Quantum Weighted Fractional Fourier Transform
Abstract
1. Introduction
2. Preparation
3. Unitarity of Weighted Fractional Fourier Transform
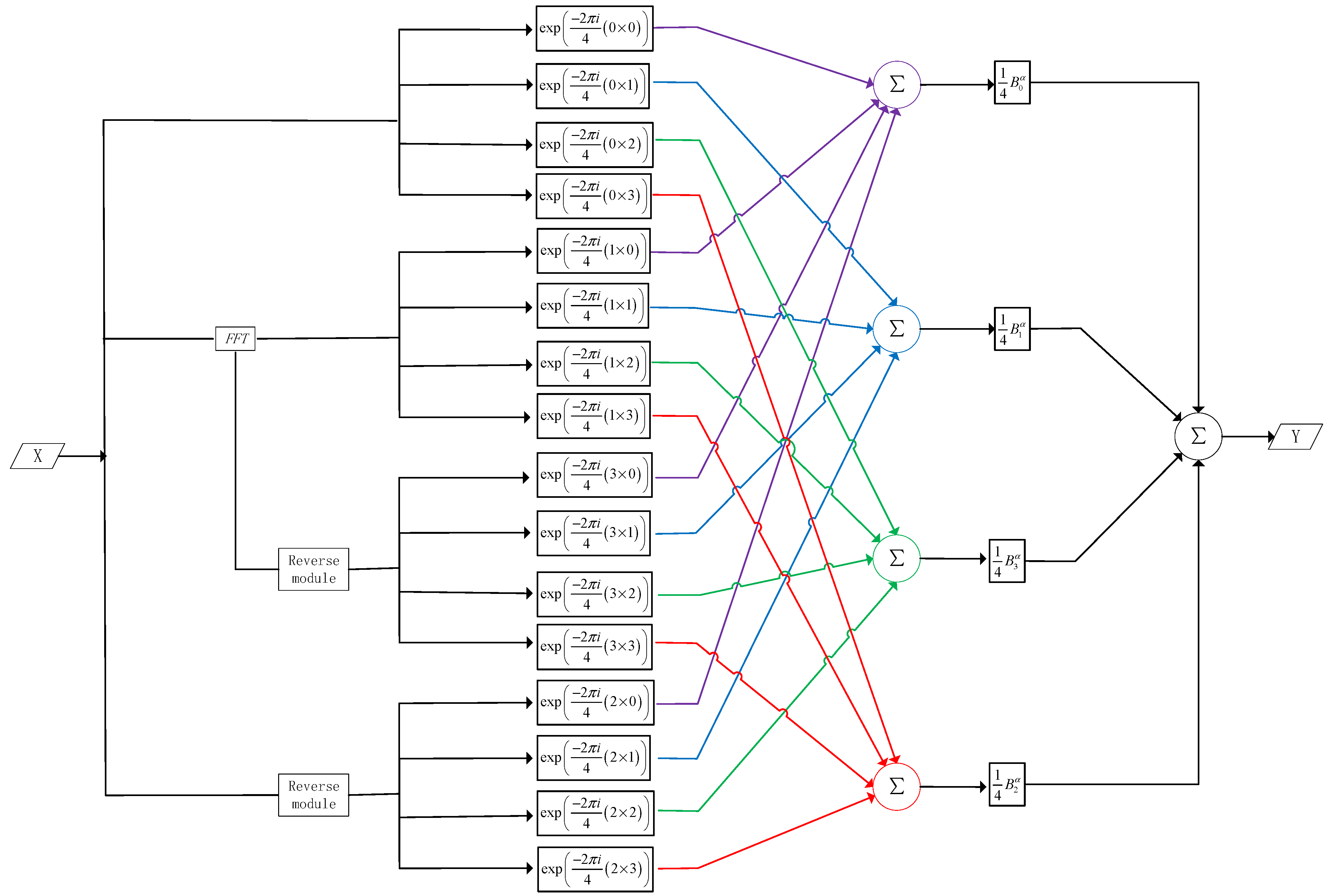
4. Quantum Weighted Fractional Fourier Transform
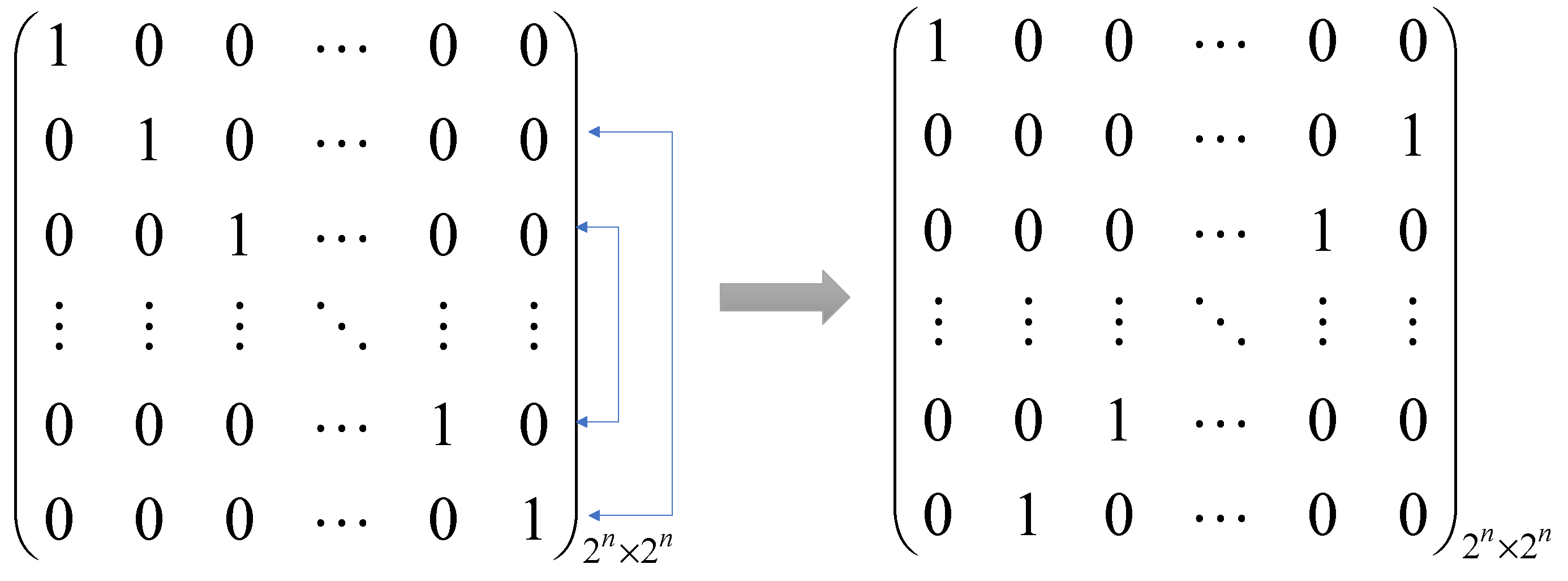
- We know that , and is the identity matrix; obviously, this is a unitary operator. Then, its operation can be expressed as
- The QFT is a unitary operator. The Fourier transform of a quantum state can be expressed as
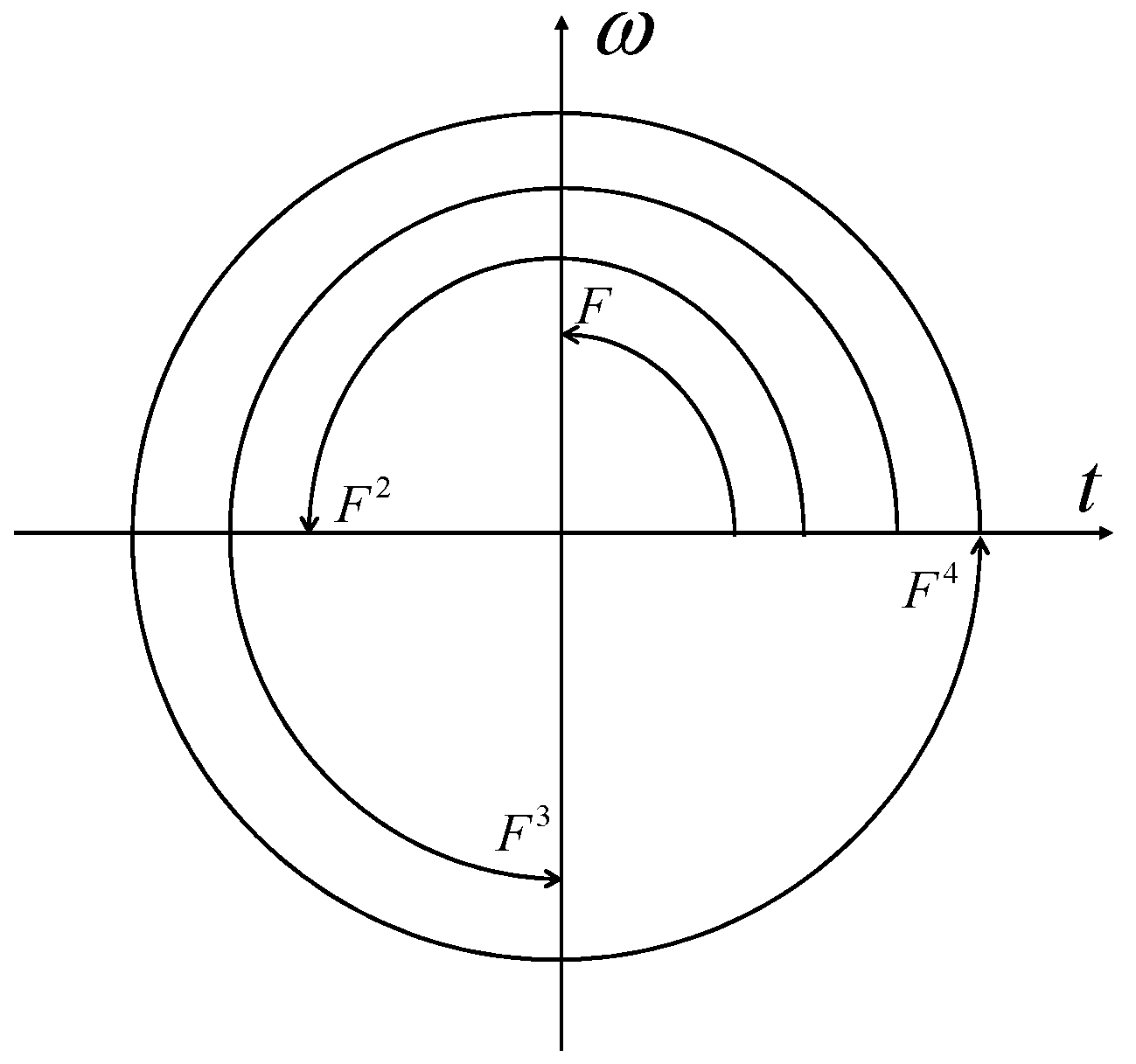
- The quadratic power of the QFT can be expressed as
- The third power of the QFT, which is equivalent to the inverse operation of the QFT, is also a unitary operator.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 97–117. [Google Scholar]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual IEEE Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th Annual ACM Symposium on the Theory of Computing, New York, NY, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Biham, E.; Biham, O.; Biron, D.; Grassl, M.; Lidar, D.A. Grover’s quantum search algorithm for an arbitrary initial amplitude distribution. Phys. Rev. A 1999, 60, 2742–2745. [Google Scholar] [CrossRef]
- Boyer, M.; Brassard, G.; Høyer, P.; Tapp, A. Tight bounds on quantum searching. Fortschr. Der Phys. Prog. Phys. 1998, 46, 493–505. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum computers can search rapidly by using almost any transformation. Phys. Rev. Lett. 1998, 80, 4329–4332. [Google Scholar] [CrossRef]
- GuiLu, L.; WeiLin, Z.; YanSong, L.; Li, N. Arbitrary phase rotation of the marked state cannot be used for Grover’s quantum search algorithm. Commun. Theor. Phys. 1999, 32, 335–338. [Google Scholar] [CrossRef][Green Version]
- Long, G.L.; Li, Y.S.; Zhang, W.L.; Niu, L. Phase matching in quantum searching. Phys. Lett. A 1999, 262, 27–34. [Google Scholar] [CrossRef]
- Narayanan, A.; Moore, M. Quantum-inspired genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 61–66. [Google Scholar]
- Shenvi, N.; Kempe, J.; Whaley, K.B. Quantum random-walk search algorithm. Phys. Rev. A 2003, 67, 052307. [Google Scholar] [CrossRef]
- Han, K.-H.; Kim, J.-H. Genetic quantum algorithm and its application to combinatorial optimization problem. In Proceedings of the IEEE Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; pp. 1354–1360. [Google Scholar]
- Chen, L.B. Mitochondrial membrane potential in living cells. Annu. Rev. Cell Biol. 1988, 4, 155–181. [Google Scholar] [CrossRef]
- Høyer, P.; Špalek, R. Quantum fan-out is powerful. Theory Comput. 2005, 1, 81–103. [Google Scholar] [CrossRef]
- Sun, J.; Wu, X.; Palade, V.; Fang, W.; Lai, C.-H.; Xu, W. Convergence analysis and improvements of quantum-behaved particle swarm optimization. Inf. Sci. 2012, 193, 81–103. [Google Scholar] [CrossRef]
- Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef] [PubMed]
- Childs, A.M.; Kothari, R.; Somma, R.D. Quantum algorithm for systems of linear equations with exponentially improved dependence on precision. SIAM J. Comput. 2017, 46, 1920–1950. [Google Scholar] [CrossRef]
- Clader, B.D.; Jacobs, B.C.; Sprouse, C.R. Preconditioned quantum linear system algorithm. Phys. Rev. Lett. 2013, 110, 250504. [Google Scholar] [CrossRef]
- Wossnig, L.; Zhao, Z.; Prakash, A. Quantum linear system algorithm for dense matrices. Phys. Rev. Lett. 2018, 120, 050502. [Google Scholar] [CrossRef]
- Arrazola, J.M.; Kalajdzievski, T.; Weedbrook, C.; Lloyd, S. Quantum algorithm for nonhomogeneous linear partial differential equations. Phys. Rev. A 2019, 100, 032306. [Google Scholar] [CrossRef]
- Lloyd, S.; De Palma, G.; Gokler, C.; Kiani, B.; Liu, Z.-W.; Marvian, M.; Tennie, F.; Palmer, T. Quantum algorithm for nonlinear differential equations. arXiv 2020, arXiv:2011.06571. [Google Scholar]
- Childs, A.M.; Liu, J.-P. Quantum spectral methods for differential equations. Commun. Math. Phys. 2020, 375, 1427–1457. [Google Scholar] [CrossRef]
- Childs, A.M.; Liu, J.-P.; Ostrander, A. High-precision quantum algorithms for partial differential equations. Quantum 2021, 5, 574. [Google Scholar] [CrossRef]
- Coppersmith, D. An approximate Fourier transform useful in quantum factoring. arXiv 2002, arXiv:quant-ph/0201067. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum computation and quantum information. Phys. Today 2001, 54, 60. [Google Scholar]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Namias, V. The fractional order Fourier transform and its application to quantum mechanics. IMA J. Appl. Math. 1980, 25, 241–265. [Google Scholar] [CrossRef]
- Candan, C.; Kutay, M.A.; Ozaktas, H.M. The discrete fractional Fourier transform. IEEE Trans. Signal Process. 2000, 48, 1329–1337. [Google Scholar] [CrossRef]
- Shih, C.C. Fractionalization of Fourier transform. Opt. Commun. 1995, 118, 495–498. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Arikan, O.; Kutay, M.A.; Bozdagt, G. Digital computation of the fractional Fourier transform. IEEE Trans. Signal Process. 1996, 44, 2141–2150. [Google Scholar] [CrossRef]
- Parasa, V.; Perkowski, M. Quantum pseudo-fractional fourier transform using multiple-valued logic. In Proceedings of the IEEE 42nd International Symposium on Multiple-Valued Logic, Victoria, BC, Canada, 14–16 May 2012; pp. 311–314. [Google Scholar]
- Bailey, D.H.; Swarztrauber, P.N. The fractional Fourier transform and applications. SIAM Rev. 1991, 33, 389–404. [Google Scholar] [CrossRef]
- Cao, H.; Cao, F.; Wang, D. Quantum artificial neural networks with applications. Inf. Sci. 2015, 290, 1–6. [Google Scholar] [CrossRef]
- da Silva, A.J.; de Oliveira, W.R. Comments on “quantum artificial neural networks with applications”. Inf. Sci. 2016, 370, 120–122. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Nearby states in non-Hermitian quantum systems I: Two states. Eur. Phys. J. D 2015, 69, 229. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Clustering of exceptional points and dynamical phase transitions. Phys. Rev. A 2016, 93, 042116. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Yang, T.; Chi, Y. Quantum Weighted Fractional Fourier Transform. Mathematics 2022, 10, 1896. https://doi.org/10.3390/math10111896
Zhao T, Yang T, Chi Y. Quantum Weighted Fractional Fourier Transform. Mathematics. 2022; 10(11):1896. https://doi.org/10.3390/math10111896
Chicago/Turabian StyleZhao, Tieyu, Tianyu Yang, and Yingying Chi. 2022. "Quantum Weighted Fractional Fourier Transform" Mathematics 10, no. 11: 1896. https://doi.org/10.3390/math10111896
APA StyleZhao, T., Yang, T., & Chi, Y. (2022). Quantum Weighted Fractional Fourier Transform. Mathematics, 10(11), 1896. https://doi.org/10.3390/math10111896




