Generalized Proportional Caputo Fractional Differential Equations with Delay and Practical Stability by the Razumikhin Method

Abstract

Practical stability properties of generalized proportional Caputo fractional differential equations with bounded delay are studied in this paper. Two types of stability, practical stability and exponential practical stability, are defined and considered, and also some sufficient conditions to guarantee stability are presented. The study is based on the application of Lyapunov like functions and their generalized proportional Caputo fractional derivatives among solutions of the studied system where appropriate Razumikhin like conditions are applied (appropriately modified in connection with the fractional derivative considered). The theory is illustrated with several nonlinear examples.

1. Introduction

Fractional differential equations have been studied extensively in the literature mainly because of their applications in various fields of engineering and science (see, for example, the monographs [1,2], and the cited references therein, and the papers [3,4]). In the literature, we note there are various types of fractional derivatives with different properties and the main common property of fractional derivatives is connected with the memory which differs from the case of integer order derivatives. Recently ([5,6]) generalized proportional fractional integrals and derivatives were introduced and applied to differential equations (see, for examples, [7,8,9,10]). These integrals and derivatives generalize classical Riemann–Liouville and Caputo fractional integrals and derivatives, respectively ([11,12]), and give the opportunity for more adequate modeling of complicated real world phenomena.

In the qualitative study for nonlinear systems, stability properties play an important role. For example, several stability results for fractional order systems with delay were obtained in [13]. One of the most successful methods to study the stability properties of the solutions is the second method of Lyapunov. When this method is applied to differential equations with delays, there are two approaches to consider: the Lyapunov–Krasovskii method via Lyapunov functionals and the Razumikhin method with Lyapunov functions. In this paper, we will apply the Razumikhin method (see, for example, [14] for stability of fractional delay differential equations) and its appropriate modification. LaSalle and Lefschetz [15] introduced the so-called practical stability, which does not provide stability of the equilibrium point, but it is connected with its boundedness. This type of stability is studied for various types of differential equations (for differential equations with integer order derivatives [16], and for Caputo fractional differential equations [17]).

The main goal of this paper is to define and study practical stability properties of generalized proportional Caputo fractional delay differential equations. We study the case of bounded time variable delays. To the best of our knowledge, this is the first paper that studies practical stability properties of generalized proportional Caputo fractional differential equation with delays. The investigation is based on the fractional modification of the Razumikhin method. In connection with the considered generalized proportional Caputo fractional derivative, we modified the classical Razumikhin condition of the type $V(t,y\left(t\right))={sup}_{s\in [-r,0]}V(t+s,y(t+s))$ to $V(t,y\left(t\right))={sup}_{s\in [-r,0]}V(t+s,y(t+s))e^{\frac{\rho -1}{\rho }s}$, which is useful and natural here. Note that this condition is deeply connected with the type of fractional derivative considered (for the Caputo fractional derivative, see, for example [14]) for the generalized proportional Caputo fractional derivative [9]. Several examples of nonlinear generalized proportional Caputo fractional differential equations are provided to illustrate the application of the sufficient conditions we obtain.

2. Preliminary Notes

Recall that the generalized proportional fractional integral and the generalized Caputo proportional fractional derivative of a function $u:[a,\infty )\to ℝ$ are defined, respectively, by (as long as all integrals are well defined, see [5,6])

$$\begin{array}{cc}& \left({}_a{\mathcal{I}}^{q,\rho }u\right)\left(t\right)=\frac{1}{{\rho }^q\Gamma \left(q\right)}{\int }_a^t{e}^{\frac{\rho -1}{\rho }\left(t-s\right)}{\left(t-s\right)}^{q-1}u\left(s\right)ds,t\in (a,b],q\ge 0,\rho \in (0,1],\hfill \end{array}$$

and

$$\begin{array}{cc}& \left({}_a^C{\mathcal{D}}^{q,\rho }u\right)\left(t\right)=\frac{1}{{\rho }^{1-q}\Gamma (1-q)}{\int }_a^t{e}^{\frac{\rho -1}{\rho }\left(t-s\right)}{\left(t-s\right)}^{-q}\left({\mathcal{D}}^{1,\rho }u\right)\left(s\right)ds,\hfill \\ & \mathrm{for}t\in (a,b],q\in (0,1),\rho \in (0,1],\hfill \end{array}$$

(1)

where $\left({\mathcal{D}}^{1,\rho }u\right)\left(t\right)=(1-\rho )u\left(t\right)+\rho u^{\prime }\left(t\right)$.

Remark 1.

If $\rho =1$, then the generalized Caputo proportional fractional derivative is reduced to the classical Caputo fractional derivative of order $q\in (0,1):{}_a^C{\mathcal{D}}^{q}u\left(t\right)$ ([12]).

Remark 2.

Note that the generalized proportional Caputo fractional derivative easily could be generalized for $f\in C([a,b],{ℝ}^n)$ via component-wise.

Remark 3.

The generalized proportional Caputo fractional derivative of a constant is not zero for $\rho \in (0,1)$.

Remark 4

(see [5] [Remark 3.2]). The relation $\left({}_a^C{\mathcal{D}}^{q,\rho }{e}^{\frac{\rho -1}{\rho }(.)}\right)\left(t\right)=0$ for $t>a$ holds.

We recall some results about generalized proportional Caputo fractional derivatives and their applications in differential equations, which will be applied to the main result in the paper.

Lemma 1

([5] [Proposition 5.2]). For $\rho \in (0,1]$ and $q\in (0,1)$ we have

$$({}_a^C{\mathcal{D}}^{q,\rho }\left(e^{\frac{\rho -1}{\rho }t}{(t-a)}^{\beta -1}\right)\left(t\right)=\frac{{\rho }^q\Gamma \left(\beta \right)}{\Gamma (\beta -q)}{e}^{\frac{\rho -1}{\rho }t}{(t-a)}^{\beta -1-q},\beta >0.$$

Lemma 2

([9] [Lemma 3.2]). Let the function $u\in C^1([a,b],ℝ)$ with $a,b\in ℝ,b\le \infty$ (if $b=\infty$ then the interval is half open), and $q\in (0,1),\rho \in (0,1]$ be two real numbers. Then,

$$\left({}_a^C{\mathcal{D}}^{q,\rho }{u}^2\right)\left(t\right)\le 2u\left(t\right)\left({}_a^C{\mathcal{D}}^{q,\rho }u\right)\left(t\right),t\in (a,b].$$

Lemma 3

([7] [Lemma 5]). Let $u\in C([t_0,T,ℝ)$, $T>t_0$, and there exists a point $t^{*}\in (t_0,T]$ such that $u\left(t^{*}\right)=0$, and $u\left(t\right)<0$, for $t_0\le t<t^{*}.$ Then, if the generalized proportional Caputo fractional derivative of u exists for $t=t^{*}$, then the inequality $\left({}_{t_0}^c{\mathcal{D}}^{q,\rho }u\right)\left(t\right){|}_{t=t^{*}}>0$ holds.

Lemma 4

([5] [Example 5.7]). The solution of the scalar linear generalized proportional Caputo fractional initial value problem

$$\left({}_a^C{\mathcal{D}}^{q,\rho }u\right)\left(t\right)=\lambda u\left(t\right),u\left(a\right)=u_0,q\in (0,1),\rho \in (0,1]$$

has a solution

$$u\left(t\right)=u_0{e}^{\frac{\rho -1}{\rho }(t-a)}{E}_q\left(\lambda {\left(\frac{t-a}{\rho }\right)}^q\right),$$

where $E_q\left(t\right)$ is the Mittag-Leffler function of one parameter, $\lambda \in ℝ$.

3. Statement of the Problem

Let ${ℝ}_{+}=[0,\infty )$ and $r>0$ be a given number. Consider the space $C_0=C([-r,0],{ℝ}^n)$ with the norm ${\parallel y\parallel }_0={sup}_{t\in [-r,0]}\{\parallel y\left(t\right)\parallel :y\in C_0\},$ where $\parallel ·\parallel$ is a norm in ${ℝ}^n$.

Consider the initial value problem (IVP) for a nonlinear system of generalized proportional Caputo fractional differential equations with bounded time dependent delay (FrDDE) with $q\in (0,1),\rho \in (0,1]$:

$$\begin{array}{cc}& {}_{t_0}^C{\mathcal{D}}_t^{q,\rho }y\left(t\right)=f(t,y\left(t\right),y(t+\tau \left(t\right))),\mathrm{for}t>t_0,\hfill \\ & y(t+t_0)=\varphi \left(t\right),\mathrm{for}t\in [-r,0],\hfill \end{array}$$

(2)

where $t_0\ge 0$ is the initial time, ${}_{t_0}^C{\mathcal{D}}_t^{q,\rho }x\left(t\right)$ denotes the generalized proportional Caputo fractional derivative for the state y, $f:[t_0,\infty )\times {ℝ}^n\times {ℝ}^n\to {ℝ}^n$, $\varphi \in C_0$, $\tau \in C([t_0,\infty ),[-r,0])$ is the delay.

We introduce the following assumption:

A1. 

The function $f\in C([t_0,\infty )\times {ℝ}^n\times {ℝ}^n,{ℝ}^n)$.

A2. 

$f(t,0,0)=0$ for $t\ge t_0$.

A3. 

For any initial function $\varphi \in C_0$ the IVP for FrDDE (2) has a solution $y(t;t_0,\varphi )$ defined for $t\ge t_0$.

Now, we will define practical stability for the nonlinear Caputo FrDDE following the ideas for practical stability for ordinary differential equations ([15]).

Definition 1.

The zero solution of FrDDE (2) with zero initial function is called

-

Practically stable with respect to $(\lambda ,A)$, if for any initial function $\varphi \in C_0:{\parallel \varphi \parallel }_0<\lambda$, the inequality $∥y(t;t_0,\varphi )∥<A,fort\ge t_0,$ holds, where the positive real numbers $(\lambda ,A)$ with $0<\lambda <A$ are given;

-

Exponentially practically stable with respect to $(\lambda ,A,K)$, if for any initial function $\varphi \in C_0:{\parallel \varphi \parallel }_0<\lambda$, the inequality $∥y(t;t_0,\varphi )∥<A{e}^{K\frac{\rho -1}{\rho }(t-t_0)},fort\ge t_0,$ holds, where the positive real numbers $(\lambda ,A,K)$ with $0<\lambda <A$ are given.

Here, $y(t;t_0,\varphi )$ is a solution of the IVP for FrDDE (2).

Remark 5.

If the zero solution of (2) is exponentially practically stable, then it is practically stable, but the opposite is not true.

Remark 6.

We note that the change of the initial time $t_0$ leads to a change of the differential equation and not only on the initial condition (see, Lemma 4). This property is different from the case of integer order differential equations. As a result, we will consider the case when the initial time is fixed.

Define the following sets:

$$\begin{array}{ccc}\hfill \mathcal{K}& =& \{a\in C({\mathbb{R}}_{+},{\mathbb{R}}_{+}):a\mathrm{is}\mathrm{strictly}\mathrm{increasing}\mathrm{and}a\left(0\right)=0\};\hfill \\ \hfill \mathcal{M}& =& \{a\in \mathcal{K}:\mathrm{there}\mathrm{exist}\mathrm{a}\mathrm{positive}\mathrm{constant}K\mathrm{and}\mathrm{a}\mathrm{function}b\in \mathcal{K}\mathrm{such}\mathrm{that}\hfill \\ & & a^{-1}\left(C{e}^{\frac{\rho -1}{\rho }s}\right)\le b\left(C\right)e^{K\frac{\rho -1}{\rho }s}\mathrm{for}\mathrm{any}C>0\mathrm{and}s\ge 0\};\hfill \\ \hfill S_A& =& \{x\in {ℝ}^n:\parallel x\parallel \le A\},A>0.\hfill \end{array}$$

Remark 7.

The function $a\left(s\right)=\sqrt{s}$ is from the set $\mathcal{M}$ with $K=1,b\left(s\right)=s^2$ because $a^{-1}\left(s\right)=s^2$ and $e^{\frac{\rho -1}{\rho }s}\le 1$.

The function $a\left(s\right)=s^2$ is from the set $\mathcal{M}$ with $K=0.5,b\left(s\right)=\sqrt{s}$ because $a^{-1}\left(s\right)=\sqrt{s}$ and $a^{-1}\left(C{e}^{\frac{\rho -1}{\rho }s}\right)=\sqrt{C{e}^{\frac{\rho -1}{\rho }s}}=\sqrt{C}{e}^{0.5\frac{\rho -1}{\rho }s}.$

Remark 8.

Note when $f(t,x)\equiv F\left(t\right)$, the FrDDE (2) will not have a zero solution, so we will not consider practical stability in this case.

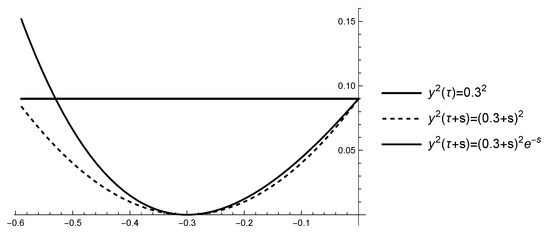
Example 1.

Consider the scalar FrDDE with $\tau \left(t\right)\equiv 0$

$$\begin{array}{cc}& {}_0^C{D}_t^{0.25,0.5}u\left(t\right)=\frac{0.5^{0.25}\Gamma \left(7\right)}{\Gamma \left(6.75\right)}{t}^{5.75}fort>0,u\left(0\right)=u_0.\hfill \end{array}$$

(3)

From Remark 4 the FrDE (3) does not have a zero solution. From Lemma 1 we get the equality $({}_0^C{\mathcal{D}}^{0.25,0.5}\left(e^{-t}{t}^6\right)\left(t\right)=\frac{0.5^{0.25}\Gamma \left(7\right)}{\Gamma (7-0.25)}{e}^{-t}{t}^{6-0.25}$ and thus FrDE (3) has a solution $u\left(t\right)=(u_0+t^6)e^{-t},t>0$. Now ${sup}_{t>0}{e}^{-t}{t}^6\approx 115.6487=e^{-6}{6}^6$ and let $M>115.64866155454445$ and $\delta =e^6(M-115.6487)$. Now for $|u_0|<\delta$ the inequality $\left|u\left(t\right)\right|<\delta e^{-t}+115.6487<M,t\ge 0$ holds (see Figure 1).

Figure 1. Graphs of the solutions of (3) with various initial values.

We introduce the classes of Lyapunov-like functions that will be used to investigate the practical stability of the system FrDDE (2).

Definition 2.

Let$I\subset {\mathbb{R}}_{+}$ and $\mathcal{D}\subset {\mathbb{R}}^n.$ We say that the function $V:I\times \Omega \to {\mathbb{R}}_{+}$ belongs to the class $\Lambda (I,\Omega )$ if V is continuous and locally Lipschitzian with respect to its second argument in $I\times \Omega .$

Definition 3.

Let $\mathcal{D}\subset {\mathbb{R}}^n.$ We say that the function $V:\Omega \to {\mathbb{R}}_{+}$ belongs to the class $\mathcal{L}(\Omega )$ if V is continuous and locally Lipschitzian.

In this paper, the results on practical stability properties for systems of the type (2) will be given where the generalized proportional Caputo fractional derivatives of the Lyapunov functions from the class $\Lambda (I,\Omega )$ are estimated only on points $\tau \ge t_0$ for which the following condition called the Razumikhin condition

$$V(\tau ,y(\tau ;t_0,\varphi ))=\underset{s\in [-r,0]}{sup}V(\tau +s,y(\tau +s;t_0,\varphi ))$$

(4)

holds; here $y(t;t_0,\varphi ),t\ge t_0-r,$ is a solution of the IVP for FrDDE(2).

In connection with the applied type of fractional derivative, we will also use the following modified Razumikhin condition:

$$V(\tau ,y(\tau ;t_0,\varphi ))=\underset{s\in [-r,0]}{sup}V(\tau +s,y(\tau +s;t_0,\varphi ))e^{\frac{1-\rho }{\rho }s}.$$

(5)

Remark 9.

Note if the Razumikhin type condition (4) is satisfied for a point τ, then the modified Razumikhin condition (5) holds. However, the opposite is not true.

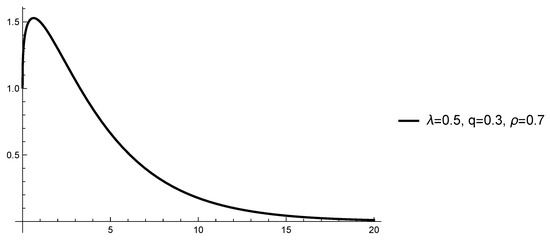
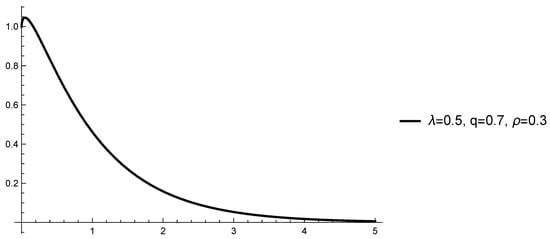
Example 2.

Let $t_0=0$, $\Omega \subset ℝ$ and $V(t,x)=x^2{e}^{\frac{\rho -1}{\rho }t},x\in \Omega$, $\rho =0.5$, $\tau =0.3$, $r=0.59$.

Let $y\left(t\right)=e^t$. Then, both the Razumikhin condition (4) and the modified Razumikhin condition (5) hold (see Figure 2).

Figure 2. Graphs of the Razumikhin condition (4) and modified Razumikhin condition (5) for the function $e^t$.

Let $y\left(t\right)=t$. Then, the inequality $y^2(\tau +s)e^{\frac{\rho -1}{\rho }(\tau +s)}{e}^{\frac{1-\rho }{\rho }s}<y^2\left(\tau \right)e^{\frac{\rho -1}{\rho }\tau }$ is satisfied for all $s\in [-0.59,0)$ because ${(\tau +s)}^2<{\tau }^2$, i.e., the modified Razumikhin condition (5) holds.

However, the inequality $y^2\left(\tau \right)e^{\frac{\rho -1}{\rho }\tau }>y^2(\tau +s)e^{\frac{\rho -1}{\rho }(\tau +s)}$ or its equivalent $y^2\left(\tau \right)>y^2(\tau +s)e^{\frac{\rho -1}{\rho }s}$ does not hold for all $s\in [-0.59,0)$ (see the Figure 3 for $s\in [-0.59,0)$ and $\tau =0.3$). Thus, the Razumikhin condition (4) does not hold.

Figure 3. Illustrations of the Razumikhin condition (4) and the modified Razumikhin condition (5).

Remark 10.

Razumikhin type conditions (4) and (5) can also be written for the functions of the class $\mathcal{L}(\Omega ).$

4. Practical Stability Results

We will use generalized proportional Caputo fractional derivatives of Lyapunov functions to obtain sufficient conditions for both practical stability and exponential practical stability. The study is based on the application of the Razumikhin method applying both condition (4) and (5).

First, we will obtain sufficient conditions for practical stability of FrDDE (2) applying the generalized proportional Caputo fractional derivative of the Lyapunov function for points satisfying the classical Razhumikhin condition (4).

Theorem 1.

Let conditions A1, A2, and A3 be satisfied for a given number $t_0\ge 0$ and there exists a continuously differentiable Lyapunov function $V\in \Lambda ([t_0-r,\infty ),{ℝ}^n)$ with $V(t,0)=0,$ such that

(i) 

the inequalities

$$\begin{array}{cc}& {\alpha }_1(\parallel x\parallel )\le V(t,x),fort\ge t_0,x\in {ℝ}^n\hfill \\ & V(t,x)\le {\alpha }_2(\parallel x\parallel ),fort\ge t_0,x\in S_{\lambda },\hfill \end{array}$$

hold, where ${\alpha }_i\in \mathcal{K},i=1,2$, and $\lambda >0$ is a given number.

(ii) 

for any $\tau >t_0$ and for any solution $y\left(t\right)=y(t;t_0,\varphi )$ of (2) with $\varphi \in C_0$ such that

$$\underset{s\in [-r,0]}{sup}V(\tau +s,y(\tau +s))=V(\tau ,y\left(\tau \right)),$$

the inequality

$${}_{t_0}^C{\mathcal{D}}^{q,\rho }{V(.,y(.))\left(t\right)|}_{t=\tau }\le 0$$

holds.

Then, the zero solution of FrDDE (2) is practically stable with respect to $(\lambda ,{\alpha }_1^{-1}\left({\alpha }_2\left(\lambda \right)\right))$.

Proof. 

Let $y\left(t\right)=y(t;t_0,\varphi )$ be a solution of FrDDE (2) with the initial function $\varphi \in C_0:{\parallel \varphi \parallel }_0<\lambda$. Define the function

$$v\left(t\right)=\underset{s\in [t_0-r,t]}{sup}V(s,y\left(s\right)),t\ge t_0.$$

Clearly, the function v is non-decreasing. We will prove that

$$v\left(t\right)=v\left(t_0\right),fort\ge t_0.$$

(6)

Theequality (6) is satisfied for $t=t_0$.

Assume (6) is not true, i.e., there exists a small enough number $\epsilon >0$, and a point $T\ge t_0$ such that $v\left(t\right)=v\left(t_0\right)$, for $t\in [t_0,T]$, but $v\left(t\right)>v\left(t_0\right)$ and v is strictly increasing for $t\in (T,T+\epsilon ]$, i.e., $v\left(t\right)=V(t,y(t\left)\right)$ for every $t\in (T,T+\epsilon ]$. Then, for every $\sigma \in [t_0,T]$ the inequality $V(\sigma ,y\left(\sigma \right))\le {sup}_{s\in [t_0-r,\sigma ]}V(s,y\left(s\right))=v\left(\sigma \right)=v\left(t_0\right)={sup}_{s\in [t_0-r,t_0]}V(s,y\left(s\right))={sup}_{s\in [t_0-r,T]}V(s,y\left(s\right))$ holds, and $v\left(t\right)=V(t,y\left(t\right))>v\left(t_0\right)={sup}_{s\in [t_0-r,t_0]}V(s,y\left(s\right))$, for $t\in (T,T+\epsilon ]$.

Let $\Theta \in (T,T+\epsilon ]$. Then, the inequality

$$\underset{s\in [\Theta -r,\Theta ]}{sup}V(s,y\left(s\right))\le \underset{s\in [t_0-r,\Theta ]}{sup}V(s,y\left(s\right))=v(\Theta )=V(\Theta ,y(\Theta ))$$

holds. Thus, ${sup}_{s\in [-r,0]}V(\Theta +s,y(\Theta +s))=V(\Theta ,y(\Theta ))$. According to condition (ii) with $\tau =\Theta$, we get the inequality

$${(}_{t_0}^C{\mathcal{D}}^{q,\rho }v)\left(t\right){{|}_{t=\Theta }{=}_{t_0}^C{\mathcal{D}}^{q,\rho }V(t,y\left(t\right))|}_{t=\Theta }\le 0.$$

(7)

From Equation (1), we obtain

$$\begin{array}{cc}& \left({}_{t_0}^c{\mathcal{D}}^{q,\rho }v\right)\left(t\right){|}_{t=\Theta }=\frac{1}{{\rho }^{1-q}\Gamma (1-q)}{\int }_{t_0}^T{e}^{\frac{\rho -1}{\rho }\left(\Theta -s\right)}{\left(\Theta -s\right)}^{-q}\left({\mathcal{D}}^{1,\rho }v\right)\left(s\right)ds\hfill \\ & +\frac{1}{{\rho }^{1-q}\Gamma (1-q)}{\int }_T^{\Theta }{e}^{\frac{\rho -1}{\rho }\left(\Theta -s\right)}{\left(\Theta -s\right)}^{-q}\left({\mathcal{D}}^{1,\rho }v\right)\left(s\right)ds\hfill \end{array}$$

(8)

where $\left({\mathcal{D}}^{1,\rho }v\right)\left(t\right)=(1-\rho )v\left(t\right)+\rho v^{\prime }\left(t\right)$.

Case 1. Let $s\in [t_0,T]$. Then, we have $v\left(s\right)=v\left(t_0\right)\ge 0$, $v^{\prime }\left(s\right)=0$ and $\left({\mathcal{D}}^{1,\rho }v\right)\left(s\right)=(1-\rho )v\left(s\right)\ge 0$.

Case 2. Let $s\in (T,\Theta ]$. Then, we have $v\left(s\right)=V(t,y(t\left)\right)\ge 0$, $v^{\prime }\left(s\right)>0$ and $\left({\mathcal{D}}^{1,\rho }v\right)\left(s\right)=(1-\rho )v\left(s\right)+\rho v^{\prime }\left(s\right)>0$.

Thus,

$$\begin{array}{cc}& \left({}_{t_0}^c{\mathcal{D}}^{q,\rho }v\right)\left(t\right){|}_{t=\Theta }>0.\hfill \end{array}$$

(9)

Inequality(9) contradicts (7). Therefore, equality (6) is true.

From condition (i), and equality (6), we get

$$\begin{array}{cc}& {\alpha }_1(\parallel y\left(t\right)\parallel )\le V(t,y\left(t\right))\le v\left(t\right)=v\left(t_0\right)=\underset{s\in [t_0-r,t_0]}{sup}V(s,\varphi (s-t_0))\hfill \\ & \le \underset{s\in [t_0-r,t_0]}{sup}{\alpha }_2(\parallel \varphi (s-t_0)\parallel )=\underset{s\in [-r,0]}{sup}{\alpha }_2(\parallel \varphi \left(s\right)\parallel )={\alpha }_2{(\parallel \varphi \parallel }_0)\le {\alpha }_2\left(\lambda \right),\hfill \end{array}$$

(10)

i.e., $\parallel y\left(t\right)\parallel \le {\alpha }_1^{-1}\left({\alpha }_2\left(\lambda \right)\right),t>t_0$. □

We will obtain sufficient conditions for the exponential practical stability of the system FrDDE (2) by an application of the Lyapunov function, which does not depend directly on the time variable and using the generalized proportional Caputo fractional derivative of Lyapunov function with the modified Razumikhin condition (5).

Theorem 2.

Let the following conditions be satisfied:

1 

The conditions A1, A2, and A3 are satisfied for a given $t_0$.

2 

There exists a function $V\in \mathcal{L}\left({ℝ}^n\right)$ with $V\left(0\right)=0,$ such that

(i) 

the inequality

$$\begin{array}{cc}& a(\parallel x\parallel )\le V\left(x\right)forx\in {ℝ}^n,\hfill \end{array}$$

holds, where $a\in \mathcal{K}$;

(ii) 

for any $\tau >t_0$ and for any solution $y\left(t\right)=y(t;t_0,\varphi )$ of (2) with $\varphi \in C_0$ such that the Lyapunov function $V\left(y\left(t\right)\right)\in S_{a\left(A\right)},t\in [t_0,\tau ]$ and

$$V\left(y\left(\tau \right)\right)=\underset{s\in [-r,0]}{sup}V\left(y(\tau +s)\right)e^{\frac{1-\rho }{\rho }s},$$

(11)

the inequality

$$\left({}_{t_0}^C{\mathcal{D}}^{q,\rho }V\left(y(.)\right)\right){\left(t\right)|}_{t=\tau }\le 0$$

(12)

holds, where $A>0$ is a given number.

Then, the zero solution of FrDDE (2) is practically stable.

Proof. 

From $V\left(0\right)=0$, it follows there exists a number $\lambda \in (0,A)$ such that

$$V\left(x\right)\le a\left(A\right)for\left|\right|x\left|\right|<\lambda .$$

Choose the initial function $\varphi \in C_0:{\parallel \varphi \parallel }_0<\lambda$. Thus, $V\left(\varphi \right(s\left)\right)<a\left(A\right)$ for $s\in [-r,0]$.

Consider the solution $y\left(t\right)=y(t;t_0,\varphi ),t\ge t_0-r$ of the IVP for FrDDE (2) with the above chosen initial function $\varphi$. Define the function $m\left(t\right)=V\left(y\right(t\left)\right)$ for $t\ge t_0-r$.

We will prove that

$$m\left(t\right)<a\left(A\right)e^{\frac{\rho -1}{\rho }(t-t_0)},t\ge t_0.$$

(13)

From the choice of the constant $\lambda$ and the initial function, we have $m\left(t_0\right)=V\left(\varphi \left(0\right)\right)\le a\left(A\right)$, i.e., inequality (13) holds for $t=t_0$.

Assume the contrary, i.e., there exists a point $T>t_0$ such that

$$m\left(s\right)<a\left(A\right)e^{\frac{\rho -1}{\rho }(s-t_0)},s\in [t_0,T),m\left(T\right)=a\left(A\right)e^{\frac{\rho -1}{\rho }(T-t_0)}.$$

Therefore, $m\left(t\right)\le a\left(A\right)e^{\frac{\rho -1}{\rho }(t-t_0)}\le a\left(A\right)$ for $t\in [t_0,T]$, i.e., $V\left(y\left(t\right)\right)\in S_{a\left(A\right)}$ for $t\in [t_0,T]$.

Consider the function $\eta \left(t\right)=m\left(t\right)-a\left(A\right)e^{\frac{\rho -1}{\rho }(t-t_0)}t\in [t-0,T]$. According to Lemma 3 with $t^{*}=T$ the inequality $\left({}_{t_0}^c{\mathcal{D}}^{q,\rho }\eta (.)\right){\left(t\right)|}_{t=T}>0$ holds. Applying Remark 4 with $a=t_0$ we obtain

$$\left({}_{t_0}^c{\mathcal{D}}^{q,\rho }m(.)\right){\left(t\right)|}_{t=T}>0.$$

(14)

Case 1. Let $T\ge t_0+r$. Then $T-r\ge t_0$ and we obtain

$$m\left(s\right)e^{\frac{1-\rho }{\rho }(s-T)}<a\left(A\right)e^{\frac{\rho -1}{\rho }(s-t_0)}{e}^{\frac{1-\rho }{\rho }(s-T)}=a\left(A\right)e^{\frac{\rho -1}{\rho }(T-t_0)}=m\left(T\right)s\in [T-r,T),$$

or

$$m(s+T)e^{\frac{1-\rho }{\rho }s}<m\left(T\right)s\in [-r,0),$$

i.e., inequality (11) holds for $t^{*}=T$.

Case 2. Let $T<t_0+r$. Then, $t_0-T>-r$, $[T-r,T]=[T-r,t_0)\cup [t_0,T]$ and $[-r,0]=[-r,t_0-T)\cup [t_0-T,0]$.

Case 2.1. Consider the interval $[t_0,T]$. Then, we get

$$m\left(s\right)e^{\frac{1-\rho }{\rho }(s-T)}<a\left(A\right)e^{\frac{\rho -1}{\rho }(T-t_0)}=m\left(T\right)fors\in [t_0,T].$$

Denote $\sigma =s-T\in [t_0-T,0]$ for $s\in [t_0,T]$ and we obtain

$$m(\sigma +T)e^{\frac{1-\rho }{\rho }\sigma }<m\left(T\right),\sigma \in [t_0-T,0],$$

or

$$V\left(y(\sigma +T)\right)e^{\frac{1-\rho }{\rho }\sigma }<V\left(y\left(T\right)\right),\sigma \in [t_0-T,0].$$

Case 2.2. Consider the interval $[T-r,t_0)$. Denote $\sigma =s-T$. Then, $\sigma \in [-r,t_0-T)$ for $s\in [T-r,t_0)$, $y(\sigma +T)=\varphi (\sigma +T-t_0)$ and

$$V\left(y(\sigma +T)\right)e^{\frac{1-\rho }{\rho }\sigma }=V\left(\varphi (\sigma +T-t_0)\right)e^{\frac{1-\rho }{\rho }\sigma }<a\left(A\right)e^{\frac{1-\rho }{\rho }\sigma }<a\left(A\right)e^{\frac{1-\rho }{\rho }(t_0-T)}=m\left(T\right)=V\left(y\left(T\right)\right).$$

Therefore, inequality (11) holds for $t^{*}=T$.

From the choice of the point T we have that $m\left(t\right)\le a\left(A\right)$ for $t\in [t_0,T]$, i.e., $m\left(t\right)\in S_{a\left(A\right)}$ on $[t_0,T]$. From condition 2(ii) with $t^{*}=T$, the inequality

$$\left({}_{t_0}^C{\mathcal{D}}^{q,\rho }m(.)\right)\left(t\right){{|}_{t=T}=\left({}_{t_0}^C{\mathcal{D}}^{q,\rho }V\left(y(.)\right)\right)\left(t\right)|}_{t=T}\le 0.$$

(15)

holds.

Inequality (15) contradicts (14).

From inequality (13) and condition 2(i), we have

$$a\left(\right|\left|y\left(t\right)\right|\left|\right)\le a\left(A\right)e^{\frac{\rho -1}{\rho }(t-t_0)}\le a\left(A\right),t\ge t_0$$

Thus, $\left|\right|y\left(t\right)\left|\right|\le A,t\ge t_0.$

Therefore, the zero solution of FrDDE (2) is practically stable with respect to $(\lambda ,A)$. □

Remark 11.

If conditions 2(i) and 2(ii) of Theorem 1 are satisfied for the function $V\in \mathcal{L}\left({ℝ}^n\right)$, then the condition 2(ii) of Theorem 2 is satisfied with $A=a_1^{-1}\left(a_2\left(\lambda \right)\right)$.

Corollary 1.

Let all conditions of Theorem 2 be satisfied with $a\in \mathcal{M}$. Then, the zero solution of FrDDE (2) is exponentially practically stable.

Proof. 

As in the proof of Theorem 2 we prove the inequality (13). From $a\in \mathcal{M}$ it follows there exist a function $b\in \mathcal{K}$ and a constant $K>0$ such that $a^{-1}(C{e}^{\frac{\rho -1}{\rho }(t-t_0)}\le b\left(C\right)e^{K\frac{\rho -1}{\rho }(t-t_0)}$. Thus, from inequality (13) and condition (i) we get

$$\parallel y\left(t\right)\parallel \le a^{-1}\left(a\left(A\right)e^{\frac{\rho -1}{\rho }(t-t_0)}\right)\le b\left(a\left(A\right)\right)e^{K\frac{\rho -1}{\rho }(t-t_0)},t\ge t_0.$$

□

In the case generalized proportional Caputo fractional derivative of Lyapunov function is positive we obtain the following sufficient conditions.

Theorem 3.

Let the following conditions be satisfied:

1 

The conditions A1, A2, and A3 are satisfied for a given $t_0$.

2 

There exists a function $V\in \mathcal{L}\left({ℝ}^n\right)$ with $V\left(0\right)=0$, such that

(i) 

The inequality

$$\begin{array}{cc}& a(\parallel x\parallel )\le V\left(x\right)forx\in {ℝ}^n,\hfill \end{array}$$

holds, where $a\in \mathcal{K}$;

(ii) 

For any $\tau >t_0$ and for any solution $y\left(t\right)=y(t;t_0,\varphi )$ of (2) with $\varphi \in C_0$ such that the Lyapunov function $V\left(y\left(t\right)\right)\in S_{a\left(A\right)K},t\in [t_0,\tau ]$ and

$$V(\tau ,y\left(\tau \right))=\underset{s\in [-r,0]}{sup}V\left(y(\tau +s)\right)e^{\frac{1-\rho }{\rho }s},$$

(16)

the inequality

$$\left({}_{t_0}^C{\mathcal{D}}^{q,\rho }V\left(y(.)\right)\right){\left(t\right)|}_{t=\tau }\le \lambda V\left(y\left(\tau \right)\right)$$

(17)

holds, where $A>0$ is a given number and the constants $\lambda ,q,\rho ,K$ are such that $a\left(\lambda \right)<a\left(A\right)K$ and $E_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t-t_0)}\le K$ for $t\ge t_0$.

Then, the zero solution of FrDDE (2) is practically stable with respect to $(\lambda ,a^{-1}\left(a\left(A\right)K)\right)$.

Proof. 

From $V\left(0\right)=0$, it follows there exists a number $\lambda \in (0,A)$ such that

$$V\left(x\right)<a\left(A\right)for\left|\right|x\left|\right|<\lambda .$$

Choose the initial function $\varphi \in C_0:{\parallel \varphi \parallel }_0<\lambda$. Thus, $V\left(\varphi \right(s\left)\right)<a\left(A\right)$ for $s\in [-r,0]$.

Consider the solution $y\left(t\right)=y(t;t_0,\varphi ),t\ge t_0$ of the IVP for FrDDE (2) with the above chosen initial function $\varphi$. Define the function $m\left(t\right)=V\left(y\right(t\left)\right)$ for $t\ge t_0-r$.

We will prove that

$$m\left(t\right)<a\left(A\right)E_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t-t_0)},t\ge t_0.$$

(18)

From the choice of the constant $\lambda$ and the initial function we have $m\left(t_0\right)=V\left(\varphi \left(0\right)\right)<a\left(A\right)=a\left(A\right)E_q\left(\lambda {\left(\frac{t_0-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t_0-t_0)}$, i.e., inequality (18) holds for $t=t_0$.

Assume the contrary, i.e., there exists a point $T>t_0$ such that

$$\begin{array}{cc}& m\left(s\right)<a\left(A\right)E_q\left(\lambda {\left(\frac{s-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(s-t_0)},s\in [t_0,T),\hfill \\ & m\left(T\right)=a\left(A\right)E_q\left(\lambda {\left(\frac{T-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(T-t_0)}.\hfill \end{array}$$

Therefore, by condition 2(ii) $m\left(t\right)\le a\left(A\right)E_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t-t_0)}\le a\left(A\right)K$ for $t\in [t_0,T]$, i.e., $V\left(y\left(t\right)\right)\in S_{a\left(A\right)K}$ for $t\in [t_0,T]$.

Consider the function $\eta \left(t\right)=m\left(t\right)-a\left(A\right)E_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t-t_0)}t\in [t-0,T]$. According to Lemma 3 with $t^{*}=T$, the inequality $\left({}_{t_0}^c{\mathcal{D}}^{q,\rho }\eta (.)\right){\left(t\right)|}_{t=T}>0$ holds. Apply the equality $\left({}_{t_0}^c{\mathcal{D}}^{q,\rho }h(.)\right)\left(t\right)=\lambda E_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t-t_0)}$ where the function $h\left(t\right)=E_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t-t_0)}$ and obtain

$$\left({}_{t_0}^c{\mathcal{D}}^{q,\rho }m(.)\right)\left(t\right){{|}_{t=T}=\left({}_{t_0}^c{\mathcal{D}}^{q,\rho }\eta (.)\right)\left(t\right)|}_{t=T}+\lambda E_q\left(\lambda {\left(\frac{T-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(T-t_0)}>0.$$

(19)

Case 1. Let $T\ge t_0+r$. For any $\Theta \in [-r,0)$ we have $T+\Theta \in [t_0,T)$ and using the monotonicity property of the Mittag-Leffler function $E_q(.)$ we get

$$\begin{array}{cc}& V\left(y(T+\Theta )\right)e^{\frac{1-\rho }{\rho }\Theta }=m(T+\Theta )e^{\frac{1-\rho }{\rho }\Theta }\hfill \\ & =\eta (T+\Theta )e^{\frac{1-\rho }{\rho }\Theta }+a\left(A\right)E_q\left(\lambda {\left(\frac{T+\Theta -t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(T+\Theta -t_0)}{e}^{\frac{1-\rho }{\rho }\Theta }\hfill \\ & <a\left(A\right)E_q\left(\lambda {\left(\frac{T-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(T-t_0)}\hfill \\ & =m\left(T\right)=V\left(y\right(T\left)\right),\hfill \end{array}$$

(20)

i.e., inequality (16) holds for $\tau =T$.

Case 2. Let $T\in (t_0,t_0+r)$. For any $\Theta \in [-r,0)$ we have $T+\Theta \in [t_0,T)$ or $T+\Theta \in [t_0-r,t_0)$.

Case 2.1. Let $T+\Theta \in [t_0,T)$. Similar to Case 1, we obtain the inequality (20).

Case 2.2. Let $T+\Theta \in [t_0-r,t_0)$. Then we obtain $\Theta \in [t_0-T-r,t_0-T)\subset [-r,0)$ and

$$\begin{array}{cc}& V\left(y(T+\Theta )\right)e^{\frac{1-\rho }{\rho }\Theta }=V\left(\varphi (T+\Theta -t_0)\right)e^{\frac{1-\rho }{\rho }\Theta }\hfill \\ & \le a\left(A\right)e^{\frac{1-\rho }{\rho }\Theta }<a\left(A\right)e^{\frac{1-\rho }{\rho }(t_0-T)}\hfill \\ & <a\left(A\right)E_q\left(\lambda {\left(\frac{T-t_0}{\rho }\right)}^q\right)e^{\frac{1-\rho }{\rho }\Theta }=m\left(T\right)=V\left(y\left(T\right)\right).\hfill \end{array}$$

(21)

Therefore, inequality (16) holds for $\tau =T$ and according to condition 2(ii) we get

$$\left({}_{t_0}^C{\mathcal{D}}^{q,\rho }m(.)\right)\left(t\right){{|}_{t=T}=\left({}_{t_0}^C{\mathcal{D}}^{q,\rho }V\left(y(.)\right)\right)\left(t\right)|}_{t=T}\le 0.$$

(22)

holds.

Inequality (22) contradicts (19).

From inequality (13) and condition 2(i), we have

$$a\left(\right|\left|y\left(t\right)\right|\left|\right)\le a\left(A\right)E_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)e^{\frac{\rho -1}{\rho }(t-t_0)}\le a\left(A\right)K,t\ge t_0$$

Thus, $\left|\right|y\left(t\right)\left|\right|\le a^{-1}\left(a\left(A\right)K\right),t\ge t_0.$

Therefore, the zero solution of FrDDE (2) is practically stable with respect to $(\lambda ,a^{-1}\left(a\left(A\right)K\right))$. □

The main condition in Theorem 3 is connected with the boundedness of the function $h\left(t\right)=e^{\frac{\rho -1}{\rho }(t-t_0)}{E}_q\left(\lambda {\left(\frac{t-t_0}{\rho }\right)}^q\right)$. Its behavior depends significantly on the values of q and $\rho$, and we will illustrate this in the following example.

Example 3.

The function $h\left(t\right)$ could be unbounded, for $\lambda =1$, $q=0.8$ and $\rho =0.7$ (see Figure 4) and bounded with $K=1.6$ for $\lambda =0.5$, $q=0.3$ and $\rho =0.7$ (see Figure 5) or with $K=1.1$ for $\lambda =0.5$, $q=0.7$ and $\rho =0.3$ (see Figure 6).

Figure 4. Graph of the function $h\left(t\right)$ for $\lambda =1$, $q=0.8$ and $\rho =0.7$.

Figure 5. Graphs of $h\left(t\right)$ for $\lambda =0.5$, $q=0.3$ and $\rho =0.7$.

Figure 6. Graph of $h\left(t\right)$ for $\lambda =0.5$, $q=0.7$ and $\rho =0.3$.

5. Applications

We will provide some examples to illustrate the application of our criteria and the modified Razumikhin condition. First, we will consider a scalar nonlinear equation with a generalized proportional Caputo fractional derivative.

Example 4.

Consider the IVP for the scalar nonlinear FrDDE

$$\begin{array}{cc}& \left({}_0^C{\mathcal{D}}^{q,\rho }x(.)\right)\left(t\right)=-x\left(t\right)+x(t-{sin}^2\left(t\right))fort>0,\hfill \\ & x\left(s\right)=\varphi \left(s\right)fors\in [-1,0].\hfill \end{array}$$

(23)

Let $V(t,x)=x^2$ with $\parallel x\parallel =\left|x\right|$. Then, ${\alpha }_1(\parallel x\parallel )\le V(t,x)$ for $t\ge 0,x\in ℝ$ with ${\alpha }_1\left(u\right)=u^2$ and $V(t,x)\le {\alpha }_2(\parallel x\parallel )$ for $t\ge 0,x\in S_{\lambda }$ with ${\alpha }_2\left(u\right)=u$, and $\lambda =1$.

Let the point $\tau >0$ be such that ${sup}_{s\in [-1,0]}{x}^2(\tau +s)=x^2\left(\tau \right)$. Then, by Lemma 2 and inequality $2ab\le a^2+b^2,a,b\in ℝ$ we obtain

$$\begin{array}{cc}& \left({}_0^C{\mathcal{D}}^{q,\rho }{x}^2(.)\right)\left(t\right){{|}_{t=\tau }\le 2x\left(\tau \right)\left({}_0^C{\mathcal{D}}^{q,\rho }{x}^2(.)\right)\left(t\right)|}_{t=\tau }\hfill \\ & =2x\left(\tau \right)\left(-x\left(\tau \right)+x(\tau -{sin}^2\left(\tau \right))\right)\le 2x^2\left(\tau \right)+x^2\left(\tau \right)+x^2(\tau -{sin}^2\left(\tau \right))\hfill \\ & \le -2x^2\left(\tau \right)+x^2\left(\tau \right)+x^2\left(\tau \right)=0.\hfill \end{array}$$

(24)

According to Theorem 1, the zero solution of (23) is practically stable with respect to $(1,1)$.

Next, we consider (23) with a slight change.

Example 5.

Consider the IVP for the scalar nonlinear FrDDE

$$\begin{array}{cc}& \left({}_0^C{\mathcal{D}}^{q,\rho }x(.)\right)\left(t\right)=-x\left(t\right)+x(t-{sin}^2\left(t\right))e^{\frac{\rho -1}{2\rho }{sin}^2\left(t\right)}fort>0,\hfill \\ & x\left(s\right)=\varphi \left(s\right)fors\in [-1,0].\hfill \end{array}$$

(25)

Let $V\left(x\right)=x^2$ with $\parallel x\parallel =\left|x\right|$. Then, $a(\parallel x\parallel )\le V\left(x\right)$ for $x\in ℝ$ with $a\left(u\right)=u^2$.

Let the point $\tau >0$ be such that ${sup}_{s\in [-1,0]}{x}^2(\tau +s)e^{\frac{1-\rho }{\rho }s}=x^2\left(\tau \right)$. Then, by Lemma 2 and inequality $2ab\le a^2+b^2,a,b\in ℝ$, we obtain

$$\begin{array}{cc}& \left({}_0^C{\mathcal{D}}^{q,\rho }{x}^2(.)\right)\left(t\right){{|}_{t=\tau }\le 2x\left(\tau \right)\left({}_0^C{\mathcal{D}}^{q,\rho }{x}^2(.)\right)\left(t\right)|}_{t=\tau }\hfill \\ & =2x\left(\tau \right)\left(-x\left(\tau \right)+x(\tau -{sin}^2\left(\tau \right))e^{\frac{\rho -1}{2\rho }{sin}^2\left(\tau \right)}\right)\hfill \\ & \le -2x^2\left(\tau \right)+x^2\left(\tau \right)+x^2(\tau -{sin}^2\left(\tau \right))e^{\frac{1-\rho }{\rho }(-{sin}^2\left(\tau \right))}\hfill \\ & \le 0.\hfill \end{array}$$

(26)

According to Theorem 2, the zero solution of (25) is practically stable with respect to $(1,1)$.

We will consider a system of FrDDE.

Example 6.

Consider the IVP for the system of nonlinear FrDDE

$$\begin{array}{cc}& \left({}_0^C{\mathcal{D}}^{0.7,0.3}{x}_1(.)\right)\left(t\right)=-0.75x_1\left(t\right)+x_2\left(t-\frac{t}{t+1}\right)e^{\frac{-7}{6}\frac{t}{t+1}}fort>0,\hfill \\ & \left({}_0^C{\mathcal{D}}^{0.7,0.3}{x}_2(.)\right)\left(t\right)=-0.75x_2\left(t\right)+x_1\left(t-\frac{t}{t+1}\right)e^{\frac{-7}{6}\frac{t}{t+1}}fort>0,\hfill \\ & x_k\left(s\right)={\varphi }_k\left(s\right)fors\in [-1,0],k=1,2,\hfill \end{array}$$

(27)

where $\frac{\rho -1}{2\rho }=\frac{-7}{6}$.

Let $V\left(x\right)=x_1^2+x_2^2$ with $x=(x_1,x_2),\parallel x\parallel =\sqrt{x_1^2+x_2^2}$. Then, $a(\parallel x\parallel )\le V\left(x\right)$ for $x=(x_1,x_2)\in {ℝ}^2$ with $a\left(u\right)=u^2$.

Let the point $\tau >0$ be such that ${sup}_{s\in [-1,0]}\left(x_1^2(\tau +s)+x_2^2(\tau +s)\right)e^{\frac{7}{3}s}=x_1^2\left(\tau \right)+x_2^2\left(\tau \right)$. Then, by Lemma 2 and inequality $2ab\le a^2+b^2,a,b\in ℝ$ we obtain

$$\begin{array}{cc}& \left({}_0^C{\mathcal{D}}^{0.7,0.3}V\left(x(.)\right)\right)\left(t\right){{|}_{t=\tau }=\left({}_0^C{\mathcal{D}}^{0.7,0.3}\left(x_1^2(.)+x_2^2(.)\right)\right)\left(t\right)|}_{t=\tau }\hfill \\ & \le 2x_1\left(\tau \right)\left({}_0^C{\mathcal{D}}^{0.7,0.3}{x}_1^2(.)\right)\left(t\right){{|}_{t=\tau }+2x_2\left(\tau \right)\left({}_0^C{\mathcal{D}}^{0.7,0.3}{x}_2^2(.)\right)\left(t\right)|}_{t=\tau }\hfill \\ & =2x_1\left(\tau \right)\left(-0.75x_1\left(\tau \right)+x_2\left(\tau -\frac{\tau }{\tau +1}\right)e^{\frac{-7}{6}\frac{\tau }{\tau +1}}\right)\hfill \\ & +2x_2\left(\tau \right)\left(-0.75x_2\left(\tau \right)+x_1\left(\tau -\frac{\tau }{\tau +1}\right)e^{\frac{-7}{6}\frac{\tau }{\tau +1}}\right)\hfill \\ & \le -0.5\left(x_1^2\left(\tau \right)+x_2^2\left(\tau \right)\right)+\left(x_1^2\left(\tau -\frac{\tau }{\tau +1}\right)+x_2^2\left(\tau -\frac{\tau }{\tau +1}\right)\right)e^{\frac{7}{3}\left(-\frac{\tau }{\tau +1}\right)}\hfill \\ & \le 0.5\left(x_1^2\left(\tau \right)+x_2^2\left(\tau \right)\right)=0.5V\left(x\left(\tau \right)\right).\hfill \end{array}$$

(28)

According to Example 3 for $\lambda =0.5$, $q=0.7$, $A=0.5$, and $\rho =0.3$ the bound is $K=1.1$ (see Figure 6). Thus, according to Theorem 3, the zero solution of FrDDE (27) is practically stable with respect to $(0.5,0.5244)$.

6. Conclussions

A nonlinear system of differential equations with generalized proportional Caputo fractional derivatives and bounded delay is studied. Two types of stability, practical stability and exponential practical stability, are defined. Lyapunov like functions and their generalized proportional Caputo fractional derivatives among solutions of the studied system are applied, and in connection with this, the Razumikhin method is applied with an appropriately modified Razumikhin condition. Several sufficient conditions are obtained and illustrated with examples.

We hope to apply the modified Razumihin condition and its application to study various types of generalized proportional Caputo fractional differential equations with delays such as practical stability, Lipschitz stability, etc. Additionally we hope the ideas in this paper could be applied to study stochastic differential equations with a generalized proportional Caputo fractional derivative with appropriate changes of the Razumikhin condition.