Tell Me Why I Do Not Like Mondays
Abstract
:1. Introduction
2. Literature Review
2.1. Explanations Based on Investors’ Rational Considerations
2.2. Explanations Based on Investors’ Irrationality
3. Data
- (1)
- The first conjectures that the implied volatility is equal across weekdays. Based on the findings, we rejected this hypothesis for all of the sampled securities, as evident by the significant F-statistic values.
- (2)
- The second hypothesis postulates that changes in the VIX are equal on Monday and Friday. Based on the findings, we rejected this hypothesis as well.
- (3)
- Last, we checked whether the mean returns on the VIX are equal on Monday, Tuesday, Wednesday, and Thursday.
| Panel A: Level Data in (%). | |||||||||||
| VXAZN | VXAPL | VXGSCLS | VXGOG | VXIBM | VXD | VXN | RVX | TYVIX | |||
| Mean | 31.69 a | 28.00 a | 26.92 a | 24.61 a | 21.84 a | 14.82 a | 25.28 a | 20.13 a | 4.98 a | ||
| Med. | 29.86 | 27.33 | 25.34 | 23.86 | 20.63 | 13.93 | 20.01 | 18.56 | 4.93 | ||
| Max. | 66.06 | 62.60 | 74.88 | 55.60 | 51.72 | 42.67 | 83.00 | 57.66 | 8.62 | ||
| Min. | 5.13 | 12.52 | 16.16 | 9.21 | 13.23 | 7.58 | 10.31 | 11.83 | 3.16 | ||
| Stdev. | 8.63 | 6.55 | 7.57 | 6.20 | 4.96 | 3.72 | 13.76 | 6.01 | 0.95 | ||
| Skew. | 0.66 | 0.84 | 2.13 | 0.89 | 1.23 | 1.68 | 1.83 | 2.53 | 0.66 | ||
| Kurt. | 3.19 | 4.15 | 9.63 | 4.13 | 5.29 | 7.76 | 5.85 | 10.96 | 3.42 | ||
| #Obs | 2148 | 2148 | 2112 | 2148 | 2148 | 1602 | 4825 | 2149 | 1697 | ||
| Sample Period | 2011:08 to 2020:02 | 2011:08 to 2020:02 | 2011:10 to 2020:02 | 2011:08 to 2020:02 | 2011:08 to 2020:02 | 2013:10 to 2020:02 | 2000:10 to 2020:02 | 2011:08 to 2020:02 | 2013:05 to 2020:02 | ||
| Panel B: Correlation between the Volatility Measures. | |||||||||||
| VXD | VXN | RVX | TYVIX | VXAZN | VXAPL | VXGSCLS | VXGOG | VXIBM | |||
| VXN | 0.95 *** | 1.00 | |||||||||
| [124.97] | ----- | ||||||||||
| RVX | 0.96 *** | 0.90 *** | 1.00 | ||||||||
| [138.11] | [86.49] | ----- | |||||||||
| TYVIX | 0.53 *** | 0.46 *** | 0.60 *** | 1.00 | |||||||
| [25.85] | [21.25] | [31.11] | ----- | ||||||||
| VXAZN | 0.62 *** | 0.65 *** | 0.61 *** | 0.33 *** | 1.00 | ||||||
| [32.25] | [35.63] | [31.39] | [14.20] | ----- | |||||||
| VXAPL | 0.84 *** | 0.83 *** | 0.81 *** | 0.51 *** | 0.75 *** | 1.00 | |||||
| [63.81] | [62.29] | [57.09] | [24.58] | [46.21] | ----- | ||||||
| VXGSCLS | 0.92 *** | 0.90 *** | 0.93 *** | 0.58 *** | 0.56 *** | 0.80 *** | 1.00 | ||||
| [99.52] | [85.59] | [102.22] | [29.18] | [27.88] | [55.56] | ----- | |||||
| VXGOG | 0.81 *** | 0.83 *** | 0.78 *** | 0.41 *** | 0.85 *** | 0.86 *** | 0.77 *** | 1.00 | |||
| [56.07] | [61.17] | [51.75] | [18.80] | [67.45] | [68.91] | [49.67] | ----- | ||||
| VXIBM | 0.86 *** | 0.86 *** | 0.84 *** | 0.43 *** | 0.61 *** | 0.80 *** | 0.89 *** | 0.80 *** | 1.00 | ||
| [70.39] | [70.00] | [62.95] | [19.82] | [32.07] | [54.84] | [81.31] | [54.73] | ----- | |||
| Panel C: Rate of Change in Volatility across Weekdays. | |||||||||||
| Mon () | TUE () | WED () | THU () | FRI () | H0: α2= α3= α4= α5= α6 | H0: α2= α6 | H0: α2=α3= α4= α5 | ||||
| VXAZN | 2.228 a | 0.619 c | 0.419 | 0.839 b | −2.549 a | 26.54 a | 9.87 a | 5.65 a | |||
| (6.39) | (1.85) | (1.25) | (2.49) | (−7.59) | |||||||
| VXAPL | 1.264 a | −0.245 | −1.255 a | 0.335 | 0.146 | 7.36 a | 2.33 b | 9.76 a | |||
| (3.65) | (−0.74) | (−3.79) | (1.01) | (0.44) | |||||||
| VXGSCLS | 1.243 a | −0.149 | −0.133 | −0.026 | −0.888 a | 6.45 a | 4.99 a | 4.93 a | |||
| (4.04) | (−0.51) | (−0.45) | (−0.09) | (−2.99) | |||||||
| VXGOG | 2.626 a | 0.345 | 0.158 | 0.66 c | −2.167 a | 24.18 a | 9.75 a | 10.55 a | |||
| (7.41) | (1.02) | (0.47) | (1.94) | (−6.35) | |||||||
| VXIBM | 1.599 a | 0.262 | −0.832 b | 0.049 | −0.822 b | 7.99 a | 4.86 a | 8.14 a | |||
| (4.46) | (0.76) | (−2.42) | (0.14) | (−2.38) | |||||||
| VXD | 1.596 a | 0.657 | −0.644 | 0.589 | −0.527 | 5.13 a | 3.64 a | 5.03 a | |||
| (3.81) | (1.63) | (−1.60) | (1.45) | (−1.30) | |||||||
| VXN | 1.678 a | 0.009 | −0.243 | 0.06 | −0.571 a | 19.18 a | 8.06 a | 19.57 a | |||
| (8.36) | (0.05) | (−1.26) | (0.31) | (−2.9) | |||||||
| RVX | 1.944 a | 0.259 | −0.143 | −0.118 | −0.855 a | 11.85 a | 6.56 a | 10.59 a | |||
| (6.32) | (0.88) | (−0.49) | (−0.39) | (−2.89) | |||||||
| TYVIX | 2.039 a | 0.403 | −0.740 a | −0.214 | −1.288 a | 24.74 a | 9.16 a | 21.89 a | |||
| (7.80) | (1.61) | (−2.95) | (−0.85) | (−5.10) | |||||||
4. Empirical Findings
| Panel A: Amazon. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| First Friday | Second Friday | Third Friday | Fourth Friday | Fifth Friday | First Three Fridays | Last Two Fridays | Difference in the Two Periods | All Fridays | |
| 1.08/2011–02/2020 | |||||||||
| Mean | −3.066 a | −0.913 | −1.314 a | −1.471 | −6.684 a | −1.445 a | −3.942 a | −2.549 | |
| T-Statistic | (−3.13) | (−1.64) | (−2.88) | (−1.64) | (−5.06) | (−4.21) | (−4.90) | −2.497 a | (−6.25) |
| Welch F-test | (−2.84) | ||||||||
| Percentage negative | 68.29% | 72.00% | 64.36% | 55.45% | 60.44% | 68.18% | 57.81% | (−2.70) | 63.59% |
| #Obs | 41 | 100 | 101 | 101 | 91 | 242 | 192 | 434 | |
| 2.08/2011–12/2015 | |||||||||
| Mean | −1.704 c | −1.458 a | −0.827 | −3.096 b | −6.127 a | −1.225 a | −4.551 a | −2.730 a | |
| T-Statistic | (−1.89) | (−2.92) | (−1.34) | (−2.05) | (−3.52) | (−3.38) | (−3.95) | −3.326 a | (−4.81) |
| Welch F-test | (−2.89) | ||||||||
| Percentage negative | 68.42% | 74.00% | 61.54% | 61.54% | 60.42% | 67.77% | 61.00% | (−2.75) | 64.71% |
| #Obs | 19 | 50 | 52 | 52 | 48 | 121 | 100 | 221 | |
| 3.01/2016–02/2020 | |||||||||
| Mean | −4.243 b | −0.367 | −1.830 a | 0.254 | −7.306 a | −1.664 a | −3.279 a | 1.943 b | |
| T-Statistic | (−2.59) | (−0.37) | (−2.73) | -0.29 | (−3.60) | (−2.85) | (−2.93) | −1.615 | −2.51 |
| Welch F-test | (−1.18) | ||||||||
| Percentage negative | 68.18% | 70.00% | 67.35% | 48.98% | 60.47% | 68.60% | 54.35% | (−1.07) | 62.44% |
| #Obs | 22 | 50 | 49 | 49 | 43 | 121 | 92 | 213 | |
4.1. Do Monday’s Price Changes Depend on Friday’s Price Changes?
4.2. A Comparison of Monday and Other Days of the Week
4.3. Potential Drivers
4.3.1. Investors’ Irrationality
4.3.2. Investors’ Rational Considerations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- French, K.R. Stock returns and the weekend effect. J. Financ. Econ. 1980, 8, 55–69. [Google Scholar] [CrossRef]
- Birru, J. Day of the week and the cross-section of returns. J. Financ. Econ. 2018, 130, 182–214. [Google Scholar] [CrossRef]
- Blose, L.E.; Gondhalekar, V. Weekend gold returns in bull and bear markets. Account. Financ. 2013, 53, 609–622. [Google Scholar] [CrossRef]
- Gondhalekar, V.; Mehdian, S. The blue-Monday hypothesis: Evidence based on Nasdaq stocks, 1971–2000. Q. J. Bus. Econ. 2003, 42, 73–89. [Google Scholar]
- Zhang, T.W.; Chueh, H.; Hsu, Y.H. Day-of-the-week trading patterns of informed and uninformed traders in Taiwan’s foreign exchange market. Econ. Model. 2015, 47, 271–279. [Google Scholar] [CrossRef]
- Caporale, G.M.; Plastun, A. The day of the week effect in the cryptocurrency market. Financ. Res. Lett. 2019, 31. [Google Scholar] [CrossRef]
- Aharon, D.Y.; Qadan, M. Bitcoin and the day-of-the-week effect. Financ. Res. Lett. 2019, 31, 415–424. [Google Scholar] [CrossRef]
- Johnston, E.T.; Kracaw, W.A.; McConnell, J.J. Day-of-the-Week Effects in Financial Futures: An Analysis of GNMA, T-Bond, T-Note, and T-Bill Contracts. J. Financ. Quant. Anal. 1991, 26, 23–44. [Google Scholar] [CrossRef] [Green Version]
- Jordan, S.D.; Jordan, B.D. Seasonality in daily bond returns. J. Financ. Quant. Anal. 1991, 26, 269–285. [Google Scholar] [CrossRef]
- Gonzalez-Perez, M.T.; Guerrero, D.E. Day-of-the-week effect on the VIX. A parsimonious representation. N. Am. J. Econ. Financ. 2013, 25, 243–260. [Google Scholar] [CrossRef]
- Plastun, A.; Sibande, X.; Gupta, R.; Wohar, M.E. Rise and fall of calendar anomalies over a century. N. Am. J. Econ. Financ. 2019, 49, 181–205. [Google Scholar] [CrossRef] [Green Version]
- Boubaker, S.; Essaddam, N.; Nguyen, D.K.; Saadi, S. On the robustness of week-day effect to error distributional assumption: International evidence. J. Int. Financial Mark. Inst. Money 2017, 47, 114–130. [Google Scholar] [CrossRef]
- Brusa, J.; Liu, P.; Schulman, C. The “reverse” weekend effect: The US market versus international markets. Int. Rev. Financ. Anal. 2003, 12, 267–286. [Google Scholar] [CrossRef]
- Stivers, C.; Sun, L. Returns and option activity over the option-expiration week for S&P 100 stocks. J. Bank. Financ. 2013, 37, 4226–4240. [Google Scholar] [CrossRef]
- Baker, S.R.; Bloom, N.; Davis, S.J. Measuring Economic Policy Uncertainty. Q. J. Econ. 2016, 131, 1593–1636. [Google Scholar] [CrossRef]
- Areni, C.S.; Burger, M. Memories of “bad” days are more biased than memories of “good” days: Past Saturdays vary, but past Mondays are always blue. J. Appl. Soc. Psychol. 2008, 38, 1395–1415. [Google Scholar] [CrossRef]
- Ryan, R.M.; Bernstein, J.H.; Brown, K.W. Weekends, Work, and Well-Being: Psychological Need Satisfactions and Day of the Week Effects on Mood, Vitality, and Physical Symptoms. J. Soc. Clin. Psychol. 2010, 29, 95–122. [Google Scholar] [CrossRef]
- Wright, W.F.; Bower, G.H. Mood effects on subjective probability assessment. Organ. Behav. Hum. Decis. Process. 1992, 52, 276–291. [Google Scholar] [CrossRef]
- Kostopoulos, D.; Meyer, S. Disentangling investor sentiment: Mood and household attitudes towards the economy. J. Econ. Behav. Organ. 2018, 155, 28–78. [Google Scholar] [CrossRef]
- Qadan, M.; Aharon, D.Y.; Cohen, G. Everybody likes shopping, including the US capital market. Phys. A Stat. Mech. Appl. 2020, 551, 124173. [Google Scholar] [CrossRef]
- Aydogan, B. Sentiment dynamics and volatility of international stock markets. Eurasian Bus. Rev. 2017, 7, 407–419. [Google Scholar] [CrossRef]
- Chen, M.P.; Lee, C.C.; Hsu, Y.C. Investor sentiment and country exchange traded funds: Does economic freedom matter? N. Am. J. Econ. Financ. 2017, 42, 285–299. [Google Scholar] [CrossRef]
- Qadan, M.; Aharon, D.Y. How much happiness can we find in the US fear Index? Financ. Res. Lett. 2019, 30, 246–258. [Google Scholar] [CrossRef]
- Keim, D.B.; Stambaugh, R.F. A further investigation of the weekend effect in stock returns. J. Financ. 1984, 39, 819–835. [Google Scholar] [CrossRef]
- Groth, J.C.; Lewellen, W.G.; Schlarbaum, G.G.; Lease, R.C. An Analysis of Brokerage House Securities Recommendations. Financ. Anal. J. 1979, 35, 32–40. [Google Scholar] [CrossRef]
- Dimson, E.; Marsh, P. An analysis of brokers’ and analysts’ unpublished forecasts of UK stock returns. J. Financ. 1984, 39, 1257–1292. [Google Scholar] [CrossRef]
- Ritter, J.R. The buying and selling behavior of individual investors at the turn of the year. J. Financ. 1988, 43, 701–717. [Google Scholar] [CrossRef]
- Lakonishok, J.; Maberly, E. The weekend effect: Trading patterns of individual and institutional investors. J. Financ. 1990, 45, 231–243. [Google Scholar] [CrossRef]
- Abraham, A.; Ikenberry, D.L. The Individual Investor and the Weekend Effect. J. Financ. Quant. Anal. 1994, 29, 263. [Google Scholar] [CrossRef]
- Singal, V.; Tayal, J. Risky short positions and investor sentiment: Evidence from the weekend effect in futures markets. J. Futur. Mark. 2020, 40, 479–500. [Google Scholar] [CrossRef]
- Bariviera, A.F.; Plastino, A.; Judge, G. Spurious Seasonality Detection: A Non-Parametric Test Proposal. Econometrics 2018, 6, 3. [Google Scholar] [CrossRef] [Green Version]
- Patell, J.M.; Wolfson, M.A. Good news, bad news, and the intraday timing of corporate disclosures. Account. Rev. 1982, 57, 509–527. [Google Scholar]
- Penman, S.H. The distribution of earnings news over time and seasonalities in aggregate stock returns. J. Financ. Econ. 1987, 18, 199–228. [Google Scholar] [CrossRef]
- Dellavigna, S.; Pollet, J.M. Investor Inattention and Friday Earnings Announcements. J. Financ. 2009, 64, 709–749. [Google Scholar] [CrossRef] [Green Version]
- Michaely, R.; Rubin, A.; Vedrashko, A. Further evidence on the strategic timing of earnings news: Joint analysis of weekdays and times of day. J. Account. Econ. 2016, 62, 24–45. [Google Scholar] [CrossRef]
- Carretta, A.; Farina, V.; Martelli, D.; Fiordelisi, F.; Schwizer, P. The Impact of Corporate Governance Press News on Stock Market Returns. Eur. Financ. Manag. 2011, 17, 100–119. [Google Scholar] [CrossRef]
- Tetlock, P.C. Giving Content to Investor Sentiment: The Role of Media in the Stock Market. J. Financ. 2007, 62, 1139–1168. [Google Scholar] [CrossRef]
- Tetlock, P.C.; Saar-Tsechansky, M.; Macskassy, S. More Than Words: Quantifying Language to Measure Firms’ Fundamentals. J. Financ. 2008, 63, 1437–1467. [Google Scholar] [CrossRef]
- Batrancea, L. An Econometric Approach Regarding the Impact of Fiscal Pressure on Equilibrium: Evidence from Electricity, Gas and Oil Companies Listed on the New York Stock Exchange. Mathematics 2021, 9, 630. [Google Scholar] [CrossRef]
- Batrancea, L. The Influence of Liquidity and Solvency on Performance within the Healthcare Industry: Evidence from Publicly Listed Companies. Mathematics 2021, 9, 2231. [Google Scholar] [CrossRef]
- Batrancea, L.; Rus, M.I.; Masca, E.S.; Morar, I.D. Fiscal Pressure as a Trigger of Financial Performance for the Energy Industry: An Empirical Investigation across a 16-Year Period. Energies 2021, 14, 3769. [Google Scholar] [CrossRef]
- Saunders, E.M. Stock prices and wall street weather. Am. Econ. Rev. 1993, 83, 1337–1345. [Google Scholar]
- Kamstra, M.J.; Kramer, L.; Levi, M.D. Winter Blues: A SAD Stock Market Cycle. Am. Econ. Rev. 2003, 93, 324–343. [Google Scholar] [CrossRef] [Green Version]
- Rystrom, D.S.; Benson, E.D. Investor Psychology and the Day-of-the-Week Effect. Financ. Anal. J. 1989, 45, 75–78. [Google Scholar] [CrossRef]
- Yang, C.-M.; Spielman, A.J. The effect of a delayed weekend sleep pattern on sleep and morning functioning. Psychol. Health 2001, 16, 715–725. [Google Scholar] [CrossRef]
- Wen, H.; Sun, J.; Zhang, X. Study on Traffic Congestion Patterns of Large City in China Taking Beijing as an Example. Procedia Soc. Behav. Sci. 2014, 138, 482–491. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Lu, F.; Liu, Y.; Guo, J. How does a driving restriction affect transportation patterns? The medium-run evidence from Beijing. J. Clean. Prod. 2018, 204, 270–281. [Google Scholar] [CrossRef]
- Starcke, K.; Brand, M. Decision making under stress: A selective review. Neurosci. Biobehav. Rev. 2012, 36, 1228–1248. [Google Scholar] [CrossRef]
- Stack, S. Temporal Disappointment, Homicide and Suicide: An Analysis of Nonwhites and Whites. Sociol. Focus 1995, 28, 313–328. [Google Scholar] [CrossRef]
- Jessen, G.; Jensen, B.F.; Steffensen, P. Seasons and meteorological factors in suicidal behaviour. Arch. Suicide Res. 1998, 4, 263–280. [Google Scholar] [CrossRef]
- Golder, S.A.; Macy, M.W. Diurnal and Seasonal Mood Vary with Work, Sleep, and Daylength Across Diverse Cultures. Science 2011, 333, 1878–1881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stone, A.A.; Schneider, S.; Harter, J.K. Day-of-week mood patterns in the United States: On the existence of ‘Blue Monday’,’Thank God it’s Friday’ and weekend effects. J. Posit. Psychol. 2012, 7, 306–314. [Google Scholar] [CrossRef]
- Qadan, M.; Idilbi-Bayaa, Y. The day-of-the-week-effect on the volatility of commodities. Resour. Policy 2020, 71, 101980. [Google Scholar] [CrossRef]
- Abu Bakar, A.; Siganos, A.; Vagenas Nanos, E. Does mood explain the Monday effect? J. Forecast. 2014, 33, 409–418. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.-M.; Spielman, A.J.; D’Ambrosio, P.; Serizaw, S.; Nunes, J.; Birnbaum, J. A Single Dose of Melatonin Prevents the Phase Delay Associated with a Delayed Weekend Sleep Pattern. Sleep 2001, 24, 272–281. [Google Scholar] [CrossRef] [Green Version]
- Taylor, A.; Wright, H.R.; Lack, L.C. Sleeping-in on the weekend delays circadian phase and increases sleepiness the following week. Sleep Biol. Rhythm. 2008, 6, 172–179. [Google Scholar] [CrossRef]
- Newey, W.; West, K. A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix. Econometrica 1987, 55, 703. [Google Scholar] [CrossRef]
- Connolly, R.A. A posterior odds analysis of the weekend effect. J. Econ. 1991, 49, 51–104. [Google Scholar] [CrossRef]
- Chiang, C.-H. Stock returns on option expiration dates: Price impact of liquidity trading. J. Empir. Financ. 2014, 28, 273–290. [Google Scholar] [CrossRef]
- Wang, K.; Li, Y.; Erickson, J. A new look at the Monday effect. J. Financ. 1997, 52, 2171–2186. [Google Scholar] [CrossRef]
- Bampinas, G.; Fountas, S.; Panagiotidis, T. The day-of-the-week effect is weak: Evidence from the European real estate sector. J. Econ. Finance 2016, 40, 549–567. [Google Scholar] [CrossRef] [Green Version]
- Schwert, G.W. Anomalies and market efficiency. Handb. Econ. Financ. 2003, 1, 939–974. [Google Scholar]
- Doyle, J.R.; Chen, C.H. The wandering weekday effect in major stock markets. J. Bank. Financ. 2009, 33, 1388–1399. [Google Scholar] [CrossRef] [Green Version]
- You, W.; Guo, Y.; Peng, C. Twitter’s daily happiness sentiment and the predictability of stock returns. Financ. Res. Lett. 2017, 23, 58–64. [Google Scholar] [CrossRef]
- McFarlane, J.M.; Martin, C.L.; Williams, T.M. Mood Fluctuations: Women Versus Men and Menstrual Versus Other Cycles. Psychol. Women Q. 1988, 12, 201–223. [Google Scholar] [CrossRef]
- Hibbert, A.M.; Daigler, R.T.; Dupoyet, B. A behavioral explanation for the negative asymmetric return–volatility relation. J. Bank. Financ. 2008, 32, 2254–2266. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T.; Diebold, F.X.; Labys, P. Modeling and Forecasting Realized Volatility. Econometrica 2003, 71, 579–625. [Google Scholar] [CrossRef] [Green Version]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Smales, L.A. Risk-on/Risk-off: Financial market response to investor fear. Financ. Res. Lett. 2016, 17, 125–134. [Google Scholar] [CrossRef] [Green Version]
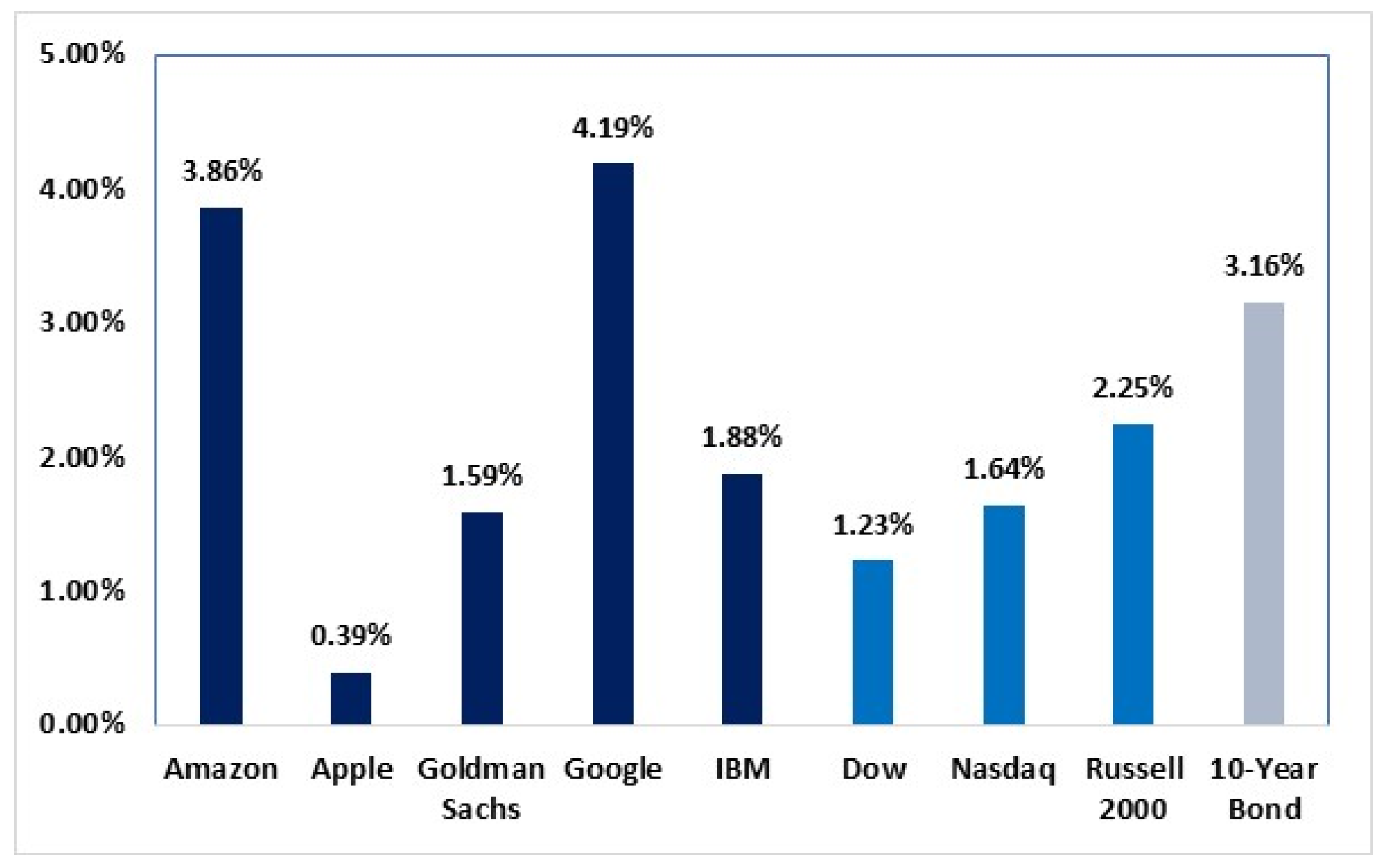
| Security/Index | Ticker Symbol | Sample Period |
|---|---|---|
| Amazon | VXAZN | 16 August 2011–28 February 2020 |
| Apple | VXAPL | 16 August 2011–28 February 2020 |
| Goldman Sachs | VXGSCLS | 6 October 2011–28 February 2020 |
| VXGOG | 16 August 2011–28 February 2020 | |
| IBM | VXIBM | 16 August 2011–28 February 2020 |
| DOW | VXD | 2 October 2013–28 February 2020 |
| NASDAQ | VXN | 10 October 2000–28 February 2020 |
| Russell 2000 | RVX | 15 August 2011–28 February 2020 |
| 10-Year Treasury notes | TYVIX | 30 May 2013–28 February 2020 |
| VXAZN (2011:08–2020:02) | VXAPL (2011:08–2020:02) | |||||
| Friday | Monday | Friday | Monday | |||
| Number of times the Index advanced | 156 | 261 | 198 | 243 | ||
| Number of times the Index declined | 276 | 141 | 233 | 158 | ||
| Number of times the Index was unchanged | 2 | 0 | 3 | 1 | ||
| Total | 434 | 402 | 434 | 402 | ||
| Percentage of times the Index advanced (1) (Sign Test t-stat.) | 35.94% *** (5.66) | 64.93% *** (5.99) | 45.62% * (1.54) | 60.45% *** (4.19) | ||
| Percentage of times the Index declined (2) | 63.59% *** (5.66) | 35.07% *** (5.99) | 53.69% * (1.54) | 39.30%*** (4.19) | ||
| Difference (2)-(1) (Sign Test t-stat.) | 27.65% *** (8.47) | 29.85% *** (8.86) | 8.06% ** (2.38) | 21.14%*** (6.13) | ||
| Mean percentage change (t-stat.) | −2.55 *** (−6.25) | 2.23 *** (5.12) | 0.15 (0.46) | 1.26 *** (3.55) | ||
| Median percentage change | −1.59 | 2.21 | −0.45 | 1.44 | ||
| VXGSCLS (2011:10–2020:02) | VXGOG (2011:08–2020:02) | VXIBM (2011:08–2020:02) | ||||
| Friday | Monday | Friday | Monday | Friday | Monday | |
| Number of times the Index advanced | 154 | 235 | 158 | 272 | 183 | 255 |
| Number of times the Index declined | 269 | 160 | 275 | 129 | 241 | 143 |
| Number of times the Index was unchanged | 4 | 1 | 1 | 1 | 10 | 4 |
| Total | 427 | 396 | 434 | 402 | 434 | 402 |
| Percentage of times the Index advanced (1) (Sign Test t-stat.) | 36.07% *** (5.37) | 59.34% *** (3.72) | 36.41% *** (5.57) | 67.66% *** (7.08) | 42.17% *** (2.30) | 63.43% *** (5.39) |
| Percentage of times the Index declined (2) | 63.00% *** (5.37) | 40.40% *** (3.72) | 63.36% *** (5.57) | 32.09% *** (7.08) | 55.53% *** (2.30) | 35.57% *** (5.39) |
| Difference (2)-(1) (Sign Test t-stat.) | 26.93% *** (8.16) | 18.94% *** (5.42) | 26.96% *** (8.24) | 35.57% *** (10.78) | 13.36% *** (3.97) | 27.86% *** (8.22) |
| Mean percentage change (t-stat.) | −0.89 *** (−2.95) | 1.24 *** (3.84) | −2.17 *** (−5.15) | 2.63 *** (6.33) | −0.82 ** (−2.37) | 1.60 *** (4.98) |
| Median percentage change | −1.28 | 1.05 | −1.20 | 2.43 | −0.57 | 1.42 |
| VXD (2013:10–2020:02) | VXN (2000:10–2020:02) | RVX (2011:08–2020:02) | ||||
| Friday | Monday | Friday | Monday | Friday | Monday | |
| Number of times the Index advanced | 126 | 174 | 363 | 536 | 170 | 242 |
| Number of times the Index declined | 196 | 128 | 600 | 366 | 260 | 159 |
| Number of times the Index was unchanged | 1 | 0 | 6 | 5 | 4 | 2 |
| Total | 323 | 302 | 969 | 907 | 434 | 403 |
| Percentage of times the Index advanced (1) (Sign Test t-stat.) | 39.01% *** (3.84) | 57.62% *** (2.65) | 37.46% *** (7.42) | 59.10% *** (5.48) | 39.17% *** (4.13) | 60.05% *** (4.04) |
| Percentage of times the Index declined (2) | 60.68% *** (3.84) | 42.38% *** (2.65) | 61.92% *** (7.42) | 40.35% *** (2.65) | 59.91% *** (4.13) | 39.45% *** (4.04) |
| Difference (2)-(1) (Sign Test t-stat.) | 21.67% *** (3.04) | 15.23% *** (2.25) | 24.46% *** (11.09) | 18.74% *** (8.12) | 20.74% *** (6.24) | 20.60% *** (5.98) |
| Mean percentage change (t-stat.) | −0.53 (−1.25) | 1.60 *** (3.52) | −0.57 *** (−2.92) | 1.68 *** (7.50) | −0.85 *** (−2.91) | 1.94 *** (5.06) |
| Median percentage change | −1.51 | 1.13 | −1.30 | 1.34 | −1.25 | 1.32 |
| TYVIX (2013:05–2020:02) | ||||||
| Friday | Monday | |||||
| Number of times the Index advanced | 119 | 224 | ||||
| Number of times the Index declined | 219 | 88 | ||||
| Number of times the Index was unchanged | 4 | 7 | ||||
| Total | 342 | 319 | ||||
| Percentage of times the Index advanced (1) (Sign Test t-stat.) | 34.80% *** (5.19) | 70.22% *** (7.22) | ||||
| Percentage of times the Index declined (2) | 64.04% *** (5.19) | 27.59% *** (7.22) | ||||
| Difference (2)-(1) (Sign Test t-stat.) | 29.24% *** (7.99) | 42.63% *** (11.89) | ||||
| Mean percentage change (t-stat.) | −1.29 *** (−4.40) | 2.04 *** (7.90) | ||||
| Median percentage change | −1.65 | 1.86 | ||||
| VXAZN (2011:08–2020:02) | VXAPL (2011:08–2020:02) | VXIBM (2011:08–2020:02) | ||||
| Friday | Monday | Friday | Monday | Friday | Monday | |
| Number of times the Index advanced | 118 | 208 | 149 | 207 | 143 | 213 |
| Number of times the Index declined | 213 | 102 | 181 | 102 | 181 | 94 |
| Number of times the Index was unchanged | 2 | 0 | 3 | 1 | 9 | 3 |
| Total | 333 | 310 | 333 | 310 | 333 | 310 |
| Percentage of times the Index advanced (1) (Sign Test t-stat.) | 35.44% *** (5.09) | 67.10% *** (6.20) | 44.74% * (1.59) | 66.77% *** (5.91) | 42.94% * (1.59) | 68.71% *** (6.59) |
| Percentage of times the Index declined (2) | 63.96% | 32.90% | 54.35% | 32.90% | 54.35% | 30.32% |
| Difference (2)–(1) (Sign Test t-stat.) | 28.53% *** (7.67) | 34.19% *** (9.05) | 9.61% ** (2.49) | 33.87% *** (8.95) | 11.41% *** (2.96) | 38.39% *** (10.34) |
| Mean percentage change (t-stat.) | −3.17 *** (−6.11) | 2.10 (4.11) | −0.11 (−0.31) | 1.74 *** (4.29) | −0.06 (−0.19) | 2.19 *** (6.11) |
| Median percentage change | −1.62 | 2.82 | −0.59 | 2.22 | −0.45 | 2.18 |
| VXGSCLS (2011:10–2020:02) | VXGOG (2011:08–2020:02) | TYVIX (2013:05–2020:02) | ||||
| Friday | Monday | Friday | Monday | Friday | Monday | |
| Number of times the Index advanced | 149 | 207 | 123 | 216 | 92 | 174 |
| Number of times the Index declined | 181 | 102 | 209 | 93 | 169 | 67 |
| Number of times the Index was unchanged | 3 | 1 | 1 | 1 | 2 | 5 |
| Total | 333 | 310 | 333 | 310 | 263 | 246 |
| Percentage of times the Index advanced (1) (Sign Test t-stat.) | 44.74% * (1.59) | 66.77% *** (5.91) | 36.94% *** (4.66) | 69.68% *** (6.93) | 34.98% *** (4.63) | 70.73% *** (6.50) |
| Percentage of times the Index declined (2) | 54.35% | 32.90% | 62.76% | 30.00% | 64.26% | 27.24% |
| Difference (2)–(1) (Sign Test t-stat.) | 9.61% ** (2.49) | 33.87% *** (9.06) | 25.83% *** (6.89) | 39.68% *** (10.75) | 29.28% *** (7.01) | 43.50% *** (10.70) |
| Mean percentage change (t-stat.) | −0.11 (−0.31) | 1.74 *** (4.29) | −1.75 *** (−3.95) | 2.39 *** (5.62) | −1.38 *** (−4.16) | 2.15 *** (7.35) |
| Median percentage change | −0.59 | 2.22 | −0.94 | 2.61 | −1.61 | 1.88 |
| VXD (2013:10–2020:02) | VXN (2000:10–2020:02) | RVX (2011:08–2020:02) | ||||
| Friday | Monday | Friday | Monday | Friday | Monday | |
| Number of times the Index advanced | 100 | 133 | 287 | 433 | 136 | 186 |
| Number of times the Index declined | 148 | 100 | 452 | 264 | 194 | 124 |
| Number of times the Index was unchanged | 1 | 0 | 4 | 4 | 3 | 1 |
| Total | 249 | 233 | 743 | 701 | 333 | 311 |
| Percentage of times the Index advanced (1) (Sign Test t-stat.) | 40.16% *** (2.98) | 57.08% ** (2.16) | 38.63% *** (5.91) | 61.77% *** (6.23) | 40.84% *** (3.01) | 59.81% *** (3.46) |
| Percentage of times the Index declined (2) | 59.44% | 42.92% | 60.83% | 37.66% | 58.26% | 39.87% |
| Difference (2)–(1) (Sign Test t-stat.) | 19.28% *** (2.68) | 14.16% *** (2.05) | 22.21% *** (8.77) | 24.11% *** (9.29) | 17.42% *** (4.56) | 19.94% *** (5.07) |
| Mean percentage change (t-stat.) | −0.38 (−0.79) | 1.78 *** (3.46) | −0.40 * (−1.79) | 2.02 *** (8.03) | −0.53 (−1.57) | 1.94 *** (4.33) |
| Median percentage change | −1.50 | 1.14 | −1.09 | 1.63 | −1.15 | 1.03 |
| Panel A: Amazon. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| First Monday | Second Monday | Third Monday | Fourth Monday | Fifth Monday | First Three Mondays | Last Two Mondays | Difference in the Two Periods | All Mondays | |
| 1.08/2011–02/2020 | |||||||||
| Mean | 3.520 a | 3.208 a | −0.939 | 2.713 a | 3.626 a | 1.529 b | 3.144 a | 1.614 c | 2.228 a |
| T-Statistic | (3.52) | (5.71) | (−0.72) | (3.26) | (4.68) | (2.43) | (5.50) | (1.84) | (5.12) |
| Welch F-test | (3.61) | ||||||||
| Percentage positive | 75.00% | 78.35% | 53.68% | 57.61% | 65.85% | 67.54% | 61.49% | 64.93% | |
| #Obs | 36 | 97 | 95 | 92 | 82 | 228 | 174 | 402 | |
| 2.08/2011−12/2015 | |||||||||
| Mean | 4.343 a | 2.353 a | 0.826 | 2.206 c | 4.098 a | 2.039 a | 3.089 a | 1.05 | 2.493 a |
| T-Statistic | (5.37) | (4.61) | (0.82) | (1.96) | (4.19) | (4.09) | (4.09) | (1.20) | (5.76) |
| Welch F-test | (1.34) | ||||||||
| Percentage positive | 84.21% | 76.00% | 55.10% | 56.25% | 76.19% | 68.64% | 65.56% | 67.31% | |
| #Obs | 19 | 50 | 49 | 48 | 42 | 118 | 90 | 208 | |
| 3.01/2016–02/2020 | |||||||||
| Mean | 2.6 | 4.117 a | −2.819 | 3.267 b | 3.131 b | 0.982 | 3.202 a | 2.22 | 1.943 b |
| T-Statistic | (1.35) | (4.06) | (−1.15) | (2.62) | (2.57) | (0.83) | (3.69) | (1.43) | (2.51) |
| Welch F-test | (2.28) | ||||||||
| Percentage positive | 64.71% | 80.85% | 52.17% | 59.09% | 55.00% | 66.36% | 57.14% | 62.37% | |
| #Obs | 17 | 47 | 46 | 44 | 40 | 110 | 84 | 194 | |
| Performance of the Index on Monday | VXAZN | VXAPL | |||||
| After an Advance on Friday | After a Decline on Friday | After an Advance on Friday | After a Decline on Friday | ||||
| Number of times the Index advanced | 97 | 152 | 103 | 126 | |||
| Number of times the Index declined | 47 | 94 | 79 | 79 | |||
| Number of times the Index was unchanged | 0 | 0 | 1 | 0 | |||
| Total | 144 | 246 | 183 | 205 | |||
| Percentage of times the Index advanced (t-stat.) | 67.36% *** (4.17) | 61.79% *** (3.69) | 56.28% ** (1.70) | 61.46% *** (3.28) | |||
| Percentage of times the Index declined (t-stat.) | 32.64% *** (4.17) | 38.21% *** (3.69) | 43.17% ** (1.70) | 38.54% *** (3.28) | |||
| Difference (2)–(1) (t-stat.) | 34.72% *** (5.98) | 23.58% *** (5.07) | 13.11% ** (2.43) | 22.93% *** (4.49) | |||
| Mean percentage change (t-stat.) | 3.00 *** (3.85) | 1.39 *** (2.59) | 1.02 * (1.74) | 1.06 ** (2.23) | |||
| Median percentage change | 2.66 | 1.91 | 1.33 | 1.31 | |||
| Performance of the Index on Monday | VXGSCLS | VXGOG | VXIBM | ||||
| After an Advance on Friday | After a Decline on Friday | After an Advance on Friday | After a Decline on Friday | After an Advance on Friday | After a Decline on Friday | ||
| Number of times the Index advanced | 72 | 149 | 90 | 170 | 99 | 143 | |
| Number of times the Index declined | 69 | 90 | 51 | 78 | 64 | 75 | |
| Number of times the Index was unchanged | 1 | 0 | 0 | 1 | 1 | 0 | |
| Total | 142 | 239 | 141 | 249 | 164 | 218 | |
| Percentage of times the Index advanced (t-stat.) | 50.70% (0.17) | 62.34% *** (3.82) | 63.83% *** (3.28) | 68.27% *** (5.77) | 60.37% *** (2.66) | 65.60% *** (4.61) | |
| Percentage of times the Index declined (t-stat.) | 48.59% | 37.66% | 36.17% *** (3.28) | 31.33% *** (5.77) | 39.02% *** (2.66) | 34.40% *** (4.61) | |
| Difference (2)–(1) (t-stat.) | 2.11% (0.34) | 24.69% *** (5.24) | 27.66% *** (4.54) | 36.95% *** (8.37) | 21.34% *** (3.74) | 31.19% *** (6.48) | |
| Mean percentage change (t-stat.) | 0.47 (0.67) | 1.40 *** (3.87) | 2.39 *** (3.58) | 2.64 *** (4.81) | 1.52 *** (2.77) | 1.49 *** (3.67) | |
| Median percentage change | 0.33 | 1.27 | 2.66 | 2.29 | 1.22 | 1.56 | |
| Performance of the Index on Monday | VXD | VXN | RVX | ||||
| After an Advance on Friday | After a Decline on Friday | After an Advance on Friday | After a Decline on Friday | After an Advance on Friday | After a Decline on Friday | ||
| Number of times the Index advanced | 56 | 108 | 186 | 323 | 85 | 147 | |
| Number of times the Index declined | 58 | 67 | 144 | 212 | 70 | 84 | |
| Number of times the Index was unchanged | 0 | 0 | 1 | 4 | 1 | 0 | |
| Total | 114 | 175 | 331 | 539 | 156 | 231 | |
| Percentage of times the Index advanced (t-stat.) | 49.12% (0.43) | 61.71% *** (3.10) | 56.19% ** (2.25) | 59.93% *** (4.61) | 54.49% (1.12) | 63.64% *** (4.15) | |
| Percentage of times the Index declined | 50.88% (0.38) | 38.29% *** (3.00) | 43.50% | 39.33% | 44.87% | 36.36% | |
| Difference (2)–(1) (t-stat.) | 1.75% (0.47) | 23.43% *** (2.66) | 12.69% *** (3.15) | 20.59% *** (6.56) | 9.62% (1.63) | 27.27% *** (5.74) | |
| Mean percentage change (t-stat.) | 1.39 (1.56) | 1.47 *** (2.94) | 1.94 *** (4.32) | 1.30 *** (5.24) | 2.17 *** (2.74) | 1.52 *** (3.80) | |
| Median percentage change | −0.09 | 1.26 | 0.96 | 1.17 | 0.46 | 1.60 | |
| Performance of the Index on Monday | TYVIX | ||||||
| After an Advance on Friday | After a Decline on Friday | ||||||
| Number of times the Index advanced | 68 | 146 | |||||
| Number of times the Index declined | 38 | 47 | |||||
| Number of times the Index was unchanged | 2 | 4 | |||||
| Total | 108 | 197 | |||||
| Percentage of times the Index advanced (t-stat.) | 62.96% *** (2.69) | 74.11% *** (6.77) | |||||
| Percentage of times the Index declined | 35.19% | 23.86% | |||||
| Difference (2)–(1) (t-stat.) | 27.78% *** (4.04) | 50.25% *** (10.92) | |||||
| Mean percentage change (t-stat.) | 1.67 *** (3.27) | 2.27 *** (7.48) | |||||
| Median percentage change | 1.48 | 1.97 | |||||
| Percentage of Times the Index Advanced | VXAZN | VXAPL | ||||
| On Monday | On Other Days | On Monday | On Other Days | |||
| After an Advance the previous day (t-stat.) | 67.36% *** (4.17) | 47.52% (1.14) | 56.28% ** (1.70) | 47.61% (1.19) | ||
| After a decline the previous day (t-stat.) | 61.79% *** (3.69) | 48.66% (0.39) | 61.46% *** (3.28) | 54.33% *** (2.57) | ||
| Mean Percentage Change | ||||||
| After an Advance the previous day (t-stat.) | 3.00 *** (3.85) | −0.38 * (−1.82) | 1.02 * (1.74) | −0.35 (−1.43) | ||
| After a decline the previous day (t-stat.) | 1.39 *** (2.59) | 0.10 (0.41) | 1.06 ** (2.23) | −0.16 (−0.72) | ||
| Percentage of Times the Index Advanced | VXGSCLS | VXGOG | VXIBM | |||
| On Monday | On Other Days | On Monday | On Other Days | On Monday | On Other Days | |
| After an Advance the previous day (t-stat.) | 50.70% (0.17) | 43.82% *** (3.36) | 63.83% *** (3.28) | 48.75% (0.45) | 60.37% *** (2.66) | 48.42% (0.56) |
| After a decline the previous day (t-stat.) | 62.34% *** (3.82) | 56.46% *** (3.82) | 68.27% *** (3.58) | 52.52% (1.40) | 65.60% *** (4.61) | 51.07% (0.60) |
| Mean Percentage Change | ||||||
| After an Advance the previous day (t-stat.) | 0.47 (0.67) | −0.44 ** (−2.09) | 2.39 *** (3.58) | −0.31 (−1.54) | 1.52 *** (2.77) | −0.57 ** (−2.14) |
| After a decline the previous day (t-stat.) | 1.40 *** (3.87) | −0.16 (−0.79) | 2.64 *** (4.81) | −0.18 (−0.67) | 1.49 *** (3.67) | −0.09 (−0.38) |
| Percentage of Times the Index Advanced | VXD | VXN | RVX | |||
| On Monday | On Other Days | On Monday | On Other Days | On Monday | On Other Days | |
| After an Advance the previous day (t-stat.) | 49.12% (0.43) | 45.09% *** (2.47) | 56.19% *** (2.25) | 43.19% *** (5.56) | 54.49% (1.12) | 42.51% *** (3.99) |
| After a decline the previous day (t-stat.) | 61.71% *** (3.10) | 43.63% *** (3.29) | 59.93% *** (4.61) | 42.45% *** (6.27) | 63.64% *** (4.15) | 46.28% ** (1.73) |
| Mean Percentage Change | ||||||
| After an Advance the previous day (t-stat.) | 1.39 (1.56) | −0.16 (−0.57) | 1.94 *** (4.32) | −0.25 * (−1.90) | 2.17 *** (2.74) | −0.48 ** (−2.45) |
| After a decline the previous day (t-stat.) | 1.47 *** (2.94) | 00.19 (0.61) | 1.30 *** (5.24) | −0.11 (0.83) | 1.52 *** (3.80) | 0.01 (0.07) |
| Percentage of Times the Index Advanced | TYVIX | |||||
| On Monday | On Other Days | |||||
| After an Advance the previous day (t-stat.) | 62.96% *** (2.69) | 43.40% ** (2.25) | ||||
| After a decline the previous day (t-stat.) | 74.11% *** (6.77) | 40.18% *** (3.92) | ||||
| Mean Percentage Change | ||||||
| After an Advance the previous day (t-stat.) | 1.67 *** (3.27) | −0.38 ** (−2.03) | ||||
| After a decline the previous day (t-stat.) | 2.27 *** (7.48) | −0.57 *** (−3.21) | ||||
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday | |
|---|---|---|---|---|---|---|---|
| Mean | 6.011 *** | 6.009 *** | 6.010 *** | 6.015 *** | 6.031 *** | 6.034 *** | 6.024 *** |
| Med. | 6.010 | 6.010 | 6.010 | 6.010 | 6.030 | 6.030 | 6.020 |
| Max. | 6.250 | 6.210 | 6.250 | 6.360 | 6.340 | 6.290 | 6.260 |
| Min. | 5.770 | 5.880 | 5.870 | 5.890 | 5.780 | 5.870 | 5.840 |
| Stdev. | 0.043 | 0.042 | 0.044 | 0.050 | 0.049 | 0.046 | 0.049 |
| Skew. | −0.039 | 0.309 | 0.841 | 1.556 | 0.545 | 0.247 | 0.352 |
| Kurt. | 5.289 | 3.783 | 6.434 | 9.794 | 7.947 | 4.292 | 4.628 |
| #Obs | 598 | 599 | 599 | 599 | 599 | 596 | 598 |
| MON | TUE | WED | THU | FRI | ||||
|---|---|---|---|---|---|---|---|---|
| VXAZN | 1.93 a | 0.34 | 0.21 | 0.45 | −2.81 a | 26.26 a | 9.85 a | 22.23 a |
| (5.58) | (1.03) | (0.63) | (1.36) | (−8.40) | ||||
| VXAPL | −1.39 a | −0.24 | −1.27 a | 0.17 | 0.07 | 8.27 a | 2.81 a | 4.11 a |
| (4.10) | (−0.75) | (−3.92) | (0.52) | (0.21) | ||||
| VXGSCLS | 1.29 a | −0.12 | −0.04 | −0.06 | −0.988 a | 7.36 a | 5.38 a | 2.44 c |
| (4.24) | (−0.41) | (−0.13) | (−0.20) | (−3.35) | ||||
| VXGOG | 2.36 a | 0.12 | −0.02 | 0.26 | −2.57 a | 26.48 a | 10.22 a | 16.29 a |
| (6.81) | (0.36) | (−0.05) | (0.79) | (−7.67) | ||||
| VXIBM | 1.55 a | 0.27 | −0.81 b | 0.01 | −0.90 a | 7.97 a | 4.94 a | 2.90 b |
| (4.34) | (0.78) | (−2.37) | (0.03) | (−2.61) | ||||
| VXD | −0.14 | 0.73 c | 0.77 b | −1.05 a | −0.34 | 3.86 a | 0.37 | 5.09 a |
| (−0,34) | (1.87) | (1.98) | (−2.67) | (−0.88) | ||||
| VXN | 1.50 a | −0.13 | −0.36 c | −0.14 | −0.77 a | 19.39 a | 8.21 a | 2.47 c |
| (7.55) | (−0.67) | (−1.89) | (−0.71) | (−4.01) | ||||
| RVX | 1.75 a | 0.08 | −0.23 | −0.38 | −1.11 a | 12.55 a | 6.79 a | 3.00 b |
| (5.78) | (0.29) | (−0.77) | (−1.30) | (−3.79) | ||||
| TYVIX | 2.03 a (7.83) | 0.47 c (1.89) | −0.69 a (−2.77) | −0.20 (−0.80) | −1.49 a (−5.91) | 27.03 a | 9.73 a | 10.86 a |
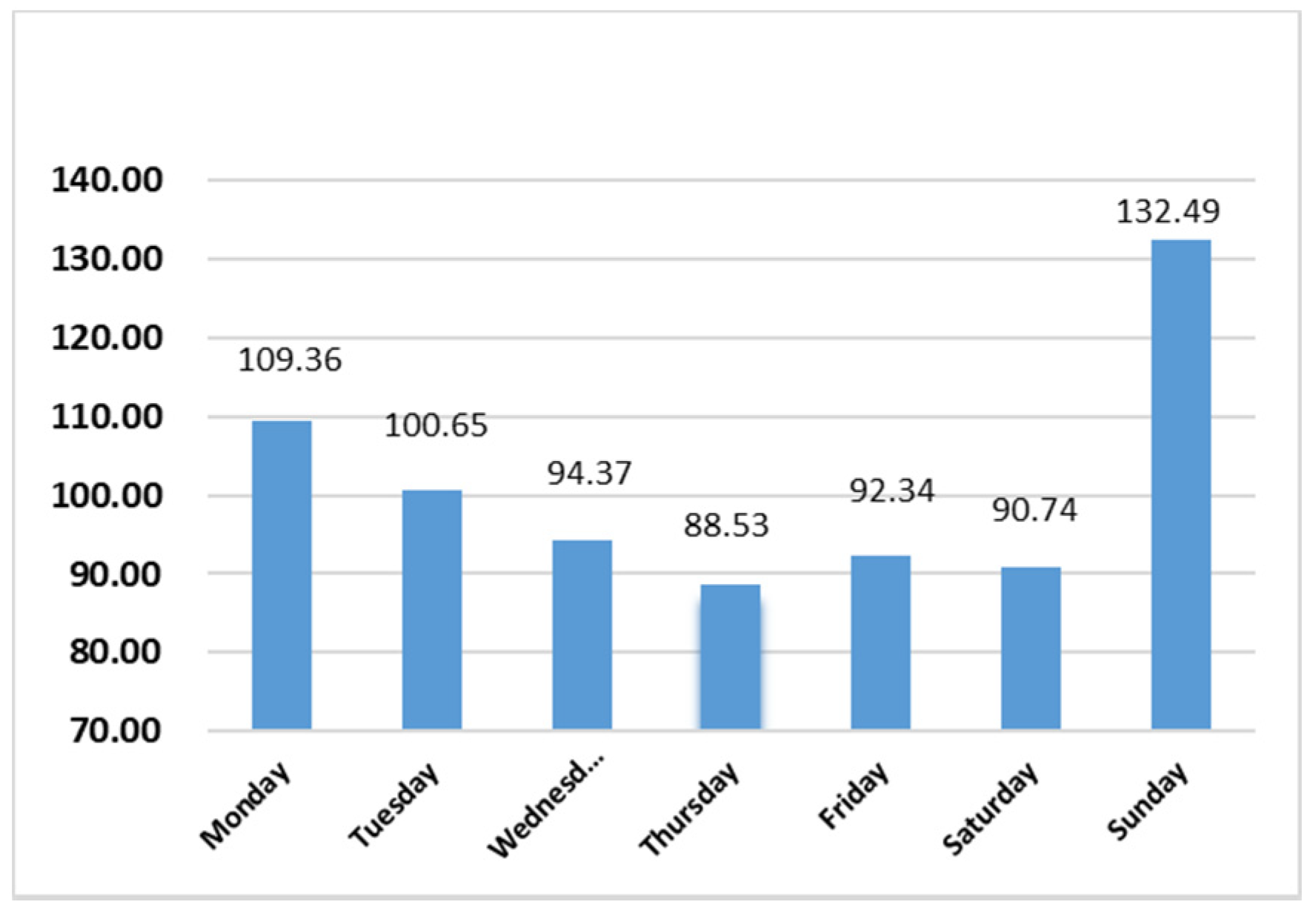
| Panel A. Full Sample. | |||||||
|---|---|---|---|---|---|---|---|
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday | |
| Mean | 109.36 *** | 100.65 *** | 94.37 *** | 88.53 *** | 92.34 *** | 90.74 *** | 132.49 *** |
| Med. | 92.74 | 83.69 | 76.74 | 71.27 | 75.88 | 74.25 | 118.11 |
| Max. | 623.45 | 719.07 | 690.81 | 515.61 | 560.12 | 586.55 | 496.43 |
| Min. | 5.80 | 5.93 | 3.38 | 4.75 | 3.32 | 4.15 | 4.05 |
| Stdev. | 67.65 | 69.96 | 67.18 | 62.39 | 62.16 | 64.78 | 69.97 |
| Skew. | 1.81 | 2.32 | 2.22 | 1.96 | 1.78 | 2.01 | 1.29 |
| Kurt. | 8.85 | 13.44 | 11.79 | 8.65 | 7.95 | 9.94 | 5.23 |
| #Obs | 1834 | 1835 | 1835 | 1835 | 1835 | 1834 | 1834 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Idilbi-Bayaa, Y.; Qadan, M. Tell Me Why I Do Not Like Mondays. Mathematics 2022, 10, 1850. https://doi.org/10.3390/math10111850
Idilbi-Bayaa Y, Qadan M. Tell Me Why I Do Not Like Mondays. Mathematics. 2022; 10(11):1850. https://doi.org/10.3390/math10111850
Chicago/Turabian StyleIdilbi-Bayaa, Yasmeen, and Mahmoud Qadan. 2022. "Tell Me Why I Do Not Like Mondays" Mathematics 10, no. 11: 1850. https://doi.org/10.3390/math10111850
APA StyleIdilbi-Bayaa, Y., & Qadan, M. (2022). Tell Me Why I Do Not Like Mondays. Mathematics, 10(11), 1850. https://doi.org/10.3390/math10111850





