A Positivity-Preserving Improved Nonstandard Finite Difference Method to Solve the Black-Scholes Equation
Abstract
:1. Introduction
- K is the exercise price;
- T is the maturity;
- is the interest rate;
- is the reference volatility.
2. Finite Difference Approaches
2.1. The -Method
2.2. The Mixed Method
2.3. The Richardson Method
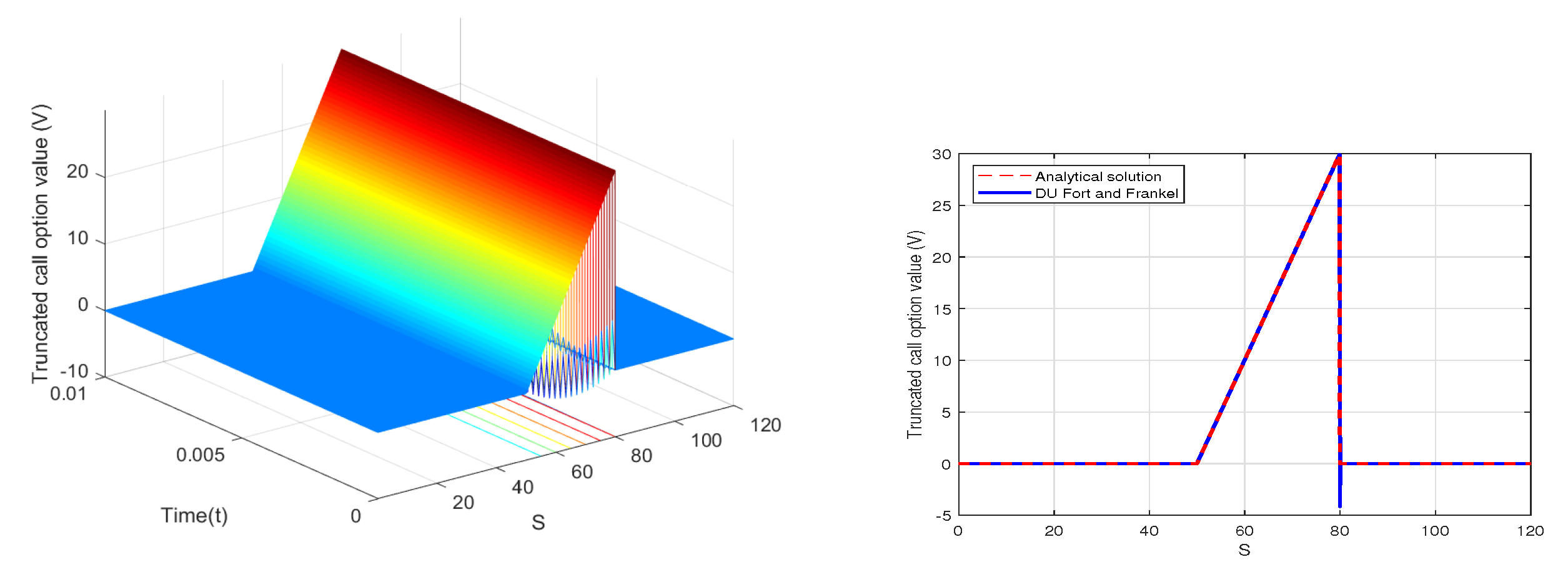
2.4. The Du Fort and Frankel Method
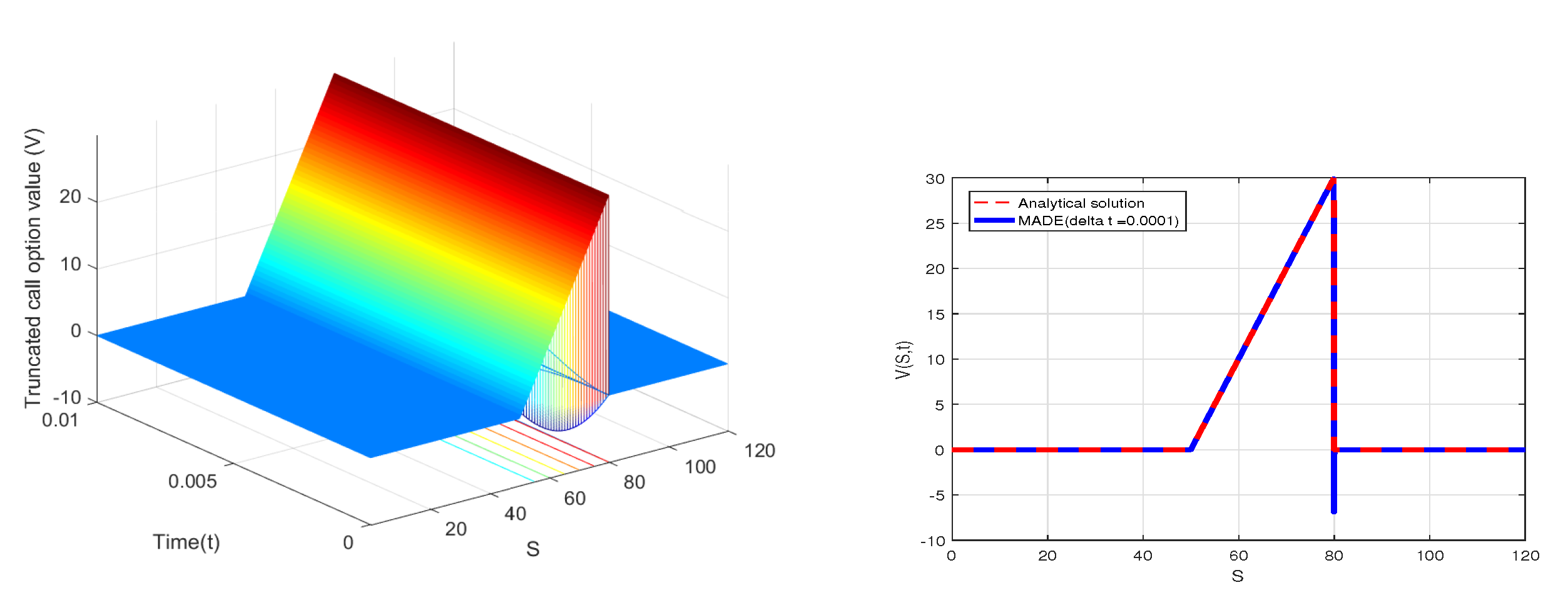
2.5. The MADE Method
3. Nonstandard Finite-Difference Strategy
- The function in the denominator of the approximation of the discrete derivative must be expressed in terms of a function of the step size, provided that (16) holds. This rule allows the introduction of a complex analytic function of h in the denominator with the condition thatExamples of functions that satisfy this condition are [40]:
4. Scheme Construction
5. Analysis of the New Scheme
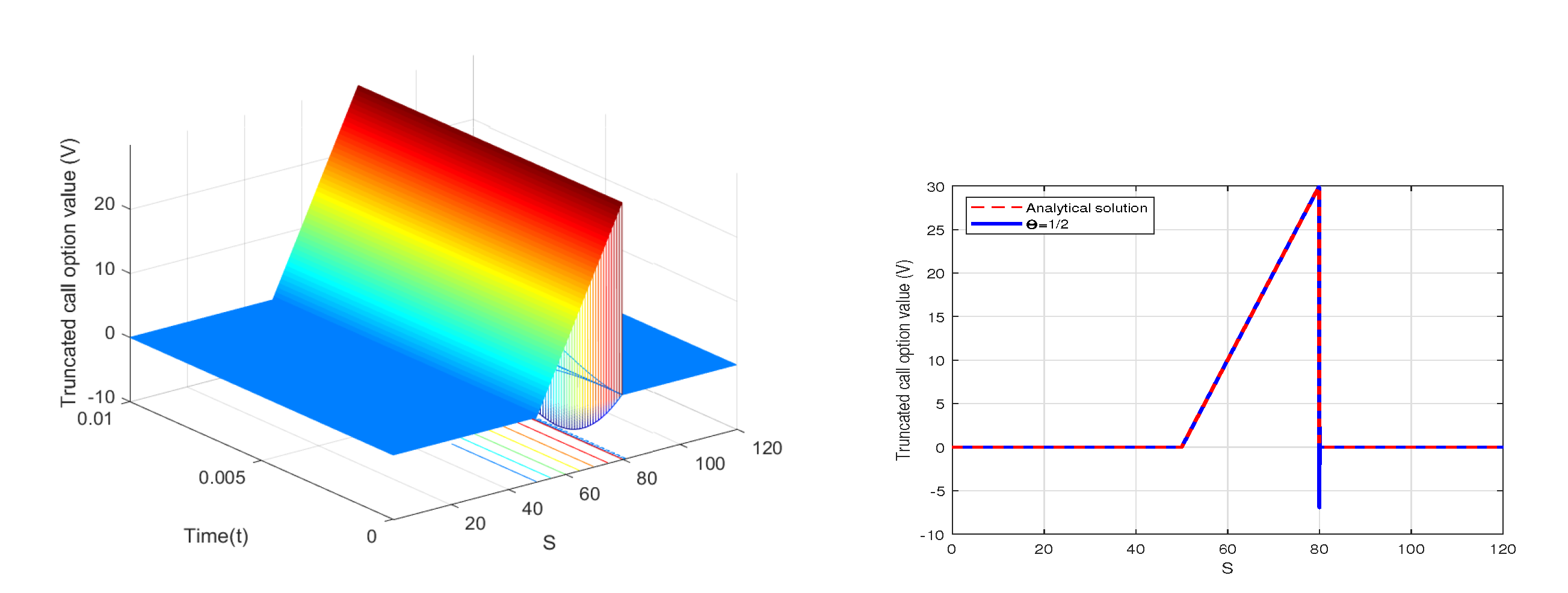
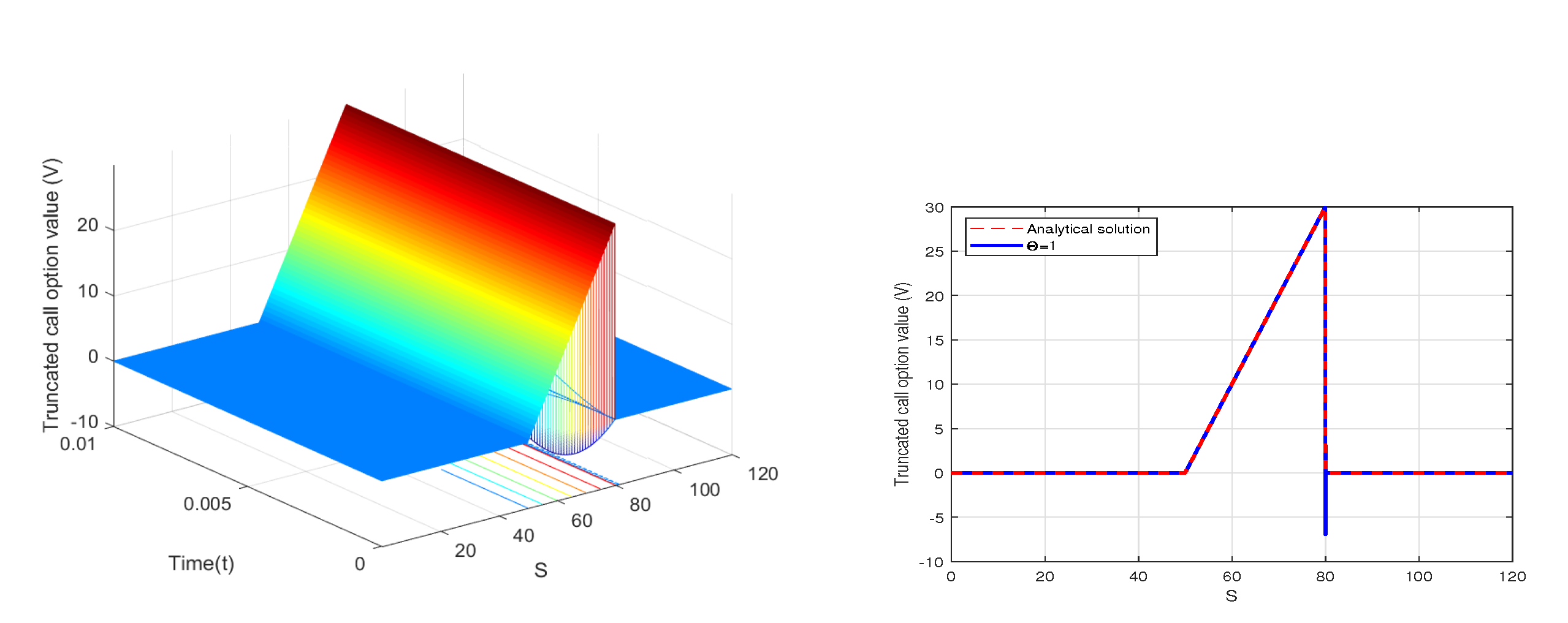
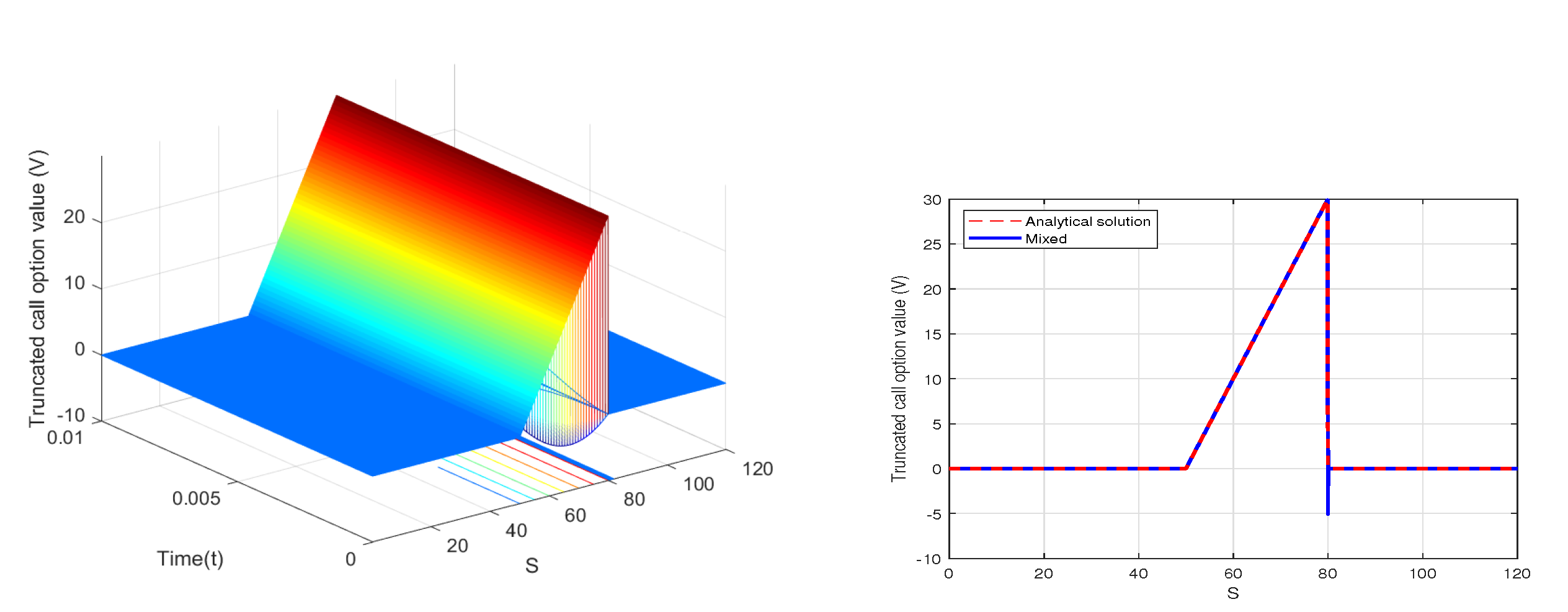
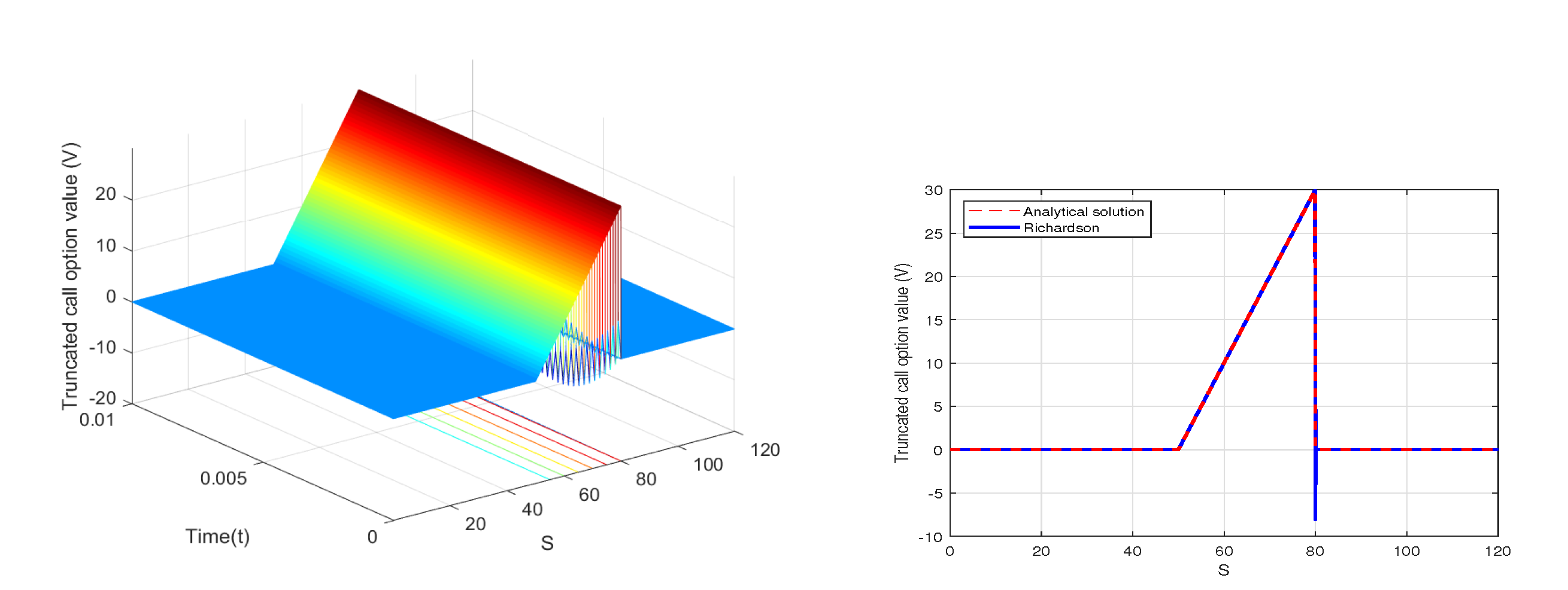
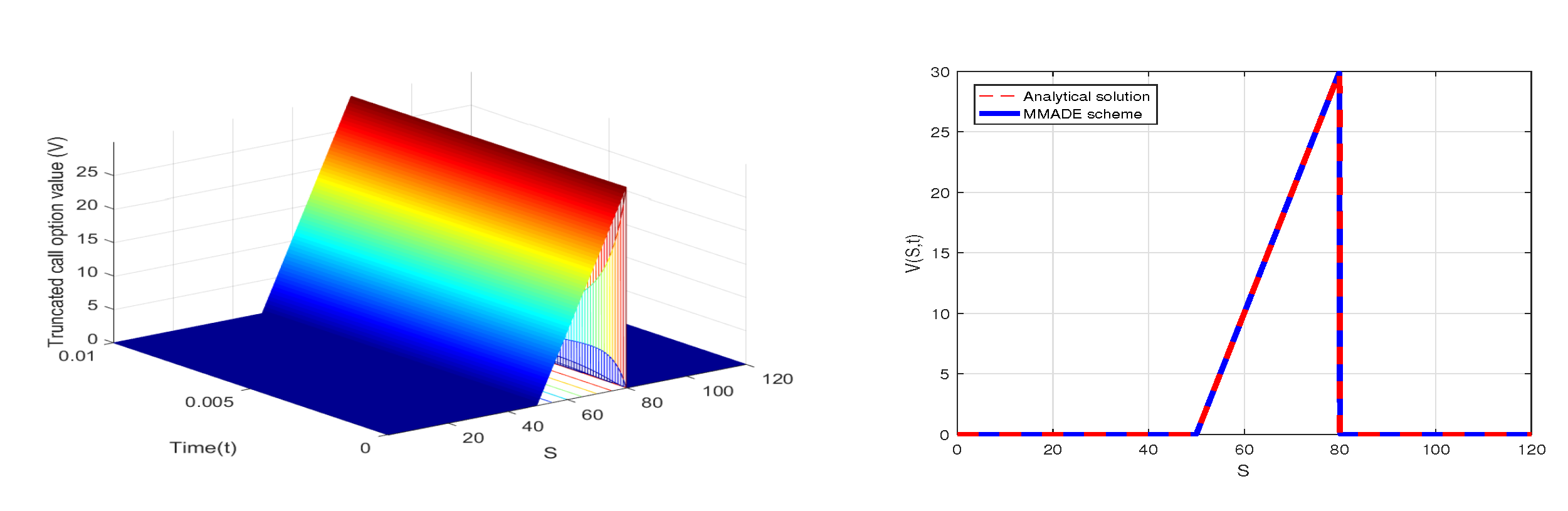
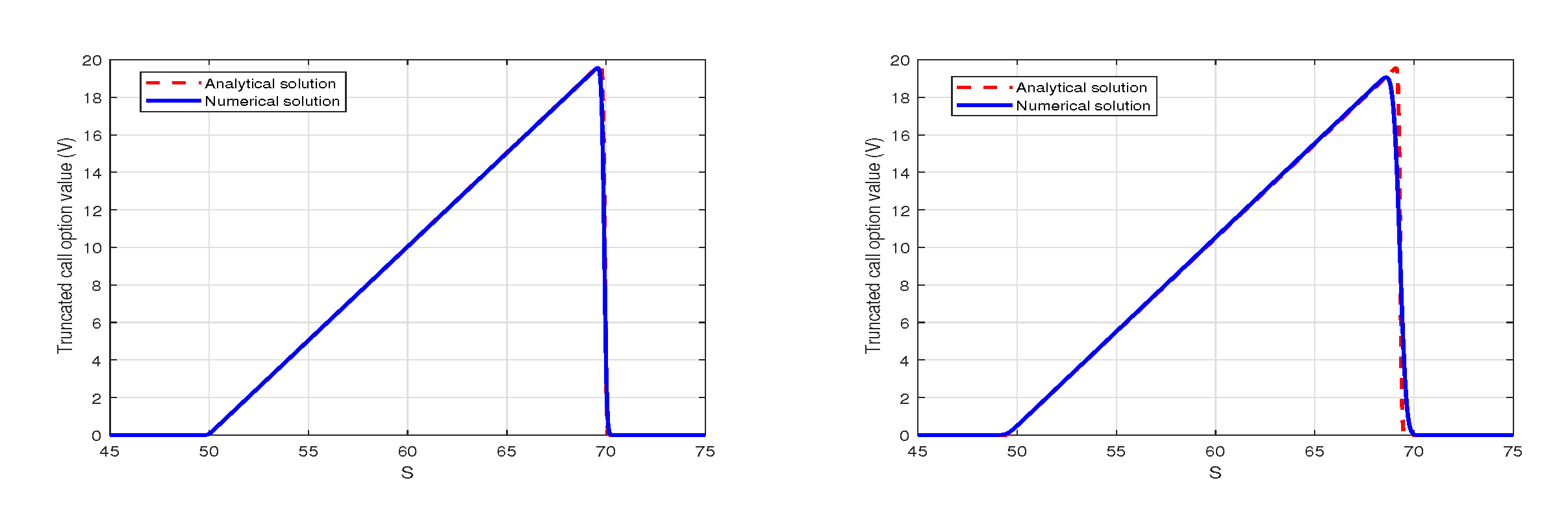
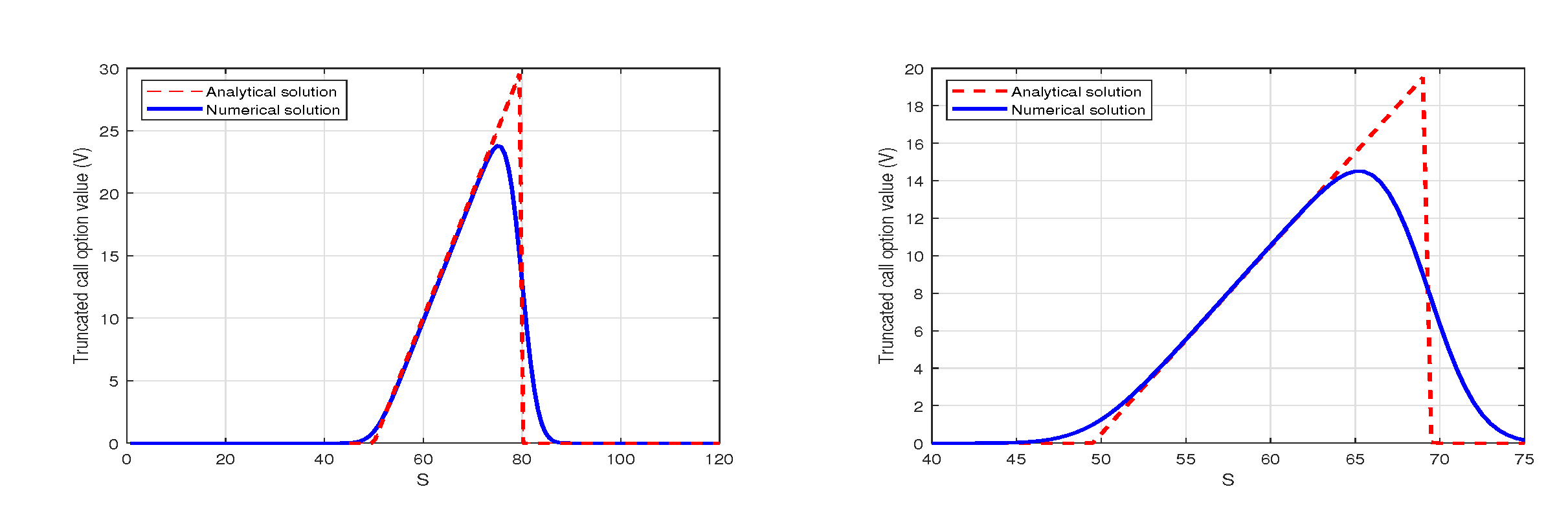
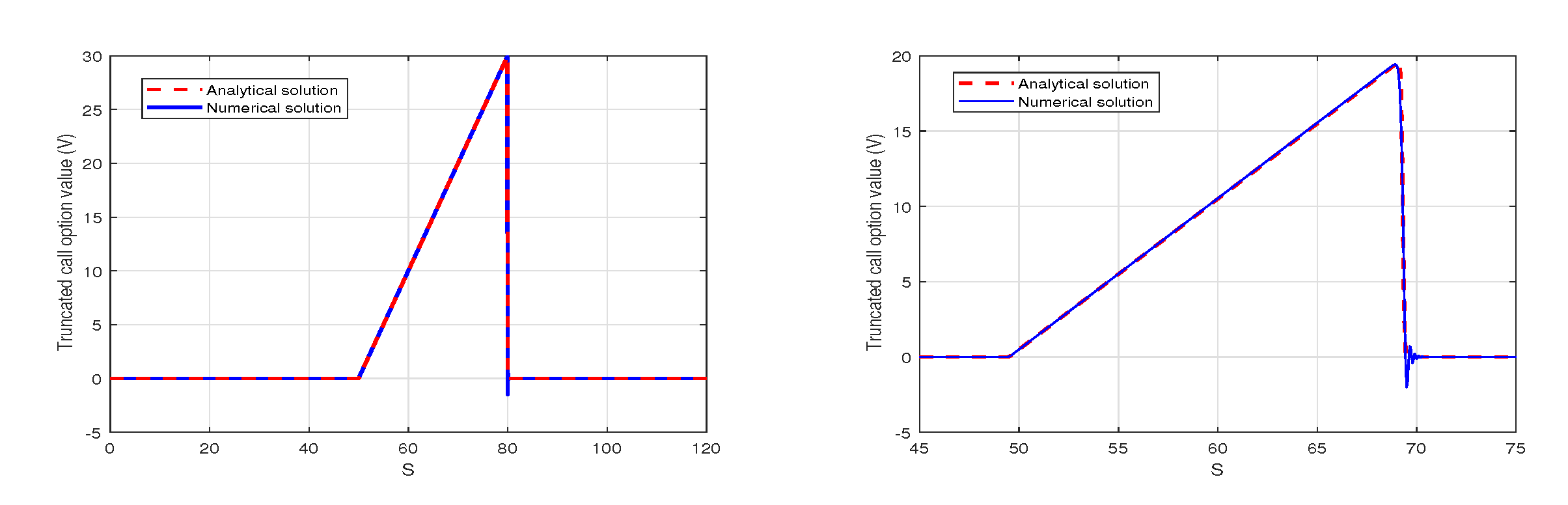
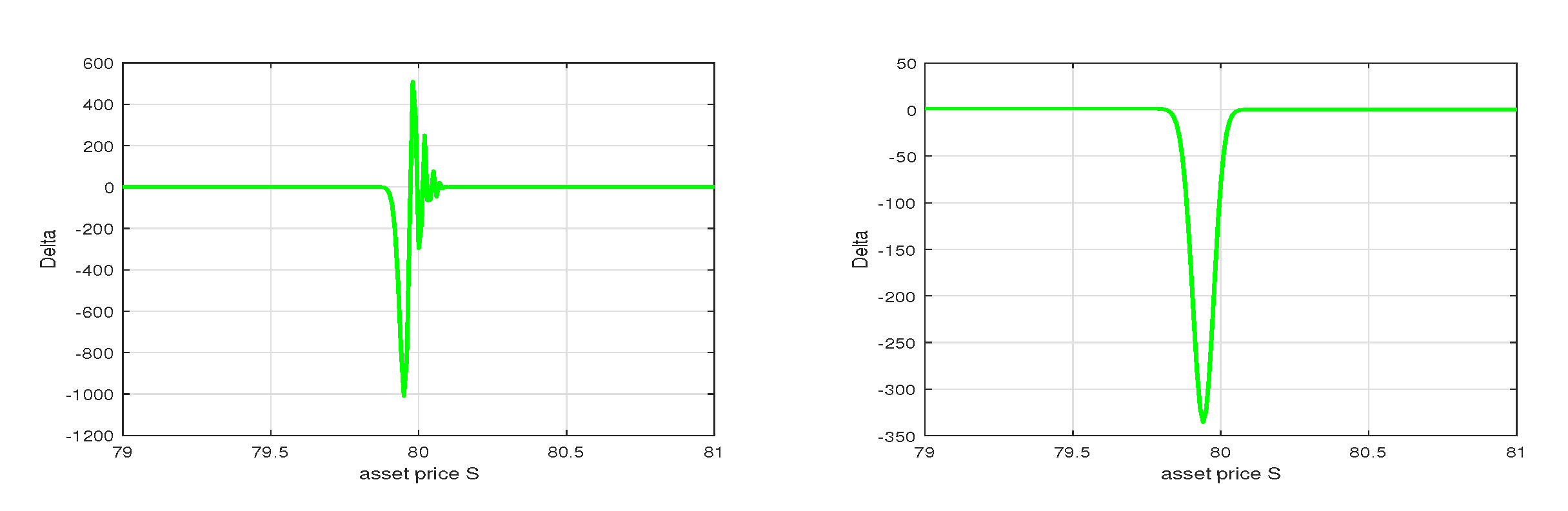
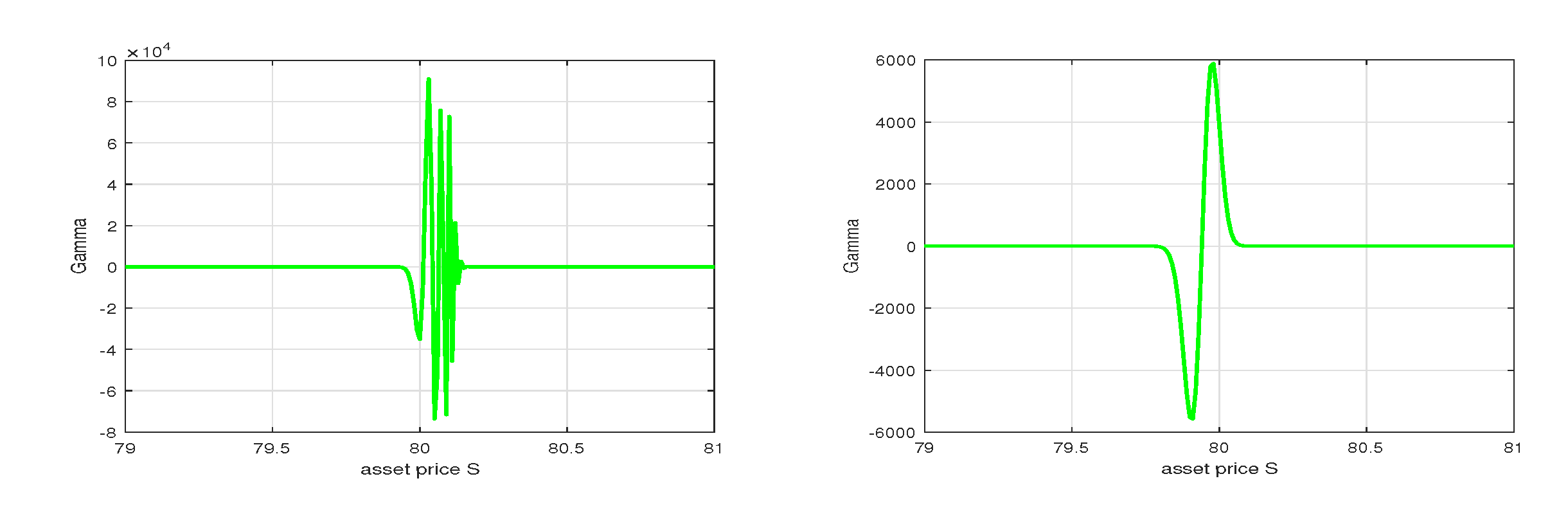
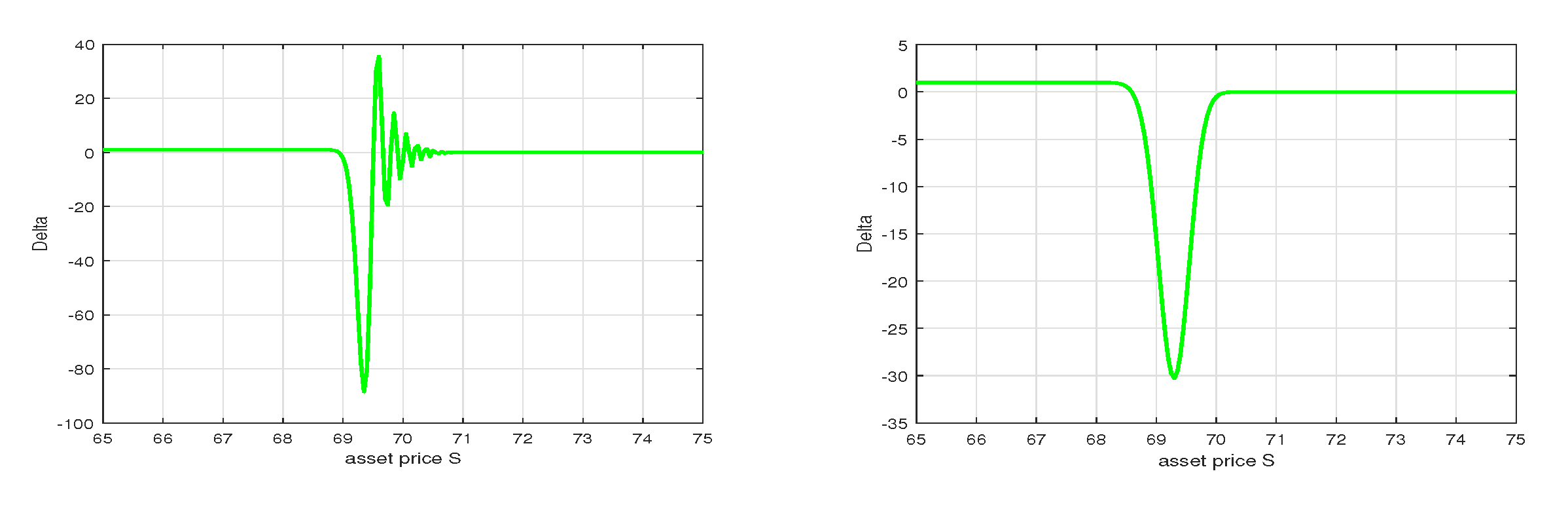
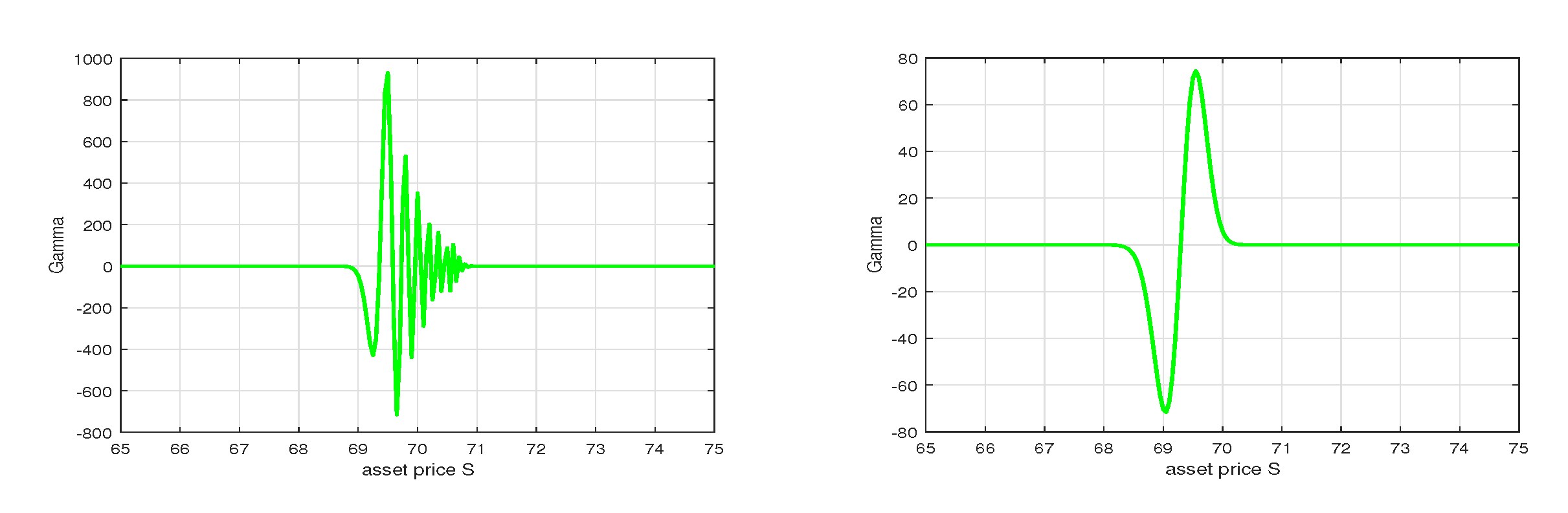
6. Numerical Results with MMADE
7. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–659. [Google Scholar] [CrossRef] [Green Version]
- Widdicks, M.; Duck, P.W.; Andricopoulos, A.D.; Newton, D.P. The Black–Scholes equation revisited: Asymptotic expansions and singular perturbationss. Math Financ. 2005, 15, 373–391. [Google Scholar] [CrossRef]
- Xi, L.; Cen, Z.; Chen, J. A Second-order Finite Difference Scheme for a Type of Black–Scholes Equation. Int. J. Nonlinear Sci. 2008, 6, 238–245. [Google Scholar]
- Milev, M.; Tagliani, A. Numerical valuation of discrete double barrier options. J. Comput. Appl. Math. 2010, 233, 2468–2480. [Google Scholar] [CrossRef] [Green Version]
- Milev, M.; Tagliani, A. Nonstandard finite difference schemes with application to finance: Option pricing. Serdica Math. J. 2010, 36, 75–88. [Google Scholar]
- Pealat, G.; Duffy, D.J. The Alternating Direction Explicit (ADE) Method for One-Factor Problems. Wilmott 2011, 2011, 54–60. [Google Scholar] [CrossRef]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. A modified explicit method for the Black–Scholes equation with positivity preserving property. J. Math. Comput. Sci. 2015, 15, 299–305. [Google Scholar] [CrossRef]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. An efficient nonstandard numerical method with positivity preserving property. J. Math. Model. 2016, 4, 161–169. [Google Scholar]
- Jeong, D.; Yoo, M.; Kim, J. Finite Difference Method for the Black–Scholes Equation Without Boundary Conditions. Comput. Econ. 2018, 51, 961–972. [Google Scholar] [CrossRef]
- Anwar, M.N.; Andallah, L.S. A Study on Numerical Solution of Black–Scholes Model. Math Financ. 2018, 8, 372–381. [Google Scholar] [CrossRef] [Green Version]
- Aliev Fikret, A.; Aliev, N.A.; Mutallimov, M.M.; Namazov, A.A. Algorithm for Solving the Identification Problem for Determining the Fractional-Order Derivative of an Oscillatory System. Appl. Comput. Math. 2020, 19, 415–422. [Google Scholar] [CrossRef]
- Ashyralyev, A.; Agirseven, D.; Agarwal, R.P. Stability Estimates for Delay Parabolic Differential and Difference Equations. Appl. Comput. Math. 2020, 19, 175–204. [Google Scholar]
- Assari, P.; Dehghan, M. The Numerical Solution of Nonlinear Weakly Singular Fredholm Integral Equations Based on the Dual-Chebyshev Wavelets. Appl. Comput. Math. 2020, 19, 3–19. [Google Scholar]
- Iskenderov, N.S.; Allahverdiyeva, S.I. An Inverse Boundary Value Problem for the Boussinesq-Love Equation with Nonlocal Integral Condition. TWMS J. Pure Appl. Math. 2020, 11, 226–237. [Google Scholar]
- Mahmudov, N.I.; Huseynov, I.T.; Aliev, N.A.; Aliev, F.A. Analytical Approach to a Class of Bagley-Torvik Equations. TWMS J. Pure Appl. Math. 2020, 11, 238–258. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri, A. The New Classes of High Order Implicit Six-Step P-Stable Multiderivative Methods for The Numerical Solution of Schrodinger Equation. Appl. Comput. Math. 2020, 19, 59–86. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri, A.; Mohammadnia, Z.; Sedighi, H.M. Qualitatively Stable Nonstandard Finite Difference Scheme for Numerical Solution of the Nonlinear Black–Scholes. J. Math. 2021, 2021, 6679484. [Google Scholar] [CrossRef]
- Moshtaghi, N.; Saadatmandi, A. Numerical Solution for Diffusion Equations with Distributed-Order in Time Based on Sinc-Legendre Collocation Method. Appl. Comput. Math. 2020, 19, 317–355. [Google Scholar]
- Noeiaghdam, S.; Sidorov, D.; Sizikov, V.; Sidorov, N. Control of Accuracy of Taylor-Collocation Method to Solve The Weakly Regular Volterra Integral Equations of The First Kind by Using the Cestac Method. Appl. Comput. Math. 2020, 19, 87–105. [Google Scholar] [CrossRef]
- Odibat, Z. Fractional Power Series Solutions of Fractional Differential Equations by Using Generalized Taylor Series. Appl. Comput. Math. 2020, 19, 47–58. [Google Scholar]
- Omarova, M.N. Parabolic Non-Singular Integral Operator and its Commutators on Parabolic Vanishing Generalized Orlicz-Morrey Spaces. TWMS J. Pure Appl. Math. 2020, 11, 213–225. [Google Scholar]
- Ozyapici, A.; Karanfiller, T. New Integral Operator for Solutions of Differential Equations. TWMS J. Pure Appl. Math. 2020, 11, 131–143. [Google Scholar]
- Qalandarov, A.; Khaldjigitov, A.A. Mathematical and Numerical Modeling of the Coupled Dynamic Thermoelastic Problems for Isotropic Bodies. TWMS J. Pure Appl. Math. 2020, 11, 119–126. [Google Scholar]
- Set, E.; Ocak Akdemir, A.; Ozata, F. Grüss Type Inequalities for Fractional Integral Operator Involving the Extended Generalized Mittag-Leffler Function. Appl. Comput. Math. 2020, 19, 402–414. [Google Scholar]
- Simos, T.E.; Tsitouras, C. 6th Order Runge-Kutta Pairs for Scalar Autonomous IVP. Appl. Comput. Math. 2020, 19, 392–401. [Google Scholar]
- Sweilam, N.H.; Nagy, A.M.; El-Sayed, A.A. Sinc-Chebyshev Collocation Method for Time-Fractional Order Telegraph Equation. Appl. Comput. Math. 2020, 19, 162–174. [Google Scholar]
- Tunc, T.; Sarikaya, M.Z.; Yaldiz, H. Fractional Hermite Hadamards Type Inequality for the Co-Ordinated Convex Functions. TWMS J. Pure Appl. Math. 2020, 11, 3–29. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. Positivity Preserving Schemes for Black–Scholes Equation. RJFA 2015, 6, 1697–2222. [Google Scholar]
- Milev, M.; Tagliani, A. Laplace Transform and finite difference methods for the Black–Scholes equation. Appl. Math. Comput. 2013, 220, 649–658. [Google Scholar] [CrossRef]
- Cohen, A.M. Numerical Methods for Laplace Transform Inversion; Springer: New York, NY, USA, 2007. [Google Scholar]
- Bouwer, A. The Du Fort and Frankel Finite Difference Scheme Applied to and Adapted for a Class of Finance Problems. Master’s Thesis, Department of Mathematics and Applied Mathematics, The University of Pretoria, Pretoria, Cape Town, South Africa, 2008. [Google Scholar]
- Du Fort, E.C.; Frankel, S.P. Stability conditions in the numerical treatment of parabolic differential equations. Math. Tables Other Aids Comput. 1953, 7, 135–152. [Google Scholar] [CrossRef]
- Mehdizadeh Khalsaraeia, M.; Shokri, A.; Ramos, H.; Heydari, S. A positive and elementary stable nonstandard explicit scheme for a mathematical model of the influenza disease. Math Comput Simul. 2021, 182, 397–410. [Google Scholar] [CrossRef]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. Positivity-preserving nonstandard finite difference schemes for simulation of advection-diffusion reaction equations. Comput. Methods Differ. Equ. 2014, 2, 256–267. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. Positivity preserving schemes with application to finance: Option pricing. Appl. Math. Eng. 2015, 3, 212–220. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. A family of positivity preserving schemes for numerical solution of Black–Scholes equation. Int. J. Financ. Eng. 2016, 4, 1650025. [Google Scholar] [CrossRef]
- Mehdizadeh Khalsaraei, M.; Shokri Jahandizi, R. Efficient Explicit Nonstandard Finite Difference Scheme with Positivity-Preserving Property. J. Sci. 2017, 30, 259–268. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Usmani, N. A family of positive nonstandard numerical methods with application to Black–Scholes equation. Sahand Commun. Math. Anal. 2017, 5, 31–40. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing, Bell J. Econo. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef] [Green Version]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar] [CrossRef]
- Mickens, R.E.; Jordan, P.M. A positivity-preserving nonstandard finite difference scheme for the Damped Wave Equation. Numer. Methods Partial Differ. Equ. 2004, 20, 639–649. [Google Scholar] [CrossRef]
- Mickens, R.E.; Jordan, P.M. A new positivity-preserving nonstandard finite difference scheme for the DWE. Numer. Methods Partial Differ. Equ. 2005, 21, 976–985. [Google Scholar] [CrossRef]
- Mickens, R.E. Advances in the Applications of Nonstandard Finite Difference Schemes; World Scientific Publishing Company: Singapore, 2005. [Google Scholar] [CrossRef]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1985. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehdizadeh Khalsaraei, M.; Shokri, A.; Ramos, H.; Mohammadnia, Z.; Khakzad, P. A Positivity-Preserving Improved Nonstandard Finite Difference Method to Solve the Black-Scholes Equation. Mathematics 2022, 10, 1846. https://doi.org/10.3390/math10111846
Mehdizadeh Khalsaraei M, Shokri A, Ramos H, Mohammadnia Z, Khakzad P. A Positivity-Preserving Improved Nonstandard Finite Difference Method to Solve the Black-Scholes Equation. Mathematics. 2022; 10(11):1846. https://doi.org/10.3390/math10111846
Chicago/Turabian StyleMehdizadeh Khalsaraei, Mohammad, Ali Shokri, Higinio Ramos, Zahra Mohammadnia, and Pari Khakzad. 2022. "A Positivity-Preserving Improved Nonstandard Finite Difference Method to Solve the Black-Scholes Equation" Mathematics 10, no. 11: 1846. https://doi.org/10.3390/math10111846
APA StyleMehdizadeh Khalsaraei, M., Shokri, A., Ramos, H., Mohammadnia, Z., & Khakzad, P. (2022). A Positivity-Preserving Improved Nonstandard Finite Difference Method to Solve the Black-Scholes Equation. Mathematics, 10(11), 1846. https://doi.org/10.3390/math10111846







