Topological Data Analysis with Spherical Fuzzy Soft AHP-TOPSIS for Environmental Mitigation System
Abstract
:1. Introduction
- The notion of a spherical fuzzy soft set (SFSS) is a combination of an SFS and a SS. An SFSS is a new approach for computational intelligence, data analysis, and fuzzy modeling.
- We define some new operations on SFSSs for the construction of SFSS-topology. The idea of spherical fuzzy soft set topology (SFSS-topology) is defined with the help of null SFSS, absolute SFSS, SFSS-extended union, and SFSS-restricted intersection.
- Novel conceptualizations of SFSS-topology are explored, such as, SFSS-open set, SFSS-closed set, SFSS-interior, SFSS-closure, SFSS-base and SFSS-subbase. These notions are illustrated with some numerical examples.
- The concepts of spherical fuzzy soft set separation axioms are proposed and related results are explored.
- We developed an extended choice value method (CVM) and the AHP-TOPSIS for SSFSs, respectively.
- The suggested methods are efficient tools for MCDGDM of an environmental mitigation system. An application is designed to identify the ability of the suggested approach to focus the crises addressed by the environmental mitigation system, as well as to signify the validity of numerous major findings through case studies. It is presented in order to justify our technique and demonstrate its applicability and effectiveness.
- The efficiency of suggested methods is demonstrated by a comparative analysis and sensitivity analysis.
2. Preliminaries
- If then precedes i.e., ;
- If then succeeds i.e., ;
- If then .
- If and coincide and exceeds then ;
- If both and coincide then
- Inclusion: If ;
- Equality: If and then ;
- Union: ;
- Intersection: ;
- Complement: .
- Inclusion: If .
- Intersection: .
| ⋯ | ||||
| ⋯ | ||||
| ⋯ | ||||
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| ⋯ |
- (i)
- , and
- (ii)
- is SFSS-subset of for all .
3. Spherical Fuzzy Soft Set Topology
- (i)
- ;
- (ii)
- then ;
- (iii)
- If , then .
- (1)
- SFSS interior:The interior of is the SFSS extended union of all SFSS-open subsets of . Note that is the largest SFSS-open subset of .
- (2)
- SFSS closure:The closure of is the SFSS restricted intersection of all SFSS-closed supersets of . Note that is the smallest SFSS-closed superset of .
- (3)
- SFSS frontier:The boundary or frontier of is defined as
- (4)
- SFSS exterior:The exterior of is defined as
- and .
- .
- A is an SFSS open set ⇔.
- .
- This is obvious by Definition 24.
- This is obvious by Definition 24.
- If is an SFSS open set in X, then is itself an SFSS open set in X which contains . Therefore, itself is the largest SFSS open set contained in and . Conversely, suppose that . Since is always SFSS open, must be SFSS open.
- Let . Then, from (3) and then, .
- Consider as is an SFSS open subset of , so, by the definition, we have that .
- It is clear that and . Thus, and . Therefore, we have that , using 5.
- It is known that and by 5. Therefore, that . In addition, from and , we have . These imply that
- and ;
- ;
- A is an SFSS closed set ⇔;
- ;
- ;
- ;
- .
- (1)
- , and
- (2)
- .
4. SFSS-Separation Axioms
5. MCDGM by Using SFSS Information
| Algorithm 1 Choice value method. |
|
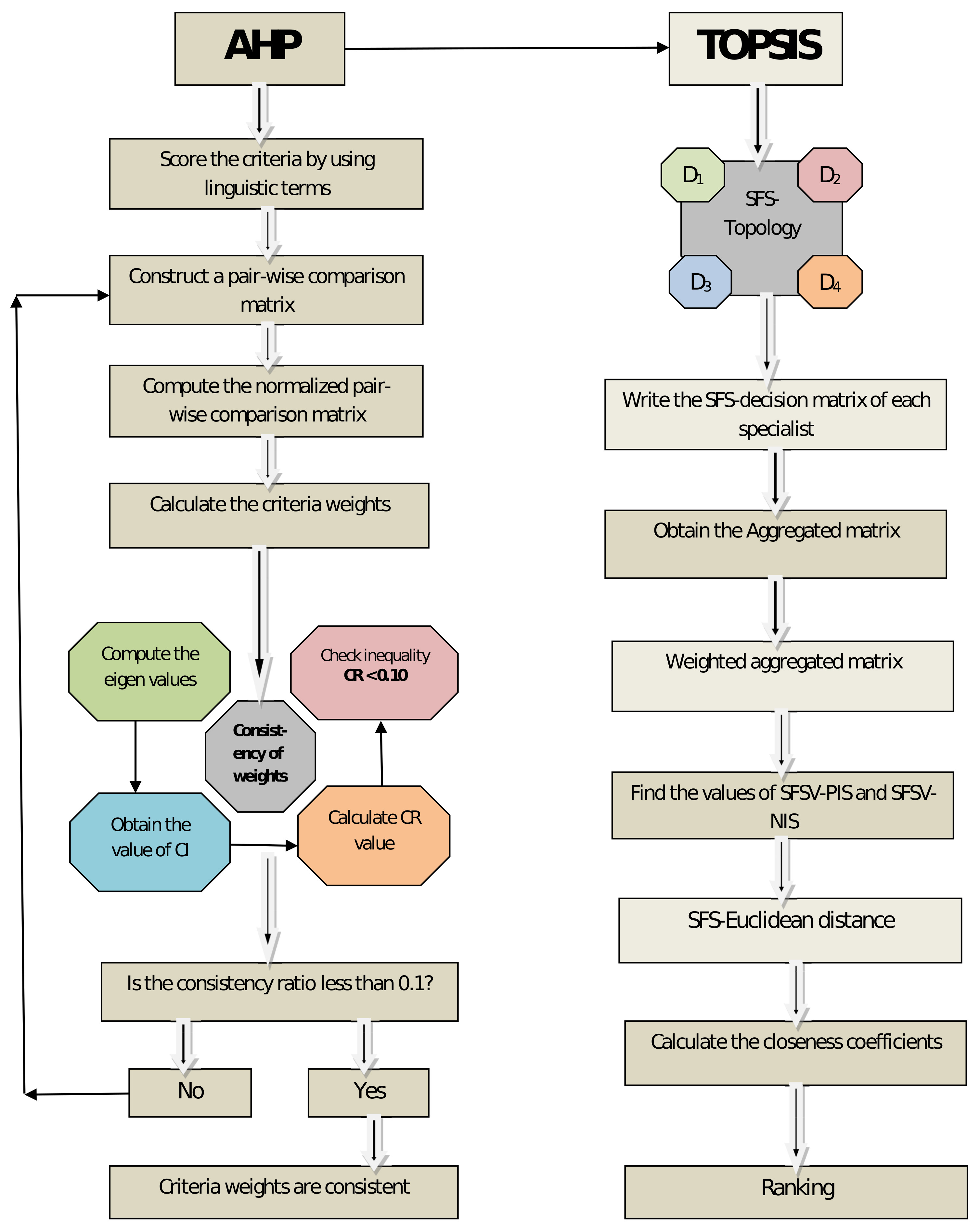
6. AHP-TOPSIS Approach for Environmental Mitigation with SFS-Topology
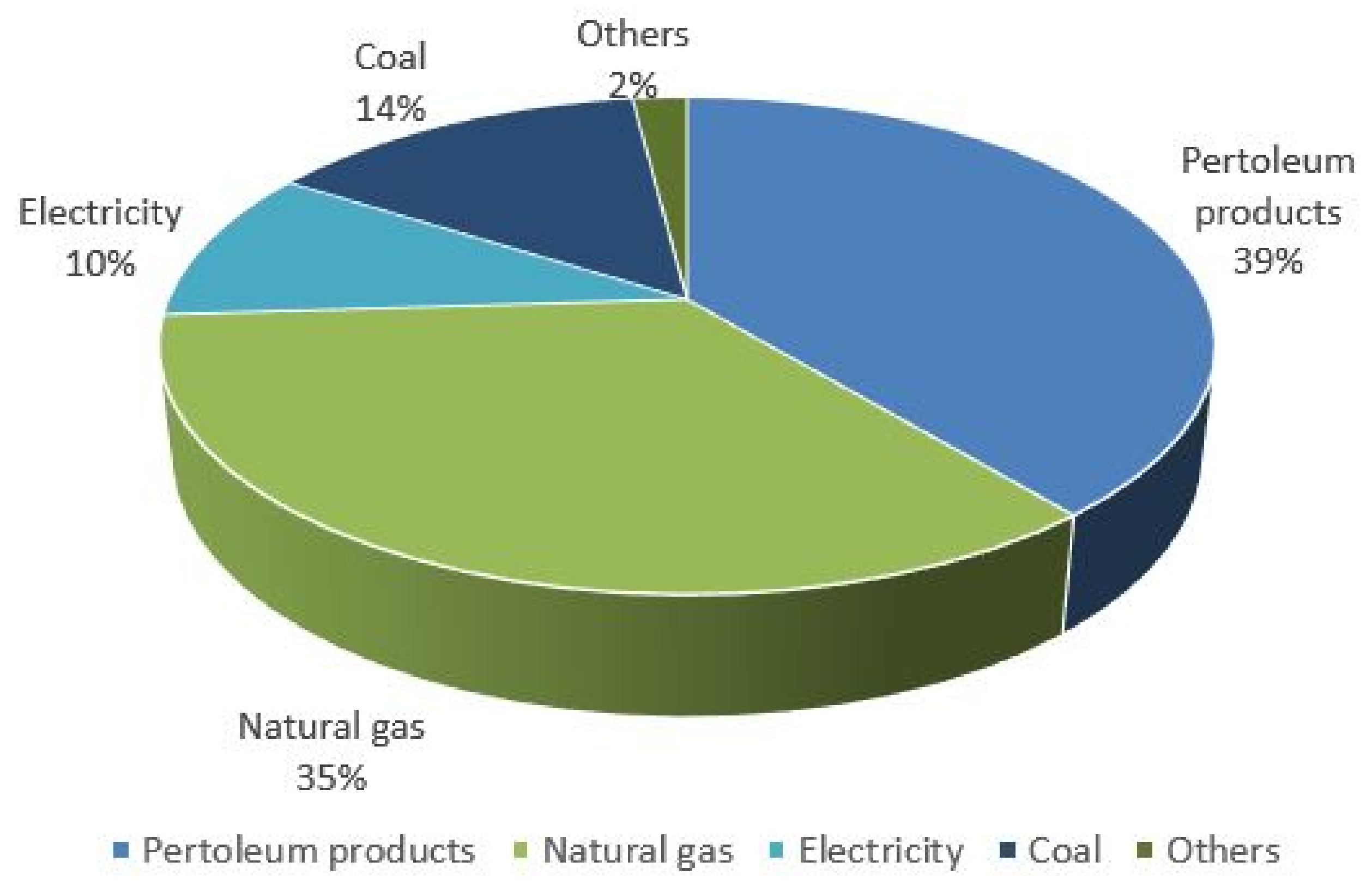
- Case studyEnvironmental degradation in Pakistan comprises air quality, water contamination, traffic noise, global warming, chemical abuse, desertification, natural catastrophes, dunes, and storms. A worldwide environmental-performance index (EPI) has previously labelled Pakistan’s air quality as deplorable. Global warming poses a serious threat to the lives of the citizens in the state. Emissions of greenhouse gases, increasing urbanization, and deforestation all play a role in the current state of affairs. Climate change is running amok in low-income countries such as Pakistan. It is not alone in being helpless, as advanced economies—most notably China and the United States—postpone lowering emissions. Global warming will have a significant impact on Pakistan, as well as the Maldives and many other island nations. In contrast to many other countries that have addressed the issue of global emissions at the UN, Pakistan is doing little to safeguard its future. Regular agricultural cycles have helped Pakistan’s economy weather several crises. However, if the IPCC Article is accurate, the country will be underwater by 2050. Already, Pakistan is struggling with a slew of environmental challenges. Many lives have been lost due to weather extremes, which also have a major impact on crop cycles and harvests. Floods decimated Pakistan’s two main cities this year: Karachi and Islamabad. Due to landslides, Pakistan’s commercial lifeline with China, the 806-kilometer Karakoram Highway, was shut down many times for multiple days. There was considerable deforestation in the northern part of Kohistan and the southern part of Jaglot, which led to the deadly landslides. The logging mafias are swiftly clearing old-growth forests north of Shimshal and east of the Skardu Valley, virtually insuring future environmental catastrophes. The state government appears utterly unconcerned about the looming crisis. Not much effort has been put towards meeting its goal of producing 60% of its power from renewable sources by 2030. More than 60% of the country’s electricity is generated from fossil fuels at the moment. Figure 3 shows the key environmental issues in Pakistan.
- Economic ramifications of environmental devastationAgriculture and fishing employ more than two-thirds of the workforce in Pakistan and produce over a quarter of the country’s total output. Increased use of finite natural resources is necessary for economic growth. Oddly, the very thing that is enabling this country to develop also constitutes a danger to its long-term safety and stability. A total of 70 percent of Pakistan’s population lives in rural areas and suffers from high poverty levels, according to the World Bank. To make money, these people rely on utilization and conservation, which they tend to misuse. This leads to greater ecological damage, which in turn, enhances impoverishment. This has culminated in a “vicious downward spiral of impoverishment and environmental degradation,” as stated by the World Bank. Pollution-related wellness factors influence both urban and rural dwellers, as per a 2013 World Bank evaluation. Air quality is the state’s most critical environmental challenge. Not only do these global impacts harm Pakistanis, but they often put the country’s business in jeopardy. In the article, growing industrialization, globalization, and vehicular use are anticipated to aggravate the situation.
- Water pollutionPakistan is rated as a water-stressed country by the World Economic forum. The Kabul River flows from Afghanistan into Pakistan; whereas the Indus, Jhelum, Chenab, Ravi, and Sutlej Rivers flow from India into Pakistan. Under the Indus Waters Treaty of 1960, water from the Ravi and Sutlej waters is redirected upstream to India for household consumption. The Indus (main stem), Jhelum, and Chenab rivers supply water to the agricultural lands of Punjab and Sindh, though not to the remainder of the region. Pakistan’s economy and the welfare of millions of Pakistanis are strongly effected by resource depletion. With the Law of the Sea Convention and canal diversion, Pakistan’s rivers have fewer diluting flows. The size of the economy, as well as a lack of water treatment, have caused a spike in water pollution. To provide water to people, dumped raw sewage is drained into rivers and the ocean, and unsanitary pipes are used. Water contamination makes it increasingly challenging to acquire safe drinking water and elevates the likelihood of developing an illness carried through raw sewage. There are many ailments that may be largely attributed to filthy water in Pakistan, because of this. Indeed, 45 percent of infant deaths and 60 percent of aquatic infections are caused by diarrhoea.
- Noise pollutionSome of Pakistan’s urbanized areas are plagued by a substantial amount of noise pollution. Noise pollution is generally triggered by traffic, including vehicles, automobiles, lorries, wheelers, and water tankers. An analysis found that Karachi’s main route seemed to have an average noise level of 90 dB and may reach as high as 110 dB. As a matter of fact, this surpasses the 70 dB limit set by the “International Organization for Standardization (ISO)”. According to the studies, the Environmental Quality Agency’s ambient noise standard in Pakistan is 85 decibels (dB). This threshold of noise pollution might have an influence on both auditory and quasi abilities. There seems to be a diversity of non-auditory clinical depression, notably insomnia, hearing and myocardial sickness, neuroendocrine sensitivity to loudness, and mental disorders. There are only a few, inconsistent noise regulations and policies in place. There is no culpability and the municipal and regional environmental conservation agencies are unable to intervene due to various statutory limitations and a loss of specific norms and regulations, which hinders them from doing so.
- Air pollutionWellbeing has been shown to be disproportionately affected by air pollution. For Pakistanis who habitually inhale dirty air, nanoparticle matter variations are a big concern. Respiratory difficulties have been associated to SPM in Pakistan’s largest cities, according to the research. Sustainable fuels such as liquefied petroleum gas (LPG) and improved transportation construction and sustainability can significantly minimize urban air pollution in Pakistan. The government can also adopt mitigation policies to reduce emissions. Pollution levels are increasing in Pakistan’s metro areas. Karachi’s urban air pollution is one of the worst in the world, having a devastating impact on both human development and health. Unsustainable energy use combined with the increased utilisation of automobiles, unauthorized corporate emissions, and debris and polymer combustion have all contributed to urban air pollution. According to the Sindh Environmental Conservation Department, urban air quality is approximately four times that proposed by the World Health Organization. These contaminants contribute to “respiratory disorders, impaired vision, vegetation degradation, and crop production”. Economic production leads to air pollution. An unavoidable byproduct and insufficient air pollution legislation have led to cities’ poor air quality. Abid Omar founded the Pakistan ambient air initiative in 2018, to evaluate the country’s major cities’ air quality. In Pakistan, the US State Department has established three elevated air-quality monitoring units. To overcome such environmental issues, various aspects should be taken under view and numerous efforts are required in order to obtain environmentally friendly conditions. Some are listed below:
- The establishment of a large tree plantation.
- Going paperless has the potential to significantly reduce the rate of deforestation on Earth.
- The number of diesel-powered automobiles that pollute the atmosphere should be reduced.
- An effective system for treating and managing sewage should be put in place.
- The practice of living a water-conserving lifestyle should be encouraged.
One of the most crucial objectives is to achieve an appropriate and effective level of environmental remediation and protection. Policymakers and decision makers must acknowledge that a sustainable plan for solving global crises must be a consistent effort comes from a long approach that combines all stakeholders. Inevitably, the project’s performance is determined by organizational commitment and dedication at every phase of the process, in addition to endorsement of adequate systems and guidelines at all levels. A method to tackle the ecological disaster has several merits, some of which are listed below.- Recovering a susceptible and priceless expedient.
- Increasing the efficacy of currently available systems.
- Exploiting infrastructure’s massive financial assets.
- Extending the systems’ average life duration.
- Increasing revenue from environmental mitigation services.
- Energy-demand reduction.
- Decrease in the service’s carbon footprint.
In order to locate and accentuate the finest solution to environmental issues, a thorough structure of tactics is developed in this study. To be sustainable, the plan chosen must be in harmony with the ecological sector’s integrated approach. Rather than a laborious process of making recommendations that account for the fact that many particular objectives and opportunities exist in the market, a well-organized approach that can be articulated promptly and succinctly must account for concerns of various individuals and those of the constitutionally sound authorities. Decisions are being made by legislators and selection analysts who are well-versed in the process. A review of the literature on environmental strategic planning undertaken with professionals and authorities, as well as information concerning the region of convenience’s domestic life, resulted in the improvement of these measures. Climate-remediation approaches were applied in the environmental distribution network. When a long-term ecological safeguard system exists, clear provisions are often in place. Appraisal attributes are used to assess the effectiveness of each methodology. To choose the optimal method, first, the critical nature of grading parameters should be understood. Attributes are given in Table 5 as the strategies to overcome environmental crises, and judgement criteria are given in Table 6.The linguistic terms for judging alternatives are listed in Table 7.
- Intermediate values for two consecutive linguistic terms will be as 2, 4, 6, 8, respectively
- Values for inverse composition for each linguistic term will be the reciprocal of its score index.
| Algorithm 2 AHP-TOPSIS. |
|
- Step 1
- Let be the collection of alternatives and be the collection of evaluation criteria as given in Table 3 and Table 4, respectively. We will use the set to refer to a group of policymakers / decision makers who have been asked to score each approach on the basis of how well it meets each of the evaluation criteria in terms of SFNs.
- Step 2
- Step 3
- Then, we obtained normalized pair-wise comparison matrix, which is given in Table 10.
- Step 4
- Therefore, the required criteria weights are calculated, as shown in Table 11.
- Step 5
- Criteria weights are consistent, as they fulfil the requirement that .
- Step 6
- The evaluations of decision makers in terms of decision matrices , , , and are expressed in Table 12, Table 13, Table 14, and Table 15, respectively. The rows represent the alternatives and the columns represent the parameters in these matrices. Then, the collection of decision matrices forms an SFSS-topology.As a result, we arrive at an aggregated decision matrix that looks like Table 16, computed by using
- Step 7
- Then, we calculated the weighted SFSS decision matrix, given in Table 17.
- Step 8
- Then, we obtained the SFSS-valued positive ideal solution (SFSV-PIS) and SFSS-valued negative ideal solution (SFSV-NIS)...
- Step 9
- Step 10
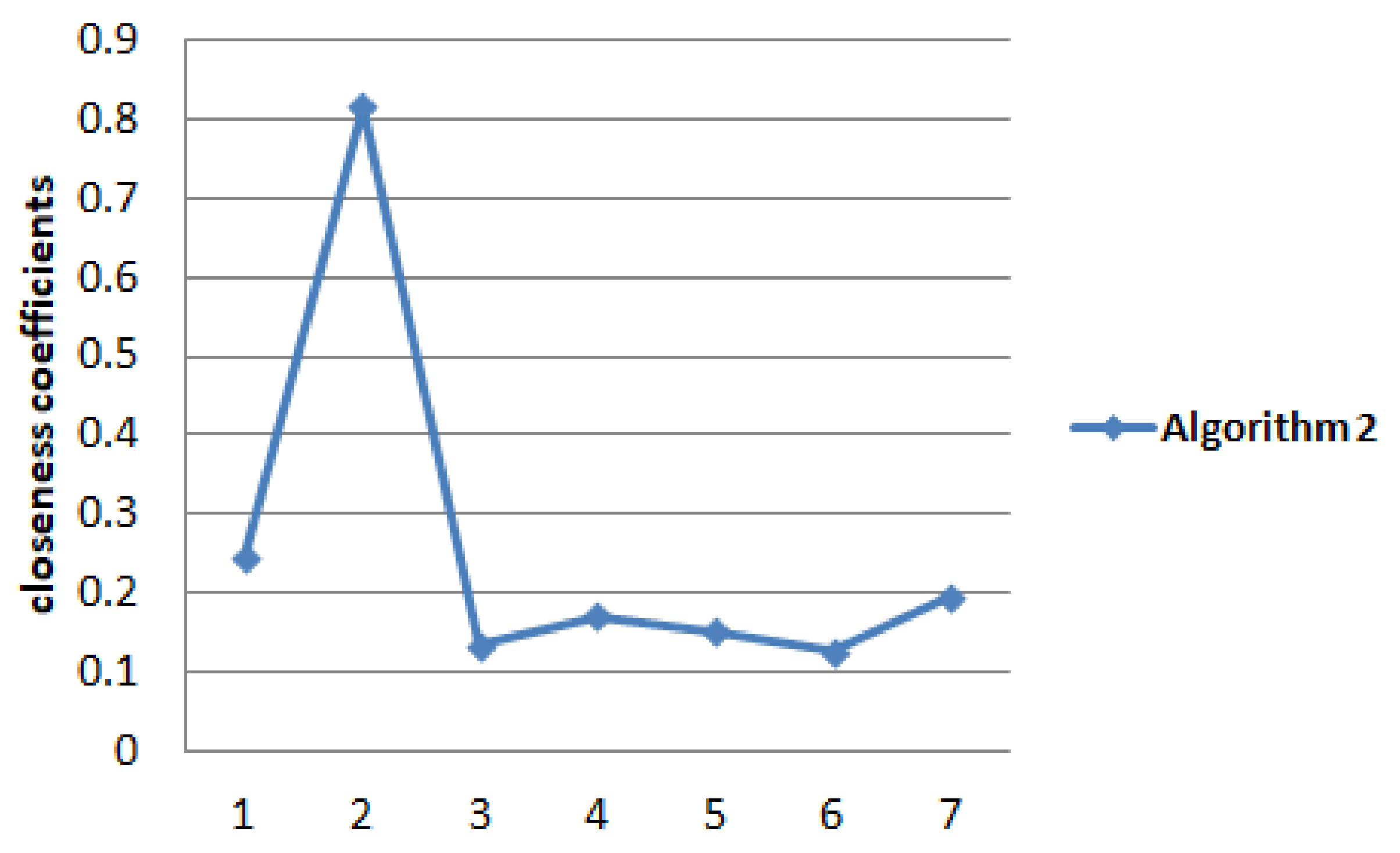
- Each alternative was compared to the ideal solution in Table 20, in order to compute its closeness coefficient.
- Step 11
- The preference order of the alternatives, therefore, is
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sardiu, M.E.; Gilmore, J.M.; Groppe, B.; Florens, L.; Washburn, M.P. Identification of topological network modules in perturbed protein Interaction networks. Sci. Rep. 2017, 7, 43845. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lum, P.Y.; Singh, G.; Lehman, A.; Ishkanov, T.; Johansson, M.V.; Alagappan, M.; Carlsson, J.; Carlsson, G. Extracting insights from the shape of complex data using topology. Sci. Rep. 2013, 3, 1236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicolau, M.; Levine, A.J.; Carlsson, G. Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proc. Natl. Acad. Sci. USA 2011, 108, 72657270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Cheng, W.Y.; Glicksberg, B.S.; Gottesman, O.; Tamler, R.; Chen, R.; Bottinger, E.P.; Dudley, J.T. Identification of type 2 diabetes subgroups through topological analysis of patient similarity. Sci. Transl. Med. 2015, 7, 311ra174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hofer, C.; Kwitt, R.; Niethammer, M. Deep learning with topological signatures. Adv. Neural Inf. Process. Syst. 2017, 30, 1634–1644. [Google Scholar]
- Witten, E. Reflections on the fate of spacetime. Phys. Today 1996, 96, 2430. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Set Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), 2013 JoInt, Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Pythagorean membership grades in multi criteria decision-making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis; American Research Press: Champaign, IL, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single Valued Neutrosophic Sets; Infinite Study: Dubai, United Arab Emirates, 2010; pp. 1–4. [Google Scholar]
- Cuong, B.C. Picture fuzzy sets—First results, Part 1. In Seminar Neuro-Fuzzy Systems with Applications; Institute of Mathematics, Vietnam Academy of Science and Technology: Hanoi, Vietnam, 2013. [Google Scholar]
- Cuong, B.C. Picture fuzzy sets—First results, Part 2. In Seminar Neuro-Fuzzy Systems with Applications; Institute of Mathematics, Vietnam Academy of Science and Technology: Hanoi, Vietnam, 2013. [Google Scholar]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An Approach towards decision making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S.; Mahmood, T.; Ghani, F.; Mahmood, T. Spherical fuzzy sets and their applications in multi-attribute decision making problems. J. Intell. Fuzzy Syst. 2019, 36, 2829–2844. [Google Scholar] [CrossRef]
- Gündogdu, F.K.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2018, 36, 337–352. [Google Scholar] [CrossRef]
- Chang, C.L. Fuzzy topological spaces. J. Math. Anal. Appl. 1968, 24, 182–190. [Google Scholar] [CrossRef] [Green Version]
- Kelley, J.L. General Topology; Van Nostrand: Princeton, NJ, USA, 1955. [Google Scholar]
- Wong, C.K. Fuzzy point and local properties of fuzzy topology. J. Math. Anal. Appl. 1974, 46, 316–328. [Google Scholar] [CrossRef] [Green Version]
- Lowen, R. Fuzzy topological spaces and compactness. J. Math. Anal. Appl. 1976, 56, 621–633. [Google Scholar] [CrossRef] [Green Version]
- Hutton, B. Normality in fuzzy topological spaces. J. Math. Anal. Appl. 1975, 50, 74–79. [Google Scholar] [CrossRef] [Green Version]
- Ming, P.P.; Ming, L.Y. Fuzzy topology I, Neighborhood structure of a fuzzy point and Moore—Smith convergence. J. Math. Anal. Appl. 1980, 76, 571–599. [Google Scholar] [CrossRef] [Green Version]
- Ying, M. A new approach for fuzzy topology (I). Fuzzy Sets Syst. 1991, 39, 302–321. [Google Scholar] [CrossRef]
- Ying, M. A new approach for fuzzy topology (II). Fuzzy Sets Syst. 1992, 47, 221–232. [Google Scholar] [CrossRef]
- Shen, J. Separation axiom in fuzzifying topology. Fuzzy Sets Syst. 1993, 57, 111–123. [Google Scholar] [CrossRef]
- Coker, D. An Introduction to Intuitionistic fuzzy topological spaces. Fuzzy Sets Syst. 1997, 88, 81–89. [Google Scholar] [CrossRef]
- Coker, D.; Haydar, E.A. On fuzzy compactness in Intuitionistic fuzzy topological spaces. J. Fuzzy Math. 1995, 3, 899–910. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets; Studies in Fuzziness and Soft Computing Physica; Soft Computing Physica: Heidelberg, Germany, 1999; Volume 35, pp. 1–137. [Google Scholar]
- Atanassov, K.T.; Stoeva, S. Intuitionistic fuzzy sets. In Polish Symp; On Interval and Fuzzy Mathematics: Poznan, Poland, 1983; pp. 23–26. [Google Scholar]
- Riaz, M.; Hashmi, M.R. Fuzzy parameterized fuzzy soft compact spaces with decision-making. Punjab Univ. J. Math. 2018, 50, 131–145. [Google Scholar]
- Riaz, M.; Hashmi, M.R. Fuzzy parameterized fuzzy soft topology with applications. Ann. Fuzzy Math. Informat. 2017, 13, 593–613. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory-first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Maji, P.K.; Biswas, R.; Roy, A.R. Fuzzy soft sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Ahmad, B.; Hussain, S. On some structures of soft topology. Math. Sci. 2012, 6, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Cagman, N.; Karatas, S.; Enginoglu, S. Soft topology. Comput. Math. Appl. 2011, 62, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Hazra, H.; Majumdar, P.; Samanta, S.K. Soft Topology. Fuzzy Inf. Eng. 2012, 1, 105–115. [Google Scholar] [CrossRef]
- Roy, S.; Samanta, T.K. A note on soft topological space. Punjab Univ. J. Math. 2014, 46, 19–24. [Google Scholar]
- Shabir, M.; Naz, M. On soft topological spaces. Comput. Math. Appl. 2011, 61, 1786–1799. [Google Scholar] [CrossRef] [Green Version]
- Varol, B.P.; Shostak, A.; Aygun, H. A new approach to soft topology. Hacet. J. Math. Stat. 2012, 41, 731–741. [Google Scholar]
- Aygunoglu, A.; Cetkin, V.; Aygun, H. An introduction to fuzzy soft topological spaces. Hacet. J. Math. Stat. 2014, 43, 193–204. [Google Scholar]
- Zorlutuna, I.; Atmaca, S. Fuzzy parameterized fuzzy soft topology. New Trends Math. Sci. 2016, 4, 142–152. [Google Scholar] [CrossRef]
- Osmanoglu, I.; Tokat, D. On intutionistic fuzzy soft topology. Gen. Math. Notes 2013, 19, 59–70. [Google Scholar]
- Li, Z.; Cui, R. On the topological structure of intuitionistic fuzzy soft sets. Ann. Fuzzy Math. Informat. 2013, 5, 229–239. [Google Scholar]
- Riaz, M.; Cagman, N.; Zareef, I.; Aslam, M. N-soft topology and its applications to multi-criteria group decision makin. J. Intell. Fuzzy Syst. 2019, 36, 6521–6536. [Google Scholar] [CrossRef]
- Riaz, M.; Smarandache, F.; Firdous, A.; Fakhar, A. On soft rough topology with-attribute group decision making. Mathematics 2019, 7, 67. [Google Scholar] [CrossRef] [Green Version]
- Riaz, M.; Davvaz, B.; Firdous, A.; Fakhar, A. Novel concepts of soft rough set topology with applications. J. Intell. Fuzzy Syst. 2019, 36, 3579–3590. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186, pp. 58–191. [Google Scholar]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Akram, M.; Shumaiza; Arshad, M. Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 2020, 39, 1–21. [Google Scholar] [CrossRef]
- Eraslan, S.; Karaaslan, F. A group decision making method based on TOPSIS under fuzzy soft environment. J. New Theory 2015, 3, 30–40. [Google Scholar]
- Garg, H.; Arora, R. TOPSIS method based on correlation coefficient for solving decision-making problems with intuitionistic fuzzy soft set information. AIMS Math. 2020, 5, 2944–2966. [Google Scholar] [CrossRef]
- Kahraman, C.; Gundogdu, F.K.; Onar, S.C.; Oztaysi, B. Hospital Location Selection Using Spherical Fuzzy TOPSIS. In Proceedings of the 11th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT 2019), Prague, Czech Republic, 9–13 September 2019. [Google Scholar] [CrossRef] [Green Version]
- Naeem, K.; Riaz, M.; Afzal, D. Pythagorean m-polar fuzzy sets and TOPSIS method for the selection of advertisement mode. J. Intell. Fuzzy Syst. 2019, 37, 8441–8458. [Google Scholar] [CrossRef]
- Senvar, O.; Otay, I.; Bolturk, E. Hospital Site Selection via Hesitant Fuzzy TOPSIS. Ifac-Pap. Online 2016, 49, 1140–1145. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to multi criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Kahraman, C.; Engin, O.; Kabak, O.; Kaya, I. Information systems outsourcing decisions using a group decision-making approach. Eng. Appl. Artif. Intell. 2009, 22, 832–841. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Prakash, C.; Barua, M.K. Integration of AHP-TOPSIS method for prioritizing the solutions of reverse logistics adoption to overcome its barriers under fuzzy environment. J. Manuf. Syst. 2015, 37, 599–615. [Google Scholar] [CrossRef]
- Arslan, T. A hybrid model of fuzzy and AHP for handling public assessments on transportation projects. Transportation 2009, 36, 97–112. [Google Scholar] [CrossRef]
- Calabrese, A.; Costa, R.; Levialdi, N.; Menichini, T. A fuzzy analytic hierarchy process method to support materiality assessment in sustainability reporting. J. Clean. Prod. 2016, 121, 248–264. [Google Scholar] [CrossRef]
- Mangla, S.K.; Kumar, P.; Barua, M.K. Risk analysis in green supply chain using fuzzy AHP approach: A case study. Resour. Conserv. Recy. 2015, 104, 375–390. [Google Scholar] [CrossRef]
- Jayawickrama, H.M.M.M.; Kulatunga, A.K.; Mathavan, S. Fuzzy AHP based plant sustainability evaluation method. Procedia Manuf. 2017, 8, 571–578. [Google Scholar] [CrossRef]
- Lamba, D.; Yadav, D.K.; Brave, A.; Panda, G. Prioritizing barriers in reverse logistics of E-commerce supply chain using fuzzy-analytic hierarcy process. Electron Commer. Res. 2019, 20, 381–403. [Google Scholar] [CrossRef]
- Panjwani, S.; Kumar, S.N.; Ahuja, L.; Islam, A. Prioritization of global climate models using fuzzy analytic hierarchy process and reliability index. Ther. Appl. Climatol. 2019, 137, 2381–2392. [Google Scholar] [CrossRef]
- Khushand, A.; Rahimi, K.; Ehteshami, M.; Gharaei, S. Fuzzy AHP approach for prioritizing electronic waste management options: A case study of Tehran. Iran Environ. Sci. Pollut. Res. 2019, 26, 9649–9660. [Google Scholar] [CrossRef]
- Maldonado-Macias, A.; Gracia, J.L.; Alvarado, A.; Balderrama, C.O. A hierarchical fuzzy axiomatic design methodology for ergonomic compatibility evaluation of advanced manufacturing technology. Int. J. Adv. Manuf. Technol. 2013, 66, 171–186. [Google Scholar] [CrossRef]
- Maldonado-Macias, A.; Gracia-Alcaraz, J.; Reyes, R.M.; Hernandez, J. Application of a fuzzy axiomatic design methodology for ergonomic compatibility evaluation on the selection of plastic molding machines: A case study. Procedia Manuf. 2015, 3, 5769–5776. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.K.; Sarkar, P. A framework based on fuzzy AHP-TOPSIS for prioritizing solutions to overcome the barriers in the implementation of ecodesign practices in SMEs. Int. J. Sustain. Dev. World Ecol. 2019, 26, 506–521. [Google Scholar] [CrossRef]
- Onar, S.C.; Oztaysi, B.; Kahraman, C. Strategic decision selection using hesitant fuzzy TOPSIS and interval type-2 fuzzy AHP: A case study. Int. J. Comput. Intell. Syst. 2014, 7, 1002–1021. [Google Scholar] [CrossRef] [Green Version]
- Junaid, M.; Xue, Y.; Syed, M.W.; Li, J.Z.; Ziaullah, M. A neutrosophic AHP and TOPSIS frsmework for supply chain risk assessment in automotive industry of Pakistan. Sustainability 2020, 12, 154. [Google Scholar] [CrossRef] [Green Version]
- Ak, M.F.; Gul, M. AHP-TOPSIS integration extended with Pythagorean fuzzy setsfor information security risk analysis. Complex Intell. Syst. 2019, 5, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Kusumawardani, R.P.; Agintiara, M. Application of fuzzy AHP-TOPSIS method for decision making in human resource manager selection process. Procedia Comput. Sci. 2015, 72, 638–646. [Google Scholar] [CrossRef] [Green Version]
- Dooki, A.E.; Bolhasani, P.; Fallah, M. An integrated fuzzy AHP and fuzzy TOPSIS approach for ranking and selecting the chief inspectors of bank: A case study. J. Appl. Res. Ind. Eng. 2017, 4, 8–23. [Google Scholar]
- Panchal, D.; Kumar, D. Maintenance decision-making for power generating unit in thermal power plant using combined fuzzy AHP-TOPSIS approach. Int. J. Oper. Res. 2017, 29, 248–272. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. A novel spherical fuzzy analytic hierarchy process and its renewable energy application. Soft Comput. 2020, 24, 4607–4621. [Google Scholar] [CrossRef]
- Roman, R.C.; Precup, R.E.; Petriu, E.M. Hybrid data-driven fuzzy active disturbance rejection control for tower crane systems. Eur. J. Control 2020, 58, 373–387. [Google Scholar] [CrossRef]
- Zhu, Z.; Pan, Y.; Zhou, Q.; Lu, C. Event-triggered adaptive fuzzy control for stochastic nonlinear systems with unmeasured states and unknown backlash-like hysteresis. IEEE Trans. Fuzzy Syst. 2020, 29, 1273–1283. [Google Scholar] [CrossRef]
- Sarkar, B.; Biswas, A. Pythagorean fuzzy AHP-TOPSIS integrated approach for transportation management through a new distance measure. Soft Comput. 2021, 25, 4073–4089. [Google Scholar] [CrossRef]
- Perveen, P.A.F.; John, S.J.; Babitha, K.V. Spherical fuzzy soft sets. In Decision Making with Spherical Fuzzy Sets; Kahraman, C., Kutlu Gündogdu, F., Eds.; Studies in Fuzziness and Soft Computing; Springer: Cham, Switzerland, 2021; Volume 392, pp. 8237–8250. [Google Scholar]
- Ashraf, A.; Ullah, K.; Hussain, A.; Bari, M. Interval-Valued Picture Fuzzy Maclaurin Symmetric Mean Operator with application in Multiple Attribute Decision-Making. Rep. Mech. Eng. 2022, 3, 301–317. [Google Scholar] [CrossRef]
- Narang, M.; Joshi, M.C.; Bisht, K.; Pal, A. Stock portfolio selection using a new decision-making approach based on the integration of fuzzy CoCoSo with Heronian mean operator. Decis. Making Appl. Manag. Eng. 2022, 5, 90–112. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Stevic, Z.; Mardani, A. Modelling procedure for the selection of steel pipes supplier by applying fuzzy AHP method. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 39–53. [Google Scholar] [CrossRef]
- Blagojevic, A.; Veskovic, S.; Kasalica, S.; Gojic, A.; Allamani, A. The application of the fuzzy AHP and DEA for measuring the efficiency of freight transport railway undertakings. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 1–23. [Google Scholar] [CrossRef]
- Badi, L.; Pamucar, D. Supplier selection for steel making company by using combined Grey-MARCOS methods. Decis. Making Appl. Manag. Eng. 2020, 3, 37–48. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Ullah, K.; Khan, Q. Einstein Geometric Aggregation Operators using a novel complex interval-valued Pythagorean fuzzy setting with application in green supplier chain management. Rep. Mech. Eng. 2021, 2, 105–134. [Google Scholar] [CrossRef]


| Fuzzy Models | Constraints | |||
|---|---|---|---|---|
| Fuzzy set (FS) [7] | 🗸 | × | × | An FS deals with vagueness |
| in terms of with | ||||
| Intuitionistic fuzzy set | 🗸 | × | 🗸 | An IFS assigns a pair of PMD and |
| (IFS) [8] | NMD with | |||
| Pythagorean fuzzy set | 🗸 | × | 🗸 | A PFS assigns a pair of PMD and |
| (PFS) [9,10] | NMD with | |||
| q-Rung orthopair fuzzy set | 🗸 | × | 🗸 | A q-ROFS assigns a pair of PMD and |
| (q-ROFS) [11] | NMD with | |||
| Neutrosophic set | 🗸 | 🗸 | 🗸 | An NS assigns three indexes, truthness T, |
| (NS) [12] | indeterminacy I, and falsity F, with | |||
| , | ||||
| Single-valued neutrosophic | 🗸 | 🗸 | 🗸 | An NS assigns three indexes, truthness T, |
| set (SVNS) [13] | indeterminacy I, and falsity F, with | |||
| , | ||||
| Picture fuzzy set | 🗸 | 🗸 | 🗸 | A PFS assigns PMD, ND, and NMD, |
| (PFS) [14,15,16] | such that | |||
| Spherical fuzzy set | 🗸 | 🗸 | 🗸 | A PFS assigns PMD, ND, and NMD, |
| (SFS) [17,18,19] | such that |
| Models | Researchers | Applications |
|---|---|---|
| Crisp-TOPSIS | Hwang and Yoon [50] | The fighter aircraft problem |
| Fuzzy-TOPSIS | Chen [51] | Selection of a system-analysis engineer |
| BF-TOPSIS | Akram et al. [52] | Skin disorder diagnosis |
| FSS-TOPSIS | Eraslan and Karaaslan [53] | Selection of a house |
| IFSS-TOPSIS | Garg and Arora [54] | Supplier-selection problem |
| SF-TOPSIS | Kahraman et al. [55] | Selection of a hospital location |
| PmpF-TOPSIS | Naeem et al. [56] | Selection of an advertisement mode |
| HFS-TOPSIS | Senvar et al. [57] | Hospital-site selection |
| PF-TOPSIS | Zhang and Xu [58] | MCDM based on PFSs to examine efficiency among domestic airlines |
| TOPSIS | Kahraman et al. [59] | Ranking of alternatives for location problem in supply-chain management |
| (0.469, 0.131, 0.630) | (0.589, 0.128, 0.338) | (0.811, 0.008, 0.213) | (0.638, 0.213, 0.419) | (0.291, 0.316, 0.362) | (0.429, 0.214, 0.586) | |
| (0.234, 0.346, 0.189) | (0.000, 0.000, 1.000) | (0.783, 0.132, 0.189) | (0.789, 0.102, 0.289) | (0.278, 0.118, 0.346) | (0.000, 0.000, 1.000) | |
| (0.271, 0.213, 0.348) | (0.769, 0.139, 0.169) | (0.000, 0.000, 1.000) | (0.532, 0.243, 0.411) | (0.291, 0.381, 0.293) | (0.781, 0.131, 0.639) | |
| (0.795, 0.142, 0.231) | (0.249, 0.321, 0.256) | (0.330, 0.142, 0.479) | (0.359, 0.134, 0.651) | (0.594, 0.287, 0.367) | (0.801, 0.095, 0.121) | |
| (0.256, 0.389, 0.180) | (0.393, 0.102, 0.597) | (0.435, 0.134, 0.596) | (0.795, 0.112, 0.280) | (0.000, 0.000, 1.000) | (0.286, 0.327, 0.179) | |
| (0.692, 0.134, 0.128) | (0.643, 0.260, 0.189) | (0.000, 0.000, 1.000) | (0.279, 0.321, 0.340) | (0.788, 0.103, 0.211) | (0.327, 0.256, 0.441) | |
| (0.297, 0.216, 0.310) | (0.781, 0.118, 0.171) | (0.181, 0.310, 0.490) | (0.497, 0.115, 0.324) | (0.237, 0.310, 0.212) | (0.505, 0.123, 0.486) |
| X | Ranking | |
|---|---|---|
| 2 | ||
| 7 | ||
| 6 | ||
| 3 | ||
| 5 | ||
| 1 | ||
| 4 |
| Code | Strategies |
|---|---|
| Forest conservation | |
| Disaster mitigation | |
| Environmental legislation | |
| Eliminate the use of fossil-fuel vehicles | |
| Eliminate single-use plastics | |
| Agriculture that is sustainable | |
| Mitigation of environmental aspects of aviation |
| Code | Strategies | Explanation |
|---|---|---|
| Cost figure | Expenditure associated with the implementation of the criteria | |
| Benefit period | Calculation of the effective life span of the criteria | |
| Energy Saved | For a solution to be viable, it must be able to cut energy consumption and global-warming emissions. | |
| Supply reliability | The criteria may be preferable if it is capable of saving a long-term service and easing supply constraints. | |
| Flexibility | The criteria should be tailored to meet diverse needs and uncertainties in order to be more flexible. | |
| Social acceptance | If the criteria has ability to be accepted by the localities. |
| Linguistic Terms | Score Index |
|---|---|
| Equal importance (EI) | 1 |
| Moderate importance (MI) | 3 |
| Strong important (SI) | 5 |
| Very-strong importance (VI) | 7 |
| Extreme importance (EXI) | 9 |
| 0.2454 | |
| 0.8167 | |
| 0.1351 | |
| 0.1712 | |
| 0.1515 | |
| 0.1261 | |
| 0.1965 |
| Models | Advantages and Limitations |
|---|---|
| Soft set (SS) (Molodtsov [35]) | An SS deals with uncertainty in terms of a parameterized collection of the subsets of the universe. |
| It can not deal with spherical fuzzy information. | |
| Spherical fuzzy set (SFS) ([17,18,19]) | It deals with spherical fuzzy information in terms of three indexes of PMD, ND, and NMD. |
| It can not deal with parameterizations. | |
| Spherical fuzzy soft set ([82]) | A strong hybrid model of SS and SFS to deal with uncertainty in terms of a parameterized collection of spherical fuzzy subsets. |
| It defines classes of parameters and their approximate elements. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.; Tanveer, S.; Pamucar, D.; Qin, D.-S. Topological Data Analysis with Spherical Fuzzy Soft AHP-TOPSIS for Environmental Mitigation System. Mathematics 2022, 10, 1826. https://doi.org/10.3390/math10111826
Riaz M, Tanveer S, Pamucar D, Qin D-S. Topological Data Analysis with Spherical Fuzzy Soft AHP-TOPSIS for Environmental Mitigation System. Mathematics. 2022; 10(11):1826. https://doi.org/10.3390/math10111826
Chicago/Turabian StyleRiaz, Muhammad, Shaista Tanveer, Dragan Pamucar, and Dong-Sheng Qin. 2022. "Topological Data Analysis with Spherical Fuzzy Soft AHP-TOPSIS for Environmental Mitigation System" Mathematics 10, no. 11: 1826. https://doi.org/10.3390/math10111826
APA StyleRiaz, M., Tanveer, S., Pamucar, D., & Qin, D.-S. (2022). Topological Data Analysis with Spherical Fuzzy Soft AHP-TOPSIS for Environmental Mitigation System. Mathematics, 10(11), 1826. https://doi.org/10.3390/math10111826








