Queueing-Inventory System for Two Commodities with Optional Demands of Customers and MAP Arrivals

Abstract

This research analyses the performance of a perishable queueing-inventory system for two commodities with optional customers demands. We assume in the article that all customers who come to the system can only purchase the first item or the second item or service (they do not purchase both items). This is the original aspect of the paper. We show the significance of the impact of optional demands on the system’s performance, which is the purpose of the paper. In this system, customers arrive, using the Markovian arrival process (MAP), to a demand for a single unit. The system is composed of a waiting hall with a limited capacity of F. The arriving customer observes the waiting hall is filled to capacity or the stock stage is zero, and they decide to leave the system. In the steady-state case, the joint probability distribution for the first commodity, the second commodity, and the number of customers in the system are computed using matrix geometric methods. We evaluate diverse system performance measures. Finally, we provide a numerical illustration of the optimal value for diverse parameters of the system, which highlights the results and implications of the article.

1. Introduction

One of the critical problems in an inventory system is having a large number of items which can affect its integrated functioning. To avoid this problem, multiple commodity systems are used. To manage such systems numerous models have been proposed with various sorts of ordering policies. The joint ordering policy was introduced by [1] and developed by [2]. A two commodity inventory system with zero lead time and with the same demand process were inspected by [3,4], respectively. The authors of [5,6] analyzed a joint ordering policy with a substitutable inventory system. A queueing-inventory system can be manipulated according to a number of factors, such as arrival/service processes, waiting hall capacity, service interruption, and vacation assumptions. See [7,8] review articles and [9,10,11,12,13,14,15,16,17,18,19] articles for discussion of a two commodity queueing-inventory system.

A system needs to satisfy different kinds of customer demands to achieve profit. Sometimes customers need only service without purchasing an item. For example, in a mechanic shop, customers may come to repair their vehicle. Some customers come to the system with a required item—they only need service. Some customers come to the system without items—they need service with the item. In a similar way, we can observe this sort of circumstance in a tailoring shop, card printers, etc. In this circumstance, the system provides the same services for both demands.

Motivated by practical situations that arise, we consider how arriving customers may choose either service with or without an item. The present article also considers a perishable $(s,Q)$ queueing-inventory system for two commodities in which customers arrive according to a Markovian arrival process (MAP) to a single unit or for service at a certain time.

A MAP is a type of tractable class of the Markov renewal process. The arrival process can be modified to be a renewal process by adjusting the MAP’s parameters. The MAP is a diverse class of point processes that also includes the Poisson process. The purpose of MAP is to generalize the Poisson process and create more flexibility for modeling purposes. MAP may be used for both discrete and continuous time frames, but this paper focuses only on continuous-time frames. An explanation of MAP is provided by [20]. The states of the Markov chain are $\left\{1,2,\dots y\right\}$. When the chain goes into the state u, $1\le u\le y$, it remains with parameter $m_u$ for an exponential time. When the sojourn period is over, the chain may shift to a transition until arrival occurs; then the chain goes into the state v with the probability $c_{uv},1\le v\le y$, or if transition occurs without arrival, then the chain goes into the state v with probability $d_{uv},1\le v\le y$, $u\ne v$. When an arrival occurs, the chain might return to the same state. We describe the square matrices $D_f,f=0,1$, of size y by ${\left[D_0\right]}_{uu}=-m_u$ and ${\left[D_0\right]}_{uv}=m_u{d}_{uv}$, $u\ne v$, ${\left[D_1\right]}_{uv}=m_u{c}_{uv}$, $1\le u,v\le y$. $\chi$ represents the continuous time Markov chain’s unique probability vector with an infinitesimal generator matrix $D(=D_0+D_1)$, and $\chi$ is obtained from $\chi D=0$, $\chi \mathbf{e}=1$.

Let $\phi$ represent the initial probability vector of the underlying MAP-based Markov process. We have an independent arrival, the end of an interval with minimum k arrivals, and the moment at which the system enters or exits a certain state, such as when a busy period begins or ends, etc.; by choosing a suitable $\phi$, we can obtain the kind of time. The main purpose is that we obtain the unique probability vector of MAP by $\phi =\chi$. The average arrival rate $\lambda =\chi D_1\mathbf{e}$ provides the mean number of customers occurring per unit time. The MAP-described point process is a special category of semi-Markov processes with a transition probability matrix provided by

$${\displaystyle {\int }_0^x{e}^{D_{0}t}dt{D}_1=[I-e^{D_{0}x}]{(-D_0)}^{-1}{D}_1,x\ge 0.}$$

For more information on MAP, readers can refer to [21,22,23]. Table 1 summarizes the overview of literature review.

Table 1. Literature review overview.

Author(s)	Poisson Arrivals	MAP Arrivals	Joint Replenishment	Optional Demand	Exponentially Distributed Lead Time	Perishable Inventory
Balintfy [1]	✓		✓
Silver [2]	✓		✓
Krishnamoorthy [3]	✓				✓
Anbazhagan [4]	✓		✓		✓
Anbazhagan [5]	✓		✓		✓
Anbazhagan [6]	✓		✓		✓
Karthikeyan [7]	✓					✓
Krishnamoorthy [8]	✓
Sivakumar [9]	✓		✓		✓	✓
Benny [10]	✓
Ozkar [11]		✓	✓	✓	✓
Senthil Kumar [12]	✓
Sinu Lal [13]	✓				✓
Senthil Kumar [14]	✓		✓
Yadavalli [15]	✓	✓				✓
Nahmias [16]						✓
Murthy [17]				✓
Uzunoglu Kocer [18]	✓			✓	✓	✓
Jacob [19]		✓		✓	✓
Lucantoni [20]		✓
Latouche [21]		✓
Lee [22]		✓
Chakravarthy [23]		✓
This paper		✓	✓	✓	✓	✓

✓ Factors included in the research.

The findings of the above survey inspired our research, since, to our knowledge, there has been little study into two commodities with three forms of service, which is a common occurrence in business administration. Section 2 discusses the detailed description of our model. In Section 3, we provide an analysis of our prescriptive model. Analysis of the model’s steady-state is described in Section 4. In Section 5, we develop several aspects of system performance for the steady-state case. In Section 6, the total expected cost rate (TCR) is calculated. In Section 7, numerical examples are provided.

2. Model Narrations

A two-commodity perishable queueing-inventory system is considered. The system has a maximum capacity of $S_1$ items for the first commodity, and $S_2$ items for the second commodity. The system provides the finite waiting room size of F along with one getting service. The customers show up as per MAP, with demand for a single unit. A single item of the first commodity is required by the customer (i.e., a high quality and high price item) with probability $b_1$ or the second commodity (i.e., a normal quality and cheap price item) with probability $b_2$ or service only with probability $b_3$. The server’s service is the same for each demand. With parameter $b_i\mu ,(i=1,2,3)$, three different kinds of service times are exponentially distributed. We take the parameter ${\gamma }_1$ as the lifetime of the first commodity and ${\gamma }_2$ for the second commodity follows an exponential distribution. If both stock levels are close to their respective reorder levels $s_i\left(i=1,2\right)$, then an order is made for both commodities. $Q_i\left(>s_i,i=1,2\right)$ units are considered the ordering quantity for the i-th commodity. The lead time follows an exponential distribution with parameter $\beta (>0)$. The customer arrives during a stock-out period and the full system is considered to be lost. Customers leave the system after receiving the required service performances of the item.

3. Analysis

We consider $I^{\left(1\right)}\left(t\right)$ to represent the number of items in the first commodity at time t, $I^{\left(2\right)}\left(t\right)$ to represent the number of items in the second commodity at time t, $N\left(t\right)$ to represent the number of customers in the system at time t and $J\left(t\right)$ to represent the phase of the arrival process at time t. The Markov process $\left\{\left(I^{\left(1\right)}\left(t\right),I^{\left(2\right)}\left(t\right),N\left(t\right),J\left(t\right)\right);t\ge 0\right\}$ with discrete state space $\mathbf{E}=E_1\times E_2\times E_3\times E_4$, where $0\le E_1\le S_1$, $0\le E_2\le S_2$, $0\le E_3\le F$, $1\le E_4\le y$. The infinitesimal generator matrix ${\left[\mathbb{W}\right]}_{ij}=\left\{\begin{array}{cc}{\mathbb{O}}_i,\hfill & j=i\times 1, i=1,2,\dots S_1\hfill \\ {\mathbb{P}}_i,\hfill & j=i, i=0,1,\dots S_1\hfill \\ \mathbb{R},\hfill & j=i+Q_1, i=0,1,\dots s_1\hfill \\ \mathbf{0},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$ where ${\left[\mathbb{R}\right]}_{kl}=\left\{\begin{array}{cc}\beta I_Z\otimes I_y,\hfill & l=k+Q_2, k=0,1,\dots s_2,\hfill \\ \mathbf{0},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$ where, $Z=F+1$

Here, $i=1,2,\dots S_1$ and $A_Z$ = ${\left[a_{ij}\right]}_{Z\times Z}$ = $\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j=i-1,i=1,2,\dots F\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$

${\left[{\mathbb{O}}_i\right]}_{kl}=\left\{\begin{array}{cc}\left(i{\gamma }_1{I}_Z+b_1\mu A_Z\right)\otimes I_y,\hfill & l=k,k=0,1,\dots S_2,\hfill \\ \mathbf{0},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Here, $B_Z={\left[b_{ij}\right]}_{Z\times Z}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j=i+1,i=0,1,\dots F-1\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$

$C_Z={\left[c_{ij}\right]}_{Z\times Z}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j=i,i=F\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$

$G_Z={\left[g_{ij}\right]}_{Z\times Z}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j=i,i=0,1,\dots F-1\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$

$H_Z={\left[h_{ij}\right]}_{Z\times Z}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j=i,i=1,2,\dots F\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$

For $i=0$,

${\left[{\mathbb{P}}_i\right]}_{kl}=\left\{\begin{array}{cc}\left(k{\gamma }_2{I}_Z+b_2\mu A_Z\right)\otimes I_y,\hfill & l=k-1,k=1,2,\dots S_2,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)\right.\hfill \\ \left.+\left(C_Z\otimes D\right)\right)-\left(\left(I_Z\otimes \beta I_y\right)+\left(H_Z\otimes \left(b_3\mu \right)I_y\right)\right)),\hfill & l=k,k=0,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)+\left(C_Z\otimes D\right)\right)\hfill \\ -\left(\left(I_Z\otimes \left(\beta +k{\gamma }_2\right)I_y\right)+\left(H_Z\otimes (b_3\mu +b_2\mu )I_y\right)\right)),\hfill & l=k,k=1,2,\cdots s_2,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)+\left(C_Z\otimes D\right)\right)\hfill \\ -\left(\left(I_Z\otimes \left(k{\gamma }_2\right)I_y\right)+\left(H_Z\otimes (b_3\mu +b_2\mu )I_y\right)\right)),\hfill & l=k,\hfill \\ & k=s_2+1,s_2+2,\cdots S_2,\hfill \\ \mathbf{0},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

For $i=1,2,\dots s_1$,

${\left[{\mathbb{P}}_i\right]}_{kl}=\left\{\begin{array}{cc}\left(k{\gamma }_2{I}_Z+b_2\mu A_Z\right)\otimes I_y,\hfill & l=k-1,\hfill \\ & k=1,2,\dots S_2,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)+\left(C_Z\otimes D\right)\right)\hfill \\ -\left(\left(I_Z\otimes \left(\beta +i{\gamma }_1\right)I_y\right)+\left(H_Z\otimes (b_3\mu +b_1\mu )I_y\right)\right)),\hfill & l=k,k=0,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)+\left(C_Z\otimes D\right)\right)\hfill \\ -\left(\left(I_Z\otimes \left(\beta +i{\gamma }_1+k{\gamma }_2\right)I_y\right)+\left(H_Z\otimes (b_3\mu +b_1\mu +b_2\mu )I_y\right)\right)),\hfill & l=k,\hfill \\ & k=1,2,\cdots s_2,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)+\left(C_Z\otimes D\right)\right)\hfill \\ -\left(\left(I_Z\otimes \left(i{\gamma }_1+k{\gamma }_2\right)I_y\right)+\left(H_Z\otimes (b_3\mu +b_1\mu +b_2\mu )I_y\right)\right)),\hfill & l=k,\hfill \\ & k=s_2+1,\cdots S_2,\hfill \\ \mathbf{0},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

For $i=s_1+1,\dots S_1$,

${\left[{\mathbb{P}}_i\right]}_{kl}=\left\{\begin{array}{cc}\left(k{\gamma }_2{I}_Z+b_2\mu A_Z\right)\otimes I_y,\hfill & l=k-1,\hfill \\ & k=1,2,\dots S_2,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)+\left(C_Z\otimes D\right)\right)\hfill \\ -\left(\left(I_Z\otimes \left(i{\gamma }_1\right)I_y\right)+\left(H_Z\otimes (b_3\mu +b_1\mu )I_y\right)\right)),\hfill & l=k,k=0,\hfill \\ \left(b_3\mu A_Z\otimes I_y\right)+\left(B_Z\otimes D_1\right)+(\left(\left(G_Z\otimes D_0\right)+\left(C_Z\otimes D\right)\right)\hfill \\ -\left(\left(I_Z\otimes \left(i{\gamma }_1+k{\gamma }_2\right)I_y\right)+\left(H_Z\otimes (b_3\mu +b_1\mu +b_2\mu )I_y\right)\right)),\hfill & l=k,\hfill \\ & k=1,2,\cdots S_2,\hfill \\ \mathbf{0},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

4. Steady State Analysis

From the structure of $\mathbb{W}$, the Markov process $\left\{I^{\left(1\right)}\left(t\right),I^{\left(2\right)}\left(t\right),N\left(t\right),J\left(t\right);t\ge 0\right\}$ on the state space $\mathbf{E}$ is irreducible, and the limiting distribution Y$(i_1,i_2,i_3,i_4)=\underset{t\to \infty }{lim}Pr[I^{\left(1\right)}\left(t\right)=i_1,I^{\left(2\right)}\left(t\right)=i_2,N\left(t\right)=i_3,J\left(t\right)=i_4;I^{\left(1\right)}\left(0\right),I^{\left(2\right)}\left(0\right),N\left(0\right),J\left(0\right)]$, exists.

The limiting distribution Y$(i_1,i_2,i_3,i_4)$ is independent of the starting condition.

Take

$$\begin{array}{ccc}\hfill \mathbf{Y}& =& (\mathbf{Y}\left(0\right),\mathbf{Y}\left(1\right),\dots ,\mathbf{Y}\left(S_1\right)),\hfill \\ \hfill \mathrm{where} \mathbf{Y}\left(i_1\right)& =& (\mathbf{Y}(i_1,0),\mathbf{Y}(i_1,1),\dots ,\mathbf{Y}(i_1,S_2)),i_1=0,1,\dots ,S_1\hfill \\ \hfill \mathbf{Y}(i_1,i_2)& =& (\mathbf{Y}(i_1,i_2,0),\mathbf{Y}(i_1,i_2,1),\dots ,\mathbf{Y}(i_1,i_2,F)),i_2=0,1,\dots ,S_2\hfill \\ \hfill \mathbf{Y}(i_1,i_2,i_3)& =& (\mathbf{Y}(i_1,i_2,i_3,1),\mathbf{Y}(i_1,i_2,i_3,2),\dots ,\mathbf{Y}(i_1,i_2,i_3,y)),i_3=0,1,\dots ,F\hfill \end{array}$$

The steady-state probability vector $\mathbf{Y}$ obtained from $\mathbf{Y}\mathbb{W}$ = 0, $\mathbf{Y}\mathbf{e}$ = 1.

Theorem 1.

The steady-state probability vector $\mathbf{Y}$ for the Markov process whose rate matrix $\mathbb{W}$ is given by

$$\mathbf{Y}\left(i_1\right)=\mathbf{Y}\left(Q_1\right){\Omega }_{i_1}, i_1=0,1,\dots ,S_1$$

where

${\Omega }_{i_1}=\left\{\begin{array}{cc}{(-1)}^{Q_1-i_1}{\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1},\hfill & i_1=0,1\dots ,Q_1-1;\hfill \\ I,\hfill & i_1=Q_1;\hfill \\ {(-1)}^{2Q_1-i_1+1}{\displaystyle {\displaystyle \sum _{j=0}^{S_1-i_1}}}\left\{({\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{s_1+1-j}{\mathbb{P}}_{s_1-j}^{-1})\right.\hfill & \\ \left.\mathbb{R}{\mathbb{P}}_{S_1-j}^{-1}({\mathbb{O}}_{S_1-j}{\mathbb{P}}_{S_1-j-1}^{-1}{\mathbb{O}}_{S_1-j-1}\dots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1})\right\},\hfill & i_1=Q_1+1,\dots ,S_1;\hfill \end{array}\right.$

The following two equations can be used to arrive to $\mathbf{Y}\left(Q_1\right)$:

$$\begin{array}{c}\hfill (i.e)\mathbf{Y}\left(Q_1\right)({(-1)}^{Q_1}{\displaystyle \sum _{j=0}^{s_1-1}}({\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\cdots {\mathbb{O}}_{s_1+1-j}{\mathbb{P}}_{s_1-j}^{-1})\mathbb{R}{\mathbb{P}}_{S_1-j}^{-1}\\ \hfill ({\mathbb{O}}_{S_{1-j}}{\mathbb{P}}_{S_{1-j-1}}^{-1}{\mathbb{O}}_{S_{1-j-1}}\dots {\mathbb{O}}_{Q_{1+2}}{\mathbb{P}}_{Q_{1+1}}^{-1}){\mathbb{O}}_{Q_{1+1}}+{\mathbb{P}}_{Q_1}+\\ \hfill \left\{{(-1)}^{Q{}_1}{\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_{1-1}}^{-1}{\mathbb{O}}_{Q_{1-1}}\dots {\mathbb{O}}_1{\mathbb{P}}_0^{-1}\right\}\mathbb{R})=0\end{array}$$

and

$$\begin{array}{c}\hfill \mathbf{Y}\left(Q_1\right)({\displaystyle \sum _{i_1=o}^{Q_1-1}}\left\{{(-1)}^{Q_1-i_1}{\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1}\right\}+I+\\ \hfill {\displaystyle \sum _{i_1=Q_1+1}^{S_1}}\left\{{(-1)}^{2Q_1-i_1+1}{\displaystyle \sum _{j=0}^{S_1-i_1}}\right\{({\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{s_1+1-j}{\mathbb{P}}_{s_1-j}^{-1})\\ \hfill \mathbb{R}{\mathbb{P}}_{S_1-j}^{-1}({\mathbb{O}}_{S_1-j}{\mathbb{P}}_{S_1-j-1}^{-1}{\mathbb{O}}_{S_1-j-1}\cdots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1})\left\}\right\})\mathbf{e}=1\end{array}$$

Proof. 

We know that

$$\mathbf{Y}\mathbb{W}=0 \mathrm{and} \mathbf{Y}\mathbf{e}=\mathbf{1}.$$

The equation $\mathbf{Y}\mathbb{W}=0$ can be written as

$$\begin{array}{ccc}\hfill \mathbf{Y}(i_1+1){\mathbb{O}}_{i_1+1}+\mathbf{Y}\left(i_1\right){\mathbb{P}}_{i_1}& =& 0,i_1=0,1,\dots Q_1-1\hfill \\ \hfill \mathbf{Y}(i_1+1){\mathbb{O}}_{i_1+1}+\mathbf{Y}\left(i_1\right){\mathbb{P}}_{i_1}+\mathbf{Y}(i_1-Q_1)\mathbb{R}& =& 0,i_1=Q_1\hfill \\ \hfill \mathbf{Y}(i_1+1){\mathbb{O}}_{i_1+1}+\mathbf{Y}\left(i_1\right){\mathbb{P}}_{i_1}+\mathbf{Y}(i_1-Q_1)\mathbb{R}& =& 0,i_1=Q_1+1,Q_1+2,\dots S_1-1\hfill \\ \hfill \mathbf{Y}\left(i_1\right){\mathbb{P}}_{i_1}+\mathbf{Y}(i_1-Q_1)\mathbb{R}& =& 0,i_1=S_1.\hfill \end{array}$$

(1)

The equations, except (1), can be solved recursively, yielding

$$\mathbf{Y}\left(i_1\right)=\mathbf{Y}\left(Q_1\right){\Omega }_{i_1}, i=0,1,\dots ,S_1$$

where

$${\Omega }_{i_1}=\left\{\begin{array}{cc}{(-1)}^{Q_1-i_1}{\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1},\hfill & i_1=0,1\dots ,Q_1-1;\hfill \\ I,\hfill & i_1=Q_1;\hfill \\ {(-1)}^{2Q_1-i_1+1}{\displaystyle {\displaystyle \sum _{j=0}^{S_1-i_1}}}\left\{({\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{s_1+1-j}{\mathbb{P}}_{s_1-j}^{-1})\right.\hfill & \\ \left.\mathbb{R}{\mathbb{P}}_{S_1-j}^{-1}({\mathbb{O}}_{S_1-j}{\mathbb{P}}_{S_1-j-1}^{-1}{\mathbb{O}}_{S_1-j-1}\dots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1})\right\},\hfill & i_1=Q_1+1,\dots ,S_1;\hfill \end{array}\right.$$

After placing the value of ${\Omega }_{i_1}$ in (1) and in the normalizing condition, we acquire $\mathbf{Y}\left(Q_1\right)$

$$\begin{array}{c}\hfill (i.e)\mathbf{Y}\left(Q_1\right)({(-1)}^{Q_1}{\displaystyle \sum _{j=0}^{s_1-1}}({\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\cdots {\mathbb{O}}_{s_1+1-j}{\mathbb{P}}_{s_1-j}^{-1})\mathbb{R}{\mathbb{P}}_{S_1-j}^{-1}\\ \hfill ({\mathbb{O}}_{S_1-j}{\mathbb{P}}_{S_1-j-1}^{-1}{\mathbb{O}}_{S_1-j-1}\dots {\mathbb{O}}_{Q_1+2}{\mathbb{P}}_{Q_1+1}^{-1}){\mathbb{O}}_{Q_1+1}+{\mathbb{P}}_{Q_1}+\\ \hfill \left\{{(-1)}^{Q_1}{\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_1{\mathbb{P}}_0^{-1}\right\}\mathbb{R})=0\end{array}$$

and

$$\begin{array}{c}\hfill \mathbf{Y}\left(Q_1\right)({\displaystyle \sum _{i_1=o}^{Q_1-1}}\left\{{(-1)}^{Q_1-i_1}{\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1}\right\}+I+\\ \hfill {\displaystyle \sum _{i_1=Q_1+1}^{S_1}}\left\{{(-1)}^{2Q_1-i_1+1}{\displaystyle \sum _{j=0}^{S_1-i_1}}\right\{({\mathbb{O}}_{Q_1}{\mathbb{P}}_{Q_1-1}^{-1}{\mathbb{O}}_{Q_1-1}\dots {\mathbb{O}}_{s_1+1-j}{\mathbb{P}}_{s_1-j}^{-1})\\ \hfill \mathbb{R}{\mathbb{P}}_{S_1-j}^{-1}({\mathbb{O}}_{S_1-j}{\mathbb{P}}_{S_1-j-1}^{-1}{\mathbb{O}}_{S_1-j-1}\cdots {\mathbb{O}}_{i_1+1}{\mathbb{P}}_{i_1}^{-1})\left\}\right\})\mathbf{e}=1\end{array}$$

□

5. System Performance Measures

In this division, we surmise a few performance measures in the system.

5.1. Mean Inventory Level

Let $M^{I^{\left(1\right)}}$ and $M^{I^{\left(2\right)}}$ be the mean inventory levels of the first and second commodities, respectively, in a steady state, which can be expressed as

$$M^{I^{\left(1\right)}}={\displaystyle \sum _{i_1=1}^{S_1}}{i}_1\left({\displaystyle \sum _{i_2=0}^{S_2}}{\displaystyle \sum _{i_3=0}^F}\mathbf{Y}(i_1,i_2,i_3)\right)\mathbf{e}$$

$$M^{I^{\left(2\right)}}={\displaystyle \sum _{i_2=1}^{S_2}}{i}_2\left({\displaystyle \sum _{i_1=0}^{S_1}}{\displaystyle \sum _{i_3=0}^F}\mathbf{Y}(i_1,i_2,i_3)\right)\mathbf{e}$$

5.2. Mean Reorder Rate

In a stable state, the $M^R$ represents the mean reorder rate. The joint inventory level decreases to $(s_1,s_2)$ or $(s_1,i_2),i_2<s_2$ or $(i_1,s_2),i_1<s_1$ if once service is performed, or if any of the $(s_i+1),i=1,2$ items are perishable.

$$\begin{array}{ll}{M}^R=& (s_1+1){\gamma }_1{\displaystyle \sum _{i_2=0}^{s_2}}{\displaystyle \sum _{i_3=0}^F}\mathbf{Y}(s_1+1,i_2,i_3)\mathbf{e}+(s_2+1){\gamma }_2{\displaystyle \sum _{i_1=0}^{s_1}}{\displaystyle \sum _{i_3=0}^F}\mathbf{Y}(i_1,s_2+1,i_3)\mathbf{e}\\ & +b_1\mu {\displaystyle \sum _{i_3=1}^F}{\displaystyle \sum _{i_2=0}^{s_2}}\mathbf{Y}(s_1+1,i_2,i_3)\mathbf{e}+b_2\mu {\displaystyle \sum _{i_3=1}^F}{\displaystyle \sum _{i_1=0}^{s_1}}\mathbf{Y}(i_1,s_2+1,i_3)\mathbf{e}.\end{array}$$

5.3. Mean Perishable Rate

Let $M^{P_1}$ and $M^{P_2}$ be the mean perishable rates of the first and second commodity, respectively, in a steady state and are given by

$$M^{P_1}={\displaystyle \sum _{i_1=1}^{S_1}}{\displaystyle \sum _{i_2=0}^{S_2}}{\displaystyle \sum _{i_3=0}^F}{i}_1{\gamma }_1\mathbf{Y}(i_1,i_2,i_3)\mathbf{e}$$

$$M^{P_2}={\displaystyle \sum _{i_1=0}^{S_1}}{\displaystyle \sum _{i_2=1}^{S_2}}{\displaystyle \sum _{i_3=0}^F}{i}_2{\gamma }_2\mathbf{Y}(i_1,i_2,i_3)\mathbf{e}.$$

6. Cost Analysis

For the total expected cost function per unit time, we have evaluated the cost aspects listed below.

• $C^{C_i}$: Carrying cost of i-th commodity per unit time ($i=1,2$)
• $C^S$: Setup cost per order
• $C^{P_1}$: First-commodity perishable cost per item per unit time
• $C^{P_2}$: Second-commodity perishable cost per item per unit time

The total expected cost function is given by

$$\begin{array}{ccc}\hfill TC(S_1,s_1,S_2,s_2,F)& =& C^{C_1}{M}^{I^{\left(1\right)}}+C^{C_2}{M}^{I^{\left(2\right)}}+C^S{M}^R+C^{P_1}{M}^{P_1}+C^{P_2}{M}^{P_2}\hfill \end{array}$$

where $M^{I^{\left(i\right)}}$, $M^R$ and $M^{P_i}$ (i = 1, 2) are given in Section 5.

7. Numerical Illustration

The convexity of the TCR is demonstrated using numerical examples. We presume the below numerical example: The arrival process is hyper-exponential. As a MAP, its parameters are given by ($D_0$,$D_1$) where

$$D_0=\left(\begin{array}{cc}-10& 0\\ 0& -1\end{array}\right) \mathrm{and} D_1=\left(\begin{array}{cc}9& 1\\ 0.9& 0.1\end{array}\right)$$

Let F = 6, $s_1=3$, $s_2=2$, $\beta =0.45$, $\mu =1.6$, ${\gamma }_1=0.7$, ${\gamma }_2=0.5$, $b_1=0.4$, $b_2=0.32$, $b_3=0.28$; $C^{C_1}=1.4$, $C^{C_2}=1.35$, $C^{P_1}=1.28$, $C^{P_2}=2.7$, $C^S=1$;

Furthermore, let $T{C}^{\prime }$($S_1,S_2$) = $TC(S_1,3,S_2,2,6)$.

This gives the expected cost rate for different values of $S_1$ and of $S_2$.

In Table 2, we present the $T{C}^{\prime }$($S_1,S_2$) values. Here, the row minimum is represented in boldface and the column minimum is underlined. A convex function of ($S_1,S_2$) is $T{C}^{\prime }$($S_1,S_2$), and the optimum at ($S_1,S_2$) = (21, 16).

Table 2. TCR as a function of $S_1$ and $S_2$.

${\mathit{S}}_1/{\mathit{S}}_2$	13	14	15	16	17
20	0.95816	0.93312	0.91461	0.91429	0.99542
21	0.93239	0.78797	0.66773	0.56698	0.68216
22	0.92900	0.86021	0.85043	0.84890	0.90087
23	0.98022	0.94679	0.90740	0.90105	0.90133
24	1.10383	0.96021	0.94100	1.48230	1.49438

Let $S_2=12$, $s_1=2$, $s_2=1$, $\beta =1.4$, $\mu =1.7$, ${\gamma }_1=1.01$, ${\gamma }_2=0.05$, $b_1=0.4$, $b_2=0.32$, $b_3=0.28$; $C^{C_1}=1.1$, $C^{C_2}=0.35$, $C^{P_1}=1.28$, $C^{P_2}=2.78$, $C^S=1.76$;

Furthermore, let $T{C}^{\prime }$($S_1,F$) = TC($S_1,2,12,1,F$).

This provides the TCR for different values of $S_1$ and of F.

In Table 3, we present the $T{C}^{\prime }$($S_1,F$) values. Here, the row minimum is represented in boldface and the column minimum is underlined. A convex function of ($S_1,F$) is $T{C}^{\prime }$($S_1,F$), and the optimum at ($S_1,F$) = (7, 6).

Table 3. TCR as a function of $S_1$ and F.

${\mathit{S}}_1/\mathit{F}$	5	6	7	8	9
5	0.8065	0.7642	0.7512	1.1471	1.3590
6	0.7631	0.6991	0.7172	1.1319	1.3489
7	0.8025	0.6944	0.7081	1.1281	1.3487
8	0.8277	0.7062	0.7073	1.1225	1.3438
9	0.8376	0.7136	0.7114	1.1232	1.3430
10	0.8413	0.7165	0.7137	1.1246	1.3434
11	0.8426	0.7176	0.7146	1.1254	1.3439

Let $S_1=6$, $s_1=2$, $s_2=3$, $\beta =1.4$, $\mu =1.7$, ${\gamma }_1=1.01$, ${\gamma }_2=0.05$, $b_1=0.4$, $b_2=0.32$, $b_3=0.28$; $C^{C_1}=1.1$, $C^{C_2}=0.35$, $C^{P_1}=1.13$, $C^{P_2}=2.78$, $C^S=2.5$;

Furthermore, let $T{C}^{\prime }$($S_2,F$) = $TC(6,2,S_2,3,F)$.

This provides the TCR for different values of $S_2$ and of F.

The $T{C}^{\prime }$($S_2,F$) values are presented in Table 4. The optimal cost for each $S_2$ and F are displayed in boldface and underlined, respectively. A convex function of ($S_2,F$) is $T{C}^{\prime }$($S_2,F$), and the optimum takes place at ($S_2,F$) = (13, 8).

Table 4. TCR as a function of $S_2$ and F.

${\mathit{S}}_2/\mathit{F}$	5	6	7	8	9
12	0.76205	0.72886	0.72567	0.71925	0.84315
13	0.69172	0.63563	0.63280	0.58965	0.61770
14	0.73478	0.65798	0.64908	0.59718	0.61275
15	0.81303	0.69213	0.66818	0.60717	0.62222
16	0.81599	0.76243	0.73614	0.71850	0.73127

Let F = 4, $S_2=18$, $s_2=2$, $\beta =0.3$, $\mu =1.7$, ${\gamma }_1=1.01$, ${\gamma }_2=0.05$, $b_1=0.4$, $b_2=0.32$, $b_3=0.28$; $C^{C_1}=1.09$, $C^{C_2}=0.35$, $C^{P_1}=1.28$, $C^{P_2}=2.78$, $C^S=1.77$;

Furthermore, let $T{C}^{\prime }$($S_1,s_1$) = $TC(S_1,s_1,18,2,4)$.

This provides the TCR for different values of $S_1$ and of $s_1$.

In Table 5, we present the $T{C}^{\prime }$($S_1,s_1$) values. Here, the row minimum is represented in boldface and the column minimum is underlined. A convex function of ($S_1,s_1$) is $T{C}^{\prime }$($S_1,s_1$), and the optimum takes place at ($S_1,s_1$) = (19, 5).

Table 5. TCR as a function of $S_1$ and $s_1$.

${\mathit{S}}_1/{\mathit{s}}_1$	2	3	4	5	6	7	8
18	0.67208	0.66955	0.65955	0.65436	0.65222	0.65190	0.65216
19	0.65650	0.65287	0.65073	0.64893	0.64894	0.65007	0.65168
20	0.66838	0.65296	0.65385	0.65768	0.66257	0.66786	0.67321
21	0.70294	0.70154	0.66367	0.66487	0.67006	0.68021	0.69014
22	0.78844	0.77510	0.76728	0.76571	0.68173	0.68243	0.69431

Let F = 5, $S_1=12$, $s_1=2$, $\beta =0.37$, $\mu =0.3$, ${\gamma }_1=1.01$, ${\gamma }_2=0.05$, $b_1=0.4$, $b_2=0.32$, $b_3=0.28$; $C^{C_1}=1.1$, $C^{C_2}=0.35$, $C^{P_1}=1.28$, $C^{P_2}=2.78$, $C^S=1.77$;

Furthermore, let $T{C}^{\prime }$($S_2,s_2$) = $TC(12,2,S_2,s_2,5)$.

This provides the TCR for different values of $S_2$ and of $s_2$.

The $T{C}^{\prime }$($S_2,s_2$) values are presented in Table 6. The optimal cost for each $S_2$ and $s_2$ are displayed in boldface and underlined, respectively. A convex function of ($S_2,s_2$) is $T{C}^{\prime }$($S_2,s_2$), and the optimum takes place at ($S_2,s_2$) = (16, 3).

Table 6. TCR as a function of $S_2$ and $s_2$.

${\mathit{S}}_2/{\mathit{s}}_2$	2	3	4	5	6
15	0.58260	0.57920	0.57942	0.58109	0.59306
16	0.58204	0.57138	0.57226	0.58004	0.58615
17	0.58123	0.58038	0.58045	0.59580	0.60113
18	0.59235	0.58550	0.58857	0.59855	0.60828
19	0.67502	0.59628	0.59979	0.60156	0.60891

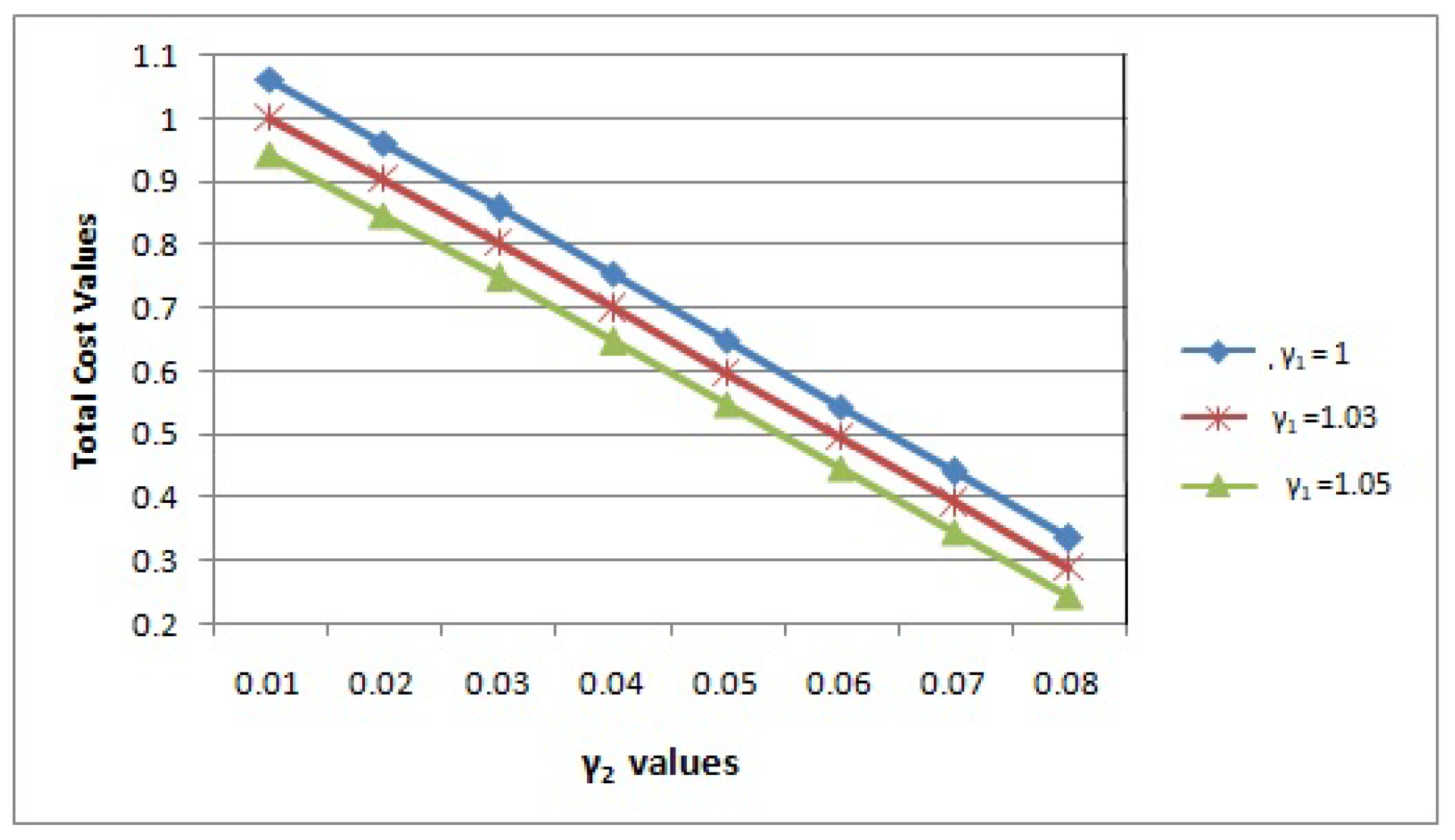
The impact of the second commodity perishable rate (${\gamma }_2$) on the TCR is shown in Figure 1 via three curves which relate to ${\gamma }_1=1,1.03,1.05$. We discovered that the TCR diminishes whenever the perishable rate of the first commodity (${\gamma }_1$) and the perishable rate of the second commodity (${\gamma }_2$) increase.

Figure 1. TC versus ${\gamma }_2$. $S_1=19$, $S_2=18$, F = 4, $s_1=5$, $s_2=2$, $\beta =0.3$, $\mu =1.7$, $\alpha =0.01$; $b_1=0.4$, $b_2=0.32$, $b_3=0.28$, $C^{C_1}=1.09$, $C^{C_2}=0.35$, $C^{P_1}=1.28$, $C^{P_2}=2.78$, $C^S=1.77$.

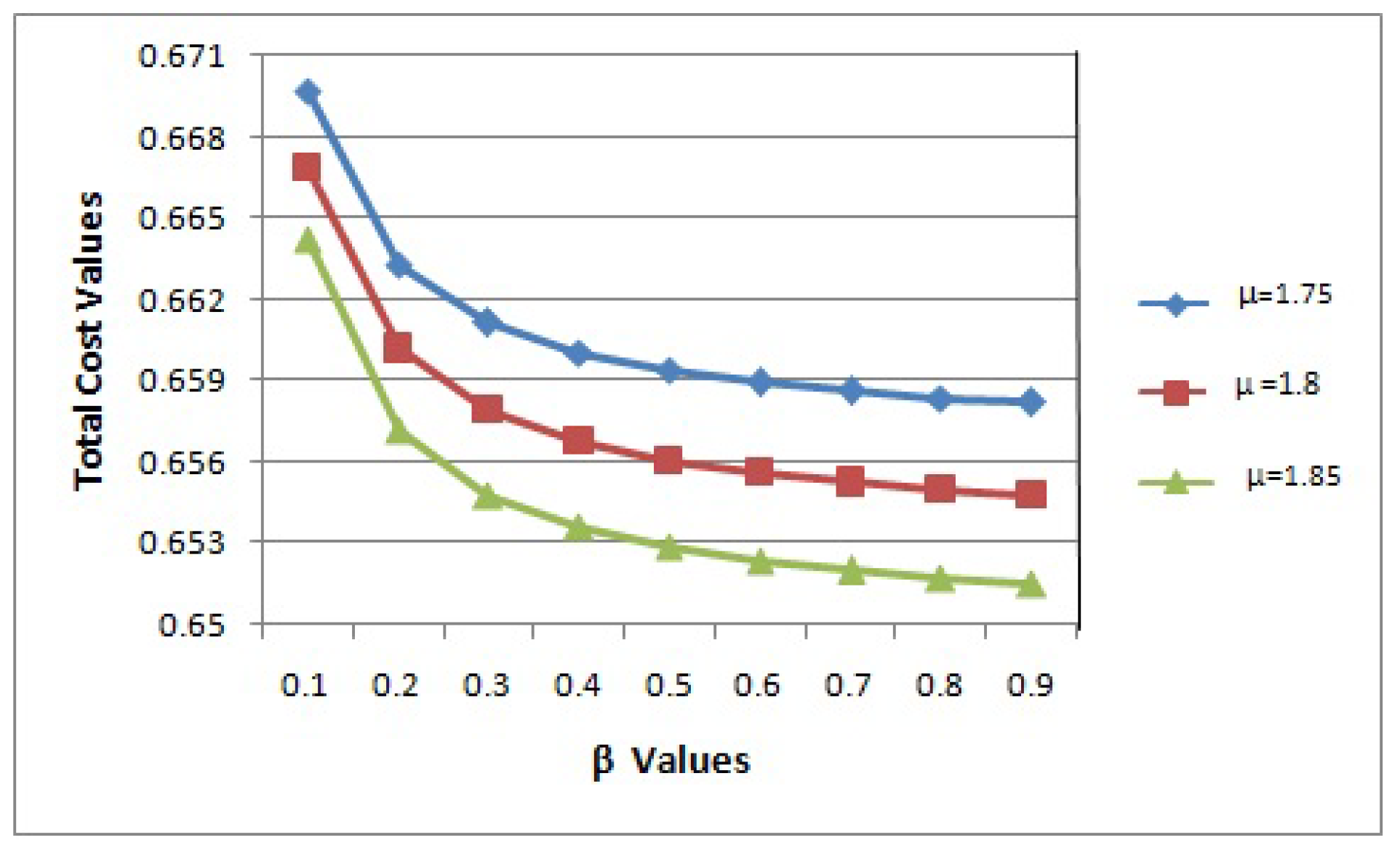
The outcome of the replenishment rate $\left(\beta \right)$ on the TCR is depicted in Figure 2 via three curves which relate to $\left(\mu \right)=1.75,1.8,1.85$. We discovered that the TCR diminishes whenever the service rate $\left(\mu \right)$ and the replenishment rate $\left(\beta \right)$ increase.

Figure 2. TC versus $\mu$. $S_1=19$, $S_2=18$, F = 4, $s_1=5$, $s_2=2$, ${\gamma }_1=1.01$, ${\gamma }_2=0.05$, $\alpha =0.01$; $b_1=0.4$, $b_2=0.32$, $b_3=0.28$, $C^{C_1}=1.09$, $C^{C_2}=0.35$, $C^{P_1}=1.28$, $C^{P_2}=2.78$, $C^S=1.77$.

In Table 7, Table 8 and Table 9, we demonstrate the outcome of the setup cost $C^S$ and the carrying cost of the first commodity $C^{C_1}$, and, similarly, the second commodity $C^{C_2}$ on the optimal point $(S_1^{*},s_1^{*})$ and the corresponding TCR $T{C}^{\prime }$. The other parameters and cost values are $S_1=19$, $S_2=18$, F = 4, $s_1=5$, $s_2=2$, ${\gamma }_1=1.01$, ${\gamma }_2=0.05$, $\alpha =0.01$; $b_1=0.4$, $b_2=0.32$, $b_3=0.28$, $C^{C_1}=1.09$, $C^{C_2}=0.35$, $C^{P_1}=1.28$, $C^{P_2}=2.78$, $C^S=1.77$;

Table 7. Impact of $C^{C_1}$ and $C^{C_2}$ costs on the optimal values.

${\mathit{C}}^{{\mathit{C}}_1}$/${\mathit{C}}^{{\mathit{C}}_2}$	0.33		0.34		0.35		0.36		0.37
	21	5	21	5	21	5	21	5	21	5
1.07	0.50896		0.54967		0.59039		0.63110		0.67181
	21	5	21	5	21	5	19	5	19	5
1.08	0.54520		0.58592		0.62663		0.66310		0.69720
	19	5	19	5	19	5	19	5	19	5
1.09	0.58074		0.61483		0.64893		0.68303		0.71713
	15	5	15	5	15	5	15	5	15	5
1.10	0.60066		0.63476		0.70296		0.73706		0.76484
	15	5	15	5	15	5	15	4	15	4
1.11	0.64349		0.71233		0.72289		0.78482		0.81679

Table 8. Impact of $C^{C_1}$ and $C^S$ costs on the optimal values.

${\mathit{C}}^{{\mathit{C}}_1}$/${\mathit{C}}^{\mathit{S}}$	1.75		1.76		1.77		1.78		1.79
	20	5	20	5	20	5	20	5	20	5
1.07	0.59257		0.59342		0.59426		0.59510		0.59594
	20	5	20	5	20	5	20	5	20	5
1.08	0.62292		0.62377		0.62461		0.63245		0.64230
	20	5	20	5	19	5	19	5	19	5
1.09	0.63327		0.63412		0.64893		0.66241		0.67195
	19	5	15	5	15	5	15	5	15	5
1.10	0.68520		0.68919		0.69501		0.69591		0.69821
	18	5	15	5	15	5	15	4	15	4
1.11	0.68663		0.69770		0.69877		0.69950		0.70116

Table 9. Impact of $C^{C_2}$ and $C^S$ costs on the optimal values.

${\mathit{C}}^{{\mathit{C}}_2}$/${\mathit{C}}^{\mathit{S}}$	1.75		1.76		1.77		1.78		1.79
	20	6	20	6	20	6	20	6	20	5
0.33	0.57182		0.57566		0.57950		0.58934		0.59919
	20	5	20	5	20	5	20	5	20	5
0.34	0.61555		0.61629		0.61723		0.62607		0.62692
	19	5	19	5	19	5	19	5	19	5
0.35	0.65187		0.65578		0.64893		0.66758		0.67748
	19	5	15	5	15	5	15	5	15	5
0.36	0.69012		0.69336		0.70359		0.71081		0.73876
	18	5	15	5	15	5	15	4	15	4
0.37	0.73502		0.75162		0.78509		0.79530		0.79741

From the Table 7, Table 8 and Table 9, we discover the monotonic behavior of $(S_1^{*},s_1^{*})$ as detailed below:

In Table 7, the TCR increases whenever both the carrying cost of the first commodity $C^{C_1}$ and the second commodity $C^{C_2}$ increases. In Table 8, the TCR increases when the carrying cost of the first commodity $C^{C_1}$ and $C^S$ both increase. Similarly, Table 9 shows that the TCR increases whenever the carrying cost of the second commodity $C^{C_2}$ and $C^S$ both increase. In addition, $(S_1^{*},s_1^{*})$ monotonically decrease for all the Table 7, Table 8 and Table 9. The carrying cost, as well as the set-up cost, are components of the TC function, so, whenever the holding cost and setup cost increase, the total cost value also increases.

Furthermore, acquiring a significant amount of inventory increases a company’s carrying costs, whereas ordering smaller amounts of items more regularly increases a company’s setup costs. However, we want to minimize both costs so the TC is determined to do this work.

8. Conclusions

In this article, we studied a two-commodity inventory system that consists of a finite waiting hall. We investigated performance analyses of a perishable $(s,Q)$ queueing-inventory system of two commodities with optional demands from customers. To obtain either a single item or only service without items, customer arrivals are analyzed using the MAP. We also obtained a steady-state vector. Furthermore, the outcomes were exemplified with numerical patterns to determine the convexity of the TCR. Similarly, we provided a numerical illustration that depicts the effect of the service rate on the inventory system’s TCR. In the numerical illustration, it is shown that the TCR diminishes because the service rates and replenishment rates are increased. The model describes the contribution of customers’ optional demands to the two-commodity system. We believe that the model portrayed and the investigation described have implications for a range of modern organisations since there are various kinds of customer demands, such as service requests without items. In the future, our proposed model can be used to explore more conditions, such as service and lead times under PH distribution, to assess whether customer arrivals might follow a batch Markovian arrival process, and to determine whether the server might also work under a vacation policy.