Multi-View Cosine Similarity Learning with Application to Face Verification
Abstract
:1. Introduction
2. Related Work
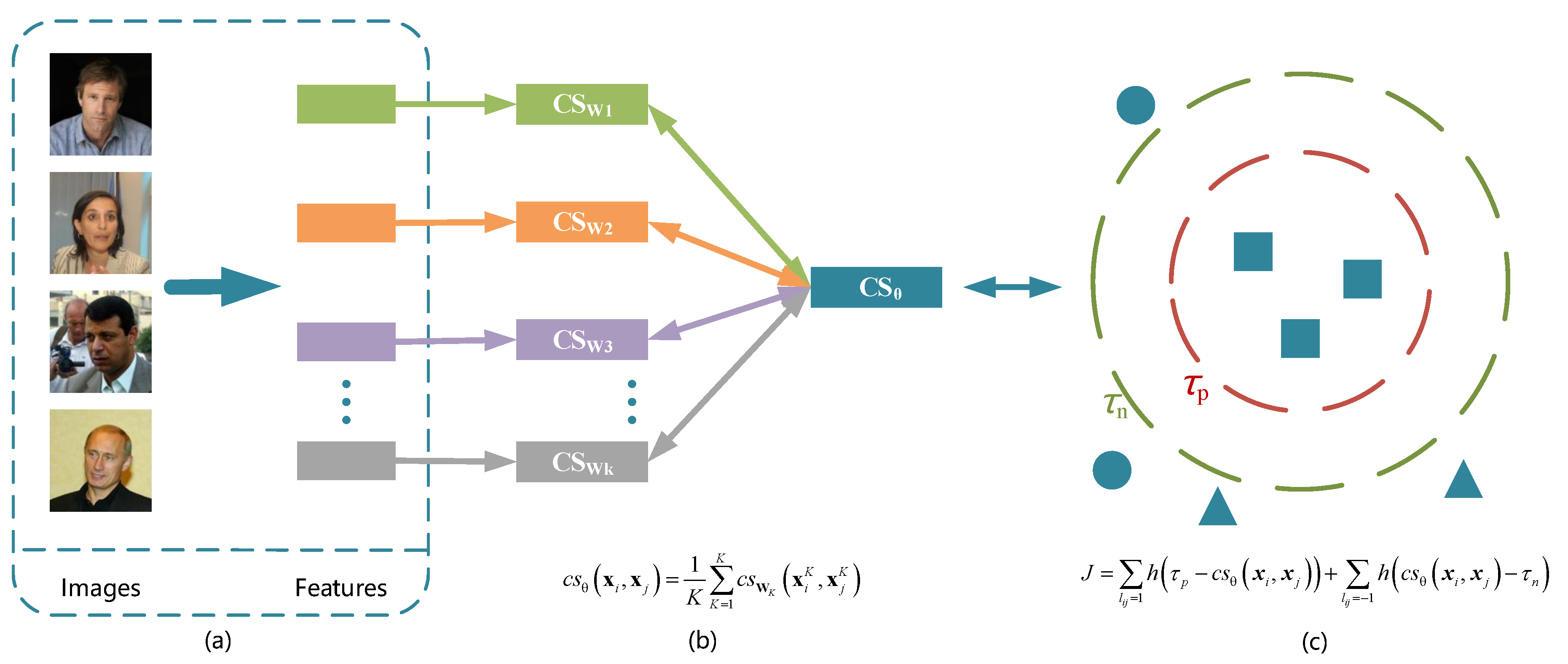
3. Multi-View Cosine Similarity Learning
| Algorithm 1: MVCSL |
| Input: Training set of the -th view; thresholds and ; learning rate ; total iterative number T; convergence error . Output: .
|
4. Experiments
- MVC-s: This is the single-view cosine similarity learning method that learns a single similarity metric via the objective function (3) using the single-view feature representation;
- Concatenation (abbrev., Con): All the multi-view feature representations are concatenated as a high-dimension feature vector, and then, the MVC-s method is employed to find out the cosine similarity;
- MVC-i: We independently learn the mapping for each view, and then, we add up the cosine similarities of all views as the final cosine similarity of a sample pair.
4.1. Fine-Grained Face Verification
4.1.1. Dataset and Settings
- LBP [12]: we partition an image into segments and obtain a 59-dimensional LBP for each segment; then, we finally achieve a 3776-dimensional feature representation by concatenating them.
- HOG [13]: we split an image into non-overlapping blocks and with two different sizes and compute a nine-dimensional HOG feature on each block. Finally, we achieve a feature representation of 2880 dimensions for each image.
- SIFT [11]: each facial image is segmented into 49 blocks to extract a feature representation of 6272 dimensions.
4.1.2. Experimental Results
4.2. Kinship Verification
4.2.1. Dataset and Settings
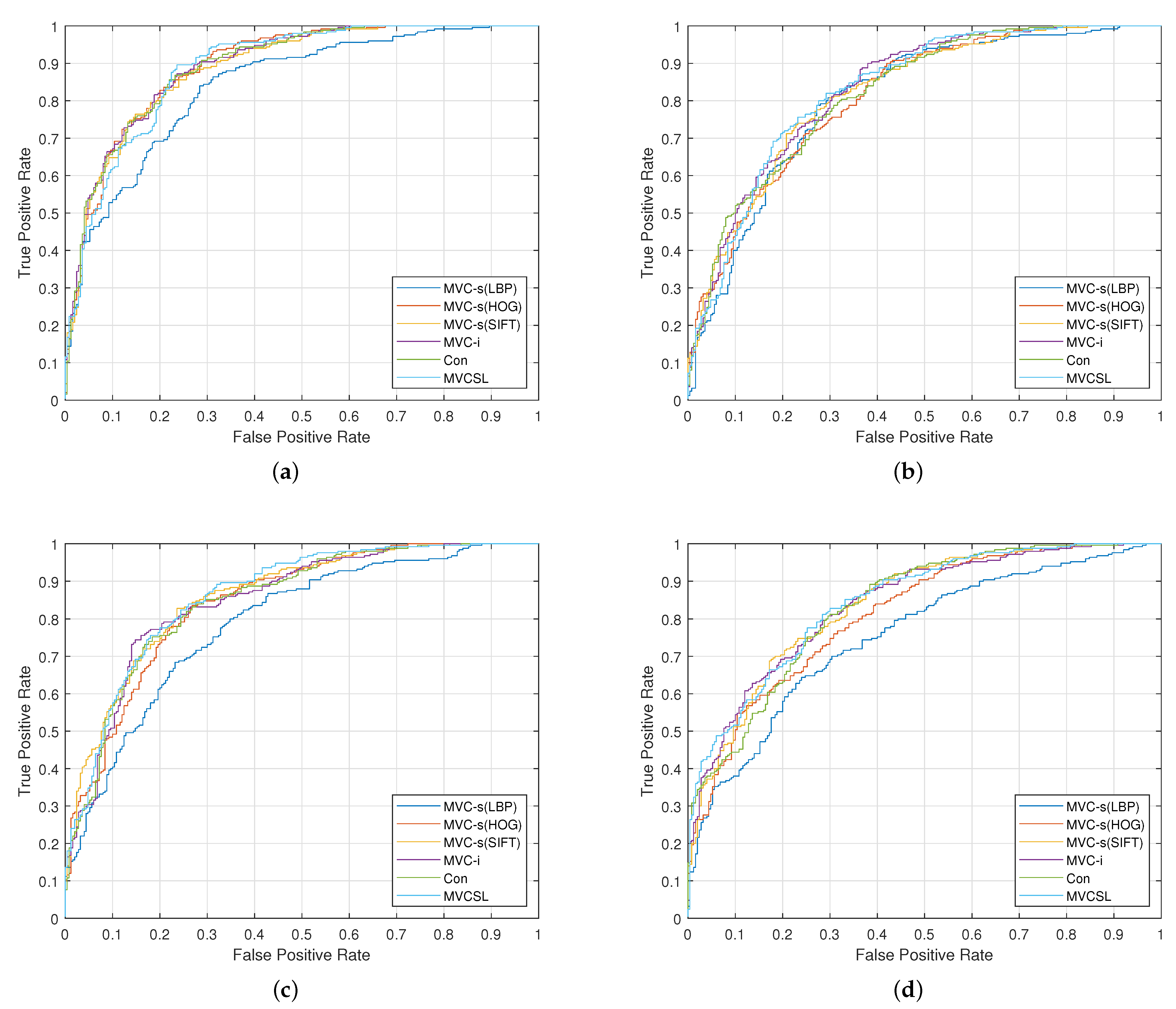
4.2.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suárez, J.L.; García, S.; Herrera, F. A tutorial on distance metric learning: Mathematical foundations, algorithms, experimental analysis, prospects and challenges. Neurocomputing 2021, 425, 300–322. [Google Scholar] [CrossRef]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Zheng, W.; Lu, J.; Zhou, J. Hardness-Aware Deep Metric Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3214–3228. [Google Scholar] [CrossRef] [PubMed]
- Karlinsky, L.; Shtok, J.; Harary, S.; Schwartz, E.; Aides, A.; Feris, R.; Giryes, R.; Bronstein, A.M. Repmet: Representative-based metric learning for classification and few-shot object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5197–5206. [Google Scholar]
- Huang, G.B.; Ramesh, M.; Berg, T.; Learned-Miller, E. Labeled Faces in the Wild: A Database for Studying Face Recognition in Unconstrained Environments; Technical Report 07-49; University of Massachusetts: Amherst, MA, USA, 2007. [Google Scholar]
- Kemelmacher-Shlizerman, I.; Seitz, S.M.; Miller, D.; Brossard, E. The megaface benchmark: 1 million faces for recognition at scale. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4873–4882. [Google Scholar]
- Lu, J.; Zhou, X.; Tan, Y.; Shang, Y.; Zhou, J. Neighborhood Repulsed Metric Learning for Kinship Verification. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 331–345. [Google Scholar] [PubMed]
- Wang, M.; Deng, W. Deep face recognition: A survey. Neurocomputing 2021, 429, 215–244. [Google Scholar] [CrossRef]
- Guillaumin, M.; Verbeek, J.; Schmid, C. Is that you? Metric learning approaches for face identification. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 498–505. [Google Scholar]
- Koestinger, M.; Hirzer, M.; Wohlhart, P.; Roth, P.M.; Bischof, H. Large scale metric learning from equivalence constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2288–2295. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Ahonen, T.; Hadid, A.; Pietikainen, M. Face description with local binary patterns: Application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 2037–2041. [Google Scholar] [CrossRef] [PubMed]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 886–893. [Google Scholar]
- Chen, N.; Zhu, J.; Sun, F.; Xing, E.P. Large-margin predictive latent subspace learning for multiview data analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2365–2378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, J.; Lu, J.; Tan, Y.P. Sharable and individual multi-view metric learning. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2281–2288. [Google Scholar] [CrossRef] [PubMed]
- Xing, E.P.; Jordan, M.I.; Russell, S.J.; Ng, A.Y. Distance metric learning with application to clustering with side-information. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 521–528. [Google Scholar]
- Weinberger, K.Q.; Saul, L. Distance Metric Learning for Large Margin Nearest Neighbor Classification. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2005; pp. 1473–1480. [Google Scholar]
- Davis, J.V.; Kulis, B.; Jain, P.; Sra, S.; Dhillon, I.S. Information-theoretic metric learning. In Proceedings of the Twenty-Fourth International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 209–216. [Google Scholar]
- Nguyen, H.V.; Bai, L. Cosine similarity metric learning for face verification. In Proceedings of the 10th Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; pp. 709–720. [Google Scholar]
- Tang, Z.; Wu, X.; Fu, B.; Chen, W.; Feng, H. Fast face recognition based on fractal theory. Appl. Math. Comput. 2018, 321, 721–730. [Google Scholar] [CrossRef]
- Gdawiec, K.; Domanska, D. Partitioned iterated function systems with division and a fractal dependence graph in recognition of 2D shapes. Int. J. Appl. Math. Comput. Sci. 2011, 21, 757–767. [Google Scholar] [CrossRef]
- Tan, T.; Yan, H. Face recognition using the weighted fractal neighbor distance. IEEE Trans. Syst. Man, Cybern. Part C (Appl. Rev.) 2005, 35, 576–582. [Google Scholar] [CrossRef]
- Wang, X.; Han, X.; Huang, W.; Dong, D.; Scott, M.R. Multi-similarity loss with general pair weighting for deep metric learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5022–5030. [Google Scholar]
- Xie, P.; Xing, E. Multi-Modal Distance Metric Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 1806–1812. [Google Scholar]
- Hu, J.; Lu, J.; Tan, Y.P.; Yuan, J.; Zhou, J. Local large-margin multi-metric learning for face and kinship verification. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 1875–1891. [Google Scholar] [CrossRef]
- Jia, X.; Jing, X.Y.; Zhu, X.; Chen, S.; Du, B.; Cai, Z.; He, Z.; Yue, D. Semi-supervised Multi-view Deep Discriminant Representation Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2496–2509. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Lu, J.; Tan, Y.P. Fine-grained face verification: Dataset and baseline results. In Proceedings of the International Conference on Biometrics, Phuket, Thailand, 19–22 May 2015; pp. 79–84. [Google Scholar]
- Deng, W.; Hu, J.; Zhang, N.; Chen, B.; Guo, J. Fine-grained face verification: FGLFW database, baselines, and human-DCMN partnership. Pattern Recognit. 2017, 66, 63–73. [Google Scholar] [CrossRef]
- Kan, M.; Shan, S.; Xu, D.; Chen, X. Side-Information based Linear Discriminant Analysis for Face Recognition. In Proceedings of the British Machine Vision Conference, Dundee, Scotland, 29 August–2 September 2011; pp. 1–12. [Google Scholar]
- Cao, Q.; Ying, Y.; Li, P. Similarity metric learning for face recognition. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2408–2415. [Google Scholar]
- Patel, B.; Maheshwari, R.; Raman, B. Evaluation of periocular features for kinship verification in the wild. Comput. Vis. Image Underst. 2017, 160, 24–35. [Google Scholar] [CrossRef]
- Zadeh, P.; Hosseini, R.; Sra, S. Geometric Mean Metric Learning. In Proceedings of the 33nd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2464–2471. [Google Scholar]
- Hu, J.; Lu, J.; Liu, L.; Zhou, J. Multi-view geometric mean metric learning for kinship verification. In Proceedings of the IEEE International Conference on Image Processing, Taipei, China, 22–25 September 2019; pp. 1178–1182. [Google Scholar]
- Yan, H. Learning discriminative compact binary face descriptor for kinship verification. Pattern Recognit. Lett. 2019, 117, 146–152. [Google Scholar] [CrossRef]
- Chen, J.; Hu, J. Weakly Supervised Compositional Metric Learning for Face Verification. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]


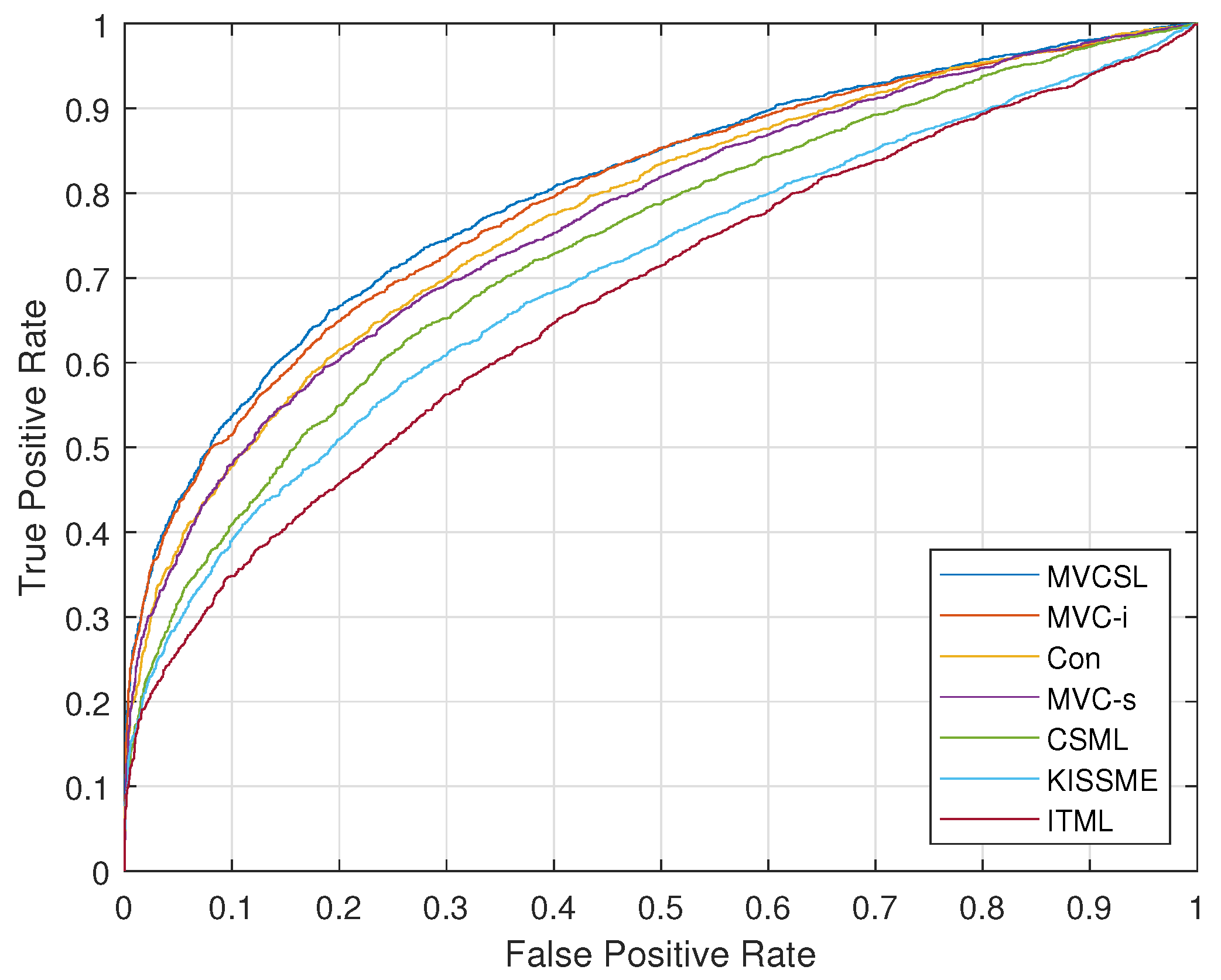
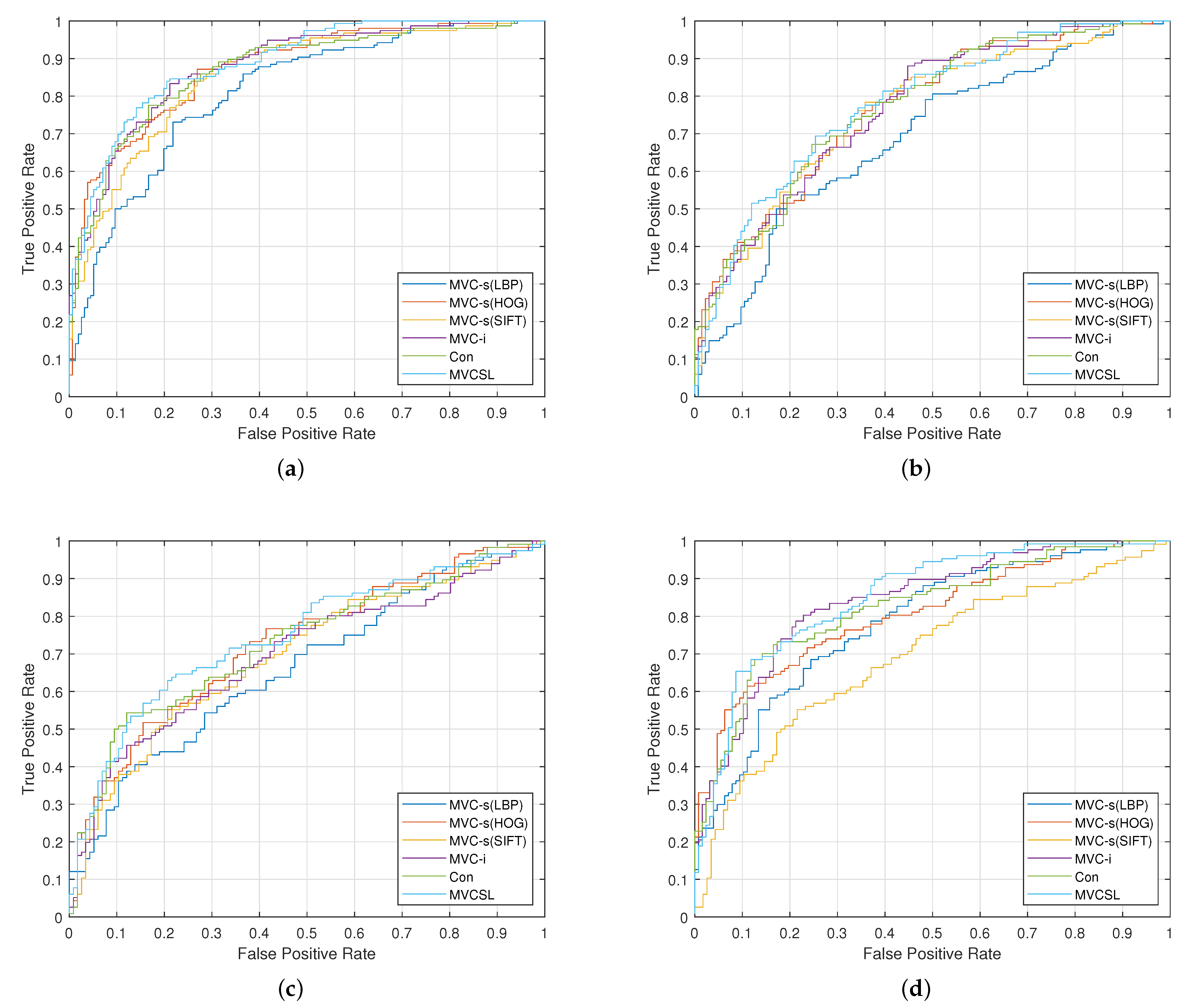
| Method | HOG | LBP | SIFT |
| ITML | 63.52 ± 4.41 | 62.86 ± 3.84 | 64.29 ± 4.29 |
| KISSME | 69.67 ± 3.37 | 68.35 ± 3.26 | 69.67 ± 3.40 |
| SILD | 70.00 ± 3.68 | 62.53 ± 3.17 | 68.57 ± 3.53 |
| CSML | 71.43 ± 1.94 | 72.31 ± 3.53 | 72.31 ± 3.24 |
| MVC-s | 79.23 ± 3.35 | 81.43 ± 1.96 | 78.90 ± 3.49 |
| Method | HOG, LBP, SIFT | ||
| Con | 84.95 ± 2.29 | ||
| MVC-i | 82.31 ± 2.73 | ||
| MVCSL | 86.70 ± 2.62 | ||
| Method | HOG | LBP | SIFT |
| ITML | 64.48 ± 1.54 | 65.07 ± 1.74 | 62.32 ± 1.84 |
| KISSME | 65.43 ± 1.29 | 66.60 ± 2.04 | 63.17 ± 2.36 |
| Sub-SML | 67.88 ± 2.32 | 69.18 ± 0.78 | 65.83 ± 2.01 |
| CSML | 68.00 ± 2.30 | 68.98 ± 2.83 | 67.87 ± 1.67 |
| MVC-s | 70.52 ± 2.22 | 71.18 ± 2.89 | 70.00 ± 1.39 |
| Method | HOG, LBP, SIFT | ||
| Con | 71.62 ± 1.51 | ||
| MVC-i | 73.33 ± 2.40 | ||
| MVCSL | 74.23 ± 2.14 | ||
| Method | F-S | F-D | M-S | M-D | Mean |
|---|---|---|---|---|---|
| MVC-s (LBP) | 77.57 | 70.17 | 68.04 | 76.84 | 73.15 |
| MVC-s (HOG) | 82.37 | 73.53 | 73.22 | 79.16 | 77.07 |
| MVC-s (SIFT) | 81.42 | 74.27 | 71.52 | 76.41 | 75.91 |
| MVC-i | 82.69 | 73.53 | 71.97 | 80.36 | 77.14 |
| Con | 83.01 | 74.64 | 72.81 | 79.96 | 77.61 |
| MVCSL | 84.30 | 75.38 | 74.53 | 81.16 | 78.84 |
| BNRML [31] | 76.28 | 70.51 | 73.70 | 72.47 | 73.24 |
| GMML [33] | 69.28 | 72.42 | 69.42 | 74.36 | 71.37 |
| MVGMML [33] | 69.25 | 75.00 | 69.40 | 72.76 | 71.13 |
| D-CBFD [34] | 79.60 | 73.60 | 76.10 | 81.50 | 77.60 |
| WSCML [35] | 81.90 | 73.95 | 72.88 | 72.90 | 75.21 |
| Method | F-S | F-D | M-S | M-D | Mean |
|---|---|---|---|---|---|
| MVC-s (LBP) | 78.80 | 76.80 | 74.60 | 71.80 | 75.50 |
| MVC-s (HOG) | 83.80 | 76.40 | 79.60 | 76.40 | 79.05 |
| MVC-s (SIFT) | 83.00 | 77.60 | 81.00 | 78.60 | 80.05 |
| MVC-i | 83.80 | 77.60 | 81.20 | 78.80 | 80.35 |
| Con | 83.60 | 78.03 | 81.00 | 78.00 | 80.15 |
| MVCSL | 84.80 | 79.00 | 81.80 | 78.40 | 81.00 |
| BNRML [31] | 79.40 | 79.00 | 77.00 | 72.80 | 77.05 |
| GMML [33] | 68.60 | 73.20 | 67.80 | 68.40 | 69.50 |
| MVGMML [33] | 70.40 | 73.40 | 65.80 | 69.20 | 69.70 |
| D-CBFD (HOG) [34] | 81.00 | 76.20 | 77.40 | 79.30 | 78.50 |
| [25] | 82.40 | 78.20 | 78.80 | 80.40 | 80.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Chen, J.; Hu, J. Multi-View Cosine Similarity Learning with Application to Face Verification. Mathematics 2022, 10, 1800. https://doi.org/10.3390/math10111800
Wang Z, Chen J, Hu J. Multi-View Cosine Similarity Learning with Application to Face Verification. Mathematics. 2022; 10(11):1800. https://doi.org/10.3390/math10111800
Chicago/Turabian StyleWang, Zining, Jiawei Chen, and Junlin Hu. 2022. "Multi-View Cosine Similarity Learning with Application to Face Verification" Mathematics 10, no. 11: 1800. https://doi.org/10.3390/math10111800
APA StyleWang, Z., Chen, J., & Hu, J. (2022). Multi-View Cosine Similarity Learning with Application to Face Verification. Mathematics, 10(11), 1800. https://doi.org/10.3390/math10111800






