A New Method for Reconstructing Data Considering the Factor of Selected Provider Nodes Set in Distributed Storage System

Abstract

In the distributed storage system, when data need to be recovered after node failure, the erasure code redundancy method occupies less storage space than the multi-copy method. At present, the repair mechanism using erasure code to reconstruct the failed node only considers the improvement of link bandwidth on the repair rate and does not consider the impact of the selection of data providing node-set on the repair performance. A single node fault data reconstruction method based on the Software Defined Network (SDN) using the erasure code method is designed to solve the above problems. This method collects the network link-state through SDN, establishes a multi-attribute decision-making model of the data providing node-set based on the node performance, and determines the data providing nodes participating in providing data through the ideal point method. Then, the data recovery problem of a single fault node is modeled as the optimization problem of an optimal repair tree, and a hybrid genetic algorithm is designed to solve it. The experimental results show that under the same erasure code scale, after selecting the nodes of the data providing node-set, compared with the traditional tree topology and star topology, the repair delay distribution of the designed single fault node repair method for a distributed storage system is reduced by 15% and 45% respectively, and the repair flow is close to the star topology, which is reduced by 40% compared with the traditional tree repair.

1. Introduction

With the rapid development of computer technology and internet applications, data services grow exponentially, resulting in an increasing demand for storage space. Under this trend, distributed storage has become the mainstream storage structure of large-scale data centers because of its high-cost performance and scalability [1]. However, a distributed storage system contains many storage nodes, and the problem of data failure caused by node failure often occurs.

Distributed storage often adopts the method of increasing data redundancy and data reconstruction to solve the problem of data failure of failed nodes. Common data redundancy methods include multi-copy technology [2] and erasure code technology [3]. Although the multi-copy technology is simple and easy to implement, it needs to consume a lot of storage space in the process of storage redundancy. Erasure code correction technology [4] has the advantages of high storage efficiency and good flexibility, but its repair flow is high and the repair rate is slow. With the increase in the number of nodes in distributed storage, the advantage of low overhead of erasure code storage [5] is becoming more and more obvious. The research on erasure code storage has gradually become a hot spot.

When the fault node is repaired by erasure code, a new node (called newcomer) will be obtained from the idle node-set named N_n to replace the node. The newcomer will select multiple surviving nodes (called providers) from the surviving node-set named N_p to download data blocks, transfer data to the newcomer node, and reconstruct the failed node. This process produces a lot of network overhead, resulting in a low repair rate of erasure code. Additionally, this process can be modeled as a decision-making problem; the authors in [6] proves the effectiveness of cluster analysis as a decision-making tool. The authors in [7] combine the net present value (NPV) and break-even point (BEP) analysis, and realize the integration of battery energy storage system into photovoltaic (PV) power station in residential environment. In the traditional erasure code data repair process, providers use the star topology to transfer the repair data to the newcomer; in this case, the newcomer needs to receive data from all nodes before starting the repair work. Therefore, the repair delay depends on the link with the slowest transmission in the topology, and the link with the smallest bandwidth is called the bottleneck link. In the star topology, if the bottleneck bandwidth is low, the repair delay of the whole topology will be greatly increased. In the later research, the researchers proposed a tree repair topology to replace the original star topology. With the newcomer as the root node and providers as the child nodes, the links with higher available bandwidth were selected to join the repair topology to reduce the repair delay.

Compared with the star repair topology, the traditional tree repair topology does improve the data repair rate, but it brings greater traffic overhead to the storage cluster network. Then, finding the optimal repair tree through the greedy algorithm in traditional tree repair topology is a locally optimal solution. Constructing the optimal repair tree is a subtree of the generating tree in the graph, it can be abstracted as a Stener Problem, and it is an NP-hard problem. With the increase in storage scale, the construction time of repair topology will increase exponentially, which will bring huge repair delays to the storage system with a large cluster scale. In addition, in the distributed storage system, the number of storage nodes is huge and the performance among nodes is heterogeneous. If the newcomer participating in the repair has poor performance, it will increase the repair delay caused by the calculation of erasure codes. If there are nodes far away from the newcomer in the selected provider, a repair tree with bigger hops will be obtained, resulting in greater repair traffic, which will greatly affect the repair efficiency of nodes. In traditional tree repair, the selection of repair node-set is random and only considers the heterogeneity of link bandwidth between nodes, but ignores the impact of heterogeneous performance between different nodes and the number of repair tree hops on repair traffic. Therefore, selecting a repair node-set with better performance and smaller distance will greatly reduce the repair overhead. This lays a good foundation for establishing a tree repair topology with better repair delay and repair traffic.

In the process of repairing the faulty node, it is also necessary to obtain the network state through measurement. The pieces of information such as link bandwidth and transmission delay are conducive to the construction of the repair topology when reconstructing the data. In the past, the traditional network measurement methods either have cumbersome configuration or high measurement overhead, which brings a lot of measurement tasks to node repair and reduces the rate of node repair. With the emergence of more flexible network measurement methods called Software Defined Network [8] SDN, it simplifies network measurement and management, provides flexible and efficient maintenance strategies, and effectively solves the problems of traditional network measurement methods, but it is rarely used in the link-state measurement of distributed storage.

To solve the above problems, this paper combines SDN technology to measure and obtain the link bandwidth, transmission delay, and other network state information of the link between nodes and then establishes a multi-attribute decision-making model that comprehensively considers the adjacent bandwidth, storage performance, CPU core number, and I/O performance of the nodes in the set of all surviving nodes. The ideal point method is used to select the newcomer node and providers’ node-set for fault data reconstruction. With the selected newcomer and providers, to build a repair tree topology with optimal repair time performance and repair traffic performance, a Steiner tree optimization model with constraints is established. A hybrid genetic algorithm based on the K-shortest path is designed to solve this NP-hard discrete optimization problem.

In summary, the innovations of this paper are as follows:

(1) In the actual data reconstruction of the fault node, the performance of selecting different nodes to participate in the repair process is different. This paper considers the selection of the newcomer and the providers node-set for the first time and builds this problem into a multi-attribute decision-making model to solve, to determine the reasonable node-set to participate in the repair.

(2) To build a repair tree topology with optimal repair time performance and repair traffic performance, a Steiner tree optimization model with constraints is established, which is solved by designing a hybrid genetic algorithm based on the k-shortest path. k-path is used for node preprocessing to screen out some links with poor performance for hybrid genetic algorithms. The designed method can obtain the approximate global optimal solution in a short time, which effectively solves the NP-hard problem of traditional tree repair when there are too many nodes and the problem that traditional tree repair easily falls into the dilemma of local optimization.

(3) The final experiments show that the single node repair scheme designed in this paper reduces the repair delay by 15% and 45%, respectively, compared with the traditional tree repair and traditional star repair, and the repair flow is also reduced by 40% compared with the traditional tree repair.

The rest of this paper is organized as follows. Section 2 introduces the research status of erasure code in the distributed storage system. Section 3 analyzes the influence of topology, repair traffic, and node performance on the repair process, deduces the node selection strategy, and establishes the mathematical model of topology construction. Section 4 describes in detail the design and algorithm flow of each operator of the genetic algorithm proposed in this paper. Section 5 designs experiments to compare and analyze the performance differences between this algorithm and traditional star and tree repair algorithms, and also analyzes the influence of parameters in the algorithm. Section 6 summarizes the full text and prospects the future research direction.

2. Related Work

There are two main storage redundancy strategies, one is multi-copy, the other is erasure code [9]. Erasure codes originated in the field of communication and transmission. With the growth of storage reliability requirements, erasure codes are gradually applied to data error detection and error correction in storage systems [10].

With the continuous expansion of the scale of the storage system, it is difficult for the multi-copy method to meet the requirements of the massive storage system for the redundant backup mechanism due to its low disk utilization [11]. The advantages of the erasure code method in its low storage overhead are becoming more and more obvious. The research related to erasure code technology has also become a research hotspot in the industry. The existing research on erasure code [12] storage mainly focuses on two aspects: the improvement of the coding mechanism and the construction of topology in the repair process.

On the improvement of erasure code coding mechanism: Lin Xuan, Wang Yijie, et al. [13] proposed grouping repair code (GRC) to overcome the high cost of multi-node failure repair and created a code with both global check and local check. Wang Jing et al. [14] took the minimum storage regeneration code (MSR code) as the local code and constructed the local repair code on the premise of ensuring the maximum distance separability and simple repair characteristics. Zhou Yue et al. [15] proposed a new piggyback code based on MDS code and gave its general construction and repair algorithm. By constructing new piggybacks addition rules, the problem of solving equations in finite fields is effectively avoided. Zhang Xiaoyang et al. [16] designed a PLRC code that uses node prediction technology to predict bad node blocks and reduce the group leader of bad blocks, to reduce the consumption of repair bandwidth. However, this coding relies too much on the accuracy of node prediction. Wang Zizhong et al. [17] designed a hybrid code based on the characteristics of fast repair efficiency of local repair code and low storage overhead of the Hitchhiker code, which uses LRC to store hot data and the Hitchhiker code to store cold data, but its coding conversion mechanism is too ideal.

In terms of topology construction in the process of erasure code repair [18,19,20]: Huang Jianzhong et al. [21] proposed a pipeline repair scheme. Each surviving node transmits data and integrates into a one-to-one mode, which improves the efficiency of the repair process and reduces its network overhead. However, this is essentially a serial transmission mode, so it cannot achieve the optimal repair rate. Xie Xianzhong [22] designed an MDS dual-code architecture and proposed a multi-node cooperative precise repair scheme (MER) suitable for simultaneous repair of multiple system nodes and redundant nodes through the expansion of E-MDS code. Jun Li et al. [23] proposed to design a new repair model tree based on the principle of regenerative code and network topology selection for the storage cluster with regenerative code mechanism, but its repair topology still has the problem of large repair traffic. Wan Xiaoyong et al. [24] comprehensively considered the impact of the actual network topology on the repair process and proposed the STNR algorithm to integrate the repair traffic at the intermediate node. Through the combination of the minimum cost path heuristic algorithm and ant colony algorithm to construct the optimal repair topology, it can not only improve the repair efficiency, but also reduce the repair traffic in the cluster, but its network measurement efficiency is low. H. Zhang et al. [25] considered the actual network topology and used the idea of k-path and heuristic greedy algorithm to build the topology, but they only considered that the greedy algorithm would easily fall into the dilemma of local optimization, did not consider other performance characteristics of the link, and did not achieve load balancing. Evolutionary algorithms are global optimization methods with high robustness and applicability [26,27,28,29]. The authors in [30] applied machine learning to evolutionary algorithms to improve the overall quality and performances of the prediction model. In [31], some specifically designed genetic operators are proposed, and two classical MOEA frameworks are adaptively combined. K.SEO et al. [32], using the idea of maximum cut, used a genetic algorithm to calculate the maximum cut of the link to build the optimal repair topology, however, it only considers the nodes providing data in the link, and there is no intermediate node transmission.

In addition, the acquisition of link information is essential in the construction and repair of topology. The traditional network measurement method has complex configurations and difficult operations. Due to its simple configuration and flexible operation, SDN has gradually replaced the traditional network measurement method in the application of large-scale clusters and data centers. The research on SDN technology is also becoming more and more mature, and the application of software-defined networks in large-scale clusters and data centers has become a research hotspot. Literature [33] proposed that SDN should be applied to the network architecture of data centers to use its programmability for centralized network configuration and management. Literature [34] uses an SDN method similar to OpenFlow and applies it to Ethernet fiber channel (FCoE) networks to control storage traffic. Furthermore, [35] proposes an SDN multipath routing scheme to dynamically control data routing according to the network state in the storage cluster. Although the research on SDN is very mature, it is rarely applied to network condition measurement in node repair. In [36], we adopted SDN and proposed a hybrid genetic algorithm to solve the one single failure node repair problem, but it did not consider the factor of data providers set, it will affect the performance directly.

In this paper, the network condition measurement based on SDN is considered. For the failure of the most widely used RS codes storage nodes, the multi-attribute decision-making method is used for node selection, and a hybrid genetic algorithm for constructing an approximate global optimal repair topology with optimal repair performance is designed to complete the repair of the failed nodes. Finally, it solves the problem of large repair overhead and computational overhead of traditional repair topology in dealing with large-scale storage redundancy.

3. Description and Modeling of Single Node Failure Repair Problem

Aiming at the problems faced in the process of erasure code repair mentioned above, this chapter first introduces the principle of erasure code repair and then analyzes the impact of repair topology and topology repair flow on the repair process. Then, the mathematical model of node selection is established, and the repair topology model is proposed.

3.1. Repair Principle of Erasure Code

RS coding was first proposed by Reed et al. [37], which is an error correction coding widely used in the field of data communication. Due to the characteristics of MDS code, the RS code storage system has the best storage efficiency. Compared with our previous work [38], we have research the write operation in distributed storage system in the multi-copy way, both the multi-copy and RS coding way should both conduct the multicast problem.

Taking the classical vandermond RS code (k + r, k) as an example, the original data with the size of M is divided into k data blocks with the size of M/k. By performing multiplication with the vandermond generated matrix in Galois domain GW (2^w), r check blocks are obtained. The loss within any r block in the k + r block can be obtained by the replacement node from any k nodes in the remaining surviving nodes, performing encoding and decoding operations to obtain the original data and repair the lost data.

3.2. Influence of Network Topology on Repair Delay

In the actual physical network, the link bandwidth between nodes is often different. In the process of node repair, the delay of system transmission mainly depends on the bottleneck bandwidth on the data block transmission link. In the process of data block transmission, the appropriate transmission path can be selected for a specific data block to avoid those links with low bandwidth, so as to reduce the transmission delay.

To show the impact of network topology on repair delay, we assume a network topology using the erasure code disaster recovery cluster. There are five nodes: V0, V1, V2, V3, and V4. The link bandwidth between them has been marked (unit Mbps) and M = 500 Mb data is stored in it. If (5,2,4) coding is adopted and V0 is the newcomer node, the repair topology is shown in Figure 1a. During the repair process of the topology, each node needs to pass β = M/(k (d − k + 1)) = 100 Mb, repair delay t = β/20 Mbps = 5 s. If the tree repair topology is adopted, as shown in Figure 1b, the repair delay t = max (β/40 Mbps, 2β/100 Mbps) = 2.5 s, the bottleneck chain route (V0, V3) becomes (V0, V4). It can be found that because the tree repair topology is more diversified in the selection of the optimal repair path than the star topology, and it can make full use of some relatively idle links in the cluster network to improve the overall repair efficiency. Therefore, the problem of finding the optimal repair delay topology can be transformed into a classical minimum spanning tree problem. Find a tree repair topology t = (V_T, E_T) in the whole network topology. At this time, if you want to minimize the repair delay of the whole topology, that is, if the bottleneck bandwidth W_ij of the topology is the shortest, then the optimal repair tree T^* satisfies Formula (1).

$$T^{*}=\underset{T}{\arg }max(min{w}_{ij}),e_{ij}\in E_T$$

(1)

From the above analysis, the delay of parallel tree repair is much smaller than that of star repair direct transmission path. It can be seen that different logical network topologies have obvious differences in the repair performance of erasure codes. In the single-node repair process of erasure code, by making rational use of the actual network topology and link bandwidth information and using the coding operation ability of intermediate nodes, a tree repair path for the data block to be repaired can be constructed, which can effectively reduce the repair delay.

3.3. Repair Flow

Although the repair speed of tree repair is higher than that of star repair, due to the complexity of repair topology, the selection of provider with high link bandwidth also brings huge repair traffic, and the traffic required to be transmitted by each link is the number of providers in its connected subtree multiplied by the amount of transmitted data β, which makes the burden of links close to newcomer much greater than that of links close to providers, more likely causing the problem of congestion. With the increase in the scale of erasure code, the repair topology is more complex, and the problem of repair traffic is more obvious. Through the combination of intermediate node aggregation and reducing the number of hops of repair topology, the problem of excessive repair traffic in traditional tree repair can be effectively reduced.

3.3.1. Repair Flow

Some received data packets are aggregated through the intermediate node, and the data recovery operation is carried out immediately and then forwarded. Due to the strong operation ability of the current computer and the small amount of calculation of erasure code repair, the proportion of operation time in transmission time is very small, which can be ignored. As shown in Figure 2, Figure 2a shows the repair flow on each link in the topology when performing traditional tree repair; the repair traffic of each link is β. It can be seen that when the data in newcomer need to be repaired, the traffic in the overall repair topology is traffic = {a + b + c + a + b + d} = 6β. In Figure 2b, the data are preliminarily calculated and processed in each node, then the repair traffic of its subtree is aggregated at the intermediate node V2, and finally, the complete decoding operation is completed at the newcomer. At this time, the traffic in the repair topology is traffic = {a + 2b + 3c + (a + 2b + 4d)} = 4β. At this time, the repair traffic is aggregated through the intermediate node, which reduces by 1β repair traffic. The larger the size of the erasure code cluster, the more repair traffic will be reduced in this mode. For link S_i, the reduced repair traffic satisfies Formula (2).

$$\phi (S_i)=in(S_i)-out(S_i)$$

(2)

The total traffic saved is:

$$\phi (T)={\displaystyle {\sum }_1^{N-2}\phi (S_i)}$$

(3)

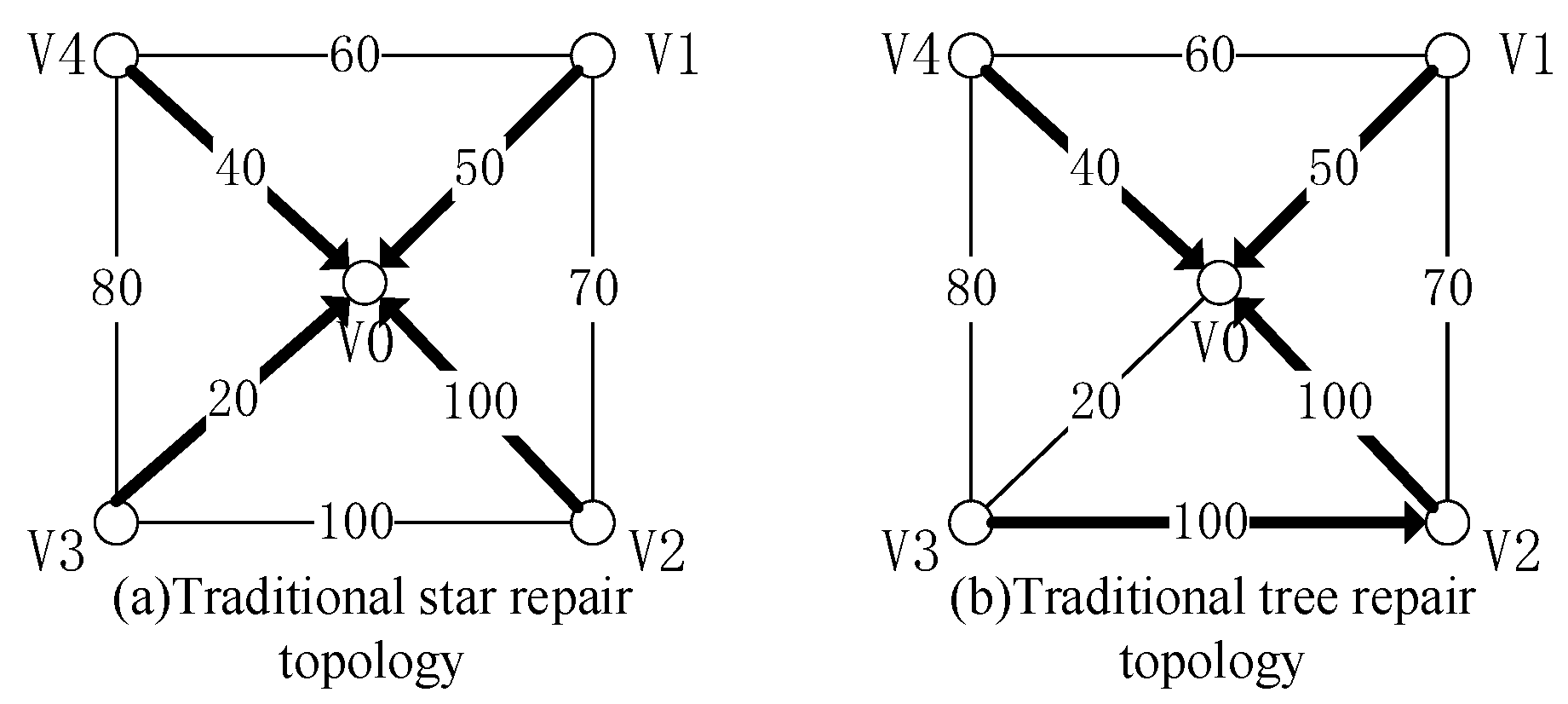
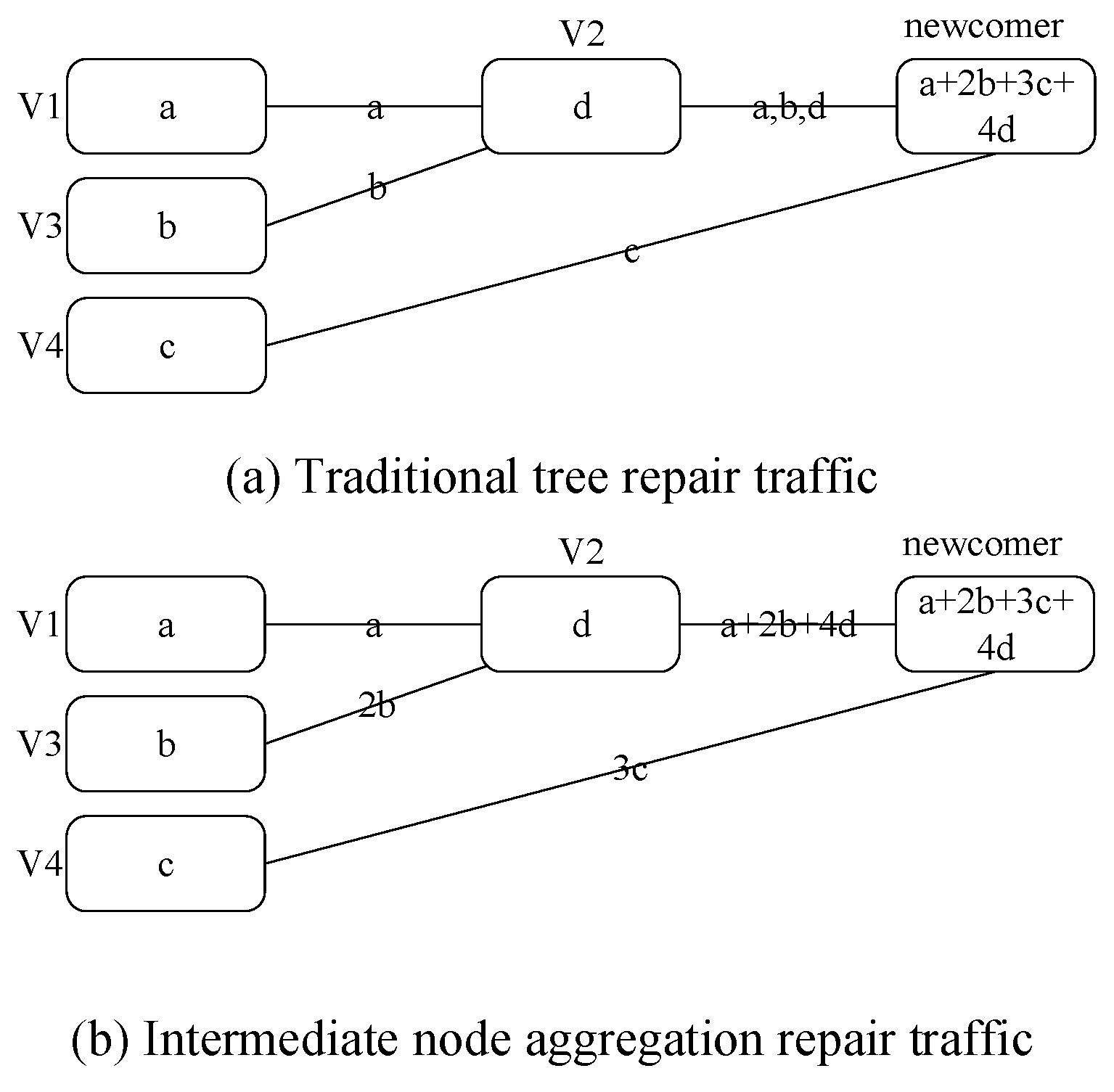
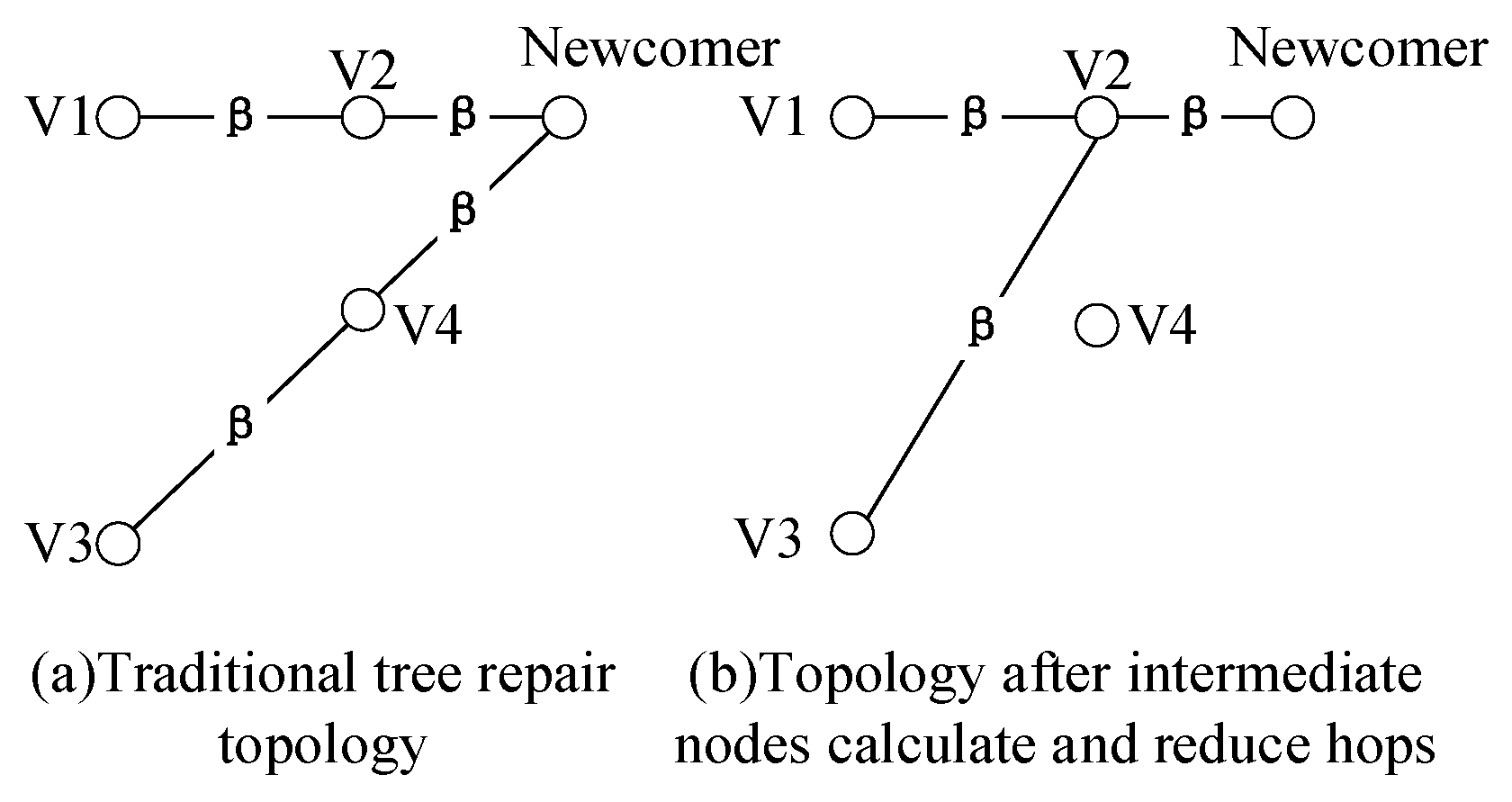
3.3.2. Minimum Hops

With the addition of the intermediate node aggregation mechanism in Section 3.3.1, when more traffic consolidation is in the whole repair topology, the repair traffic will be further reduced. As shown in Figure 3, Figure 3a shows a repair topology in the traditional tree repair. It can be seen from the figure that when the failed node is repaired, even though, in the aggregation of intermediate nodes, the repair traffic of 1β needs to be transmitted from V1, V2, V3, and V4 nodes, and a total of 4β needs to be transmitted.

Figure 3b reduces the number of links in the repair topology through the topology construction. By transmitting the data of nodes V1 and V3 to V2, the repair traffic of 3β in the topology is reduced by 1β compared with that in the traditional topology. Therefore, in the topology construction, when the number of hops is reduced, the overall repair traffic will also be reduced. In the repair process, the relationship between the required repair traffic and the amount β and hops of data transmitted by each node meets the following formula:

$$\varphi (T)=\min (\beta *{\displaystyle \sum hop})$$

(4)

3.4. Node Selection for Single Node Fault Repair

Node selection is very important for node repair. The speed of node processing capacity directly affects the speed of node repair and the quality of topology construction. This section designs a node selection scheme for single node fault repair to select supply nodes and newcomer nodes with better performance for later topology construction.

Referring to the definition of node processing capacity in the repair topology in the research of Qi Fenglin et al. [39], each node V_i has independent adjacency bandwidth, memory attributes, CPU cores, and Disk I/O. For these attributes γ₁, γ₂, …, γ_k, …, γ_m, m corresponds to the serial number of attributes, α₁, …, α_i is the weight of different attributes, and the processing capacity of the node is:

$$proces{s}_i={\displaystyle {\sum }_{k=1}^m{\alpha }_k{\gamma }_k}$$

(5)

Assuming that the repair traffic on node V_i is represented by M_i, the processing time of the node for reading, encoding, and forwarding the repair traffic is:

$$t_{V_i}=\epsilon \frac{D_i}{proces{s}_i}$$

(6)

In Formula (6), $\epsilon$ is the capacity conversion coefficient. Considering the processing delay of intermediate nodes, the repair delay t (V_i, V_j) of link (V_i, V_j) is transformed from β/ω to:

$$t_{(V_i,V_j)}=\epsilon \frac{D_i}{proces{s}_i}+\frac{\beta }{\omega (V_i,Vj)}+\epsilon \frac{D_j}{proces{s}_i}$$

(7)

How the node with better processing capacity is selected will directly determine the node processing capacity of single node repair and the overall repair rate after the repair topology is established. Therefore, we need to consider designing a better node selection algorithm and selecting a better set of repair nodes. Therefore, starting from the node performance, this paper designs a single node repair node selection scheme, which effectively selects a better node-set to participate in the construction of repair topology.

3.5. The Optimal Repair Tree Construction Problem after Repairing the Node-Set Is Determined

Based on the previous analysis of the coding mechanism and the two main problems in the process of tree repair topology repair, the optimal repair topology based on a hybrid genetic algorithm can be obtained through the repair node-set obtained by node selection.

Based on the sub-cluster design after considering the node selection, this section uses undirected connected graph G = (V, E, P, W) to represent the topology of the distributed storage system, where V = {v₁, v₂, …, v_n} represents the set of n nodes in the distributed storage system. E= {e₁, e₂, …, e_m}, where e_s (1 ≤ s ≤ m) = (v_i, v_j) represents the link between any two nodes v_i, v_j in the topology. W = {ω(v_i, v_j)|(v_i, v_j)∈E} represents the remaining bandwidth on the link and represents the processing capacity of the v_i node itself when v_i = v_j. P = {p₁, p₂, …, p_k}, where p_r(1 ≤ r ≤ k) = (v_i, v_n)|v_i∈V_p) represents the r best path cost between node v_i and node v_n in the topology.

For the single node failure scenario in which the repair node-set is determined, starting from the comprehensive optimization of the repair traffic and repair delay of the repair topology, based on the bandwidth sensing and preprocessing of SDN, a globally optimal repair tree is constructed by using the hybrid meta-heuristic algorithm. Combined with Formula (4) and Formula (7), the repair tree needs to meet the following Formula (8), where 1 and 2 are the weights of bandwidth attribute and hop attribute, respectively.

$$\begin{array}{l}\min \{{\alpha }_{bw}\max [\epsilon \frac{D_i}{proces{s}_i}+\frac{\beta }{\omega (V_i,Vj)}+\epsilon \frac{D_j}{proces{s}_i}\\ |(V_i,V_j\in E)]+{\alpha }_{hop}\min (\beta *{\displaystyle \sum hop})\}\end{array}$$

(8)

Constructing an optimal repair tree topology that meets the above conditions and has the optimal repair rate and minimum repair flow will greatly reduce the repair rate and repair flow of the whole single node repair process and occupy fewer system resources. Therefore, we need to consider designing a better topology construction algorithm and constructing a globally optimal repair topology. Therefore, based on the selection of node-set, this paper initializes its path and encodes it into a single node repair topology construction scheme. This scheme not only solves the NP-hard problem of traditional repair topology when there are too many nodes but also constructs an optimal Steiner tree repair model with approximate global optimization.

4. Considering the Single Node Fault Repair Method Based on SDN and Genetic Algorithm after Repairing the Node-Set

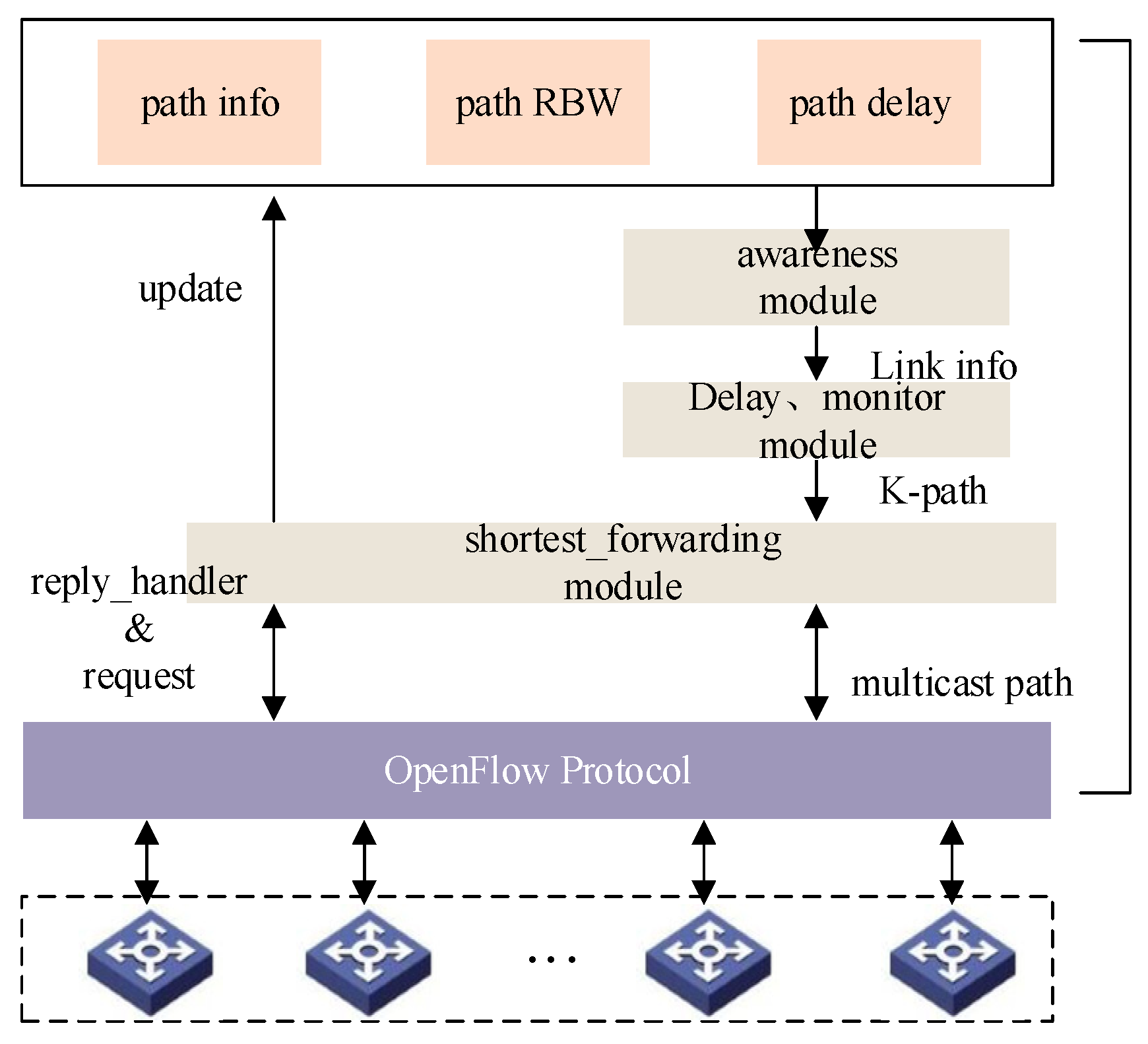
4.1. SDN Network Measurement

Ryu is an open-source SDN controller, which is completely implemented by Python. Ryu currently supports all versions of the OpenFlow protocol. Users can write code in the app module to meet their own needs. Mininet is a lightweight network simulator based on Linux container virtualization technology. It can create an openvswitch supporting the OpenFlow protocol. It is also the distributed storage network simulator used in this paper. Ryu controller senses the topology information through the awareness module through the OpenFlow protocol, collects the link delay and bandwidth status using the delay and monitor modules, and packet_in the path between nodes in mininet through the forwarding module. Refer to our original working literature [38], and its system structure is shown in Figure 4 below.

4.2. Node Selection Strategy

The selection of nodes is divided into two steps. Firstly, select the newcomer node. For this, this paper uses multi-attribute decision-making to sort the node attributes and selects the nodes with better processing capacity and adjacent bandwidth attributes from N_n as the newcomer node. Then, since the nodes in the idle node-set are basically in the same area in distributed storage, we rank the bandwidth attributes of the direct bandwidth between the nodes in N_p node-set and N_n node-set to obtain the providers nodes with good bandwidth performance and close to the newcomer node.

4.2.1. Newcomer Node Selection Based on the Multi-Attribute Decision

The following describes the process of multi-attribute decision-making for N_n nodes and the process of obtaining the required newcomer node. Formula (10) is used to normalize the decision matrix M; a standardized decision matrix M′ can be obtained by the attributes as rows and nodes as columns in N_n, where i and j are the row and column numbers of the matrix M′ and n is the number of nodes.

$$M=\left[\begin{array}{llll}{B}_1& -L_1& -C_1& -R_1\\ B_2& -L_2& -C_2& -R_2\\ B_3& -L_3& -C_3& -R_3\\ B_n& -L_n& -C_n& -R_n\end{array}\right]$$

(9)

$$M_{ij}^{\prime }=\frac{f_{ij}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{f}_{ij}^2}}},i=1,2,\dots ,n;j=1,2,3,4$$

(10)

The obtained decision matrix is weighted, and the standardized weighted decision matrix Z is obtained through the appropriate weighting coefficient W. The weight value in Formula (11) is generally obtained through experiments. In the later experiment, we find set W = [0.4, 0.3, 0.2, 0.1] will achieve the best performance.

$$W=[W_1,W_2,W_3,W_4]$$

(11)

$$Z=W*M_{ij}^{\prime },i=1,\dots ,n;j=1,2,3,4$$

(12)

Take the positive ideal solution and negative ideal solution as the maximum and minimum values of each attribute value in Z, respectively, and calculate the distance D⁺ and D⁻ from each node to the positive and negative ideal solution through Formula (13).

$$\begin{gathered} D_i^{+}=\sqrt{{\displaystyle {\sum }_{j=1}^4{(Z_{ij}-Z_j^{+})}^2}} \\ {D}_i^{-}=\sqrt{{\displaystyle {\sum }_{j=1}^4{(Z_{ij}-Z_j^{-})}^2}} \end{gathered}$$

(13)

Finally, the relative sticking progress between each node and the optimal solution point is calculated. The larger is the value, the better the performance of the node is.

$$C_i^{+}=\frac{D_i^{-}}{D_i^{+}+D_i^{-}},i=1,2,\dots ,n$$

(14)

For the node with the largest relative pasting progress, we select it as the newcomer node.

4.2.2. Provider Nodes Selection Based on Bandwidth Ranking among Node Sets

The selection of provider nodes is mainly obtained by sorting the bandwidth between the surviving node-set and the idle node-set. Select the provider nodes with high transmission efficiency and low repair traffic for the newcomer. The pseudo-code of the algorithm is presented in table Algorithm 1.

Algorithm 1 Providers node selection based on bandwidth sorting between node sets

Input: Nn node-set and Np node-set.

Output: provider nodes.

1:     SDN get bandwidth from Nn and Np.

2:     Bandwidth = {}

3:     for bandwidth of ni in Nn and nj in Np do

4:            if bandwidth is true then Bandwidth.set((ni,nj),bandwidth)

5:            else pass

6:            end if

7:     end for

8:     Sort edge.bandwidth from Bandwidth.

9:     for edge in Bandwidth do

10:         Get (ni,nj) from Bandwidth, Provider.append(nj);

11:    end for

12:    return Provider

4.3. Solution of Optimal Repair Tree Based on Genetic Algorithm

4.3.1. k-Path Encoding, Decoding, Population Initialization, and Fitness Function

The subsequent cross mutation and other operations of the genetic algorithm are based on population coding. The superiority of population coding has a direct impact on the search rate of the whole algorithm. In the whole coding process, we refer to the idea of k-shortest-path in reference [26], adopt the path coding method, and take the k-shortest-path under SDN operation as the coding. The so-called shortest path is the shortest path between node A and node B in the topology. We run the Dijkstra algorithm many times to get the top k shortest path from a provider node to the newcomer node.

Any population individual in this paper is coded as (p₁, p₂, …, p_i, …, p_d), where p_i = random (1, k) = j represents the j best cost path randomly selected from node i to the destination node. As shown in Figure 5, for the original undirected graph of Figure 5a, the k-path (k = 2) from each providing node (1, 2, 3) to the destination node 4 has been listed. At this time, a coding individual is shown in Figure 5b, and its coding can also be given according to the k-path.

From the above, the initialization process of this paper is the population initialization process with the population size of popsize based on k-path coding. To ensure the genetic diversity of the population, the pseudo-code of the initialization algorithm designed in this paper is as follows:

Fitness function is the main index to evaluate and describe the individual quality of the population, and it is also an important reference factor for the genetic algorithm to obtain high-quality solutions. The objective of the algorithm optimization problem in this paper is to improve the repair efficiency of the failed node repair process and reduce the repair traffic as much as possible. The overall hops and bottleneck bandwidth of the local optimal tree generated by each generation are searched, and then the fitness function based on hops and bandwidth is brought in to obtain the comprehensive fitness value. The fitness function is given in Equation (15), and the pseudo-code of initial population is presented in table Algorithm 2.

$$\begin{array}{l}f={\alpha }_{bw}\max [\epsilon \frac{D_i}{proces{s}_i}+\frac{\beta }{\omega (V_i,Vj)}+\epsilon \frac{D_j}{proces{s}_i}\\ |(V_i,V_j\in E)]+{\alpha }_{hop}\min (\beta *{\displaystyle \sum hop})\end{array}$$

(15)

Algorithm 2 Initial population

Input: population size popsize, provider nodes and the newcomer node. Output: population.

1:     Popsize = {}

2:     Get all k-paths between the provider nodes and the newcomer node.

3:     while Popsize does not meet the requirements do

4:            for node in Providers do

5:         individual append the i-path between the node and newcomer;

6:            end for

7:            Popsize append the individual;

8:     end while

9:     return Popsize

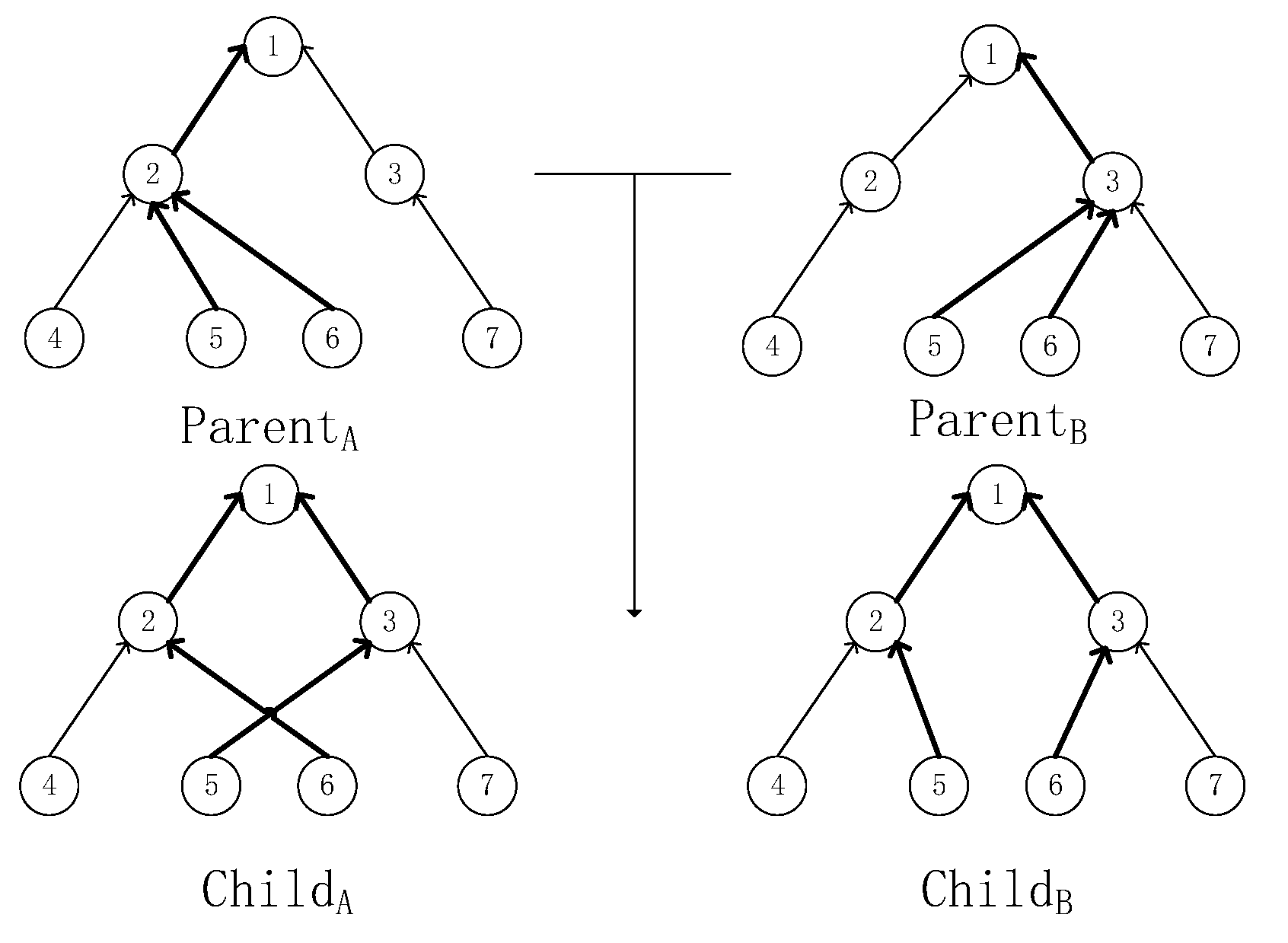
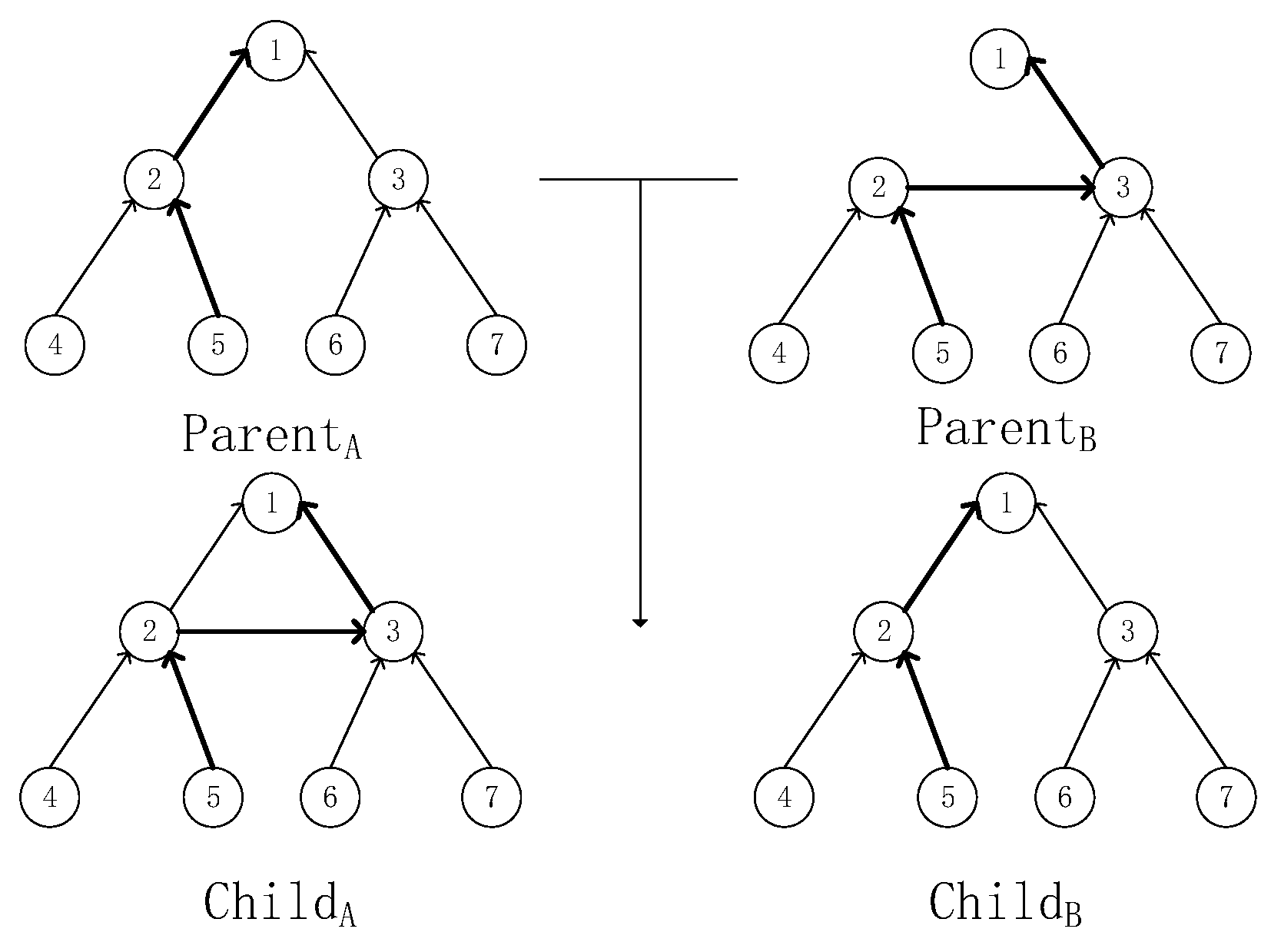
4.3.2. Crossover Operator

The purpose of crossover is to produce new individuals in the next generation. Through crossover operation, the searchability of the genetic algorithm can be greatly improved. Gene cross recombination is the most important means for the genetic algorithm to obtain new and excellent individuals. Common crossover methods include real value recombination (discrete recombination, intermediate recombination, linear recombination) and binary crossover (single-point crossover, multi-point crossover, uniform crossover). The crossover operator ensures that the offspring individuals maintain the diversity of the population based on inheriting the parental gene fragments, to improve the searchability of the algorithm.

In this section, the initial population is used for the crossover transformation of the side path, and the multi-point crossover in the binary crossover is adopted. It is assumed that the new individual form (x₁, x₂, …, x_d), (y₁, y₂, …, y_d) is the value of a certain two individuals in the population after crossing. For any x_i, y_j, i, j∈1, …, d, x_i∈N_xi.k-path, y_j∈N_yi.k-path, as shown in Figure 6, the individual codes of Parent_A and Parent_B are [2-1,3-1,4-2-1,5-2-1,6-2-1,7-3-1] and [2-1,3-1,4-2-1,5-3-1,6-3-1,7-3-1], respectively. The [5-2-1,6-2-1] gene fragment of Parent_A and the [5-3-1,6-3-1] gene fragment of Parent_B are exchanged to obtain the offspring individual Child_A and Child_B, respectively. The generation pseudo-code of crossover operator is presented in table Algorithm 3.

Algorithm 3 Crossover operation

Input: old population, cross probability Pc.

Output: new population.

1:     newPopsize= {}

2:     for i in len(oldPopsize) do

3:      Get parent x and parent y: randomly selected two individuals without crossover;

4:      if Random.Random<Pc then

5:         Get the gene fragments of the parent: x[i:j] and y[i:j];

6:         Change x[i:j] and y[i:j];

7:         Get child1 [x1,…,y1,…,yj,…,xd] and child2 [y1,…,xi,…,yj,…,yd];

8:         newPopsize.append(child1,child2);

9:           else newPopsize.append(x,y)

10:        end if

11:   end for

12:   return newPopsize

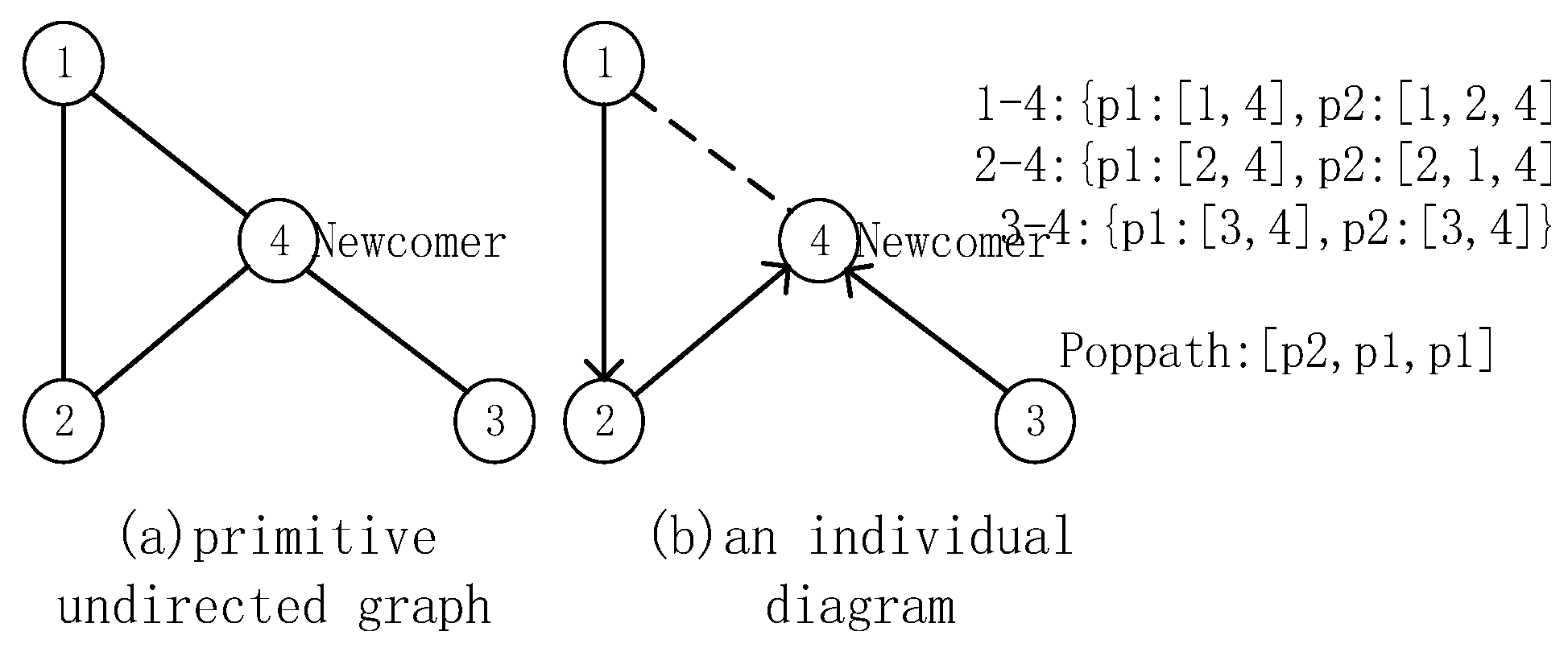
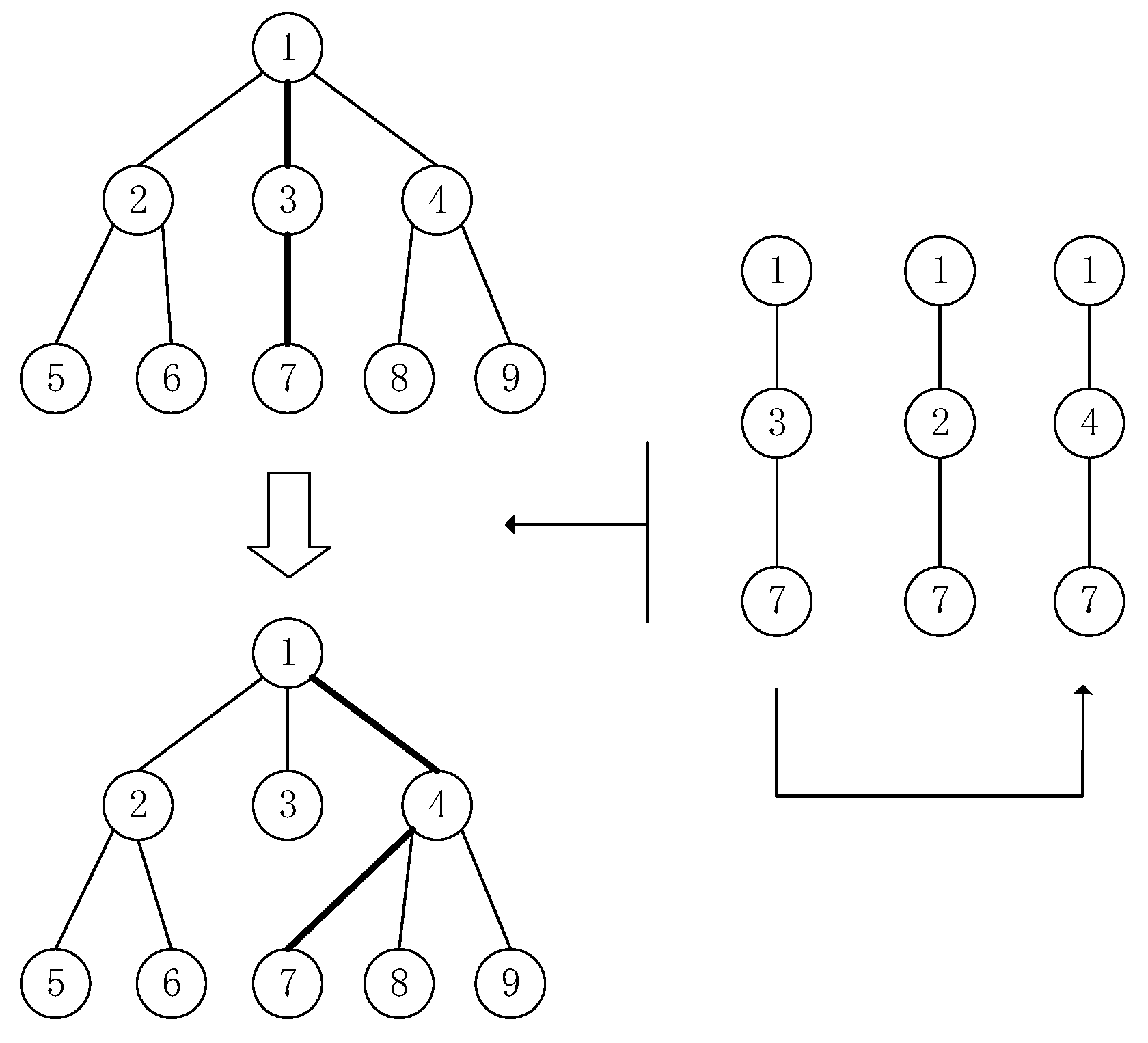
4.3.3. Remove Loop Operation

The “spanning tree” corresponding to the offspring generated after the crossover operation is likely to become an infeasible solution due to the loop. As shown in Figure 7, at this time, the Child_A generated by the parent’s path exchange for node 5 changes from [5,2,1] to [5,2,3,1]. In this way, the topology corresponding to the individual offspring is no longer a tree and does not meet our requirements for achieving the minimum repair traffic, Therefore, it is necessary to design an appropriate de looping operation to change the infeasible solution into a feasible solution.

According to the previous analysis, it is best to achieve the effect of repairing the local minimum flow at the same time when correcting the infeasible solution, that is, after de looping, the maximum weight of the edge of the spanning tree is the smallest among all spanning trees, which is the bottleneck spanning tree of the graph. Therefore, only the bottleneck spanning tree of the graph corresponding to the infeasible solution is required; this can be accomplished by solving the minimum spanning tree. The following theorems and proofs ensure that the de looping operation designed in this paper can not only correct the infeasible solution but also achieve the local repair flow optimization.

Theorem 1.

The minimum spanning tree must be the bottleneck spanning tree.

Proof of Theorem 1.

It can be proved by the method of counter-evidence. Assuming that the minimum spanning tree is not a bottleneck tree and the maximum weight edge of the minimum spanning tree T is e, there is a bottleneck tree T_b whose weight of all edges is less than w(e). Delete e in T to form two trees T’ and T’’ and use the edge to connect the two trees T’ and T’’ in T_b to obtain a new spanning tree. Its weight is less than t, which is in contradiction with t being the minimum spanning tree. □

The Proof of Theorem 1 shows that the minimum spanning tree can not only meet the requirements of the minimum bottleneck tree but also reduce the search times for the minimum traffic. In this paper, the minimum spanning tree is constructed directly for the crossed topology to achieve the purpose of de ring and constructing the optimal repair tree. The minimum spanning tree construction method used in this paper is the Kruskal algorithm, that is, the Kruskal algorithm is used to construct the optimal repair tree with the newcomer as the root. In the screening undirected subgraph with a small number of nodes, the search time is also greatly reduced. The pseudo-code of the ring module is presented in table Algorithm 4.

Algorithm 4 Loop removal operation

Input: population with infeasible solution

Output: new population of fully feasible solutions

1:     Get oldPopsize from the previous step.

2:     newPopsize = {}

3:     treePopsize = {}

4:     for Poppath in oldPopsize do

5:            if Poppath has a loop then

6:          Get kruskalTree from creating Newcomer-rooted kruskal Tree          for Poppath;

7:          Convert tree attribute paths to graph paths and get newPoppath          from kruskalTree;

8:          treePopsize.append(newPoppath);

9:        else newPopsize.append(newPoppath);

10:         end if

11:   end for

12:   return newPopsize, treePopsize

4.3.4. Mutation Operator

The mutation operator maintains the search range of the algorithm in the individual neighborhood of the population, which ensures that each solution in the mutation parent neighborhood can be reached and causes the algorithm shed the dilemma of local optimization. The mutation itself is a kind of local random search, which is combined with the selection/recombination operator to ensure the effectiveness of the genetic algorithm, cause the genetic algorithm to have the ability of local random search, and ensure the diversity of the population. However, in the mutation operation, the mutation rate cannot be too large. If the mutation rate is greater than 0.5, the genetic algorithm will degenerate into a random search; this will also eliminate some important mathematical features and searchability in the genetic algorithm. In this paper, the variation rate P_M is set to 0.05–0.15. If it is large, the search ability of the genetic algorithm is poor, and the variation rate is modified based on the optimal topology search.

The variation used in this paper is still path variation. For the individual (x₁, x₂, …, x_i, …, x_d), the mutant individual (x₁, x₂, …, x_i’, …, x_d) is obtained after mutating the random individual gene random(x_i), x_i’ ∈P_i, as shown in Figure 8. The variation operation is carried out for a gene fragment of an individual. The gene fragment is mutated from 1-3-7 to 1-4-7 to obtain the mutated offspring individual. At the same time, if an individual has variation under probability, a de looping operation is also required after the variation operation. Refer to Section 4.3.3 for the specific de looping process.

4.3.5. Selection Operator

The progeny individuals after cross mutation need to be selected to obtain individuals with higher fitness for gene retention and inheritance to the next generation. The quality of selection operation also determines the excellence of gene retention. The first step of selection is to calculate the fitness, that is, the bandwidth and hop attributes in the subtree after cross mutation are brought into Formula (11). After obtaining the fitness value, two selection methods are carried out for the fitness value selection: elite selection and roulette selection. The probability of the selection is 50%. The pseudo-code of the two selection methods is presented in table Algorithm 5.

Algorithm 5 Select operator

Input: population from the previous step, old population

Output: next generation population

1:    pm = random [0,1].

2:    if pm < 0.5 then go to step 5

3:    else go to step 10

4:    end if

5:    allPopsize = newPopsize + oldPopsize

6:    Function (select operator 1)

7:    sort(allPopsize) and go straight to the top 20

8:    then the rest of individuals are randomly selected.

9:    EndFunction

10:  Function (select operator 2)

11:  sort(allPopsize) Individuals with higher population fitness     values were given higher selection probability and selected     only until the population size was reached

12:   EndFunction

4.3.6. Optimal Topology Construction Method Based on Hybrid Genetic Algorithm

Based on the various operators designed above, the overall steps of the genetic algorithm proposed in this chapter are presented in table Algorithm 6.

Algorithm 6 Optimal topology construction method based on Hybrid Genetic Algorithm

Input: population size as popsize, the maximum number of evolutionary genera-tions G and cross probability PC, mutation probability PM.

Output: the optimal individual, which can be used to repair process of the optimal tree repair topology.

1:   execute algorithm 2 to obtain the initialization population P(0) with the number of popsize.

2:   for individual∈ p(0) do

3:    calculate the fitness value of each individual according to Formula (15).

4:   end for

5:   while current number of evolutionary generations t < G do

6:     clear crossed offspring, mutant offspring.

7:     while crossed offspring number < popsize do

8:         ifPC > Random value then

9:           two individuals are randomly selected from the current population P(t), and           algorithm 3 is executed with probability PC to generate individuals to join cross           offspring.

10:         else

11:           parent individuals directly join the cross offspring.

12:        end if

13:       end while

14:       the set of crossed individuals is marked as O1.

15:       if the topology containing loop then

16:        use Kruskal minimum spanning tree search to create a new topology.

17:       end if

18:       if the individual set is marked as O1 then

19:         while mutant offspring number < popsize do

20:          if PM > Random value then

21:           from an individual randomly in the current population P(t), execute             Section 4.3.4 with probability PM to generate individual to join mutation offspring.

22:           else

23:            the parent individual will directly join the mutation offspring

24:           end if

25:           the return value treepopsize skips the mutation operation and saves it, and the            remaing individuals form newpopsize to replace the original individual set for            subsequent operations.

26:         end while

27:    else

28:         the individual set is marked as O2.

29:         execute algorithm 5 on the set newpopsize∪oldpopsize, obtain the selection method          according to the probability PM.

30:         select the number of individuals with the population as the population P(t + 1) of          the next generation, so that t = t + 1.

31:         newpopsize = treepopsize (O1) + treepopsize (O2).

32:   end while

33:   output the individual with the lowest fitness function value in the traversal population.

The limitation of the proposed method is mainly in the demand of the computing complexity. The proposed genetic algorithm has two parts: first is the initial operation, wherein the time complexity is proportional to the number of nodes n, the k value set in the k-path algorithm, and the size of the population; therefore, the time complexity of part 1 is O(n*k²*popsize). The second part is the evolutionary operation, wherein the time complexity is O(G*popsize*e*loge), where popsize denotes the population size, G denotes the maximum generation iterations, and e denotes the number of edge of the graph. The limitation of the method is that it is hard to evaluate the computing time of each iteration; we usually obtain it by experiments.

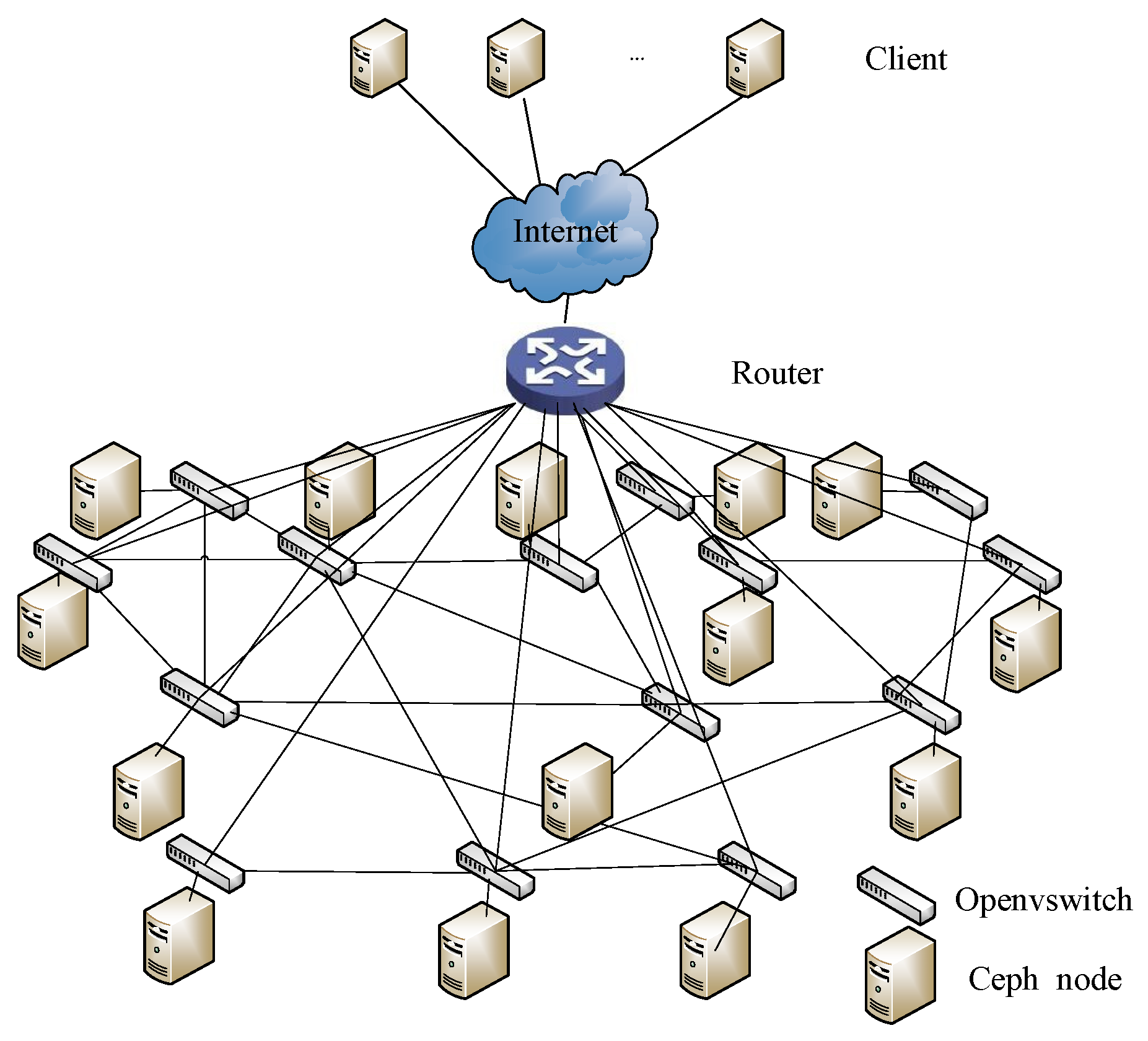
5. Experiment and Evaluation

5.1. Experimental Environment

The experiment uses mininet to simulate the real network conditions. The virtual machine environment is VMware Workstation Pro Ubuntu 16.04–64 bit, and the Ryu environment is Python 2.7 (Python Software Foundation, https://www.python.org/). the node selection and genetic algorithm simulation program is written in Pycharm 2019.2.3 x64 Python 3.5 (Python Software Foundation, https://www.python.org/). The comparative experiment is carried out in the hardware environment of AMD Ryzen 7 5800 H with Radeon Graphics 3.20 GHz 16 GB memory and 512 g SSD. The performance parameters of each storage node in the cluster topology generated by the experimental simulation are link bandwidth, memory capacity, CPU performance, and I/O performance. The corresponding weights of each parameter are 40%, 30%, 20%, and 10%. The corresponding value range is [21, 265], [1, 90], [0.3, 76], [0.5, 23]. The topology prototype used in the experiment is the network topology diagram set according to the network topology diagram of mininet simulation in downtown New York, as shown in Figure 9, in which a host terminal is connected to each openvswitch, and the original data M size in the experiment is 1 GB. After many experiments, the algorithm in this paper sets the crossover probability as 0.95 and the mutation probability as 0.15.

5.2. Node Attribute

The node selection model based on Software Defined Network (SDN) and multi-attribute decision-making is proposed in this paper. Compared with the star selection (S-SPA-C) and random selection (R-SPA-C) proposed in reference [33], the node comprehensive attribute selected in this paper has the advantage of absolute node attribute value among the five different link bandwidth attributes, which also means that a better set of nodes will be provided. Figure 10 below shows the repair delay distribution diagram of three algorithms in condition of five different link bandwidth attributes. In this paper, after selecting nodes under different bandwidth attributes, the traditional tree repair is used to build the topology, and then the repair delay is obtained through the calculation of file size and bottleneck bandwidth. The average repair rate is much higher than R-SPA-C and faster than S-SPA-C. At the same time, Figure 11 shows the average comprehensive attribute change diagram of the nodes screened by the three algorithms. In different bandwidth ranges, the comprehensive attribute values of the nodes obtained by the node selection algorithm designed in this paper are greater than S-SPA-C. When the bandwidth range gradually shrinks to the maximum value, the node attribute tends to be the same, but is still less than the node attribute obtained by us, which is also consistent with our prediction.

5.3. Algorithm Parameters

By changing and testing the fitness parameters α_bw and α_hop, we analyze the impact of different fitness parameters on the repair delay and repair flow. The larger α_bw indicates that the algorithm is more inclined to find the topology with reduced repair delay, and the increase in α_bw value will reduce the repair delay of the topology constructed by the algorithm. Similarly, α_hop is more inclined to find the repair traffic and reduce the topology. When α_hop = 1, it means that the topology will reduce the repair traffic as much as possible at the cost of increasing the repair rate. At this time, the topology repair traffic will reach the shortest measurement. When (α_bw, α_hop) is (0.25,0.75), (0.5,0.5), (12,6,7), and (10,4,7), the repair delay of topology is reduced to a certain extent. When (α_bw, α_hop) is (0.75,0.25), (1,0), (12,6,7), and (10,4,7) topology, the repair traffic decreases to a certain extent, which is consistent with our analysis. In this paper, the selection of parameters of maximum bottleneck bandwidth and minimum repair hops in the fitness value of the genetic algorithm is tested. For a variety of repair situations with different proportions, the experimental results of repair rate and repair delay are integrated. Finally, the parameter settings with (α_bw, α_hop) of (0.6, 0.4) are used for synchronous comparison experiments, the average optimal fitness value is obtained to optimize the repair rate and repair traffic in the repair topology at the same time.

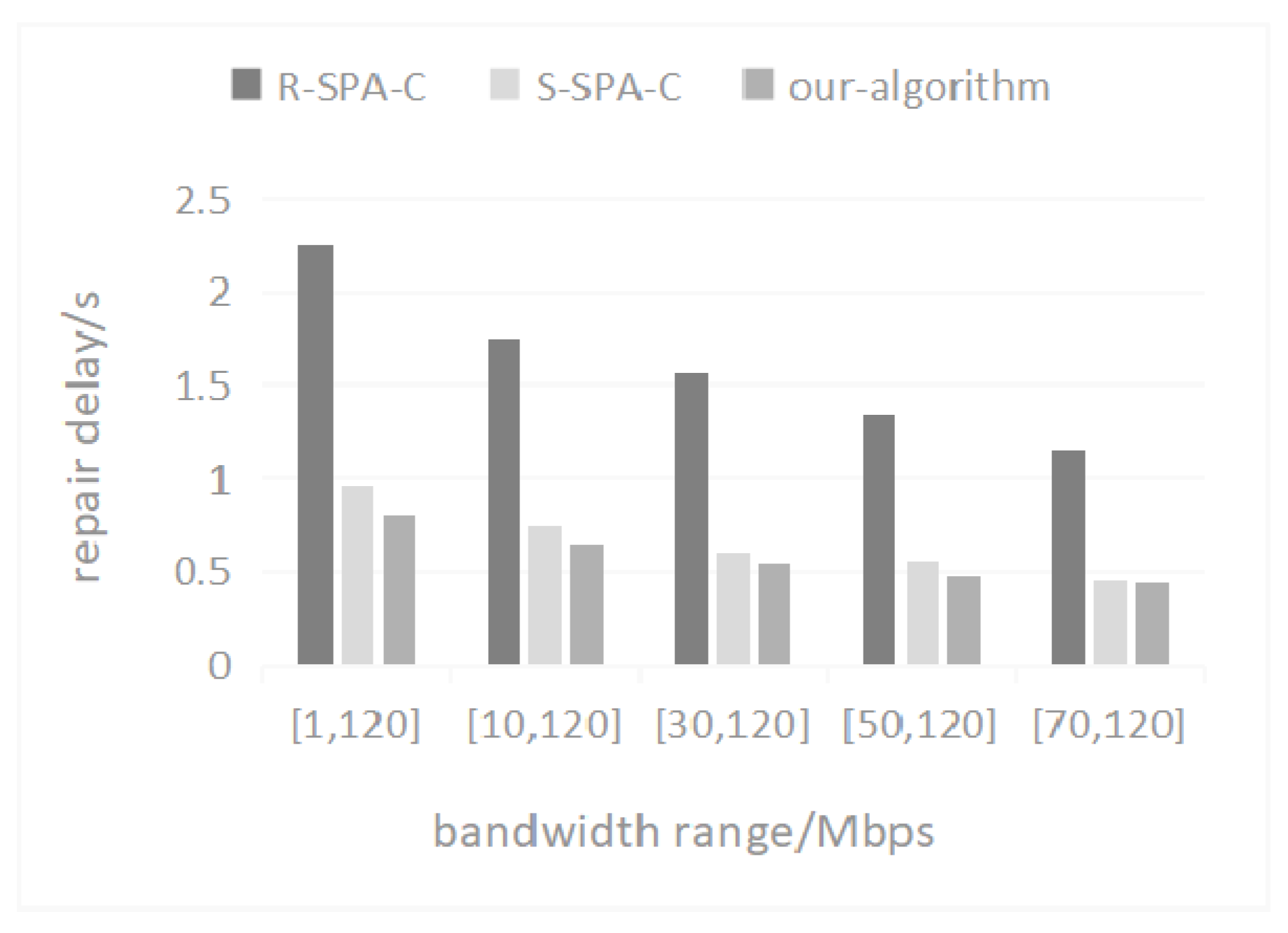
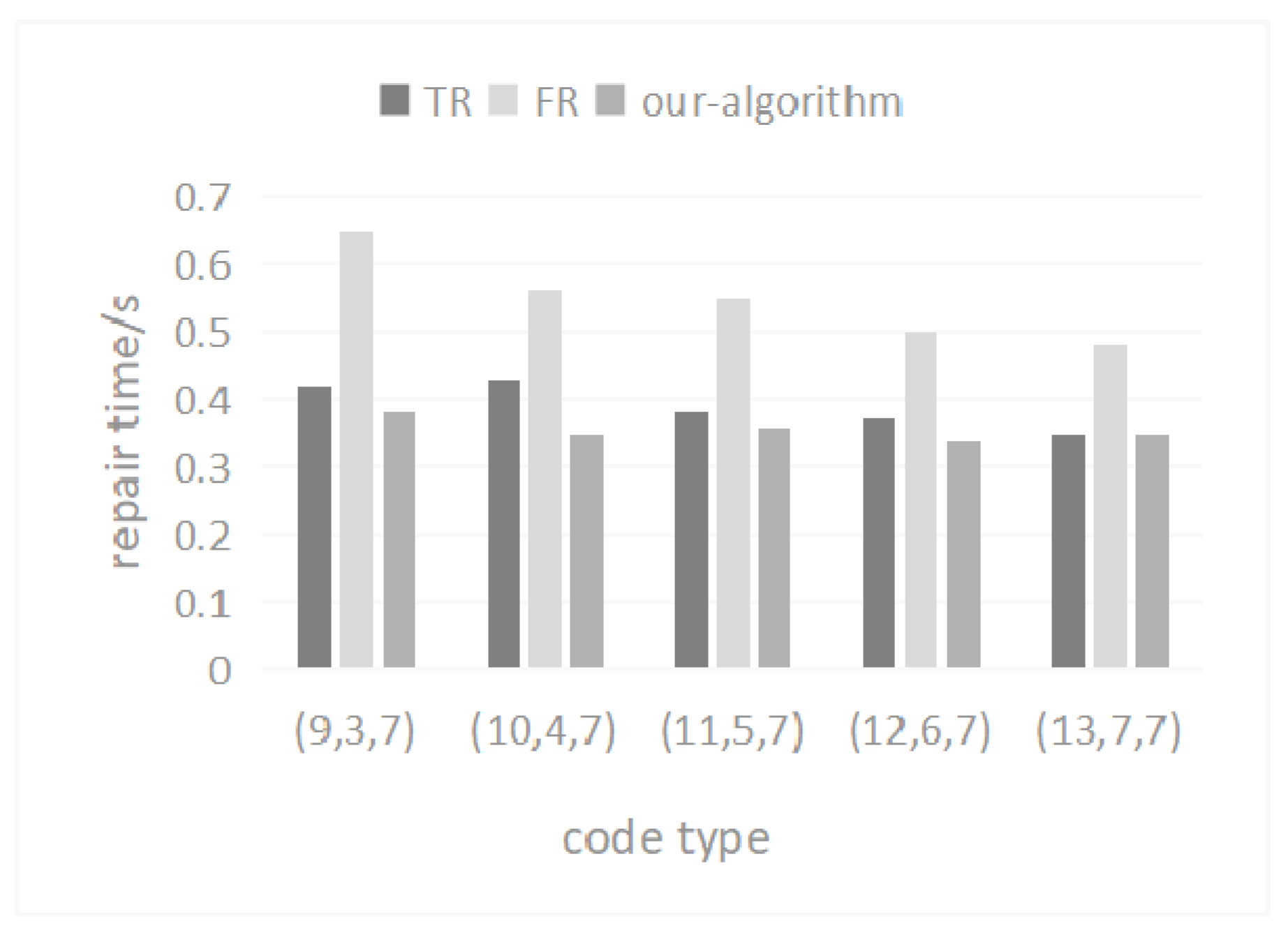
5.4. Repair Rate

After the node selection is completed, we continue our repair tree construction through appropriate parameter settings. In the traditional repair tree construction algorithm, we only consider the repair delay, that is, the bottleneck bandwidth of the repair tree. Alternatively, as in literature [34], we only consider the repair traffic, that is, the minimization of the number of repair tree hops. In this paper, the method of combining the genetic algorithm and the greedy algorithm is used to design the repair tree with the best comprehensive attribute by integrating the repair delay and repair flow. According to the k-path proposed in document [34], the k-path is improved and encoded, and then the better path is selected in the genetic algorithm to obtain the repair tree with the best comprehensive hop number and bandwidth performance. Compared with the traditional tree repair topology (TR) and star topology (SR), the repair rate of the repair topology obtained by the algorithm in the case of single-node repair is greater than that of the traditional tree repair topology and star topology under five different code types. As shown in Figure 12, below, the repair delay distribution diagram of the three algorithms under the condition of five different code type node selection is obtained respectively:

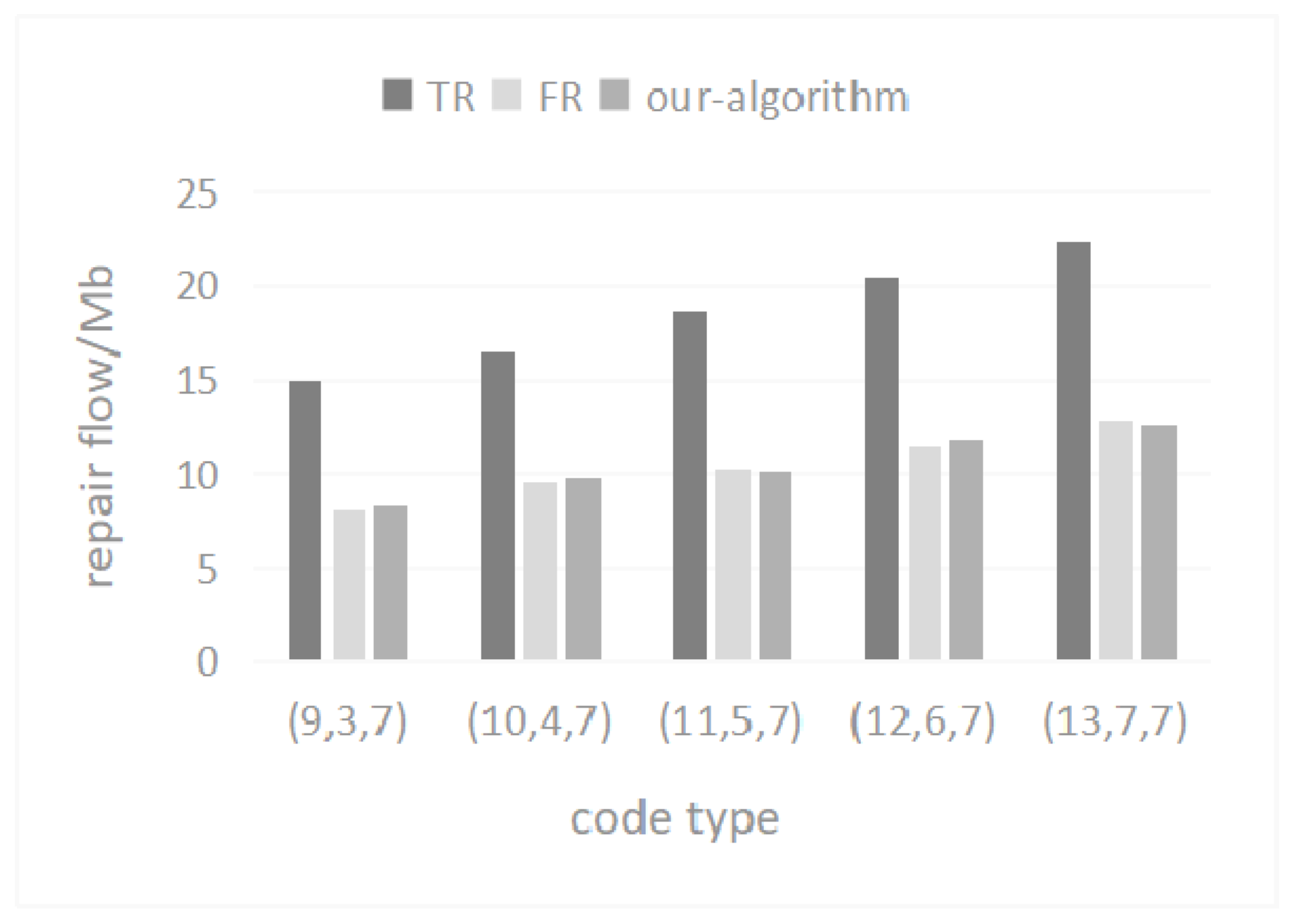
5.5. Repair Flow

As mentioned in Section 3.3 of this paper, the repair traffic in the repair topology is also an important index to judge the advantages and disadvantages of the repair topology. No matter what size of the erasure code cluster, the repair tree topology created by the FR algorithm in literature [34] based on the minimum hops will always produce the lowest repair traffic, but its repair rate is slower than the algorithm designed in this paper under five different code types. Combined experiments show that the traffic gap between the algorithm involved in this paper and the FR algorithm is very small and can be almost ignored, but it has much faster repair efficiency. Combined with the experimental results in the previous section, it can be found that this method has higher repair efficiency than the TR algorithm, and the traffic in the topology is only 50% to 60% of tr. In addition, although the star topology increases the traffic overhead due to the additional path brought by the absence of intermediate nodes, the tree topology algorithm can choose the link with a large available bandwidth in the topology to transmit the repair traffic, so the repair efficiency is far higher than that of the star topology. Secondly, the star repair rate is very slow, which cannot adapt to the current node repair with high requirements. Considering the two factors of repair efficiency and repair traffic, the comprehensive performance of this method exceeds the two traditional topology algorithms and FR algorithm, which is also consistent with the original design goal. As shown in Figure 13 below, the repair traffic distribution diagram of this paper and the other two tree algorithms TR and FR are shown.

6. Summary and Prospects

For the practical distributed storage system, the heterogeneous link bandwidth in the cluster topology, the heterogeneous performance between different nodes, and the huge repair flow in the repair process cannot be ignored. Aiming at the scenario of single node failure in the distributed storage system with traditional RS erasure code, this paper uses SDN technology to monitor the network status, and node performance comprehensively considers the impact of node processing capacity on node repair rate and the impact of repair traffic in repair topology on cluster business and also uses multi-attribute decision-making to select the repair node-set, An optimal repair topology construction method based on hybrid genetic algorithm is proposed to optimize the repair rate and repair flow of the repair topology at the same time. Through simulation experiments, the performance gap between the repair topology constructed by the node-set selected by this method and the traditional star repair topology, the traditional tree repair topology, and other literature algorithms are compared, and the influence of the algorithm parameters on the results, the repair efficiency, and the repair flow of the repair topology are discussed. The method proposed in this paper is only for the repair scenario of single node failure in the distributed storage system. How to construct a tree repair topology for multiple nodes while taking into account the optimization objectives of this paper will be worthy of further research.