Convection in a Ferromagnetic Fluid Layer Influenced by Changeable Gravity and Viscosity
Abstract
:1. Introduction
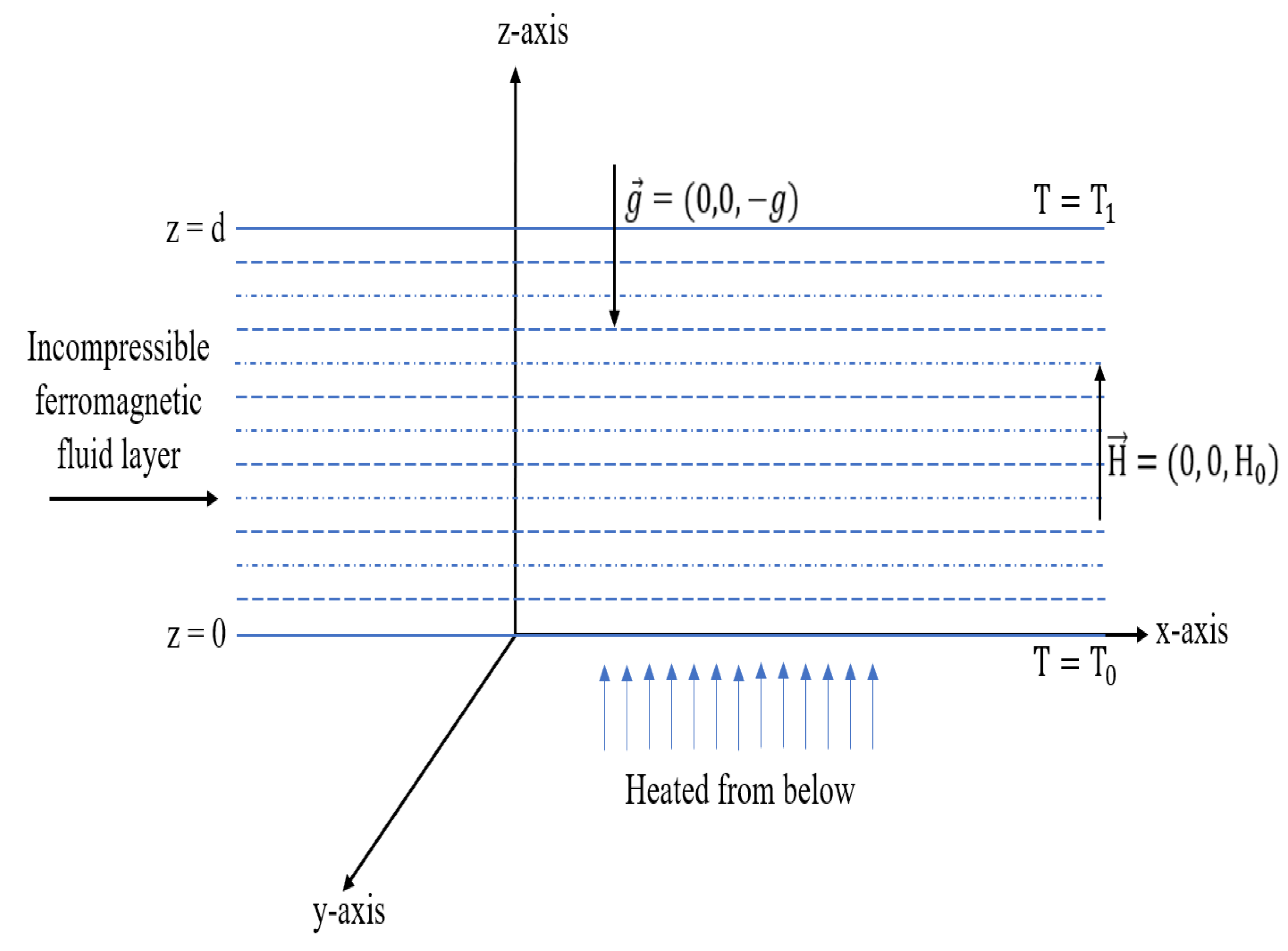
2. Mathematical Analysis
3. The Initial State
4. The Perturbation Equation
5. Normal Mode Analysis
6. Solution Methodology
7. Results and Explanation
7.1. Stationary Convection
7.2. Oscillatory Convection
8. Numerical Results and Discussion
- Increasing gravitational field variation
- Decreasing gravitational field variation
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Operators | |
| ∇ | |
| Greek Symbols | |
| Co-efficient of thermal expansion (1/K) | |
| Temperature gradient (K/m) | |
| Magnetic susceptibility | |
| Viscosity variation parameter | |
| Gravity variation parameter | |
| Variable viscosity of fluid | |
| Free space magnetic permeability of vacuum (N/A | |
| Viscosity of fluid in absence of applied magnetic field (Pa·s) | |
| Scalar magnetic potential (A) | |
| Density of fluid (Kg/m | |
| Reference density of fluid | |
| Time factor | |
| List of Symbols | |
| a | Dimensionless wave number |
| Magnetic induction (T) | |
| C | Constant |
| Specific heat at constant volume and magnetic field | |
| d | Thickness of fluid (m) |
| f | Changeable gravity function |
| g | Changeable gravity |
| Reference gravity (m/s2) | |
| Magnetic field (T) | |
| Uniform vertical magnetic field | |
| k | Resultant wave number |
| Coefficient of thermal conductivity (W/m/K) | |
| Wave number along x-axis | |
| Wave number along y-axis | |
| K | Pyromagnetic coefficient (A/mK) |
| Magnetization vector (A/m) | |
| Constant mean value of magnetization | |
| Buoyancy magnetization parameter | |
| Non-dimensional parameter | |
| Non-buoyancy magnetization parameter | |
| n | Real or complex constant |
| N | Magnetic Rayleigh number |
| p | Pressure of fluid (Pa) |
| P | Prandtl number |
| Velocity of fluid (m/s) | |
| R | Rayleigh number |
| t | Time (s) |
| T | Temperature (K) |
| Temperature at bottom surface | |
| Temperature at top surface | |
| Average temperature | |
| Superscripts/Subscripts | |
| Perturbations quantity | |
| ∗ | Dimensionless quantity |
| b | Basic state |
| c | Critical value |
References
- Neuringer, J.L.; Rosensweig, R.E. Ferrohydrodynamics. Phys. Fluids 1964, 7, 1927–1937. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Fluid dynamics and science of magnetic liquids. Adv. Electron. Electron. Phys. 1979, 48, 103–199. [Google Scholar]
- Hathaway, D. Use of ferrofluid in moving-coil loudspeakers. Db-Sound Eng. Mag. 1979, 13, 42–44. [Google Scholar]
- Bailey, R. Lesser known applications of ferrofluids. J. Magn. Magn. Mater. 1983, 39, 178–182. [Google Scholar] [CrossRef]
- Rosenweig, R. Ferrohydrodynamics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Dover Publication: Mineola, NY, USA, 1981. [Google Scholar]
- Finlayson, B. Convective instability of ferromagnetic fluids. J. Fluid Mech. 1970, 40, 753–767. [Google Scholar] [CrossRef] [Green Version]
- Lalas, D.; Carmi, S. Thermoconvective stability of ferrofluids. Phys. Fluids 1971, 14, 436–438. [Google Scholar] [CrossRef]
- Gotoh, K.; Yamada, M. Thermal convection in a horizontal layer of magnetic fluids. J. Phys. Soc. Jpn. 1982, 51, 3042–3048. [Google Scholar] [CrossRef]
- Zebib, A. Thermal convection in a magnetic fluid. J. Fluid Mech. 1996, 321, 121–136. [Google Scholar] [CrossRef]
- Schwab, L.; Hildebrandt, U.; Stierstadt, K. Magnetic Bénard convection. J. Magn. Magn. Mater. 1983, 39, 113–114. [Google Scholar] [CrossRef]
- Stiles, P.J.; Kagan, M. Thermoconvective instability of a horizontal layer of ferrofluid in a strong vertical magnetic field. J. Magn. Magn. Mater. 1990, 85, 196–198. [Google Scholar] [CrossRef]
- Vaidyanathan, G.; Sekar, R.; Balasubramanian, R. Ferroconvective instability of fluids saturating a porous medium. Int. J. Eng. Sci. 1991, 29, 1259–1267. [Google Scholar] [CrossRef]
- Gupta, M.D.; Gupta, A. Convective instability of a layer of a ferromagnetic fluid rotating about a vertical axis. Int. J. Eng. Sci. 1979, 17, 271–277. [Google Scholar] [CrossRef]
- Sekar, R.; Vaidyanathan, G.; Ramanathan, A. The ferroconvection in fluids saturating a rotating densely packed porous medium. Int. J. Eng. Sci. 1993, 31, 241–250. [Google Scholar] [CrossRef]
- Sekar, R.; Vaidyanathan, G. Convective instability of a magnetized ferrofluid in a rotating porous medium. Int. J. Eng. Sci. 1993, 31, 1139–1150. [Google Scholar] [CrossRef]
- Venkatasubramanian, S.; Kaloni, P. Effects of rotation on the thermoconvective instability of a horizontal layer of ferrofluids. Int. J. Eng. Sci. 1994, 32, 237–256. [Google Scholar] [CrossRef]
- Vaidyanathan, G.; Sekar, R.; Vasanthakumari, R.; Ramanathan, A. The effect of magnetic field dependent viscosity on ferroconvection in a rotating sparsely distributed porous medium. J. Magn. Magn. Mater. 2002, 250, 65–76. [Google Scholar] [CrossRef]
- Sharma, R. The effect of magnetic field dependent viscosity on thermosolutal convection in a ferromagnetic fluid saturating a porous medium. Transp. Porous Media 2005, 60, 251–274. [Google Scholar]
- Sharma, A.; Shandil, R. Effect of magnetic field dependent viscosity on ferroconvection in the presence of dust particles. J. Appl. Math. Comput. 2008, 27, 7–22. [Google Scholar]
- Ram, P.; Bhandari, A.; Sharma, K. Effect of magnetic field-dependent viscosity on revolving ferrofluid. J. Magn. Magn. Mater. 2010, 322, 3476–3480. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A.V. The onset of convection in a horizontal nanofluid layer of finite depth. Eur. J. Mech. B/Fluids 2010, 29, 217–223. [Google Scholar] [CrossRef]
- Gupta, U.; Ahuja, J.; Wanchoo, R. Magneto convection in a nanofluid layer. Int. J. Heat Mass Transf. 2013, 64, 1163–1171. [Google Scholar] [CrossRef]
- Haq, R.U.; Raza, A.; Algehyne, E.A.; Tlili, I. Dual nature study of convective heat transfer of nanofluid flow over a shrinking surface in a porous medium. Int. Commun. Heat Mass Transf. 2020, 114, 104583. [Google Scholar] [CrossRef]
- Dadheech, P.; Agrawal, P.; Mebarek-Oudina, F.; Abu-Hamdeh, N.; Sharma, A. Comparative Heat Transfer Analysis of MoS2/C2H6O2 and SiO2-MoS2/C2H6O2 Nanofluids with Natural Convection and Inclined Magnetic Field. J. Nanofluids 2020, 9, 161–167. [Google Scholar] [CrossRef]
- Marzougui, S.; Mebarek-Oudina, F.; Magherbi, M.; Mchirgui, A. Entropy generation and heat transport of Cu-water nanoliquid in porous lid-driven cavity through magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 2047–2069. [Google Scholar] [CrossRef]
- Mahmoud, E.; Algehyne, E.; Alqarni, M.; Afzal, A.; Ibrahim, M. Investigating the thermal efficiency and pressure drop of a nanofluid within a micro heat sink with a new circular design used to cool electronic equipment. Chem. Eng. Commun. 2021, 1–13. [Google Scholar] [CrossRef]
- El-Shorbagy, M.; Algehyne, E.; Ibrahim, M.; Ali, V.; Kalbasi, R. Effect of fin thickness on mixed convection of hybrid nanofluid exposed to magnetic field-Enhancement of heat sink efficiency. Case Stud. Therm. Eng. 2021, 26, 101037. [Google Scholar] [CrossRef]
- Chabani, I.; Mebarek-Oudina, F.; Ismail, A. MHD Flow of a Hybrid Nano-Fluid in a Triangular Enclosure with Zigzags and an Elliptic Obstacle. Micromachines 2022, 13, 224. [Google Scholar] [CrossRef]
- Algehyne, E.; Areshi, M.; Saeed, A.; Bilal, M.; Kumam, W.; Kumam, P. Numerical Simulation of Bioconvective Darcy Forchhemier Nanofluid Flow with Energy Transition over a Permeable Vertical Plate. Sci. Rep. 2022, 12, 3228. [Google Scholar] [CrossRef]
- Algehyne, E.; El-Zahar, E.; Elhag, S.; Bayones, F.; Nazir, U.; Sohail, M.; Kumam, P. Investigation of thermal performance of Maxwell hybrid nanofluid boundary value problem in vertical porous surface via finite element approach. Sci. Rep. 2022, 12, 2335. [Google Scholar] [CrossRef]
- Pradhan, G.; Samal, P.; Tripathy, U. Thermal stability of a fluid layer in a variable gravitational field. Indian J. Pure Appl. Math 1989, 20, 736–745. [Google Scholar]
- Straughan, B. Convection in a variable gravity field. J. Math. Anal. Appl. 1989, 140, 467–475. [Google Scholar] [CrossRef] [Green Version]
- Rionero, S.; Straughan, B. Convection in a porous medium with internal heat source and variable gravity effects. Int. J. Eng. Sci. 1990, 28, 497–503. [Google Scholar] [CrossRef]
- Alex, S.M.; Patil, P.R. Effect of a variable gravity field on convection in an anisotropic porous medium with internal heat source and inclined temperature gradient. J. Heat Transf. 2002, 124, 144–150. [Google Scholar] [CrossRef]
- Kaloni, P.; Qiao, Z. Non-linear convection in a porous medium with inclined temperature gradient and variable gravity effects. Int. J. Heat Mass Transf. 2001, 44, 1585–1591. [Google Scholar] [CrossRef]
- Chand, R.; Rana, G.; Kumar, S. Variable gravity effects on thermal instability of nanofluid in anisotropic porous medium. Int. J. Appl. Mech. Eng. 2013, 18, 631–642. [Google Scholar] [CrossRef] [Green Version]
- Harfash, A. Three-dimensional simulations for convection in a porous medium with internal heat source and variable gravity effects. Transp. Porous Media 2014, 101, 281–297. [Google Scholar] [CrossRef]
- Harfash, A. Convection in a porous medium with variable gravity field and magnetic field effects. Transp. Porous Media 2014, 103, 361–379. [Google Scholar] [CrossRef]
- Chand, R.; Rana, G.; Kango, S. Effect of variable gravity on thermal instability of rotating nanofluid in porous medium. FME Trans. 2015, 43, 62–69. [Google Scholar] [CrossRef] [Green Version]
- Pant, S.; Bhagat, N.; Kharayat, H. Effect of Suspended Particles and Magnetic Field on Thermal Convection in Ferromagnetic Fluid with Varying Gravitational Field in Porous Medium. Int. J. Adv. Res. 2016, 4, 939–946. [Google Scholar] [CrossRef] [Green Version]
- Mahabaleshwar, U.; Basavaraja, D.; Wang, S.; Lorenzini, G.; Lorenzini, E. Convection in a porous medium with variable internal heat source and variable gravity. Int. J. Heat Mass Transf. 2017, 111, 651–656. [Google Scholar] [CrossRef]
- Mahajan, A.; Sharma, M.K. Convection in a magnetic nanofluid saturating a porous medium under the influence of a variable gravity field. Eng. Sci. Technol. Int. J. 2018, 21, 439–450. [Google Scholar] [CrossRef]
- Mahajan, A.; Sharma, M.K. The onset of convection in a magnetic nanofluid layer with variable gravity effects. Appl. Math. Comput. 2018, 339, 622–635. [Google Scholar] [CrossRef]
- Yadav, D. Numerical investigation of the combined impact of variable gravity field and throughflow on the onset of convective motion in a porous medium layer. Int. Commun. Heat Mass Transf. 2019, 108, 104274. [Google Scholar] [CrossRef]
- Nagarathnamma, H.; Gangadharaiah, Y.; Ananda, K. Effects of variable internal heat source and variable gravity field on convection in a porous layer. Malaya J. Mat. 2020, 8, 915–919. [Google Scholar]
- Yadav, D. Effects of rotation and varying gravity on the onset of convection in a porous medium layer: A numerical study. World J. Eng. 2020, 17, 785–793. [Google Scholar] [CrossRef]
- Yadav, D.; Chu, Y.M.; Li, Z. Examination of the nanofluid convective instability of vertical constant throughflow in a porous medium layer with variable gravity. Appl. Nanosci. 2021, 1–14. [Google Scholar] [CrossRef]
- Shekhar, S.; Ragoju, R.; Yadav, D. The effect of variable gravity on rotating Rayleigh–Bénard convection in a sparsely packed porous layer. Heat Transfer. 2022, 1–18. [Google Scholar] [CrossRef]
- Yadav, D. The density-driven nanofluid convection in an anisotropic porous medium layer with rotation and variable gravity field: A numerical investigation. J. Appl. Comput. Mech. 2020, 6, 699–712. [Google Scholar]
- Fletcher, C.A. Computational Galerkin Methods; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]






| Researcher(s) | Ferrofluid/ Nanofluid | Free-Free Boundary | Galerkin Single Term Approach | Magnetic Field Dependent Viscosity | Increasing Gravitational Field Variation | Decreasing Gravitational Field Variation |
|---|---|---|---|---|---|---|
| [7] | ✓ | ✓ | ||||
| [18] | ✓ | ✓ | ✓ | |||
| [20] | ✓ | ✓ | ✓ | |||
| [22] | ✓ | ✓ | ✓ | |||
| [23] | ✓ | ✓ | ✓ | |||
| [40] | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [43,44] | ✓ | ✓ | ✓ | ✓ | ||
| [50] | ✓ | ✓ | ||||
| [46] | ✓ | ✓ | ||||
| [48] | ✓ | ✓ | ||||
| [49] | ✓ | |||||
| Present Paper | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Increasing Gravitational Field Variation | ||
| Case (i) | Linear Increasing | |
| Case (ii) | Convex Increasing | |
| Case (iii) | Concave Increasing | |
| Decreasing Gravitational Field Variation | ||
| Case (iv) | Linear Decreasing | |
| Case (v) | Concave Decreasing | |
| Case (vi) | Convex Decreasing | |
| Case | f(z) | N | Non-Linear Equation |
|---|---|---|---|
| (i) | z | ||
| (ii) | |||
| (iii) | |||
| (iv) | |||
| (v) | |||
| (vi) |
| 1 | 5 | 10 | 15 | 20 | |
|---|---|---|---|---|---|
| 0 | 1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case (i) | Case (ii) | Case (iii) | Case (i) | Case (ii) | Case (iii) | Case (i) | Case (ii) | Case (iii) | |
| 0 | 1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case (iv) | Case (v) | Case (vi) | Case (iv) | Case (v) | Case (vi) | Case (iv) | Case (v) | Case (vi) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pant, S.; Algehyne, E.A. Convection in a Ferromagnetic Fluid Layer Influenced by Changeable Gravity and Viscosity. Mathematics 2022, 10, 1737. https://doi.org/10.3390/math10101737
Pant S, Algehyne EA. Convection in a Ferromagnetic Fluid Layer Influenced by Changeable Gravity and Viscosity. Mathematics. 2022; 10(10):1737. https://doi.org/10.3390/math10101737
Chicago/Turabian StylePant, Sumit, and Ebrahem A. Algehyne. 2022. "Convection in a Ferromagnetic Fluid Layer Influenced by Changeable Gravity and Viscosity" Mathematics 10, no. 10: 1737. https://doi.org/10.3390/math10101737
APA StylePant, S., & Algehyne, E. A. (2022). Convection in a Ferromagnetic Fluid Layer Influenced by Changeable Gravity and Viscosity. Mathematics, 10(10), 1737. https://doi.org/10.3390/math10101737







