Optimization of Observer Feedback Gains for Stable Sensorless IM Drives at Very Low Frequencies: A Comparative Study between GA and PSO
Abstract
:1. Introduction
2. Mathematical Models
2.1. Induction Motor Model
2.2. Adaptive Flux Observer Model
2.3. Speed Observer Analysis
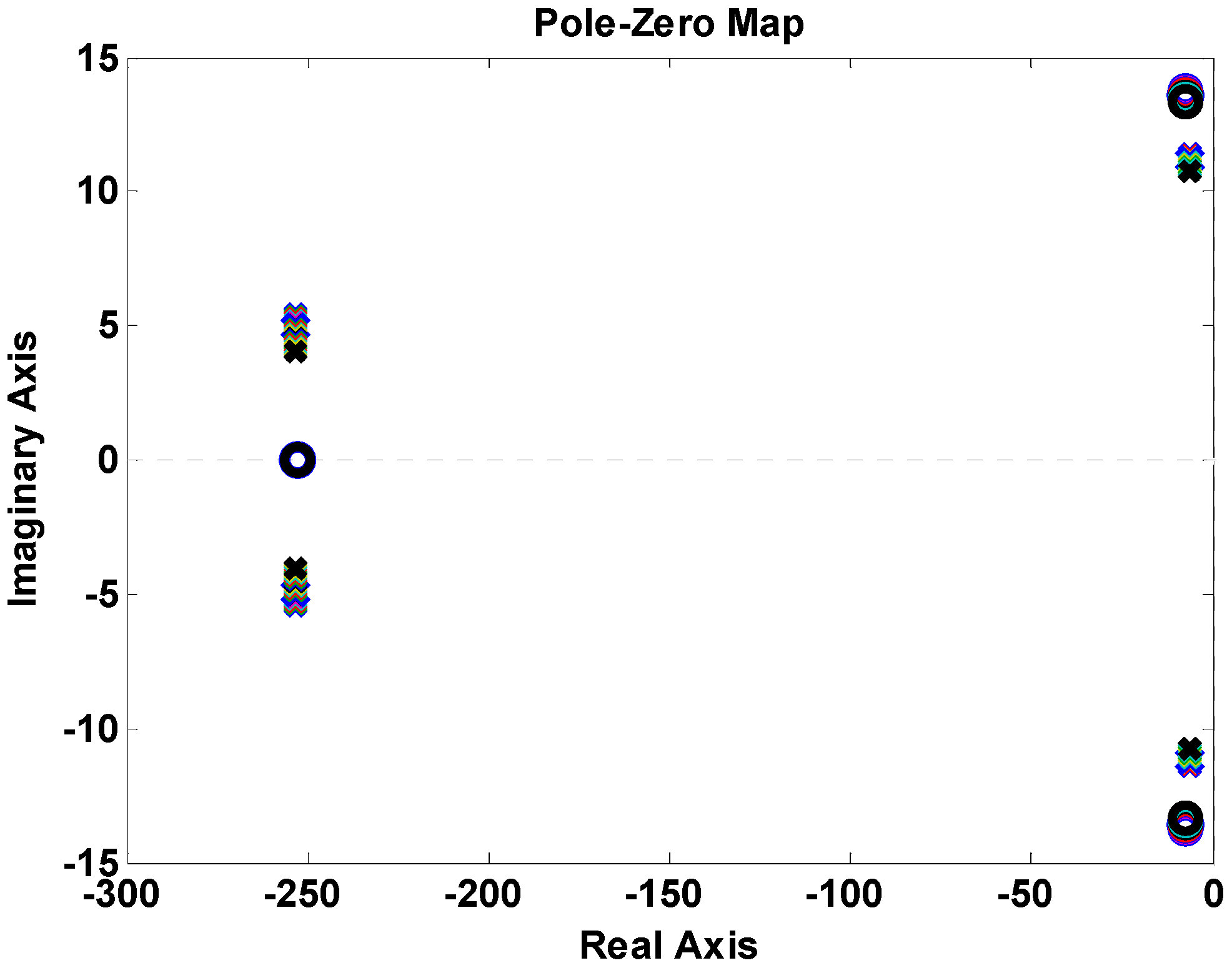
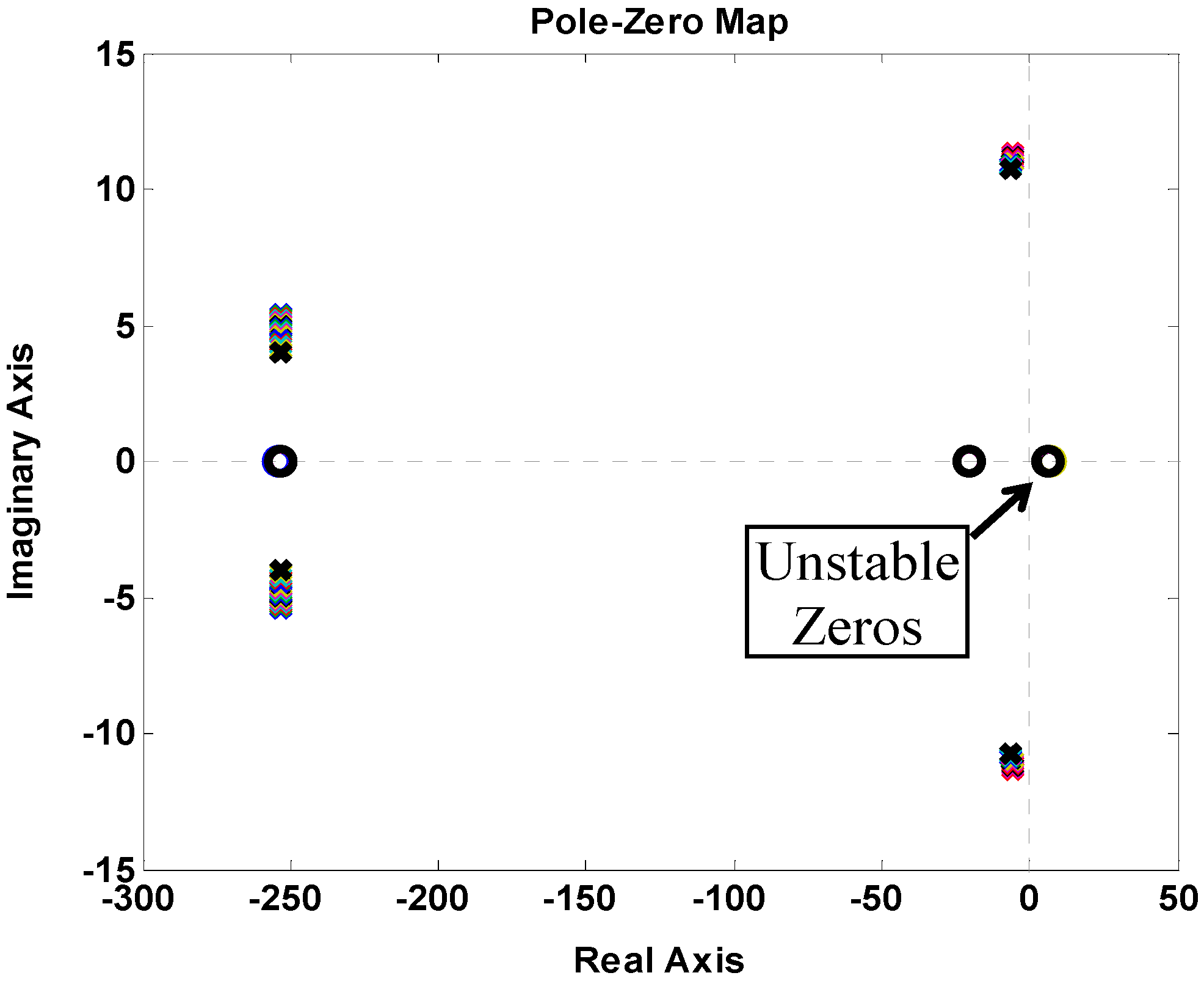
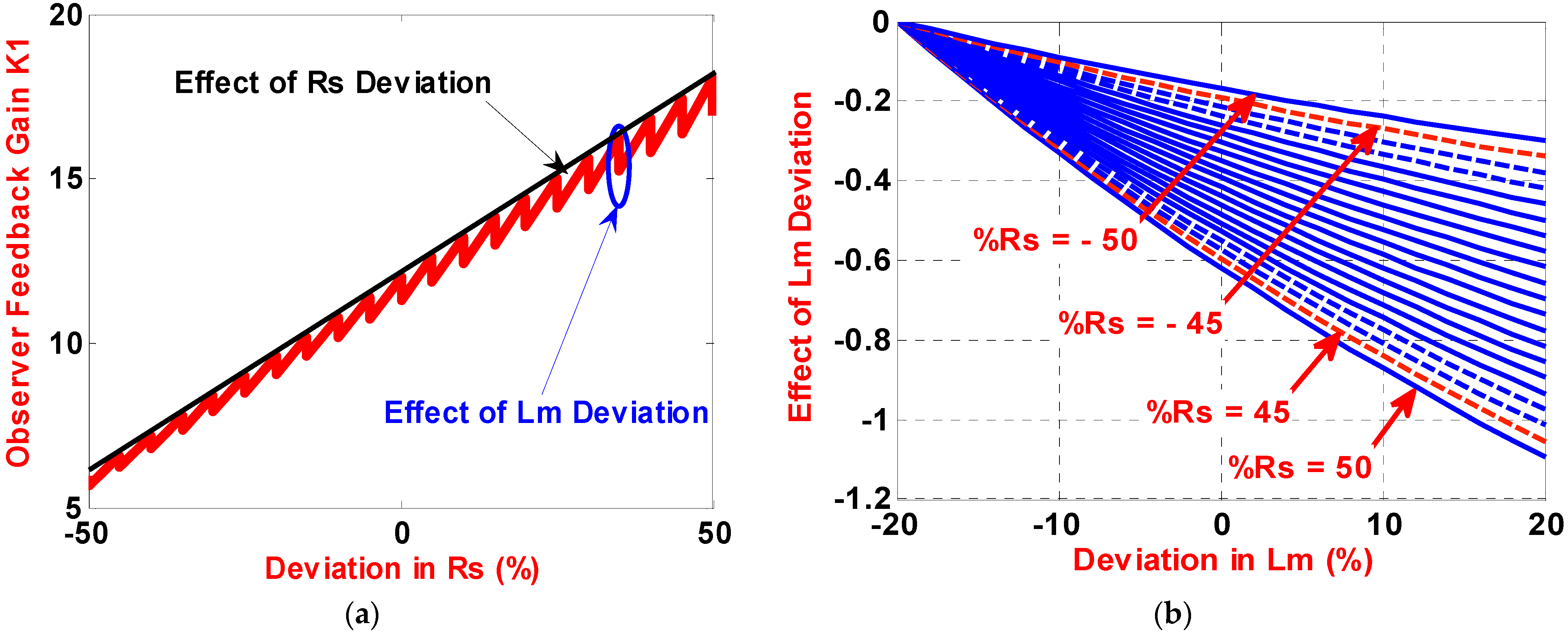
3. Derivation of AFO Stability Conditions
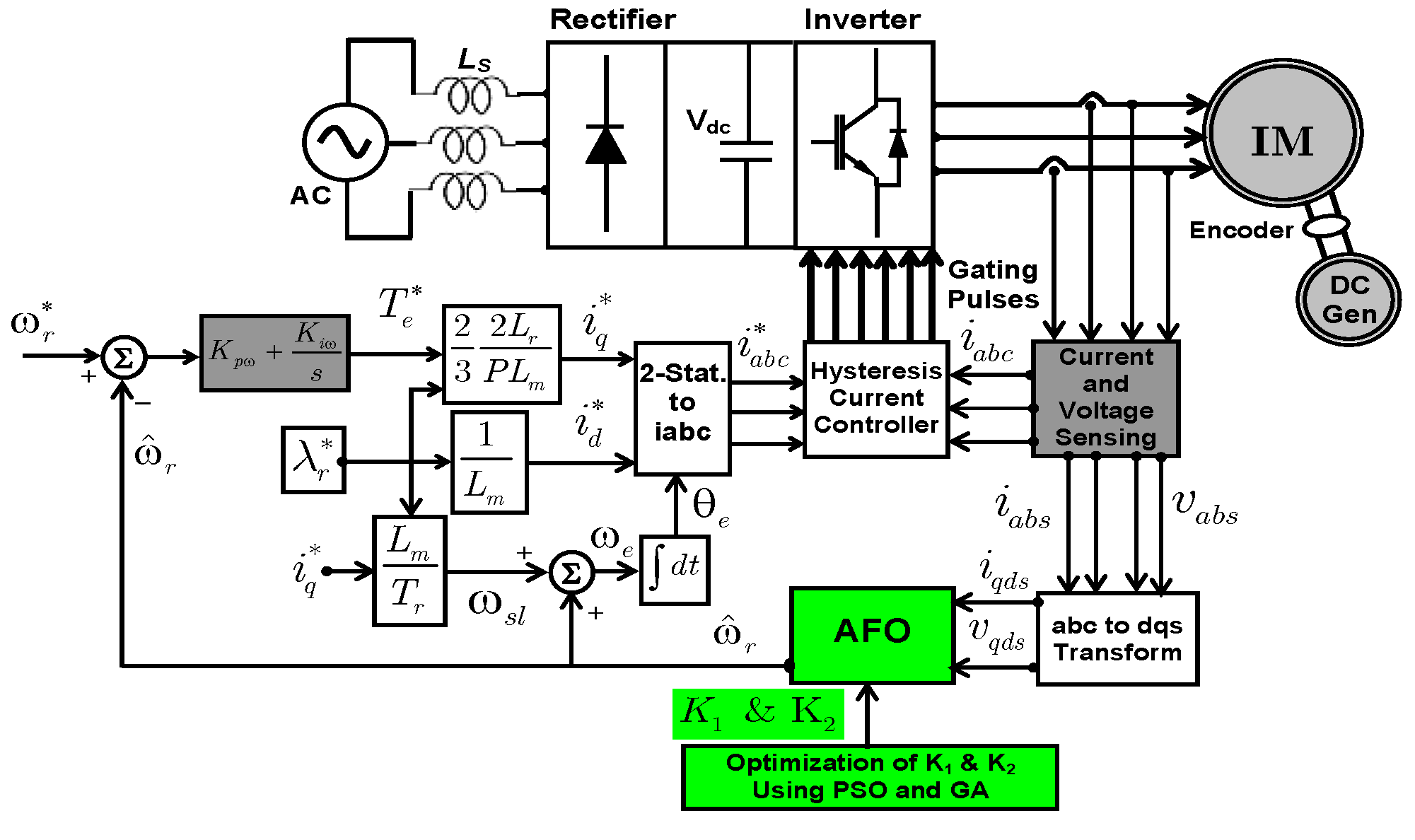
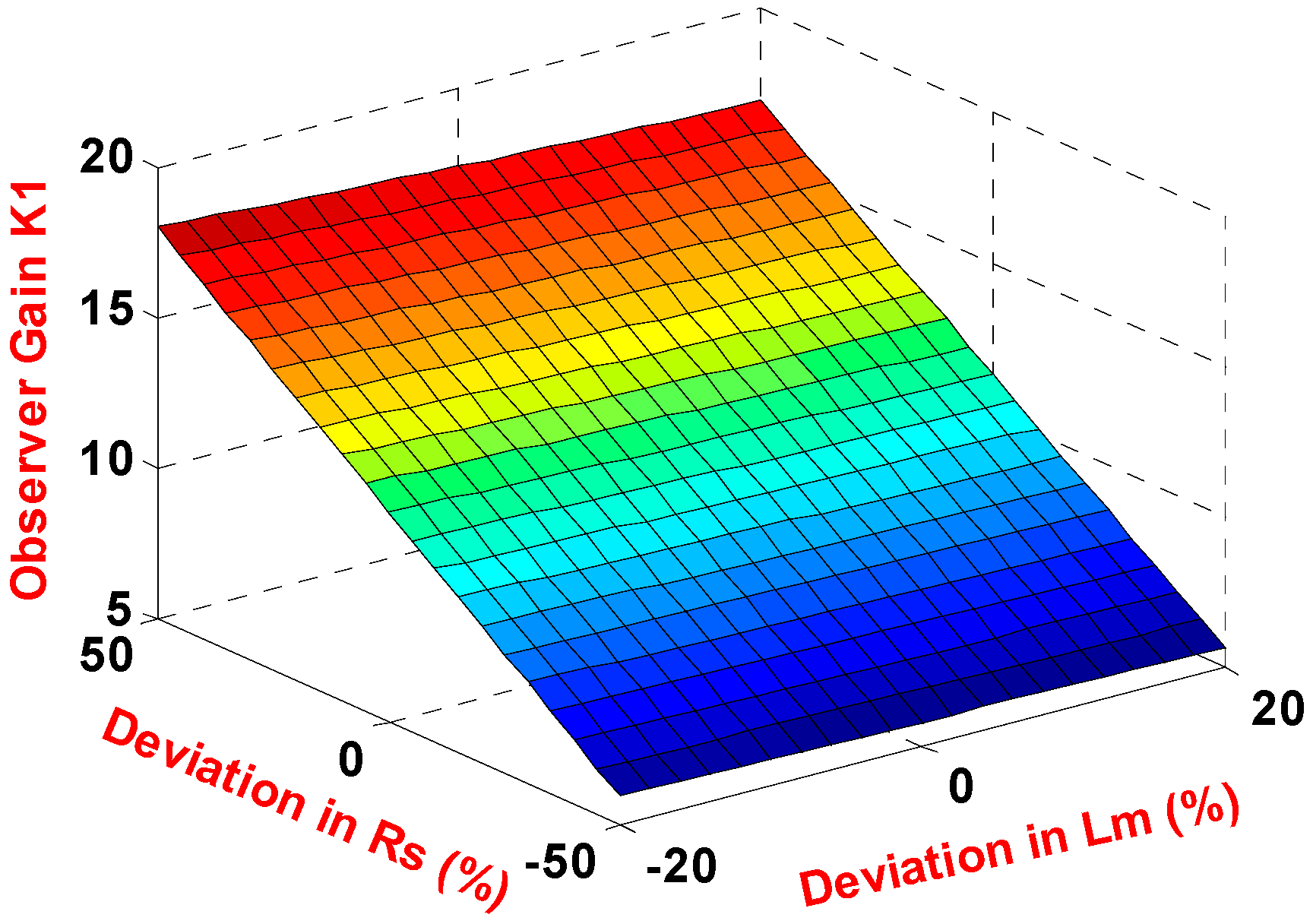
4. Optimization of OFGs Using GA and PSO
4.1. Genetic Algorithm
4.2. Particle Swarm Optimization Technique
5. Simulation and Experimental Results
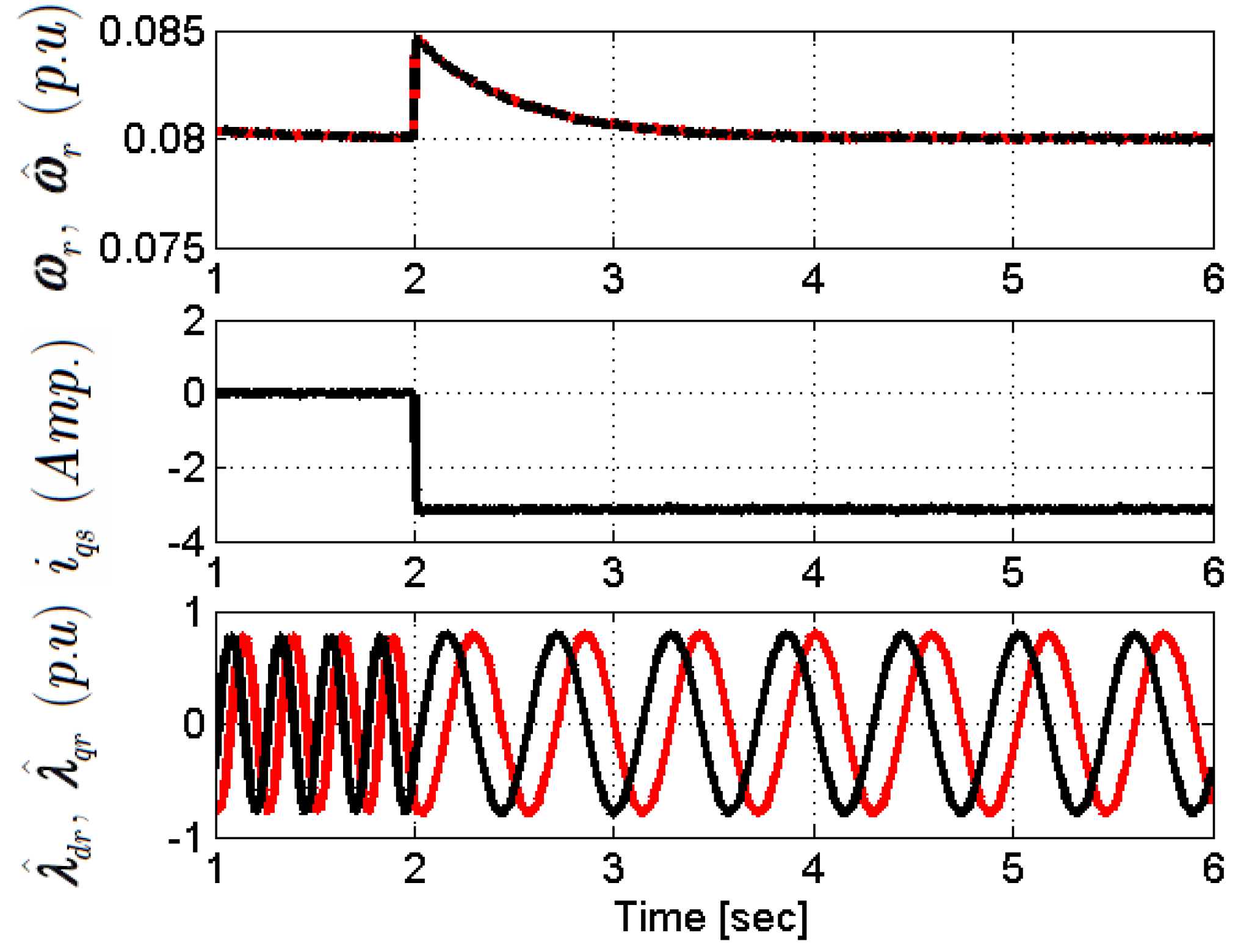
5.1. Performance at Very Low Speed during Motoring Mode
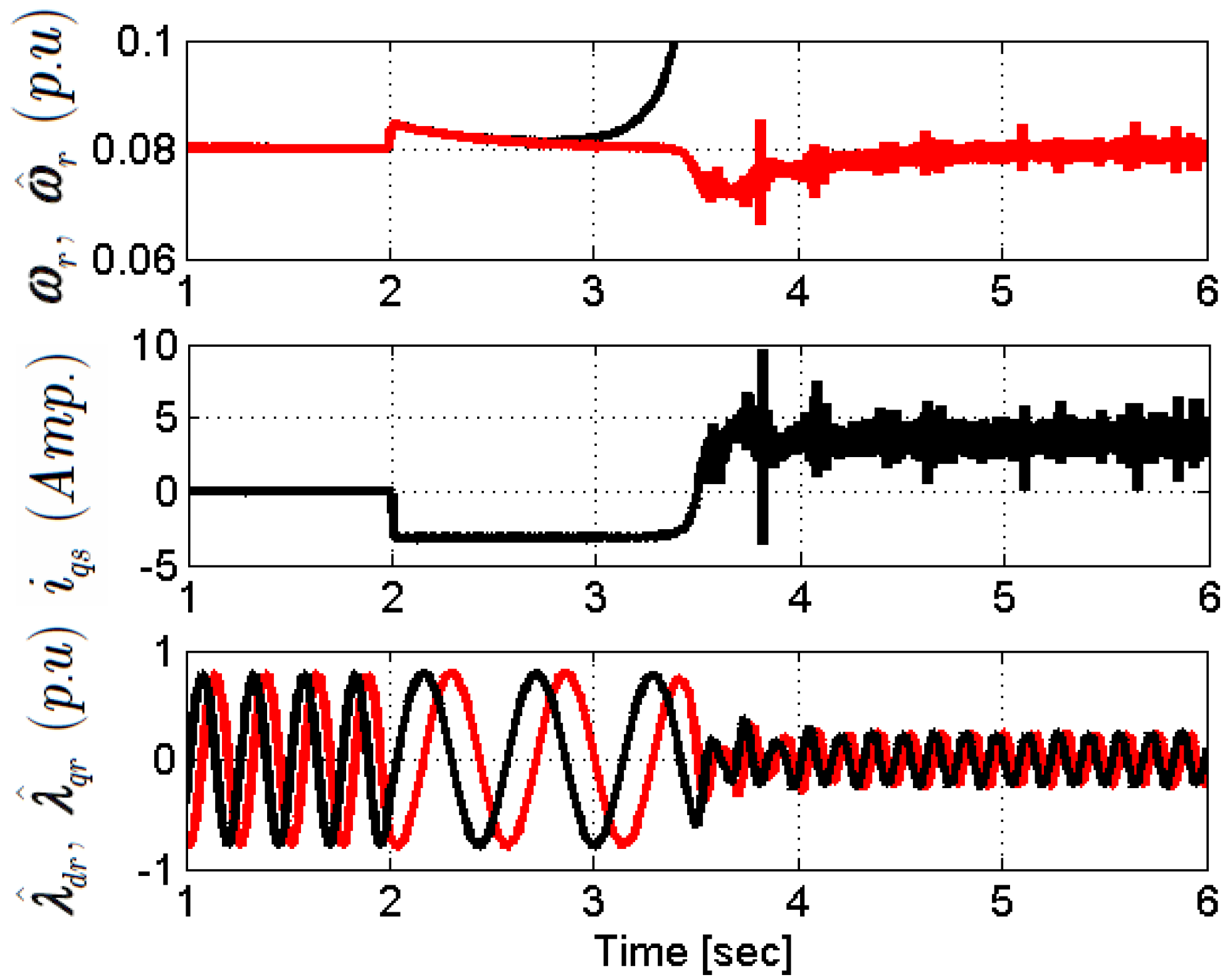
5.2. Working at Very Low Speed during Regenerating Mode
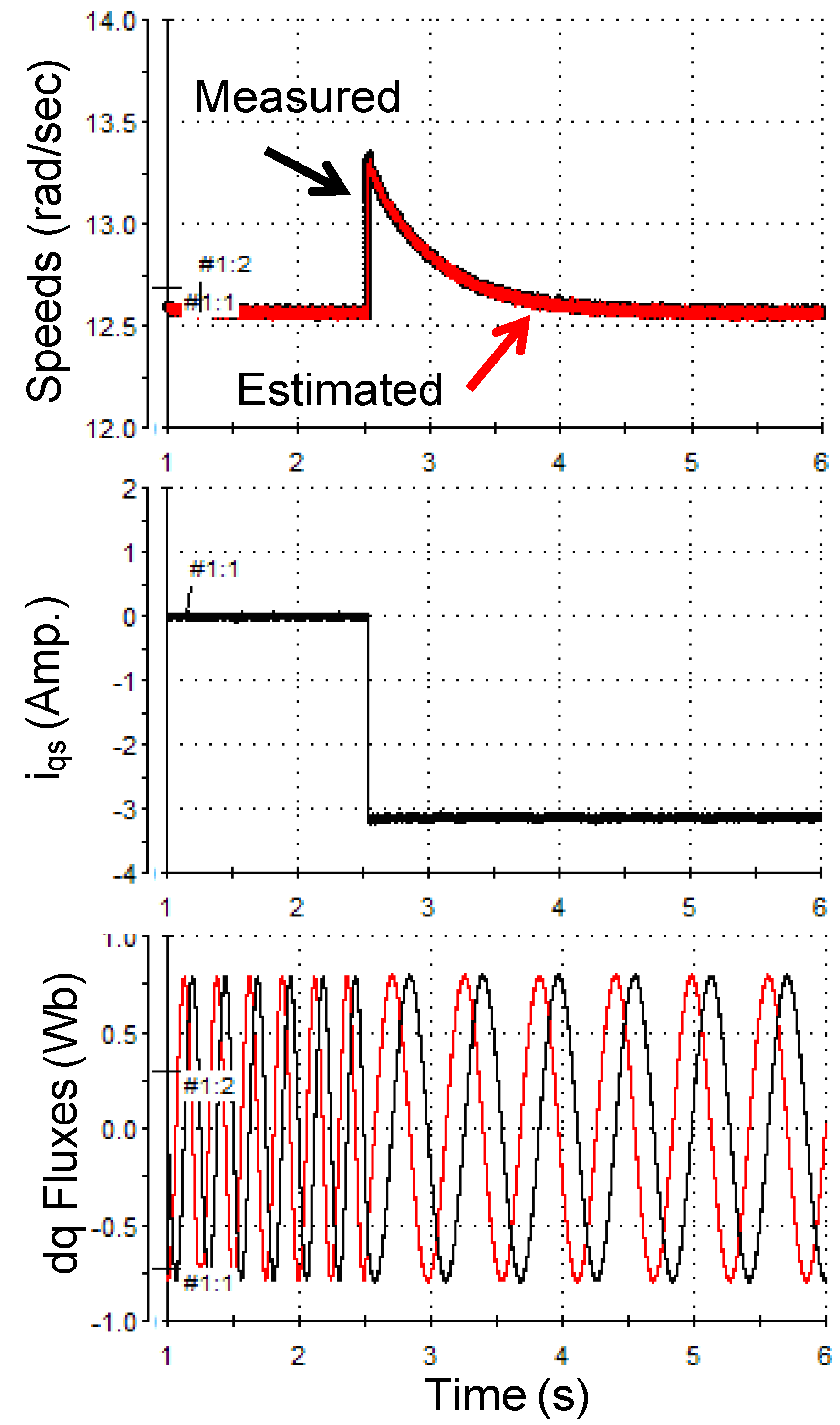
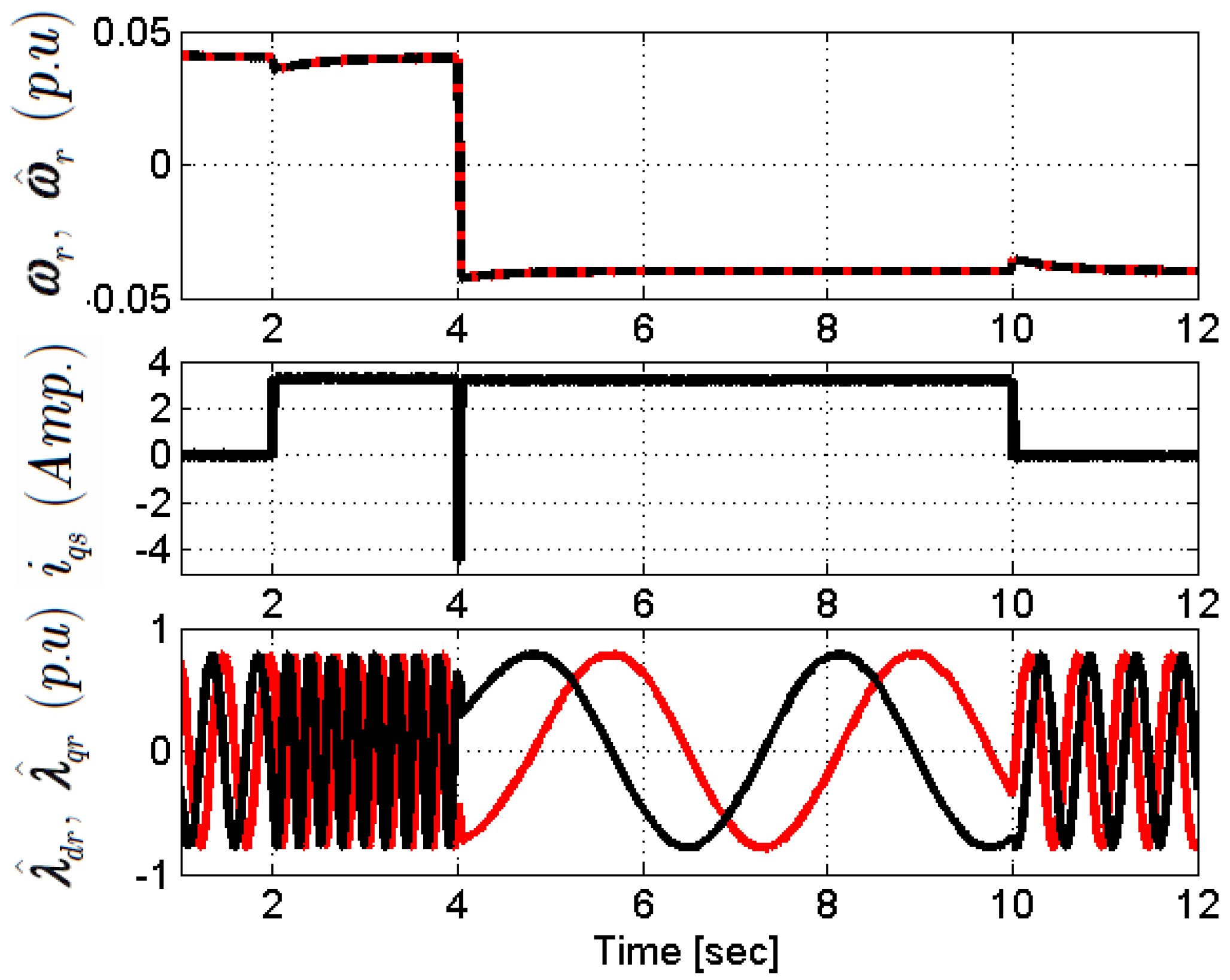
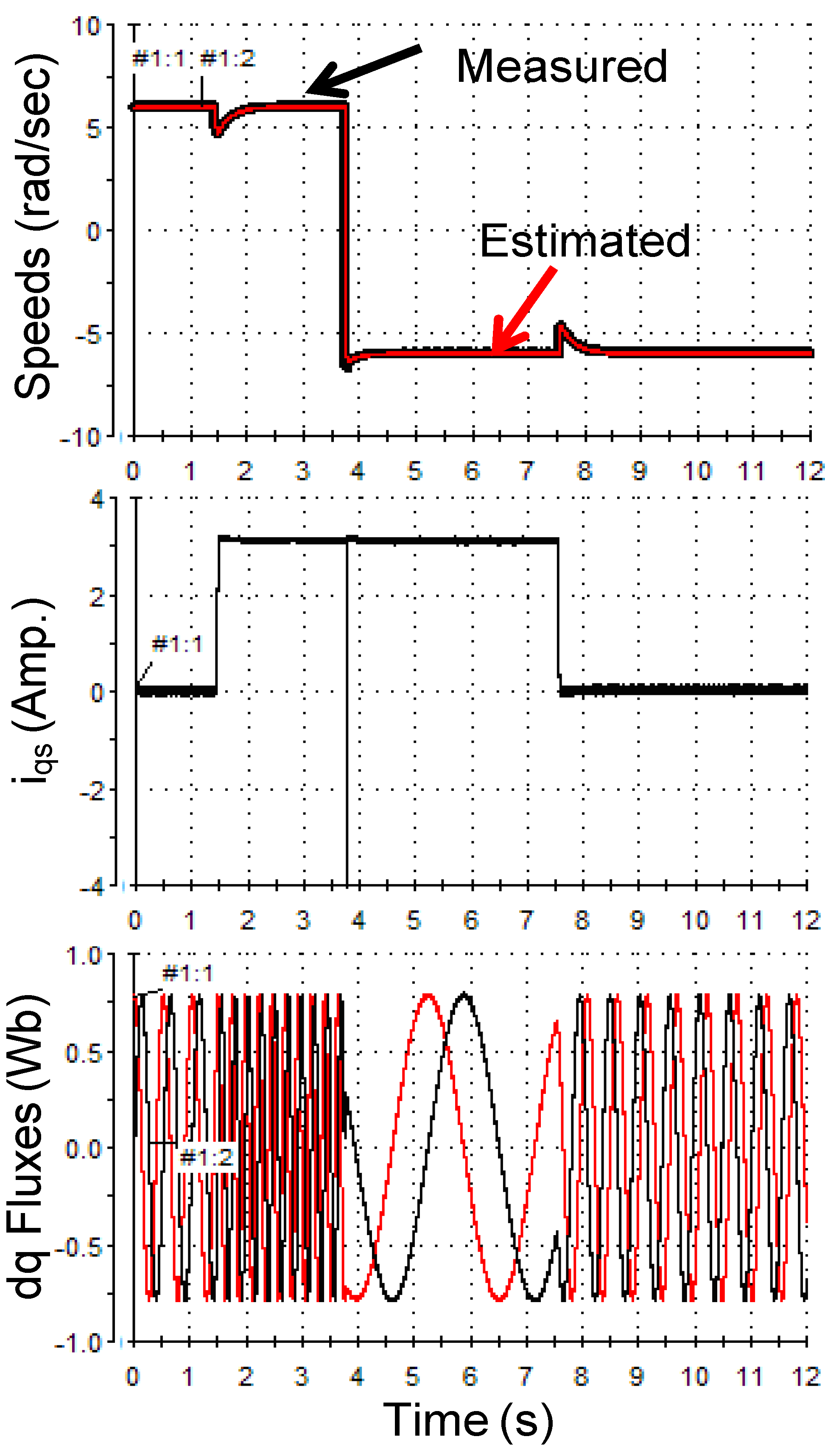
5.3. Fast Speed Reversal
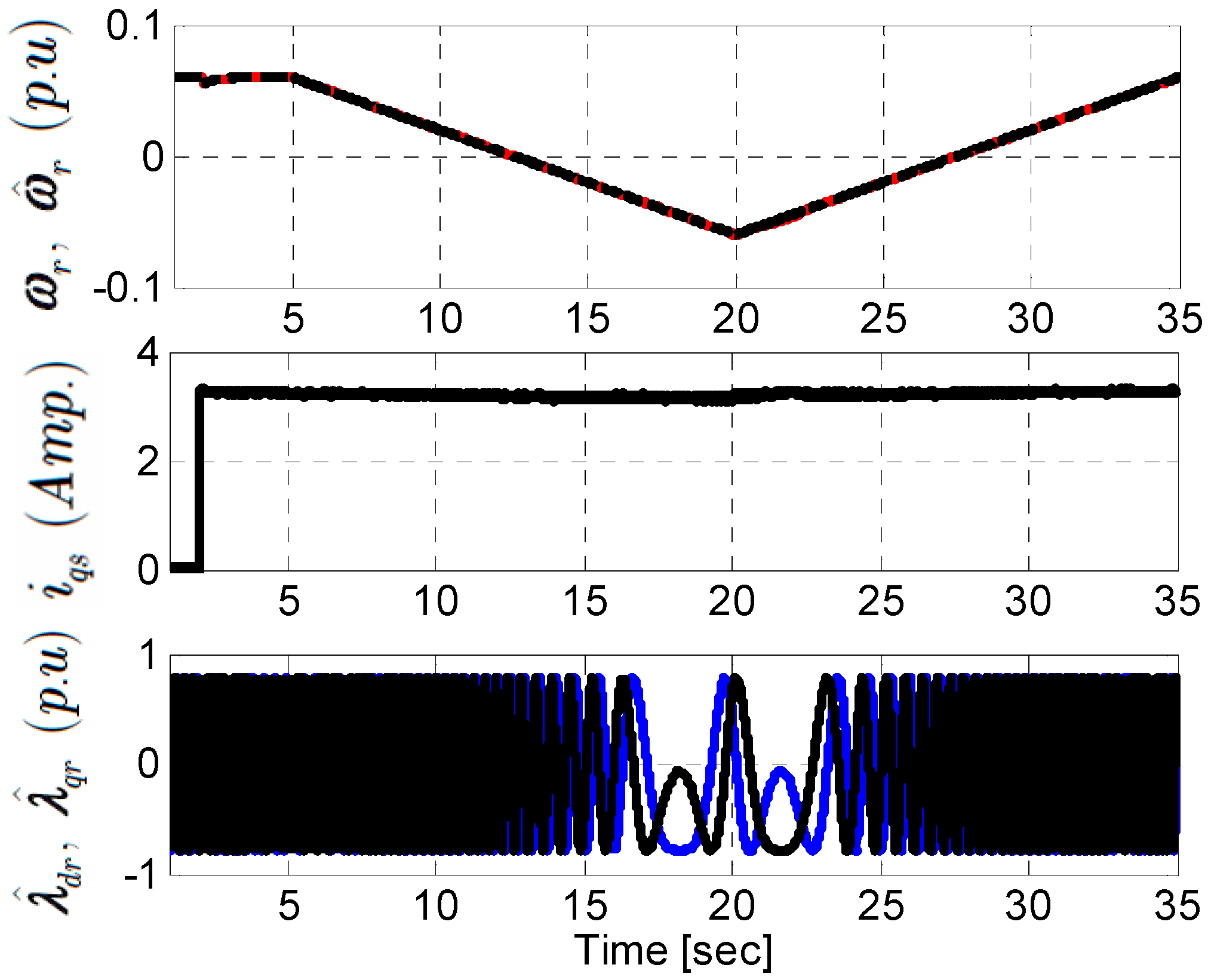
5.4. Slow Speed Reversal
5.5. Zero Speed
6. Comparison with Previous Works
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Rated output power | 5.5 kW | Stator self-inductance | 57.3 mH |
| Rated voltage | 186 V | Rotor self-inductance | 57.3 mH |
| Rated frequency | 50 Hz | Mutual inductance | 56.43 mH |
| No. of pole pairs | 2 | Stator resistance | 0.294 Ω |
| Rotor resistance | 0.14325 Ω |
References
- Pacas, M. Sensorless drives in industrial applications. IEEE Ind. Electron. Mag. 2011, 5, 16–23. [Google Scholar] [CrossRef]
- Holtz, J. Sensorless control of induction machines—With or without signal injection? IEEE Trans. Ind. Electron. 2006, 53, 7–30. [Google Scholar] [CrossRef] [Green Version]
- Kubota, H.; Matsuse, K.; Nakano, T. DSP-based speed adaptive flux observer of induction motor. IEEE Trans. Ind. Appl. 1993, 29, 344–348. [Google Scholar] [CrossRef]
- Kubota, H.; Matsuse, K. Speed sensorless field-oriented control of induction motor with rotor resistance adaptation. IEEE Trans. Ind. Appl. 1994, 30, 1219–1224. [Google Scholar] [CrossRef]
- Sun, W.; Yu, Y.; Wang, G. Design method of adaptive full order observer with or without estimated flux error in speed estimation algorithm. IEEE Trans. Power Electron. 2016, 31, 2609–2626. [Google Scholar] [CrossRef]
- Xu, W.; Dian, R.; Liu, Y.; Hu, D.; Zhu, J. Robust flux estimation method for linear induction motors based on improved extended state observers. IEEE Trans. Power Electron. 2019, 34, 4628–4640. [Google Scholar] [CrossRef]
- Devanshu, A.; Singh, M.; Kumar, N. An improved nonlinear flux observer based sensorless FOC IM drive with adaptive predictive current control. IEEE Trans. Power Electron. 2020, 35, 652–666. [Google Scholar] [CrossRef]
- Alonge, F.; Cirrincione, M.; Pucci, M.; Sferlazza, A. A nonlinear observer for rotor flux estimation of induction motor considering the estimated magnetization characteristic. IEEE Trans. Ind. Appl. 2017, 53, 5952–5965. [Google Scholar] [CrossRef]
- Zaky, M.S.; Metwaly, M.K.; Azazi, H.Z.; Deraz, S.A. A new adaptive smo for speed estimation of sensorless induction motor drives at zero and very low frequencies. IEEE Trans. Ind. Electron. 2018, 65, 6901–6911. [Google Scholar] [CrossRef]
- Lascu, C.; Andreescu, G.-D. Sliding-mode observer and improved integrator with DC-offset compensation for flux estimation in sensorless-controlled induction motors. IEEE Trans. Ind. Electron. 2006, 53, 785–794. [Google Scholar] [CrossRef]
- Suwankawin, S.; Sangwongwanich, S. A speed-sensorless IM drive with decoupling control and stability analysis of speed estimation. IEEE Trans. Ind. Electron. 2002, 49, 444–455. [Google Scholar] [CrossRef]
- Suwankawin, S.; Sangwonwanich, S. Design Strategy of an Adaptive Full-Order Observer for Speed Sensorless Induction Motor Drives-Tracking Performance and Stabilization. IEEE Trans. Ind. Electron. 2006, 53, 96–119. [Google Scholar] [CrossRef]
- HMaksoud, A.; Shaaban, S.M.; Zaky, M.S.; Azazi, Z.H. Performance and Stability Improvement of AFO for Sensorless IM Drives in Low Speeds Regenerating Mode. IEEE Trans. Power Electron. 2019, 34, 7812–7825. [Google Scholar] [CrossRef]
- Saejia, M.; Sangwongwanich, S. Averaging analysis approach for stability analysis of speed-sensorless induction motor drives with stator resistance estimation. IEEE Trans. Ind. Electron. 2006, 53, 162–177. [Google Scholar] [CrossRef]
- Zaky, M. Stability Analysis of Speed and Stator Resistance Estimators for Sensorless Induction Motor Drives. IEEE Trans. Ind. Electron. 2012, 59, 858–870. [Google Scholar] [CrossRef]
- Zaky, M.; Metwaly, M.K. Sensorless Torque/Speed Control of Induction Motor Drives at Zero and Low Frequency with Stator and Rotor Resistance Estimation. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1416–1429. [Google Scholar] [CrossRef]
- Chang, C.-M.; Liu, C.-H. A new MRAS based strategy for simultaneous estimation and control of a sensorless induction motor drive. J. Chin. Inst. Eng. 2010, 33, 451–462. [Google Scholar] [CrossRef]
- Harnefors, L.; Hinkkanen, M. Complete stability of reduced-order and full-order observers for sensorless IM drives. IEEE Trans. Ind. Electron. 2002, 55, 1319–1329. [Google Scholar] [CrossRef]
- Kubota, H.; Sato, I.; Tamura, Y.; Matsuse, K.; Ohta, H.; Hori, Y. Regenerating-mode low-speed operation of sensorless induction motor drive with adaptive observer. IEEE Trans. Ind. Appl. 2002, 38, 1081–1086. [Google Scholar] [CrossRef]
- Tsuji, M.; Chen, S.; Izumi, K.; Yamada, E. A sensorless vector control system for induction motors using q-axis flux with stator resistance identification. IEEE Trans. Ind. Electron. 2001, 48, 185–194. [Google Scholar] [CrossRef]
- Hinkkanen, M. Analysis and design of full-order flux observers for sensorless induction motors. IEEE Trans. Ind. Electron. 2004, 51, 1033–1040. [Google Scholar] [CrossRef] [Green Version]
- Etien, E.; Chaigne, C.; Bensiali, N. On the stability of full adaptive observer for induction motor in regenerating mode. IEEE Trans. Ind. Electron. 2010, 57, 1599–1608. [Google Scholar] [CrossRef]
- Hinkkanen, M.; Luomi, J. Stabilization of regenerating-mode operation in sensorless induction motor drives by full-order flux observer design. IEEE Trans. Ind. Electron. 2004, 51, 1318–1328. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Wang, T.; Yao, W.; Lee, K.; Lu, Z. Speed Convergence Rate-Based Feedback Gains Design of Adaptive Full-Order Observer in Sensorless Induction Motor Drives. IET Electr. Power Appl. 2014, 8, 12–22. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Korzonek, M.; Tarchała, G. Stability Analysis of Selected Speed Estimators for Induction Motor Drive in Regenerating Mode—A Comparative Study. IEEE Trans. Ind. Electron. 2017, 64, 7721–7730. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, Y.; Du, C.; Liu, J.; Sun, X.; Zhong, Y. Research on Anti-Error Performance of Speed and Flux Estimation for Induction Motors Based on Robust Adaptive State Observer. IEEE Trans. Ind. Electron. 2016, 63, 3499–3510. [Google Scholar] [CrossRef]
- Sun, W.; Liu, X.; Gao, J.; Yu, Y.; Wang, G.; Xu, D. Zero Stator Current Frequency Operation of Speed-Sensorless Induction Motor Drives Using Stator Input Voltage Error for Speed Estimation. IEEE Trans. Ind. Electron. 2016, 63, 1490–1498. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Korzonek, M.; Tarchala, G. Stability Improvement Methods of the Adaptive Full-Order Observer for Sensorless Induction Motor Drive—Comparative Study. IEEE Trans. Ind. Inform. 2019, 15, 6114–6126. [Google Scholar] [CrossRef]
- Sun, W.; Xu, D.; Jiang, D. Observability Analysis for Speed Sensorless Induction Motor Drives with and Without Virtual Voltage Injection. IEEE Trans. Power Electron. 2019, 34, 9236–9246. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Z.; Xu, D.G.; Yu, X.; Jiang, D. Stable Operation Method for Speed Sensorless Induction Motor Drives at Zero Synchronous Speed with Estimated Speed Error Compensation. IEEE Trans. Power Electron. 2019, 34, 11454–11466. [Google Scholar] [CrossRef]
- Chen, J.; Huang, J.; Sun, Y. Resistances and Speed Estimation in Sensorless Induction Motor Drives Using a Model with Known Regressors. IEEE Trans. Ind. Electron. 2019, 66, 2659–2667. [Google Scholar] [CrossRef]
- Chen, B.; Yao, W.; Chen, F.; Lu, Z. Parameter sensitivity in sensorless induction motor drives with the adaptive full-order observer. IEEE Trans. Ind. Electron. 2015, 62, 4307–4318. [Google Scholar] [CrossRef]
- Hinkkanen, M.; Luomi, J. Parameter Sensitivity of Full-Order Flux Observers for Induction Motors. IEEE Trans. Ind. Appl. 2003, 39, 1127–1135. [Google Scholar] [CrossRef] [Green Version]
- Hinkkanen, M.; Harnefors, L.; Luomi, J. Reduced-order flux observers with stator-resistance adaptation for speed-sensorless induction motor drives. IEEE Trans. Power Electron. 2010, 25, 1173–1183. [Google Scholar] [CrossRef]
- Luo, C.; Wang, B.; Yu, Y.; Chen, C.; Huo, Z.; Xu, D. Operating-point tracking method for sensorless induction motor stability enhancement in low-speed regenerating mode. IEEE Trans. Ind. Electron. 2020, 67, 3386–3397. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Z.; Xu, D.; Wang, B. Robust stability improvement for speed sensorless induction motor drive at low speed range by virtual voltage injection. IEEE Trans. Ind. Electron. 2020, 67, 2642–2654. [Google Scholar] [CrossRef]
- Morawiec, M.; Kroplewski, P.; Odeh, C. Nonadaptive rotor speed estimation of induction machine in an adaptive full-order observer. IEEE Trans. Ind. Electron. 2022, 69, 2333–2344. [Google Scholar] [CrossRef]
- Zaky, M.S.; Fetouh, T.; Shaban, S.M.; Azazi, H.Z. A Novel Analytical Approach using Rough Set and Genetic Algorithm of a Stable Sensorless Induction Motor Drives in the Regenerating Mode. IEEE Access 2020, 8, 157748–157761. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; Fetouh, T.; Bishr, M.A.; Saleh, R.A.F. Power System Operation using Particle Swarm Optimization Technique. Electr. Power Syst. Res. 2008, 78, 1906–1913. [Google Scholar] [CrossRef]









| Formula/Constant | Curve Fitting Value | |
|---|---|---|
| a1 | 0.116270 | |
| a2 | 11.633000 | |
| b1 | 0.116600 | |
| b2 | 11.662000 | |
| b3 | −0.025000 | |
| b4 | 0.007938 | |
| b5 | 0.696600 | |
| c1 | 1.29830 × 10−6 | |
| c2 | 1.13030 × 10−4 | |
| c3 | −1.97280 × 10−4 | |
| c4 | −0.017315 | |
| c5 | 0.116080 | |
| c6 | 11.617000 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaky, M.S.; Shaaban, S.M.; Fetouh, T.; Azazi, H.Z.; Mesalam, Y.I. Optimization of Observer Feedback Gains for Stable Sensorless IM Drives at Very Low Frequencies: A Comparative Study between GA and PSO. Mathematics 2022, 10, 1710. https://doi.org/10.3390/math10101710
Zaky MS, Shaaban SM, Fetouh T, Azazi HZ, Mesalam YI. Optimization of Observer Feedback Gains for Stable Sensorless IM Drives at Very Low Frequencies: A Comparative Study between GA and PSO. Mathematics. 2022; 10(10):1710. https://doi.org/10.3390/math10101710
Chicago/Turabian StyleZaky, Mohamed S., Shaaban M. Shaaban, Tamer Fetouh, Haitham Z. Azazi, and Yehya I. Mesalam. 2022. "Optimization of Observer Feedback Gains for Stable Sensorless IM Drives at Very Low Frequencies: A Comparative Study between GA and PSO" Mathematics 10, no. 10: 1710. https://doi.org/10.3390/math10101710
APA StyleZaky, M. S., Shaaban, S. M., Fetouh, T., Azazi, H. Z., & Mesalam, Y. I. (2022). Optimization of Observer Feedback Gains for Stable Sensorless IM Drives at Very Low Frequencies: A Comparative Study between GA and PSO. Mathematics, 10(10), 1710. https://doi.org/10.3390/math10101710








