Neural Adaptive Fixed-Time Attitude Stabilization and Vibration Suppression of Flexible Spacecraft
Abstract
:1. Introduction
- Rather than the terminal sliding mode control technique, the proposed controller was developed under the fixed-time backstepping control framework. In this way, the proposed controller does not have the chattering phenomenon and singularity problem existing in the terminal sliding mode control.
- The NN was integrated with the proposed controller to compensate the lumped unknown item. Benefiting from the NN compensation, the proposed controller is not only robust against uncertain inertia and external disturbance, but also insensitive to elastic vibrations of the flexible appendages.
2. Problem Description and Preliminaries
2.1. Problem Description
2.2. Preliminaries
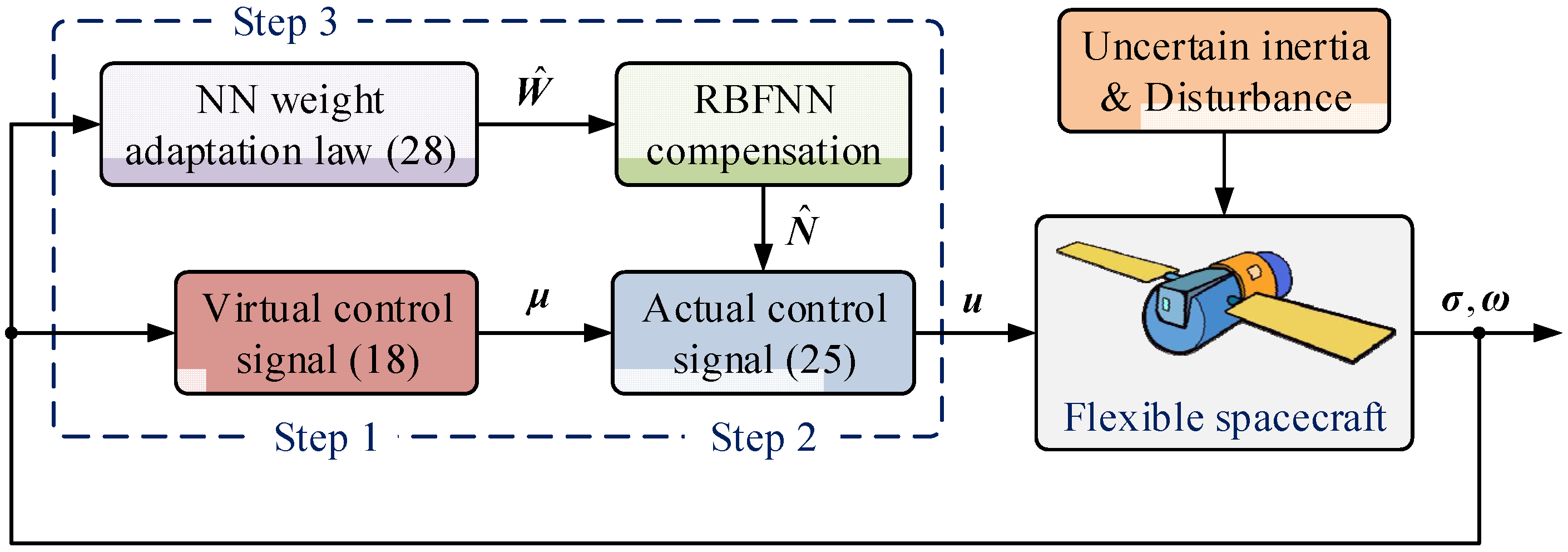
3. Control Design and Lyapunov Analysis
3.1. Control Design
3.2. Lyapunov Analysis
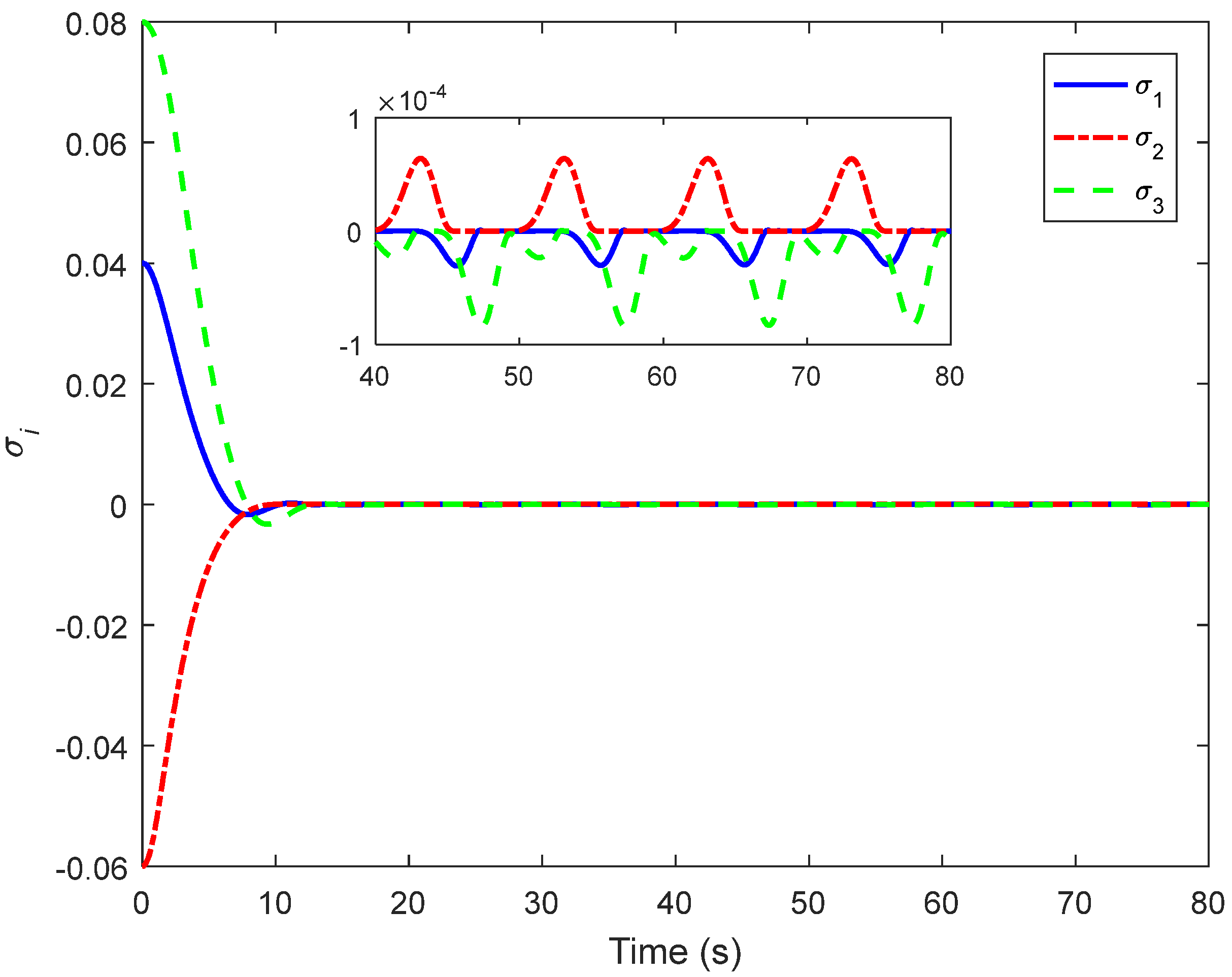
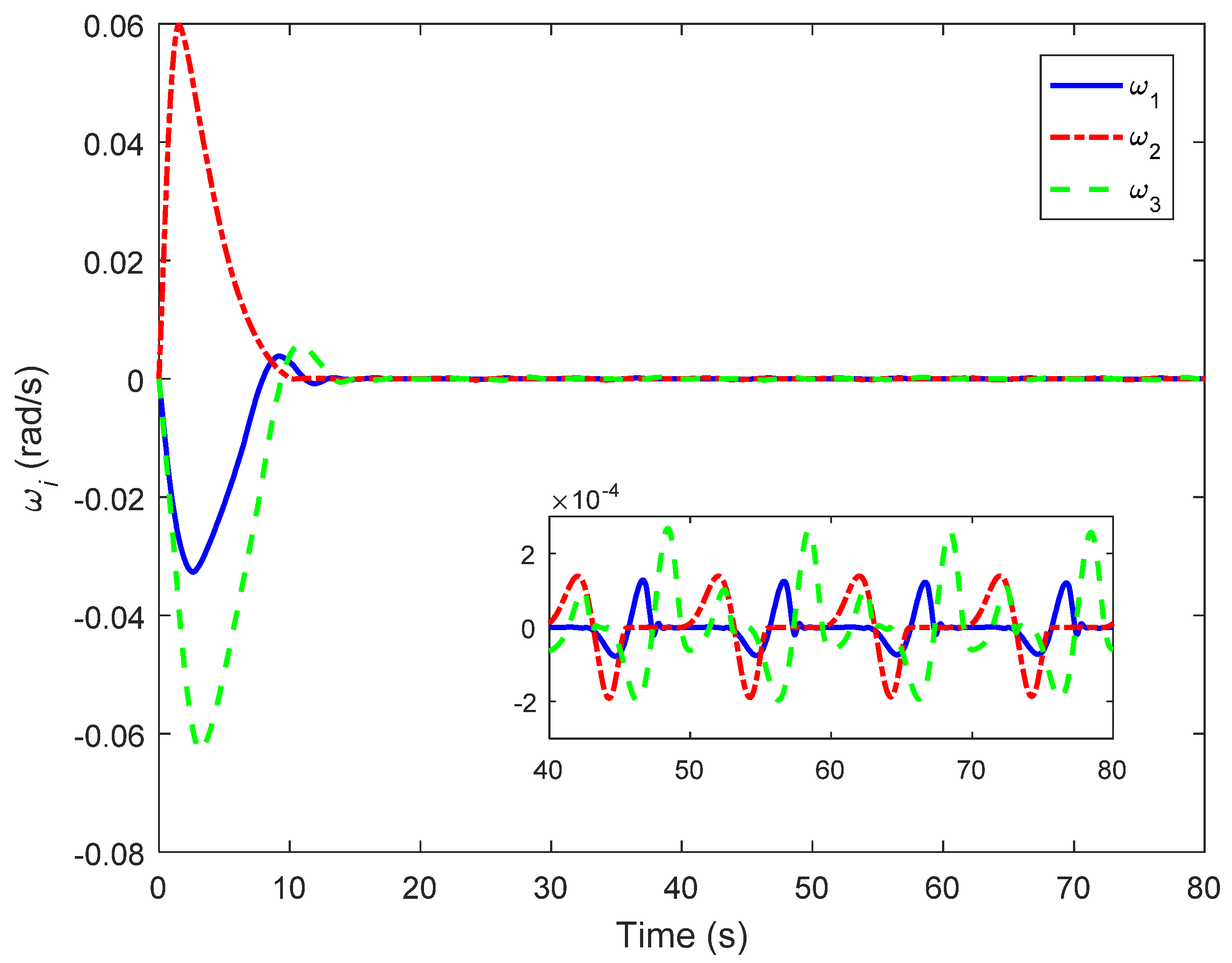
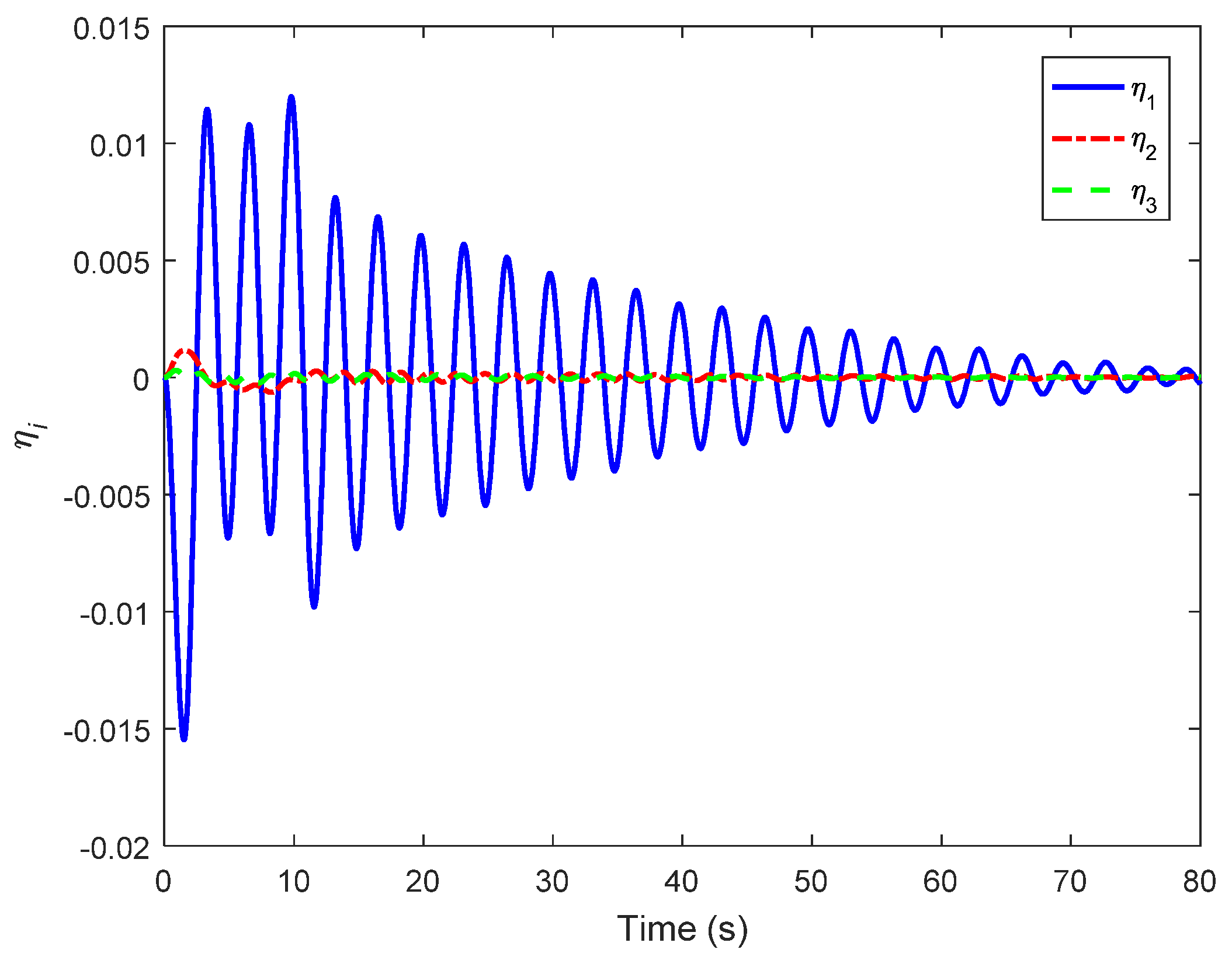
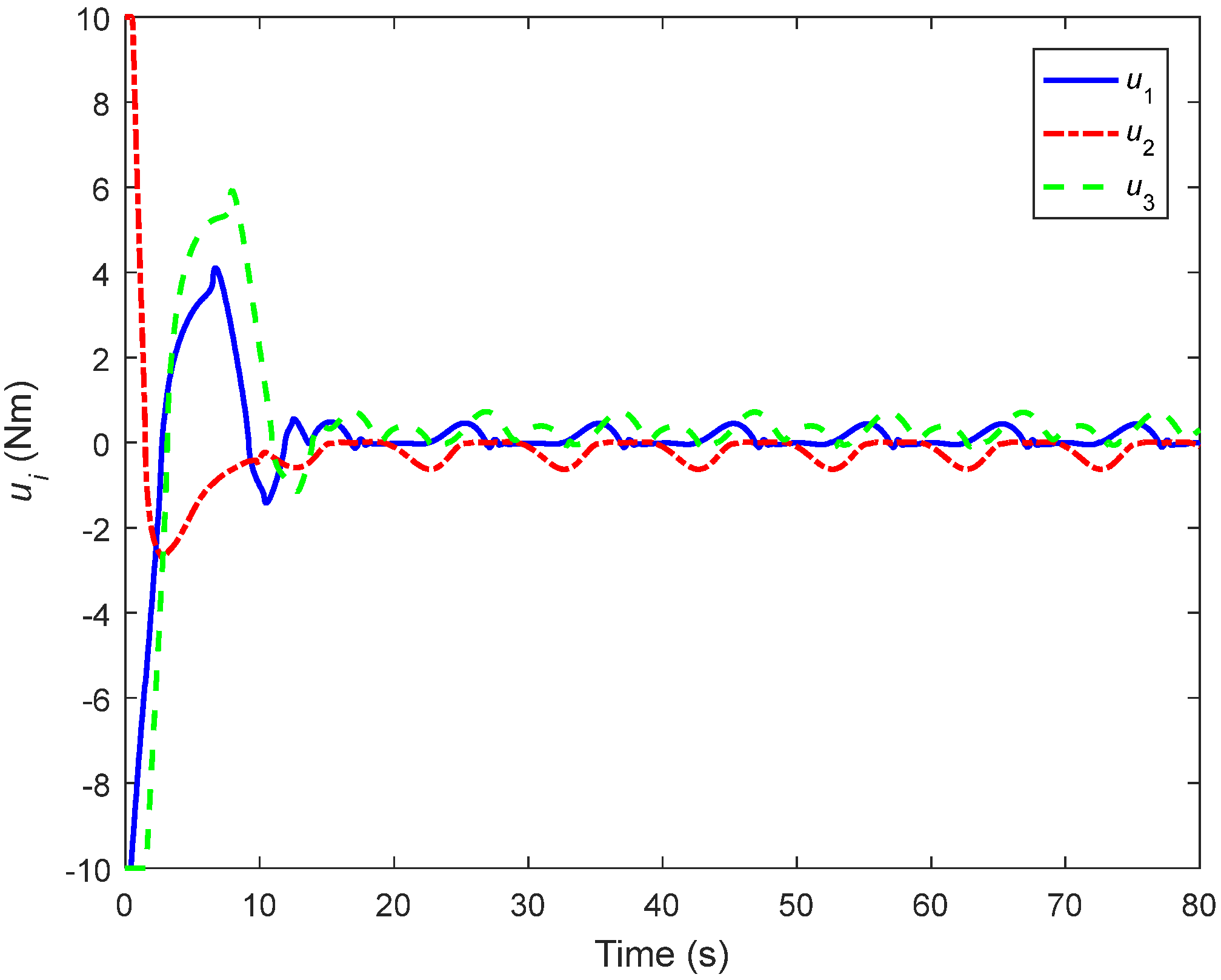
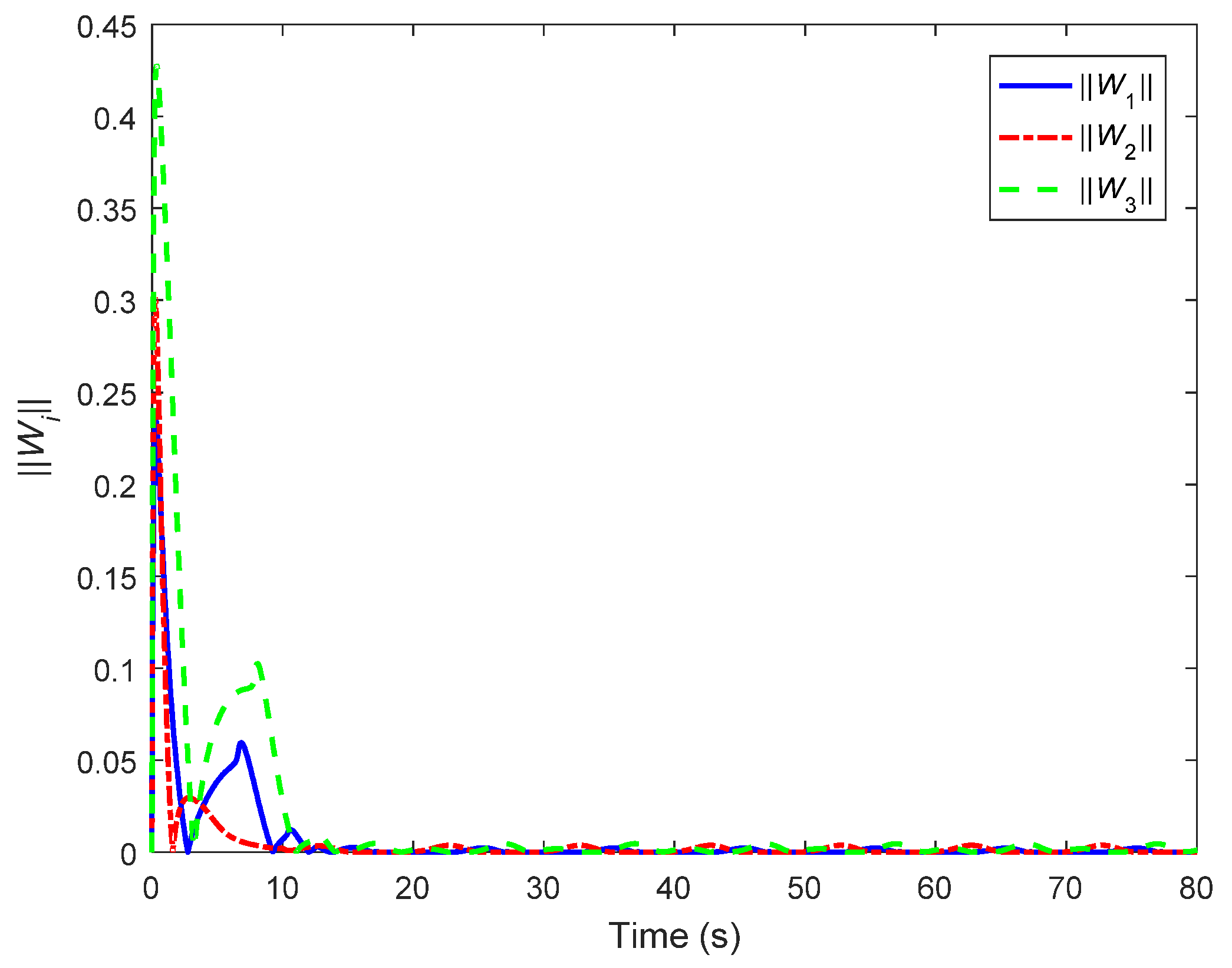
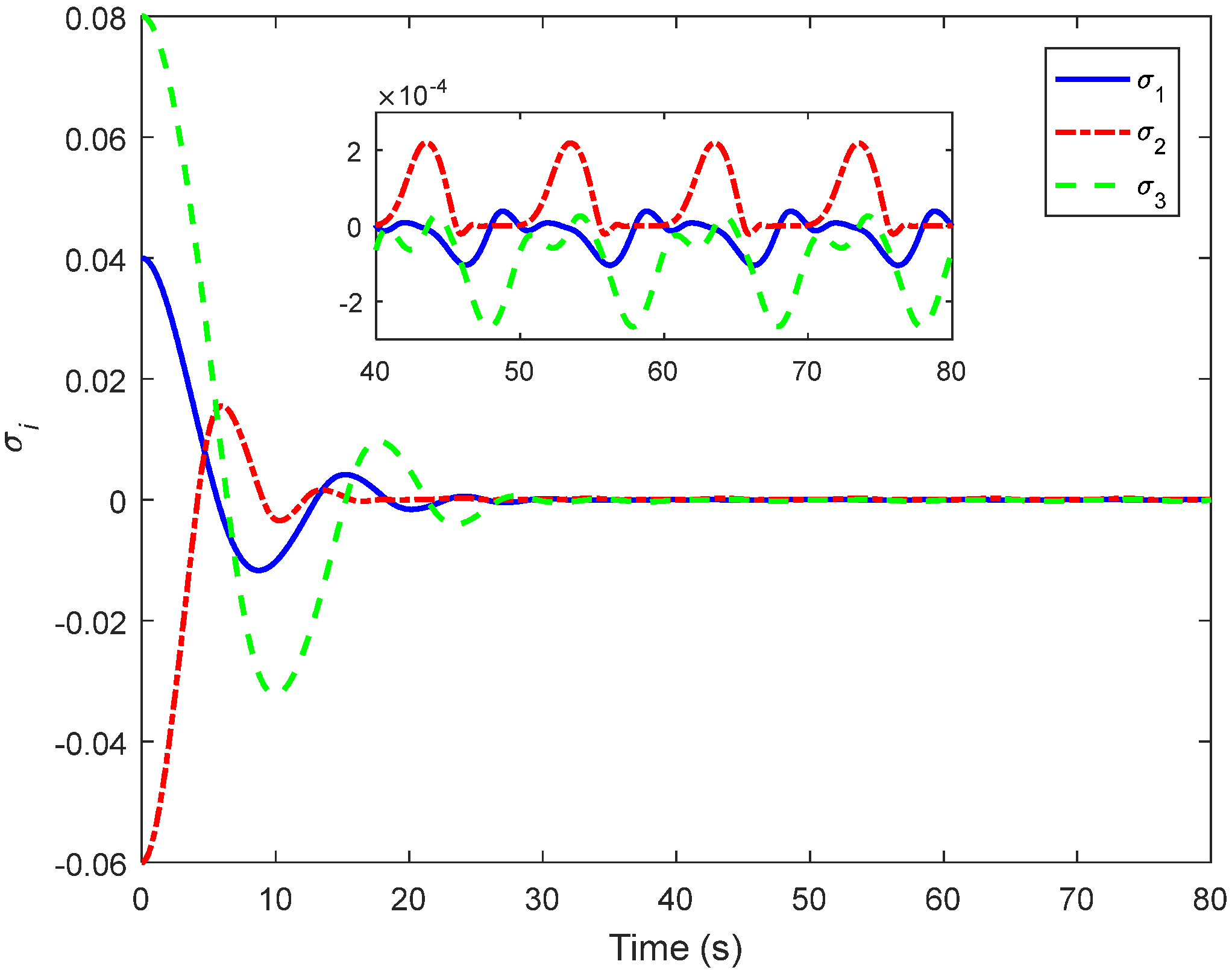
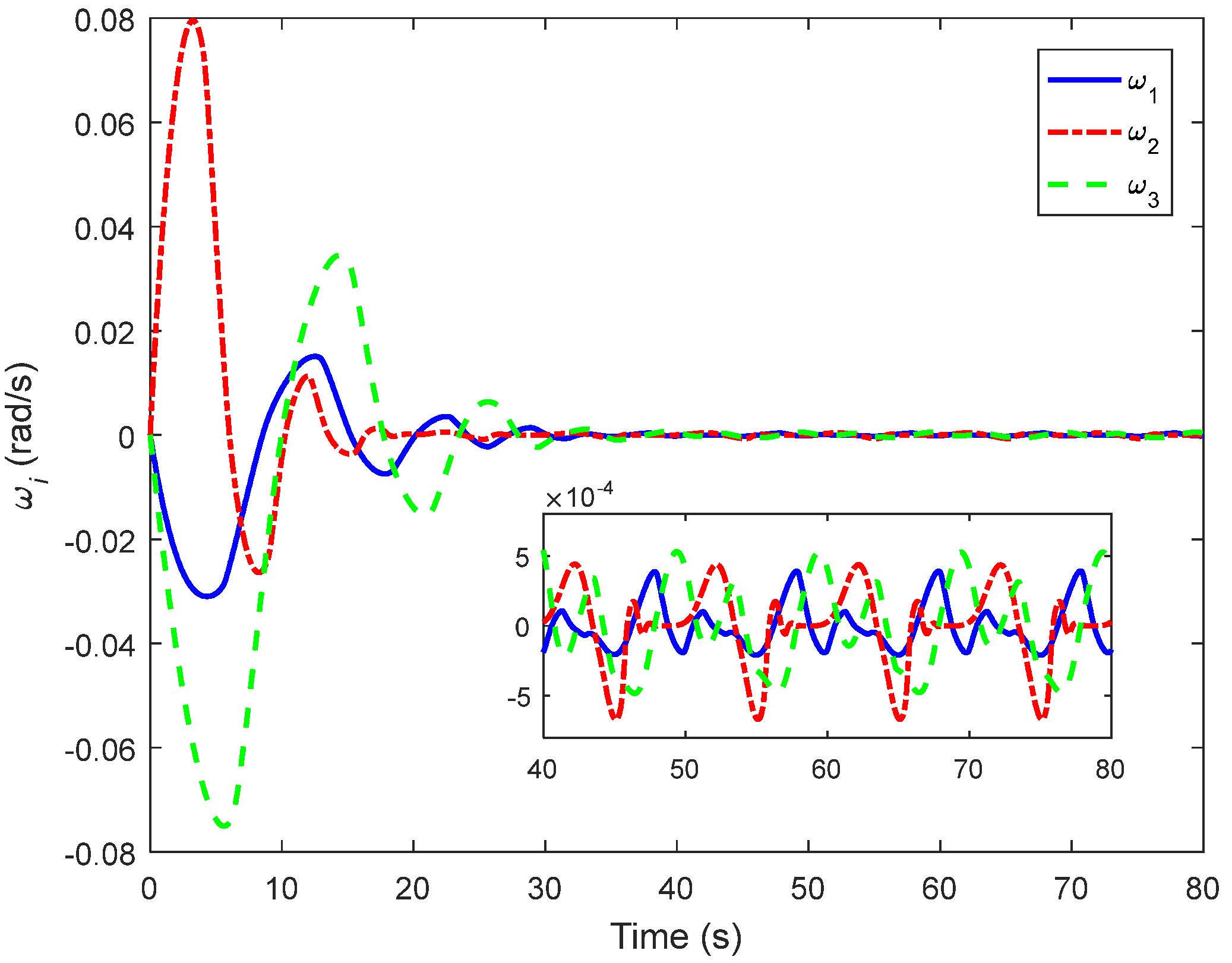
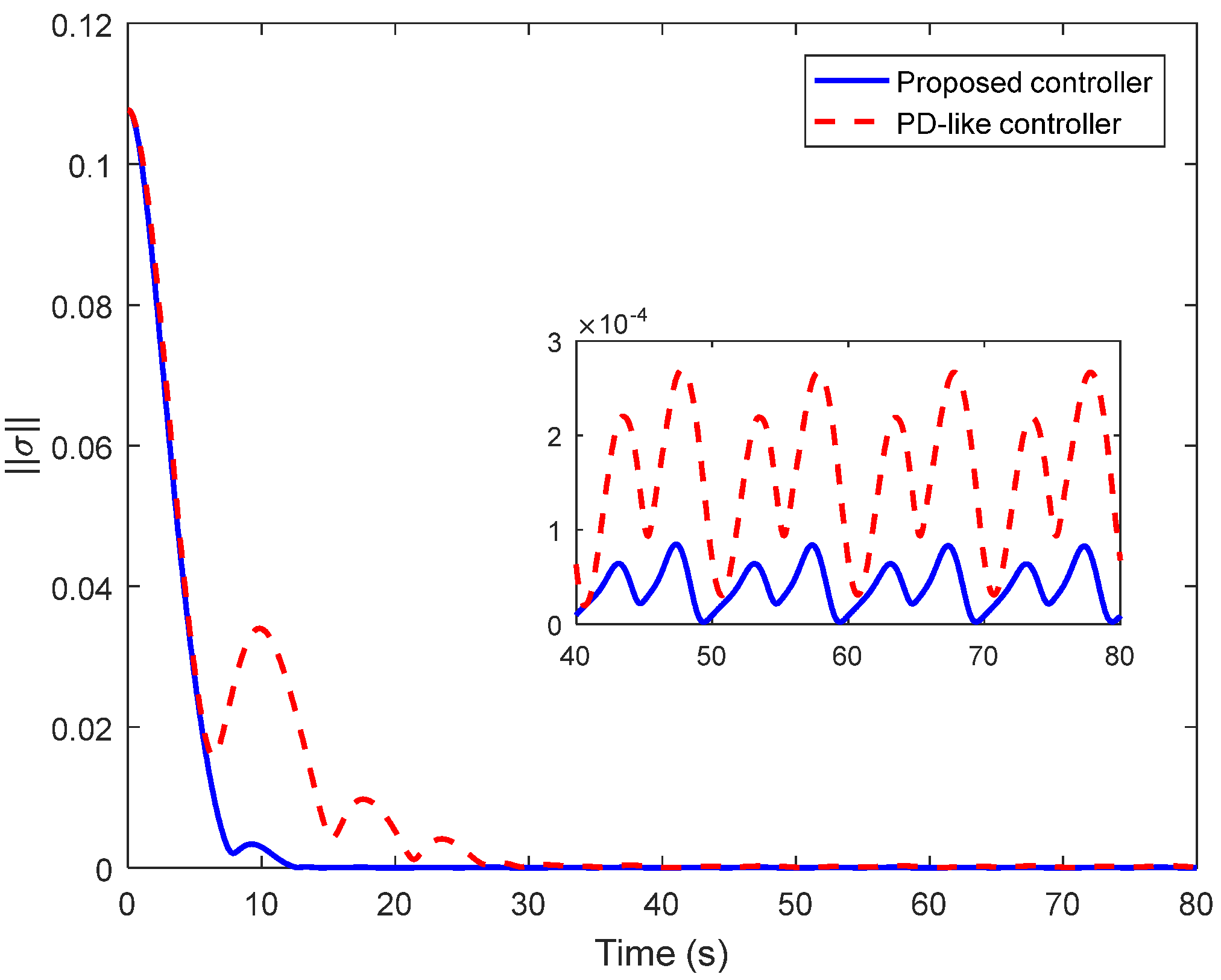
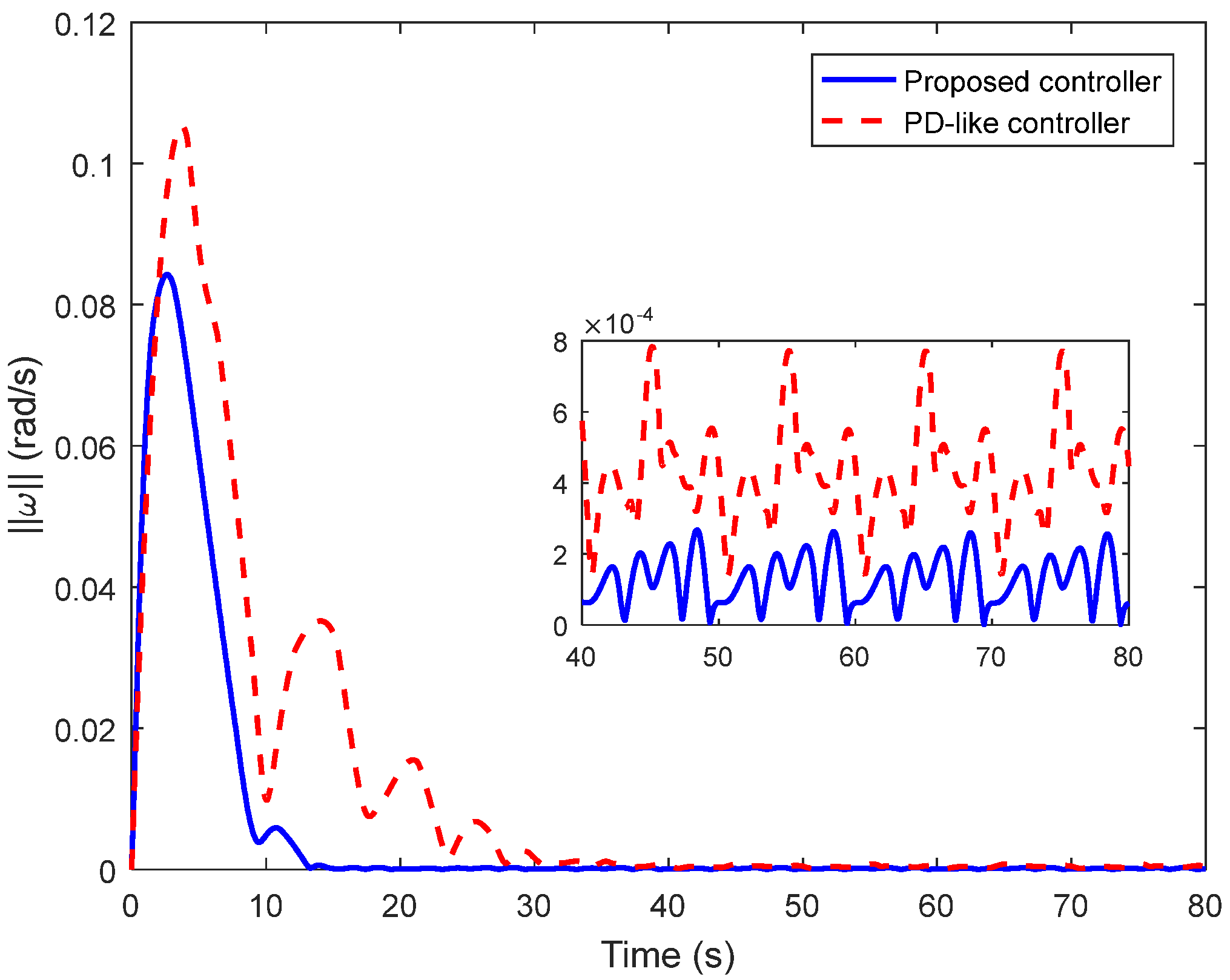
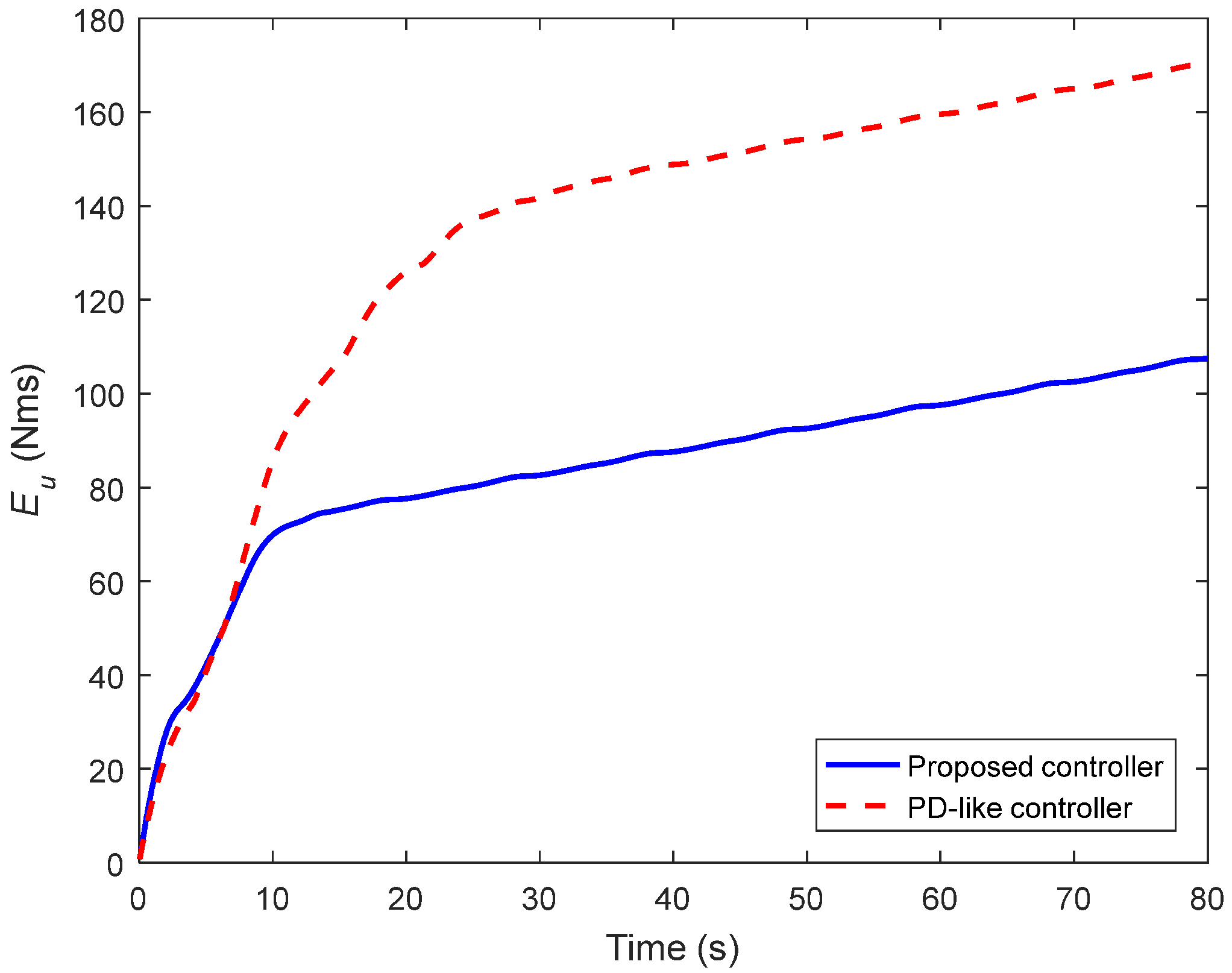
4. Simulations and Comparisons
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nagashio, T.; Kida, T.; Ohtani, T.; Hamada, Y. Design and implementation of robust symmetric attitude controller for ETS-VIII spacecraft. Control Eng. Pract. 2010, 18, 1440–1451. [Google Scholar] [CrossRef]
- Nagashio, T.; Kida, T.; Hamada, Y.; Ohtani, T. Robust two-degrees-of-freedom attitude controller design and flight test result for engineering test satellite-VIII spacecraft. IEEE Trans. Control Syst. Technol. 2014, 22, 157–168. [Google Scholar] [CrossRef]
- Luo, J.; Wei, C.; Dai, H.; Yin, Z.; Wei, X.; Yuan, J. Robust inertia-free attitude takeover control of postcapture combined spacecraft with guaranteed prescribed performance. ISA Trans. 2018, 74, 28–44. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Ma, G.; Lv, Y.; Guo, Y. Forecasting-based data-driven model-free adaptive sliding mode attitude control of combined spacecraft. Aerosp. Sci. Technol. 2019, 86, 364–374. [Google Scholar] [CrossRef]
- Huang, X.; Duan, G. Fault-tolerant attitude tracking control of combined spacecraft with reaction wheels under prescribed performance. ISA Trans. 2020, 98, 161–172. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ma, G.; Lyu, Y.; Wang, P. Neural network-based reinforcement learning control for combined spacecraft attitude tracking maneuvers. Neurocomputing 2022, 484, 67–78. [Google Scholar] [CrossRef]
- Modi, V.J. Attitude dynamics of satellites with flexible appendages—A brief review. J. Spacecr. Rocket. 1974, 11, 743–751. [Google Scholar] [CrossRef]
- Likins, P. Spacecraft attitude dynamics and control—A personal perspective on early developments. J. Guid. Control Dyn. 1986, 9, 129–134. [Google Scholar] [CrossRef]
- Li, H.; Guo, L.; Zhang, Y. An anti-disturbance PD control scheme for attitude control and stabilization of flexible spacecrafts. Nonlinear Dyn. 2012, 67, 2081–2088. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Li, L.; Yuan, J. A composite anti-disturbance control scheme for attitude stabilization and vibration suppression of flexible spacecrafts. J. Vib. Control 2017, 23, 2470–2477. [Google Scholar] [CrossRef]
- Sun, H.; Hou, L.; Zong, G.; Guo, L. Composite anti-disturbance attitude and vibration control for flexible spacecraft. IET Control Theory Appl. 2017, 11, 2383–2390. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, L.; Qiao, J.; Li, W. An enhanced anti-disturbance attitude control law for flexible spacecrafts subject to multiple disturbances. Control Eng. Pract. 2019, 84, 274–283. [Google Scholar] [CrossRef]
- Singh, S.N.; Zhang, R. Adaptive output feedback control of spacecraft with flexible appendages by modeling error compensation. Acta Astronaut. 2004, 54, 229–243. [Google Scholar] [CrossRef]
- Maganti, G.B.; Singh, S.N. Simplified adaptive control of an orbiting flexible spacecraft. Acta Astronaut. 2007, 61, 575–589. [Google Scholar] [CrossRef]
- Guan, P.; Liu, X.-J.; Liu, J.-Z. Adaptive fuzzy sliding mode control for flexible satellite. Eng. Appl. Artif. Intell. 2005, 18, 451–459. [Google Scholar] [CrossRef]
- Dong, C.; Xu, L.; Chen, Y.; Wang, Q. Networked flexible spacecraft attitude maneuver based on adaptive fuzzy sliding mode control. Acta Astronaut. 2009, 65, 1561–1570. [Google Scholar] [CrossRef]
- Hu, Q.; Xiao, B. Intelligent proportional-derivation control for flexible spacecraft attitude stabilization with unknown input saturation. Aerosp. Sci. Technol. 2012, 23, 63–74. [Google Scholar] [CrossRef]
- Sendi, C.; Ayoubi, M.A. Robust-optimal fuzzy model-based control of flexible spacecraft with actuator constraint. J. Dyn. Syst. Meas. Control 2016, 138, 091004. [Google Scholar] [CrossRef]
- Sendi, C. Attitude control of a flexible spacecraft via fuzzy optimal variance technique. Mathematics 2022, 10, 179. [Google Scholar] [CrossRef]
- Di Gennaro, S. Active vibration suppression in flexible spacecraft attitude tracking. J. Guid. Control Dyn. 1998, 21, 400–408. [Google Scholar] [CrossRef]
- Di Gennaro, S. Output stabilization of flexible spacecraft with active vibration suppression. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 747–759. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.; Ma, G. Variable structure control and active vibration suppression of flexible spacecraft during attitude maneuver. Aerosp. Sci. Technol. 2005, 9, 307–317. [Google Scholar] [CrossRef]
- Azadi, M.; Fazelzadeh, S.A.; Eghtesad, M.; Azadi, E. Vibration suppression and adaptive-robust control of a smart flexible satellite with three axes maneuvering. Acta Astronaut. 2011, 69, 307–322. [Google Scholar] [CrossRef]
- Azadi, M.; Eghtesad, M.; Fazelzadeh, S.A.; Azadi, E. Dynamics and control of a smart flexible satellite moving in an orbit. Multibody Syst. Dyn. 2015, 35, 1–23. [Google Scholar] [CrossRef]
- Wu, S.; Radice, G.; Sun, Z. Robust finite-time control for flexible spacecraft attitude maneuver. J. Aerosp. Eng. 2014, 27, 185–190. [Google Scholar] [CrossRef]
- Yan, R.; Wu, Z. Finite-time attitude stabilization of flexible spacecrafts via reduced-order SMDO and NTSMC. J. Aerosp. Eng. 2018, 31, 04018023. [Google Scholar] [CrossRef]
- Zhang, X.; Zong, Q.; Dou, L.; Tian, B.; Liu, W. Finite-time attitude maneuvering and vibration suppression of flexible spacecraft. J. Frankl. Inst. 2020, 357, 11604–11628. [Google Scholar] [CrossRef]
- Hasan, M.N.; Haris, M.; Qin, S. Vibration suppression and fault-tolerant attitude control for flexible spacecraft with actuator faults and malalignments. Aerosp. Sci. Technol. 2022, 120, 107290. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, A.; Efimov, D.; Perruquetti, W. Finite-time and fixed-time stabilization: Implicit Lyapunov function approach. Automatica 2015, 51, 332–340. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-time attitude control for rigid spacecraft with actuator saturation and faults. IEEE Trans. Control Syst. Technol. 2016, 24, 1892–1898. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M. Robust fixed-time attitude stabilization control of flexible spacecraft with actuator uncertainty. Nonlinear Dyn. 2020, 100, 2505–2519. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M.; Ran, D. Faster fixed-time control of flexible spacecraft attitude stabilization. IEEE Trans. Ind. Informat. 2020, 16, 1281–1290. [Google Scholar] [CrossRef]
- Esmaeilzadeh, S.M.; Golestani, M.; Mobayen, S. Chattering-free fault-tolerant attitude control with fast fixed-time convergence for flexible spacecraft. Int. J. Control Autom. Syst. 2021, 19, 767–776. [Google Scholar] [CrossRef]
- Golestani, M.; Esmaeilzadeh, S.M.; Mobayen, S. Fixed-time control for high-precision attitude stabilization of flexible spacecraft. Eur. J. Control 2021, 57, 222–231. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley and Sons: New York, NY, USA, 2006. [Google Scholar]
- Sanner, R.M.; Slotine, J.-J.E. Gaussian networks for direct adaptive control. IEEE Trans. Neural Netw. 1992, 3, 837–863. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Du, H.; Li, S. Finite-time attitude stabilization for a spacecraft using homogeneous method. J. Guid. Control Dyn. 2012, 35, 740–748. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Q.; Jahanshahi, H.; Moroz, I.; Alotaibi, N.D.; Bekiros, S. Neural Adaptive Fixed-Time Attitude Stabilization and Vibration Suppression of Flexible Spacecraft. Mathematics 2022, 10, 1667. https://doi.org/10.3390/math10101667
Yao Q, Jahanshahi H, Moroz I, Alotaibi ND, Bekiros S. Neural Adaptive Fixed-Time Attitude Stabilization and Vibration Suppression of Flexible Spacecraft. Mathematics. 2022; 10(10):1667. https://doi.org/10.3390/math10101667
Chicago/Turabian StyleYao, Qijia, Hadi Jahanshahi, Irene Moroz, Naif D. Alotaibi, and Stelios Bekiros. 2022. "Neural Adaptive Fixed-Time Attitude Stabilization and Vibration Suppression of Flexible Spacecraft" Mathematics 10, no. 10: 1667. https://doi.org/10.3390/math10101667
APA StyleYao, Q., Jahanshahi, H., Moroz, I., Alotaibi, N. D., & Bekiros, S. (2022). Neural Adaptive Fixed-Time Attitude Stabilization and Vibration Suppression of Flexible Spacecraft. Mathematics, 10(10), 1667. https://doi.org/10.3390/math10101667






