Barrier Function-Based Nonsingular Finite-Time Tracker for Quadrotor UAVs Subject to Uncertainties and Input Constraints

Abstract

This study proposes an adaptive barrier functions-based non-singular terminal sliding mode control approach for the trajectory tracking of a quadrotor unmanned aerial vehicle subject to bounded uncertainties and input constraints. First, the state-space equations of the six degrees-of-freedom quadrotor system is introduced in the presence of bounded uncertainty and constrained input. Then, a compensation system is designed with the aim of removing the constrained input and leading to high performance. Afterwards, a linear switching surface is defined using the tracking error and virtual control input to guarantee the convergence of the tracking error in the presence of parametric uncertainties and input saturation. Later, a non-singular terminal sliding surface is proposed for fast convergence of the linear switching surface. To eliminate the need for approximating the upper bounds of uncertainties and ensure the fast convergence of the non-singular terminal sliding surface to a pre-specified neighborhood of the origin, we considered an adaptive barrier function scheme. The fast convergence rate of the proposed approach is verified via the Lyapunov stability theory. The accuracy and performance of the proposed approach is assessed using MATLAB/Simulink simulations and robustness analysis using the random number noise.

1. Introduction

Recent years have witnessed a substantial increase in the development and use of robotic technology for industrial, military, commercial and educational usages [1,2]. Aerial robots, specially Unmanned Aerial Vehicles (UAVs), are one of the most popular types of robots. They exist in various types, such as a fixed-wing aircraft, single-rotor quadcopter and quadrotor [3,4]. The latter are the most prominent due to their simple structure, low cost and ease of use [5,6]. This has motivated research efforts in quadrotor control design [7]. Quadrotors typically have six different directions, i.e., three transitional movements along the coordinates axis, to specify the position of quadrotor, and three rotational motions around the coordinates axis, to determine attitude of quadrotor [8,9]. Hence, various linear and nonlinear control schemes have been proposed for the quadrotor control, including the Proportional-Integral-Derivative (PID), Linear Quadratic Regulator (LQR) [10], feedback linearization [11], Sliding Mode Control (SMC) [12], Adaptive Siding Mode Control (ASMC) [13], Terminal Sliding Mode Control (TSMC) [14,15] and non-singular SMC [16], which have been extended and employed for quadrotor path tracking. In practical applications, the control inputs of the quadrotor system have constraints that can potentially decrease the performance of the system. Hence, some compensation mechanisms are designed and added to the control strategy to improve the system performance against input saturation [17,18]. Furthermore, accurate tracking with a fast convergence rate is another important issue, which should be considered when designing a control strategy for quadrotors. This has motivated the use of a non-singular TSMC to yield fast convergence in the tracking performance of the quadrotor system [19,20]. Moreover, model uncertainties are ubiquitous in the dynamical model of the quadrotor UAV, and not taking them into consideration can lead to performance degradation. Accordingly, some techniques should be used to estimate parametric uncertainties and ensure the accurate performance of the quadrotor UAV. For instance, when designing controllers for the quadrotor system, some model uncertainties, including battery voltage drop, payload variation and flight condition change, should be considered. To this end, a robust control technique-based feedback approach was proposed in [21] to mitigate model uncertainties in the quadrotor UAV system. The efficiency of the proposed method was assessed using a set of real-time outdoor flight experiments. One of the methods, which can be used to remove the effects of uncertainties, is the barrier function technique. Not only does this method approximate the upper bound of model uncertainties with a high precise rate, but it also guarantees the convergence of the system states in the shortest time possible. Besides, the barrier function technique deals with the increase of parametric uncertainties very well. Structural symmetric systems, which own the symmetric transfer function matrix, can be applied to various engineering fields. This structure possesses several problems, including model reduction, stabilization and control synthesis, controller failure time analysis, etc. Hence, some valuable control techniques are used for symmetric systems, such as the $H_{\infty }$ norm in order to obtain the optimal control gain [22,23] and the feedback control technique for stabilization [24].

In [25], a first-order SMC scheme is suggested based on the adaptive control technique using the barrier function. This method ensures the finite-time convergence of the trajectories of the disturbed system with the approximation of the upper bound of disturbances. However, the above-mentioned work overlooked the rejection of uncertainties and did not take into consideration existing constraints on the control input. In [26], an adaptive high-order SMC method based on barrier function was suggested for the finite-time stability of systems with bounded uncertainty. In [27], a barrier function-based adaptive feedback control technique was proposed to stabilize a spacecraft subject to parameter uncertainties and perturbations. In [28], a non-singular TSMC method was proposed for the fast-tracking control of a quadrotor system under total rotor failure and wind perturbation. The approach considered an estimation scheme to compensate for the wind disturbance and rotor failure. In [29], path tracking of the quadrotor in the presence of parameter uncertainty and perturbation was accomplished using an adaptive non-singular TSMC technique. Besides the fast convergence rate, the upper bounds of model uncertainties and external perturbations were estimated online via the designed adaptive law. In [30], a non-singular TSMC scheme is suggested with the aim of fast tracking of a quadrotor under model uncertainties and external disturbances. Thus, to obtain smooth tracking signals and their derivatives, a tracking differentiator based on the extended state-observer was recommended to approximate uncertainties and perturbations. In [31], an incremental non-singular TSMC process is offered to design a fast tracker for a quadrotor system subject to uncertainties, perturbations and actuator faults. According to this control strategy, the offered incremental technique removed model uncertainties, perturbations and faults and resulted in a simple control technique. In [32], two control schemes were proposed using an adaptive non-singular TSMC and backstepping SMC for the path tracking control of quadrotor systems subject to external perturbations. In [33], an image-based visual servoing via non-singular TSMC approach is recommended for a quadrotor system subject to image uncertainty and external disturbances. The method was shown to achieve finite-time disturbance rejection. Two different robust control algorithms were used for the quadrotor system in [34]. The first is based on the backstepping nonsingular TSMC method with adaptive gain to achieve fast convergence and high robustness. The second relies on a nonlinear disturbance observer-based integral SMC approach combined with an adaptive procedure. However, none of the above approaches considered a compensation system for the rejection of control inputs saturation [26,27,28,29,30,31,32,33,34]. In [35], the attitude tracking of a quadrotor system under a constrained actuator is carried out using an adaptive control approach. Hence, an anti-windup procedure was adopted to compensate for actuator constraints. In [36], an integrated estimation control technique is offered for quadrotors with a constrained input. This method has two functions, including desired tracking and relative localization by means of distance measurement. In [37], an SMC observer-based finite-time controller was suggested for a quadrotor subject to actuator faults and constrained inputs. Then, a neural-network procedure based on the sliding mode control was applied to tackle the constraints on input. However, whereas in [35,36,37], the variation rejection of the adaptive gain due to the usage of the common adaptive control technique was not investigated in these researches, the adaptive barrier function technique was suggested as a potential solution to tackle this phenomenon.

A review of the recently-published papers that investigated the stabilization/tracking control of quadrotor UAVs led us to conclude that no work has been done for the path-tracking control of quadrotor UAV systems with model uncertainties and input constraints using the adaptive barrier function-based non-singular TSMC method. Hence, this paper proposes a Barrier function-based nonsingular finite-time tracker for quadrotor UAVs subject to uncertainties and input constraints. Its main contributions are as follows:

• The design of a novel compensator for quadrotor UAVs subject to model uncertainties and input saturation;
• The proposition of a non-singular terminal siding surface that yields fast reachability of the sliding surface, which is defined based on the tracking errors and virtual control inputs;
• Employment of the barrier-function technique for the accurate estimation of the unknown upper bounds of model uncertainties.

The remainder of this paper is organized as follows. The dynamical model of a quadrotor system subject to bounded uncertainties and input saturation is given in Section 2. The details of compensation system, tracking error, linear sliding surface, non-singular terminal sliding surface and barrier function procedure are given in Section 3. Simulation results and the robustness analysis are presented in Section 4. Lastly, conclusions are provided in Section 5.

2. Presentation of the Model of a Quadrotor

The dynamical model of the six degrees-of-freedom quadrotor UAV system is briefly introduced in this section. The state-space formation of the quadrotor is presented in the presence of bounded uncertainties and constrained inputs. Afterwards, some assumptions required in the design of the suggested method are given.

The dynamic equations of the quadrotor system are expressed as follows [38]:

$$\begin{gathered} \ddot{x}\left(t\right)=\frac{1}{m}\left[-K_{fd}{}_x\dot{x}\left(t\right)+\left(C_{\varphi }{C}_{\theta }{C}_{\psi }+S_{\varphi }{S}_{\psi }\right)u_z\left(t\right)\right], \\ \ddot{y}\left(t\right)=\frac{1}{m}\left[-K_{fd}{}_y\dot{y}\left(t\right)+\left(C_{\varphi }{S}_{\theta }{S}_{\psi }-S_{\varphi }{S}_{\psi }\right)u_z\left(t\right)\right], \\ \ddot{z}\left(t\right)=\frac{1}{m}\left[-K_{fd}{}_z\dot{z}\left(t\right)+C_{\varphi }{C}_{\theta }{u}_z\left(t\right)\right]-g, \\ \ddot{\varphi }\left(t\right)=\frac{1}{I_x}\left[\left(I_y-I_z\right)\dot{\psi }\left(t\right)\dot{\theta }\left(t\right)-K_{fa}{}_x{\dot{\varphi }}^2\left(t\right)-J_r\overline{\Omega }\dot{\theta }\left(t\right)+d{u}_{\varphi }\left(t\right)\right], \\ \ddot{\theta }\left(t\right)=\frac{1}{I_y}\left[\left(I_z-I_x\right)\dot{\psi }\left(t\right)\dot{\varphi }\left(t\right)-K_{fa}{}_y{\dot{\theta }}^2\left(t\right)+J_r\overline{\Omega }\dot{\varphi }\left(t\right)+d{u}_{\theta }\left(t\right)\right], \\ \ddot{\psi }\left(t\right)=\frac{1}{I_z}\left[\left(I_x-I_y\right)\dot{\varphi }\left(t\right)\dot{\theta }\left(t\right)-K_{fa}{}_z{\dot{\psi }}^2\left(t\right)+C_D{u}_{\psi }\left(t\right)\right]. \end{gathered}$$

(1)

where $\left\{x,y,z\right\}$ and $\left\{\varphi ,\theta ,\psi \right\}$ are the position and attitude vector of the quadrotor system; $\left\{I_x,I_y,I_z\right\}$, $\left\{K_{fd}{}_x,K_{fd}{}_y,K_{fd}{}_z\right\}$ and $\left\{K_{fa}{}_x,K_{fa}{}_y,K_{fa}{}_z\right\}$ are the inertia, drag coefficient and aerodynamic fiction vectors, respectively; $J_r$, $C_D$, $d$ and $m$ denote the rotor-inertia, drag factor, distance between the center of the quad-rotor and rotation axis and mass of the quad-rotor, respectively; $C_j=cos\left(j\right)$ and $S_j=\mathit{sin}\left(j\right),\forall j=\varphi ,\theta ,\psi$; $\overline{\Omega }=w_1-w_2+w_3-w_4$, such that $w_i$’s are the angular velocities; $u_x\left(t\right)$ and $u_y\left(t\right)$ are the supplementary control inputs; $\left[u_x\left(t\right),u_{\varphi }\left(t\right), u_{\theta }\left(t\right), u_{\psi }\left(t\right)\right]$ are the control input vectors by:

$$\begin{gathered} u_x\left(t\right)=K_p\left(w_1^2+w_2^2+w_3^2+w_4^2\right), \\ {u}_{\varphi }\left(t\right)=-K_p{w}_1^2+K_p{w}_3^2, \\ {u}_{\theta }\left(t\right)=-K_p{w}_2^2+K_p{w}_4^2, \\ {u}_{\psi }\left(t\right)=C_d\left(w_1^2-w_2^2+w_3^2-w_4^2\right) \end{gathered}$$

(2)

where $K_p$ is the lift power factor. Now, the state-space form of the dynamical Equation (1) under bounded uncertainties and constrained input is given by:

$$\begin{gathered} {\dot{x}}_1\left(t\right)=x_2\left(t\right), \\ {\dot{x}}_2\left(t\right)=f_x\left(x,t\right)+g_x\left(x,t\right)sat\left(u_z\left(t\right)\right), \\ {\dot{x}}_3\left(t\right)=x_4\left(t\right), \\ {\dot{x}}_4\left(t\right)=f_y\left(x,t\right)+g_y\left(x,t\right)sat\left(u_z\left(t\right)\right), \\ {\dot{x}}_5\left(t\right)=x_6\left(t\right), \\ {\dot{x}}_6\left(t\right)=f_z\left(x,t\right)+g_z\left(x,t\right)sat\left(u_z\left(t\right)\right), \\ {\dot{x}}_7\left(t\right)=x_8\left(t\right), \\ {\dot{x}}_8\left(t\right)=f_{\varphi }\left(x,t\right)+g_{\varphi }\left(x,t\right)sat\left(u_{\varphi }\left(t\right)\right), \\ {\dot{x}}_9\left(t\right)=x_{10}\left(t\right), \\ {\dot{x}}_{10}\left(t\right)=f_{\theta }\left(x,t\right)+g_{\theta }\left(x,t\right)sat\left(u_{\theta }\left(t\right)\right), \\ {\dot{x}}_{11}\left(t\right)=x_{12}\left(t\right), \\ {\dot{x}}_{12}\left(t\right)=f_{\psi }\left(x,t\right)+g_{\psi }\left(x,t\right)sat\left(u_{\psi }\left(t\right)\right). \end{gathered}$$

(3)

where $f_i\left(x,t\right)=f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right), \left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$, such that

$$\begin{gathered} f_{0x}\left(x,t\right)=a_1{x}_2\left(t\right), g_x\left(x,t\right)=\frac{u_x}{m} \\ {f}_{0y}\left(x,t\right)=a_2{x}_4\left(t\right), g_y\left(x,t\right)=\frac{u_y}{m}. \\ {f}_{0z}\left(x,t\right)=a_3{x}_6\left(t\right)-g, g_z\left(x,t\right)=\frac{C_{\varphi }{C}_{\theta }}{m} \\ {f}_{0\varphi }\left(x,t\right)=a_4{x}_{12}\left(t\right)x_{10}\left(t\right)+a_5{x}_8{}^2\left(t\right)+a_6\overline{\Omega }{x}_{10}\left(t\right), g_{\varphi }\left(x,t\right)=b_1 \\ {f}_{0\theta }\left(x,t\right)=a_7{x}_{12}\left(t\right)x_8\left(t\right)+a_8{x}_{10}{}^2\left(t\right)+a_9\overline{\Omega }{x}_8\left(t\right), g_{\theta }\left(x,t\right)=b_2 \\ {f}_{0\psi }\left(x,t\right)=a_{10}{x}_8\left(t\right)x_{10}\left(t\right)+a_{11}{x}_{12}{}^2\left(t\right), g_{\psi }\left(x,t\right)=b_3 \end{gathered}$$

(4)

with $a_1=\frac{-K_{fd}{}_x}{m}$, $a_2=\frac{-K_{fd}{}_y}{m}$, $a_3=\frac{-K_{fd}{}_z}{m}$, $a_4=\frac{I_y-I_z}{I_x}$, $a_5=\frac{-K_{fa}{}_x}{I_x}$, $a_6=-\frac{J_r}{I_x}$, $a_7=\frac{I_z-I_x}{I_y}$, $a_8=\frac{-K_{fa}{}_y}{I_y}$, $a_9=\frac{J_r}{I_y}$, $a_{10}=\frac{I_x-I_y}{I_z}$, $a_{11}=\frac{-K_{fa}{}_z}{I_z}$, $b_1=\frac{d}{I_x}$, $a_2=\frac{d}{I_y}$ and $a_3=\frac{C_D}{I_z}$; $\mathrm{\Delta }{f}_i\left(x,t\right), \forall i=x,y,z,\varphi ,\theta ,\psi$ is the uncertain bounded function. Furthermore, $u_x=C_{\varphi }{C}_{\theta }{C}_{\psi }+S_{\varphi }{S}_{\psi }$ and $u_y=C_{\varphi }{S}_{\theta }{S}_{\psi }-S_{\varphi }{S}_{\psi }$ are the auxiliary control inputs. Moreover, the term $sat\left(u_i\left(t\right)\right),\forall i=z,\varphi ,\theta ,\psi$ indicates the consideration of the constraint on the control inputs.

Assumption 1.

It is assumed that there is a known function,$M_i\left(x,t\right), \left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$, so that the uncertain function,$\mathrm{\Delta }{f}_i\left(x,t\right)$, fulfills the conditions$\left|\mathrm{\Delta }{f}_i\left(x,t\right)\right|\le M_i\left(x,t\right)$.

3. Main Results

The main control objectives are to force the quadrotor to accurately track the desired path despite disturbances and input saturation. Hence, the convergence of the tracking error is the key objective in the control of the quadrotor system. In this part, the compensation system is defined for the rejection of control inputs saturation. To this end, the tracking errors of the quadrotor system are first defined; then, their convergence is investigated in two subsystems. In the first subsystem, a siding surface based on the position errors of the quadrotor system and virtual control input is defined, while the sliding surface for the attitude of the quadrotor system and virtual control input is determined in the second subsystem. Moreover, for the fast convergence of the sliding surface, the non-singular terminal sliding surface is suggested. Finally, in order to remove the requirement to know the upper bounds of uncertainties, the barrier function approach is adopted.

3.1. Compensation System

Remark 1

[39]. The term$sat\left(u_i\left(t\right)\right)\left(\forall i=z,\varphi ,\theta ,\psi \right)$is described as

$$sat\left(u_i\left(t\right)\right)=\left\{\begin{array}{c}{u}_{i max} u_i\left(t\right)\ge u_{i max}\\ u_i\left(t\right) u_{i min}<u_i\left(t\right)<u_{i max}\\ u_{i min} u_i\left(t\right)\le u_{i min}\end{array}\right.$$

(5)

where$u_{i min}$and$u_{i max}$are the minimum and maximum values of the control inputs, respectively. Therefore, the compensation system is defined to cope with input saturation as follows:

$${\mathrm{\Sigma }}_i\left(u_i\left(t\right)\right)=\left\{\begin{array}{c}{u}_{i max}.\mathit{tanh}\left(\frac{u_i}{u_{i max}}\right) u_i\ge 0\\ u_{i min}.\mathit{tanh}\left(\frac{u_i}{u_{i min}}\right) u_i<0\end{array}\right.$$

(6)

Then, the term$sat\left(u_i\left(t\right)\right)$is considered as$sat\left(u_i\left(t\right)\right)={\mathrm{\Sigma }}_i\left(u_i\left(t\right)\right)+H_i\left(u_i\right),$with$\left|H_i\left(u_i\right)\right|=\left|sat\left(u_i\left(t\right)\right)-{\mathrm{\Sigma }}_i\left(u_i\left(t\right)\right)\right|\le max\left\{u_{i min}\left(\mathit{tanh}\left(1\right)-1\right), u_{i max}\left(1-tanh\left(1\right)\right)\right\}$. Without loss of generality, there exists a constant$0<{\mu }_i<1,$such that${\mathrm{\Sigma }}_i\left(u_i\left(t\right)\right)={\mu }_i\left(u_i\left(t\right)-u_i\left(0\right)\right)+{\mathrm{\Sigma }}_i\left(u_i\left(0\right)\right)$. Whereas for$u_i\left(0\right)=0$, it is concluded that$sat\left(u_i\left(t\right)\right)={\mu }_i{u}_i\left(t\right)+H_i\left(u_i\right)$.

3.2. Tracking Errors and Sliding Surface

Consider $x_{xd}\left(t\right)$, $x_{yd}\left(t\right)$, $x_{zd}\left(t\right)$, $x_{\varphi d}\left(t\right)$, $x_{\theta d}\left(t\right)$ and $x_{\psi d}\left(t\right)$ as the reference trajectory signals which have to be tracked by quadrotor system and $x_1\left(t\right)=x_x\left(t\right)$, $x_3\left(t\right)=x_y\left(t\right)$, $x_5\left(t\right)=x_z\left(t\right)$, $x_7\left(t\right)=x_{\varphi }\left(t\right)$, $x_9\left(t\right)=x_{\theta }\left(t\right)$ and $x_{11}\left(t\right)=x_{\psi }\left(t\right)$ as the outputs of the quadrotor UAV system. Hence, the tracking errors are determined as:

$$e_i\left(t\right)=x_i\left(t\right)-x_{id}\left(t\right), \left(\forall i=x,y,z,\varphi ,\theta ,\psi \right).$$

(7)

Because the positions of the quadrotor system, $x,y,z,$ are controlled by $u_x\left(t\right)$, $u_y\left(t\right)$, $u_z\left(t\right)$, the sliding surfaces are defined as:

$$s_i\left(t\right)={\dot{e}}_i\left(t\right)+c_0{e}_i\left(t\right),\left(\forall i=x,y\right)$$

(8)

$$s_z\left(t\right)={\dot{e}}_z\left(t\right)+c_0{e}_z\left(t\right)-c_1{{\displaystyle \int }}_0^t{\gamma }_z\left(\tau \right)d\tau ,$$

(9)

where $c_0$ and $c_1$ are the constants; ${\gamma }_z$ is the virtual control input, which is obtained as:

$${\gamma }_z=\frac{1}{c_1}{g}_{\mathrm{z}}\left(x,t\right)H_z\left(u_z\right)$$

(10)

The time-derivatives of sliding surfaces, $s_i,$ are found as:

$${\dot{s}}_i\left(t\right)={\ddot{e}}_i\left(t\right)+c_0{\dot{e}}_i\left(t\right),,\left(\forall i=x,y\right)$$

(11)

$${\dot{s}}_z\left(t\right)={\ddot{e}}_z\left(t\right)+c_0{\dot{e}}_z\left(t\right)-c_1{\gamma }_z,$$

(12)

Substituting (3), (4) and (7) into the above equations, it gives:

$${\dot{s}}_i\left(t\right)={\dot{s}}_i\left(t\right)=f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+\frac{sat\left(u_z\left(t\right)\right)}{m}{u}_i-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right),$$

(13)

$${\dot{s}}_z\left(t\right)=f_{0z}\left(x,t\right)+\mathrm{\Delta }{f}_z\left(x,t\right)+g_z\left(x,t\right)sat\left(u_z\left(t\right)\right)-{\ddot{x}}_{zd}\left(t\right)+c_0\left({\dot{x}}_z\left(t\right)-{\dot{x}}_{zd}\left(t\right)\right)-c_1{\gamma }_z$$

(14)

Considering Remark 1 and using Equation (14) yields:

$${\dot{s}}_z\left(t\right)=f_{0z}\left(x,t\right)+\mathrm{\Delta }{f}_z\left(x,t\right)+g_z\left(x,t\right){\mu }_z{u}_z\left(t\right)+g_z\left(x,t\right)H_z\left(u_z\right)-{\ddot{x}}_{zd}\left(t\right)+c_0\left({\dot{x}}_z\left(t\right)-{\dot{x}}_{zd}\left(t\right)\right)-c_1{\gamma }_z$$

(15)

Using the virtual control input (10) and doing some simplifications, one obtains:

$${\dot{s}}_z\left(t\right)=f_{0z}\left(x,t\right)+\mathrm{\Delta }{f}_z\left(x,t\right)+g_z\left(x,t\right){\mu }_z{u}_z\left(t\right)-{\ddot{x}}_{zd}\left(t\right)+c_0\left({\dot{x}}_z\left(t\right)-{\dot{x}}_{zd}\left(t\right)\right)$$

(16)

For the control of the attitude of the quadrotor system, $\varphi ,\theta ,\psi$, the sliding surfaces are defined as:

$$s_i\left(t\right)={\dot{e}}_i\left(t\right)+c_0{e}_i\left(t\right)-c_1{{\displaystyle \int }}_0^t{\gamma }_i\left(\tau \right)d\tau , \left(\forall i=\varphi ,\theta ,\psi \right)$$

(17)

where ${\gamma }_{\varphi }$, ${\gamma }_{\theta }$ and ${\gamma }_{\psi }$ are the virtual control inputs obtained using:

$${\gamma }_i=\frac{1}{c_1}{g}_i\left(x,t\right)H_i\left(u_i\right).$$

(18)

The time-derivative of the sliding surfaces (17) are found as:

$${\dot{s}}_i\left(t\right)={\ddot{e}}_i\left(t\right)+c_0{\dot{e}}_i\left(t\right)-c_1{\gamma }_i.$$

(19)

Substituting (3), (4) and (7) into ${\dot{s}}_i\left(t\right)$, it attains:

$$\begin{gathered} {\dot{s}}_i\left(t\right)=f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+g_i\left(x,t\right)sat\left(u_i\left(t\right)\right)-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right) \\ -c_1{\gamma }_i \end{gathered}$$

(20)

The consideration of Remark 1 yields:

$$\begin{gathered} {\dot{s}}_i\left(t\right)=f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+g_i\left(x,t\right){\mu }_i{u}_i\left(t\right)+g_i\left(x,t\right)H_i\left(u_i\right)-{\ddot{x}}_{id}\left(t\right) \\ +c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)-c_1{\gamma }_i \end{gathered}$$

(21)

Using the virtual control input (18) and doing some simplifications, one obtains:

$$\begin{gathered} {\dot{s}}_i\left(t\right)=f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+g_i\left(x,t\right){\mu }_i{u}_i\left(t\right)-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right). \left(\forall i \\ =\varphi ,\theta , \psi \right) \end{gathered}$$

(22)

3.3. Nonsingular Terminal Sliding Mode Control

In this part, it is presumed that the upper bounds of the uncertainties are known. Hence, in order to obtain the finite-time reachability of the sliding surfaces based on the desired tracking errors, the non-singular sliding surface is applied.

We define the non-singular sliding surface as:

$${\sigma }_i\left(t\right)=s_i\left(t\right)+\frac{1}{{\beta }_i}{s}_i{\left(t\right)}^{\frac{{\varrho }_1}{{\varrho }_2}}, \left(\forall i=x,y,z,\varphi ,\theta , \psi \right)$$

(23)

where ${\beta }_i$’s are positive constants, and $1<\frac{{\varrho }_1}{{\varrho }_2}<2$ with ${\varrho }_1$ and ${\varrho }_2$, which are two odd positive integers. Now, taking the time-derivative of (23) and using (13), (16) and (22), yields:

$$\begin{gathered} {\dot{\sigma }}_i\left(t\right)={\overline{\beta }}_i\left(f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+\frac{sat\left(u_z\left(t\right)\right)}{m}{u}_i-{\ddot{x}}_{id}\left(t\right) \\ +c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)\right),\left(\forall i=x,y\right) \end{gathered}$$

(24)

$$\begin{gathered} {\dot{\sigma }}_i\left(t\right)={\overline{\beta }}_i\left(f_{0i}\left(x,t\right)-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)+g_i\left(x,t\right){\mu }_i{u}_i\left(t\right) \\ +\mathrm{\Delta }{f}_i\left(x,t\right)\right).\left(\forall i=z,\varphi ,\theta , \psi \right) \end{gathered}$$

(25)

where ${\overline{\beta }}_i=1+\frac{1}{{\beta }_i}\frac{{\varrho }_1}{{\varrho }_2}{s}_i{}^{\frac{{\varrho }_1}{{\varrho }_2}-1}\left(t\right)$. Hence, the non-singular TSMC laws $u_i\left(t\right)\left(\forall i=x,y,z,\varphi ,\theta , \psi \right)$ are designed as:

$$u_i\left(t\right)=u_{ieq}\left(t\right)+u_{ins}\left(t\right), \left(\forall i=x,y,z,\varphi ,\theta , \psi \right)$$

(26)

such that:

$$u_{ieq}\left(t\right)=\left\{\begin{array}{c}-\frac{m}{sat\left(u_z\left(t\right)\right)}\Xi , \forall i=x,y\\ -\frac{1}{{\mu }_i{g}_i\left(x,t\right)}\Xi , \forall i=z,\varphi ,\theta , \psi \end{array}\right.$$

(27)

where $\Xi =f_{0i}\left(x,t\right)-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)$, and:

$$u_{ins}\left(t\right)=\left\{\begin{array}{c}-\frac{m}{{\overline{\beta }}_{i}sat\left(u_z\left(t\right)\right)}{\rm Y}, \forall i=x,y\\ -\frac{1}{{\overline{\beta }}_i{\mu }_i{g}_i\left(x,t\right)}{\rm Y}, \forall i=z,\varphi ,\theta , \psi \end{array}\right.$$

(28)

where $\mathsf{{\rm Y}}=\left({\delta }_i+{\eta }_i\right)\mathit{sgn}({\sigma }_i)$, ${\eta }_i$’s are the positive constants and:

$${\delta }_i\ge {\overline{\beta }}_i{M}_i\left(x,t\right), \left(\forall i=x,y,z,\varphi ,\theta , \psi \right).$$

(29)

In what follows, in order to obtain the finite-time convergence of the sliding surfaces $s_i\left(t\right) \left(\forall i=x,y,z,\varphi ,\theta , \psi \right)$, the following theorem is presented.

Theorem 1.

Consider the uncertain quadrotor system with input saturation (3); tracking errors (7); sliding variables (8), (9) and (17), and the nonsingular TSMC surfaces (23). The designed control laws (26) are applied on the quadrotor UAV to force the sliding surfaces to be converged to origin in the finite time and keep on it afterward. Hence, the tracking errors are converged to zero, and the states of the quadrotor system track the desired position and attitude properly.

Proof. 

Construct the Lyapunov candidate function as $V_i{}_1\left(t\right)=0.5{\sigma }_i{}^2\left(t\right), \left(\forall i=x,y,z,\varphi ,\theta , \psi \right)$, where its time-derivate is obtained by using (24) and (25), as follows:

$$\begin{gathered} {\dot{V}}_i{}_1\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\left(f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+\frac{sat\left(u_z\left(t\right)\right)}{m}{u}_i-{\ddot{x}}_{id}\left(t\right) \\ +c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)\right)\right\},\left(\forall i=x,y\right) \end{gathered}$$

(30)

$$\begin{gathered} {\dot{V}}_i{}_1\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\left(f_{0i}\left(x,t\right)-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)+g_i\left(x,t\right){\mu }_i{u}_i\left(t\right) \\ +\mathrm{\Delta }{f}_i\left(x,t\right)\right)\right\}. \left(\forall i=z,\varphi ,\theta , \psi \right) \end{gathered}$$

(31)

Substituting the control laws (26) into the above equation yields:

$$\begin{gathered} {\dot{V}}_i{}_1\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\mathrm{\Delta }{f}_i\left(x,t\right)-\left(\left({\delta }_i+{\eta }_i\right)\mathit{sgn}({\sigma }_i\right))\right\} \\ {\dot{V}}_i{}_1\left(t\right)\le \left|{\sigma }_i\left(t\right)\right|\left\{{\overline{\beta }}_i{M}_i\left(x,t\right)\right\}-{\delta }_i\left|{\sigma }_i\left(t\right)\right|-{\eta }_i\left|{\sigma }_i\left(t\right)\right| \end{gathered}$$

(32)

Considering (29), one obtains:

$${\dot{V}}_i{}_1\left(t\right)\le -\sqrt{2}{\eta }_i{V}_i{{}_1}^{0.5}\left(t\right).$$

(33)

This confirms that the state responses of the uncertain quadrotor system converge from the initial conditions to the desired trajectories in finite time. □

3.4. Barrier Function Based-Nonsingular Terminal Sliding Mode Control

It is assumed that the term $\left|\mathrm{\Delta }{f}_i\left(x,t\right)\right|$ is an unknown but bounded function, where $M_i\left(x,t\right)$ is its upper bound. In practical usage, this upper bound is unknown, and there are some challenges in determining it. In what follows, a new barrier function-based adaptive nonsingular TSMC law is proposed, such that the system uncertainties are estimated by using the barrier adaptation laws more effectively, and the tracking objective is achieved. The non-singular TSMC laws (28) are updated as:

$$u_{ins}\left(t\right)=\left\{\begin{array}{c}-\frac{m}{{\overline{\beta }}_{i}sat\left(u_z\left(t\right)\right)}\widehat{{\rm Y}}, \forall i=x,y\\ -\frac{1}{{\overline{\beta }}_i{\mu }_i{g}_i\left(x,t\right)}\widehat{{\rm Y}}, \forall i=z,\varphi ,\theta , \psi \end{array}\right.$$

(34)

while $\widehat{{\rm Y}}=\left({\widehat{\delta }}_i+{\eta }_i\right)\mathit{sgn}({\sigma }_i)$, and:

$${\widehat{\delta }}_i=\left\{\begin{array}{c}{\delta }_a{}_i, 0<t\le \stackrel{-}{t}\\ {\delta }_{pb}{}_i, t>\stackrel{-}{t}\hfill \end{array}\right., \left(\forall i=x,y,z,\varphi , \theta ,\psi \right)$$

(35)

where $\stackrel{-}{t}$ is the convergence time that the error trajectories reach the neighborhood ${\epsilon }_i$ of the non-singular TSMC surface. The adaptation gains ${\delta }_a{}_i$ and ${\delta }_{pb}{}_i$ are obtained by:

$${\dot{\delta }}_a{}_i={\phi }_i\left|{\sigma }_i\left(t\right)\right|,$$

(36)

$${\delta }_{pb}{}_i=\frac{{\epsilon }_i{\overline{F}}_i}{{\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|} st {\delta }_{pb}{}_i\left(0\right)=\overline{F}>0$$

(37)

where ${\phi }_i$ and ${\epsilon }_i$ denote two positive scalars. Using the adaptive tuning law (36), the controller gain ${\delta }_a{}_i$ is adjusted to be increased until the error trajectories reach the neighborhood ${\epsilon }_i$ of ${\sigma }_i\left(t\right)$ at the barrier function time $\stackrel{-}{t}$. For times that are bigger than $\stackrel{-}{t}$, the adaptive controller gain is converted to the positive-definite barrier function ${\delta }_{pb}{}_i$ which reduces the convergence region and retains the tracking errors there. The following subsections explain the stability procedure of the system:

Condition (1): $0<t\le \stackrel{-}{t}$

Theorem 2.

Consider the uncertain quadrotor system (3); tracking errors (7); sliding variables (8), (9) and (17), and the nonsingular TSMC surfaces (23). By using the adaptive TSMC inputs (26) and (34) with${\widehat{\delta }}_i={\delta }_a{}_i$and the adaptive-tuning law (36), the tracking error signals then reach the neighborhood${\epsilon }_i$of the nonsingular TSMC surface in the finite time.

Proof. 

The positive-definite Lyapunov candidate function is considered as:

$$V_i{}_2\left(t\right)=0.5\left\{{\sigma }_i{}^2\left(t\right)+\frac{1}{{\phi }_i}{({\delta }_a{}_i-{\delta }_i)}^2\right\}$$

(38)

Differentiating the above Lyapunov function, one has:

$${\dot{V}}_i{}_2\left(t\right)={\sigma }_i\left(t\right){\dot{\sigma }}_i\left(t\right)+\frac{1}{{\phi }_i}\left({\delta }_a{}_i-{\delta }_i\right){\dot{\delta }}_a{}_i$$

(39)

Substituting Equations (24), (25) and (36) into (39), one obtains:

$$\begin{gathered} {\dot{V}}_i{}_2\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\left(f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+\frac{sat\left(u_z\left(t\right)\right)}{m}{u}_i-{\ddot{x}}_{id}\left(t\right) \\ +c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)\right)\right\}+\left({\delta }_a{}_i-{\delta }_i\right)\left|{\sigma }_i\left(t\right)\right|,\left(\forall i=x,y\right) \end{gathered}$$

(40)

$$\begin{gathered} {\dot{V}}_i{}_2\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\left(f_{0i}\left(x,t\right)-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)+g_i\left(x,t\right){\mu }_i{u}_i\left(t\right) \\ +\mathrm{\Delta }{f}_i\left(x,t\right)\right)\right\}+\left({\delta }_a{}_i-{\delta }_i\right)\left|{\sigma }_i\left(t\right)\right|.\left(\forall i=z,\varphi ,\theta , \psi \right) \end{gathered}$$

(41)

Using the adaptive controllers (26) and (34) in the above equations, one has:

$$\begin{gathered} {\dot{V}}_i{}_2\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\mathrm{\Delta }{f}_i\left(x,t\right)-\left({\widehat{\delta }}_i+{\eta }_i\right)\mathit{sgn}({\sigma }_i\left(t\right))\right\}+\left({\delta }_a{}_i-{\delta }_i\right)\left|{\sigma }_i\left(t\right)\right|, \\ {\dot{V}}_i{}_2\left(t\right)\le -{\eta }_i\left|{\sigma }_i\left(t\right)\right|+{\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i{M}_i\left(x,t\right)\right\}-{\delta }_i\left|{\sigma }_i\left(t\right)\right|,\left(\forall i=x,y,z,\varphi ,\theta , \psi \right) \end{gathered}$$

(42)

From (29), it is found:

$${\dot{V}}_i{}_2\left(t\right)\le -\sqrt{2}{\eta }_i{V}_i{{}_1}^{0.5}\left(t\right).$$

(43)

□

Condition (2): $t>\stackrel{-}{t}$

Theorem 3.

Consider the uncertain quadrotor UAV system (3); tracking errors (7); sliding variables (8), (9) and (17) and the nonsingular TSMC surfaces (23). The control inputs are designed as (26) with (27), and by considering${\widehat{\delta }}_i={\delta }_{pb}{}_i=\frac{{\epsilon }_i{\overline{F}}_i}{{\epsilon }_i-\left|{\sigma }_i\right|}$, the adaptive non-singular TSMC laws are updated as follows:

$$u_{ins}\left(t\right)=\left\{\begin{array}{l}-\frac{m}{{\overline{\beta }}_{i}sat\left(u_z\left(t\right)\right)}{\rm N}, i=x,y\\ -\frac{1}{{\overline{\beta }}_i{\mu }_i{g}_i\left(x,t\right)}{\rm N}, \forall i=z,\varphi ,\theta , \psi \end{array}\right.$$

(44)

with${\rm N}=\left(\left|{\sigma }_i\left(t\right)\right|{\overline{F}}_i{({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|)}^{-1}+{\eta }_i\right)\mathit{sgn}({\sigma }_i)$; then, the error states reach the region$\left|{\sigma }_i\left(t\right)\right|\le {\epsilon }_i$in the finite time.

Proof. 

Construct the Lyapunov candidate function as:

$$V_i{}_3\left(t\right)=0.5\left({\sigma }^2\left(t\right)+{\delta }_{pb}{{}_i}^2\right)$$

(45)

where the time-derivative of the above function is:

$${\dot{V}}_i{}_3\left(t\right)={\sigma }_i\left(t\right){\dot{\sigma }}_i\left(t\right)+{\delta }_{pb}{}_i{\dot{\delta }}_{pb}{}_i$$

(46)

Substituting (24) and (25) into the above equation, one achieves:

$$\begin{gathered} {\dot{V}}_i{}_3\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\left(f_{0i}\left(x,t\right)+\mathrm{\Delta }{f}_i\left(x,t\right)+\frac{sat\left(u_z\left(t\right)\right)}{m}{u}_i-{\ddot{x}}_{id}\left(t\right) \\ +c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)\right)\right\}+\frac{{\epsilon }_i{\overline{F}}_i{\dot{\sigma }}_i\left(t\right)sign\left({\sigma }_i\left(t\right)\right)}{{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^2}{\delta }_{pb}{}_i,\left(\forall i \\ =x,y\right). \end{gathered}$$

(47)

$$\begin{gathered} {\dot{V}}_i{}_3\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\left(f_{0i}\left(x,t\right)-{\ddot{x}}_{id}\left(t\right)+c_0\left({\dot{x}}_i\left(t\right)-{\dot{x}}_{id}\left(t\right)\right)+g_i\left(x,t\right){\mu }_i{u}_i\left(t\right)+ \\ \mathrm{\Delta }{f}_i\left(x,t\right)\right)\right\}+\frac{{\epsilon }_i{\overline{F}}_i{\dot{\sigma }}_i\left(t\right)sign\left({\sigma }_i\left(t\right)\right)}{{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^2}{\delta }_{pb}{}_i,\left(\forall i=z,\varphi ,\theta , \psi \right) \end{gathered}$$

(48)

From the control inputs (26) and (44), one has:

$$\begin{gathered} {\dot{V}}_i{}_3\left(t\right)={\sigma }_i\left(t\right)\left\{{\overline{\beta }}_i\left(\mathrm{\Delta }{f}_i\left(x,t\right)\right)+\left(\left(\left|{\sigma }_i\left(t\right)\right|{({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|)}^{-1}+{\eta }_i\right)\mathit{sgn}({\sigma }_i)\right)\right\} \\ +\frac{{\epsilon }_i{\overline{F}}_i{\dot{\sigma }}_i\left(t\right)sign\left({\sigma }_i\left(t\right)\right)}{{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^2}{\delta }_{pb}{}_i, \left(\forall i=x,y,z,\varphi ,\theta , \psi \right) \end{gathered}$$

(49)

Equation (49) can be rewritten as:

$$\begin{gathered} {\dot{V}}_i{}_3\left(t\right)\le -{\eta }_i\left|{\sigma }_i\left(t\right)\right|-{({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|)}^{-1}{\left|{\sigma }_i\left(t\right)\right|}^2+\left|{\sigma }_i\left(t\right)\right|\left\{{\overline{\beta }}_i{M}_i\left(x,t\right)\right\} \\ +{\delta }_{pb}{}_i{\epsilon }_i{\overline{F}}_i{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^{-2}\mathit{sgn}({\sigma }_i\left(t\right){\dot{\sigma }}_i\left(t\right),\left(\forall i=x,y,z,\varphi ,\theta , \psi \right) \\ {\dot{V}}_i{}_3\left(t\right)\le -\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|{)}^{-1}{\left|{\sigma }_i\left(t\right)\right|}^2+\left|{\sigma }_i\left(t\right)\right|\left\{{\overline{\beta }}_i{M}_i\left(x,t\right)\right\} \\ +{\delta }_{pb}{}_i{\epsilon }_i{\overline{F}}_i{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^{-2}\left({\overline{\beta }}_i{M}_i\left(x,t\right) \\ -\left(\left|{\sigma }_i\left(t\right)\right|\left({\epsilon }_i-\left|{\sigma }_i\right|\right)+{\eta }_i\right)\mathit{sgn}({\sigma }_i)\right)\mathit{sgn}({\sigma }_i\left(t\right))\right),\left(\forall i \\ =x,y,z,\varphi ,\theta , \psi \right) \end{gathered}$$

(50)

Therefore:

$$\begin{gathered} {\dot{V}}_i{}_3\left(t\right)\le -\left({\delta }_{pb}{}_i-{\overline{\beta }}_i{M}_i\left(x,t\right)\right)\left|{\sigma }_i\left(t\right)\right|-{\eta }_i{\delta }_{pb}{}_i{\overline{F}}_i{\epsilon }_i{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^{-2} \\ -{\epsilon }_i{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^{-2}{\delta }_{pb}{}_i\left\{{\delta }_{pb}{}_i-{\overline{\beta }}_i{M}_i\left(x,t\right)\right\}, \left(\forall i=x,y,z,\varphi ,\theta , \psi \right) \end{gathered}$$

(51)

where because ${\eta }_i$ and ${\delta }_{pb}{}_i$ are positive scalars, from (29), we therefore have:

$$\begin{gathered} {\dot{V}}_i{}_3\left(t\right)\le -\sqrt{2}\left\{{\delta }_{pb}{}_i-{\overline{\beta }}_i{M}_i\left(x,t\right)\right\}\frac{\left|{\sigma }_i\left(t\right)\right|}{\sqrt{2}} \\ -\sqrt{2}{\epsilon }_i{\overline{F}}_i{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^{-2}\left\{{\delta }_{pb}{}_i-{\overline{\beta }}_i{M}_i\left(x,t\right)\right\}\frac{{\delta }_{pb}{}_i}{\sqrt{2}} \\ \le -\sqrt{2}\left\{{\delta }_{pb}{}_i-{\overline{\beta }}_i{M}_i\left(x,t\right)\right\}\min \left\{1,{\epsilon }_i{\overline{F}}_i{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^{-2}\right\}\left[\frac{\left|{\sigma }_i\left(t\right)\right|}{\sqrt{2}} \\ +\frac{{\delta }_{pb}{}_i}{\sqrt{2}}\right]\le -{\Lambda }_i\left[\frac{\left|{\sigma }_i\left(t\right)\right|}{\sqrt{2}}+\frac{{\delta }_{pb}{}_i}{\sqrt{2}}\right]\le -{\Lambda }_i{V}_i{{}_3}^{0.5}\left(t\right), \\ \left(\forall i=x,y,z,\varphi ,\theta , \psi \right) \end{gathered}$$

(52)

with:

$${\mathrm{\Lambda }}_i=\sqrt{2}\left\{{\delta }_{pb}{}_i-{\overline{\beta }}_i{M}_i\left(x,t\right)\right\}\min \left\{1,{\epsilon }_i{\overline{F}}_i{\left({\epsilon }_i-\left|{\sigma }_i\left(t\right)\right|\right)}^{-2}\right\}, \left(\forall i=x,y,z,\varphi ,\theta , \psi \right)$$

(53)

Thus, the proof is finished. □

The block diagram of the proposed technique is illustrated in Figure 1.

Remark 2 [40].

In order to overcome the chattering problem in the sliding mode control approach, the sign function$\mathit{sgn}({\sigma }_i\left(t\right)) \left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$is replaced by the hyperbolic tangent function$\mathit{tanh}\left(\frac{{\sigma }_i\left(t\right)}{{\upsilon }_i}\right)$, where ${\upsilon }_i\text{'}s$are the boundary layer thickness coefficients.

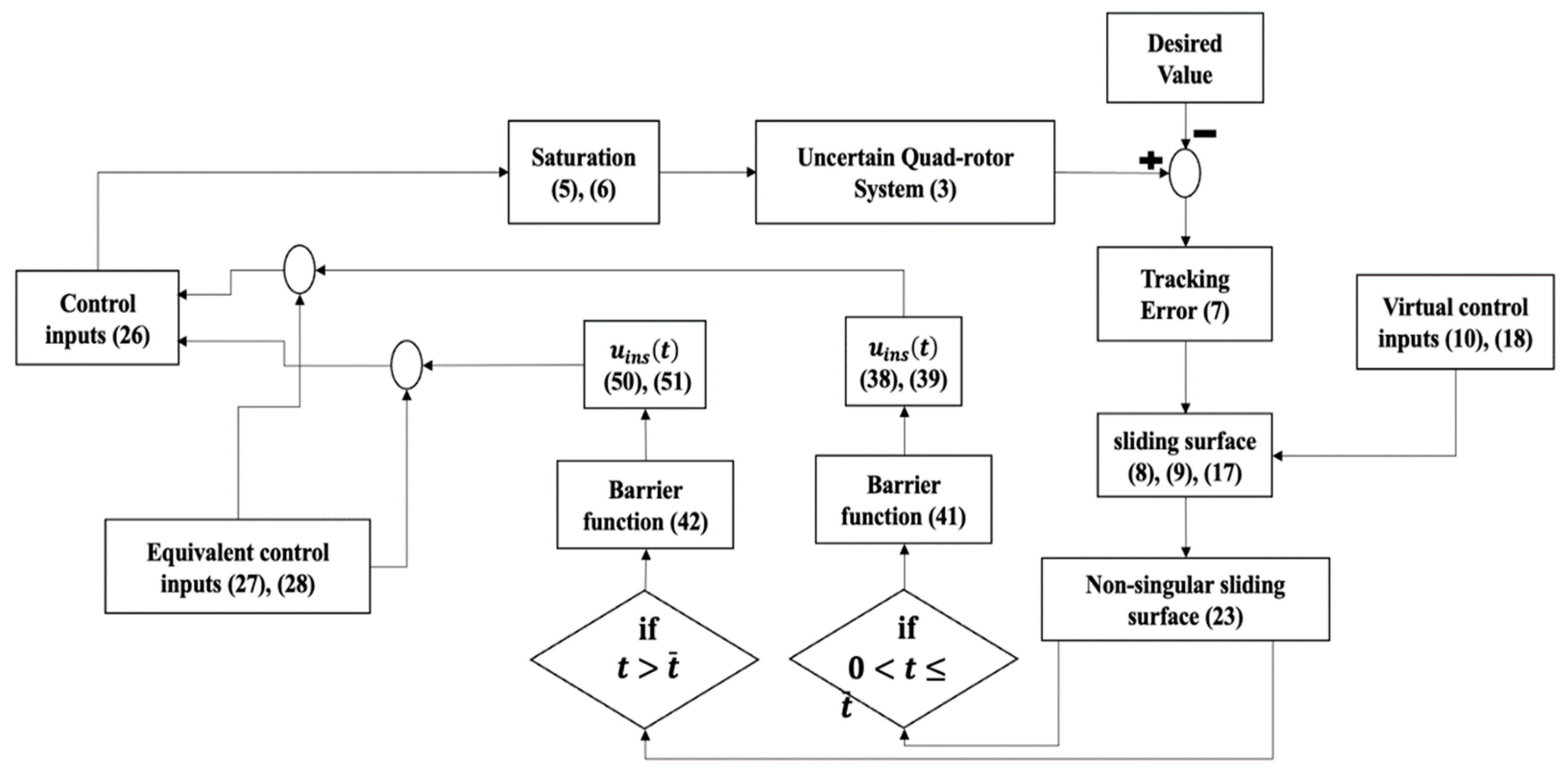
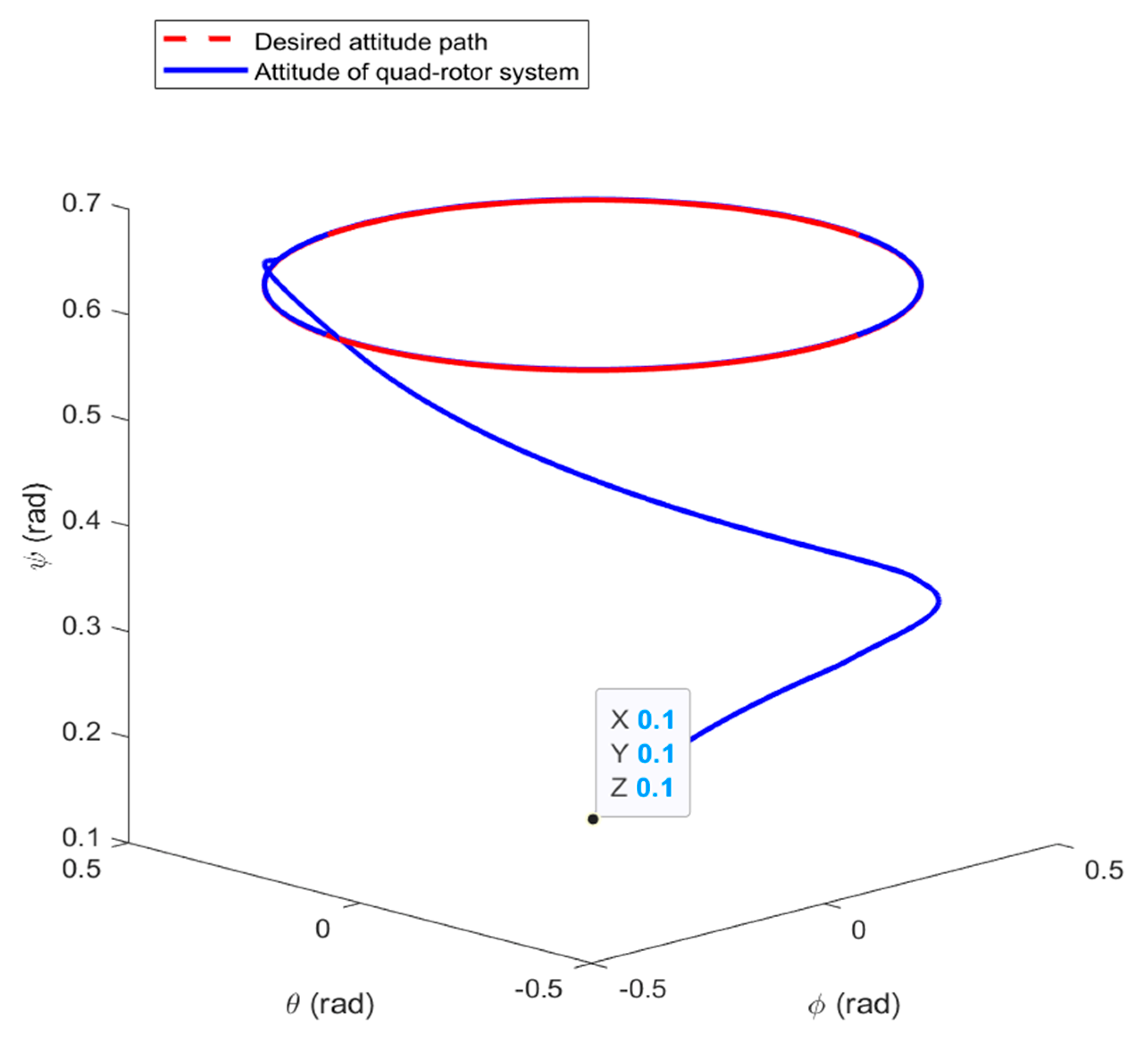
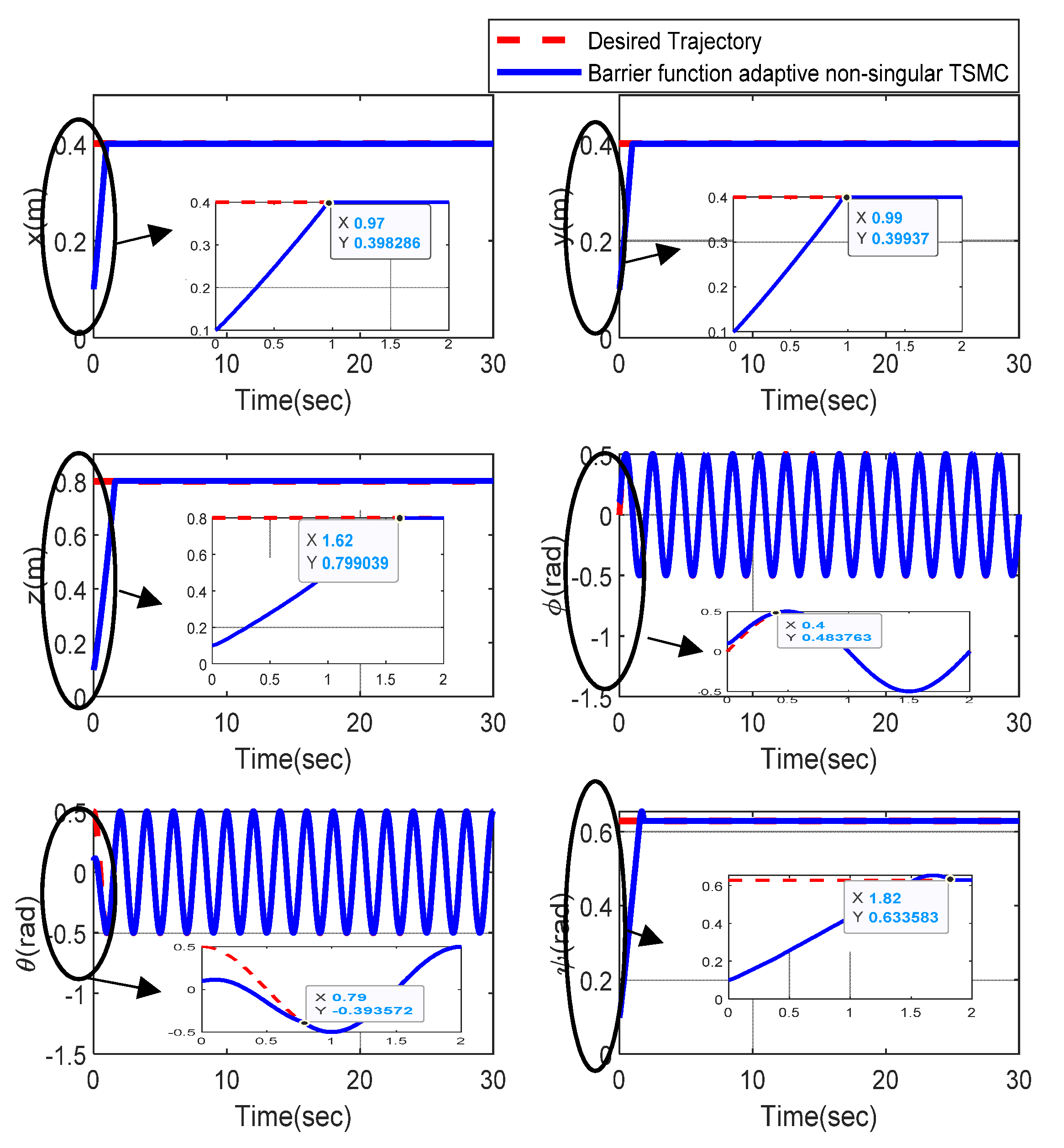
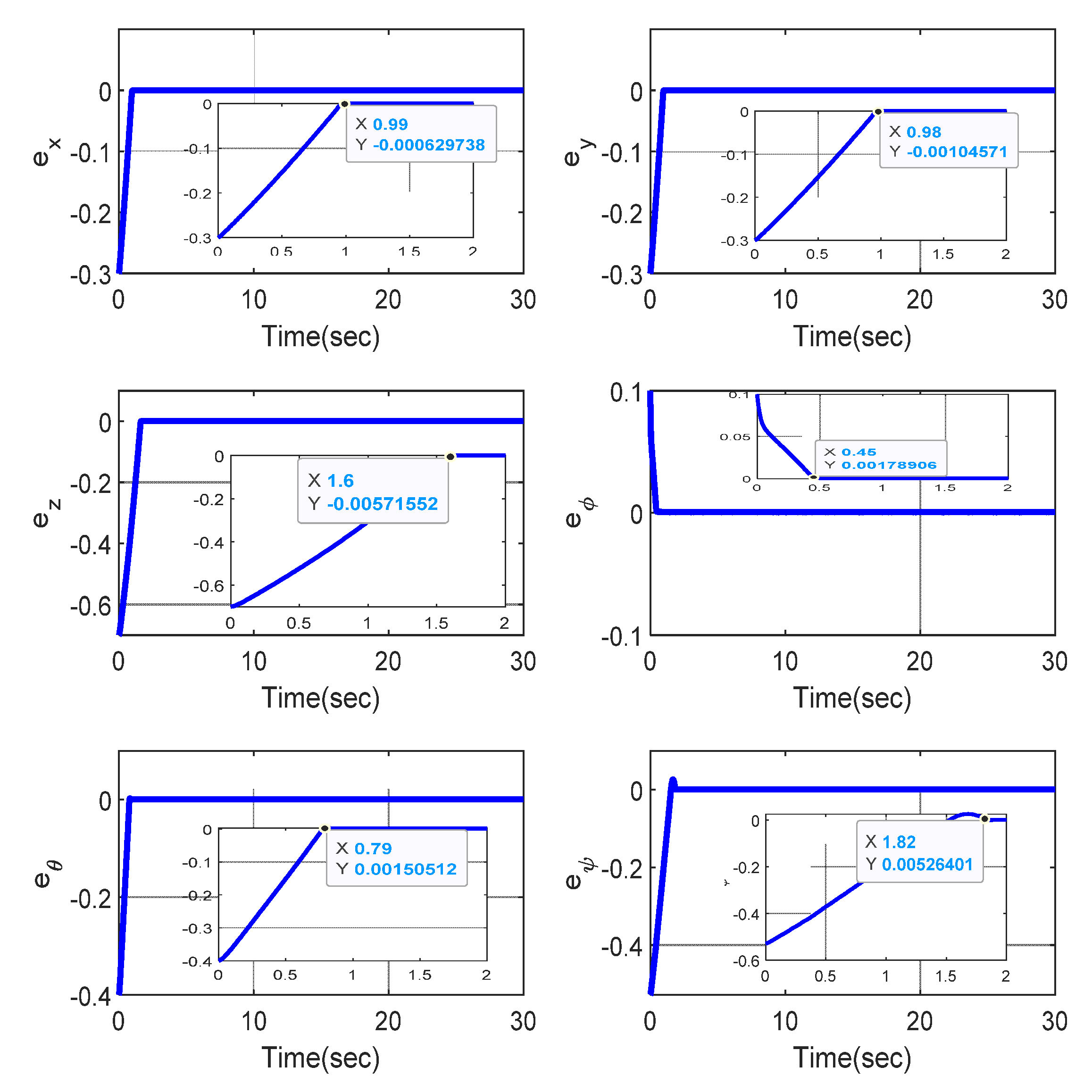
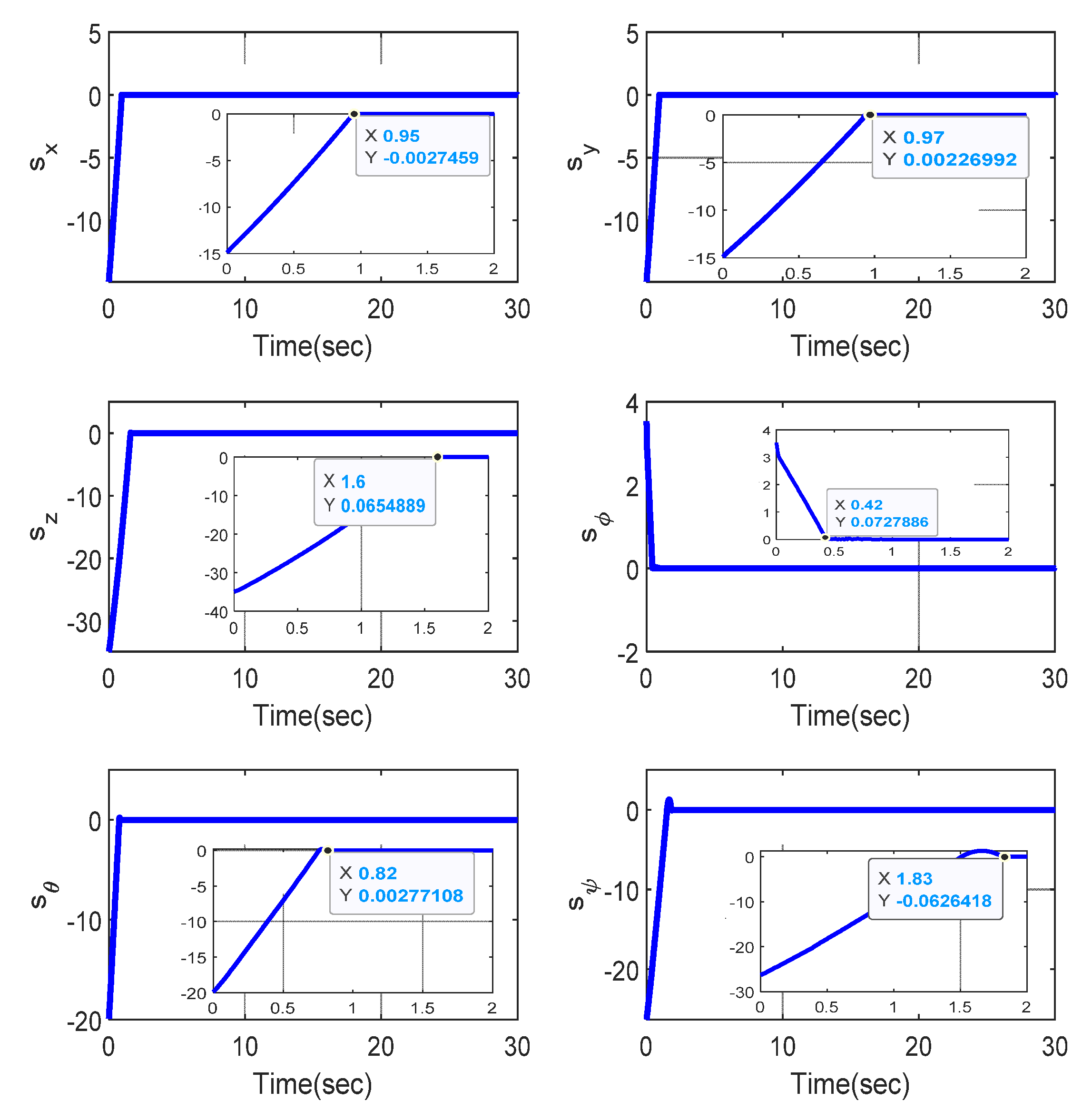
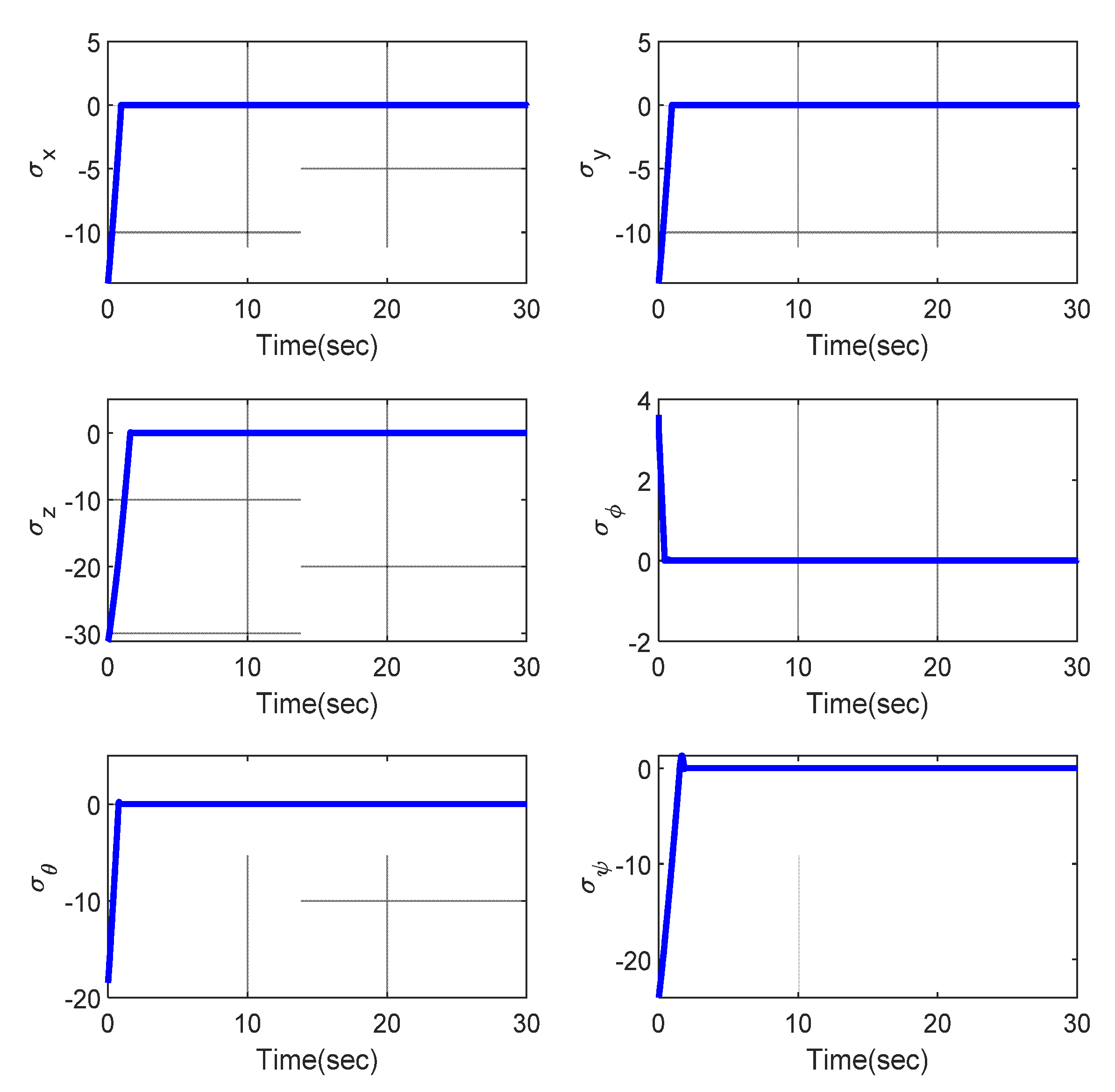
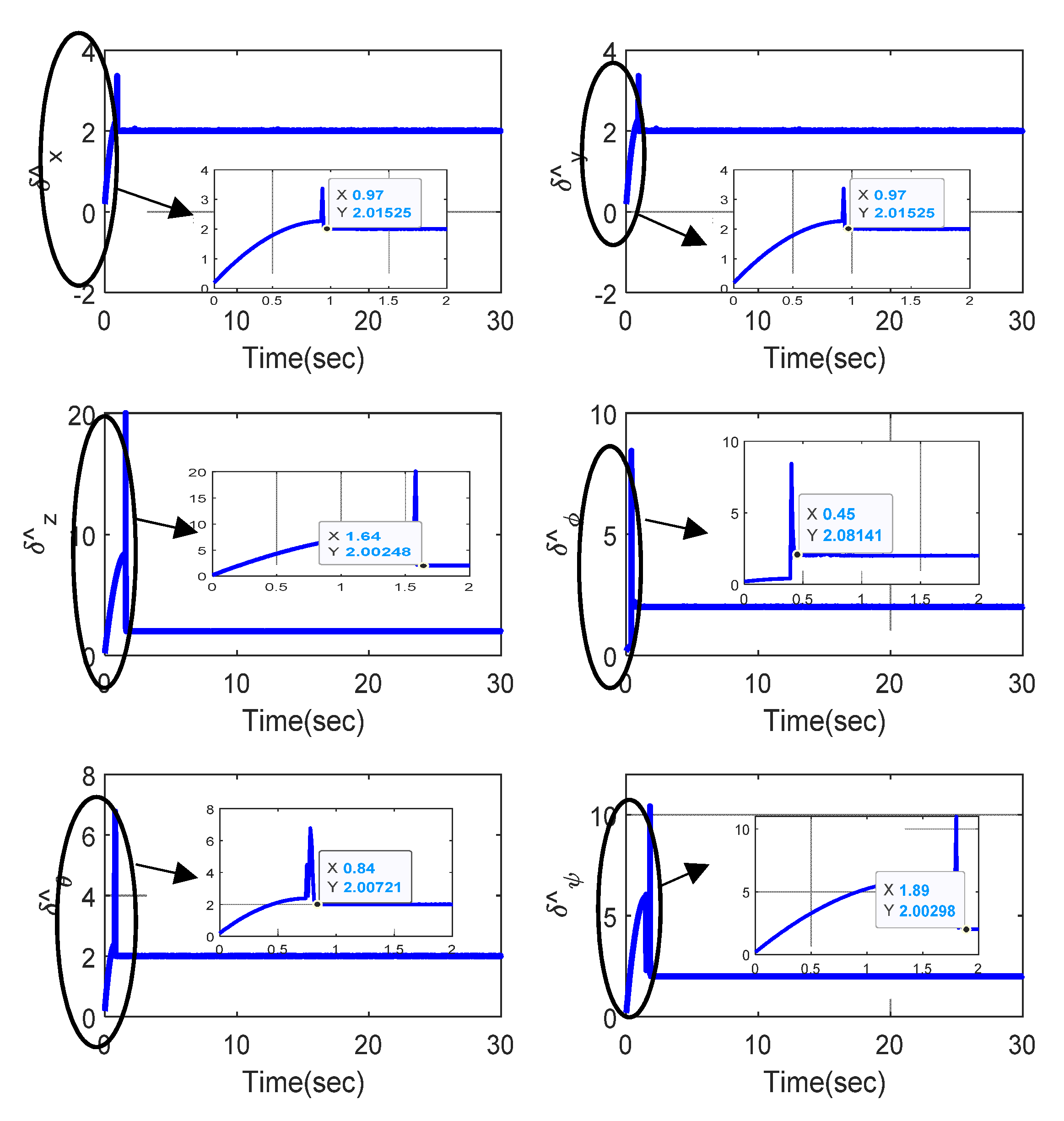
4. Simulation Results

In this section, the accuracy and performance of the proposed barrier-function-based non-singular terminal SMC is assessed using MATLAB/Simulink simulations for an uncertain quadrotor system subject to input constraints. The constant values of the quadrotor system [38] are as follows: $I_x=I_y=I_z=3.8278 \times {10}^{-3} (\mathrm{N} .\mathrm{m}/\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2$; $K_{fd}{}_x=K_{fd}{}_y=K_{fd}{}_z=K_{fa}{}_x=K_{fa}{}_y=K_{fa}{}_z=5.5670 \times {10}^{-4} \left(\mathrm{N}/\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}\right)$; $J_r=2.8385 \times {10}^{-5} \left(\mathrm{N} .\mathrm{m}/\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{s}}^2\right)$; $C_D=3.2320 \times {10}^{-2} \left(\mathrm{N} .\mathrm{m}/\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}\right)$; $d=0.25 \left(\mathrm{m}\right)$ and $m=0.486 \left(\mathrm{K}\mathrm{g}\right)$. The desired values are chosen as $x_{xd}\left(t\right)=0.4$, $x_{yd}\left(t\right)=0.4$, $x_{zd}\left(t\right)=0.8$, $x_{\varphi d}\left(t\right)=0.5sin\left(\pi t\right)$, $x_{\theta d}\left(t\right)=0.5cos\left(\pi t\right)$ and $x_{\psi d}\left(t\right)=\frac{\pi }{5}$. The bounded uncertainty $\mathrm{\Delta }{f}_i\left(x,t\right),\left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$ is selected as $0.02sin\left(0.2t\right)$. The maximum and minimum values of the control inputs are taken as $\left[u_{z min},u_{z max}\right]=\left[-10,10\right]$, $\left[u_{\varphi min},u_{\varphi max}\right]=\left[-0.5,0.5\right]$, $\left[u_{\theta min},u_{\theta max}\right]=\left[-0.5,0.5\right]$ and $\left[u_{\psi min},u_{\psi max}\right]=\left[-2,2\right]$. The parameters, which are needed for the control strategy, are gained via the trial and error method and are considered as $x_i\left(0\right)=0.1, \left(\forall i=1,\dots ,12\right)$; ${\delta }_a{}_i\left(0\right)=0.2,\left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$; $c_0=50$; $c_1=0.01$; ${\beta }_i=100,\left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$; ${\epsilon }_i=0.3,\left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$; ${\phi }_i=0.3,\left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$; ${\mu }_i=0.5,\left(\forall i=z,\varphi ,\theta ,\psi \right)$; ${\eta }_i=15,\left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$ and ${\overline{F}}_i=2,\left(\forall i=x,y,z,\varphi ,\theta ,\psi \right)$.

In Figure 2, the three-dimensional portrait of the attitude tracking dynamics of the quadrotor system in the presence of bounded uncertainty and input saturation is displayed with and without random number noise. This figure confirms that the desired path tracking of the quadrotor system is achieved in finite time. The desired position and attitude tracking of the quadrotor system in the presence of bounded uncertainty and input saturation is shown in Figure 3 with and without measurement noises. It is concluded that the desired tracking performance possesses high robustness and fast convergence. The time responses of the tracking errors, linear sliding surface and non-singular terminal sliding surface are depicted in Figure 4, Figure 5 and Figure 6, respectively. The obtained results, with/without random number noises, confirm the fast reachability and robustness of the responses. Figure 7 shows the time histories of the control inputs. According to this figure, it is demonstrated that the control inputs are bounded with suitable amplitudes. The time responses of the barrier functions are exhibited in Figure 8. With respect to the considered barrier function, for $\left|{\sigma }_i\left(t\right)\right|\le {\epsilon }_i$, the barrier function is equal to ${\overline{F}}_i=2$. Therefore, from the simulation results, it can be observed that the tracking error, linear sliding surface, non-singular terminal sliding surface and the adaptive parameter are converged to the desired values for $t_i>{\stackrel{-}{t}}_i$. From simulation results, when $\left|{\sigma }_i\left(t\right)\right|\le {\epsilon }_i$, the times ${\stackrel{-}{t}}_i$ are equal to ${\stackrel{-}{t}}_x=1$, ${\stackrel{-}{t}}_y=1$, ${\stackrel{-}{t}}_z=1.7$, ${\stackrel{-}{t}}_{\varphi }=0.5$, ${\stackrel{-}{t}}_{\theta }=0.9$ and ${\stackrel{-}{t}}_{\psi }=2$.

According to the simulation results and noise analysis, it can be inferred that the adaptive barrier non-singular TSMC method yields a robust and fast convergent performance for the quadrotor system under bounded uncertainty and constrained input.

5. Conclusions

This paper proposed a compensation system aiming at mitigating input saturation and bounded uncertainties in quadrotor UAVs. The linear sliding surface, as the combination of tracking error and virtual control input, has been designed with the goal of the reachability of the tracking error to the origin and the removal of the input saturation. In light of the importance of fast convergence of the linear sliding surface to zero, the non-singular terminal sliding surface has been suggested to ensure the finite time convergence of the linear sliding surfaces and tracking errors to zero. Because the upper bounds of uncertainties are required to be estimated, the barrier function procedure has been employed. The convergence of the non-singular terminal siding surface to the predetermined neighborhood of zero in finite time was proven using the Lyapunov theory. The obtained simulation results confirmed the effectiveness and good tracking performance of the proposed approach under bounded uncertainties and input saturation. The following topics can be considered as our future work: the design of a tracker for the quadrotor system in the presence of external disturbances, uncertainty and input saturation by using the barrier function technique and the use of an optimization algorithm to improve the quadrotor energy usage under perturbations.