Bayesian and Non-Bayesian Inference for Weibull Inverted Exponential Model under Progressive First-Failure Censoring Data
Abstract
:1. Introduction
2. Maximum Likelihood Inference
2.1. Existence of the Maximum Likelihood Estimators
- -
- For (9), when we have but when we have
- -
- Similarly, for (10), when we have but when we have or
- -
- Similarly, for (11), when we have but when we have
2.2. Asymptotic Interval Inference
3. Bayesian Inference
3.1. Lindley’s Approximation
- is the function of the parameters.
- is the log-likelihood function.
- is the log of the joint prior.
3.2. MCMC Technique
- (1):
- Start with as a guess of initial, and put
- (2):
- Generate from Gamma
- (3):
- Generate and from and , respectivily, with the proposal distributions and .
- (4):
- (5):
- Put
- (6):
- Reiterate steps N times.
- (7):
- Determine M as the burn-in period and obtain the Bayes estimates of under SE and LINEX loss functions, respectively, aswhere stands for and
- (8):
- To compute the corresponding CRIs for and , sort all the estimates in ascending order as Then the CRIs for can be obtained by
4. Simulation Study
- As the effective sample sizes m increase for fixed n, the MSEs and the average widths of and decrease.
- When n and m are fixed but k increases, the MSEs have no obvious trend on the whole.
- Lindley’s approximation performs better than the ML estimation on the basis of the smallest MSEs.
- Bayes estimates with respect to the informative priors perform better and more accurately than the ML estimators according to the MSE. When the prior information is lacking in practice, ML estimation can be taken into account as a good procedure to perform point estimates.
- Table 5 shows that the CRIs of the MCMC technique are better and more accurate than the ACIs obtained via normal approximation to the ML estimation, due to the existence of smaller widths.
- Finally, for large sample sizes, scheme I performs mostly better than schemes II and III due to the smaller MSEs.
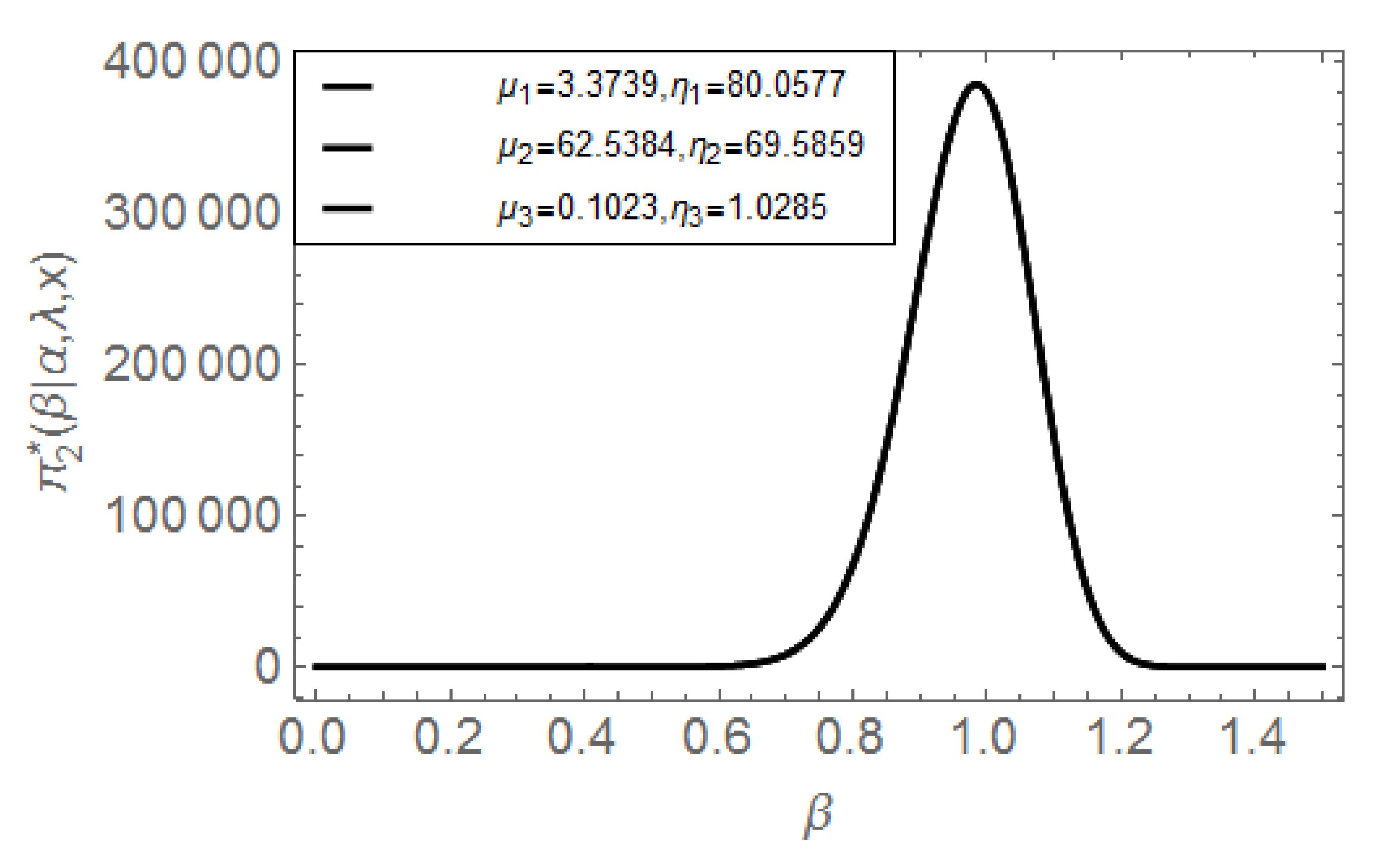
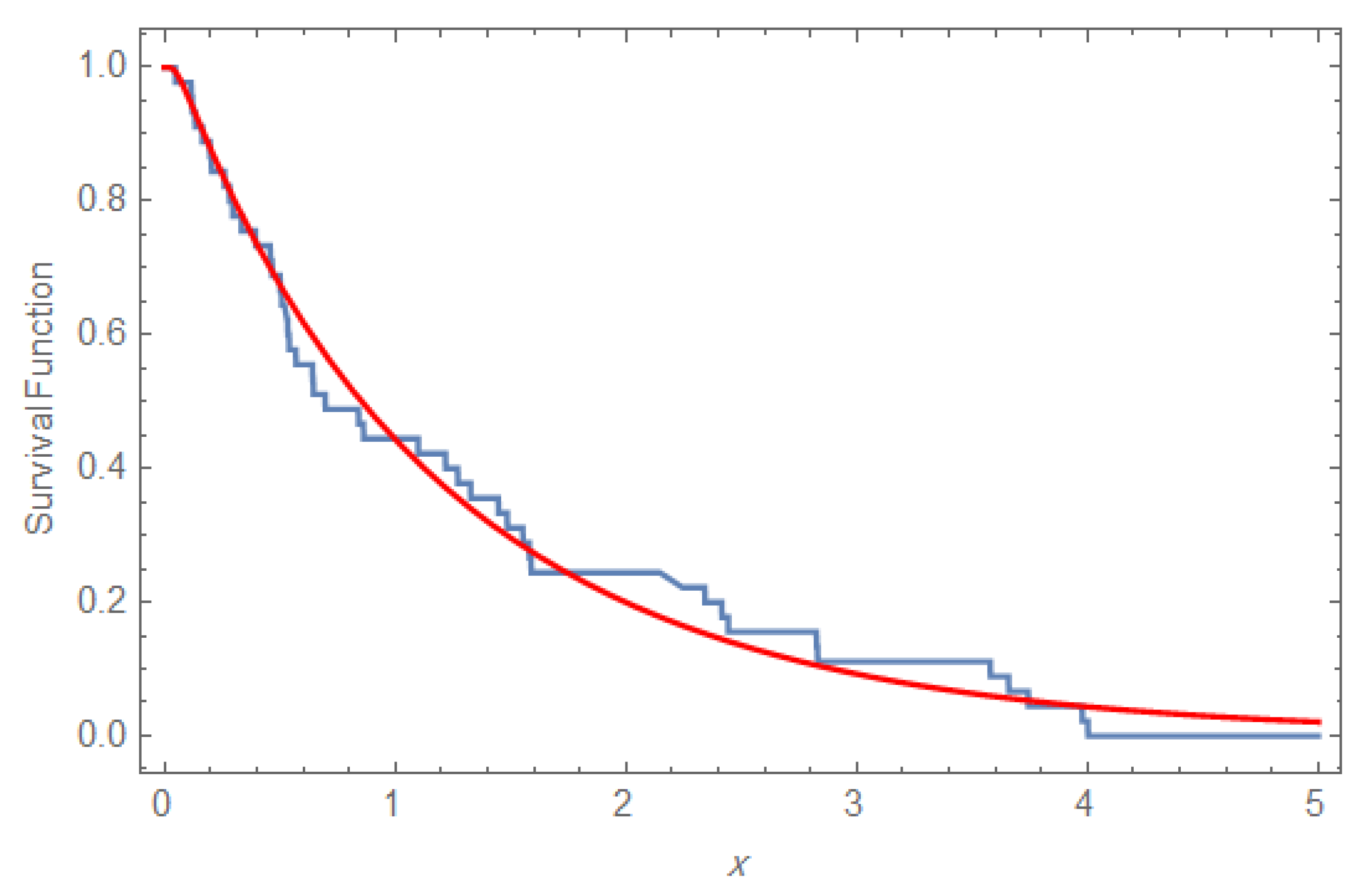
5. Numerical Example
| 0.047 | 0.132 | 0.203 | 0.296 | 0.458 | 0.507 | 0.540 | 0.644 | 0.863 | 1.271 | 1.485 | 1.589 | 2.416 | 2.830 | 3.743 |
| 0.115 | 0.164 | 0.260 | 0.334 | 0.466 | 0.529 | 0.570 | 0.696 | 1.099 | 1.326 | 1.553 | 2.178 | 2.444 | 3.578 | 3.978 |
| 0.121 | 0.197 | 0.282 | 0.395 | 0.501 | 0.534 | 0.641 | 0.841 | 1.219 | 1.447 | 1.581 | 2.342 | 2.825 | 3.658 | 4.033 |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fujii, S. Designing an optimal life test with type I censoring. Nav. Res. Logist. 2006, 38, 23–32. [Google Scholar]
- Balakrishnan, N.; Han, D. Exact Inference for a Simple Step-Stress Model with Competing Risks for Failure from Exponential Distribution under Type-II Censoring. J. Stat. Plan. Inference 2008, 138, 4172–4186. [Google Scholar] [CrossRef]
- Kundu, D.; Howlader, H. Bayesian Inference and Prediction of the Inverse Weibull Distribution for Type-II Censored Data. Comput. Stat. Data. Anal. 2010, 54, 1547–1558. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Birkhauser: Boston, MA, USA, 2000. [Google Scholar]
- Soliman, A.A. Estimation of Parameters of Life From Progressively Censored Data Using Burr-XII Model. IEEE. Trans. Reliab. 2005, 54, 34–42. [Google Scholar] [CrossRef]
- Balakrishnan, N. Progressive censoring methodology: An appraisal. Test 2007, 16, 211–259. [Google Scholar] [CrossRef]
- Du, Y.; Gui, W. Goodness of Fit Tests for the Log-Logistic Distribution Based on Cumulative Entropy under Progressive Type II Censoring. Mathematics 2019, 7, 361. [Google Scholar] [CrossRef] [Green Version]
- Alma, Ö.G.; Belaghi, R.A. Estimation in the Complementary Exponential Geometric Distribution Based on Progressive Type-II Censored Data. Commun. Math. Stat. 2020, 8, 409–441. [Google Scholar] [CrossRef]
- Wu, M.; Gui, W. Estimation and Prediction for Nadarajah-Haghighi Distribution under Progressive Type-II Censoring. Symmetry 2021, 13, 999. [Google Scholar] [CrossRef]
- Johnson, L. Theory and Technique of Variation Research; Elsevier: Amsterdam, The Netherlands, 1964. [Google Scholar]
- Wu, J.; Hung, W.; Tsai, C. Estimation of the Parameters of the Gompertz Distribution under the First Failure-Censored Sampling Plan. Statistics 2003, 37, 517–525. [Google Scholar] [CrossRef]
- Wu, J.; Yu, H. Statistical Inference about the Shape Parameter of the Burr Type XII Distribution under the Failure-Censored Sampling Plan. Appl. Math. Comput. 2005, 163, 443–482. [Google Scholar]
- Wu, S.; Kuş, C. On Estimation Based on Progressive First-Failure-Censored Sampling. Comput. Stat. Data Anal. 2009, 53, 3659–3670. [Google Scholar] [CrossRef]
- Wu, S.; Huang, S. Progressively First-Failure Censored Reliability Sampling Plans with Cost Constraint. Comput. Stat. Data Anal. 2012, 56, 2018–2030. [Google Scholar] [CrossRef]
- Mohammed, H.S.; Ateya, S.F.; AL-Hussaini, E.K. Estimation based on progressive first-failure censoring from exponentiated exponential distribution. J. Appl. Stat. 2017, 44, 1479–1494. [Google Scholar] [CrossRef]
- Ahmadi, M.V.; Doostparast, M. Pareto analysis for the lifetime performance index of products on the basis of progressively first-failure-censored batches under balanced symmetric and asymmetric loss functions. J. Appl. Stat. 2018, 46, 1–32. [Google Scholar] [CrossRef]
- Kayal, T.; Tripathi, Y.M.; Wang, L. Inference for the Chen distribution under progressive first-failure censoring. J. Stat. Theory Pract. 2019, 13, 1–27. [Google Scholar] [CrossRef]
- Zhang, F.; Gui, W. Parameter and Reliability Inferences of Inverted Exponentiated Half-Logistic Distribution under the Progressive First-Failure Censoring. Mathematics 2020, 8, 708. [Google Scholar] [CrossRef]
- Shi, X.; Shi, Y. Inference for Inverse Power Lomax Distribution with Progressive First-Failure Censoring. Entropy 2021, 23, 1099. [Google Scholar] [CrossRef]
- Chandrakant; Rastogi, M.K.; Tripathi, Y.M. On a Weibull-Inverse Exponential Distribution. Ann. Data Sci. 2018, 5, 209–234. [Google Scholar] [CrossRef]
- Cohen, A.C. Maximum Likelihood Estimation in the Weibull Distribution Based on Complete and on Censored Samples. Technometrics 1965, 7, 579–588. [Google Scholar] [CrossRef]
- Greene, W. Econometric Analysis, 4th ed.; Prentice-Hall: New York, NY, USA, 2000. [Google Scholar]
- Meeker, W.; Escobar, L. Statistical Methods for Reliability Data; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Lindley, D.V. Approximate Bayesian Methods. Trabajos de Estadística e Investigación Operativa 1980, 31, 223–237. [Google Scholar] [CrossRef]
- Kazemi, R.; Kohansal, A. Stress–Strength Parameter Estimation Based on Type-II Progressive Censored Samples for a Weibull-Half-Logistic Distribution. Bull. Malaysian Math. Sci. Soc. 2021, 44, 2531–2566. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. A Simple Simulational Algorithm for Generating Progressive Type-II Censored Samples. Am. Stat. 1995, 49, 229–230. [Google Scholar]
- Chacko, M.; Mohan, R. Bayesian Analysis of Weibull Distribution Based on Progressive Type-II Censored Competing Risks Data with Binomial Removals. Comput. Stat. 2019, 34, 233–252. [Google Scholar] [CrossRef]
- Stablein, D.M.; Carter, W.H., Jr.; Novak, J.W. Analysis of Survival Data with Nonproportional Hazard Functions. Control. Clin. Trials 1981, 2, 149–159. [Google Scholar] [CrossRef]
- Bekker, A.; Roux, J.J.J.; Mostert, P.J. A Generalization of the Compound Rayleigh Distribution: Using a Bayesian Method on Cancer Survival Times. Commun. Stat. Theory Methods 2000, 29, 1419–1433. [Google Scholar] [CrossRef]



| k,(n,m),CS | p | ML | Lindley | MCMC | ||||
|---|---|---|---|---|---|---|---|---|
| SE | LINEX | SE | LINEX | |||||
| 2,(40,15),I | 0.3268 (1.7743) | 0.2784 (0.2892) | 0.2744 (0.3872) | 0.2805 (0.2770) | 0.3166 (0.2172) | 0.3193 (0.2321) | 0.3140 (0.2042) | |
| 0.2064 (0.3473) | 0.1939 (0.0392) | 0.1925 (0.0485) | 0.1950 (0.0339) | 0.2003 (0.0136) | 0.2006 (0.0137) | 0.2000 (0.0134) | ||
| 0.1319 (1.8066) | 0.1346 (1.6667) | 0.1350 (1.6689) | 0.1343 (1.6646) | 0.1165 (0.0748) | 0.1172 (0.0780) | 0.1159 (0.0722) | ||
| S | 0.7010 (0.6218) | 0.7385 (0.2295) | 0.7381 (0.2192) | 0.7392 (0.2552) | 0.7062 (0.1306) | 0.7075 (0.1283) | 0.7048 (0.1332) | |
| H | 0.3736 (1.1400) | 0.3328 (0.6975) | 0.3312 (0.8259) | 0.3337 (0.7629) | 0.3686 (0.4132) | 0.3720 (0.4455) | 0.3652 (0.3849) | |
| 2,(40,15),II | 0.3256 (1.4734) | 0.2846 (0.1831) | 0.2819 (0.2525) | 0.2860 (0.1728) | 0.3149 (0.2188) | 0.3175 (0.2339) | 0.3123 (0.2056) | |
| 0.2055 (0.2789) | 0.1842 (0.0771) | 0.1826 (0.0958) | 0.1855 (0.0644) | 0.1997 (0.0106) | 0.2001 (0.0107) | 0.1994 (0.0105) | ||
| 0.1249 (1.2708) | 0.1233 (1.1102) | 0.1234 (1.1086) | 0.1231 (1.1115) | 0.1114 (0.0701) | 0.1118 (0.0719) | 0.1109 (0.0683) | ||
| S | 0.6979 (0.5212) | 0.7295 (0.1192) | 0.7296 (0.1191) | 0.7295 (0.1243) | 0.7051 (0.1372) | 0.7064 (0.1342) | 0.7038 (0.1405) | |
| H | 0.3799 (1.2693) | 0.3158 (0.4996) | 0.3140 (0.6574) | 0.3164 (0.4321) | 0.3669 (0.3742) | 0.3710 (0.4097) | 0.3629 (0.3439) | |
| 2,(40,15),III | 0.2770 (0.4099) | 0.2887 (0.1166) | 0.2908 (0.1195) | 0.2865 (0.1155) | 0.2897 (0.1634) | 0.2917 (0.1642) | 0.2877 (0.1635) | |
| 0.1780 (0.3617) | 0.1903 (0.1965) | 0.1873 (0.2263) | 0.1932 (0.1780) | 0.1989 (0.0031) | 0.1993 (0.0030) | 0.1985 (0.0032) | ||
| 0.1352 (0.6320) | 0.1203 (0.1653) | 0.1200 (0.1573) | 0.1205 (0.1729) | 0.1110 (0.0586) | 0.1114 (0.0602) | 0.1105 (0.0570) | ||
| S | 0.7387 (0.3133) | 0.7346 (0.1430) | 0.7360 (0.1484) | 0.7331 (0.1383) | 0.7240 (0.1330) | 0.7252 (0.1347) | 0.7228 (0.1316) | |
| H | 0.2909 (1.4838) | 0.3193 (0.8273) | 0.3145 (0.9498) | 0.3245 (0.7676) | 0.3385 (0.2683) | 0.3429 (0.2775) | 0.3344 (0.2639) | |
| 2,(40,30),I | 0.3287 (1.9205) | 0.3035 (0.5014) | 0.3015 (0.4535) | 0.3042 (0.5596) | 0.3145 (0.2182) | 0.3164 (0.2278) | 0.3126 (0.2096) | |
| 0.1977 (0.2668) | 0.1943 (0.1181) | 0.1943 (0.1178) | 0.1943 (0.1183) | 0.1995 (0.0157) | 0.1997 (0.0158) | 0.1992 (0.0156) | ||
| 0.1458 (3.8393) | 0.1474 (3.7420) | 0.1477 (3.7434) | 0.1471 (3.7407) | 0.1093 (0.0620) | 0.1097 (0.0634) | 0.1090 (0.0606) | ||
| S | 0.6993 (0.5233) | 0.7172 (0.1817) | 0.7174 (0.1677) | 0.7171 (0.1777) | 0.7037 (0.1316) | 0.7045 (0.1297) | 0.7028 (0.1336) | |
| H | 0.3595 (0.5778) | 0.3509 (0.3644) | 0.3533 (0.3689) | 0.3486 (0.3642) | 0.3642 (0.3648) | 0.3662 (0.3806) | 0.3622 (0.3503) | |
| 2,(40,30),II | 0.3257 (1.4327) | 0.3226 (1.3586) | 0.3246 (1.4020) | 0.3207 (1.3172) | 0.3353 (1.0795) | 0.3397 (1.1521) | 0.3310 (1.0145) | |
| 0.2054 (0.3311) | 0.2032 (0.3113) | 0.2035 (0.3127) | 0.2029 (0.3098) | 0.2033 (0.1851) | 0.2041 (0.1878) | 0.2025 (0.1825) | ||
| 0.1436 (3.7529) | 0.1475 (3.7539) | 0.1478 (3.7563) | 0.1472 (3.7515) | 0.1245 (0.2849) | 0.1258 (0.3007) | 0.1233 (0.2705) | ||
| S | 0.6984 (0.4126) | 0.7035 (0.3877) | 0.7046 (0.3827) | 0.7023 (0.3931) | 0.6953 (0.3269) | 0.6967 (0.3199) | 0.6939 (0.3344) | |
| H | 0.3752 (0.8326) | 0.3696 (0.7689) | 0.3736 (0.8220) | 0.3657 (0.7210) | 0.3817 (0.7383) | 0.3849 (0.7596) | 0.3786 (0.7014) | |
| 2,(40,30),III | 0.3030 (1.0318) | 0.2945 (0.4715) | 0.2954 (0.4683) | 0.2935 (0.4751) | 0.3089 (0.2019) | 0.3106 (0.2085) | 0.3074 (0.1960) | |
| 0.2090 (0.3933) | 0.1929 (0.0614) | 0.1918 (0.0651) | 0.1938 (0.0600) | 0.2007 (0.0146) | 0.2010 (0.0148) | 0.2004 (0.0145) | ||
| 0.1240 (1.6677) | 0.1238 (1.4998) | 0.1240 (1.4974) | 0.1236 (1.5018) | 0.1093 (0.0418) | 0.1097 (0.0430) | 0.1089 (0.0407) | ||
| S | 0.7109 (0.3001) | 0.7235 (0.1928) | 0.7242 (0.1901) | 0.7227 (0.1908) | 0.7080 (0.1095) | 0.7088 (0.1084) | 0.7072 (0.1106) | |
| H | 0.3568 (0.6204) | 0.3314 (0.5151) | 0.3299 (0.6474) | 0.3319 (0.4504) | 0.3604 (0.3123) | 0.3626 (0.3288) | 0.3581 (0.2975) | |
| k,(n,m),CS | p | ML | Lindley | MCMC | ||||
|---|---|---|---|---|---|---|---|---|
| SE | LINEX | SE | LINEX | |||||
| 2,(60,35),I | 0.2038 (1.1646) | 0.2165 (0.9084) | 0.2170 (0.9022) | 0.2159 (0.9148) | 0.2638 (0.2141) | 0.2651 (0.2061) | 0.2625 (0.2224) | |
| 0.2344 (0.1875) | 0.2189 (0.0631) | 0.2190 (0.0639) | 0.2189 (0.0630) | 0.2046 (0.0097) | 0.2048 (0.0100) | 0.2043 (0.0095) | ||
| 0.0670 (0.1205) | 0.0765 (0.0652) | 0.0766 (0.0648) | 0.0764 (0.0645) | 0.0895 (0.0127) | 0.0897 (0.0123) | 0.0892 (0.0112) | ||
| S | 0.7688 (0.4897) | 0.7659 (0.4391) | 0.7665 (0.4256) | 0.7652 (0.4327) | 0.7338 (0.1084) | 0.7345 (0.1115) | 0.7331 (0.1054) | |
| H | 0.2919 (0.5397) | 0.2848 (0.5784) | 0.2866 (0.5601) | 0.2831 (0.5971) | 0.3158 (0.2439) | 0.3170 (0.2380) | 0.3146 (0.2500) | |
| 2,(60,35),II | 0.3200 (1.0117) | 0.3082 (0.4398) | 0.3091 (0.4349) | 0.3073 (0.4247) | 0.3137 (0.2109) | 0.3153 (0.2192) | 0.3121 (0.2032) | |
| 0.2007 (0.2435) | 0.1948 (0.1021) | 0.1947 (0.1014) | 0.1948 (0.1008) | 0.2005 (0.0178) | 0.2007 (0.0179) | 0.2003 (0.0177) | ||
| 0.1347 (3.0075) | 0.1362 (2.9820) | 0.1364 (2.9827) | 0.1360 (2.9813) | 0.1071 (0.0332) | 0.1074 (0.0338) | 0.1068 (0.0325) | ||
| S | 0.7007 (0.3029) | 0.7112 (0.1404) | 0.7119 (0.1418) | 0.7106 (0.1392) | 0.7034 (0.1091) | 0.7042 (0.1074) | 0.7027 (0.1108) | |
| H | 0.3632 (0.5333) | 0.3511 (0.2482) | 0.3533 (0.2606) | 0.3490 (0.2395) | 0.3651 (0.3040) | 0.3671 (0.3185) | 0.3632 (0.2906) | |
| 2,(60,35),III | 0.3109 (0.5593) | 0.3066 (0.3147) | 0.3078 (0.3217) | 0.3053 (0.3089) | 0.3115 (0.1885) | 0.3128 (0.1945) | 0.3101 (0.1829) | |
| 0.1980 (0.4121) | 0.1846 (0.1055) | 0.1834 (0.1130) | 0.1856 (0.1001) | 0.1989 (0.0104) | 0.1993 (0.0105) | 0.1986 (0.0102) | ||
| 0.1390 (2.957) | 0.1362 (2.7725) | 0.1363 (2.7703) | 0.1361 (2.7744) | 0.1077 (0.0368) | 0.1081 (0.0376) | 0.1074 (0.0360) | ||
| S | 0.7044 (0.1820) | 0.7153 (0.1145) | 0.7161 (0.1148) | 0.7145 (0.1144) | 0.7050 (0.1075) | 0.7057 (0.1061) | 0.7043 (0.1090) | |
| H | 0.3571 (1.0249) | 0.3294 (0.4391) | 0.3260 (0.5977) | 0.3316 (0.3642) | 0.3616 (0.3204) | 0.3642 (0.3397) | 0.3592 (0.3032) | |
| 2,(60,50),I | 0.2999 (0.5571) | 0.2968 (0.3990) | 0.2977 (0.4036) | 0.2959 (0.3949) | 0.3083 (0.1997) | 0.3097 (0.2049) | 0.3069 (0.1949) | |
| 0.2026 (0.0473) | 0.2010 (0.0207) | 0.2011 (0.0208) | 0.2009 (0.0206) | 0.1984 (0.0081) | 0.1986 (0.0083) | 0.1982 (0.0080) | ||
| 0.0955 (0.0252) | 0.0997 (0.0162) | 0.0999 (0.0163) | 0.0995 (0.0160) | 0.1016 (0.0038) | 0.1019 (0.0039) | 0.1014 (0.0037) | ||
| S | 0.7100 (0.2434) | 0.7143 (0.1817) | 0.7149 (0.1813) | 0.7136 (0.1823) | 0.7058 (0.1007) | 0.7064 (0.0998) | 0.7051 (0.1017) | |
| H | 0.3474 (0.2708) | 0.3449 (0.2435) | 0.3467 (0.2480) | 0.3430 (0.2399) | 0.3525 (0.1716) | 0.3536 (0.1751) | 0.3513 (0.1684) | |
| 2,(60,50),II | 0.3170 (0.9423) | 0.3092 (0.6391) | 0.3102 (0.6485) | 0.3083 (0.6306) | 0.3211 (0.3665) | 0.3225 (0.3772) | 0.3197 (0.3564) | |
| 0.2154 (0.2314) | 0.2071 (0.0839) | 0.2071 (0.0838) | 0.2071 (0.0841) | 0.2062 (0.0419) | 0.2064 (0.0424) | 0.2060 (0.0415) | ||
| 0.1167 (0.1805) | 0.1169 (0.1362) | 0.1172 (0.1377) | 0.1167 (0.1347) | 0.1178 (0.0576) | 0.1181 (0.0591) | 0.1174 (0.0562) | ||
| S | 0.7034 (0.4082) | 0.7116 (0.2802) | 0.7122 (0.2795) | 0.7110 (0.2811) | 0.7025 (0.2154) | 0.7031 (0.2136) | 0.7019 (0.2172) | |
| H | 0.3911 (1.1964) | 0.3685 (0.5069) | 0.3701 (0.5137) | 0.3670 (0.5031) | 0.3840 (0.7294) | 0.3856 (0.7544) | 0.3825 (0.7055) | |
| 2,(60,50),III | 0.2908 (0.8311) | 0.2882 (0.5846) | 0.2890 (0.5894) | 0.2874 (0.5805) | 0.3064 (0.2987) | 0.3077 (0.3043) | 0.3051 (0.2936) | |
| 0.2149 (0.1189) | 0.2072 (0.0310) | 0.2073 (0.0314) | 0.2071 (0.0300) | 0.2033 (0.0089) | 0.2036 (0.0091) | 0.2031 (0.0087) | ||
| 0.0952 (0.1008) | 0.0983 (0.0758) | 0.0985 (0.0762) | 0.0981 (0.0753) | 0.1030 (0.0381) | 0.1033 (0.0386) | 0.1027 (0.0376) | ||
| S | 0.7134 (0.3532) | 0.7186 (0.2676) | 0.7192 (0.2674) | 0.7180 (0.2679) | 0.7061 (0.1901) | 0.7067 (0.1889) | 0.7055 (0.1914) | |
| H | 0.3615 (0.4949) | 0.3489 (0.4211) | 0.3510 (0.4323) | 0.3469 (0.4111) | 0.3626 (0.3740) | 0.3640 (0.3850) | 0.3611 (0.3637) | |
| k,(n,m),CS | p | ML | Lindley | MCMC | ||||
|---|---|---|---|---|---|---|---|---|
| SE | LINEX | SE | LINEX | |||||
| 4,(40,15),I | 0.3118 (1.2240) | 0.2829 (0.2343) | 0.2817 (0.2921) | 0.2831 (0.2241) | 0.3116 (0.2188) | 0.3140 (0.2313) | 0.3092 (0.2079) | |
| 0.2061 (0.3967) | 0.1828 (0.1241) | 0.1802 (0.1615) | 0.1849 (0.1005) | 0.1989 (0.0080) | 0.1993 (0.0081) | 0.1986 (0.0078) | ||
| 0.1264 (2.0566) | 0.1304 (1.9802) | 0.1307 (1.9815) | 0.1302 (1.9790) | 0.1079 (0.0433) | 0.1083 (0.0443) | 0.1075 (0.0423) | ||
| S | 0.7037 (0.4341) | 0.7335 (0.1623) | 0.7340 (0.1622) | 0.7331 (0.1663) | 0.7061 (0.1225) | 0.7074 (0.1201) | 0.7048 (0.1254) | |
| H | 0.3660 (1.3632) | 0.3108 (0.9157) | 0.3125 (0.7432) | 0.3151 (0.6543) | 0.3619 (0.3635) | 0.3659 (0.3954) | 0.3580 (0.3369) | |
| 4,(40,15),II | 0.3262 (1.4934) | 0.2827 (0.1858) | 0.2793 (0.2776) | 0.2845 (0.1711) | 0.3155 (0.2288) | 0.3183 (0.2457) | 0.3128 (0.2141) | |
| 0.2082 (0.4115) | 0.1776 (0.1334) | 0.1745 (0.1855) | 0.1801 (0.1009) | 0.1981 (0.0087) | 0.1985 (0.0088) | 0.1978 (0.0086) | ||
| 0.1133 (0.3545) | 0.1125 (0.2551) | 0.1127 (0.2562) | 0.1124 (0.2540) | 0.1077 (0.0336) | 0.1080 (0.0343) | 0.1074 (0.0328) | ||
| S | 0.6926 (0.6070) | 0.7303 (0.1227) | 0.7299 (0.1245) | 0.7310 (0.1314) | 0.7036 (0.1309) | 0.7050 (0.1272) | 0.7021 (0.1350) | |
| H | 0.3964 (3.4945) | 0.2878 (1.5816) | 0.2935 (1.2547) | 0.3033 (0.6327) | 0.366 (0.4112) | 0.3710 (0.4581) | 0.3612 (0.3729) | |
| 4,(40,15),III | 0.1972 (1.1454) | 0.2362 (0.4650) | 0.2367 (0.4613) | 0.2356 (0.4695) | 0.2467 (0.3520) | 0.2484 (0.3365) | 0.2450 (0.3678) | |
| 0.2142 (0.2527) | 0.1706 (0.3258) | 0.1658 (0.4225) | 0.1746 (0.2606) | 0.1992 (0.0014) | 0.1997 (0.0013) | 0.1988 (0.0015) | ||
| 0.0875 (0.0970) | 0.0900 (0.0670) | 0.0901 (0.0672) | 0.0898 (0.0668) | 0.1031 (0.0314) | 0.1034 (0.0320) | 0.1028 (0.0309) | ||
| S | 0.7862 (0.6908) | 0.7635 (0.3393) | 0.7644 (0.3470) | 0.7627 (0.3321) | 0.7560 (0.2587) | 0.7571 (0.2679) | 0.7549 (0.2497) | |
| H | 0.2611 (1.5065) | 0.2331 (1.8222) | 0.2286 (2.0514) | 0.2367 (1.6650) | 0.2900 (0.4498) | 0.2939 (0.4126) | 0.2864 (0.4884) | |
| 4,(40,30),I | 0.3186 (0.7216) | 0.3085 (0.3583) | 0.3100 (0.3683) | 0.3071 (0.3497) | 0.3072 (0.2335) | 0.3088 (0.2403) | 0.3056 (0.2274) | |
| 0.1887 (0.4936) | 0.1799 (0.2778) | 0.1796 (0.2790) | 0.1801 (0.2767) | 0.2011 (0.0173) | 0.2014 (0.0175) | 0.2008 (0.0171) | ||
| 0.2174 (1.804) | 0.2194 (1.719) | 0.2196 (1.720) | 0.2192 (1.709) | 0.1105 (0.0306) | 0.1108 (0.0314) | 0.1102 (0.0297) | ||
| S | 0.7073 (0.2897) | 0.7201 (0.1522) | 0.7208 (0.1516) | 0.7193 (0.1521) | 0.7103 (0.1440) | 0.7111 (0.1430) | 0.7096 (0.1451) | |
| H | 0.3460 (1.3516) | 0.3332 (0.3727) | 0.3336 (0.3928) | 0.3329 (0.3561) | 0.3606 (0.4668) | 0.3631 (0.4892) | 0.3582 (0.4467) | |
| 4,(40,30),II | 0.2777 (1.0799) | 0.2747 (0.6076) | 0.2757 (0.6091) | 0.2737 (0.6072) | 0.2928 (0.2851) | 0.2943 (0.2886) | 0.2913 (0.2823) | |
| 0.2208 (0.7544) | 0.1802 (0.1497) | 0.1737 (0.3018) | 0.1846 (0.0859) | 0.1974 (0.0211) | 0.1977 (0.0211) | 0.1971 (0.0211) | ||
| 0.1054 (0.3287) | 0.1052 (0.2532) | 0.1054 (0.2546) | 0.1051 (0.2518) | 0.1053 (0.0427) | 0.1055 (0.0433) | 0.1050 (0.0420) | ||
| S | 0.7192 (0.4165) | 0.7404 (0.2907) | 0.7403 (0.2853) | 0.7406 (0.2994) | 0.7194 (0.1768) | 0.7202 (0.1764) | 0.7187 (0.1769) | |
| H | 0.3659 (2.9944) | 0.2545 (3.38398) | 0.2732 (3.4761) | 0.2851 (0.9719) | 0.3361 (0.4043) | 0.3385 (0.4149) | 0.3338 (0.3958) | |
| 4,(40,30),III | 0.3137 (0.4260) | 0.3085 (0.2065) | 0.3100 (0.2133) | 0.3070 (0.2007) | 0.3123 (0.1896) | 0.3138 (0.1971) | 0.3108 (0.1827) | |
| 0.1909 (0.4206) | 0.1802 (0.1144) | 0.1789 (0.1273) | 0.1813 (0.1046) | 0.1987 (0.0054) | 0.1991 (0.0052) | 0.1983 (0.0051) | ||
| 0.1326 (0.6375) | 0.1266 (0.3862) | 0.1268 (0.3854) | 0.1265 (0.3841) | 0.1103 (0.0407) | 0.1106 (0.0416) | 0.1100 (0.0398) | ||
| S | 0.7057 (0.1778) | 0.7168 (0.0960) | 0.7176 (0.0949) | 0.7159 (0.0956) | 0.7059 (0.1084) | 0.7067 (0.1068) | 0.7051 (0.1102) | |
| H | 0.3523 (1.4459) | 0.3217 (0.5100) | 0.3178 (0.6945) | 0.3242 (0.4160) | 0.3633 (0.3334) | 0.3667 (0.3598) | 0.3600 (0.3108) | |
| k,(n,m),CS | p | ML | Lindley | MCMC | ||||
|---|---|---|---|---|---|---|---|---|
| SE | LINEX | SE | LINEX | |||||
| 4,(60,35),I | 0.3116 (0.1522) | 0.3085 (0.0878) | 0.3098 (0.0921) | 0.3071 (0.0840) | 0.3193 (0.0635) | 0.3208 (0.0701) | 0.3178 (0.0575) | |
| 0.2060 (0.1890) | 0.1971 (0.0222) | 0.1969 (0.0219) | 0.1972 (0.0215) | 0.1977 (0.0145) | 0.1980 (0.0146) | 0.1974 (0.0142) | ||
| 0.0991 (0.1311) | 0.1011 (0.1104) | 0.1012 (0.1109) | 0.1009 (0.1098) | 0.1011 (0.0318) | 0.1013 (0.0321) | 0.1009 (0.0316) | ||
| S | 0.6928 (0.0514) | 0.7021 (0.0239) | 0.7030 (0.0223) | 0.7011 (0.0257) | 0.6941 (0.0624) | 0.6948 (0.0599) | 0.6933 (0.0651) | |
| H | 0.3806 (0.4775) | 0.3573 (0.0658) | 0.3594 (0.0742) | 0.3554 (0.0586) | 0.3697 (0.1832) | 0.3721 (0.1982) | 0.3674 (0.1697) | |
| 4,(60,35),II | 0.3165 (0.5001) | 0.3092 (0.2664) | 0.3105 (0.2734) | 0.3079 (0.2604) | 0.3071 (0.1919) | 0.3086 (0.1983) | 0.3056 (0.1862) | |
| 0.1907 (0.1560) | 0.1918 (0.0516) | 0.1919 (0.0519) | 0.1917 (0.0512) | 0.1956 (0.0174) | 0.1959 (0.0172) | 0.1953 (0.0171) | ||
| 0.1240 (0.2001) | 0.1230 (0.1677) | 0.1231 (0.1687) | 0.1228 (0.1666) | 0.1159 (0.0536) | 0.1162 (0.0547) | 0.1156 (0.0526) | ||
| S | 0.7098 (0.1842) | 0.7158 (0.0967) | 0.7166 (0.0954) | 0.7150 (0.0963) | 0.7144 (0.0914) | 0.7151 (0.0912) | 0.7137 (0.0916) | |
| H | 0.3477 (0.8513) | 0.3439 (0.3413) | 0.3461 (0.3491) | 0.3419 (0.3370) | 0.3490 (0.3927) | 0.3514 (0.4091) | 0.3466 (0.3784) | |
| 4,(60,35),III | 0.3277 (0.2958) | 0.3207 (0.1577) | 0.3222 (0.1665) | 0.3193 (0.1497) | 0.3229 (0.1524) | 0.3245 (0.1648) | 0.3213 (0.1408) | |
| 0.1748 (1.177) | 0.1588 (0.2629) | 0.1533 (0.3377) | 0.1628 (0.2306) | 0.2005 (0.0023) | 0.2009 (0.0024) | 0.2000 (0.0022) | ||
| 0.1668 (0.9714) | 0.1575 (0.7150) | 0.1577 (0.7189) | 0.1573 (0.7113) | 0.1151 (0.0441) | 0.1154 (0.0452) | 0.1148 (0.0431) | ||
| S | 0.6979 (0.5602) | 0.7189 (0.1516) | 0.7189 (0.1403) | 0.7191 (0.1429) | 0.7008 (0.0914) | 0.7016 (0.0890) | 0.7000 (0.0940) | |
| H | 0.3967(2.649) | 0.2616(2.0704) | 0.2652 (2.1037) | 0.3130 (0.6766) | 0.3798 (0.4544) | 0.3841 (0.5023) | 0.3756 (0.4131) | |
| 4,(60,50),I | 0.2581 (0.4502) | 0.2630 (0.3444) | 0.2637 (0.3424) | 0.2624 (0.3417) | 0.2826 (0.1030) | 0.2836 (0.1009) | 0.2817 (0.1007) | |
| 0.2276 (0.2174) | 0.2114 (0.0463) | 0.2113 (0.0457) | 0.2114 (0.0449) | 0.2073 (0.0207) | 0.2076 (0.0212) | 0.2070 (0.0202) | ||
| 0.1004 (0.0586) | 0.1026 (0.0481) | 0.1027 (0.0483) | 0.1025 (0.0479) | 0.1137 (0.0250) | 0.1140 (0.0258) | 0.1134 (0.0242) | ||
| S | 0.7408 (0.1804) | 0.7407 (0.1623) | 0.7412 (0.1453) | 0.7402 (0.1594) | 0.7307 (0.0785) | 0.7312 (0.0672) | 0.7303 (0.0767) | |
| H | 0.3433 (0.1923) | 0.3251 (0.1561) | 0.3267 (0.1507) | 0.3236 (0.1419) | 0.3399 (0.1144) | 0.3412 (0.1148) | 0.3385 (0.1138) | |
| 4,(60,50),II | 0.2973 (0.7149) | 0.2944 (0.5660) | 0.2953 (0.5716) | 0.2935 (0.5607) | 0.3183 (0.1648) | 0.3195 (0.1712) | 0.3171 (0.1587) | |
| 0.2388 (0.7750) | 0.2112 (0.0787) | 0.2096 (0.0594) | 0.2126 (0.0975) | 0.2083 (0.0382) | 0.2086 (0.0389) | 0.2080 (0.0375) | ||
| 0.0939 (0.1152) | 0.0952 (0.1021) | 0.0953 (0.1023) | 0.0951 (0.1019) | 0.1033 (0.0240) | 0.1035 (0.0242) | 0.1031 (0.0237) | ||
| S | 0.6977 (0.1148) | 0.7118 (0.1797) | 0.7123 (0.1768) | 0.7114 (0.1828) | 0.6957 (0.0664) | 0.6962 (0.0646) | 0.6951 (0.0684) | |
| H | 0.4161 (0.8910) | 0.3542 (0.3835) | 0.3485 (0.5900) | 0.3578 (0.2697) | 0.3869 (0.2375) | 0.3890 (0.2564) | 0.3848 (0.2198) | |
| 4,(60,50),III | 0.2989 (0.3856) | 0.2983 (0.2641) | 0.2992 (0.2674) | 0.2975 (0.2612) | 0.3053 (0.1695) | 0.3063 (0.1729) | 0.3042 (0.1663) | |
| 0.2065 (0.6123) | 0.1868 (0.1625) | 0.1844 (0.2019) | 0.1884 (0.1530) | 0.1994 (0.0124) | 0.1997 (0.0125) | 0.1990 (0.0119) | ||
| 0.1303 (1.6840) | 0.1299 (1.6347) | 0.1300 (1.6355) | 0.1298 (1.6339) | 0.1069 (0.0254) | 0.1072 (0.0259) | 0.1067 (0.0249) | ||
| S | 0.7077 (0.1616) | 0.7185 (0.1217) | 0.7187 (0.1149) | 0.7184 (0.1317) | 0.7095 (0.0894) | 0.7101 (0.0888) | 0.7090 (0.0900) | |
| H | 0.3719 (2.5367) | 0.3131 (1.4171) | 0.3118 (1.4458) | 0.3252 (0.5164) | 0.3554 (0.3151) | 0.3576 (0.3300) | 0.3533 (0.3019) | |
| k,(n,m),CS | S | H | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ML | MCMC | ML | MCMC | ML | MCMC | ML | MCMC | ML | MCMC | |
| 2,(40,15),I | 0.6320 | 0.2821 | 0.2395 | 0.0970 | 0.2545 | 0.1274 | 0.3302 | 0.1994 | 0.4429 | 0.3171 |
| (0.955) | (0.995) | (0.935) | (0.995) | (0.965) | (0.985) | (0.970) | (0.990) | (0.970) | (0.995) | |
| 2,(40,15),II | 0.6007 | 0.2806 | 0.2566 | 0.0995 | 0.2688 | 0.1109 | 0.3082 | 0.1975 | 0.5128 | 0.3433 |
| (0.990) | (0.995) | (0.975) | (0.990) | (0.965) | (0.980) | (0.965) | (0.995) | (0.990) | (0.995) | |
| 2,(40,15),III | 0.4039 | 0.2438 | 4.8236 | 0.1135 | 7.4751 | 0.1115 | 0.3343 | 0.1886 | 6.9804 | 0.3530 |
| (0.995) | (0.990) | (0.980) | (0.995) | (0.995) | (0.990) | (0.900) | (0.965) | (0.990) | (0.985) | |
| 2,(40,30),I | 0.4111 | 0.2372 | 0.1534 | 0.0859 | 0.1705 | 0.1068 | 0.2308 | 0.1637 | 0.2901 | 0.2424 |
| (0.920) | (0.995) | (0.925) | (0.990) | (0.915) | (0.980) | (0.905) | (0.980) | (0.960) | (0.980) | |
| 2,(40,30),II | 0.3829 | 0.3537 | 0.1613 | 0.1547 | 0.1670 | 0.1592 | 0.21364 | 0.2050 | 0.3058 | 0.3005 |
| (0.905) | (0.935) | (0.880) | (0.935) | (0.910) | (0.920) | (0.920) | (0.935) | (0.905) | (0.930) | |
| 2,(40,30),III | 0.372 | 0.2198 | 0.2345 | 0.0972 | 0.2676 | 0.1067 | 0.2001 | 0.1549 | 0.3273 | 0.2573 |
| (0.920) | (0.985) | (0.910) | (0.995) | (0.970) | (0.990) | (0.920) | (0.975) | (0.965) | (0.985) | |
| 2,(60,35),I | 0.2804 | 0.1988 | 0.1504 | 0.0832 | 0.1020 | 0.0850 | 0.1894 | 0.1461 | 0.2107 | 0.1923 |
| (0.900) | (0.995) | (0.950) | (0.980) | (0.995) | (0.995) | (0.905) | (0.980) | (0.925) | (0.990) | |
| 2,(60,35),II | 0.3370 | 0.2195 | 0.1469 | 0.0863 | 0.1436 | 0.0936 | 0.1912 | 0.1493 | 0.2821 | 0.2429 |
| (0.910) | (0.970) | (0.915) | (0.995) | (0.955) | (0.980) | (0.905) | (0.970) | (0.945) | (0.975) | |
| 2,(60,35),III | 0.3252 | 0.2019 | 0.3344 | 0.1034 | 0.3542 | 0.0965 | 0.1706 | 0.1452 | 0.5088 | 0.2708 |
| (0.960) | (0.985) | (0.970) | (0.995) | (0.960) | (0.995) | (0.970) | (0.985) | (0.955) | (0.990) | |
| 2,(60,50),I | 0.2957 | 0.2053 | 0.1180 | 0.0765 | 0.1179 | 0.0884 | 0.1766 | 0.1381 | 0.2085 | 0.1883 |
| (0.905) | (0.950) | (0.900) | (0.965) | (0.910) | (0.995) | (0.920) | (0.955) | (0.935) | (0.980) | |
| 2,(60,50),II | 0.2985 | 0.2045 | 0.1295 | 0.0806 | 0.1462 | 0.1016 | 0.168 | 0.1337 | 0.2432 | 0.2125 |
| (0.905) | (0.970) | (0.900) | (0.950) | (0.920) | (0.995) | (0.935) | (0.980) | (0.970) | (0.980) | |
| 2,(60,50),III | 0.2865 | 0.1947 | 0.1574 | 0.0885 | 0.1344 | 0.0915 | 0.1610 | 0.1311 | 0.2315 | 0.2060 |
| (0.900) | (0.990) | (0.905) | (0.995) | (0.925) | (0.980) | (0.950) | (0.980) | (0.910) | (0.975) | |
| 4,(40,15),I | 0.5309 | 0.2692 | 0.3404 | 0.1041 | 0.2785 | 0.1026 | 0.2786 | 0.1956 | 0.5628 | 0.3398 |
| (0.970) | (0.980) | (0.970) | (0.995) | (0.975) | (0.990) | (0.950) | (0.985) | (0.955) | (0.990) | |
| 4,(40,15),II | 0.6156 | 0.2882 | 0.4307 | 0.1063 | 0.3808 | 0.0951 | 0.3148 | 0.2058 | 0.8889 | 0.3769 |
| (0.980) | (0.995) | (0.950) | (0.970) | (0.935) | (0.975) | (0.960) | (0.995) | (0.975) | (0.995) | |
| 4,(40,15),III | 0.2999 | 0.2236 | 9.1516 | 0.1161 | 8.8717 | 0.0968 | 0.5766 | 0.1807 | 15.881 | 0.3333 |
| (0.925) | (0.945) | (0.980) | (0.995) | (0.950) | (0.990) | (0.930) | (0.950) | (0.925) | (0.980) | |
| 4,(40,30),I | 0.3510 | 0.2184 | 0.2051 | 0.0982 | 0.1683 | 0.0960 | 0.1921 | 0.1527 | 0.3432 | 0.2667 |
| (0.935) | (0.950) | (0.910) | (0.970) | (0.900) | (0.920) | (0.950) | (0.995) | (0.945) | (0.975) | |
| 4,(40,30),II | 0.3239 | 0.2106 | 0.2257 | 0.0969 | 0.1890 | 0.0913 | 0.1862 | 0.1499 | 0.3944 | 0.2604 |
| (0.900) | (0.970) | (0.935) | (0.995) | (0.910) | (0.925) | (0.980) | (0.995) | (0.945) | (0.970) | |
| 4,(40,30),III | 0.3361 | 0.2132 | 1.2621 | 0.1088 | 2.6355 | 0.0939 | 0.2055 | 0.1564 | 1.4325 | 0.3128 |
| (0.900) | (0.935) | (0.905) | (0.995) | (0.910) | (0.935) | (0.925) | (0.950) | (0.945) | (0.980) | |
| 4,(60,35),I | 0.3447 | 0.2270 | 0.2454 | 0.1018 | 0.1309 | 0.0848 | 0.1851 | 0.1561 | 0.4616 | 0.3080 |
| (0.935) | (0.995) | (0.970) | (0.980) | (0.900) | (0.910) | (0.945) | (0.950) | (0.970) | (0.990) | |
| 4,(60,35),II | 0.3339 | 0.2148 | 0.2132 | 0.0940 | 0.2018 | 0.0906 | 0.1840 | 0.1470 | 0.3616 | 0.2617 |
| (0.990) | (0.995) | (0.990) | (0.995) | (0.935) | (0.980) | (0.905) | (0.970) | (0.900) | (0.910) | |
| 4,(60,35),III | 0.3425 | 0.2182 | 7.0377 | 0.1178 | 12.388 | 0.0930 | 0.4233 | 0.1585 | 9.2061 | 0.3528 |
| (0.970) | (0.995) | (0.935) | (0.980) | (0.905) | (0.995) | (0.905) | (0.980) | (0.910) | (0.975) | |
| 4,(60,50),I | 0.2381 | 0.1738 | 0.1667 | 0.0907 | 0.1281 | 0.0903 | 0.1385 | 0.1188 | 0.2285 | 0.2014 |
| (0.980) | (0.995) | (0.910) | (0.935) | (0.905) | (0.990) | (0.980) | (0.980) | (0.915) | (0.935) | |
| 4,(60,50),II | 0.2676 | 0.1921 | 0.1948 | 0.0957 | 0.1254 | 0.0779 | 0.1494 | 0.1301 | 0.3316 | 0.2498 |
| (0.920) | (0.935) | (0.900) | (0.995) | (0.970) | (0.995) | (0.910) | (0.980) | (0.925) | (0.965) | |
| 4,(60,50),III | 0.2628 | 0.1770 | 0.2907 | 0.1023 | 0.2579 | 0.0844 | 0.1428 | 0.1253 | 0.4898 | 0.2488 |
| (0.975) | (0.995) | (0.910) | (0.935) | (0.905) | (0.990) | (0.900) | (0.980) | (0.960) | (0.990) | |
| P | ML | Lindley | MCMC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SE | LINEX | SE | LINEX | ||||||
| 0.0145 | 0.0157 | 0.0158 | 0.0157 | 0.0154 | 0.0382 | 0.0384 | 0.0382 | 0.0381 | |
| 0.9920 | 0.8875 | 0.886 | 0.8875 | 0.889 | 0.884 | 0.8885 | 0.884 | 0.8796 | |
| 0.0581 | 0.0673 | 0.0675 | 0.0673 | 0.0672 | 0.116 | 0.1181 | 0.116 | 0.1141 | |
| 0.9817 | 0.9822 | 0.9823 | 0.9822 | 0.9822 | 0.978 | 0.978 | 0.978 | 0.9779 | |
| 0.2410 | 0.2124 | 0.2184 | 0.2124 | 0.2068 | 0.2965 | 0.3026 | 0.2965 | 0.2906 | |
| P | ML | MCMC | ||
|---|---|---|---|---|
| CIs | Length | CRIs | Length | |
| (0.0000398, 5.3189) | 5.3189 | (0.01108, 0.08287) | 0.07179 | |
| (0.5424, 1.8139) | 1.2715 | (0.70618, 1.0809) | 0.37472 | |
| (0.000723, 4.6729) | 4.6722 | (0.0251, 0.26478) | 0.23968 | |
| (0.9527, 1.0115) | 0.0588 | (0.9475, 0.9953) | 0.0478 | |
| (0.0636, 0.9135) | 0.8499 | (0.1160, 0.5485) | 0.4325 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathi, A.; Farghal, A.-W.A.; Soliman, A.A. Bayesian and Non-Bayesian Inference for Weibull Inverted Exponential Model under Progressive First-Failure Censoring Data. Mathematics 2022, 10, 1648. https://doi.org/10.3390/math10101648
Fathi A, Farghal A-WA, Soliman AA. Bayesian and Non-Bayesian Inference for Weibull Inverted Exponential Model under Progressive First-Failure Censoring Data. Mathematics. 2022; 10(10):1648. https://doi.org/10.3390/math10101648
Chicago/Turabian StyleFathi, Abdullah, Al-Wageh A. Farghal, and Ahmed A. Soliman. 2022. "Bayesian and Non-Bayesian Inference for Weibull Inverted Exponential Model under Progressive First-Failure Censoring Data" Mathematics 10, no. 10: 1648. https://doi.org/10.3390/math10101648
APA StyleFathi, A., Farghal, A.-W. A., & Soliman, A. A. (2022). Bayesian and Non-Bayesian Inference for Weibull Inverted Exponential Model under Progressive First-Failure Censoring Data. Mathematics, 10(10), 1648. https://doi.org/10.3390/math10101648







