Analytical Investigation of Fractional-Order Cahn–Hilliard and Gardner Equations Using Two Novel Techniques

Abstract

In this paper, we used the natural decomposition approach with non-singular kernel derivatives to find the solution to nonlinear fractional Gardner and Cahn–Hilliard equations arising in fluid flow. The fractional derivative is considered an Atangana–Baleanu derivative in Caputo manner (ABC) and Caputo–Fabrizio (CF) throughout this paper. We implement natural transform with the aid of the suggested derivatives to obtain the solution of nonlinear fractional Gardner and Cahn–Hilliard equations followed by inverse natural transform. To show the accuracy and validity of the proposed methods, we focused on two nonlinear problems and compared it with the exact and other method results. Additionally, the behavior of the results is demonstrated through tables and figures that are in strong agreement with the exact solutions.

1. Introduction

Fractional calculus (FC) is a subject that dates back to over 324 years, but it has recently attracted the interest of many scientists and engineers working in a variety of fields. Fractional calculus (FC) is the generic generalisation of integer-order calculus to arbitrary-order integration and differentiation with non-integer order. Signal processing, electronics, viscoelasticity, finance, chemistry, biology and dynamical systems are all examples of physical phenomena that can be modelled. Several researchers are working to significantly progress and contribute to fractional calculus [1,2,3,4,5]. There are different kinds of fractional derivatives such as Riemann–Liouville derivatives [6], Caputo derivatives [7], Kolwankar–Gangal (K-G) derivatives [8], Cressons derivatives [9], Jumaries modified Riemann–Liouville derivatives [10] and Chens fractal derivatives [11]. However, due to the uniqueness of kernels, the above concept has a significant flaw. A change in the kernel in the work of Atangana and Baleanu [12] appears to have addressed this issue. It is claimed that some physics problems involving initial values provide better results and have significant advantages over other fractional operators. One of the most essential features of the new definition is that it uses a non-singular and non-local kernel in its derivation [12]. Fractional differential equations have attracted special interest during the past two decades owing to their ability to model many phenomena in different research areas and engineering applications. Many physical applications in science and engineering can be represented using fractional differential equation models, which are extremely useful for a wide range of physical problems. Fractional linear and nonlinear PDEs are used to represent these equations, and solving fractional differential equations is essential [13,14,15,16,17,18,19,20,21]. Nonlinear equations are used to describe the world’s most important processes. Finding the exact solution to nonlinear partial differential equations is still a major problem in physics and applied mathematics, necessitating the use of various techniques to obtain at innovative approximate or exact solutions. Many approximation and numerical techniques have been used to solve fractional differential equations. Lately, many new approaches to fractional differential equations have been proposed; a few of these methods are as follows: the differential transform method (FDTM) [22], the iterative Laplace transform method (ILTM) [23], the fractional Adomian decomposition method (FADM) [24], the Elzaki transform decomposition method (ETDM) [25], the fractional variational iteration method (FVIM) [26], the fractional homotopy perturbation method (FHPM) [27] and the fractional natural decomposition method (FNDM) [28]. The main theme of the present article is to solve nonlinear fractional Gardner and Cahn–Hilliard equations with the help of one of the most effective approaches, named the natural decomposition method. Natural decomposition methods avoid round off errors by not requiring prescriptive assumptions, linearisation, discretisation, or perturbation.

The Gardner equation [29] was developed from a combination of KdV and modified KdV equations and is used to describe internal solitary waves in shallow water. Gardner’s equation is widely applied in physics, including plasma physics, fluid physics and quantum field theory [30,31]. In plasma and solid state [32], it also describes a diversity of wave phenomena. The fractional Gardner (FG) equation has the following form:

$$D_{\wp }^{\beta }\xi (\psi ,\wp )+6(\xi -{\mathrm{Y}}^2{\xi }^2)\frac{\partial \xi }{\partial \psi }+\frac{\partial {\xi }^3}{\partial {\psi }^3}=0,0<\beta \le 1,$$

(1)

where $\mathrm{Y}$ is a real constant. The wave function $\xi (\psi ,\wp )$ has the scaling variables space $\left(\psi \right)$ and time $(\wp )$, the terms $\xi \frac{\partial \xi }{\partial \psi }$ and ${\xi }^2\frac{\partial \xi }{\partial \psi }$ represent nonlinear wave steepening, and $\frac{\partial {\xi }^3}{\partial {\psi }^3}$ represents dispersive wave effects.

Cahn and Hilliard [33] introduced the Cahn–Hilliard equation in 1958 to describe the process of phase separation of a binary alloy under the critical temperature. This equation is important in a variety of remarkable scientific processes, including phase separation, phase-ordering dynamics and spinodal decomposition [34,35]. We consider the fractional Cahn–Hilliard (FCH) equation in this framework:

$$D_{\wp }^{\beta }\xi (\psi ,\wp )-\frac{\partial \xi }{\partial \psi }-6\xi \frac{\partial {\xi }^2}{\partial \psi }-(3{\xi }^2-1)\frac{{\partial }^2\xi }{\partial {\psi }^2}+\frac{{\partial }^4\xi }{\partial {\psi }^4}=0,0<\beta \le 1,$$

(2)

Different methodologies have been used to investigate the Gardner and Cahn–Hilliard equations, such as (ADM) [36], the modified Kudryashov technique [37], the reduced differential transform method [38], the residual power series method (RPSM) [39], (HPM) [40] and many others. In this article, we implement the natural decomposition method to find the solution of both equations.

The rest of the paper is organised as follows: some basic definitions of fractional derivatives have been given in Section 2. The idea of using NTDM to solve partial differential equations with fractional order and non-singular definitions is given in Section 3. In Section 4, we discuss the uniqueness and convergence of the results. In Section 5, a few new exact solutions for the nonlinear fractional Gardner and Cahn–Hilliard equations are extracted via NTDM to validate the approaches. Finally, a brief conclusion is provided in the last section.

2. Basic Preliminaries

Fractional integrals and derivatives have a variety of definitions and properties. In this section, we propose modifications to several basic fractional calculus definitions and preliminaries that are used in this research.

Definition 1.

A real function $j\left(x\right),x>0,$ is said to be in the space $C_{\mu },\mu \in \mathbb{R},$ if there exists a real number $q>\mu$ such that $j\left(x\right)=x^{q}g\left(x\right),$ where $g\in C[0,\infty ),$ and it is said to be in the space $C_{\mu }^m$ if $j^{\left(m\right)}\in C_{\mu },m\in \mathbb{N}.$

Definition 2.

For a function $j\in C_{\mu },\mu \ge -1$, the Riemann–Liouville integral for fractional-order is defined as [41]

$$\begin{array}{cc}\hfill I^{\beta }j\left(\vartheta \right)=& \frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_0^{\vartheta }{(\vartheta -\mu )}^{\beta -1}j\left(\mu \right)d\mu ,\beta >0,\vartheta >0.\hfill \\ \hfill and{I}^{0}j\left(\vartheta \right)=& j\left(\vartheta \right).\hfill \end{array}$$

(3)

Definition 3.

The fractional-order derivative for $j\left(\vartheta \right)$ in Caputo sense is defined as [41]

$$\begin{array}{c}\hfill D_{\vartheta }^{\beta }j\left(\vartheta \right)=I^{m-\beta }{D}^{m}j\left(\vartheta \right)=\frac{1}{m-\beta }{\int }_0^{\vartheta }{(\vartheta -\mu )}^{m-\beta -1}{j}^{\left(m\right)}\left(\mu \right)d\mu ,\end{array}$$

(4)

for $m-1<\beta \le m,m\in N,\vartheta >0,j\in C_{\mu }^m,\mu \ge -1$.

Definition 4.

The fractional-order derivative for $j\left(\vartheta \right)$ in Caputo–Fabrizio manner is defined as [41]

$$\begin{array}{c}\hfill D_{\vartheta }^{\beta }j\left(\vartheta \right)=\frac{F\left(\beta \right)}{1-\beta }{\int }_0^{\vartheta }exp\left(\frac{-\beta (\vartheta -\mu )}{1-\beta }\right)D\left(j\left(\mu \right)\right)d\mu ,\end{array}$$

(5)

where $0<\beta <1$ and $F\left(\beta \right)$ is a normalisation function with $F\left(0\right)=F\left(1\right)=1$.

Definition 5.

The fractional-order derivative for $j\left(\vartheta \right)$ in term of Atangana–Baleanu Caputo is given as [41]

$$\begin{array}{c}\hfill D_{\vartheta }^{\beta }j\left(\vartheta \right)=\frac{B\left(\beta \right)}{1-\beta }{\int }_0^{\vartheta }{E}_{\beta }\left(\frac{-\beta (\vartheta -\mu )}{1-\beta }\right)D\left(j\left(\mu \right)\right)d\mu ,\end{array}$$

(6)

where $0<\beta <1$, where $B\left(\beta \right)$ is a normalisation function and $E_{\beta }\left(z\right)={\sum }_{m=0}^{\infty }\frac{z^m}{\mathrm{\Gamma }(m\beta +1)}$ is the Mittag–Leffler function.

Definition 6.

The natural transform of the function $\xi (\wp )$ is defined by

$$\begin{array}{c}\hfill \mathcal{N}\left(\xi (\wp )\right)=\mathcal{U}(\omega ,\upsilon )={\int }_{-\infty }^{\infty }{e}^{-\omega \wp }\xi (\upsilon \wp )d\wp ,\omega ,\upsilon \in (-\infty ,\infty ).\end{array}$$

(7)

The natural transformation of $\xi (\wp )$ for $\wp \in (0,\infty )$ is defined as

$$\begin{array}{c}\hfill \mathcal{N}\left(\xi (\wp )H(\wp )\right)={\mathcal{N}}^{+}={\mathcal{U}}^{+}(\omega ,\upsilon )={\int }_0^{\infty }{e}^{-\omega \wp }\xi (\upsilon \wp )d\wp ,\omega ,\upsilon \in (0,\infty ).\end{array}$$

(8)

where $H(\wp )$ is the Heaviside function.

Definition 7.

The inverse natural transformation of the function $\xi (\omega ,\upsilon )$ can be written as

$$\begin{array}{c}\hfill {\mathcal{N}}^{-1}\left[\mathcal{U}(\omega ,\upsilon )\right]=\xi (\wp ),\forall \wp \ge 0\end{array}$$

(9)

Lemma 1.

If ${\mathcal{U}}_1(\omega ,\upsilon )$ and ${\mathcal{U}}_2(\omega ,\upsilon )$ are the natural transformation of ${\xi }_1(\wp )$ and ${\xi }_2(\wp )$, respectively, then

$$\begin{array}{c}\hfill \mathcal{N}[c_1{\xi }_1(\wp )+c_2{\xi }_2(\wp )]=c_1\mathcal{N}\left[{\xi }_1(\wp )\right]+c_2\mathcal{N}\left[{\xi }_2(\wp )\right]=c_1{\mathcal{U}}_1(\omega ,\upsilon )+c_2{\mathcal{U}}_2(\omega ,\upsilon ),\end{array}$$

(10)

where $c_1$ and $c_2$ are constants.

Lemma 2.

If the natural inverse transformation of ${\xi }_1(\omega ,\upsilon )$ and ${\xi }_2(\omega ,\upsilon )$ are ${\xi }_1(\wp )$ and ${\xi }_2(\wp )$, respectively, then

$$\{N^{-1}[c_1{\mathcal{U}}_1(\omega ,\upsilon )+c_2{\mathcal{U}}_2(\omega ,\upsilon )]=c_1{\mathcal{N}}^{-1}\left[{\mathcal{U}}_1(\omega ,\upsilon )\right]+c_2{\mathcal{N}}^{-1}\left[{\mathcal{U}}_2(\omega ,\upsilon )\right]=c_1{\xi }_1(\wp )+c_2{\xi }_2(\wp ),$$

(11)

where $c_1$ and $c_2$ are constants.

Definition 8.

The natural transformation of $D_{\wp }^{\beta }\xi (\wp )$ in Caputo manner is given as [41]

$$\mathcal{N}\left[D_{\wp }^{\beta }\xi (\wp )\right]={\left(\frac{\omega }{\upsilon }\right)}^{\beta }\left(\mathcal{N}\left[\xi (\wp )\right]-\left(\frac{1}{\omega }\right)\xi \left(0\right)\right)$$

(12)

Definition 9.

The natural transformation of $D_{\wp }^{\beta }\xi (\wp )$ in Caputo–Fabrizio manner is given as [41]

$$\mathcal{N}\left[D_{\wp }^{\beta }\xi (\wp )\right]=\frac{1}{1-\beta +\beta \left(\frac{\upsilon }{\omega }\right)}\left(\mathcal{N}\left[\xi (\wp )\right]-\left(\frac{1}{\omega }\right)\xi \left(0\right)\right)$$

(13)

Definition 10.

The natural transformation of $D_{\wp }^{\beta }\xi (\wp )$ in Atangana–Baleanu Caputo manner is given as [41]

$$\begin{array}{c}\hfill \mathcal{N}\left[D_{\wp }^{\beta }\xi (\wp )\right]=\frac{M\left[\beta \right]}{1-\beta +\beta {\left(\frac{\upsilon }{\omega }\right)}^{\beta }}\left(\mathcal{N}\left[\xi (\wp )\right]-\left(\frac{1}{\omega }\right)\xi \left(0\right)\right)\end{array}$$

(14)

Here, $M\left[\beta \right]$ is a normalisation function.

3. Methodology

In this section, we presented the general methodology of natural transformation for solving the equation given below [42,43]

$$\begin{array}{c}\hfill D_{\wp }^{\beta }\xi (\psi ,\wp )=\mathcal{L}\left(\xi (\psi ,\wp )\right)+N\left(\xi (\psi ,\wp )\right)+h(\psi ,\wp )=M(\psi ,\wp ),\end{array}$$

(15)

having initial condition

$$\begin{array}{c}\hfill \xi (\psi ,0)=\varphi \left(\psi \right),\end{array}$$

(16)

with linear term $\mathcal{L}$, nonlinear term N and the source term $h(\psi ,\wp )$.

3.1. Case I $\left(NTD{M}_{CF}\right):$

With the help of natural transform and Caputo–Fabrizio fractional derivative, Equation (15) can be written as

$$\begin{array}{c}\hfill \frac{1}{p(\beta ,\upsilon ,\omega )}\left(\mathcal{N}\left[\xi (\psi ,\wp )\right]-\frac{\varphi \left(\psi \right)}{\omega }\right)=\mathcal{N}\left[M(\psi ,\wp )\right],\end{array}$$

(17)

with

$$\begin{array}{c}\hfill p(\beta ,\upsilon ,\omega )=1-\beta +\beta \left(\frac{\upsilon }{\omega }\right).\end{array}$$

(18)

By taking the inverse natural transformation, Equation (17) can be written as

$$\begin{array}{c}\hfill \xi (\psi ,\wp )={\mathcal{N}}^{-1}\left(\frac{\varphi \left(\psi \right)}{\omega }+p(\beta ,\upsilon ,\omega )\mathcal{N}\left[M(\psi ,\wp )\right]\right).\end{array}$$

(19)

Applying the Adomain decomposition, we have the solution in the infinite series form for $\xi (\psi ,\wp )$ given as

$$\begin{array}{c}\hfill \xi (\psi ,\wp )=\sum _{i=0}^{\infty }{\xi }_i(\psi ,\wp ),\end{array}$$

(20)

and $N\left(\xi \right(\psi ,\wp \left)\right)$ can be decomposed into

$$\begin{array}{c}\hfill N\left(\xi (\psi ,\wp )\right)=\sum _{i=0}^{\infty }{A}_i({\xi }_0,\cdots ,{\xi }_i),\end{array}$$

(21)

where $A_i$ are called the Adomian polynomials. They can be computed according to a simple rule:

$${\displaystyle A_n=\frac{1}{n!}\frac{d^n}{d{\epsilon }^n}N(t,{\sum }_{k=0}^n{\epsilon }^k{\xi }_k){|}_{\epsilon =0}}$$

Substituting Equations (20) and (21) into (19), we have

$$\begin{array}{cc}\hfill \sum _{i=0}^{\infty }{\xi }_i(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(\frac{\varphi \left(\psi \right)}{\omega }+p(\beta ,\upsilon ,\omega )\mathcal{N}\left[h(\psi ,\wp )\right]\right)\hfill \\ \hfill & +{\mathcal{N}}^{-1}\left(p(\beta ,\upsilon ,\omega )\mathcal{N}\left[\sum _{i=0}^{\infty }\mathcal{L}\left({\xi }_i(\psi ,\wp )\right)+A_{\wp }\right]\right)\hfill \end{array}$$

(22)

From (22), we have,

$$\begin{array}{cc}\hfill {\xi }_0^{CF}(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(\frac{\varphi \left(\psi \right)}{\omega }+p(\beta ,\upsilon ,\omega )\mathcal{N}\left[h(\psi ,\wp )\right]\right),\hfill \\ \hfill {\xi }_1^{CF}(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(p(\beta ,\upsilon ,\omega )\mathcal{N}\left[\mathcal{L}\left({\xi }_0(\psi ,\wp )\right)+A_0\right]\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\xi }_{l+1}^{CF}(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(p(\beta ,\upsilon ,\omega )\mathcal{N}\left[\mathcal{L}\left({\xi }_l(\psi ,\wp )\right)+A_l\right]\right),l=1,2,3,\cdots \hfill \end{array}$$

(23)

Finally, using $NTD{M}_{CF},$ we obtain the solution of (15) by substituting (23) into (20).

$$\begin{array}{c}\hfill {\xi }^{CF}(\psi ,\wp )={\xi }_0^{CF}(\psi ,\wp )+{\xi }_1^{CF}(\psi ,\wp )+{\xi }_2^{CF}(\psi ,\wp )+\cdots .\end{array}$$

(24)

3.2. Case II $\left(NTD{M}_{ABC}\right):$

With the help of natural transform and the Atangana–Baleanu fractional derivative, Equation (15) can be written as

$$\begin{array}{c}\hfill \frac{1}{q(\beta ,\upsilon ,\omega )}\left(\mathcal{N}\left[\xi (\psi ,\wp )\right]-\frac{\varphi \left(\psi \right)}{\omega }\right)=\mathcal{N}\left[M(\psi ,\wp )\right],\end{array}$$

(25)

with

$$\begin{array}{c}\hfill q(\beta ,\upsilon ,\omega )=\frac{1-\beta +\beta {\left(\frac{\upsilon }{\omega }\right)}^{\beta }}{B\left(\beta \right)}.\end{array}$$

(26)

Using the inverse natural transformation, Equation (25) can be written as

$$\begin{array}{c}\hfill \xi (\psi ,\wp )={\mathcal{N}}^{-1}\left(\frac{\varphi \left(\psi \right)}{\omega }+q(\beta ,\upsilon ,\omega )\mathcal{N}\left[M(\psi ,\wp )\right]\right).\end{array}$$

(27)

Adopting the Adomain decomposition as in the last case, we have

$$\begin{array}{cc}\hfill \sum _{i=0}^{\infty }{\xi }_i(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(\frac{\varphi \left(\psi \right)}{\omega }+q(\beta ,\upsilon ,\omega )\mathcal{N}\left[h(\psi ,\wp )\right]\right)\hfill \\ \hfill & +{\mathcal{N}}^{-1}\left(q(\beta ,\upsilon ,\omega )\mathcal{N}\left[\sum _{i=0}^{\infty }\mathcal{L}\left({\xi }_i(\psi ,\wp )\right)+A_{\wp }\right]\right)\hfill \end{array}$$

(28)

From (22), we have

$$\begin{array}{cc}\hfill {\xi }_0^{ABC}(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(\frac{\varphi \left(\psi \right)}{\omega }+q(\beta ,\upsilon ,\omega )\mathcal{N}\left[h(\psi ,\wp )\right]\right),\hfill \\ \hfill {\xi }_1^{ABC}(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(q(\beta ,\upsilon ,\omega )\mathcal{N}\left[\mathcal{L}\left({\xi }_0(\psi ,\wp )\right)+A_0\right]\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\xi }_{l+1}^{ABC}(\psi ,\wp )=& {\mathcal{N}}^{-1}\left(q(\beta ,\upsilon ,\omega )\mathcal{N}\left[\mathcal{L}\left({\xi }_l(\psi ,\wp )\right)+A_l\right]\right),l=1,2,3,\cdots .\hfill \end{array}$$

(29)

Finally, using $NTD{M}_{ABC}$, we obtain the solution of (15) as in the last case,

$$\begin{array}{c}\hfill {\xi }^{ABC}(\psi ,\wp )={\xi }_0^{ABC}(\psi ,\wp )+{\xi }_1^{ABC}(\psi ,\wp )+{\xi }_2^{ABC}(\psi ,\wp )+\cdots .\end{array}$$

(30)

4. Convergence Analysis

Here, we discuss the uniqueness and convergence of $NTD{M}_{CF}$ and $NTD{M}_{ABC}$.

Theorem 1.

Suppose that $|\mathcal{L}\left(\xi \right)-\mathcal{L}\left({\xi }^{*}\right)|<{\gamma }_1|\xi -{\xi }^{*}|$ and $|N\left(\xi \right)-N\left({\xi }^{*}\right)|<{\gamma }_2|\xi -{\xi }^{*}|$, where $\xi :=\xi (\mu ,\wp )$ and ${\xi }^{*}:={\xi }^{*}(\mu ,\wp )$ are two different function values and ${\gamma }_1$,${\gamma }_2$ are Lipschitz constants.

$\mathcal{L}$ and N are the operators defined in (15). Then, the problem (15) has a unique solution for $NTD{M}_{CF}$ when $0<({\gamma }_1+{\gamma }_2)(1-\beta +\beta \wp )<1$ for all $\wp .$

Proof. 

Let $H=\left(C\right[J],||.|\left|\right)$ with the norm $\left|\right|\varphi (\wp )\left|\right|={max}_{\wp \in J}\left|\varphi (\wp )\right|$ be the Banach space of continuous function on the interval $J=[0,T].$ Let $I:H\to H$ be a nonlinear mapping, where

$${\xi }_{l+1}^C={\xi }_0^C+{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}[\mathcal{L}\left({\xi }_l(\mu ,\wp )\right)+N\left({\xi }_l(\mu ,\wp )\right)]\right],l\ge 0.$$

$$\begin{array}{cc}\hfill \left|\right|I\left(\xi \right)-I\left({\xi }^{*}\right)\left|\right|& \le ma{x}_{\wp \in J}|{\mathcal{N}}^{-1}[p(\beta ,\upsilon ,\omega )\mathcal{N}[\mathcal{L}\left(\xi \right)-\mathcal{L}\left({\xi }^{*}\right)]\hfill \\ \hfill & +p(\beta ,\upsilon ,\omega )\mathcal{N}[N\left(\xi \right)-N\left({\xi }^{*}\right)]\left|\right]\hfill \\ \hfill & \le ma{x}_{\wp \in J}[{\gamma }_1{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\right[|\xi -{\xi }^{*}\left|\right]]\hfill \\ \hfill & +{\gamma }_2{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\right[|\xi -{\xi }^{*}\left|\right]\left]\right]\hfill \\ \hfill & \le ma{x}_{\wp \in J}({\gamma }_1+{\gamma }_2)\left[{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\right|\xi -{\xi }^{*}\left|\right]\right]\hfill \\ \hfill & \le ({\gamma }_1+{\gamma }_2)\left[{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\right||\xi -{\xi }^{*}\left|\right|]\right]\hfill \\ \hfill & =({\gamma }_1+{\gamma }_2)(1-\beta +\beta \wp )\left|\right|\xi -{\xi }^{*}\left|\right|.\hfill \end{array}$$

(31)

Therefore, I is a contraction as $0<({\gamma }_1+{\gamma }_2)(1-\beta +\beta \wp )<1$. From the Banach fixed point theorem, the result of (15) is unique. □

Theorem 2.

Under the same hypothesis as in the last theorem, the problem in (15) has a unique solution for $NTD{M}_{ABC}$ when $0<({\gamma }_1+{\gamma }_2)(1-\beta +\beta \frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)})<1$ for all $\wp .$

Proof. 

As in the last theorem, let $H=\left(C\right[J],||.|\left|\right)$ be the Banach space of a continuous function on the interval $J.$ Let $I:H\to H$ be a nonlinear mapping, where

$${\xi }_{l+1}^C={\xi }_0^C+{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}[\mathcal{L}\left({\xi }_l(\mu ,\wp )\right)+N\left({\xi }_l(\mu ,\wp )\right)]\right],l\ge 0.$$

$$\begin{array}{cc}\hfill \left|\right|I\left(\xi \right)-I\left({\xi }^{*}\right)\left|\right|& \le ma{x}_{\wp \in J}|{\mathcal{N}}^{-1}[q(\beta ,\upsilon ,\omega )\mathcal{N}[\mathcal{L}\left(\xi \right)-\mathcal{L}\left({\xi }^{*}\right)]\hfill \\ \hfill & +q(\beta ,\upsilon ,\omega )\mathcal{N}[N\left(\xi \right)-N\left({\xi }^{*}\right)]\left|\right]\hfill \\ \hfill & \le ma{x}_{\wp \in J}[{\gamma }_1{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\right[|\xi -{\xi }^{*}\left|\right]]\hfill \\ \hfill & +{\gamma }_2{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\right[|\xi -{\xi }^{*}\left|\right]\left]\right]\hfill \\ \hfill & \le ma{x}_{\wp \in J}({\gamma }_1+{\gamma }_2)\left[{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\right|\xi -{\xi }^{*}\left|\right]\right]\hfill \\ \hfill & \le ({\gamma }_1+{\gamma }_2)\left[{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\right||\xi -{\xi }^{*}\left|\right|]\right]\hfill \\ \hfill & =({\gamma }_1+{\gamma }_2)(1-\beta +\beta \frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)})\left|\right|\xi -{\xi }^{*}\left|\right|.\hfill \end{array}$$

(32)

Therefore, I is a contraction as $0<({\gamma }_1+{\gamma }_2)(1-\beta +\beta \frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)})<1$. From the Banach fixed point theorem, the result of (15) is unique. □

Theorem 3.

Suppose that $\mathcal{L}$ and N are Lipschitz functions as in the last theorems; then, the $NTD{M}_{CF}$ result of (15) is convergent.

Proof. 

Let H be the Banach space defined before, and let ${\xi }_m={\sum }_{r=0}^m{\xi }_r(\mu ,\wp )$. To show that ${\xi }_m$ is a Cauchy sequence in H. Let

$$\begin{array}{cc}\hfill \left|\right|{\xi }_m-{\xi }_n\left|\right|& =ma{x}_{\wp \in J}\left|\sum _{r=n+1}^m{\xi }_r\right|,n=1,2,3,\cdots \hfill \\ \hfill & \le ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\left[\sum _{r=n+1}^m(\mathcal{L}\left({\xi }_{r-1}\right)+N\left({\xi }_{r-1}\right))\right]\right]\right|\hfill \\ \hfill & =ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\left[\sum _{r=n+1}^{m-1}(\mathcal{L}\left({\xi }_r\right)+N\left({\xi }_r\right))\right]\right]\right|\hfill \\ \hfill & \le ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\left[(\mathcal{L}\left({\xi }_{m-1}\right)-\mathcal{L}\left({\xi }_{n-1}\right)+N\left({\xi }_{m-1}\right)-N\left({\xi }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & \le {\gamma }_{1}ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\left[(\mathcal{L}\left({\xi }_{m-1}\right)-\mathcal{L}\left({\xi }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & +{\gamma }_{2}ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\left[(N\left({\xi }_{m-1}\right)-N\left({\xi }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & =({\gamma }_1+{\gamma }_2)(1-\beta +\beta \wp )\left|\right|{\xi }_{m-1}-{\xi }_{n-1}\left|\right|\hfill \end{array}$$

(33)

Let $m=n+1$, then

$$\begin{array}{c}\hfill \left|\right|{\xi }_{n+1}-{\xi }_n\left|\right|\le \gamma \left|\right|{\xi }_n-{\xi }_{n-1}\left|\right|\le {\gamma }^2\left|\right|{\xi }_{n-1}{\xi }_{n-2}\left|\right|\le \cdots \le {\gamma }^n\left|\right|{\xi }_1-{\xi }_0\left|\right|,\end{array}$$

(34)

where $\gamma =({\gamma }_1+{\gamma }_2)(1-\beta +\beta \wp )$. Similarly, we have

$$\begin{array}{cc}\hfill \left|\right|{\xi }_m-{\xi }_n\left|\right|& \le \left|\right|{\xi }_{n+1}-{\xi }_n\left|\right|+\left|\right|{\xi }_{n+2}{\xi }_{n+1}\left|\right|+\cdots +\left|\right|{\xi }_m-{\xi }_{m-1}\left|\right|,\hfill \\ \hfill & ({\gamma }^n+{\gamma }^{n+1}+\cdots +{\gamma }^{m-1})\left|\right|{\xi }_1-{\xi }_0\left|\right|\hfill \\ \hfill & \le {\gamma }^n\left(\frac{1-{\gamma }^{m-n}}{1-\gamma }\right)\left|\right|{\xi }_1\left|\right|,\hfill \end{array}$$

(35)

As $0<\gamma <1$, we have $1-{\gamma }^{m-n}<1$. Therefore,

$$\begin{array}{c}\hfill \left|\right|{\xi }_m-{\xi }_n\left|\right|\le \frac{{\gamma }^n}{1-\gamma }ma{x}_{\wp \in J}\left|\right|{\xi }_1\left|\right|.\end{array}$$

(36)

Since $\left|\right|{\xi }_1\left|\right|<\infty ,\left|\right|{\xi }_m-{\xi }_n\left|\right|\to 0$ when $n\to \infty$. As a result, ${\xi }_m$ is a Cauchy sequence in H, implying that the series ${\xi }_m$ is convergent. □

Theorem 4.

Suppose that $\mathcal{L}$ and N are Lipschitz functions as in the last theorems; then, the $NTD{M}_{ABC}$ result of (15) is convergent.

Proof. 

Let ${\xi }_m={\sum }_{r=0}^m{\xi }_r(\mu ,\wp )$. To show that ${\xi }_m$ is a Cauchy sequence in H. Let

$$\begin{array}{cc}\hfill \left|\right|{\xi }_m-{\xi }_n\left|\right|& =ma{x}_{\wp \in J}\left|\sum _{r=n+1}^m{\xi }_r\right|,n=1,2,3,\cdots \hfill \\ \hfill & \le ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\left[\sum _{r=n+1}^m(\mathcal{L}\left({\xi }_{r-1}\right)+N\left({\xi }_{r-1}\right))\right]\right]\right|\hfill \\ \hfill & =ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\left[\sum _{r=n+1}^{m-1}(\mathcal{L}\left({\xi }_r\right)+N\left(u_r\right))\right]\right]\right|\hfill \\ \hfill & \le ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\left[(\mathcal{L}\left({\xi }_{m-1}\right)-\mathcal{L}\left({\xi }_{n-1}\right)+N\left({\xi }_{m-1}\right)-N\left({\xi }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & \le {\gamma }_{1}ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[q(\beta ,\upsilon ,\omega )\mathcal{N}\left[(\mathcal{L}\left({\xi }_{m-1}\right)-\mathcal{L}\left({\xi }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & +{\gamma }_{2}ma{x}_{\wp \in J}\left|{\mathcal{N}}^{-1}\left[p(\beta ,\upsilon ,\omega )\mathcal{N}\left[(N\left({\xi }_{m-1}\right)-N\left({\xi }_{n-1}\right))\right]\right]\right|\hfill \\ \hfill & =({\gamma }_1+{\gamma }_2)(1-\beta +\beta \frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)})\left|\right|{\xi }_{m-1}-{\xi }_{n-1}\left|\right|\hfill \end{array}$$

(37)

Let $m=n+1$; then,

$$\begin{array}{c}\hfill \left|\right|{\xi }_{n+1}-{\xi }_n\left|\right|\le \gamma \left|\right|{\xi }_n-{\xi }_{n-1}\left|\right|\le {\gamma }^2\left|\right|{\xi }_{n-1}-{\xi }_{n-2}\left|\right|\le \cdots \le {\gamma }^n\left|\right|{\xi }_1-{\xi }_0\left|\right|,\end{array}$$

(38)

where $\gamma =({\gamma }_1+{\gamma }_2)(1-\beta +\beta \frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)})$. Similarly, we have

$$\begin{array}{cc}\hfill \left|\right|{\xi }_m-{\xi }_n\left|\right|& \le \left|\right|{\xi }_{n+1}-{\xi }_n\left|\right|+\left|\right|{\xi }_{n+2}-{\xi }_{n+1}\left|\right|+\cdots +\left|\right|{\xi }_m-{\xi }_{m-1}\left|\right|,\hfill \\ \hfill & \le ({\gamma }^n+{\gamma }^{n+1}+\cdots +{\gamma }^{m-1})\left|\right|{\xi }_1-{\xi }_0\left|\right|\hfill \\ \hfill & \le {\gamma }^n\left(\frac{1-{\gamma }^{m-n}}{1-\gamma }\right)\left|\right|{\xi }_1\left|\right|,\hfill \end{array}$$

(39)

As $0<\gamma <1$, we have $1-{\gamma }^{m-n}<1$. Therefore,

$$\begin{array}{c}\hfill \left|\right|{\xi }_m-{\xi }_n\left|\right|\le \frac{{\gamma }^n}{1-\gamma }ma{x}_{\wp \in J}\left|\right|{\xi }_1\left|\right|.\end{array}$$

(40)

Since $\left|\right|{\xi }_1\left|\right|<\infty ,\left|\right|{\xi }_m-{\xi }_n\left|\right|\to 0$ when $n\to \infty$. As a result, ${\xi }_m$ is a Cauchy sequence in H, implying that the series ${\xi }_m$ is convergent. □

5. Numerical Examples

In this section, we investigate the analytical solution of nonlinear fractional-order Gardner and Cahn–Hilliard equations.

Example 1.

Consider the FG equation

$$D_{\wp }^{\beta }\xi (\psi ,\wp )+6(\xi -{\mathrm{Y}}^2{\xi }^2)\frac{\partial \xi }{\partial \psi }+\frac{\partial {\xi }^3}{\partial {\psi }^3}=00<\beta \le 1,$$

(41)

with the initial source

$$\xi (\psi ,0)=\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right),$$

(42)

With the help of natural transform, Equation (41) can be written as

$$\mathcal{N}\left[D_{\wp }^{\beta }\xi (\psi ,\wp )\right]=-\mathcal{N}\left\{6\left(\xi \frac{\partial \xi }{\partial \psi }-{\mathrm{Y}}^2{\xi }^2\frac{\partial \xi }{\partial \psi }\right)\right\}-\mathcal{N}\left\{\frac{\partial {\xi }^3}{\partial {\psi }^3}\right\},$$

(43)

Define the nonlinear operator as

$$\frac{1}{{\omega }^{\beta }}\mathcal{N}\left[\xi (\psi ,\wp )\right]-{\omega }^{2-\beta }\xi (\psi ,0)=\mathcal{N}\left[-6\left(\xi \frac{\partial \xi }{\partial \psi }-{\mathrm{Y}}^2{\xi }^2\frac{\partial \xi }{\partial \psi }\right)-\frac{\partial {\xi }^3}{\partial {\psi }^3}\right],$$

(44)

Upon simplifying, we have

$$\mathcal{N}\left[\xi (\psi ,\wp )\right]={\omega }^2\left[\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right)\right]+\frac{\beta (\omega -\beta (\omega -\beta \left)\right)}{{\omega }^2}\mathcal{N}\left[-6\left(\xi \frac{\partial \xi }{\partial \psi }-{\mathrm{Y}}^2{\xi }^2\frac{\partial \xi }{\partial \psi }\right)-\frac{\partial {\xi }^3}{\partial {\psi }^3}\right],$$

(45)

By the inverse $NT$, Equation (45) can be written as

$$\begin{array}{cc}\hfill & \xi (\psi ,\wp )=\left[\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right)\right]\hfill \\ \hfill & +{\mathcal{N}}^{-1}\left[\frac{\beta (\omega -\beta (\omega -\beta \left)\right)}{{\omega }^2}\mathcal{N}\left\{-6\left(\xi \frac{\partial \xi }{\partial \psi }-{\mathrm{Y}}^2{\xi }^2\frac{\partial \xi }{\partial \psi }\right)-\frac{\partial {\xi }^3}{\partial {\psi }^3}\right\}\right],\hfill \end{array}$$

(46)

Now, we implement $ND{M}_{CF}$

The series form solution for the unknown function $\xi (\psi ,\wp )$ is written as

$$\xi (\psi ,\wp )=\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp ).$$

(47)

The nonlinear terms with the help of Adomian polynomials are represented by $\xi {\xi }_{\psi }={\sum }_{l=0}^{\infty }{\mathcal{A}}_l$ and ${\xi }^2{\xi }_{\psi }={\sum }_{l=0}^{\infty }{\mathcal{B}}_l$; thus, with the help of these terms, Equation (46) can be rewritten as

$$\begin{array}{cc}\hfill & \sum _{l=0}^{\infty }{\xi }_{l+1}(\psi ,\wp )=\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right)\hfill \\ \hfill & +{\mathcal{N}}^{-1}\left[\frac{\beta (\omega -\beta (\omega -\beta \left)\right)}{{\omega }^2}\mathcal{N}\left\{-6\sum _{l=0}^{\infty }{\mathcal{A}}_l+6{\mathrm{Y}}^2\sum _{l=0}^{\infty }{\mathcal{B}}_l-\sum _{l=0}^{\infty }{\xi }_{l\psi \psi \psi }\right\}\right].\hfill \end{array}$$

(48)

Thus, upon comparing both sides of Equation (48), we have

$${\xi }_0(\psi ,\wp )=\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right),$$

$${\xi }_1(\psi ,\wp )=\frac{{sech}^2\left(\frac{\psi }{2}\right)(-1+(-4+3{\mathrm{Y}}^2)cosh\left(\psi \right)+3(-1+{\mathrm{Y}}^2)sinh\left(\psi \right))}{8}\left(\beta (\wp -1)+1\right),$$

(49)

$$\begin{array}{cc}\hfill & {\xi }_2(\psi ,\wp )=\frac{-{sech}^7\left(\frac{\psi }{2}\right)}{64}(-24(-1+{\mathrm{Y}}^2)cosh\left(\frac{\psi }{2}\right)-6(22-37{\mathrm{Y}}^2+15{\mathrm{Y}}^4)cosh\left(\frac{3\psi }{2}\right)\hfill \\ \hfill & +6(4-7{\mathrm{Y}}^2+3{\mathrm{Y}}^4)cosh\left(\frac{5\psi }{2}\right)+2(103-102{\mathrm{Y}}^2)sinh\left(\frac{\psi }{2}\right)-3(43-74{\mathrm{Y}}^2+30{\mathrm{Y}}^4)\hfill \\ \hfill & sinh\left(\frac{3\psi }{2}\right)+(25-42{\mathrm{Y}}^2+18{\mathrm{Y}}^4)sinh\left(\frac{5\psi }{2}\right))\left({(1-\beta )}^2+2\beta (1-\beta )\wp +\frac{{\beta }^2{\wp }^2}{2}\right),\hfill \end{array}$$

(50)

Continuing the same process, we can easily find the remaining components of ${\xi }_l$ for $(l\ge 3)$. Subsequently, we define the series form solutions as

$$\begin{array}{cc}\hfill \xi (\psi ,\wp )& =\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp )={\xi }_0(\psi ,\wp )+{\xi }_1(\psi ,\wp )+{\xi }_2(\psi ,\wp )+\cdots ,\hfill \\ \hfill \xi (\psi ,\wp )& =\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right)+\frac{{sech}^2\left(\frac{\psi }{2}\right)(-1+(-4+3{\mathrm{Y}}^2)cosh\left(\psi \right)+3(-1+{\mathrm{Y}}^2)sinh\left(\psi \right))}{8}\hfill \\ \hfill & \left(\beta (\wp -1)+1\right)+\frac{-{sech}^7\left(\frac{\psi }{2}\right)}{64}(-24(-1+{\mathrm{Y}}^2)cosh\left(\frac{\psi }{2}\right)-6(22-37{\mathrm{Y}}^2+15{\mathrm{Y}}^4)\hfill \\ \hfill & cosh\left(\frac{3\psi }{2}\right)+6(4-7{\mathrm{Y}}^2+3{\mathrm{Y}}^4)cosh\left(\frac{5\psi }{2}\right)+2(103-102{\mathrm{Y}}^2)sinh\left(\frac{\psi }{2}\right)-3(43-74{\mathrm{Y}}^2+\hfill \\ \hfill & 30{\mathrm{Y}}^4)sinh\left(\frac{3\psi }{2}\right)+(25-42{\mathrm{Y}}^2+18{\mathrm{Y}}^4)sinh\left(\frac{5\psi }{2}\right))\left({(1-\beta )}^2+2\beta (1-\beta )\wp +\frac{{\beta }^2{\wp }^2}{2}\right)+\cdots .\hfill \end{array}$$

(51)

Now, we implement $ND{M}_{ABC}$

The series form solution for the unknown function $\xi (\psi ,\wp )$ is written as

$$\xi (\psi ,\wp )=\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp ).$$

(52)

The nonlinear terms with the help of Adomian polynomials are represented by $\xi {\xi }_{\psi }={\sum }_{l=0}^{\infty }{\mathcal{A}}_l$ and ${\xi }^2{\xi }_{\psi }={\sum }_{l=0}^{\infty }{\mathcal{B}}_l$; thus, with the help of these terms Equation (46) can be rewritten as

$$\begin{array}{cc}\hfill \sum _{l=0}^{\infty }{\xi }_{l+1}(\psi ,\wp )& =\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right)\hfill \\ \hfill & +{\mathcal{N}}^{-1}\left[\frac{{\upsilon }^{\beta }({\omega }^{\beta }+\beta ({\upsilon }^{\beta }-{\omega }^{\beta }))}{{\omega }^{2\beta }}\mathcal{N}\left\{-6\sum _{l=0}^{\infty }{\mathcal{A}}_l+6{\mathrm{Y}}^2\sum _{l=0}^{\infty }{\mathcal{B}}_l-\sum _{l=0}^{\infty }{\xi }_{l\psi \psi \psi }\right\}\right].\hfill \end{array}$$

(53)

Thus, upon comparing both sides of Equation (53), we have

$${\xi }_0(\psi ,\wp )=\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right),$$

$${\xi }_1(\psi ,\wp )=\frac{{sech}^2\left(\frac{\psi }{2}\right)(-1+(-4+3{\mathrm{Y}}^2)cosh\left(\psi \right)+3(-1+{\mathrm{Y}}^2)sinh\left(\psi \right))}{8}\left(1-\beta +\frac{\beta {\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}\right),$$

(54)

$$\begin{array}{cc}\hfill & {\xi }_2(\psi ,\wp )=\frac{-{sech}^7\left(\frac{\psi }{2}\right)}{64}(-24(-1+{\mathrm{Y}}^2)cosh\left(\frac{\psi }{2}\right)-6(22-37{\mathrm{Y}}^2+15{\mathrm{Y}}^4)cosh\left(\frac{3\psi }{2}\right)\hfill \\ \hfill & +6(4-7{\mathrm{Y}}^2+3{\mathrm{Y}}^4)cosh\left(\frac{5\psi }{2}\right)+2(103-102{\mathrm{Y}}^2)sinh\left(\frac{\psi }{2}\right)-3(43-74{\mathrm{Y}}^2+30{\mathrm{Y}}^4)\hfill \\ \hfill & sinh\left(\frac{3\psi }{2}\right)+(25-42{\mathrm{Y}}^2+18{\mathrm{Y}}^4)sinh\left(\frac{5\psi }{2}\right))\left[\frac{{\beta }^2{\wp }^{2\beta }}{\mathrm{\Gamma }(2\beta +1)}+2\beta (1-\beta )\frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}+{(1-\beta )}^2\right],\hfill \end{array}$$

(55)

Continuing the same process, we can easily find the remaining components of ${\xi }_l$ for $(l\ge 3)$. Subsequently, we define the series form solutions as

$$\begin{array}{cc}\hfill \xi (\psi ,\wp )& =\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp )={\xi }_0(\psi ,\wp )+{\xi }_1(\psi ,\wp )+{\xi }_2(\psi ,\wp )+\cdots ,\hfill \\ \hfill \xi (\psi ,\wp )& =\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi }{2}\right)+\frac{{sech}^2\left(\frac{\psi }{2}\right)(-1+(-4+3{\mathrm{Y}}^2)cosh\left(\psi \right)+3(-1+{\mathrm{Y}}^2)sinh\left(\psi \right))}{8}\hfill \\ \hfill & \left(1-\beta +\frac{\beta {\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}\right)+\frac{-{sech}^7\left(\frac{\psi }{2}\right)}{64}(-24(-1+{\mathrm{Y}}^2)cosh\left(\frac{\psi }{2}\right)-6(22-37{\mathrm{Y}}^2+15{\mathrm{Y}}^4)\hfill \\ \hfill & cosh\left(\frac{3\psi }{2}\right)+6(4-7{\mathrm{Y}}^2+3{\mathrm{Y}}^4)cosh\left(\frac{5\psi }{2}\right)+2(103-102{\mathrm{Y}}^2)sinh\left(\frac{\psi }{2}\right)-3(43-74{\mathrm{Y}}^2+\hfill \\ \hfill & 30{\mathrm{Y}}^4)sinh\left(\frac{3\psi }{2}\right)+(25-42{\mathrm{Y}}^2+18{\mathrm{Y}}^4)sinh\left(\frac{5\psi }{2}\right)\left)\right[\frac{{\beta }^2{\wp }^{2\beta }}{\mathrm{\Gamma }(2\beta +1)}+2\beta (1-\beta )\frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}+\hfill \\ \hfill & {(1-\beta )}^2]+\cdots \hfill \end{array}$$

(56)

If we set $\beta =1$, we have the exact solution as

$$\xi (\psi ,\wp )=\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\psi -\wp }{2}\right),$$

(57)

Example 2.

Consider the FCH equation

$$D_{\wp }^{\beta }\xi (\psi ,\wp )-\frac{\partial \xi }{\partial \psi }-6\xi \frac{\partial {\xi }^2}{\partial \psi }-(3{\xi }^2-1)\frac{{\partial }^2\xi }{\partial {\psi }^2}+\frac{{\partial }^4\xi }{\partial {\psi }^4}=0,0<\beta \le 1,$$

(58)

with initial source

$$\xi (\psi ,0)=tanh\left(\frac{\psi }{\sqrt{2}}\right),$$

(59)

With the help of natural transform, Equation (58) can be written as

$$\mathcal{N}\left[D_{\wp }^{\beta }\xi (\psi ,\wp )\right]=\mathcal{N}\left[\frac{\partial \xi }{\partial \psi }\right]+6\mathcal{N}\left[\xi \frac{\partial {\xi }^2}{\partial \psi }\right]+3\mathcal{N}\left[{\xi }^2\frac{{\partial }^2\xi }{\partial {\psi }^2}\right]-3\mathcal{N}\left[\frac{{\partial }^2\xi }{\partial {\psi }^2}\right]-\mathcal{N}\left[\frac{{\partial }^4\xi }{\partial {\psi }^4}\right],$$

(60)

Define the nonlinear operator as

$$\frac{1}{{\omega }^{\beta }}\mathcal{N}\left[\xi (\psi ,\wp )\right]-{\omega }^{2-\beta }\xi (\psi ,0)=\mathcal{N}\left[\frac{\partial \xi }{\partial \psi }+6\xi \frac{\partial {\xi }^2}{\partial \psi }+3{\xi }^2\frac{{\partial }^2\xi }{\partial {\psi }^2}-3\frac{{\partial }^2\xi }{\partial {\psi }^2}-\frac{{\partial }^4\xi }{\partial {\psi }^4}\right],$$

(61)

Upon simplifying, we have

$$\mathcal{N}\left[\xi (\psi ,\wp )\right]={\omega }^2\left[tanh\left(\frac{\psi }{\sqrt{2}}\right)\right]+\frac{\beta (\omega -\beta (\omega -\beta \left)\right)}{{\omega }^2}\mathcal{N}\left[\frac{\partial \xi }{\partial \psi }+6\xi \frac{\partial {\xi }^2}{\partial \psi }+3{\xi }^2\frac{{\partial }^2\xi }{\partial {\psi }^2}-3\frac{{\partial }^2\xi }{\partial {\psi }^2}-\frac{{\partial }^4\xi }{\partial {\psi }^4}\right],$$

(62)

Taking the inverse $NT$, Equation (62) can be written as

$$\xi (\psi ,\wp )=tanh\left(\frac{\psi }{\sqrt{2}}\right)+{\mathcal{N}}^{-1}\left[\frac{\beta (\omega -\beta (\omega -\beta \left)\right)}{{\omega }^2}\mathcal{N}\left\{\frac{\partial \xi }{\partial \psi }+6\xi \frac{\partial {\xi }^2}{\partial \psi }+3{\xi }^2\frac{{\partial }^2\xi }{\partial {\psi }^2}-3\frac{{\partial }^2\xi }{\partial {\psi }^2}-\frac{{\partial }^4\xi }{\partial {\psi }^4}\right\}\right],$$

(63)

Now, we apply $ND{M}_{CF}$

The series form solution for the unknown function $\xi (\psi ,\wp )$ is written as

$$\xi (\psi ,\wp )=\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp ).$$

(64)

The nonlinear terms with the help of Adomian polynomials are represented by $\xi {\xi }_{\psi }^2={\sum }_{l=0}^{\infty }{\mathcal{A}}_l$, ${\xi }^2{\xi }_{\psi \psi }={\sum }_{l=0}^{\infty }{\mathcal{B}}_l$; thus, with the help of these terms, Equation (63) can be rewritten as

$$\begin{array}{cc}\hfill & \sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp )=tanh\left(\frac{\psi }{\sqrt{2}}\right)+{\mathcal{N}}^{-1}\left[\frac{\beta (\omega -\beta (\omega -\beta \left)\right)}{{\omega }^2}\mathcal{N}\right\{\sum _{l=0}^{\infty }{v}_{l\psi }+6\sum _{l=0}^{\infty }{\mathcal{A}}_l+3\sum _{l=0}^{\infty }{\mathcal{B}}_l-3\sum _{l=0}^{\infty }{v}_{l\psi \psi }-\hfill \\ \hfill & \sum _{l=0}^{\infty }{v}_{l\psi \psi \psi \psi }\left\}\right].\hfill \end{array}$$

(65)

Thus, upon comparing both sides of Equation (65), we have

$$\begin{array}{cc}\hfill {\xi }_0(\psi ,\wp )& =tanh\left(\frac{\psi }{\sqrt{2}}\right),\hfill \\ \hfill {\xi }_1(\psi ,\wp )& ={sech}^2\frac{\left(\frac{\psi }{\sqrt{2}}\right)}{\sqrt{2}}\left(\beta (\wp -1)+1\right)\hfill \end{array}$$

$${\xi }_2(\psi ,\wp )=-{sech}^2\left(\frac{\psi }{\sqrt{2}}\right)tanh\left(\frac{\psi }{\sqrt{2}}\right)\left({(1-\beta )}^2+2\beta (1-\beta )\wp +\frac{{\beta }^2{\wp }^2}{2}\right),$$

Continuing the same process, we can easily find the remaining components of ${\xi }_l$ for $(l\ge 3)$. Subsequently, we define the series form solutions as

$$\begin{array}{cc}\hfill \xi (\psi ,\wp )& =\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp )={\xi }_0(\psi ,\wp )+{\xi }_1(\psi ,\wp )+{\xi }_2(\psi ,\wp )+\cdots ,\hfill \\ \hfill \xi (\psi ,\wp )& =tanh\left(\frac{\psi }{\sqrt{2}}\right)+{sech}^2\frac{\left(\frac{\psi }{\sqrt{2}}\right)}{\sqrt{2}}\left(\beta (\wp -1)+1\right)-{sech}^2\left(\frac{\psi }{\sqrt{2}}\right)tanh\left(\frac{\psi }{\sqrt{2}}\right)({(1-\beta )}^2+\hfill \\ \hfill & 2\beta (1-\beta )\wp +\frac{{\beta }^2{\wp }^2}{2})+\cdots \hfill \end{array}$$

(66)

Now, we apply $ND{M}_{ABC}$

The series form solution for the unknown function $\xi (\psi ,\wp )$ is written as

$$\xi (\psi ,\wp )=\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp ).$$

(67)

The nonlinear terms with the help of Adomian polynomials are represented by $\xi {\xi }_{\psi }^2={\sum }_{l=0}^{\infty }{\mathcal{A}}_l$, ${\xi }^2{\xi }_{\psi \psi }={\sum }_{l=0}^{\infty }{\mathcal{B}}_l$; thus, with the help of these terms, Equation (63) can be rewritten as

$$\begin{array}{cc}\hfill \sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp )& =\left[tanh\left(\frac{\psi }{\sqrt{2}}\right)\right]+{\mathcal{N}}^{-1}\left[\frac{{\upsilon }^{\beta }({\omega }^{\beta }+\beta ({\upsilon }^{\beta }-{\omega }^{\beta }))}{{\omega }^{2\beta }}\mathcal{N}\right\{\sum _{l=0}^{\infty }{v}_{l\psi }+6\sum _{l=0}^{\infty }{\mathcal{A}}_l+3\sum _{l=0}^{\infty }{\mathcal{B}}_l-\hfill \\ \hfill & 3\sum _{l=0}^{\infty }{v}_{l\psi \psi }-\sum _{l=0}^{\infty }{v}_{l\psi \psi \psi \psi }\left\}\right].\hfill \end{array}$$

(68)

Thus, upon comparing both sides of Equation (68), we have

$$\begin{array}{cc}\hfill {\xi }_0(\psi ,\wp )& =tanh\left(\frac{\psi }{\sqrt{2}}\right),\hfill \\ \hfill {\xi }_1(\psi ,\wp )& ={sech}^2\frac{\left(\frac{\psi }{\sqrt{2}}\right)}{\sqrt{2}}\left(1-\beta +\frac{\beta {\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}\right),\hfill \end{array}$$

$${\xi }_2(\psi ,\wp )=-{sech}^2\left(\frac{\psi }{\sqrt{2}}\right)tanh\left(\frac{\psi }{\sqrt{2}}\right)\left[\frac{{\beta }^2{\wp }^{2\beta }}{\mathrm{\Gamma }(2\beta +1)}+2\beta (1-\beta )\frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}+{(1-\beta )}^2\right]$$

Continuing the same process, we can easily find the remaining components of ${\xi }_l$ for $(l\ge 3)$. Subsequently, we define the series form solutions as

$$\begin{array}{cc}\hfill \xi (\psi ,\wp )& =\sum _{l=0}^{\infty }{\xi }_l(\psi ,\wp )={\xi }_0(\psi ,\wp )+{\xi }_1(\psi ,\wp )+{\xi }_2(\psi ,\wp )+\cdots ,\hfill \\ \hfill \xi (\psi ,\wp )& =tanh\left(\frac{\psi }{\sqrt{2}}\right)+{sech}^2\frac{\left(\frac{\psi }{\sqrt{2}}\right)}{\sqrt{2}}\left(1-\beta +\frac{\beta {\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}\right)\hfill \\ \hfill & -{sech}^2\left(\frac{\psi }{\sqrt{2}}\right)tanh\left(\frac{\psi }{\sqrt{2}}\right)\left[\frac{{\beta }^2{\wp }^{2\beta }}{\mathrm{\Gamma }(2\beta +1)}+2\beta (1-\beta )\frac{{\wp }^{\beta }}{\mathrm{\Gamma }(\beta +1)}+{(1-\beta )}^2\right]+\cdots \hfill \end{array}$$

(69)

If we set $\beta =1$, we obtain the exact solution:

$$\xi (\psi ,\wp )=tanh\left(\frac{\psi +\wp }{\sqrt{2}}\right).$$

(70)

6. Results and Discussion

In this section, we present the numerical study of nonlinear fractional-order Gardner and Cahn–Hilliard equations by implementing the natural transform decomposition method. The graphical illustrations of the solutions are given in the figures and tables with the aid of Maple. In

Table 1. Absolute error comparison of problem 1 at various fractional order of $\beta$.

℘	$\psi$	$\beta =0.4$	$\beta =0.6$	$\beta =0.8$	$\beta =1\left({\mathit{NTDM}}_{\mathit{CF}}\right)$	$\beta =1\left({\mathit{NTDM}}_{\mathit{ABC}}\right)$
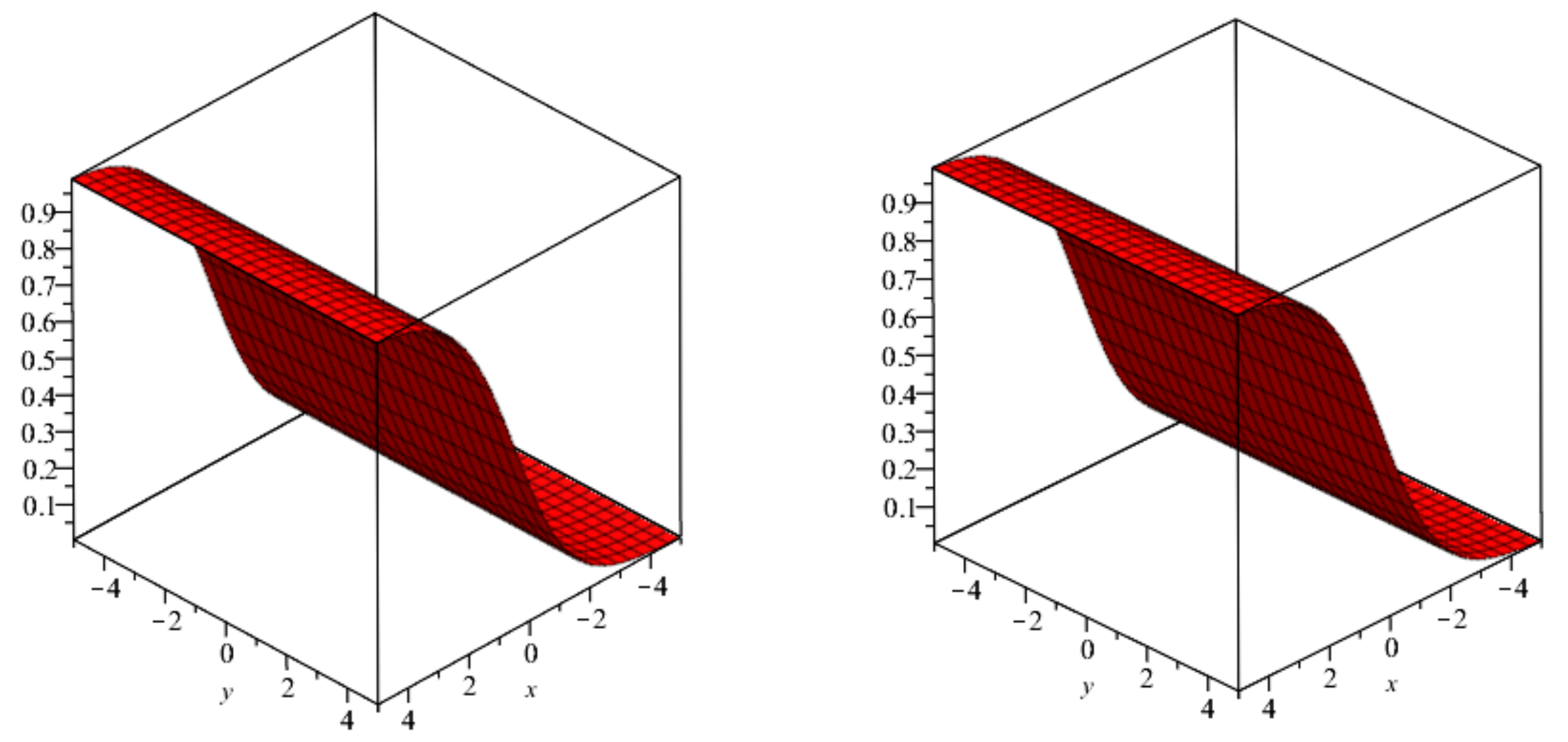
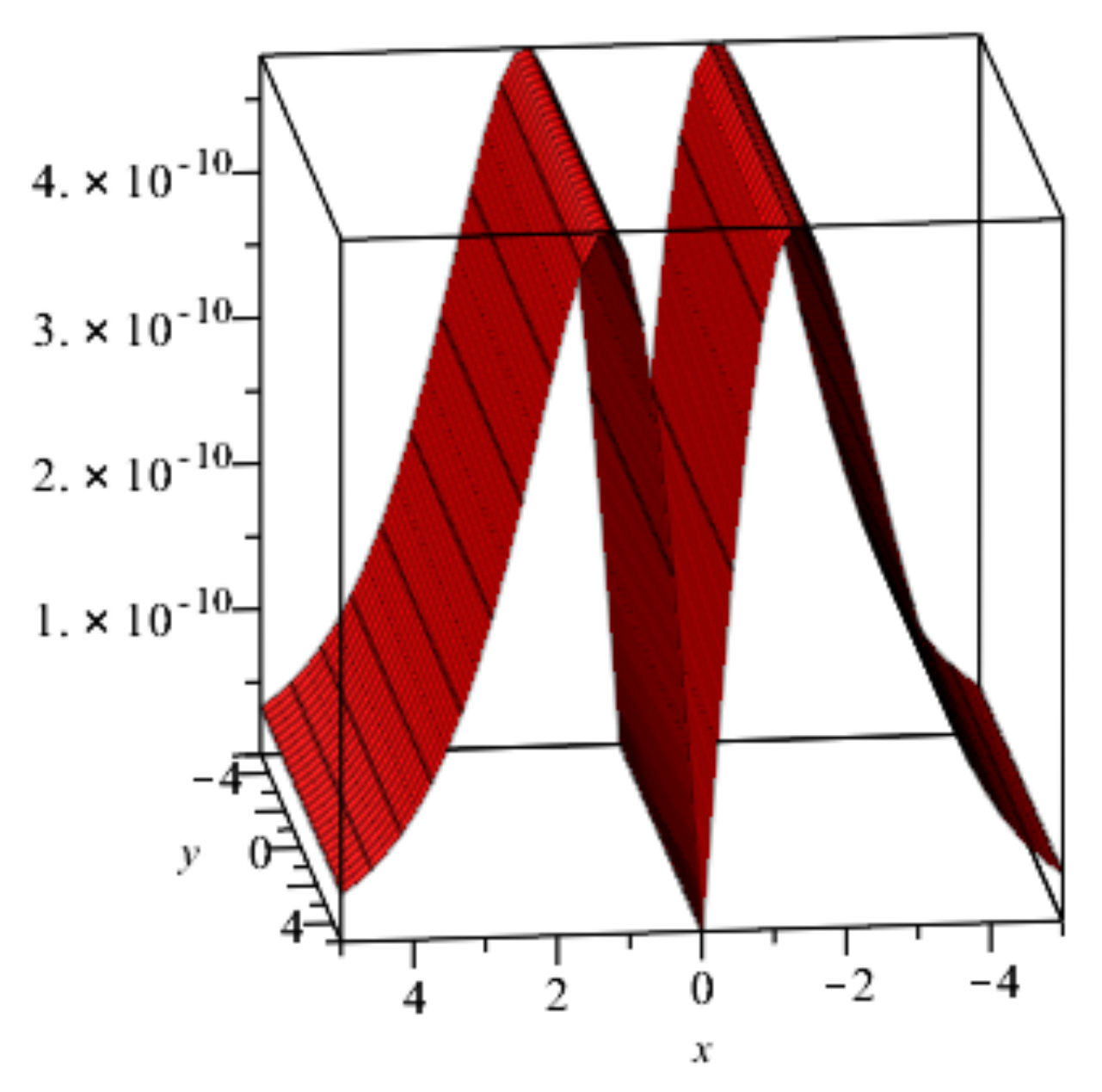
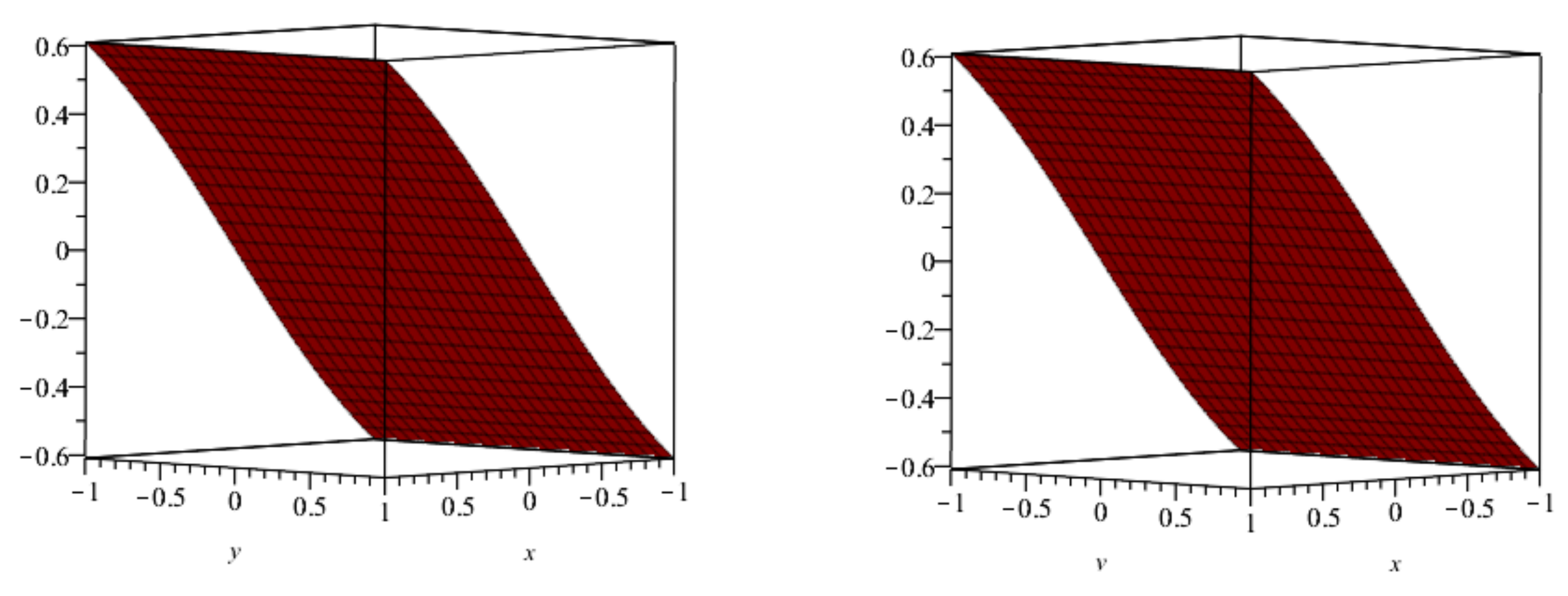
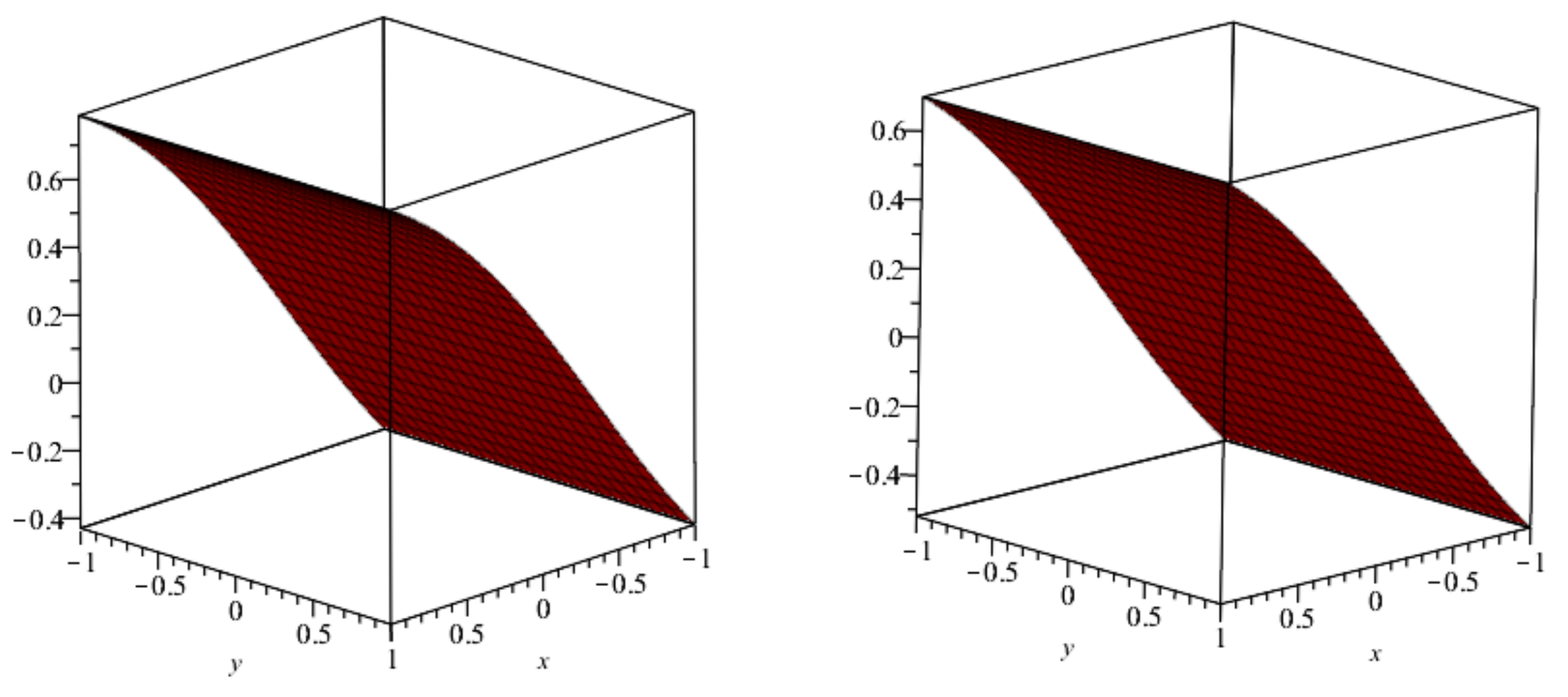
0.01	0.2	2.478508 × 10−2	1.238910 × 10−2	2.477395 × 10−3	1.000000 × 10−10	1.000000 × 10−10
	0.4	2.405852 × 10−2	1.202592 × 10−2	2.404771 × 10−3	2.000000 × 10−10	2.000000 × 10−10
	0.6	2.290932 × 10−2	1.145148 × 10−2	2.289902 × 10−3	4.000000 × 10−10	4.000000 × 10−10
	0.8	2.1419859 × 10−2	1.070696 × 10−2	2.141023 × 10−3	4.000000 × 10−10	4.000000 × 10−10
	1	1.9687746 × 10−2	9.841145 × 10−3	1.967890 × 10−3	4.000000 × 10−10	4.000000 × 10−10
0.02	0.2	2.481072 × 10−2	1.239979 × 10−2	2.479251 × 10−3	5.000000 × 10−10	5.000000 × 10−10
	0.4	2.408340 × 10−2	1.203630 × 10−2	2.406573 × 10−3	1.000000 × 10−9	1.000000 × 10−9
	0.6	2.293301 × 10−2	1.146136 × 10−2	2.291618 × 10−3	1.400000 × 10−9	1.400000 × 10−9
	0.8	2.144201 × 10−2	1.071619 × 10−2	2.142627 × 10−3	1.700000 × 10−9	1.700000 × 10−9
	1	1.970810 × 10−2	9.849635 × 10−3	1.969363 × 10−3	1.800000 × 10−9	1.800000 × 10−9
0.03	0.2	2.483378 × 10−2	1.240957 × 10−2	2.480968 × 10−3	1.100000 × 10−9	1.100000 × 10−9
	0.4	2.410579 × 10−2	1.204579 × 10−2	2.408239 × 10−3	2.100000 × 10−9	2.100000 × 10−9
	0.6	2.295433 × 10−2	1.147039 × 10−2	2.293204 × 10−3	2.900000 × 10−9	2.900000 × 10−9
	0.8	2.146194 × 10−2	1.072464 × 10−2	2.144109 × 10−3	3.700000 × 10−9	3.700000 × 10−9
	1	1.972642 × 10−2	9.857396 × 10−3	1.970725 × 10−3	4.000000 × 10−9	4.000000 × 10−9
0.04	0.2	2.485524 × 10−2	1.241876 × 10−2	2.482596 × 10−3	2.000000 × 10−9	2.000000 × 10−9
	0.4	2.412662 × 10−2	1.205471 × 10−2	2.409818 × 10−3	3.800000 × 10−9	3.800000 × 10−9
	0.6	2.297416 × 10−2	1.147889 × 10−2	2.294707 × 10−3	5.300000 × 10−9	5.300000 × 10−9
	0.8	2.148048 × 10−2	1.073258 × 10−2	2.145513 × 10−3	6.500000 × 10−9	6.500000 × 10−9
	1	1.974347 × 10−2	9.864694 × 10−3	1.972016 × 10−3	7.200000 × 10−9	7.200000 × 10−9
0.05	0.2	2.487555 × 10−2	1.242752 × 10−2	2.484156 × 10−3	3.100000 × 10−9	3.100000 × 10−9
	0.4	2.414633 × 10−2	1.206321 × 10−2	2.411331 × 10−3	5.900000 × 10−9	5.900000 × 10−9
	0.6	2.299293 × 10−2	1.148699 × 10−2	2.296147 × 10−3	8.300000 × 10−9	8.300000 × 10−9
	0.8	2.149803 × 10−2	1.074015 × 10−2	2.146859 × 10−3	1.030000 × 10−9	1.030000 × 10−9
	1	1.975959 × 10−2	9.871653 × 10−3	1.973252 × 10−3	1.130000 × 10−9	1.130000 × 10−9

and

Table 2. Error comparison among $RPS$, $q-HAM$, $FNDM$, $q-HATM$, $ND{M}_{CF}$ and $ND{M}_{ABC}$ for problem 1 at $\beta =1$.

$\psi$	$\mathit{RPS}$	$\left|q-\mathit{HAM}\right|$	$\left|\mathit{FNDM}\right|$	$\left|q-\mathit{HATM}\right|$	$|{\mathit{NTDM}}_{\mathit{CF}}|$	$|{\mathit{NTDM}}_{\mathit{ABC}}|$
0.1	1.66002 × 10−4	1.66002 × 10−4	9.95627 × 10−7	9.95627 × 10−7	2.48000 × 10−8	2.48000 × 10−8
0.2	1.62707 × 10−4	1.62707 × 10−4	2.61331 × 10−6	2.61331 × 10−6	4.92000 × 10−8	4.92000 × 10−8
0.3	1.56257 × 10−4	1.56257 × 10−4	4.12217 × 10−6	4.12217 × 10−6	7.26000 × 10−8	7.26000 × 10−8
0.4	1.46917 × 10−4	1.46917 × 10−4	5.46303 × 10−6	5.46303 × 10−6	9.47000 × 10−8	9.47000 × 10−8
0.5	1.35064 × 10−4	1.35064 × 10−4	6.58827 × 10−6	6.58827 × 10−6	1.15000 × 10−7	1.15000 × 10−7

, we present the error analysis of the fractional Gardner equation obtained with the help of the proposed method at different values of $\psi$ and ℘. Furthermore, we show a comparative study of the obtained solution for the fractional Gardner equation with $RPS$, $q-HAM$, $FNDM$, $q-HATM$, $NTD{M}_{CF}$ and $NTD{M}_{ABC}$ in terms of absolute error, which reveals that the suggested schemes are highly accurate in comparison with these methods. Similarly

Table 3. Absolute error comparison of problem 2 at various fractional orders of $\beta$.

℘	$\psi$	$\beta =0.4$	$\beta =0.6$	$\beta =0.8$	$\beta =1\left({\mathit{NTDM}}_{\mathit{CF}}\right)$	$\beta =1\left({\mathit{NTDM}}_{\mathit{ABC}}\right)$
0.01	0.2	6.843036 × 10−2	1.383664 × 10−2	6.927804 × 10−3	2.223097 × 10−10	2.223097 × 10−10
	0.4	6.362177 × 10−2	1.300789 × 10−2	6.521729 × 10−3	3.938473 × 10−10	3.938473 × 10−10
	0.6	5.705894 × 10−2	1.178846 × 10−2	5.917824 × 10−3	5.391620 × 10−10	5.391620 × 10−10
	0.8	4.954728 × 10−2	1.033387 × 10−2	5.193500 × 10−3	5.664495 × 10−10	5.664495 × 10−10
	1	4.183562 × 10−2	8.798218 × 10−3	4.426079 × 10−3	5.873327 × 10−10	5.873327 × 10−10
0.02	0.2	6.849818 × 10−2	1.384696 × 10−2	6.932795 × 10−3	7.708391 × 10−10	7.708391 × 10−10
	0.4	6.368210 × 10−2	1.301721 × 10−2	6.526244 × 10−3	1.487289 × 10−9	1.487289 × 10−9
	0.6	5.711074 × 10−2	1.179659 × 10−2	5.921768 × 10−3	1.900548 × 10−9	1.900548 × 10−9
	0.8	4.959041 × 10−2	1.034074 × 10−2	5.196840 × 10−3	2.161298 × 10−9	2.161298 × 10−9
	1	4.187066 × 10−2	8.803879 × 10−3	4.428836 × 10−3	2.265400 × 10−9	2.265400 × 10−9
0.03	0.2	6.855899 × 10−2	1.385645 × 10−2	6.937398 × 10−3	1.845587 × 10−9	1.845587 × 10−9
	0.4	6.373601 × 10−2	1.302575 × 10−2	6.530395 × 10−3	3.480376× 10−9	3.480376 × 10−9
	0.6	5.715685 × 10−2	1.180401 × 10−2	5.925381 × 10−3	4.484208 × 10−9	4.484208 × 10−9
	0.8	4.962867 × 10−2	1.034700 × 10−2	5.199890 × 10−3	4.984595 × 10−9	4.984595 × 10−9
	1	4.190163 × 10−2	8.809018 × 10−3	4.431346 × 10−3	5.034164 × 10−9	5.034164 × 10−9
0.04	0.2	6.861545 × 10−2	1.386540 × 10−2	6.941751 × 10−3	3.246556 × 10−9	3.246556 × 10−9
	0.4	6.378593 × 10−2	1.303379 × 10−2	6.534311 × 10−3	6.072957 × 10−9	6.072957 × 10−9
	0.6	5.719942 × 10−2	1.181098 × 10−2	5.928781 × 10−3	7.889992 × 10−9	7.889992 × 10−9
	0.8	4.966389 × 10−2	1.035285 × 10−2	5.202754 × 10−3	8.836192 × 10−9	8.836192 × 10−9
	1	4.193007 × 10−2	8.813821 × 10−3	4.433698 × 10−3	8.993703 × 10−9	8.993703 × 10−9
0.05	0.2	6.866877 × 10−2	1.387396 × 10−2	6.945918 × 10−3	5.073744 × 10−9	5.073744 × 10−9
	0.4	6.383297 × 10−2	1.304147 × 10−2	6.538053 × 10−3	9.365133 × 10−9	9.365133 × 10−9
	0.6	5.723945 × 10−2	1.181762 × 10−2	5.932024 × 10−3	1.231800 × 10−8	1.231800 × 10−8
	0.8	4.969693 × 10−2	1.035842 × 10−2	5.205480 × 10−3	1.381618 × 10−8	1.381618 × 10−8
	1	4.195668 × 10−2	8.818376 × 10−3	4.435932 × 10−3	1.404396 × 10−8	1.404396 × 10−8

presents the error comparison for the obtained results with the aid of the proposed methods for the corresponding equation, while

Table 4. Error comparison among $RPS$, $q-HAM$,$FNDM$,$q-HATM$, $ND{M}_{CF}$ and $ND{M}_{ABC}$ for problem 2 at $\beta =1$.

$\psi$	$\mathit{RPS}$	$\left|q-\mathit{HAM}\right|$	$\left|\mathit{FNDM}\right|$	$\left|q-\mathit{HATM}\right|$	$|{\mathit{NTDM}}_{\mathit{CF}}|$	$|{\mathit{NTDM}}_{\mathit{ABC}}|$
0.1	2.55541 × 10−5	2.55541 × 10−5	7.55258 × 10−6	7.55258 × 10−6	4.20818 × 10−8	4.20818 × 10−8
0.2	4.15291 × 10−5	4.15291 × 10−5	1.27010 × 10−5	1.27010 × 10−5	8.15279 × 10−8	8.15279 × 10−8
0.3	5.42246 × 10−5	5.42246 × 10−5	1.68403 × 10−5	1.68403 × 10−5	1.17804 × 10−7	1.17804 × 10−7
0.4	6.28898 × 10−5	6.28898 × 10−5	1.97175 × 10−5	1.97175 × 10−5	1.49799 × 10−7	1.49799 × 10−7
0.5	6.72637 × 10−5	6.72637 × 10−5	2.12349 × 10−5	2.12349 × 10−5	1.76464 × 10−7	1.76464 × 10−7

shows the error comparison of fractional Cahn–Hilliard equation results with $RPS$, $q-HAM$, $FNDM$, $q-HATM$, $NTD{M}_{CF}$ and $NTD{M}_{ABC}$. From these tables, it is clear that the proposed methods are very effective and accurate compared with other methods. Additionally, it is observed from the fractional-order solution that the solution better reflects the exact solution as the value of ℘ becomes closer to the integer order. Figure 1 shows the nature of the exact and analytical solutions of the suggested methods. The behavior of the proposed method solution at various fractional orders is shown in Figure 2. The fractional-order 3D and 2D layout of problem 1 is seen in Figure 3, while the absolute error graphical view the for corresponding equation obtained with the help of proposed techniques is plotted in Figure 4. Figure 5 shows the behaviour of the exact and natural decomposition technique results for problem 2, whereas Figure 6 illustrates the behavior of the analytical solution at various fractional orders of $\beta$. Figure 7 shows 3D and 2D solution graph for problem 2 at various fractional orders whereas, Figure 8 shows the absolute error of problem 2.

7. Conclusions

In this article, we implemented the natural decomposition method with the aid of two different fractional derivatives to find the solution of nonlinear fractional Gardner and Cahn–Hilliard equations. To demonstrate the validity of the suggested technique, we implement it to solve two nonlinear problems. The implementation of the proposed methods show that the schemes are extremely efficient in finding smooth solutions to specified equations. The convergence of the suggested method was shown analytically and graphically when applied to fractional-order Gardner and Cahn–Hilliard equations, indicating the method’s stability and effectiveness. By demonstrating specific cases, the physical and geometrical interpretations have been demonstrated, and their graphs indicate the exact solutions within certain approximation errors. As the value of the fractional-order derivatives approaches 1, the approximation solution converges to the exact solution, according to the results. The solution graphs and tables for each problem shown confirmed that the method had good agreement with the exact result of the problem. The proposed method gives a solution in the form of a series with high accuracy and minimal calculations. Finally, we conclude that the suggested methods are very efficient and accurate, which can be utilised to study any nonlinear problems that arise in complex phenomena.