Analytical Investigation of Fractional-Order Cahn–Hilliard and Gardner Equations Using Two Novel Techniques
Abstract
:1. Introduction
2. Basic Preliminaries
3. Methodology
3.1. Case I
3.2. Case II
4. Convergence Analysis
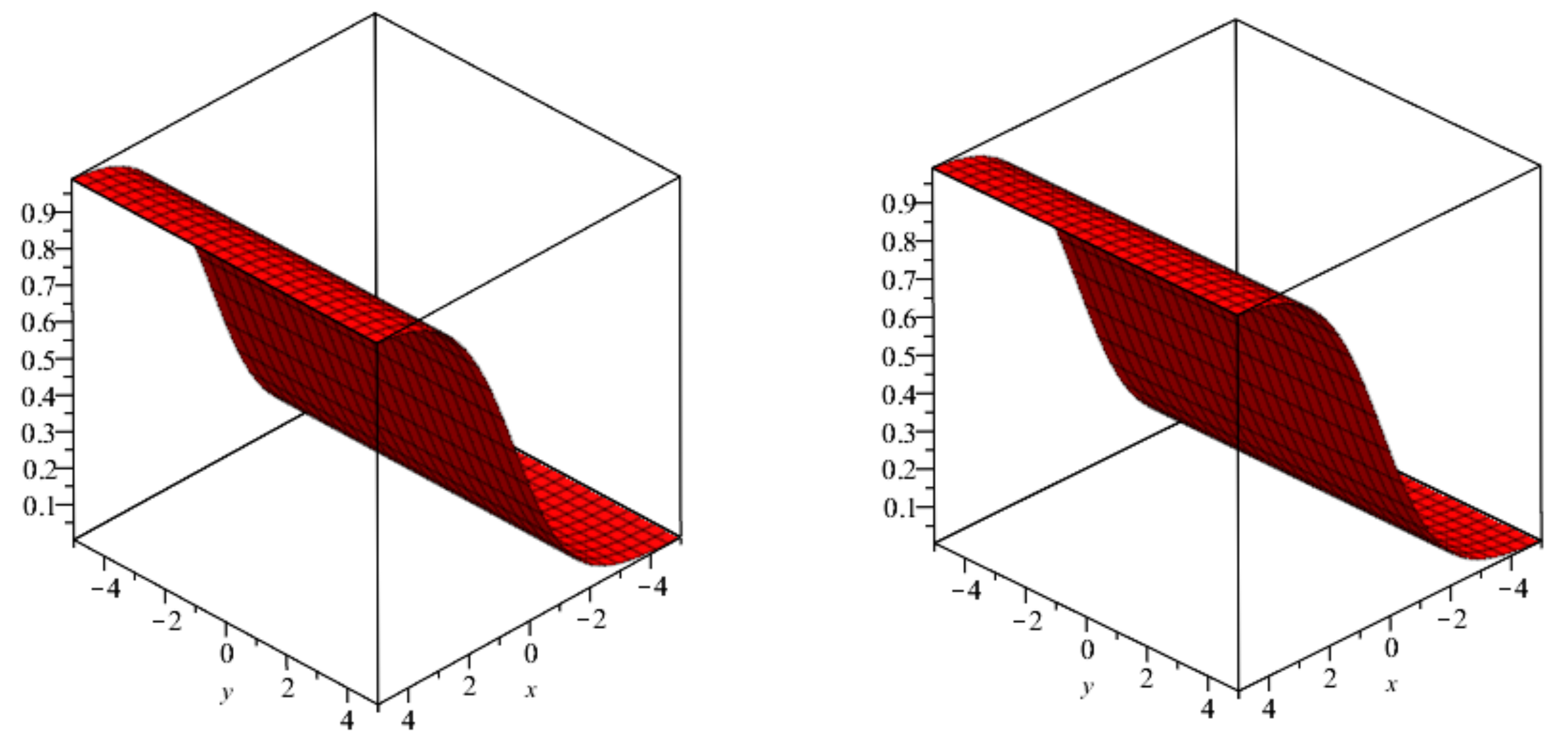
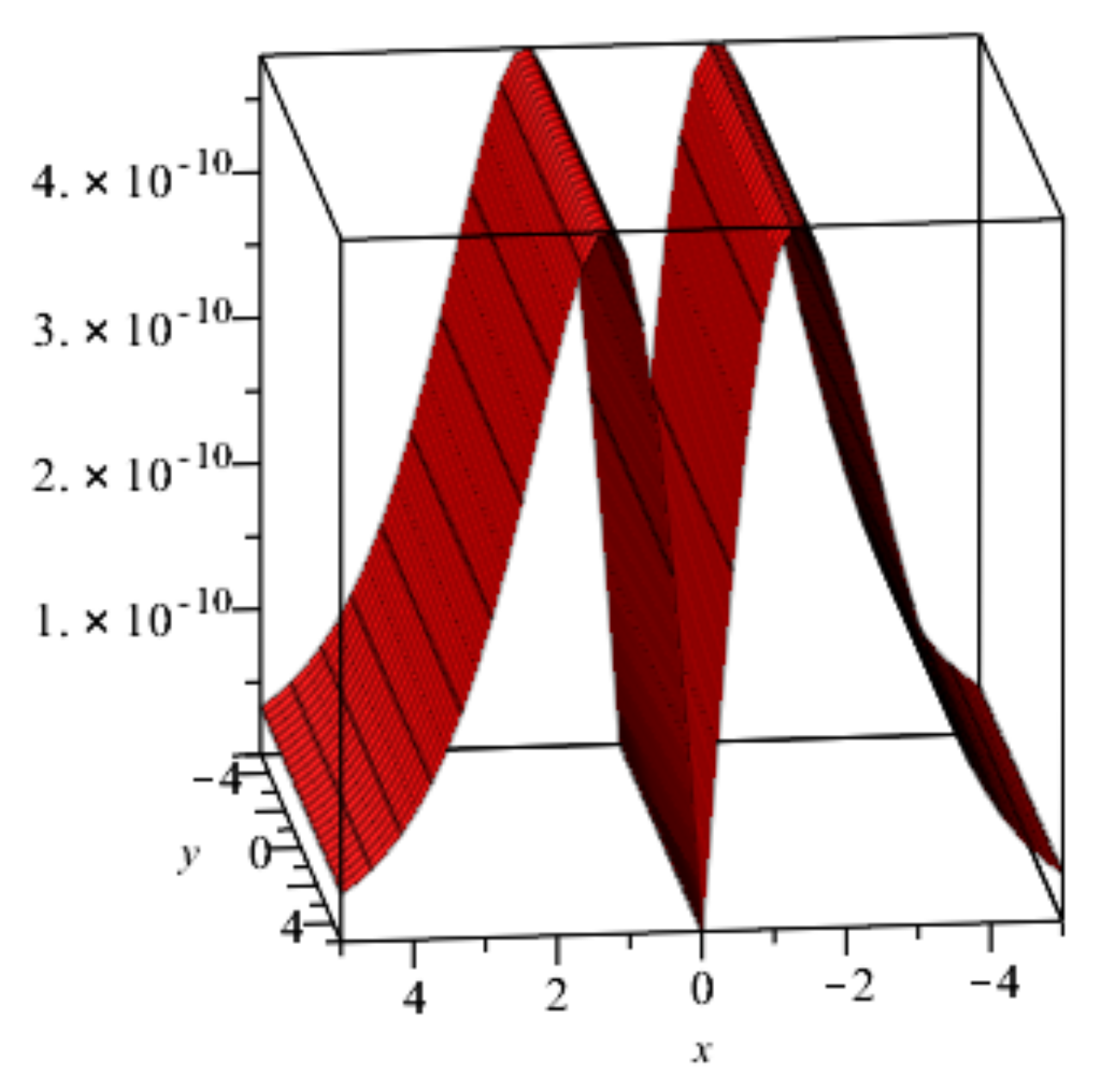
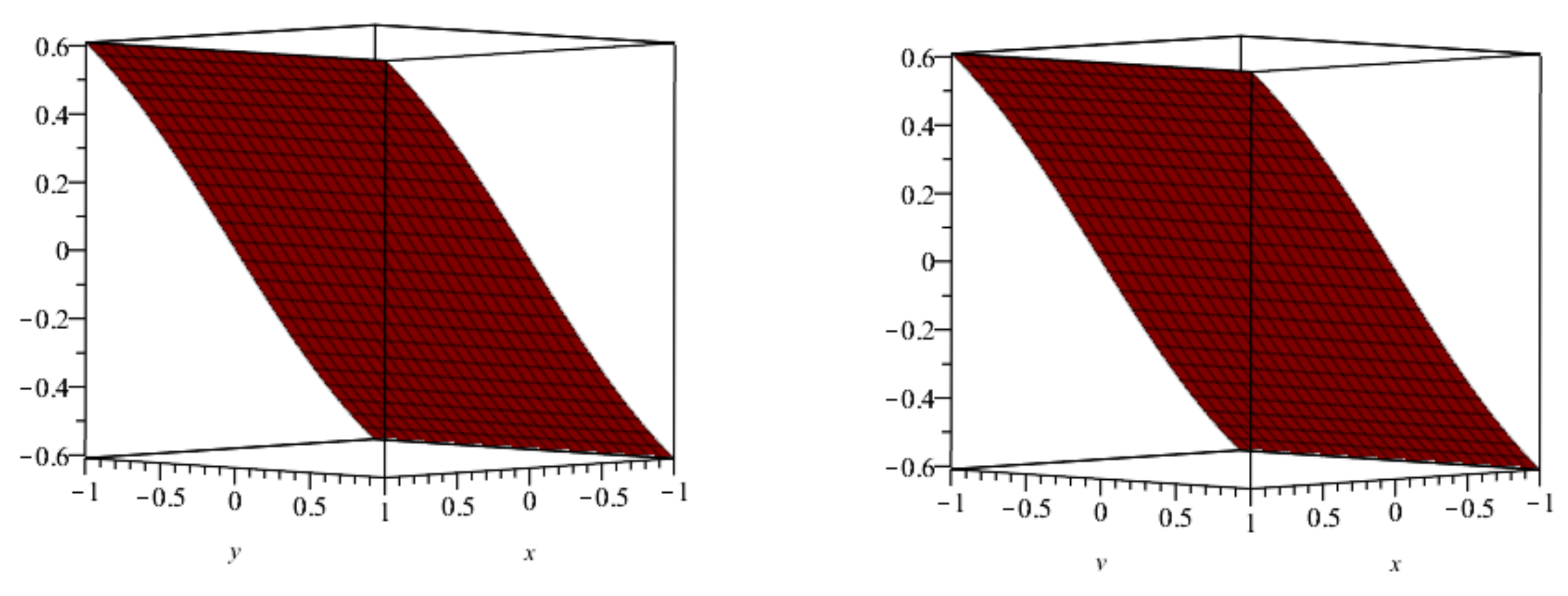
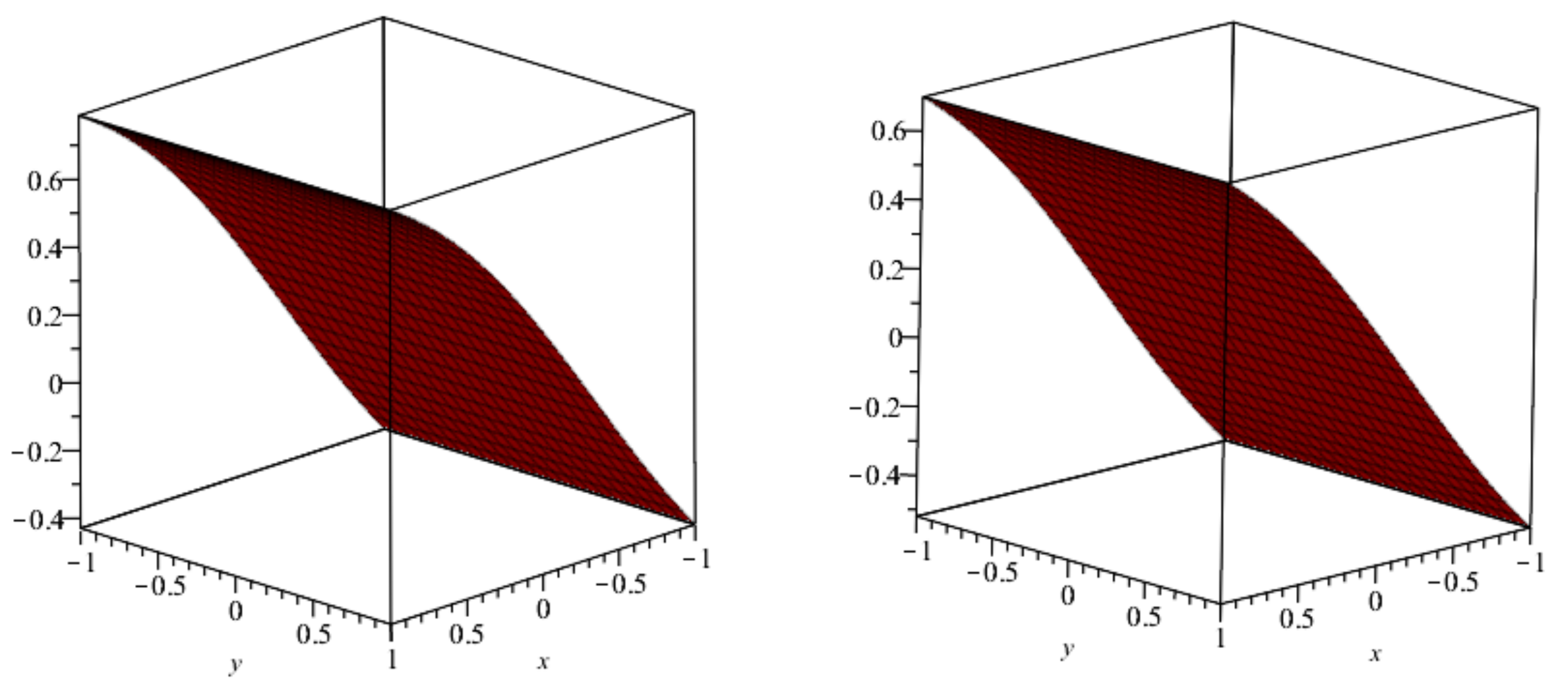
5. Numerical Examples
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 2000. [Google Scholar]
- Calderon, A.; Vinagre, B.; Feliu, V. Fractional order control strategies for power electronic buck converters. Signal Process 2006, 86, 2803–2819. [Google Scholar] [CrossRef]
- Abatier, J.; Aoun, M.; Oustaloup, A.; Grgoire, G.; Ragot, F.; Roy, P. Fractional system identification for lead acid battery state of charge estimation. Signal Process 2006, 86, 2645–2657. [Google Scholar] [CrossRef]
- Vinagre, B.; Monje, C.; Calderon, A.; Suarej, J. Fractional PID controllers for industry application: A brief introduction. J. Vib. Control 2007, 13, 1419–1430. [Google Scholar] [CrossRef]
- Baleanu, D. Fractional Calculus, Series on Complexity, Nonlinearity and Chaos, 3; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2012. [Google Scholar]
- Iqbal, N.; Akgül, A.; Shah, R.; Bariq, A.; Mossa Al-Sawalha, M.; Ali, A. On Solutions of Fractional-Order Gas Dynamics Equation by Effective Techniques. J. Funct. Spaces 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Nonlaopon, K.; Alsharif, A.; Zidan, A.; Khan, A.; Hamed, Y.; Shah, R. Numerical Investigation of Fractional-Order Swift–Hohenberg Equations via a Novel Transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Agarwal, R.; Mofarreh, F.; Shah, R.; Luangboon, W.; Nonlaopon, K. An Analytical Technique, Based on Natural Transform to Solve Fractional-Order Parabolic Equations. Entropy 2021, 23, 1086. [Google Scholar] [CrossRef] [PubMed]
- Aljahdaly, N.; Agarwal, R.; Shah, R.; Botmart, T. Analysis of the Time Fractional-Order Coupled Burgers Equations with Non-Singular Kernel Operators. Mathematics 2021, 9, 2326. [Google Scholar] [CrossRef]
- Shah, R.; Farooq, U.; Khan, H.; Baleanu, D.; Kumam, P.; Arif, M. Fractional View Analysis of Third Order Kortewege-De Vries Equations, Using a New Analytical Technique. Front. Phys. 2020, 7, 244. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Part II. Ann. Geophys. 1966, 19, 383–393. [Google Scholar] [CrossRef]
- Marin, M.; Marinescu, C. Thermoelasticity of initially stressed bodies, asymptotic equipartition of energies. Int. J. Eng. Sci. 1998, 36, 73–86. [Google Scholar] [CrossRef]
- Marin, M. A domain of influence theorem for microstretch elastic materials. Nonlinear Anal. Real World Appl. 2010, 11, 3446–3452. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Differential Equations; John Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Lin, L.; Liu, Y.; Zhao, D. Controllability of Impulsive?—Caputo Fractional Evolution Equations with Nonlocal Conditions. Mathematics 2021, 9, 1358. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Y.; Zhao, D. Study on implicit-type fractional coupled system with integral boundary conditions. Mathematics 2021, 9, 300. [Google Scholar] [CrossRef]
- Tuan, N.H. Existence and limit problem for fractional fourth order subdiffusion equation and Cahn-Hilliard equation. Discret. Contin. Dyn. Syst.-S 2021, 14, 4551. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches. Axioms 2019, 8, 125. [Google Scholar] [CrossRef] [Green Version]
- Yasmin, H.; Iqbal, N.; Hussain, A. Convective Heat/Mass Transfer Analysis on Johnson-Segalman Fluid in a Symmetric Curved Channel with Peristalsis: Engineering Applications. Symmetry 2020, 12, 1475. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Al-Qurashi, M.; Shah, R.; Baleanu, D. Modified modelling for heat like equations within Caputo operator. Energies 2020, 13, 2002. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Kumam, P.; Baleanu, D.; Arif, M. An approximate analytical solution of the Navier-Stokes equations within Caputo operator and Elzaki transform decomposition method. Adv. Differ. Equ. 2020, 2020, 1–23. [Google Scholar]
- Alesemi, M.; Iqbal, N.; Botmart, T. Novel Analysis of the Fractional-Order System of Non-Linear Partial Differential Equations with the Exponential-Decay Kernel. Mathematics 2022, 10, 615. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Shah, R.; Baleanu, D. An efficient analytical approach for the solution of certain fractional-order dynamical systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Rawashdeh, M.S. The fractional natural decomposition method: Theories and applications. Math. Methods Appl. Sci. 2017, 40, 2362–2376. [Google Scholar] [CrossRef]
- Gardner, G.H.F.; Gardner, L.W.; Gregory, A.R. Formation velocity and density-the diagnostic basics for stratigraphic traps. Geophysics 1974, 39, 770–780. [Google Scholar] [CrossRef] [Green Version]
- Fu, Z.; Liu, S.; Liu, S. New kinds of solutions to Gardner equation. Chaos Solit Fractals 2004, 20, 301–309. [Google Scholar] [CrossRef]
- Xu, G.Q.; Li, Z.B.; Liu, Y.P. Exact solutions to a large class of nonlinear evolution equations. Chin. J. Phys. 2003, 41, 232–241. [Google Scholar]
- Kuo, C.K. New solitary solutions of the Gardner equation and Whitham-Broer-Kaup equations by the modified simplest equation method. Optik 2017, 147, 128–135. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Gurtin, M.E. Generalized Ginzburg-Landau and Cahn-Hilliard equations based on a microforce balance. Phys. D Nonlinear Phenom. 1996, 92, 178–192. [Google Scholar] [CrossRef]
- Choo, S.M.; Chung, S.K.; Lee, Y.J. A conservative difference scheme for the viscous Cahn-Hilliard equation with a nonconstant gradient energy coefficient. Appl. Numer Math. 2004, 51, 207–219. [Google Scholar] [CrossRef]
- Dahmani, Z.; Benbachir, M. Solutions of the Cahn-Hilliard equation with time- and space-fractional derivatives. Int. J. Nonlinear Sci. 2009, 8, 19–26. [Google Scholar]
- Hosseini, K.; Bekir, A.; Ansari, R. New exact solutions of the conformable time-fractional Cahn-Allen and Cahn-Hilliard equations using the modified Kudryashov method. Optik 2017, 132, 203–209. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Obeidat, N.A. Applying the reduced differential transform method to solve the telegraph and Cahn-Hilliard equations. Thai J. Math. 2015, 13, 153–163. [Google Scholar]
- Arafa, A.; Elmahdy, G. Application of residual power series method to fractional coupled physical equations arising in fluids flow. Int. J. Differ Equ. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Bouhassoun, A.; Cherif, M.H. Homotopy perturbation method for solving the fractional Cahn-Hilliard equation. J. Interdiscip Math. 2015, 18, 513–524. [Google Scholar] [CrossRef]
- Zhou, M.X.; Kanth, A.S.V.; Aruna, K.; Raghavendar, K.; Rezazadeh, H.; Inc, M.; Aly, A. Numerical Solutions of Time Fractional Zakharov-Kuznetsov Equation via Natural Transform Decomposition Method with Nonsingular Kernel Derivatives. J. Funct. Spaces 2021, 2021, 9884027. [Google Scholar] [CrossRef]
- Adomian, G. A new approach to nonlinear partial differential equations. J. Math. Anal. Appl. 1984, 102, 420–434. [Google Scholar] [CrossRef] [Green Version]
- Elsayed, E.; Shah, R.; Nonlaopon, K. The Analysis of the Fractional-Order Navier-Stokes Equations by a Novel Approach. J. Funct. Spaces 2022, 2022, 1–18. [Google Scholar] [CrossRef]



| ℘ | ||||||
|---|---|---|---|---|---|---|
| 0.01 | 0.2 | 2.478508 × 10−2 | 1.238910 × 10−2 | 2.477395 × 10−3 | 1.000000 × 10−10 | 1.000000 × 10−10 |
| 0.4 | 2.405852 × 10−2 | 1.202592 × 10−2 | 2.404771 × 10−3 | 2.000000 × 10−10 | 2.000000 × 10−10 | |
| 0.6 | 2.290932 × 10−2 | 1.145148 × 10−2 | 2.289902 × 10−3 | 4.000000 × 10−10 | 4.000000 × 10−10 | |
| 0.8 | 2.1419859 × 10−2 | 1.070696 × 10−2 | 2.141023 × 10−3 | 4.000000 × 10−10 | 4.000000 × 10−10 | |
| 1 | 1.9687746 × 10−2 | 9.841145 × 10−3 | 1.967890 × 10−3 | 4.000000 × 10−10 | 4.000000 × 10−10 | |
| 0.02 | 0.2 | 2.481072 × 10−2 | 1.239979 × 10−2 | 2.479251 × 10−3 | 5.000000 × 10−10 | 5.000000 × 10−10 |
| 0.4 | 2.408340 × 10−2 | 1.203630 × 10−2 | 2.406573 × 10−3 | 1.000000 × 10−9 | 1.000000 × 10−9 | |
| 0.6 | 2.293301 × 10−2 | 1.146136 × 10−2 | 2.291618 × 10−3 | 1.400000 × 10−9 | 1.400000 × 10−9 | |
| 0.8 | 2.144201 × 10−2 | 1.071619 × 10−2 | 2.142627 × 10−3 | 1.700000 × 10−9 | 1.700000 × 10−9 | |
| 1 | 1.970810 × 10−2 | 9.849635 × 10−3 | 1.969363 × 10−3 | 1.800000 × 10−9 | 1.800000 × 10−9 | |
| 0.03 | 0.2 | 2.483378 × 10−2 | 1.240957 × 10−2 | 2.480968 × 10−3 | 1.100000 × 10−9 | 1.100000 × 10−9 |
| 0.4 | 2.410579 × 10−2 | 1.204579 × 10−2 | 2.408239 × 10−3 | 2.100000 × 10−9 | 2.100000 × 10−9 | |
| 0.6 | 2.295433 × 10−2 | 1.147039 × 10−2 | 2.293204 × 10−3 | 2.900000 × 10−9 | 2.900000 × 10−9 | |
| 0.8 | 2.146194 × 10−2 | 1.072464 × 10−2 | 2.144109 × 10−3 | 3.700000 × 10−9 | 3.700000 × 10−9 | |
| 1 | 1.972642 × 10−2 | 9.857396 × 10−3 | 1.970725 × 10−3 | 4.000000 × 10−9 | 4.000000 × 10−9 | |
| 0.04 | 0.2 | 2.485524 × 10−2 | 1.241876 × 10−2 | 2.482596 × 10−3 | 2.000000 × 10−9 | 2.000000 × 10−9 |
| 0.4 | 2.412662 × 10−2 | 1.205471 × 10−2 | 2.409818 × 10−3 | 3.800000 × 10−9 | 3.800000 × 10−9 | |
| 0.6 | 2.297416 × 10−2 | 1.147889 × 10−2 | 2.294707 × 10−3 | 5.300000 × 10−9 | 5.300000 × 10−9 | |
| 0.8 | 2.148048 × 10−2 | 1.073258 × 10−2 | 2.145513 × 10−3 | 6.500000 × 10−9 | 6.500000 × 10−9 | |
| 1 | 1.974347 × 10−2 | 9.864694 × 10−3 | 1.972016 × 10−3 | 7.200000 × 10−9 | 7.200000 × 10−9 | |
| 0.05 | 0.2 | 2.487555 × 10−2 | 1.242752 × 10−2 | 2.484156 × 10−3 | 3.100000 × 10−9 | 3.100000 × 10−9 |
| 0.4 | 2.414633 × 10−2 | 1.206321 × 10−2 | 2.411331 × 10−3 | 5.900000 × 10−9 | 5.900000 × 10−9 | |
| 0.6 | 2.299293 × 10−2 | 1.148699 × 10−2 | 2.296147 × 10−3 | 8.300000 × 10−9 | 8.300000 × 10−9 | |
| 0.8 | 2.149803 × 10−2 | 1.074015 × 10−2 | 2.146859 × 10−3 | 1.030000 × 10−9 | 1.030000 × 10−9 | |
| 1 | 1.975959 × 10−2 | 9.871653 × 10−3 | 1.973252 × 10−3 | 1.130000 × 10−9 | 1.130000 × 10−9 |
| 0.1 | 1.66002 × 10−4 | 1.66002 × 10−4 | 9.95627 × 10−7 | 9.95627 × 10−7 | 2.48000 × 10−8 | 2.48000 × 10−8 |
| 0.2 | 1.62707 × 10−4 | 1.62707 × 10−4 | 2.61331 × 10−6 | 2.61331 × 10−6 | 4.92000 × 10−8 | 4.92000 × 10−8 |
| 0.3 | 1.56257 × 10−4 | 1.56257 × 10−4 | 4.12217 × 10−6 | 4.12217 × 10−6 | 7.26000 × 10−8 | 7.26000 × 10−8 |
| 0.4 | 1.46917 × 10−4 | 1.46917 × 10−4 | 5.46303 × 10−6 | 5.46303 × 10−6 | 9.47000 × 10−8 | 9.47000 × 10−8 |
| 0.5 | 1.35064 × 10−4 | 1.35064 × 10−4 | 6.58827 × 10−6 | 6.58827 × 10−6 | 1.15000 × 10−7 | 1.15000 × 10−7 |
| ℘ | ||||||
|---|---|---|---|---|---|---|
| 0.01 | 0.2 | 6.843036 × 10−2 | 1.383664 × 10−2 | 6.927804 × 10−3 | 2.223097 × 10−10 | 2.223097 × 10−10 |
| 0.4 | 6.362177 × 10−2 | 1.300789 × 10−2 | 6.521729 × 10−3 | 3.938473 × 10−10 | 3.938473 × 10−10 | |
| 0.6 | 5.705894 × 10−2 | 1.178846 × 10−2 | 5.917824 × 10−3 | 5.391620 × 10−10 | 5.391620 × 10−10 | |
| 0.8 | 4.954728 × 10−2 | 1.033387 × 10−2 | 5.193500 × 10−3 | 5.664495 × 10−10 | 5.664495 × 10−10 | |
| 1 | 4.183562 × 10−2 | 8.798218 × 10−3 | 4.426079 × 10−3 | 5.873327 × 10−10 | 5.873327 × 10−10 | |
| 0.02 | 0.2 | 6.849818 × 10−2 | 1.384696 × 10−2 | 6.932795 × 10−3 | 7.708391 × 10−10 | 7.708391 × 10−10 |
| 0.4 | 6.368210 × 10−2 | 1.301721 × 10−2 | 6.526244 × 10−3 | 1.487289 × 10−9 | 1.487289 × 10−9 | |
| 0.6 | 5.711074 × 10−2 | 1.179659 × 10−2 | 5.921768 × 10−3 | 1.900548 × 10−9 | 1.900548 × 10−9 | |
| 0.8 | 4.959041 × 10−2 | 1.034074 × 10−2 | 5.196840 × 10−3 | 2.161298 × 10−9 | 2.161298 × 10−9 | |
| 1 | 4.187066 × 10−2 | 8.803879 × 10−3 | 4.428836 × 10−3 | 2.265400 × 10−9 | 2.265400 × 10−9 | |
| 0.03 | 0.2 | 6.855899 × 10−2 | 1.385645 × 10−2 | 6.937398 × 10−3 | 1.845587 × 10−9 | 1.845587 × 10−9 |
| 0.4 | 6.373601 × 10−2 | 1.302575 × 10−2 | 6.530395 × 10−3 | 3.480376× 10−9 | 3.480376 × 10−9 | |
| 0.6 | 5.715685 × 10−2 | 1.180401 × 10−2 | 5.925381 × 10−3 | 4.484208 × 10−9 | 4.484208 × 10−9 | |
| 0.8 | 4.962867 × 10−2 | 1.034700 × 10−2 | 5.199890 × 10−3 | 4.984595 × 10−9 | 4.984595 × 10−9 | |
| 1 | 4.190163 × 10−2 | 8.809018 × 10−3 | 4.431346 × 10−3 | 5.034164 × 10−9 | 5.034164 × 10−9 | |
| 0.04 | 0.2 | 6.861545 × 10−2 | 1.386540 × 10−2 | 6.941751 × 10−3 | 3.246556 × 10−9 | 3.246556 × 10−9 |
| 0.4 | 6.378593 × 10−2 | 1.303379 × 10−2 | 6.534311 × 10−3 | 6.072957 × 10−9 | 6.072957 × 10−9 | |
| 0.6 | 5.719942 × 10−2 | 1.181098 × 10−2 | 5.928781 × 10−3 | 7.889992 × 10−9 | 7.889992 × 10−9 | |
| 0.8 | 4.966389 × 10−2 | 1.035285 × 10−2 | 5.202754 × 10−3 | 8.836192 × 10−9 | 8.836192 × 10−9 | |
| 1 | 4.193007 × 10−2 | 8.813821 × 10−3 | 4.433698 × 10−3 | 8.993703 × 10−9 | 8.993703 × 10−9 | |
| 0.05 | 0.2 | 6.866877 × 10−2 | 1.387396 × 10−2 | 6.945918 × 10−3 | 5.073744 × 10−9 | 5.073744 × 10−9 |
| 0.4 | 6.383297 × 10−2 | 1.304147 × 10−2 | 6.538053 × 10−3 | 9.365133 × 10−9 | 9.365133 × 10−9 | |
| 0.6 | 5.723945 × 10−2 | 1.181762 × 10−2 | 5.932024 × 10−3 | 1.231800 × 10−8 | 1.231800 × 10−8 | |
| 0.8 | 4.969693 × 10−2 | 1.035842 × 10−2 | 5.205480 × 10−3 | 1.381618 × 10−8 | 1.381618 × 10−8 | |
| 1 | 4.195668 × 10−2 | 8.818376 × 10−3 | 4.435932 × 10−3 | 1.404396 × 10−8 | 1.404396 × 10−8 |
| 0.1 | 2.55541 × 10−5 | 2.55541 × 10−5 | 7.55258 × 10−6 | 7.55258 × 10−6 | 4.20818 × 10−8 | 4.20818 × 10−8 |
| 0.2 | 4.15291 × 10−5 | 4.15291 × 10−5 | 1.27010 × 10−5 | 1.27010 × 10−5 | 8.15279 × 10−8 | 8.15279 × 10−8 |
| 0.3 | 5.42246 × 10−5 | 5.42246 × 10−5 | 1.68403 × 10−5 | 1.68403 × 10−5 | 1.17804 × 10−7 | 1.17804 × 10−7 |
| 0.4 | 6.28898 × 10−5 | 6.28898 × 10−5 | 1.97175 × 10−5 | 1.97175 × 10−5 | 1.49799 × 10−7 | 1.49799 × 10−7 |
| 0.5 | 6.72637 × 10−5 | 6.72637 × 10−5 | 2.12349 × 10−5 | 2.12349 × 10−5 | 1.76464 × 10−7 | 1.76464 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kbiri Alaoui, M.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical Investigation of Fractional-Order Cahn–Hilliard and Gardner Equations Using Two Novel Techniques. Mathematics 2022, 10, 1643. https://doi.org/10.3390/math10101643
Kbiri Alaoui M, Nonlaopon K, Zidan AM, Khan A, Shah R. Analytical Investigation of Fractional-Order Cahn–Hilliard and Gardner Equations Using Two Novel Techniques. Mathematics. 2022; 10(10):1643. https://doi.org/10.3390/math10101643
Chicago/Turabian StyleKbiri Alaoui, Mohammed, Kamsing Nonlaopon, Ahmed M. Zidan, Adnan Khan, and Rasool Shah. 2022. "Analytical Investigation of Fractional-Order Cahn–Hilliard and Gardner Equations Using Two Novel Techniques" Mathematics 10, no. 10: 1643. https://doi.org/10.3390/math10101643
APA StyleKbiri Alaoui, M., Nonlaopon, K., Zidan, A. M., Khan, A., & Shah, R. (2022). Analytical Investigation of Fractional-Order Cahn–Hilliard and Gardner Equations Using Two Novel Techniques. Mathematics, 10(10), 1643. https://doi.org/10.3390/math10101643







