Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm
Abstract
:1. Introduction
- Introducing a novel geometry-based optimization method, called CSA.
- Presenting a mathematical model for the proposed CSA, including the states of exploration and exploitation processes.
- Applying the proposed CSA and other comparative algorithms to determine the optimal solution of 23 well-known functions and three engineering design issues
- Applying the CSA to solve high-dimensional functions (100 and 1000 dimensions).
- Testing the superiority and significance of the CSA in comparison with other algorithms, performed by using a variety of statistical tests, including the mean, standard deviation, rank test, and p-values.
2. Circle Search Algorithm
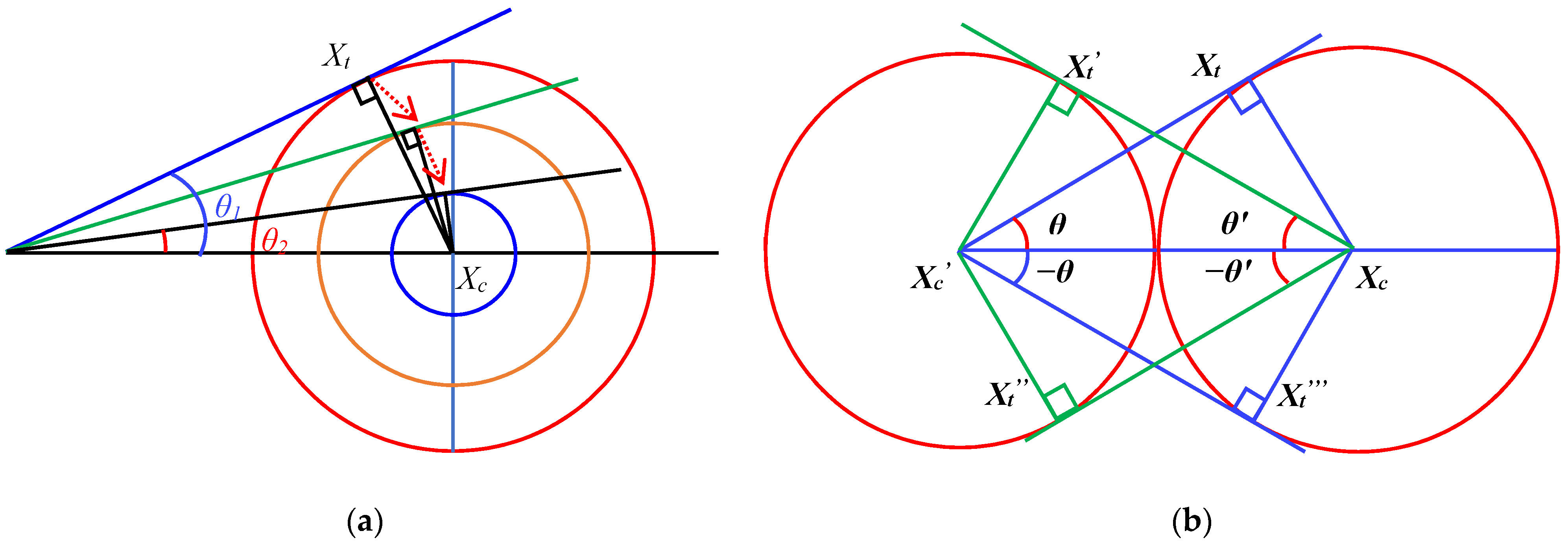
2.1. Background
2.2. CSA Formulation
- Case 1:Iter > (c.Maxiter): this case means that the angle all the time, which can applied to improve the exploration process of the CSA and escape the local stagnation.
- Case 2:Iter < (c.Maxiter): this case makes the angle all the time, which can be used to improve the exploitation process of the CSA.
| Algorithm 1 Initialization of the CSA |
| InputLBandUB. Do for all search agents r = random number between [0, 1]. Use Equation (4) to initialize the search agent Xt. End Do |
| Algorithm 2 Pseudo-code of the CSA |
| Initialize the search agentsXtusing Algorithm 1 Input the constant value c, Iter = 0, and Maxiter While Iter less than Maxiter Use Equation (8) to find the value of a Do for all search agents Use Equation (7) to find the value of w Use Equation (9) to find the value of p Use Equation (6) to find the value of the angle θ Use Equation (5) to update the search agent Xt if the updated search agents are out of the boundaries then set search agents equal to the boundaries find the fitness function f(Xt) End Do Evaluate the f(Xt) with the stored best solution f(Xc) Update f(Xc) and Xc Iter = Iter + 1 End While Output f(Xc) and Xc |
3. Computational Complexity of the CSA
4. Experimental Results and Discussion
4.1. Standard Functions
4.2. Comparative Algorithms
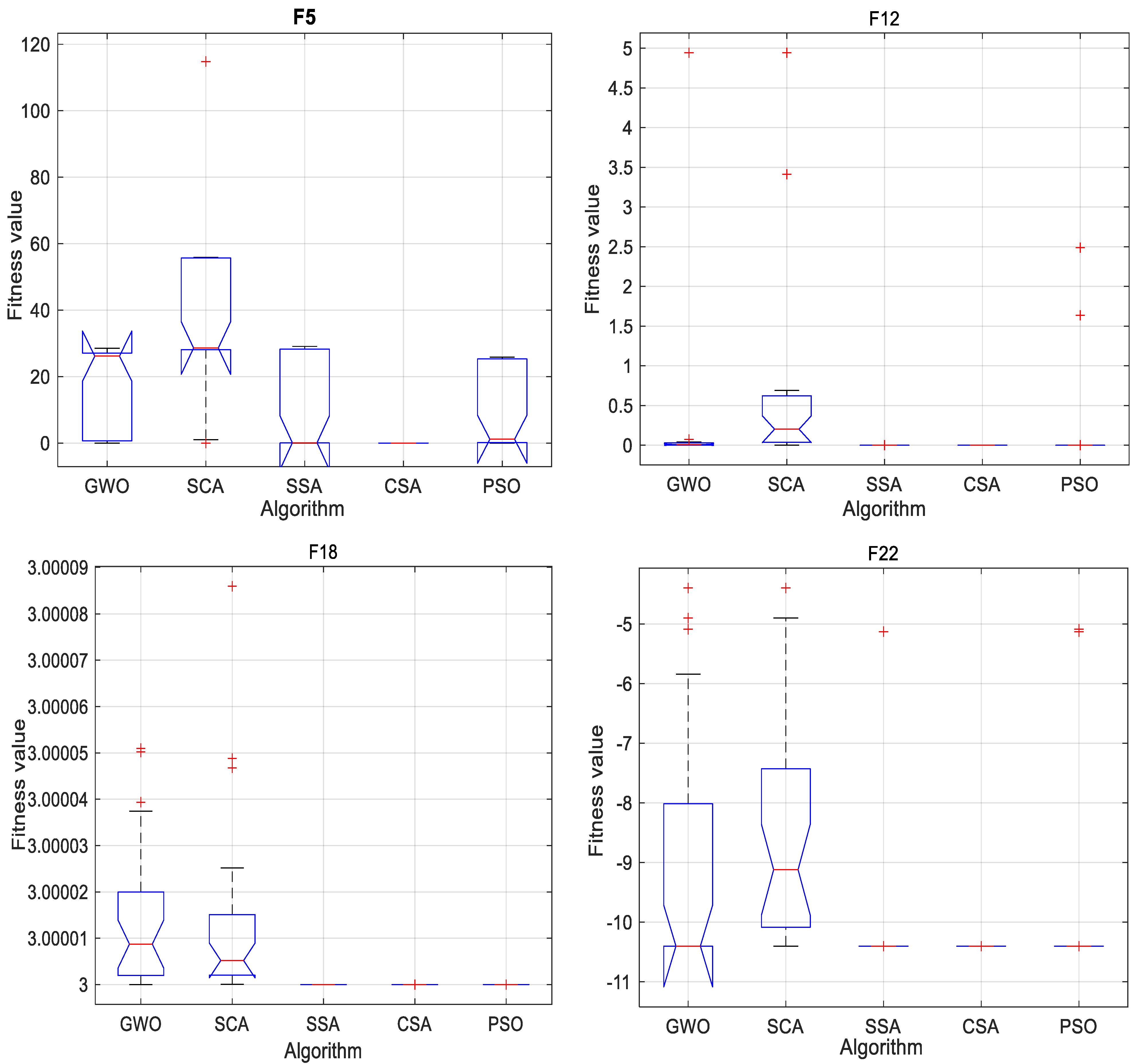
4.3. Statistical Analysis
4.4. High-Dimensional Functions
4.5. Computational Time
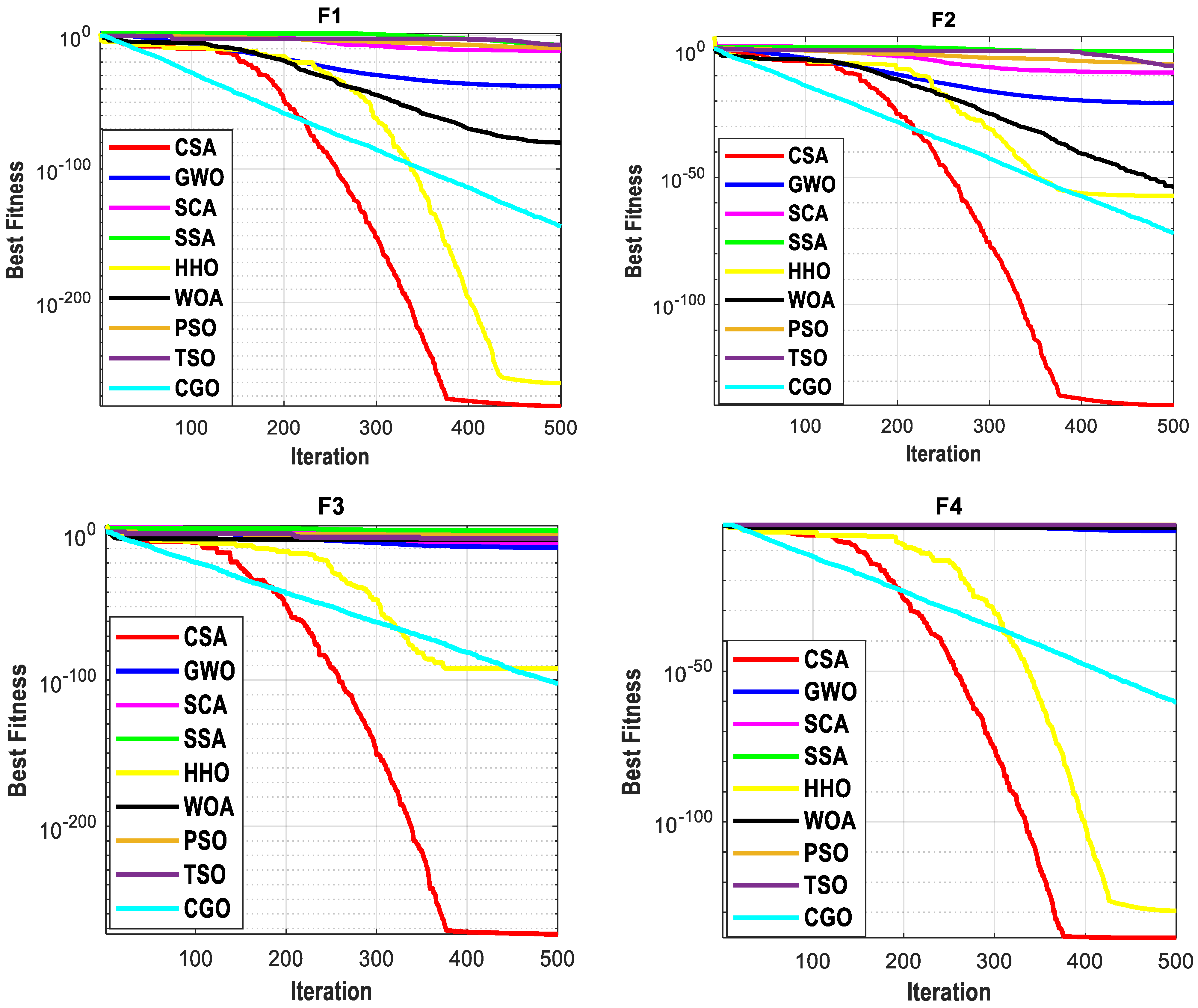
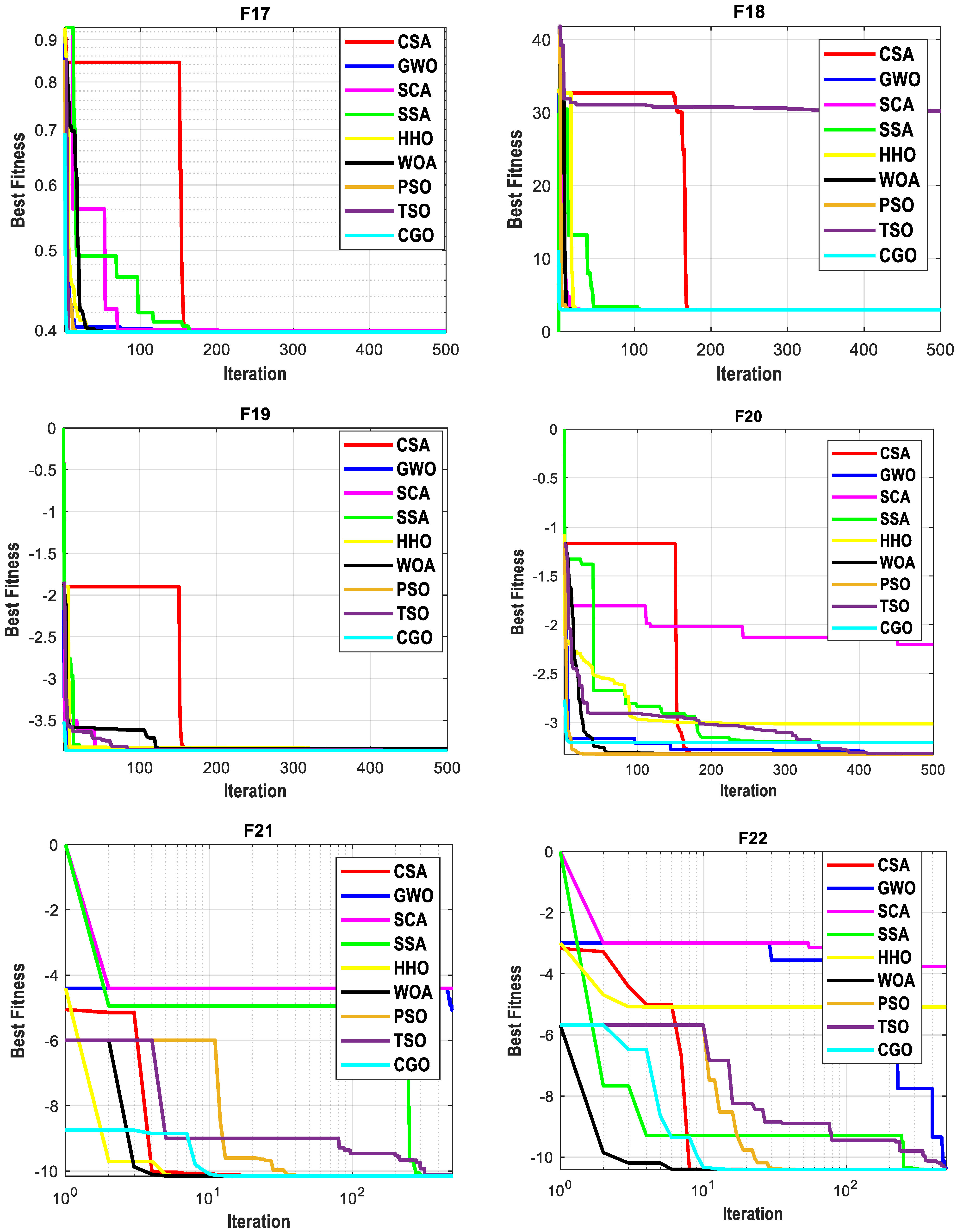
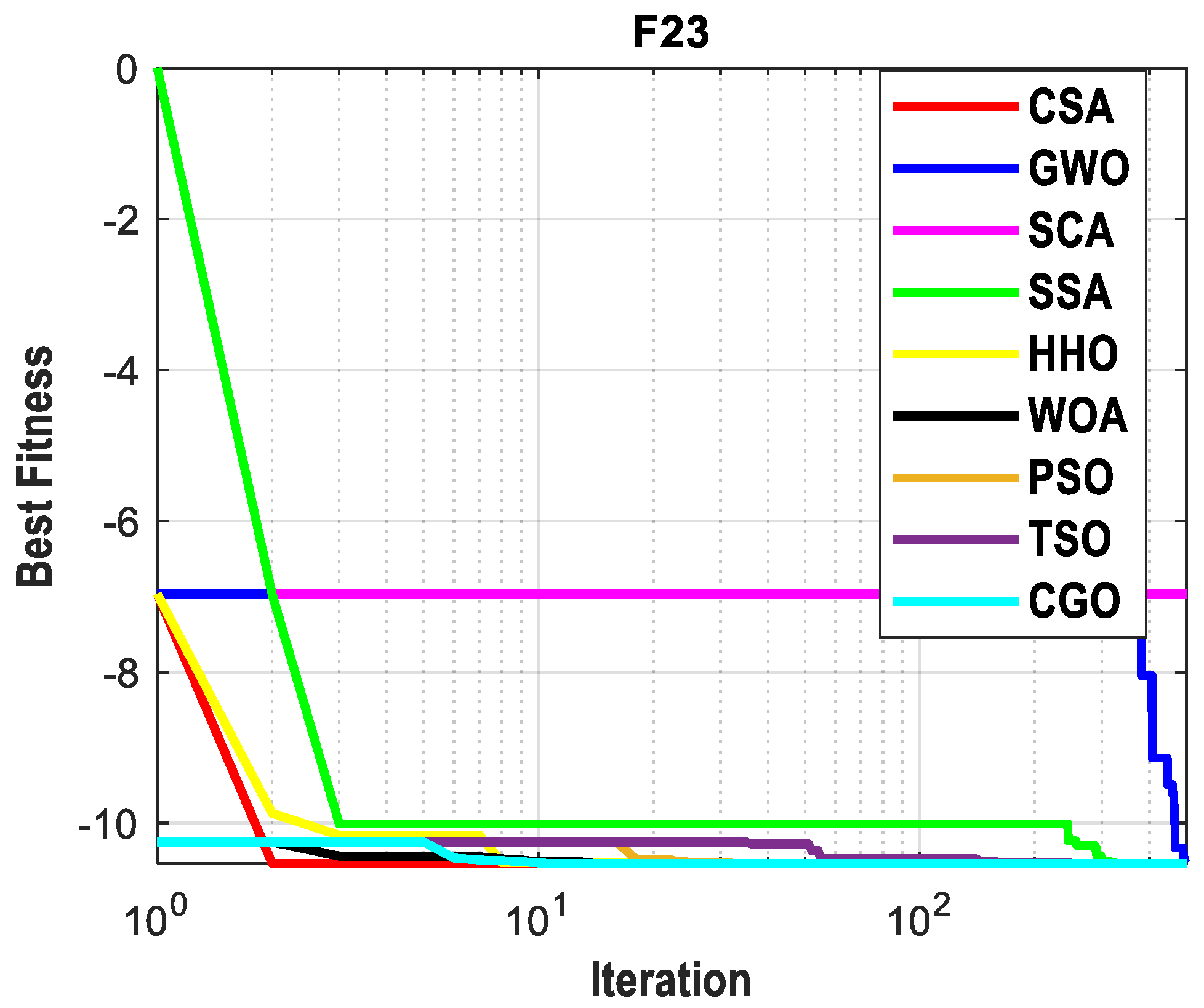
4.6. Convergence Speed
5. Real-World Engineering Problems
5.1. Welded Beam
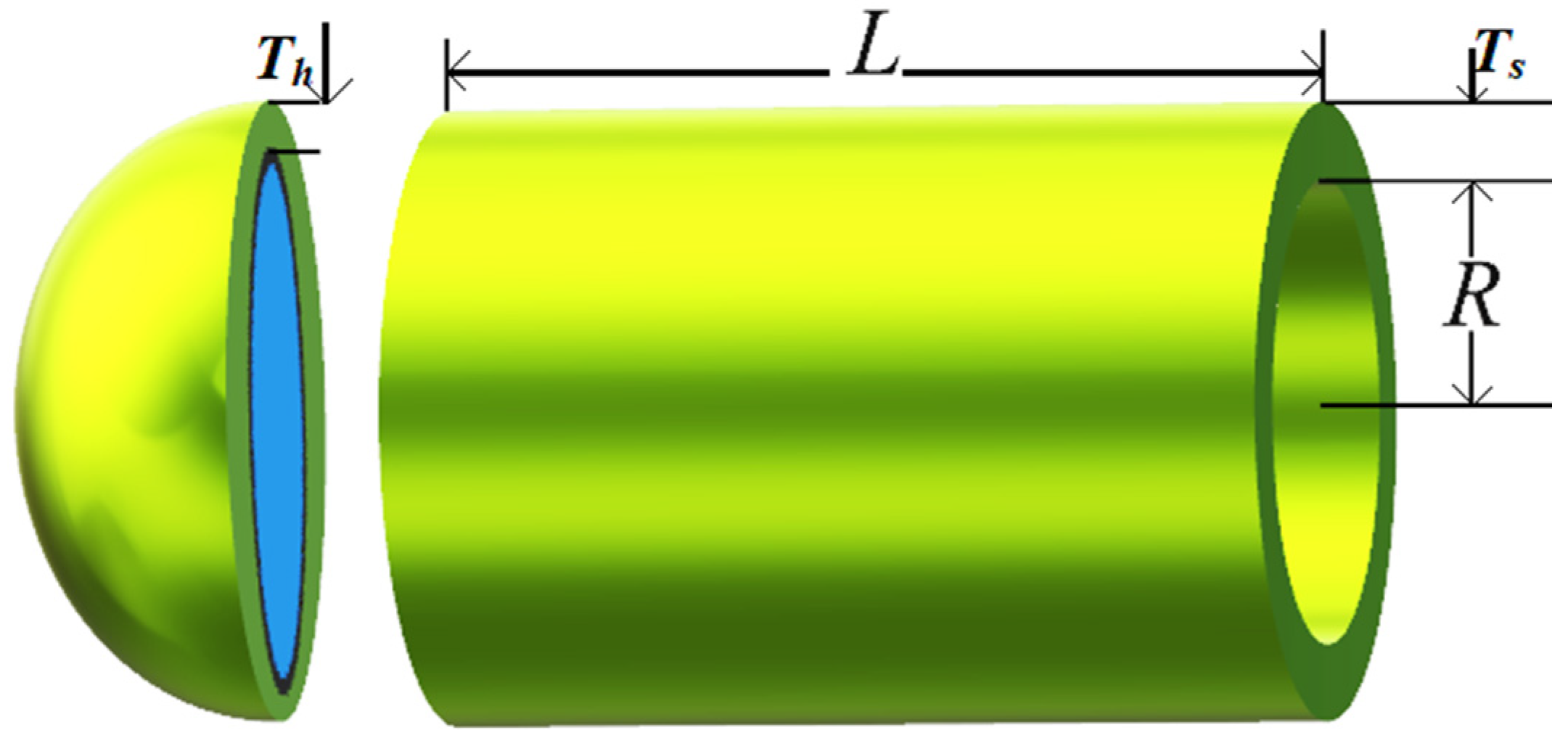
5.2. Pressure Vessel
5.3. Tension Spring
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, P.C.; Shoup, T.E. Parameter sensitivity study of the Nelder-Mead Simplex Method. Adv. Eng. Softw. 2011, 42, 529–533. [Google Scholar] [CrossRef]
- Altinoz, O.T.; Yilmaz, A.E. Multiobjective Hooke–Jeeves algorithm with a stochastic Newton–Raphson-like step-size method. Expert Syst. Appl. 2019, 117, 166–175. [Google Scholar] [CrossRef]
- Leardi, R. Genetic Algorithms. Compr. Chemom. 2009, 1, 631–653. [Google Scholar]
- Clerc, M. Particle Swarm Optimization; ISTE: London, UK, 2006; Volume 4, ISBN 9780470612163. [Google Scholar]
- Qais, M.; Abdulwahid, Z. A new method for improving particle swarm optimization algorithm (TriPSO). In Proceedings of the 2013 5th International Conference on Modeling, Simulation and Applied Optimization, Hammamet, Tunisia, 28–30 April 2013. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. Artificial Bee Colony (ABC) optimization algorithm for solving constrained optimization problems. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Cancun, Mexico, 18–21 June 2007; Melin, P., Castillo, O., Aguilar, L.T., Kacprzyk, J., Pedrycz, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4529, pp. 789–798. [Google Scholar]
- Ji, J.; Song, S.; Tang, C.; Gao, S.; Tang, Z.; Todo, Y. An artificial bee colony algorithm search guided by scale-free networks. Inf. Sci. 2019, 473, 142–165. [Google Scholar] [CrossRef]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic Bat-inspired Algorithm. In Studies in Computational Intelligence; González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. ISBN 9783642125379. [Google Scholar]
- Cheng, M.Y.; Prayogo, D. Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Qi, X.; Zhu, Y.; Zhang, H. A new meta-heuristic butterfly-inspired algorithm. J. Comput. Sci. 2017, 23, 226–239. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Oftadeh, R.; Mahjoob, M.J.; Shariatpanahi, M. A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search. Comput. Math. Appl. 2010, 60, 2087–2098. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Pierezan, J.; Dos Santos Coelho, L. Coyote Optimization Algorithm: A New Metaheuristic for Global Optimization Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Kaveh, A.; Farhoudi, N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013, 59, 53–70. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Li, V.O.K. A social spider algorithm for global optimization. Appl. Soft Comput. J. 2015, 30, 614–627. [Google Scholar] [CrossRef] [Green Version]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Askarzadeh, A. Bird mating optimizer: An optimization algorithm inspired by bird mating strategies. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1213–1228. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S.; Elgendy, M.A. Output Power Smoothing of Grid-Tied PMSG-Based Variable Speed Wind Turbine Using Optimal Controlled SMES. In Proceedings of the 2019 54th International Universities Power Engineering Conference, Bucharest, Romania, 3–6 September 2019; pp. 1–6. [Google Scholar]
- Kallioras, N.A.; Lagaros, N.D.; Avtzis, D.N. Pity beetle algorithm—A new metaheuristic inspired by the behavior of bark beetles. Adv. Eng. Softw. 2018, 121, 147–166. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Mohammadi-Balani, A.; Dehghan Nayeri, M.; Azar, A.; Taghizadeh-Yazdi, M. Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Comput. Ind. Eng. 2021, 152, 107050. [Google Scholar] [CrossRef]
- Gomes, G.F.; da Cunha, S.S.; Ancelotti, A.C. A sunflower optimization (SFO) algorithm applied to damage identification on laminated composite plates. Eng. Comput. 2019, 35, 619–626. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Yang, X.S. Flower pollination algorithm for global optimization. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Orléan, France, 3–7 September 2012; Springer: Berlin/Heidelberg, Germany; Volume 7445, pp. 240–249. [Google Scholar]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T. Water Evaporation Optimization: A novel physically inspired optimization algorithm. Comput. Struct. 2016, 167, 69–85. [Google Scholar] [CrossRef]
- Patel, V.K.; Savsani, V.J. Heat transfer search (HTS): A novel optimization algorithm. Inf. Sci. 2015, 324, 217–246. [Google Scholar] [CrossRef]
- Shayanfar, H.; Gharehchopogh, F.S. Farmland fertility: A new metaheuristic algorithm for solving continuous optimization problems. Appl. Soft Comput. J. 2018, 71, 728–746. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras Eslamlou, A. Water strider algorithm: A new metaheuristic and applications. Structures 2020, 25, 520–541. [Google Scholar] [CrossRef]
- Moazzeni, A.R.; Khamehchi, E. Rain optimization algorithm (ROA): A new metaheuristic method for drilling optimization solutions. J. Pet. Sci. Eng. 2020, 195, 107512. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Output power smoothing of grid-connected permanent-magnet synchronous generator driven directly by variable speed wind turbine: A review. J. Eng. 2017, 2017, 1755–1759. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Y.; Gao, S.; Pan, H.; Yang, G. A hierarchical gravitational search algorithm with an effective gravitational constant. Swarm Evol. Comput. 2019, 46, 118–139. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Francisco, M.B.; Diniz, C.A.; Antônio Oliver, G.; Cunha, S.S.; Gomes, G.F. Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization. Expert Syst. Appl. 2021, 170, 114522. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Futur. Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Qais, M.; Khaled, U.; Alghuwainem, S. Improved differential relay for bus bar protection scheme with saturated current transformers based on second order harmonics. J. King Saud Univ. Eng. Sci. 2018, 30, 320–329. [Google Scholar] [CrossRef] [Green Version]
- Qais, M.; Khaled, U. Evaluation of V–t characteristics caused by lightning strokes at different locations along transmission lines. J. King Saud Univ. Eng. Sci. 2018, 30, 150–160. [Google Scholar] [CrossRef] [Green Version]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V.R. Colliding bodies optimization: A novel meta-heuristic method. Comput. Struct. 2014, 139, 18–27. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl. Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray Optimization. Comput. Struct. 2012, 112–113, 283–294. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization: A new meta-heuristic optimization algorithm. Appl. Intell. 2020, 50, 3926–3941. [Google Scholar] [CrossRef]
- Muthiah-Nakarajan, V.; Noel, M.M. Galactic Swarm Optimization: A new global optimization metaheuristic inspired by galactic motion. Appl. Soft Comput. J. 2016, 38, 771–787. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization: A new nature inspired computational framework for multidimensional search and optimization. Stud. Comput. Intell. 2008, 129, 221–238. [Google Scholar]
- Javidy, B.; Hatamlou, A.; Mirjalili, S. Ions motion algorithm for solving optimization problems. Appl. Soft Comput. J. 2015, 32, 72–79. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Danesh, M.; Gheyratmand, C. A new Newton metaheuristic algorithm for discrete performance-based design optimization of steel moment frames. Comput. Struct. 2020, 234, 106250. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Azizi, M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021, 93, 657–683. [Google Scholar] [CrossRef]
- Talatahari, S.; Azizi, M. Chaos Game Optimization: A novel metaheuristic algorithm. Artif. Intell. Rev. 2021, 54, 917–1004. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Aarts, E.H.L. (Eds.) Simulated Annealing: Theory and Applications; Springer: Dordrecht, The Netherlands, 1987; pp. 7–15. ISBN 978-94-015-7744-1. [Google Scholar]
- Hasanien, H.M.; Muyeen, S.M. Particle swarm optimization-based superconducting magnetic energy storage for low-voltage ride-through capability enhancement in wind energy conversion system. Electr. Power Compon. Syst. 2015, 43, 1278–1288. [Google Scholar] [CrossRef] [Green Version]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Enhanced whale optimization algorithm for maximum power point tracking of variable-speed wind generators. Appl. Soft Comput. J. 2020, 86, 105937. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Augmented grey wolf optimizer for grid-connected PMSG-based wind energy conversion systems. Appl. Soft Comput. J. 2018, 69, 504–515. [Google Scholar] [CrossRef]
- Qais, M.; Hasanien, H.M.; Alghuwainem, S. Salp swarm algorithm-based TS-FLCs for MPPT and fault ride-through capability enhancement of wind generators. ISA Trans. 2020, 101, 211–224. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. A Grey Wolf Optimizer for Optimum Parameters of Multiple PI Controllers of a Grid-Connected PMSG Driven by Variable Speed Wind Turbine. IEEE Access 2018, 6, 44120–44128. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Whale optimization algorithm-based Sugeno fuzzy logic controller for fault ride-through improvement of grid-connected variable speed wind generators. Eng. Appl. Artif. Intell. 2020, 87, 103328. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Identification of electrical parameters for three-diode photovoltaic model using analytical and sunflower optimization algorithm. Appl. Energy 2019, 250, 109–117. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S.; Nouh, A.S. Coyote optimization algorithm for parameters extraction of three-diode photovoltaic models of photovoltaic modules. Energy 2019, 187, 116001. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Parameters extraction of three-diode photovoltaic model using computation and Harris Hawks optimization. Energy 2020, 195, 117040. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization for electrical parameters estimation of photovoltaic module based on datasheet values. Energy Convers. Manag. 2020, 214, 112904. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Optimal transient search algorithm-based PI controllers for enhancing low voltage ride-through ability of grid-linked PMSG-based wind turbine. Electronics 2020, 9, 1807. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Wu, Q.; Zhu, S.; Zhang, L. Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems. Expert Syst. Appl. 2022, 188, 116026. [Google Scholar] [CrossRef]
- Suyanto, S.; Ariyanto, A.A.; Ariyanto, A.F. Komodo Mlipir Algorithm. Appl. Soft Comput. 2022, 114, 108043. [Google Scholar] [CrossRef]
- Li, C.; Chen, G.; Liang, G.; Luo, F.; Zhao, J.; Dong, Z.Y. Integrated optimization algorithm: A metaheuristic approach for complicated optimization. Inf. Sci. 2022, 586, 424–449. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Jafari, M.; Salajegheh, E.; Salajegheh, J. Elephant clan optimization: A nature-inspired metaheuristic algorithm for the optimal design of structures. Appl. Soft Comput. 2021, 113, 107892. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Liu, S. Cooperation search algorithm: A novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems. Appl. Soft Comput. 2021, 98, 106734. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z. Group teaching optimization algorithm: A novel metaheuristic method for solving global optimization problems. Expert Syst. Appl. 2020, 148, 113246. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Shabani, A.; Asgarian, B.; Salido, M.; Asil Gharebaghi, S. Search and rescue optimization algorithm: A new optimization method for solving constrained engineering optimization problems. Expert Syst. Appl. 2020, 161, 113698. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]






| Algorithm | Name | Reference | Classification | Mimicking |
|---|---|---|---|---|
| Orca predation algorithm | OPA | [76] | Biology-based (hunters) | The orcas’ hunting habit. |
| Komodo mlipir algorithm | KMA | [77] | Biology-based | Komodo dragons and miliper foraging and reproduction |
| Integrated optimization algorithm | IOA | [78] | Evolutionarily based | Follower search, leader search, wanderer search, crossover search, and role learning are all terms used to construct IOA |
| Reptile search algorithm | RSA | [79] | Biology-based (hunters) | Crocodiles’ hunting habit |
| African vultures optimization | AVOA | [80] | Biology-based | African vultures’ feeding and navigational behaviors |
| Elephant clan optimization | ECO | [81] | Biology-based | Elephants’ clan behavior. |
| Cooperation search algorithm | CoSA | [82] | Human-learning-based | The behaviors of teamwork in contemporary business |
| Group teaching optimization | GTOA | [83] | Human-learning-based | The relationship between the instructor and his or her pupils |
| Mayfly algorithm | MA | [84] | Biology-based | Mayfly flying and mating behavior |
| Search and rescue optimization algorithm | SAR | [85] | Human-learning-based | The study of human behavior during search and rescue missions |
| Function | Expression | Dimension (d) | Solution Space | Best Solution |
|---|---|---|---|---|
| F1 | 30, 100, 1000 | [−100, 100]d | 0 | |
| F2 | 30, 100, 1000 | [−10, 10]d | 0 | |
| F3 | 30, 100, 1000 | [−100, 100]d | 0 | |
| F4 | 30, 100, 1000 | [−100, 100]d | 0 | |
| F5 | 30, 100, 1000 | [−30, 30]d | 0 | |
| F6 | 30, 100, 1000 | [−100, 100]d | 0 | |
| F7 | 30, 100, 1000 | [−1.28, 1.28]d | 0 |
| Function | Expression | Dimension (d) | Solution Space | Best Solution |
|---|---|---|---|---|
| F8 | 30, 100, 1000 | [−500, 500]d | −418.9829 × d | |
| F9 | 30, 100, 1000 | [−5.12, 5.12]d | 0 | |
| F10 | 30, 100, 1000 | [−32, 32]d | 0 | |
| F11 | 30, 100, 1000 | [−600, 600]d | 0 | |
| F12 | 30, 100, 1000 | [−50, 50]d | 0 | |
| F13 | 30, 100, 1000 | [−50, 50]d | 0 |
| Function | Expression | Dimension (d) | Solution Space | Best Solution |
|---|---|---|---|---|
| F14 | 2 | [−65, 65]d | 1 | |
| F15 | 4 | [−5, 5]d | 0.00030 | |
| F16 | 2 | [−5, 5]d | −1.0316 | |
| F17 | 2 | [−5, 5]d | 0.398 | |
| F18 | 2 | [−2, 2]d | 3 | |
| F19 | 3 | [1, 3]d | −3.86 | |
| F20 | 6 | [0, 1]d | −3.32 | |
| F21 | 4 | [0, 10]d | −10.1532 | |
| F22 | 4 | [0, 10]d | −10.4028 | |
| F23 | 4 | [0, 10]d | −10.5363 |
| Algorithm | Parameters |
|---|---|
| Proposed CSA | w decreased from 1.5 to 0 and constant c = 0.75 for F1–F13 and c = 0.3 for F14–F23 |
| PSO | Inertia weight w decreased from 0.5 to 0.3, c1 = 2, and c2 = 2 |
| GWO | The parameter a changed from 2 to 0 |
| SSA | Probability update was 0.5 |
| SCA | Constant a = 2 and probability update was 0.5 |
| WOA | The parameter a changed from 2 to 0, b = 1 |
| HHO | The decreasing energy E1 changed from 2 to 0 |
| CGO | α, β, and γ were random numbers |
| TSO | The parameter a changed from 2 to 0 |
| GWO | SCA | SSA | HHO | WOA | PSO | TSO | CGO | CSA | ||
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg. | 5.7838 × 10−38 | 6.5806 × 10−11 | 9.5464 × 10−08 | 1.4759 × 10−109 | 6.6351 × 10−69 | 4.6281 × 10−07 | 1.0826 × 10−03 | 1.1934 × 10−136 | 9.5326 × 10−219 |
| STD. | 9.1734 × 10−38 | 2.7669 × 10−10 | 5.2552 × 10−08 | 8.0839 × 10−109 | 3.6342 × 10−68 | 1.0552 × 10−06 | 3.9713 × 10−03 | 4.7846 × 10−136 | 0.0000 × 1000 | |
| Min | 1.1944 × 10−40 | 1.9641 × 10−15 | 3.3386 × 10−08 | 0.0000 × 1000 | 6.6909 × 10−86 | 2.3249 × 10−10 | 8.9536 × 10−08 | 0.0000 × 1000 | 2.9648 × 10−278 | |
| F2 | Avg. | 1.8357 × 10−22 | 3.1710 × 10−08 | 2.6003 × 10−01 | 3.4043 × 10−53 | 6.7368 × 10−50 | 5.3551 × 10−04 | 8.4374 × 10−06 | 1.7566 × 10−71 | 1.3380 × 10−92 |
| STD. | 3.6643 × 10−22 | 4.5318 × 10−08 | 1.8497 × 10−01 | 1.2317 × 10−52 | 3.3959 × 10−49 | 8.9901 × 10−04 | 1.2036 × 10−05 | 7.9508 × 10−71 | 7.3287 × 10−92 | |
| Min | 1.1603 × 10−23 | 1.1753 × 10−09 | 4.5012 × 10−03 | 9.7243 × 10−172 | 1.1799 × 10−57 | 2.8776 × 10−06 | 6.5020 × 10−07 | 0.0000 × 1000 | 3.4777 × 10−140 | |
| F3 | Avg. | 1.2328 × 10−08 | 1.0265 × 10−07 | 3.0191 × 1002 | 5.3195 × 10−78 | 1.7475 × 10−01 | 1.0393 × 1003 | 3.9684 × 1002 | 1.0135 × 10−98 | 3.5072 × 10−192 |
| STD. | 3.2665 × 10−08 | 3.1441 × 10−07 | 4.7355 × 1002 | 2.0975 × 10−77 | 4.9298 × 10−01 | 9.4985 × 1002 | 1.0181 × 1003 | 2.6061 × 10−98 | 0.0000 × 1000 | |
| Min | 3.4277 × 10−12 | 9.8383 × 10−13 | 1.1474 × 1000 | 4.6827 × 10−103 | 7.1459 × 10−08 | 3.8895 × 10−02 | 4.5120 × 10−04 | 0.0000 × 1000 | 1.2646 × 10−274 | |
| F4 | Avg. | 5.7254 × 10−01 | 1.0814 × 1000 | 1.0281 × 1000 | 1.5750 × 10−119 | 4.8675 × 10−02 | 3.0927 × 1000 | 7.2259 × 10−01 | 6.5523 × 10−59 | 1.2504 × 10−98 |
| STD. | 1.0996 × 1000 | 2.5084 × 1000 | 8.5943 × 10−01 | 8.6266 × 10−119 | 1.3524 × 10−01 | 2.9911 × 1000 | 6.7465 × 10−01 | 1.2075 × 10−58 | 6.8486 × 10−98 | |
| Min | 4.2053 × 10−08 | 9.9628 × 10−05 | 2.8062 × 10−02 | 8.0269 × 10−181 | 6.5725 × 10−06 | 2.8062 × 10−02 | 6.0508 × 10−03 | 0.0000 × 1000 | 3.0109 × 10−139 | |
| F5 | Avg. | 2.5381 × 1001 | 7.0200 × 1001 | 2.5675 × 1001 | 1.8902 × 10−06 | 8.5474 × 1000 | 1.9573 × 1001 | 1.1420 × 1001 | 1.5351 × 1001 | 0.0000 × 1000 |
| STD. | 1.5260 × 1001 | 1.3659 × 1002 | 2.4616 × 1001 | 1.0192 × 10−05 | 1.2854 × 1001 | 2.3932 × 1001 | 1.2831 × 1001 | 5.4322 × 1000 | 0.0000 × 1000 | |
| Min | 7.5169 × 10−02 | 7.5169 × 10−02 | 9.3447 × 10−04 | 0.0000 × 1000 | 2.3611 × 10−07 | 4.2949 × 10−05 | 4.6622 × 10−03 | 3.2114 × 10−06 | 0.0000 × 1000 | |
| F6 | Avg. | 5.4155 × 10−01 | 5.3173 × 1000 | 2.0211 × 10−07 | 2.8436 × 10−07 | 1.3848 × 10−02 | 4.7315 × 10−07 | 4.8451 × 10−01 | 1.8244 × 10−18 | 0.0000 × 1000 |
| STD. | 3.5419 × 10−01 | 8.0594 × 10−01 | 3.5045 × 10−07 | 1.4406 × 10−06 | 2.4111 × 10−02 | 8.7532 × 10−07 | 4.2675 × 10−01 | 5.9259 × 10−18 | 0.0000 × 1000 | |
| Min | 2.8333 × 10−04 | 1.2272 × 1000 | 2.4022 × 10−08 | 0.0000 × 1000 | 7.5679 × 10−08 | 5.0032 × 10−09 | 3.5827 × 10−02 | 6.2486 × 10−24 | 0.0000 × 1000 | |
| F7 | Avg. | 1.3202 × 10−03 | 4.7389 × 10−04 | 4.0651 × 10−02 | 1.0839 × 10−04 | 1.2714 × 10−03 | 2.7046 × 10−02 | 2.5284 × 10−03 | 4.6345 × 10−04 | 3.8180 × 10−04 |
| STD. | 6.4299 × 10−04 | 4.4640 × 10−04 | 4.0466 × 10−02 | 1.0664 × 10−04 | 2.4965 × 10−03 | 2.5014 × 10−02 | 2.8216 × 10−03 | 3.4197 × 10−04 | 6.6990 × 10−04 | |
| Min | 2.8985 × 10−04 | 4.5957 × 10−06 | 2.1466 × 10−03 | 1.3803 × 10−05 | 7.2309 × 10−07 | 7.7340 × 10−04 | 1.1353 × 10−04 | 7.3420 × 10−05 | 2.6012 × 10−05 | |
| F8 | Avg. | −1.1269 × 1004 | −1.1117 × 1004 | −1.2096 × 1004 | −1.2569 × 1004 | −1.2427 × 1004 | −1.2071 × 1004 | −1.2223 × 1004 | −1.2451 × 1004 | −1.2569 × 1004 |
| STD. | 1.6040 × 1003 | 1.5893 × 1003 | 1.2285 × 1003 | 2.3541 × 10−09 | 6.5709 × 1002 | 1.2389 × 1003 | 9.5254 × 1002 | 6.4871 × 1002 | 1.9404 × 10−12 | |
| Min | −1.2557 × 1004 | −1.2551 × 1004 | −1.2569 × 1004 | −1.2569 × 1004 | −1.2569 × 1004 | −1.2569 × 1004 | −1.2569 × 1004 | −1.2569 × 1004 | −1.2569 × 1004 | |
| F9 | Avg. | 4.1807 × 1001 | 4.0559 × 1001 | 9.9496 × 1000 | 0.0000 × 1000 | 1.8948 × 10−15 | 3.0214 × 1001 | 2.2908 × 1000 | 0.0000 × 1000 | 0.0000 × 1000 |
| STD. | 3.5269 × 1001 | 4.2016 × 1001 | 1.4311 × 1001 | 0.0000 × 1000 | 1.0378 × 10−14 | 3.3687 × 1001 | 1.2547 × 1001 | 0.0000 × 1000 | 0.0000 × 1000 | |
| Min | 0.0000 × 1000 | 0.0000 × 1000 | 2.3251 × 10−08 | 0.0000 × 1000 | 0.0000 × 1000 | 2.7281 × 10−08 | 1.7390 × 10−08 | 0.0000 × 1000 | 0.0000 × 1000 | |
| F10 | Avg. | 1.1978 × 10−01 | 2.5187 × 10−01 | 9.4409 × 10−01 | 8.8818 × 10−16 | 5.0330 × 10−15 | 9.1797 × 10−01 | 1.3331 × 10−01 | 2.7830 × 10−15 | 8.8818 × 10−16 |
| STD. | 6.5604 × 10−01 | 9.5974 × 10−01 | 1.2595 × 1000 | 0.0000 × 1000 | 2.9626 × 10−15 | 1.9652 × 1000 | 7.2493 × 10−01 | 1.8027 × 10−15 | 0.0000 × 1000 | |
| Min | 7.9936 × 10−15 | 6.1332 × 10−09 | 4.1912 × 10−05 | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.9230 × 10−06 | 7.4523 × 10−06 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| F11 | Avg. | 3.7391 × 10−03 | 2.1526 × 10−07 | 1.8495 × 10−02 | 0.0000 × 1000 | 0.0000 × 1000 | 1.1234 × 10−02 | 6.6144 × 10−02 | 0.0000 × 1000 | 0.0000 × 1000 |
| STD. | 1.0062 × 10−02 | 1.1396 × 10−06 | 1.4792 × 10−02 | 0.0000 × 1000 | 0.0000 × 1000 | 1.3511 × 10−02 | 1.5859 × 10−01 | 0.0000 × 1000 | 0.0000 × 1000 | |
| Min | 0.0000 × 1000 | 3.2196 × 10−15 | 4.8962 × 10−04 | 0.0000 × 1000 | 0.0000 × 1000 | 2.9305 × 10−09 | 1.8765 × 10−08 | 0.0000 × 1000 | 0.0000 × 1000 | |
| F12 | Avg. | 1.2064 × 1000 | 1.4563 × 1000 | 1.9961 × 10−02 | 1.0540 × 10−08 | 3.7369 × 10−04 | 7.9748 × 10−01 | 7.4001 × 10−03 | 1.3909 × 10−20 | 1.5705 × 10−32 |
| STD. | 2.5890 × 1000 | 2.4947 × 1000 | 7.7080 × 10−02 | 3.8589 × 10−08 | 1.1984 × 10−03 | 1.7667 × 1000 | 1.2526 × 10−02 | 6.6394 × 10−20 | 5.5674 × 10−48 | |
| Min | 1.6660 × 10−05 | 2.1551 × 10−04 | 4.8395 × 10−07 | 6.3387 × 10−21 | 2.1843 × 10−09 | 3.6269 × 10−13 | 1.3758 × 10−06 | 1.0149 × 10−25 | 1.5705 × 10−32 | |
| F13 | Avg. | 2.3921 × 10−01 | 1.8630 × 1000 | 4.0527 × 10−01 | 7.6694 × 10−07 | 2.4754 × 10−03 | 2.3928 × 10−01 | 1.5123 × 10−01 | 2.2315 × 10−02 | 1.3498 × 10−32 |
| STD. | 2.3561 × 10−01 | 9.1497 × 10−01 | 1.5566 × 1000 | 3.5053 × 10−06 | 6.0994 × 10−03 | 1.2677 × 1000 | 1.5863 × 10−01 | 5.2790 × 10−02 | 5.5674 × 10−48 | |
| Min | 5.3035 × 10−04 | 3.4038 × 10−02 | 7.9766 × 10−06 | 1.3498 × 10−32 | 2.8468 × 10−09 | 1.1833 × 10−10 | 6.0890 × 10−05 | 8.1780 × 10−24 | 1.3498 × 10−32 | |
| F14 | Avg. | 3.2156 × 1000 | 1.9345 × 1000 | 1.0643 × 1000 | 9.9800 × 10−01 | 9.9800 × 10−01 | 1.0311 × 1000 | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 |
| STD. | 3.8889 × 1000 | 9.9707 × 10−01 | 2.5219 × 10−01 | 1.5699 × 10−10 | 1.3046 × 10−08 | 1.8148 × 10−01 | 1.7835 × 10−07 | 0.0000 × 1000 | 1.7494 × 10−16 | |
| Min | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 | 9.9800 × 10−01 | |
| F15 | Avg. | 4.0459 × 10−04 | 5.7433 × 10−04 | 6.4506 × 10−04 | 3.2725 × 10−04 | 3.2225 × 10−04 | 4.6375 × 10−04 | 3.7770 × 10−04 | 3.3801 × 10−04 | 3.0806 × 10−04 |
| STD. | 1.1637 × 10−04 | 2.5944 × 10−04 | 3.3345 × 10−04 | 2.2421 × 10−05 | 2.5146 × 10−05 | 2.4872 × 10−04 | 1.7279 × 10−04 | 1.6718 × 10−04 | 7.8742 × 10−07 | |
| Min | 3.0749 × 10−04 | 3.3338 × 10−04 | 3.0769 × 10−04 | 3.0751 × 10−04 | 3.0784 × 10−04 | 3.0749 × 10−04 | 3.0758 × 10−04 | 3.0749 × 10−04 | 3.0749 × 10−04 | |
| F16 | Avg. | −1.0316 × 1000 | −1.0315 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 |
| STD. | 7.0549 × 10−08 | 8.7695 × 10−05 | 4.0464 × 10−14 | 3.0122 × 10−09 | 3.6944 × 10−09 | 6.6486 × 10−16 | 1.5990 × 10−05 | 6.7752 × 10−16 | 4.6137 × 10−09 | |
| Min | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | −1.0316 × 1000 | |
| F17 | Avg. | 3.9789 × 10−01 | 4.0100 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 | 3.9790 × 10−01 | 3.9789 × 10−01 | 3.9791 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 |
| STD. | 5.3714 × 10−06 | 3.2491 × 10−03 | 7.3008 × 10−15 | 5.2004 × 10−06 | 1.7830 × 10−05 | 0.0000 × 1000 | 2.2182 × 10−05 | 0.0000 × 1000 | 5.2398 × 10−08 | |
| Min | 3.9789 × 10−01 | 3.9811 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 | 3.9789 × 10−01 | |
| F18 | Avg. | 3.0000 × 1000 | 3.0000 × 1000 | 3.0000 × 1000 | 3.0000 × 1000 | 3.0001 × 1000 | 3.0000 × 1000 | 2.9715 × 1001 | 3.0000 × 1000 | 3.0000 × 1000 |
| STD. | 4.1823 × 10−05 | 3.5195 × 10−05 | 1.8243 × 10−13 | 6.0229 × 10−07 | 4.6026 × 10−04 | 9.9301 × 10−16 | 5.0596 × 1000 | 9.3663 × 10−16 | 4.9599 × 10−06 | |
| Min | 3.0000 × 1000 | 3.0000 × 1000 | 3.0000 × 1000 | 3.0000 × 1000 | 3.0000 × 1000 | 3.0000 × 1000 | 3.0032 × 1000 | 3.0000 × 1000 | 3.0000 × 1000 | |
| F19 | Avg. | −3.8616 × 1000 | −3.8507 × 1000 | −3.8628 × 1000 | −3.8583 × 1000 | −3.8518 × 1000 | −3.8628 × 1000 | −3.8040 × 1000 | −3.8628 × 1000 | −3.8625 × 1000 |
| STD. | 2.3429 × 10−03 | 7.7056 × 10−03 | 1.6209 × 10−11 | 6.6567 × 10−03 | 1.7466 × 10−02 | 2.6684 × 10−15 | 2.0896 × 10−01 | 2.7101 × 10−15 | 1.4192 × 10−03 | |
| Min | −3.8628 × 1000 | −3.8605 × 1000 | −3.8628 × 1000 | −3.8628 × 1000 | −3.8628 × 1000 | −3.8628 × 1000 | −3.8628 × 1000 | −3.8628 × 1000 | −3.8628 × 1000 | |
| F20 | Avg. | −3.3219 × 1000 | −2.6135 × 1000 | −3.2161 × 1000 | −3.0656 × 1000 | −3.3118 × 1000 | −3.2638 × 1000 | −3.3133 × 1000 | −3.2784 × 1000 | −3.3059 × 1000 |
| STD. | 2.2933 × 10−05 | 3.1389 × 10−01 | 5.5503 × 10−02 | 1.0806 × 10−01 | 3.4871 × 10−02 | 7.1334 × 10−02 | 9.1886 × 10−03 | 5.8273 × 10−02 | 4.1813 × 10−02 | |
| Min | −3.3220 × 1000 | −3.0564 × 1000 | −3.3220 × 1000 | −3.1993 × 1000 | −3.3217 × 1000 | −3.3220 × 1000 | −3.3211 × 1000 | −3.3220 × 1000 | −3.3220 × 1000 | |
| F21 | Avg. | −8.3916 × 1000 | −6.8959 × 1000 | −1.0153 × 1001 | −9.8130 × 1000 | −9.8109 × 1000 | −8.9697 × 1000 | −1.0128 × 1001 | −1.0153 × 1001 | −1.0153 × 1001 |
| STD. | 2.1174 × 1000 | 2.2821 × 1000 | 5.5169 × 10−11 | 1.2933 × 1000 | 1.2928 × 1000 | 2.1819 × 1000 | 2.7575 × 10−02 | 6.7923 × 10−15 | 1.4067 × 10−07 | |
| Min | −1.0152 × 1001 | −1.0152 × 1001 | −1.0153 × 1001 | −1.0153 × 1001 | −1.0153 × 1001 | −1.0153 × 1001 | −1.0153 × 1001 | −1.0153 × 1001 | −1.0153 × 1001 | |
| F22 | Avg. | −8.9990 × 1000 | −7.2308 × 1000 | −1.0227 × 1001 | −9.8713 × 1000 | −9.8701 × 1000 | −8.3816 × 1000 | −1.0391 × 1001 | −1.0403 × 1001 | −1.0403 × 1001 |
| STD. | 2.2109 × 1000 | 2.4640 × 1000 | 9.6292 × 10−01 | 1.6218 × 1000 | 1.6214 × 1000 | 2.7339 × 1000 | 1.0467 × 10−02 | 1.3601 × 10−15 | 3.3477 × 10−05 | |
| Min | −1.0402 × 1001 | −1.0394 × 1001 | −1.0403 × 1001 | −1.0403 × 1001 | −1.0403 × 1001 | −1.0403 × 1001 | −1.0403 × 1001 | −1.0403 × 1001 | −1.0403 × 1001 | |
| F23 | Avg. | −8.6580 × 1000 | −7.2350 × 1000 | −9.8216 × 1000 | −1.0175 × 1001 | −1.0354 × 1001 | −8.7432 × 1000 | −1.0518 × 1001 | −1.0358 × 1001 | −1.0536 × 1001 |
| STD. | 2.5993 × 1000 | 2.5826 × 1000 | 1.8535 × 1000 | 1.3719 × 1000 | 9.8705 × 10−01 | 2.5794 × 1000 | 2.0234 × 10−02 | 9.7874 × 10−01 | 2.7028 × 10−05 | |
| Min | −1.0536 × 1001 | −1.0536 × 1001 | −1.0536 × 1001 | −1.0536 × 1001 | −1.0536 × 1001 | −1.0536 × 1001 | −1.0536 × 1001 | −1.0536 × 1001 | −1.0536 × 1001 |
| GWO | SCA | SSA | HHO | WOA | PSO | TSO | CGO | |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 6.0350 × 10−03 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.9209 × 10−06 |
| F2 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 5.0383 × 10−01 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 2.3534 × 10−06 |
| F3 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 3.1817 × 10−06 |
| F4 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 3.7243 × 10−05 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 2.3534 × 10−06 |
| F5 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.5625 × 10−02 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 |
| F6 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.3183 × 10−04 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 |
| F7 | 5.3070 × 10−05 | 6.5641 × 10−02 | 1.7344 × 10−06 | 1.7088 × 10−03 | 3.3269 × 10−02 | 1.7344 × 10−06 | 5.7924 × 10−05 | 1.3194 × 10−02 |
| F8 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 6.2500 × 10−02 | 2.5631 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.2383 × 10−06 |
| F9 | 2.5631 × 10−06 | 2.5596 × 10−06 | 1.7344 × 10−06 | 1.0000 × 1000 | 1.0000 × 1000 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.0000 × 1000 |
| F10 | 1.4383 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.0000 × 1000 | 2.1912 × 10−05 | 1.7344 × 10−06 | 1.7344 × 10−06 | 6.3342 × 10−05 |
| F11 | 1.2500 × 10−01 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.0000 × 1000 | 1.0000 × 1000 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.0000 × 1000 |
| F12 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 |
| F13 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 2.7016 × 10−05 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7300 × 10−06 |
| F14 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.0231 × 10−05 | 1.8435 × 10−04 | 1.7344 × 10−06 | 1.0000 × 1000 | 1.7344 × 10−06 | 5.0000 × 10−01 |
| F15 | 2.8434 × 10−05 | 1.7344 × 10−06 | 1.9209 × 10−06 | 6.3391 × 10−06 | 2.8786 × 10−06 | 3.3173 × 10−04 | 3.5152 × 10−06 | 3.1123 × 10−05 |
| F16 | 3.8822 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 8.9443 × 10−04 | 4.1140 × 10−03 | 1.7344 × 10−06 | 2.1266 × 10−06 | 1.7344 × 10−06 |
| F17 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 5.2165 × 10−06 | 1.9209 × 10−06 | 1.7344 × 10−06 | 1.9209 × 10−06 | 1.7344 × 10−06 |
| F18 | 3.0650 × 10−04 | 1.2453 × 10−02 | 1.7344 × 10−06 | 2.1630 × 10−05 | 1.1499 × 10−04 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 |
| F19 | 1.4936 × 10−05 | 1.7344 × 10−06 | 1.7344 × 10−06 | 9.3157 × 10−06 | 1.1265 × 10−05 | 1.7344 × 10−06 | 2.3534 × 10−06 | 1.7344 × 10−06 |
| F20 | 1.5658 × 10−02 | 1.7344 × 10−06 | 5.7924 × 10−05 | 1.7344 × 10−06 | 1.1748 × 10−02 | 3.0861 × 10−01 | 1.4795 × 10−02 | 7.3433 × 10−01 |
| F21 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.3591 × 10−01 | 2.6033 × 10−06 | 6.6858 × 10−01 | 1.7344 × 10−06 | 6.0496 × 10−07 |
| F22 | 1.7344 × 10−06 | 1.7344 × 10−06 | 3.1123 × 10−05 | 1.7988 × 10−05 | 9.3157 × 10−06 | 3.8202 × 10−01 | 2.1266 × 10−06 | 1.7300 × 10−06 |
| F23 | 1.7344 × 10−06 | 1.7344 × 10−06 | 1.4795 × 10−02 | 1.9729 × 10−05 | 3.1123 × 10−05 | 6.4352 × 10−01 | 1.7344 × 10−06 | 3.1123 × 10−05 |
| Function | Test | CSA | PSO | SSA | SCA | GWO |
|---|---|---|---|---|---|---|
| F1 | Best | 4.05207 × 10−66 | 1.40909 × 10−02 | 8.41001 × 10−02 | 7.65220 × 10−05 | 1.15671 × 10−16 |
| Mean | 9.49793 × 10−37 | 3.23392 × 1001 | 1.98479 × 1001 | 4.22900 × 10−01 | 2.72480 × 10−14 | |
| Std | 5.20184 × 10−36 | 4.83756 × 1001 | 2.80619 × 1001 | 9.12128 × 10−01 | 3.45607 × 10−14 | |
| F2 | Best | 1.79982 × 10−33 | 1.51649 × 10−01 | 3.28652 × 10−01 | 9.66793 × 10−05 | 4.82345 × 10−10 |
| Mean | 2.92106 × 10−22 | 3.89166 × 1000 | 4.75249 × 1000 | 3.31250 × 10−03 | 6.43809 × 10−09 | |
| Std | 1.53426 × 10−21 | 4.88194 × 1000 | 3.71882 × 1000 | 3.35433 × 10−03 | 4.85863 × 10−09 | |
| F3 | Best | 6.77086 × 10−66 | 2.43120 × 1001 | 2.58477 × 1002 | 3.09196 × 10−04 | 5.83050 × 10−01 |
| Mean | 1.18525 × 10−40 | 8.05289 × 1004 | 2.33034 × 1004 | 4.24039 × 1000 | 1.82227 × 1002 | |
| Std | 6.39505 × 10−40 | 3.84529 × 1004 | 3.16829 × 1004 | 6.62382 × 1000 | 2.88485 × 1002 | |
| F4 | Best | 5.64112 × 10−36 | 1.97453 × 10−01 | 1.96642 × 10−01 | 1.97453 × 10−01 | 1.97453 × 10−01 |
| Mean | 3.81723 × 10−22 | 2.62001 × 1000 | 9.88436 × 10−01 | 2.62001 × 1000 | 2.59439 × 1000 | |
| Std | 1.83964 × 10−21 | 2.72100 × 1000 | 7.22522 × 10−01 | 2.72100 × 1000 | 2.71903 × 1000 | |
| F5 | Best | 0.00000 × 1000 | 8.09021 × 10−01 | 1.15830 × 1000 | 1.80961 × 1000 | 1.80961 × 1000 |
| Mean | 0.00000 × 1000 | 3.38351 × 1003 | 4.75416 × 1002 | 4.89317 × 1003 | 1.26269 × 1002 | |
| Std | 0.00000 × 1000 | 1.14975 × 1004 | 9.22158 × 1002 | 1.39892 × 1004 | 1.65257 × 1002 | |
| F6 | Best | 0.00000 × 1000 | 9.17634 × 10−05 | 3.55921 × 10−04 | 1.76154 × 10−03 | 8.62047 × 10−04 |
| Mean | 0.00000 × 1000 | 3.30019 × 1001 | 1.32821 × 1001 | 2.93302 × 1001 | 7.17494 × 1000 | |
| Std | 0.00000 × 1000 | 5.13931 × 1001 | 1.86246 × 1001 | 2.88694 × 1001 | 3.74740 × 1000 | |
| F7 | Best | 4.23203 × 10−06 | 1.54553 × 10−02 | 4.83797 × 10−03 | 3.57837 × 10−04 | 3.66995 × 10−03 |
| Mean | 4.00859 × 10−04 | 1.86225 × 10−01 | 1.41949 × 10−01 | 1.01286 × 10−01 | 8.42239 × 10−03 | |
| Std | 4.78167 × 10−04 | 1.75616 × 10−01 | 1.17454 × 10−01 | 2.46964 × 10−01 | 4.68636 × 10−03 | |
| F8 | Best | −4.18983 × 1004 | −4.18952 × 1004 | −4.18914 × 1004 | −4.18464 × 1004 | −4.18464 × 1004 |
| Mean | −4.18983 × 1004 | −3.96372 × 1004 | −4.03440 × 1004 | −3.75470 × 1004 | −3.82785 × 1004 | |
| Std | 2.96014 × 10−11 | 4.49162 × 1003 | 3.63037 × 1003 | 5.82693 × 1003 | 5.27419 × 1003 | |
| F9 | Best | 0.00000 × 1000 | 3.27575 × 10−03 | 8.23333 × 10−03 | 3.73030 × 10−05 | 3.25244 × 10−06 |
| Mean | 0.00000 × 1000 | 8.27521 × 1001 | 4.28287 × 1001 | 1.24652 × 1002 | 1.51656 × 1002 | |
| Std | 0.00000 × 1000 | 7.32871 × 1001 | 4.87230 × 1001 | 1.19664 × 1002 | 1.11244 × 1002 | |
| F10 | Best | 8.88178 × 10−16 | 7.84248 × 10−02 | 2.24259 × 10−02 | 8.35089 × 10−04 | 1.59905 × 10−09 |
| Mean | 8.88178 × 10−16 | 2.88503 × 1000 | 1.76283 × 1000 | 1.31387 × 1000 | 9.57690 × 10−01 | |
| Std | 0.00000 × 1000 | 2.62189 × 1000 | 1.12465 × 1000 | 2.18567 × 1000 | 2.49990 × 1000 | |
| F11 | Best | 0.00000 × 1000 | 4.25764 × 10−03 | 5.71780 × 10−02 | 3.41024 × 10−06 | 0.00000 × 1000 |
| Mean | 0.00000 × 1000 | 1.52847 × 1000 | 9.20741 × 10−01 | 2.27770 × 10−01 | 1.55201 × 10−03 | |
| Std | 0.00000 × 1000 | 1.66071 × 1000 | 5.63135 × 10−01 | 2.79365 × 10−01 | 5.96126 × 10−03 | |
| F12 | Best | 4.71163 × 10−33 | 1.97180 × 10−04 | 1.12509 × 10−03 | 5.24202 × 10−03 | 1.23122 × 10−04 |
| Mean | 4.71163 × 10−33 | 1.01808 × 1000 | 4.60484 × 10−01 | 1.64094 × 1000 | 1.44908 × 1000 | |
| Std | 1.39185 × 10−48 | 1.49538 × 1000 | 1.11625 × 1000 | 1.78266 × 1000 | 2.82336 × 1000 | |
| F13 | Best | 1.34978 × 10−32 | 3.52700 × 10−05 | 2.58636 × 10−04 | 7.25952 × 10−04 | 4.19563 × 10−04 |
| Mean | 1.34978 × 10−32 | 1.45863 × 1001 | 2.90656 × 1000 | 2.47516 × 1001 | 2.72461 × 1000 | |
| Std | 5.56740 × 10−48 | 2.21891 × 1001 | 5.27444 × 1000 | 4.78364 × 1001 | 2.82642 × 1000 |
| Function | Test | CSA | PSO | SSA | SCA | GWO |
|---|---|---|---|---|---|---|
| F1 | Best | 1.74114 × 10−68 | 7.86330 × 10−01 | 8.69625 × 10−01 | 9.85563 × 10−01 | 1.28824 × 10−03 |
| Mean | 6.75805 × 10−43 | 2.57658 × 1004 | 1.87823 × 1003 | 3.13124 × 1004 | 6.86880 × 1001 | |
| Std | 3.69123 × 10−42 | 5.49528 × 1004 | 4.45580 × 1003 | 6.67314 × 1004 | 1.47024 × 1002 | |
| F2 | Best | 4.94485 × 10−35 | 1.70351 × 1000 | 1.86340 × 1000 | 2.11466 × 1000 | 7.00593 × 10−04 |
| Mean | 2.44060 × 10−21 | 2.85661 × 1002 | 9.02285 × 1001 | 4.69947 × 1001 | 4.62960 × 10−02 | |
| Std | 1.33304 × 10−20 | 2.42764 × 1002 | 7.96943 × 1001 | 2.46857 × 1001 | 3.27695 × 10−02 | |
| F3 | Best | 7.28940 × 10−62 | 1.44335 × 1006 | 7.08473 × 1003 | 3.52592 × 1004 | 3.55999 × 1005 |
| Mean | 4.45675 × 10−39 | 9.83821 × 1006 | 5.17443 × 1006 | 8.89991 × 1005 | 1.07487 × 1006 | |
| Std | 2.13852 × 10−38 | 3.95888 × 1006 | 4.61038 × 1006 | 6.68057 × 1005 | 3.87543 × 1005 | |
| F4 | Best | 9.39244 × 10−41 | 2.82903 × 10−02 | 2.82903 × 10−02 | 2.82903 × 10−02 | 2.82903 × 10−02 |
| Mean | 4.97072 × 10−23 | 3.13296 × 1000 | 1.47575 × 1000 | 3.13296 × 1000 | 3.01621 × 1000 | |
| Std | 2.35097 × 10−22 | 2.36133 × 1000 | 1.34765 × 1000 | 2.36133 × 1000 | 2.28900 × 1000 | |
| F5 | Best | 0.00000 × 1000 | 1.11144 × 1002 | 1.10805 × 1002 | 1.13580 × 1002 | 1.13580 × 1002 |
| Mean | 0.00000 × 1000 | 3.96596 × 1006 | 1.47830 × 1005 | 4.84064 × 1006 | 1.08327 × 1006 | |
| Std | 0.00000 × 1000 | 1.44863 × 1007 | 7.61203 × 1005 | 1.75361 × 1007 | 4.23453 × 1006 | |
| F6 | Best | 0.00000 × 1000 | 1.11552 × 1000 | 1.18127 × 1000 | 1.37640 × 1000 | 1.16202 × 1000 |
| Mean | 0.00000 × 1000 | 9.06200 × 1003 | 1.26919 × 1003 | 1.13358 × 1004 | 1.43531 × 1002 | |
| Std | 0.00000 × 1000 | 1.17632 × 1004 | 2.22354 × 1003 | 1.46871 × 1004 | 1.19839 × 1002 | |
| F7 | Best | 1.34248 × 10−05 | 2.95314 × 10−02 | 3.36464 × 10−03 | 8.28122 × 10−03 | 5.86957 × 10−03 |
| Mean | 2.40186 × 10−04 | 3.51020 × 1001 | 7.03426 × 10−01 | 3.98208 × 1001 | 8.03855 × 1000 | |
| Std | 2.09618 × 10−04 | 1.65495 × 1002 | 1.69178 × 1000 | 1.89489 × 1002 | 2.83190 × 1001 | |
| F8 | Best | −4.18983 × 1005 | −4.18978 × 1005 | −4.18978 × 1005 | −4.18977 × 1005 | −4.18977 × 1005 |
| Mean | −4.18983 × 1005 | −3.87824 × 1005 | −3.88408 × 1005 | −3.84621 × 1005 | −3.84898 × 1005 | |
| Std | 1.18405 × 10−10 | 4.42563 × 1004 | 4.34900 × 1004 | 4.69810 × 1004 | 4.68726 × 1004 | |
| F9 | Best | 0.00000 × 1000 | 4.15359 × 10−01 | 4.65994 × 10−01 | 5.27444 × 10−01 | 5.27444 × 10−01 |
| Mean | 0.00000 × 1000 | 1.34989 × 1003 | 4.44170 × 1002 | 1.47652 × 1003 | 1.47580 × 1003 | |
| Std | 0.00000 × 1000 | 1.02977 × 1003 | 4.18444 × 1002 | 1.10934 × 1003 | 1.10745 × 1003 | |
| F10 | Best | 8.88178 × 10−16 | 1.17690 × 10−01 | 1.21822 × 10−01 | 1.30832 × 10−01 | 9.76292 × 10−04 |
| Mean | 8.88178 × 10−16 | 4.07750 × 1000 | 2.10393 × 1000 | 4.24648 × 1000 | 2.82129 × 1000 | |
| Std | 0.00000 × 1000 | 2.78347 × 1000 | 1.56515 × 1000 | 2.84110 × 1000 | 3.32683 × 1000 | |
| F11 | Best | 0.00000 × 1000 | 1.54060 × 1000 | 5.76886 × 10−01 | 1.65931 × 1000 | 4.45692 × 10−03 |
| Mean | 0.00000 × 1000 | 1.40518 × 1002 | 1.45067 × 1001 | 1.74547 × 1002 | 7.56728 × 10−01 | |
| Std | 0.00000 × 1000 | 1.93782 × 1002 | 3.49974 × 1001 | 2.45555 × 1002 | 6.70865 × 10−01 | |
| F12 | Best | 4.71163 × 10−34 | 3.49707 × 10−05 | 2.95159 × 10−05 | 3.53593 × 10−05 | 3.22334 × 10−05 |
| Mean | 4.71163 × 10−34 | 4.61458 × 1000 | 1.15674 × 1000 | 4.71509 × 1000 | 2.37655 × 1000 | |
| Std | 8.69906 × 10−50 | 7.79023 × 1000 | 2.17639 × 1000 | 8.25036 × 1000 | 3.71613 × 1000 | |
| F13 | Best | 1.34978 × 10−32 | 1.24017 × 1000 | 1.07560 × 1000 | 1.37886 × 1000 | 1.05795 × 1000 |
| Mean | 1.34978 × 10−32 | 2.66755 × 1002 | 2.86286 × 1001 | 2.83343 × 1002 | 2.02468 × 1002 | |
| Std | 5.56740 × 10−48 | 4.21627 × 1002 | 2.54245 × 1001 | 4.39341 × 1002 | 3.96828 × 1002 |
| CSA | PSO | SSA | SCA | GWO | |
|---|---|---|---|---|---|
| F1 | 0.178432 | 0.190542 | 0.302927 | 0.20064 | 0.282661 |
| F2 | 0.12315 | 0.159538 | 0.228658 | 0.195575 | 0.239618 |
| F3 | 0.568033 | 0.611411 | 0.721536 | 0.730838 | 0.698834 |
| F4 | 0.12295 | 0.188939 | 0.239374 | 0.196382 | 0.251754 |
| F5 | 0.156947 | 0.170969 | 0.235264 | 0.209225 | 0.246743 |
| F6 | 0.115594 | 0.169406 | 0.215389 | 0.193195 | 0.227015 |
| F7 | 0.275001 | 0.305304 | 0.393652 | 0.364141 | 0.403618 |
| F8 | 0.14028 | 0.223961 | 0.268633 | 0.246461 | 0.294057 |
| F9 | 0.122207 | 0.160593 | 0.262984 | 0.209103 | 0.27208 |
| F10 | 0.133938 | 0.175045 | 0.255505 | 0.214336 | 0.264772 |
| F11 | 0.13927 | 0.173938 | 0.255895 | 0.230421 | 0.256377 |
| F12 | 0.526553 | 0.582185 | 0.667134 | 0.6323 | 0.678474 |
| F13 | 0.512411 | 0.559926 | 0.652665 | 0.616762 | 0.688092 |
| Sum | 3.114766 | 3.671757 | 4.699616 | 4.239379 | 4.804095 |
| Rank | (1) | (2) | (4) | (3) | (5) |
| CSA | PSO | SSA | SCA | GWO | |
|---|---|---|---|---|---|
| F1 | 0.864606 | 0.920696 | 1.411428 | 1.526312 | 1.954178 |
| F2 | 0.8211 | 0.927257 | 1.691217 | 1.690701 | 2.304578 |
| F3 | 9.746041 | 9.914311 | 9.757791 | 9.416562 | 9.929068 |
| F4 | 0.712832 | 0.857485 | 1.391238 | 1.644103 | 2.219137 |
| F5 | 0.784051 | 0.858395 | 1.423493 | 1.550448 | 2.002662 |
| F6 | 0.764518 | 0.883734 | 1.460421 | 1.610766 | 1.972805 |
| F7 | 1.450708 | 1.453512 | 2.155236 | 2.387385 | 2.742038 |
| F8 | 0.970483 | 1.17946 | 1.778078 | 2.079184 | 2.718625 |
| F9 | 0.904283 | 1.135896 | 1.676209 | 1.895193 | 2.421654 |
| F10 | 0.918339 | 1.132918 | 1.680022 | 1.861007 | 2.290501 |
| F11 | 1.024792 | 1.171338 | 1.809926 | 2.044052 | 2.410413 |
| F12 | 2.495781 | 2.802061 | 3.292436 | 3.421013 | 4.016006 |
| F13 | 2.471004 | 2.700387 | 3.175498 | 3.381912 | 4.266181 |
| Sum | 23.92854 | 25.93745 | 32.70299 | 34.50864 | 41.24785 |
| CSA | PSO | SSA | SCA | GWO | |
|---|---|---|---|---|---|
| h | 0.205729639786 | 0.205729639786 | 0.205723211955 | 0.205811043402 | 0.205724311092 |
| l | 3.470488665628 | 7.092414276557 | 7.092727008708 | 7.380674589109 | 7.092527090825 |
| t | 9.036623910358 | 9.036623910358 | 9.036624222889 | 8.972002667140 | 9.036803373437 |
| b | 0.205729639786 | 0.205729639786 | 0.205729638416 | 0.208874244972 | 0.205728938896 |
| Minimum cost | 1.724852308597 | 2.218150861764 | 2.218172785211 | 2.273030395508 | 2.218180086668 |
| Average cost | 1.724853828957 | 2.218150861764 | 2.244245629001 | 2.291353653772 | 2.218198907121 |
| Std. | 0.000004807757 | 0.000000000000 | 0.052784172626 | 0.010496471904 | 0.000013807448 |
| CSA | PSO | SSA | SCA | GWO | |
|---|---|---|---|---|---|
| Ts | 0.77816864138 | 0.7781686414 | 0.79357920102 | 0.78922547613 | 0.007781787 |
| Th | 0.38464916263 | 0.3846491626 | 0.39226677976 | 0.40639993523 | 0.003846530 |
| R | 40.3196187241 | 40.3196187241 | 41.1180752663 | 40.6926147876 | 40.319922618 |
| L | 200.000000000 | 200.000000000 | 189.175939539 | 196.033601579 | 200.000000000 |
| Minimum cost | 5885.33277362 | 5885.33277362 | 5912.20652171 | 6004.52071673 | 5885.46666087 |
| Average cost | 6011.55334154 | 6013.40373404 | 6191.42556961 | 6198.38074830 | 5974.52840595 |
| Std | 175.417988776 | 179.129462647 | 307.601967961 | 116.552624682 | 79.439547307 |
| CSA | PSO | SSA | SCA | GWO | |
|---|---|---|---|---|---|
| D | 0.0517190259 | 0.0516975399 | 0.0500000000 | 0.0500000000 | 0.0517410542 |
| d | 0.3574390430 | 0.3569217527 | 0.3174254133 | 0.3155229746 | 0.3579696634 |
| N | 11.2468029380 | 11.2770151263 | 14.0277750624 | 14.4243340035 | 11.2159545387 |
| Min. weight | 0.0126652492 | 0.0126652341 | 0.0127190578 | 0.0129556368 | 0.0126652949 |
| Avg. weight | 0.0126789335 | 0.0133988758 | 0.0127190585 | 0.0131845009 | 0.0126662267 |
| Std | 0.0000327544 | 0.0015508356 | 0.0000000011 | 0.0001295549 | 0.0000011609 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qais, M.H.; Hasanien, H.M.; Turky, R.A.; Alghuwainem, S.; Tostado-Véliz, M.; Jurado, F. Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm. Mathematics 2022, 10, 1626. https://doi.org/10.3390/math10101626
Qais MH, Hasanien HM, Turky RA, Alghuwainem S, Tostado-Véliz M, Jurado F. Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm. Mathematics. 2022; 10(10):1626. https://doi.org/10.3390/math10101626
Chicago/Turabian StyleQais, Mohammed H., Hany M. Hasanien, Rania A. Turky, Saad Alghuwainem, Marcos Tostado-Véliz, and Francisco Jurado. 2022. "Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm" Mathematics 10, no. 10: 1626. https://doi.org/10.3390/math10101626
APA StyleQais, M. H., Hasanien, H. M., Turky, R. A., Alghuwainem, S., Tostado-Véliz, M., & Jurado, F. (2022). Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm. Mathematics, 10(10), 1626. https://doi.org/10.3390/math10101626










