Estimation of the Hurst Parameter in Spot Volatility
Abstract
:1. Introduction
- We propose a new Hurst exponent by changing the frequency method, prove consistency, and derive the asymptotic volatility of our estimator. Then we do simulations by the Monte Carlo method and compare our new Hurst estimator with existing Hurst exponents, showing its advantages.
- We introduce a non-parametric estimator for spot volatility based on the rough volatility environment proposed by Bayer et al. [12], and Gatheral et al. [13]. While Fan and Wang [28] proposed the same non-parametric estimator for spot volatility based on fractional stochastic volatility models with , we extend this estimator for all . The proof method established in this paper can be also applied to a general fractional stochastic volatility model with a bounded drift term.
- We employ the MF-DFA method proposed by Kantelhardt et al. [30] and qth-order SF method used by Gatheral et al. [13] to analyze the roughness of 10 industrial indices’ spot volatility in the Chinese financial market. Then we compared two Hurst exponents of the least square method proposed by Berzin et al. [31] with our new Hurst exponents using empirical data. Gatheral et al. [13] proved the SF method in American markets, and their numeric results are similar to ours in Chinese markets. There is much evidence showing the roughness of volatility in different sectors and markets (see Guennoun et al. [32], Funahashi and Kijima [33], Neuenkirch and Shalaiko [34]. We confirmed that the Hurst exponent we propose is universal in other markets and sectors. Our results suggest that spot volatility is also rough, and has confirmed the roughness of realized volatility (Bennedsen et al. [10]; Gatheral et al. [13]) and implied volatility (Livieri et al. [14]).
2. The Spot Volatility Model
- A1 The diffusion term in (1) satisfies:
- and.
- A2 For, whereis an arbitrarily small number.
- A3 The drift termin (1) satisfies:
- A4 Bandwidthand kernelsatisfy,is twice differentiable with supportand.
3. Estimation Methods of the Hurst Exponent
3.1. A New Hurst Exponent
3.2. Alternative Estimators for the Hurst Parameter
3.2.1. MF-DFA
3.2.2. The qth-Order SF Method
3.2.3. Two Least Square Estimation Methods
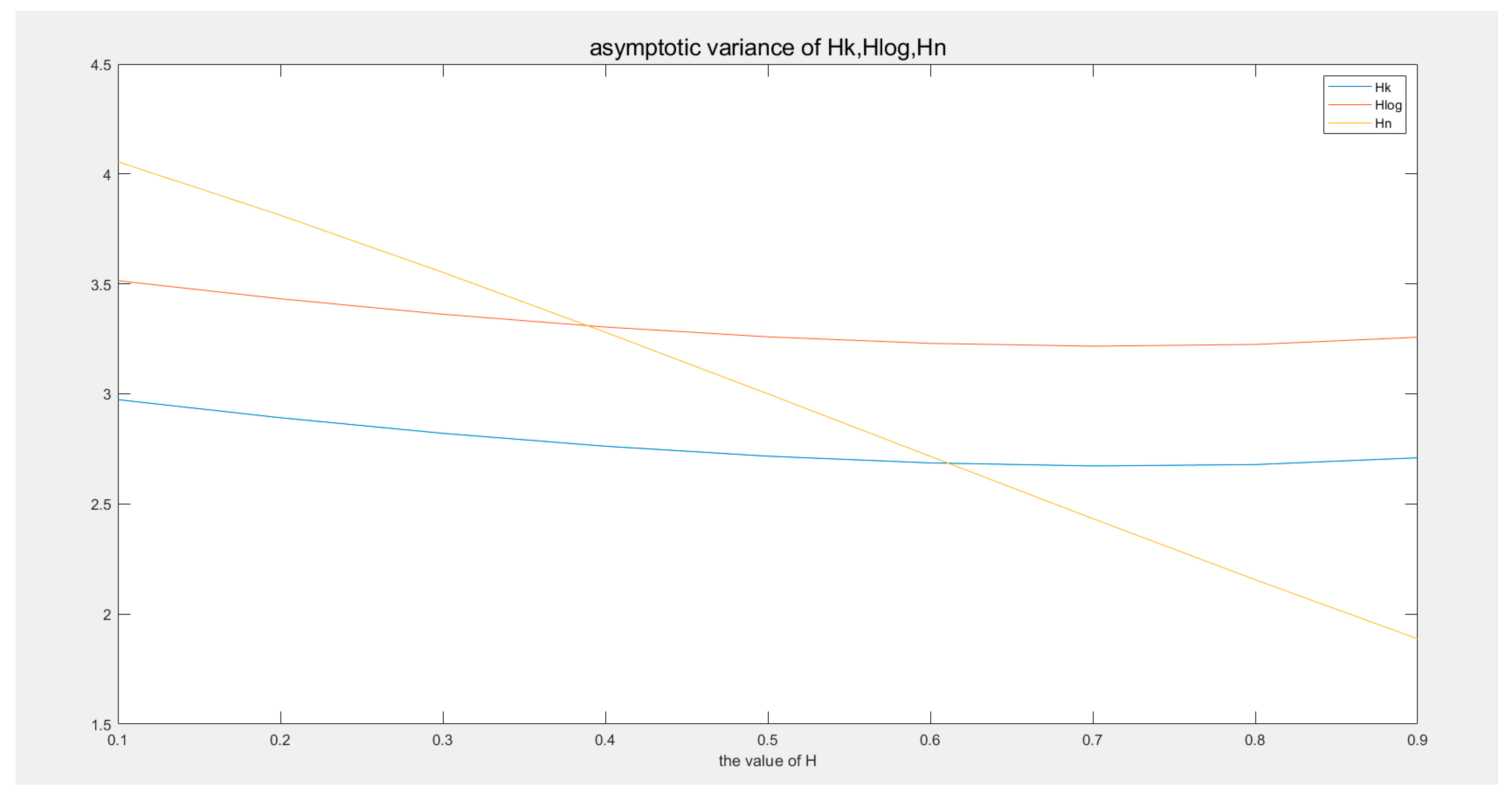
3.3. Comparison of Asymptotic Variance of , and
4. Research on the Roughness of Truncated and Non-Truncated Spot Volatility of Chinese A-Share Industry Indices Estimated by Five Hurst Exponents
4.1. Data Description
4.2. Non-Truncated Spot Volatility
4.3. Truncated Spot Volatility
4.4. Hurst Exponent Estimation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Fouque, J.-P.; Papanicolaou, G.; Sircar, K.R. Derivatives in Financial Markets with Stochastic Volatility; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Hull, J.; White, A. The pricing of options on assets with stochastic volatilities. J. Financ. 1987, 42, 281–300. [Google Scholar] [CrossRef]
- Scott, L.O. Option Pricing when the Variance Changes Randomly: Theory, Estimation, and an Application. J. Financ. Quant. Anal. 1987, 22, 419. [Google Scholar] [CrossRef]
- Stein, E.M.; Stein, J.C. Stock Price Distributions with Stochastic Volatility: An Analytic Approach. Rev. Financ. Stud. 1991, 4, 727–752. [Google Scholar] [CrossRef]
- Comte, F.; Renault, E. Long memory in continuous-time stochastic volatility models. Math. Financ. 1998, 8, 291–323. [Google Scholar] [CrossRef]
- Comte, F.; Coutin, L.; Renault, E. Affine fractional stochastic volatility models. Ann. Financ. 2012, 8, 337–378. [Google Scholar] [CrossRef]
- Chronopoulou, A.; Viens, F.G. Estimation and pricing under long-memory stochastic volatility. Ann. Financ. 2012, 8, 379–403. [Google Scholar] [CrossRef] [Green Version]
- Chronopoulou, A.; Viens, F.G. Stochastic volatility and option pricing with long-memory in discrete and continuous time. Quant. Financ. 2012, 12, 635–649. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.; Yu, J. Asymptotic theory for estimating drift parameters in the fractional vasicek model. Econ. Theory 2019, 35, 198–231. [Google Scholar] [CrossRef] [Green Version]
- Bennedsen, M.; Lunde, A.; Pakkanen, M.S. Decoupling the Short- and Long-Term Behavior of Stochastic Volatility. J. Financ. Econ. 2021, 1–46. [Google Scholar] [CrossRef]
- Bayer, C.; Friz, P.; Gatheral, J. Pricing under rough volatility. Quant. Financ. 2016, 16, 887–904. [Google Scholar] [CrossRef]
- Gatheral, J.; Jaisson, T.; Rosenbaum, M. Volatility is rough. Quant. Financ. 2018, 18, 933–949. [Google Scholar] [CrossRef]
- Livieri, G.; Mouti, S.; Pallavicini, A.; Rosenbaum, M. Rough volatility: Evidence from option prices. IISE Trans. 2018, 50, 767–776. [Google Scholar] [CrossRef]
- El Euch, O.; Rosenbaum, M. The characteristic function of rough Heston models. Math. Financ. 2019, 29, 3–38. [Google Scholar] [CrossRef] [Green Version]
- Alòs, E.; León, J.A.; Vives, J. On the short-time behavior of the implied volatility for jump-diffusion models with stochastic volatility. Financ. Stoch. 2007, 11, 571–589. [Google Scholar] [CrossRef] [Green Version]
- Fukasawa, M.; Takabatake, T. Asymptotically efficient estimators for self-similar stationary Gaussian noises under high frequency observations. Bernoulli 2019, 25, 1870–1900. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wei, Y.; Chen, X.; Ma, F.; Liang, C.; Chen, W. Which uncertainty is powerful to forecast crude oil market volatility? New evidence. Int. J. Financ. Econ. 2020, 1–19. [Google Scholar] [CrossRef]
- Wang, D.; Xin, Y.; Chang, X.; Su, X. Realized volatility forecasting and volatility spillovers: Evidence from Chinese non-ferrous metals futures. Int. J. Financ. Econ. 2020, 26, 2713–2731. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, W.; Yu, J. Modeling and forecasting realized volatility with the fractional Ornstein–Uhlenbeck process. J. Econ. 2021. [Google Scholar] [CrossRef]
- Da Fonseca, J.; Zhang, W. Volatility of volatility is (also) rough. J. Futur. Mark. 2019, 39, 600–611. [Google Scholar] [CrossRef]
- Cao, J.; Kim, J.-H.; Kim, S.-W.; Zhang, W. Rough stochastic elasticity of variance and option pricing. Financ. Res. Lett. 2019, 37, 101381. [Google Scholar] [CrossRef]
- Takaishi, T. Rough volatility of Bitcoin. Financ. Res. Lett. 2019, 32, 101379. [Google Scholar] [CrossRef]
- Fukasawa, M.; Takabatake, T.; Westphal, R. Is volatility rough? arXiv 2019, arXiv:1905.04852. [Google Scholar]
- Brandi, G.; Di Matteo, T. Multiscaling and rough volatility: An empirical investigation. arXiv 2022, arXiv:2201.10466. [Google Scholar]
- Alòs, E.; León, J. An Intuitive Introduction to Fractional and Rough Volatilities. Mathematics 2021, 9, 994. [Google Scholar] [CrossRef]
- Jacod, J.; Todorov, V. Testing for common arrivals of jumps for discretely observed multidimensional processes. Ann. Stat. 2009, 37, 1792–1838. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Wang, Y. Spot volatility estimation for high-frequency data. Stat. Interface 2008, 1, 279–288. [Google Scholar] [CrossRef] [Green Version]
- Renò, R. Nonparametric estimation of the diffusion coefficient of stochastic volatility models. Econ. Theory 2008, 24, 1174–1206. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef] [Green Version]
- Berzin, C.; Latour, A.; León, J.R. Inference on the Hurst Parameter and the Variance of Diffusions Driven by Fractional Brownian Motion; Springer: Cham, Switzerland, 2014; Volume 216, p. 200. [Google Scholar]
- Guennoun, H.; Jacquier, A.; Roome, P.; Shi, F. Asymptotic Behavior of the Fractional Heston Model. SIAM J. Financ. Math. 2018, 9, 1017–1045. [Google Scholar] [CrossRef]
- Funahashi, H.; Kijima, M. Does the Hurst index matter for option prices under fractional volatility? Ann. Financ. 2017, 13, 55–74. [Google Scholar] [CrossRef]
- Neuenkirch, A.; Shalaiko, T. The order barrier for strong approximation of rough volatility models. arXiv 2016, arXiv:1606.03854. [Google Scholar]
- Kermarrec, G. On Estimating the Hurst Parameter from Least-Squares Residuals. Case Study: Correlated Terrestrial Laser Scanner Range Noise. Mathematics 2020, 8, 674. [Google Scholar] [CrossRef]
- Jena, S.K.; Tiwari, A.K.; Dogăn, B.; Hammoudeh, S. Are the top six cryptocurrencies efficient? evidence from time-varying long memory. Int. J. Financ. Econ. 2020. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, W.; Xu, W. Parameter estimation for fractional Ornstein–Uhlenbeck processes at discrete observation. Appl. Math. Model. 2011, 35, 4196–4207. [Google Scholar] [CrossRef]
- Christensen, K.; Oomen, R.C.; Podolskij, M. Fact or friction: Jumps at ultra high frequency. J. Financ. Econ. 2014, 114, 576–599. [Google Scholar] [CrossRef]
- Cheridito, P.; Kawaguchi, H.; Maejima, M. Fractional Ornstein-Uhlenbeck processes. Electron. J. Probab. 2003, 8, 1–14. [Google Scholar] [CrossRef]
- Kubilius, K. CLT for quadratic variation of Gaussian processes and its application to the estimation of the Orey index. Stat. Probab. Lett. 2020, 165, 108845. [Google Scholar] [CrossRef]



| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 61.43384 | 60.09544 | 58.74345 | 57.42546 | 56.19696 | 55.12336 | 54.28286 | 53.77096 | 53.7078 | |
| 5 | 9.179444 | 9.099669 | 8.987028 | 8.86357 | 8.745652 | 8.646854 | 8.57992 | 8.558286 | 8.597588 | |
| 10 | 2.973535 | 2.891396 | 2.820534 | 2.762025 | 2.716779 | 2.686191 | 2.672437 | 2.678699 | 2.709498 | |
| 2 | 165.8243 | 75.86426 | 74.52995 | 73.18453 | 71.87646 | 70.66238 | 69.6092 | 68.7972 | 68.32469 | |
| 5 | 11.05752 | 10.97854 | 10.86696 | 10.74497 | 10.62911 | 10.53315 | 10.47013 | 10.45383 | 10.50042 | |
| 10 | 3.51451 | 3.432525 | 3.361931 | 3.303832 | 3.259175 | 3.229411 | 3.216792 | 3.22461 | 3.257532 |
| H | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 2.973535 | 2.891396 | 2.820534 | 2.762025 | 2.716779 | 2.686191 | 2.672437 | 2.678699 | 2.709498404 | |
| 3.51451 | 3.432525 | 3.361931 | 3.303832 | 3.259175 | 3.229411 | 3.216792 | 3.22461 | 3.257531806 | |
| 4.055571 | 3.812466 | 3.552612 | 3.280313 | 3 | 2.716159 | 2.433252 | 2.155608 | 1.887306706 | |
| stat_non_trunc | Mean | Min | Max | Median | Std.Dev | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Panel A: Non-truncated Spot Volatility | |||||||
| SSE index | 0.00022 | 9.05 × 10−6 | 0.00484 | 0.00010 | 0.00037 | 5.61360960 | 47.7565 |
| SSE Energy | 0.00025 | 1.48 × 10−5 | 0.00613 | 0.00014 | 0.00045 | 6.96110970 | 69.8107 |
| SSE Materials | 0.00026 | 1.74 × 10−5 | 0.00810 | 0.00014 | 0.00051 | 8.30235757 | 95.8771 |
| SSE Industrials | 0.00023 | 1.02 × 10−5 | 0.00787 | 0.00010 | 0.00052 | 8.19252067 | 90.0560 |
| SSE Cons Disc | 0.00021 | 9.85 × 10−6 | 0.00648 | 0.00011 | 0.00041 | 8.81983563 | 106.233 |
| SSE Cons Staples | 0.00020 | 1.14 × 10−5 | 0.00659 | 0.00012 | 0.00037 | 9.56348181 | 128.357 |
| SSE Health Care | 0.00019 | 7.73 × 10−6 | 0.00603 | 0.00011 | 0.00035 | 8.82946172 | 113.921 |
| SSE Financials | 0.00021 | 1.04 × 10−5 | 0.00562 | 0.00011 | 0.00038 | 6.87344218 | 67.1841 |
| SSE Info Technology | 0.00031 | 2.28 × 10−5 | 0.00727 | 0.00018 | 0.00048 | 7.08361470 | 76.6140 |
| SSE Telecom Svc | 0.00034 | 2.38 × 10−5 | 0.00934 | 0.00018 | 0.00061 | 7.56650831 | 79.6772 |
| SSE Utilities | 0.00017 | 1.13 × 10−5 | 0.00587 | 7.65 × 10−5 | 0.00040 | 7.96280129 | 83.3764 |
| Panel B: Logarithm of non-truncated spot volatilities | |||||||
| SSE index | −9.0228 | −11.6127 | −5.3299 | −9.1544 | 1.04418 | 0.48284956 | 2.92738 |
| SSE Energy | −8.8034 | −11.1212 | −5.0932 | −8.8651 | 0.93912 | 0.56099374 | 3.72217 |
| SSE Materials | −8.7734 | −10.959 | −4.8149 | −8.8504 | 0.92463 | 0.64137993 | 3.95554 |
| SSE Industrials | −9.0030 | −11.4906 | −4.8435 | −9.1269 | 0.95747 | 0.87836819 | 4.56345 |
| SSE Cons Disc | −8.9992 | −11.5282 | −5.0387 | −9.0412 | 0.92581 | 0.50655449 | 4.08381 |
| SSE Cons Staples | −8.9353 | −11.3815 | −5.0212 | −8.9969 | 0.82634 | 0.65934088 | 4.71016 |
| SSE Health Care | −9.0657 | −11.7707 | −5.11096 | −9.0936 | 0.94631 | 0.29717300 | 3.91282 |
| SSE Financials | −8.9995 | −11.4702 | −5.1811 | −9.0533 | 0.96055 | 0.43924226 | 3.75374 |
| SSE Info Technology | −8.4958 | −10.689 | −4.9236 | −8.5761 | 0.87165 | 0.45663801 | 3.65189 |
| SSE Telecom Svc | −8.4808 | −10.645 | −4.6731 | −8.5727 | 0.86341 | 0.78021763 | 4.49018 |
| SSE Utilities | −9.3710 | −11.3898 | −5.1368 | −9.4783 | 0.98057 | 0.94548892 | 4.67285 |
| stat_trunc | Mean | Min | Max | Median | Std.Dev | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Panel A: Truncated spot volatilities | |||||||
| SSE index | 0.00015 | 9.05 × 10−6 | 0.00093 | 9.38 × 10−5 | 0.00015 | 1.910627 | 6.71405 |
| SSE Energy | 0.00016 | 1.48 × 10−5 | 0.00089 | 0.00011 | 0.00014 | 2.162615 | 8.26727 |
| SSE Materials | 0.00016 | 1.74 × 10−5 | 0.00082 | 0.00012 | 0.00014 | 2.072311 | 7.87712 |
| SSE Industrials | 0.00014 | 1.02 × 10−5 | 0.00090 | 0.0001 | 0.00013 | 2.476477 | 9.72460 |
| SSE Cons Disc | 0.00013 | 9.85 × 10−6 | 0.00077 | 0.00010 | 0.00011 | 2.323363 | 9.81297 |
| SSE Cons Staples | 0.00014 | 1.14 × 10−5 | 0.00081 | 0.00011 | 0.00010 | 2.505865 | 11.2342 |
| SSE Health Care | 0.00013 | 7.73 × 10−6 | 0.00085 | 0.00010 | 0.00011 | 2.366167 | 10.4674 |
| SSE Financials | 0.00014 | 1.04 × 10−5 | 0.00102 | 0.00010 | 0.00013 | 2.684608 | 12.6908 |
| SSE Info Technology | 0.00021 | 2.28 × 10−5 | 0.00095 | 0.00016 | 0.00015 | 1.64547 | 5.96398 |
| SSE Telecom Svc | 0.00020 | 2.38 × 10−5 | 0.00100 | 0.00016 | 0.00014 | 1.889841 | 7.25645 |
| SSE Utilities | 0.00010 | 1.01 × 10−5 | 0.00086 | 7.26 × 10−5 | 0.00012 | 3.081249 | 13.9049 |
| Panel B: Logarithm of truncated spot volatilities | |||||||
| SSE index | −9.1803 | −11.612 | −6.9750 | −9.2744 | 0.88871 | 0.197569 | 2.41616 |
| SSE Energy | −9.0321 | −11.121 | −7.0142 | −9.0610 | 0.76953 | 0.124777 | 2.77233 |
| SSE Materials | −8.9674 | −10.959 | −7.1063 | −8.9712 | 0.74074 | 0.099774 | 2.73774 |
| SSE Industrials | −9.1668 | −11.490 | −7.0048 | −9.2100 | 0.76706 | 0.275856 | 3.15982 |
| SSE Cons Disc | −9.1697 | −11.528 | −7.1616 | −9.1632 | 0.76327 | −0.04621 | 3.00242 |
| SSE Cons Staples | −9.0922 | −11.381 | −7.1069 | −9.1035 | 0.66098 | 0.002958 | 3.49107 |
| SSE Health Care | −9.2145 | −11.770 | −7.069 | −9.1831 | 0.78518 | −0.28041 | 3.35773 |
| SSE Financials | −9.1818 | −11.470 | −6.8844 | −9.2013 | 0.79877 | −0.00218 | 3.09299 |
| SSE Info Technology | −8.6952 | −10.689 | −6.9569 | −8.7076 | 0.6935 | −0.10739 | 2.91148 |
| SSE Telecom Svc | −8.6995 | −10.645 | −6.9032 | −8.7227 | 0.65081 | 0.013933 | 3.01487 |
| SSE Utilities | −9.4973 | −11.507 | −7.0505 | −9.5307 | 0.8180 | 0.394645 | 3.19111 |
| Index | Log (Non-Truncated Spot Volatility) | Log (Truncated Spot Volatility) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MF-DFA | MF-DFA | |||||||||
| SSE index | 0.27 | 0.22 | 0.09 | 0.27 | 0.22 | 0.27 | 0.17 | 0.16 | 0.19 | 0.26 |
| SSE Energy | 0.33 | 0.28 | 0.06 | 0.33 | 0.23 | 0.33 | 0.22 | 0.05 | 0.24 | 0.26 |
| SSE Materials | 0.26 | 0.25 | 0.28 | 0.26 | 0.22 | 0.26 | 0.27 | 0.09 | 0.26 | 0.26 |
| SSE Industrials | 0.29 | 0.26 | 0.18 | 0.29 | 0.20 | 0.29 | 0.18 | 0.21 | 0.15 | 0.27 |
| SSE Cons Disc | 0.23 | 0.18 | 0.16 | 0.23 | 0.25 | 0.23 | 0.25 | 0.20 | 0.23 | 0.28 |
| SSE Cons Staples | 0.20 | 0.17 | 0.25 | 0.20 | 0.22 | 0.20 | 0.23 | 0.13 | 0.23 | 0.21 |
| SSE Health Care | 0.22 | 0.21 | 0.11 | 0.22 | 0.27 | 0.22 | 0.20 | 0.22 | 0.17 | 0.34 |
| SSE Financials | 0.23 | 0.24 | 0.27 | 0.23 | 0.15 | 0.23 | 0.21 | 0.11 | 0.20 | 0.23 |
| SSE Info Technology | 0.33 | 0.33 | 0.21 | 0.32 | 0.18 | 0.33 | 0.29 | 0.23 | 0.29 | 0.23 |
| SSE Telecom Svc | 0.37 | 0.38 | 0.10 | 0.37 | 0.21 | 0.37 | 0.31 | 0.21 | 0.30 | 0.25 |
| SSE Utilities | 0.27 | 0.22 | 0.09 | 0.27 | 0.22 | 0.27 | 0.33 | 0.15 | 0.28 | 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Teng, Y. Estimation of the Hurst Parameter in Spot Volatility. Mathematics 2022, 10, 1619. https://doi.org/10.3390/math10101619
Li Y, Teng Y. Estimation of the Hurst Parameter in Spot Volatility. Mathematics. 2022; 10(10):1619. https://doi.org/10.3390/math10101619
Chicago/Turabian StyleLi, Yicun, and Yuanyang Teng. 2022. "Estimation of the Hurst Parameter in Spot Volatility" Mathematics 10, no. 10: 1619. https://doi.org/10.3390/math10101619
APA StyleLi, Y., & Teng, Y. (2022). Estimation of the Hurst Parameter in Spot Volatility. Mathematics, 10(10), 1619. https://doi.org/10.3390/math10101619






