LPV H∞ Control with an Augmented Nonlinear Observer for Sawyer Motors
Abstract
:1. Introduction
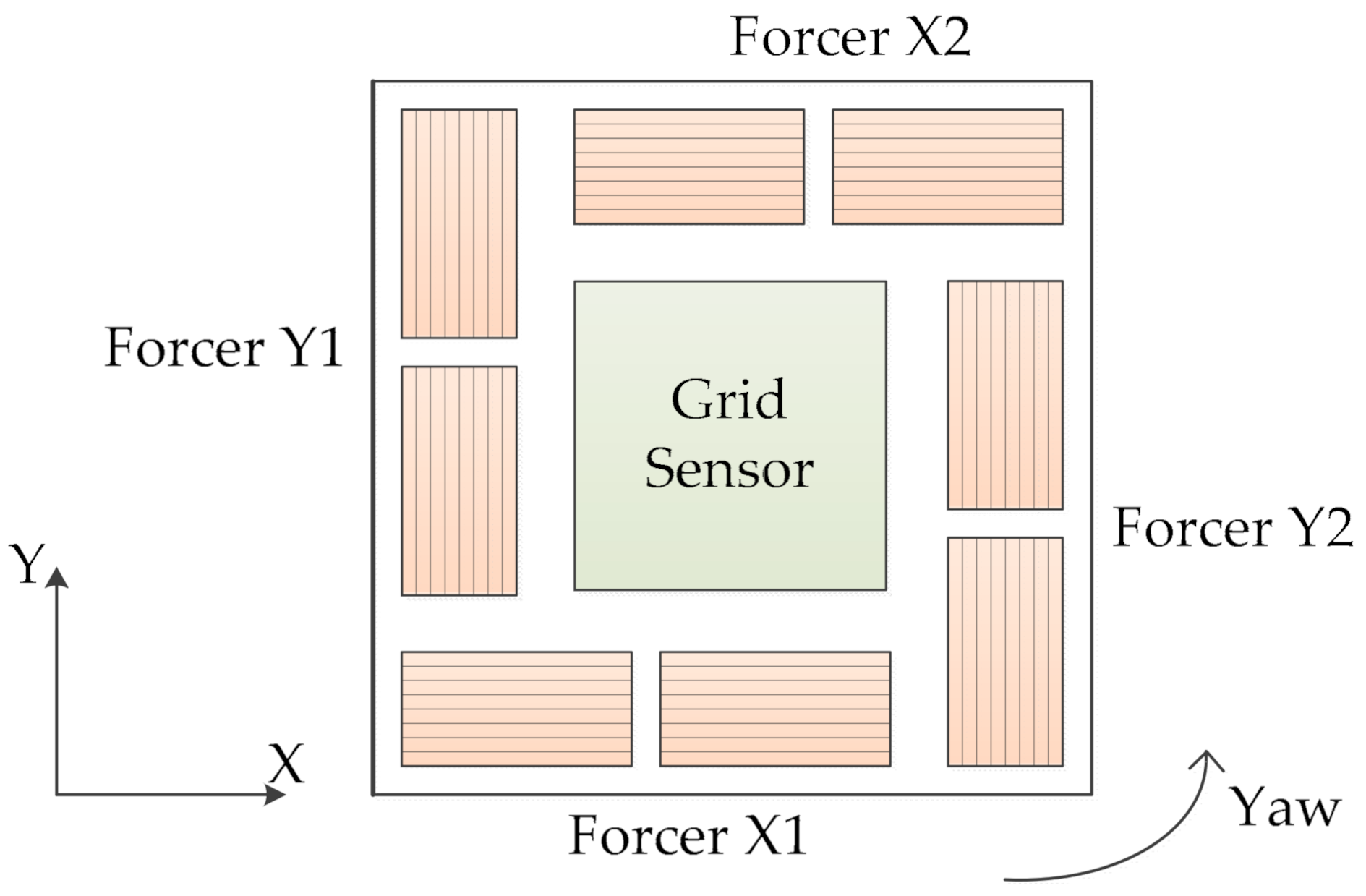
2. Mathematical Model of Sawyer Motor
3. Forces, Torque Modulation Scheme, and Lyapunov-Based Current Controller
3.1. Tracking Error Dynamics
3.2. Forces and Torque Modulation Scheme
3.3. Lyapunov-Based Current Controller
4. Configuration of LPV System
4.1. LPV System
4.2. Vertex Expansion Technique
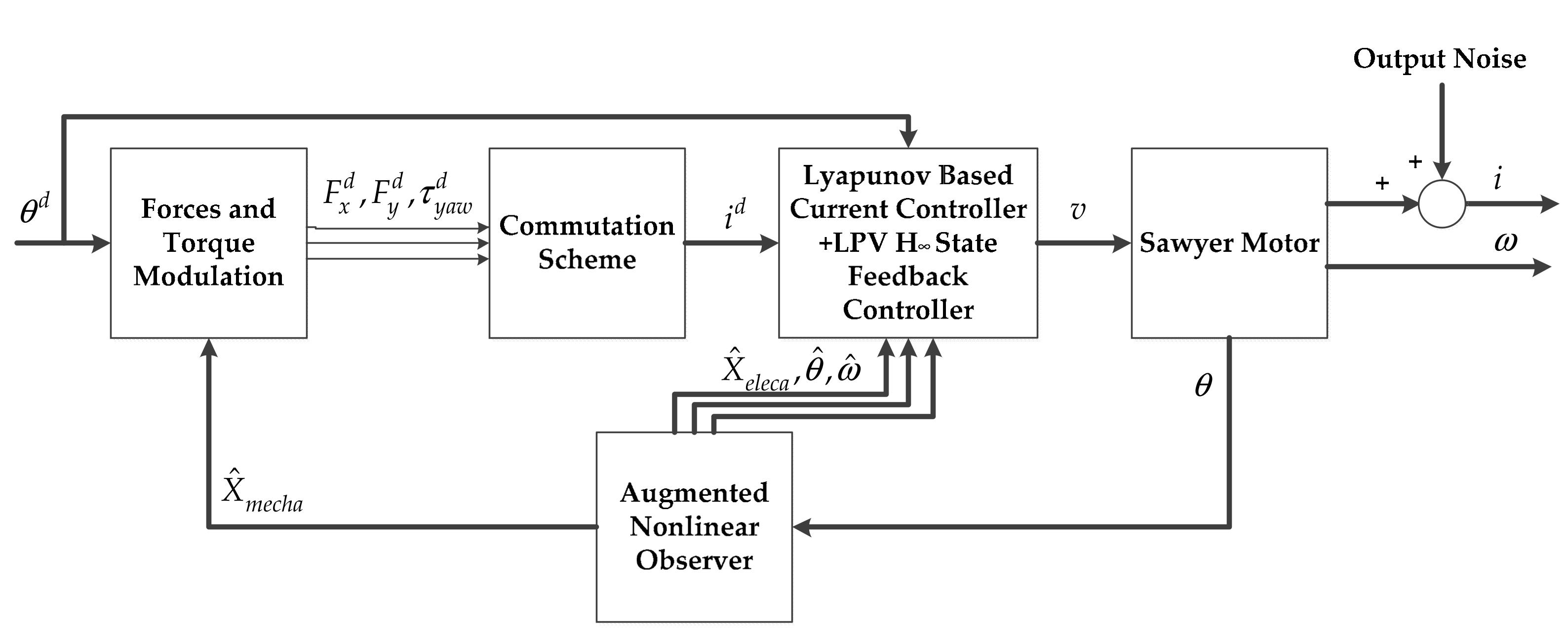
5. Augmented Nonlinear Observer and H∞ Feedback Control Design Using LPV Synthesis
5.1. Augmented Nonlinear Observer
5.2. LPV H∞ State Feedback Control and Closed-Loop Stability Analysis
- (A1)
- is stable.
- (A2)
- is invertible.
- (A3)
- .
- (A4)
- has no unobservable modes on the imaginary axis.
- There exists such that .
- There exists such that:
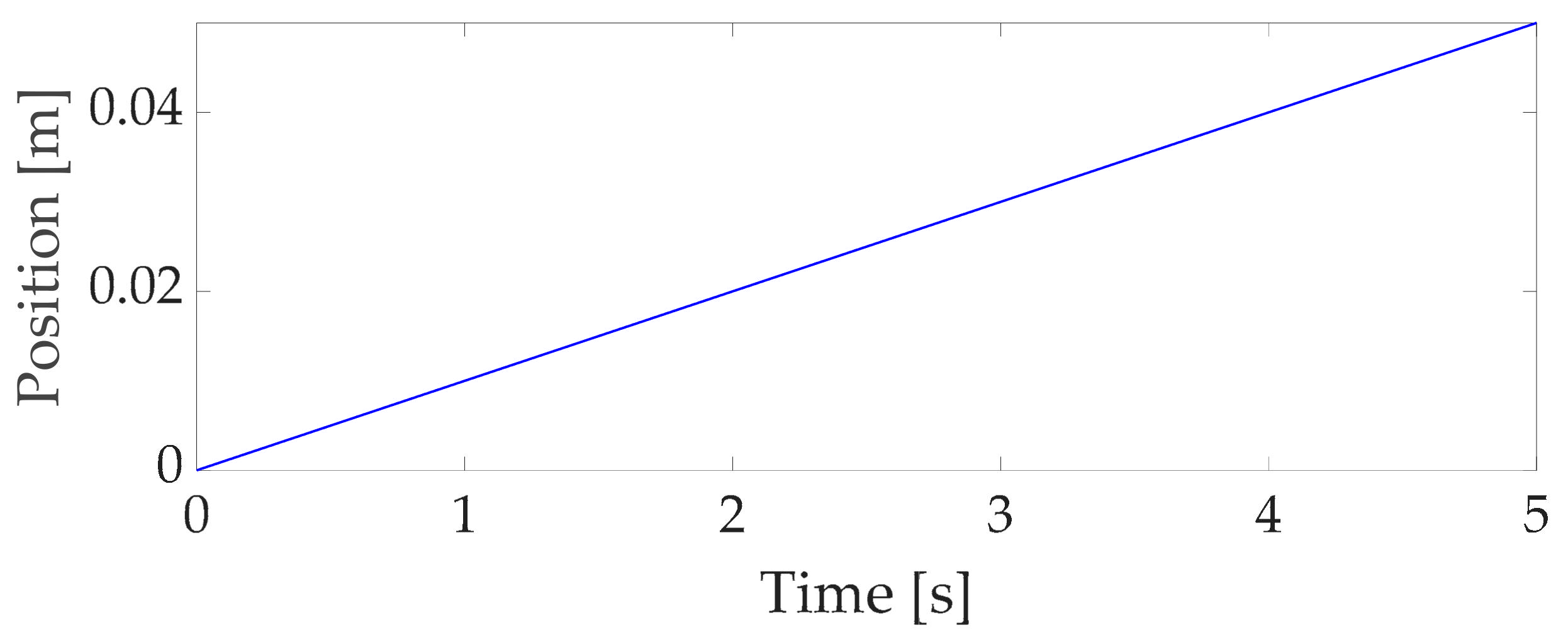
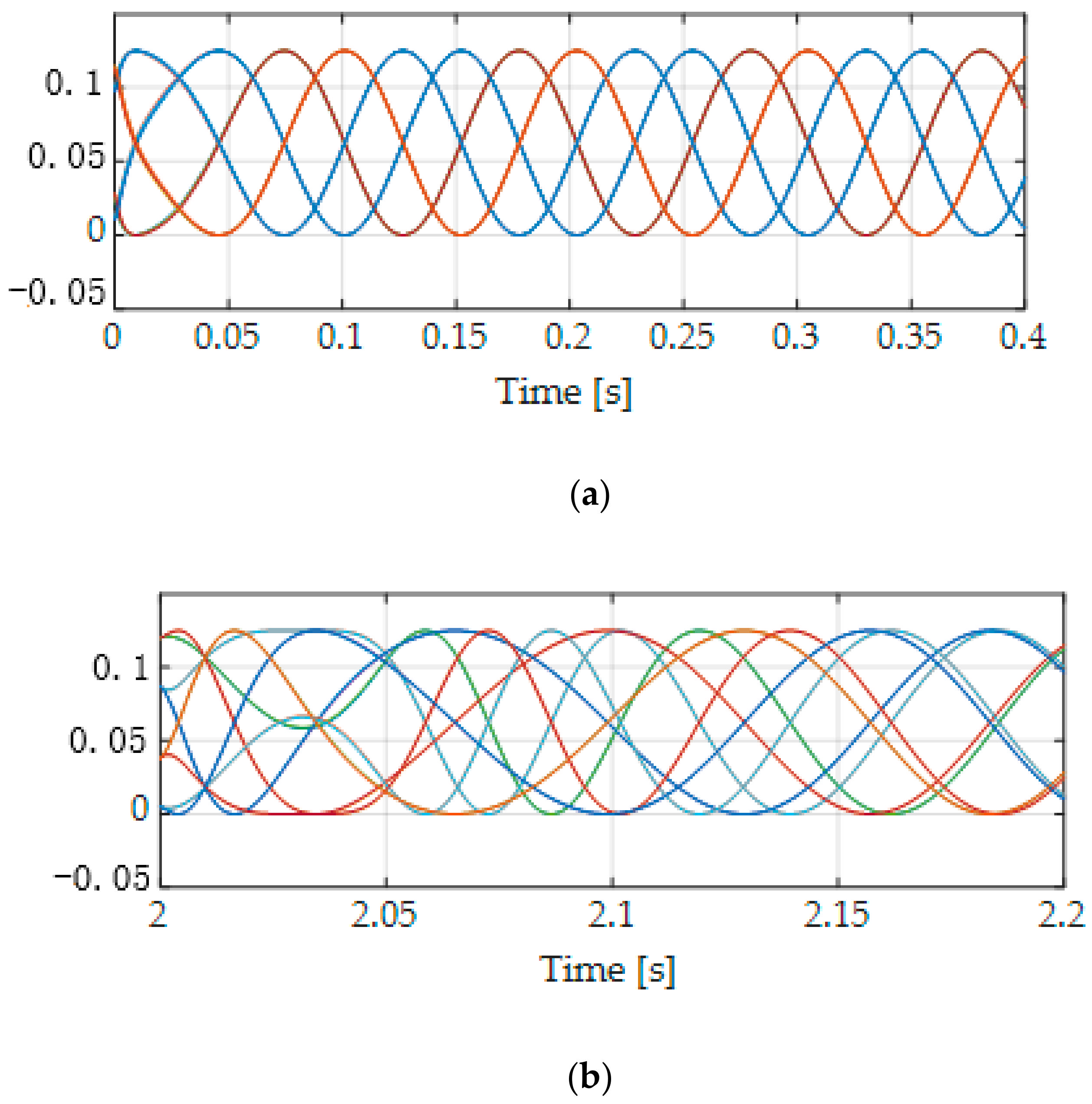
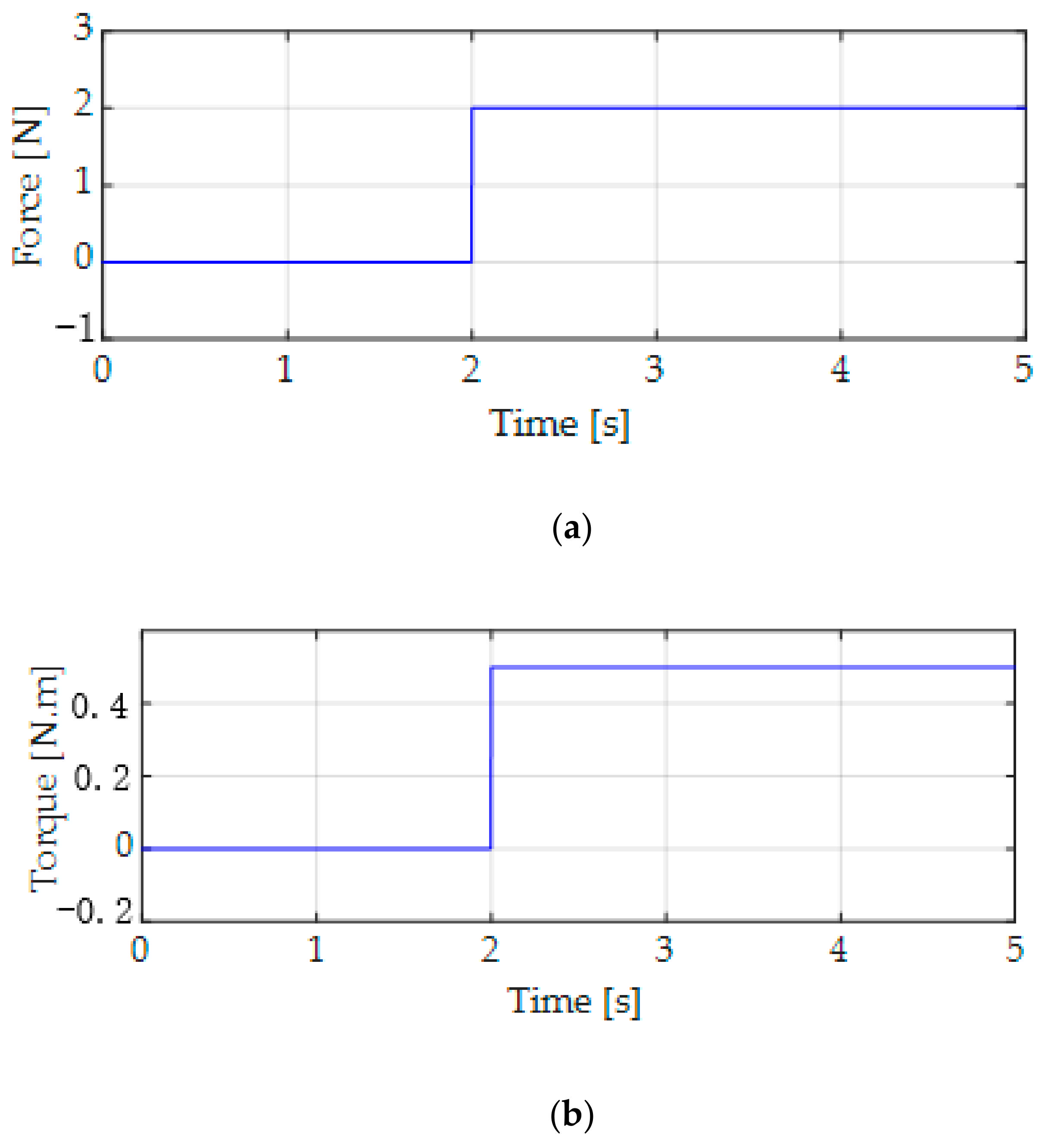
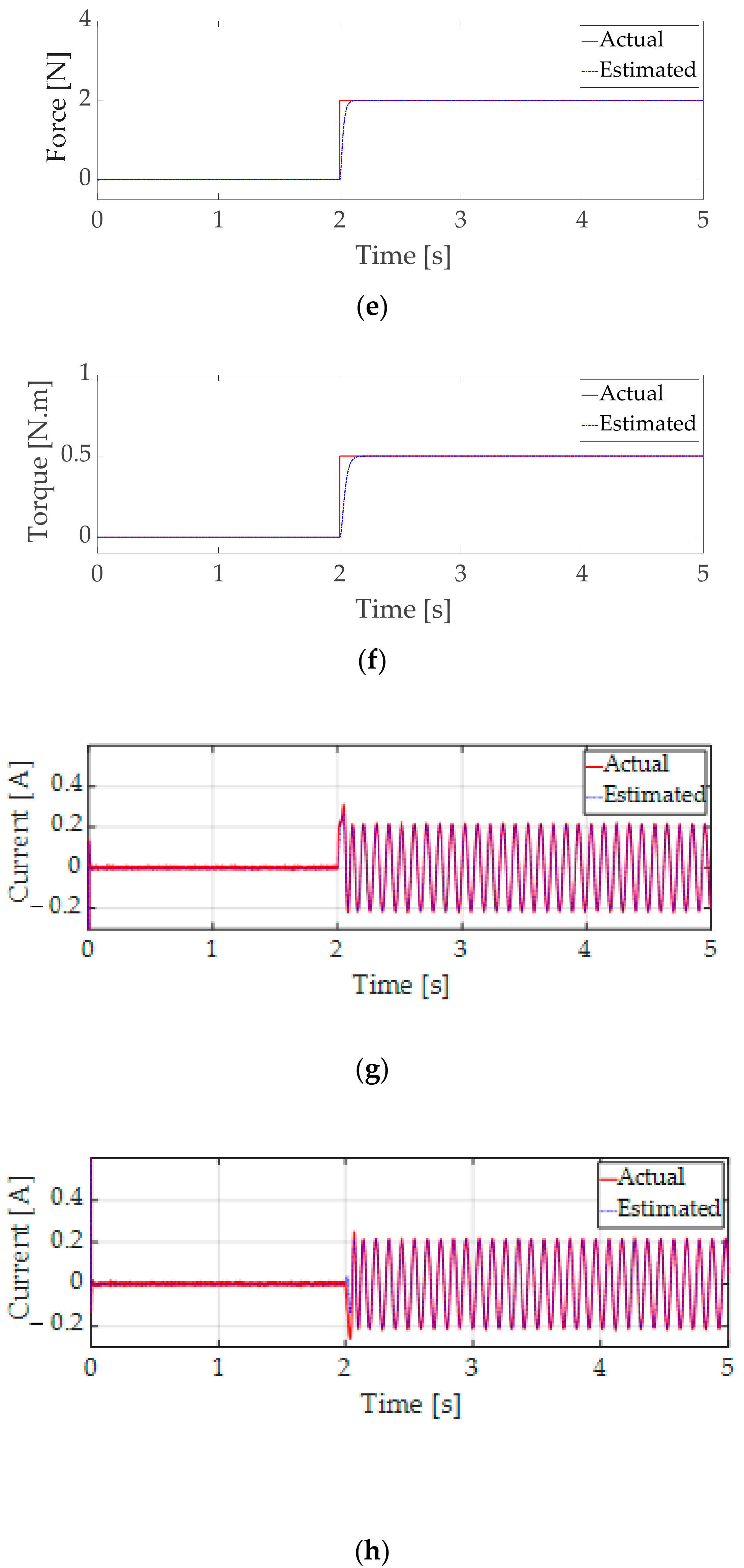
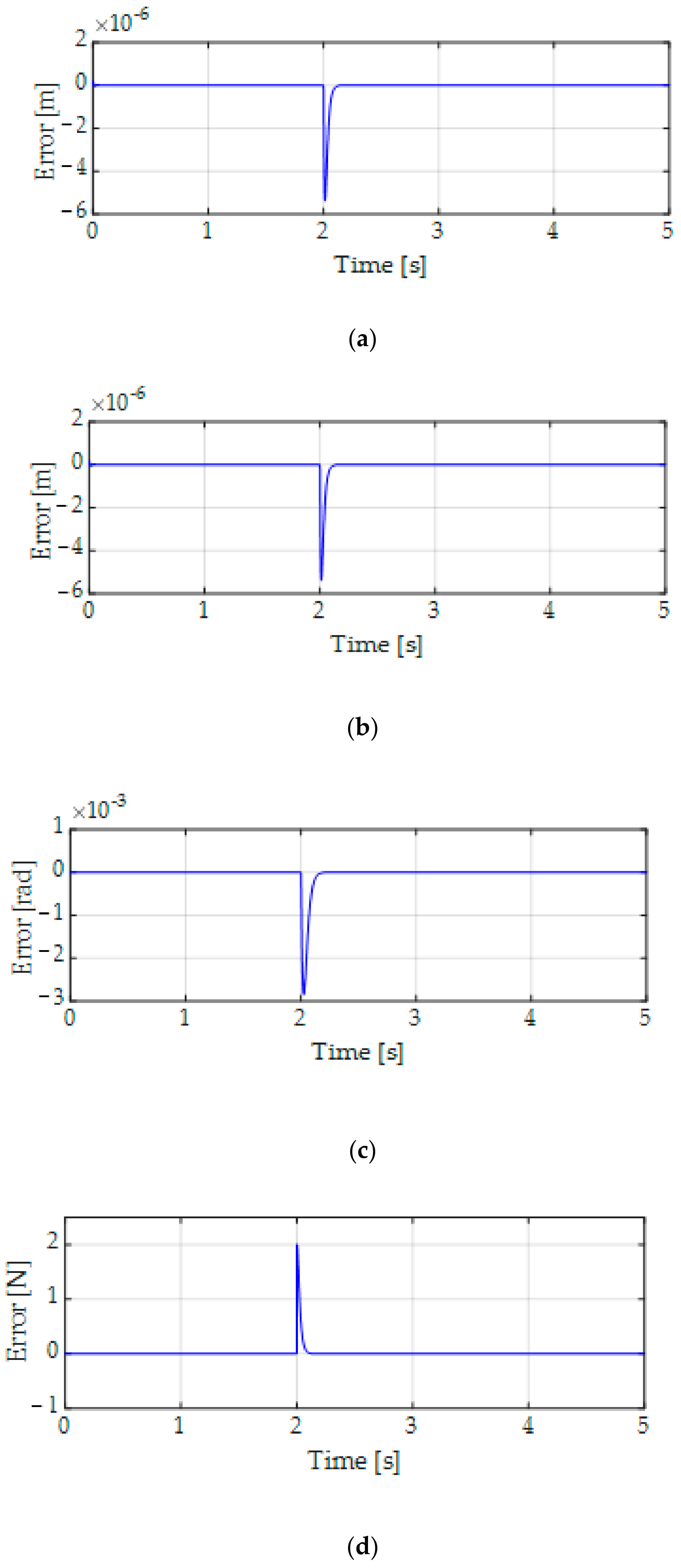
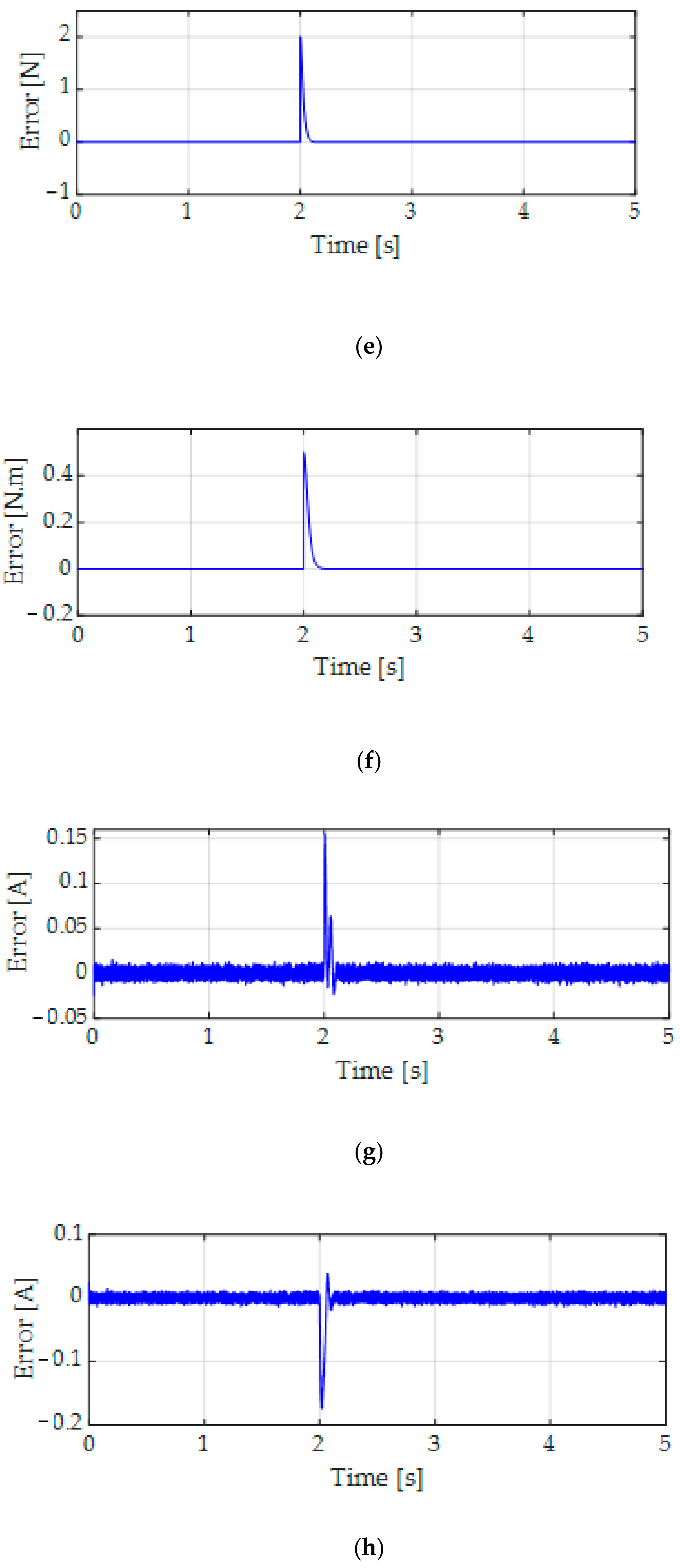
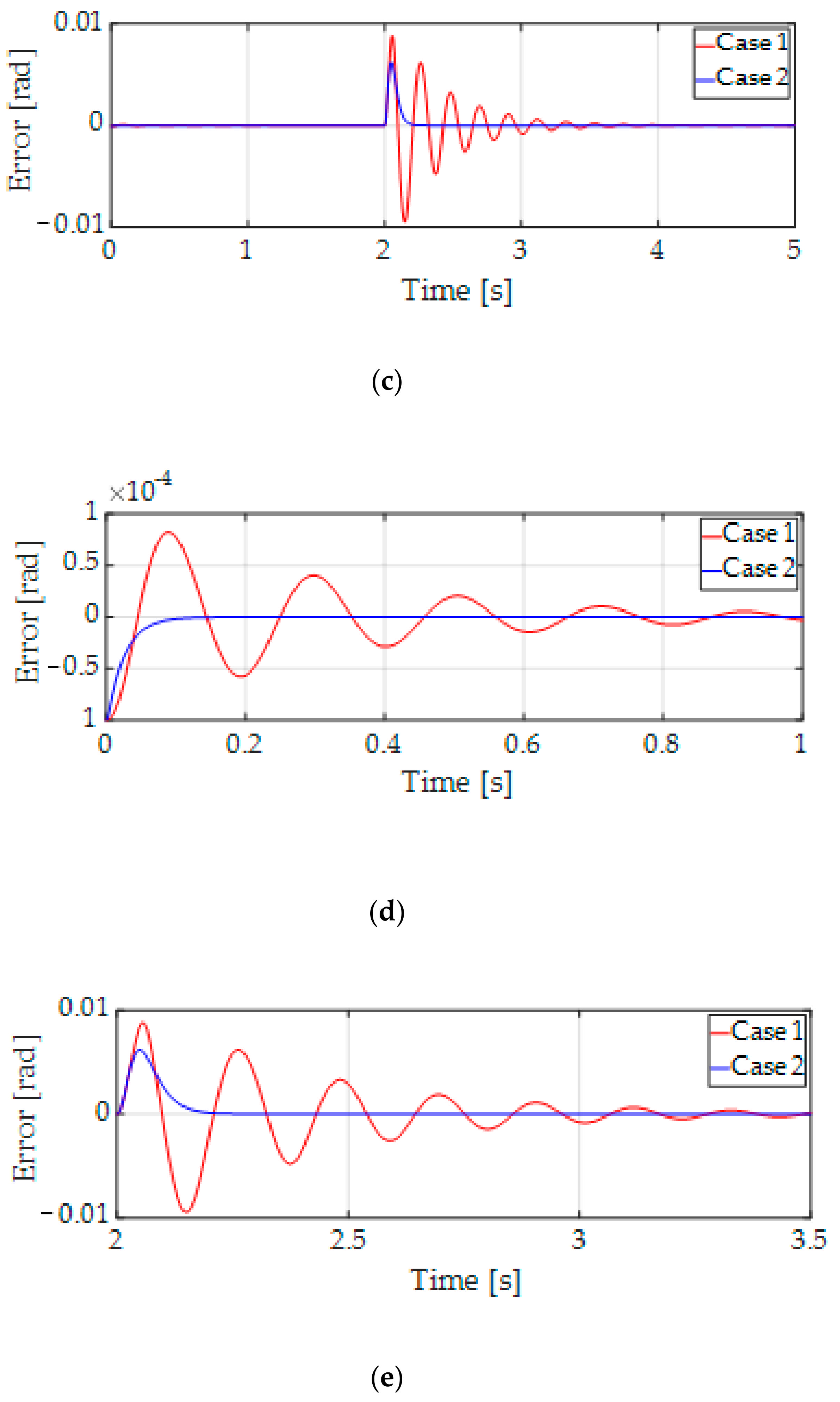
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| LPV | Linear parameter varying |
| ANOB | Augmented nonlinear observer |
| LMI | Linear matrix inequality |
| PID | Proportional integral derivative |
| DOB | Disturbance observer |
| EMF | Electromotive force |
References
- Krishnamurthy, P.; Khorrami, F. Robust adaptive control of Sawyer motors without current measurements. IEEE/ASME Trans. Mechatron. 2004, 9, 689–696. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F.; Ng, T.L.; Cherepinsky, I. Control design and implementation for Sawyer motors used in manufacturing systems. IEEE Trans. Control Syst. Technol. 2011, 19, 1467–1478. [Google Scholar] [CrossRef]
- Pan, J.; Cheung, N.C.; Yang, J. High-precision position control of a novel planar switched reluctance motor. IEEE Trans. Ind. Electron. 2005, 52, 1644–1652. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Kim, W.J. Design and control of a compact light-weight planar positioner moving over a concentrated-field magnet matrix. IEEE/ASME Trans. Mechatron. 2013, 18, 1090–1099. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Zhu, Y.; Zhang, M.; Liu, H. Performance-oriented precision LARC tracking motion control of a magnetically levitated planar motor with comparative experiments. IEEE Trans. Ind. Electron. 2016, 63, 5763–5773. [Google Scholar] [CrossRef]
- Huang, S.D.; Chen, L.; Cao, G.Z.; Wu, C.; Xu, J.; He, Z. Predictive position control of planar motors using trajectory gradient soft constraint with attenuation coefficients in the weighting matrix. IEEE Trans. Ind. Electron. 2021, 68, 821–837. [Google Scholar] [CrossRef]
- Huang, S.D.; Cao, G.Z.; Xu, J.; Cui, Y.; Wu, C.; He, J. Predictive position control of long-stroke planar motors for high-precision positioning applications. IEEE Trans. Ind. Electron. 2021, 68, 796–811. [Google Scholar] [CrossRef]
- Apkarian, P.; Gahinet, P.; Becker, G. Self-scheduled H∞ control of linear parameter-varying systems: A design example. Automatica 1995, 31, 1251–1261. [Google Scholar] [CrossRef]
- Packard, A. Gain scheduling via linear fractional transformations. Syst. Control Lett. 1994, 22, 79–92. [Google Scholar] [CrossRef]
- Shamma, S. Analysis and Design of Gain Scheduled Control Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1988. [Google Scholar]
- Kim, K.S.; Rew, K.H.; Kim, S. Disturbance observer for estimating higher order disturbances in time series expansion. IEEE Trans. Automat. Contr. 2010, 55, 1905–1911. [Google Scholar]
- Ishikawa, J.; Tomizuka, M. Pivot friction compensation using an accelerometer and a disturbance observer for hard disk drives. IEEE/ASME Trans. Mechatron. 1998, 3, 194–201. [Google Scholar] [CrossRef]
- Kim, K.H.; Youn, M.J. A nonlinear speed control for a PM synchronous motor using a simple disturbance estimation technique. IEEE Trans. Ind. Electron. 2002, 49, 524–535. [Google Scholar]
- Liu, H.; Li, S. Speed control for PMSM servo system using predictive functional control and extended state observer. IEEE Trans. Ind. Electron. 2012, 59, 1171–1183. [Google Scholar] [CrossRef]
- Cho, K.; Kim, J.; Choi, S.B.; Oh, S. A high-precision motion control based on a periodic adaptive disturbance observer in a PMLSM. IEEE/ASME Trans. Mechatron. 2015, 20, 2158–2171. [Google Scholar] [CrossRef]
- Lee, S.H.; Kang, H.J.; Chung, C.C. Robust fast seek control of a servo track writer using a state space disturbance observer. IEEE Trans. Control Syst. Technol. 2012, 20, 346–355. [Google Scholar] [CrossRef]
- Kang, H.J.; Kim, K.S.; Lee, S.H.; Chung, C.C. Bias compensation for fast servo track writer seek Control. IEEE Trans. Magn. 2011, 47, 1937–1943. [Google Scholar] [CrossRef]
- Delibas, B.; Koc, B. A method to realize low velocity movability and eliminate friction induced noise in piezoelectric ultrasonic motors. IEEE/ASME Trans. Mechatron. 2020, 25, 2677–2687. [Google Scholar] [CrossRef]
- Ding, S.; Chen, W.H.; Mei, K.; Murray-Smith, D.J. Disturbance observer design for nonlinear systems represented by input-output models. IEEE Trans. Ind. Electron. 2020, 67, 1222–1232. [Google Scholar] [CrossRef] [Green Version]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Lee, Y.W.; Lee, S.H.; Chung, C.C. LPV H∞ Control with disturbance estimation for permanent magnet synchronous motors. IEEE Trans. Ind. Electron. 2018, 65, 488–497. [Google Scholar] [CrossRef]
- Baranyi, P.; Yam, Y.; Varlaki, P. Tensor Product Model Transformation in Polytopic Model-Based Control; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Szollosi, A.; Baranyi, P. Influence of the tensor product model representation of qLPV models on the feasibility of linear matrix inequality. Asian J. Control 2016, 18, 1328–1342. [Google Scholar] [CrossRef]
- Takarics, B.; Vanek, B. Robust control design for the FLEXOP demonstrator aircraft via tensor product models. Asian J. Control 2021, 23, 1290–1300. [Google Scholar] [CrossRef]


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| M | 1.8 kg | ||
| 0.0485 m | |||
| 40 | |||
| 1 | |||
| 0.175 | |||
| 0 | |||
| 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, K.H.; Byeon, K.; Kim, W.; Lee, Y. LPV H∞ Control with an Augmented Nonlinear Observer for Sawyer Motors. Mathematics 2022, 10, 18. https://doi.org/10.3390/math10010018
Su KH, Byeon K, Kim W, Lee Y. LPV H∞ Control with an Augmented Nonlinear Observer for Sawyer Motors. Mathematics. 2022; 10(1):18. https://doi.org/10.3390/math10010018
Chicago/Turabian StyleSu, Khac Huan, Kwankyun Byeon, Wonhee Kim, and Youngwoo Lee. 2022. "LPV H∞ Control with an Augmented Nonlinear Observer for Sawyer Motors" Mathematics 10, no. 1: 18. https://doi.org/10.3390/math10010018
APA StyleSu, K. H., Byeon, K., Kim, W., & Lee, Y. (2022). LPV H∞ Control with an Augmented Nonlinear Observer for Sawyer Motors. Mathematics, 10(1), 18. https://doi.org/10.3390/math10010018







