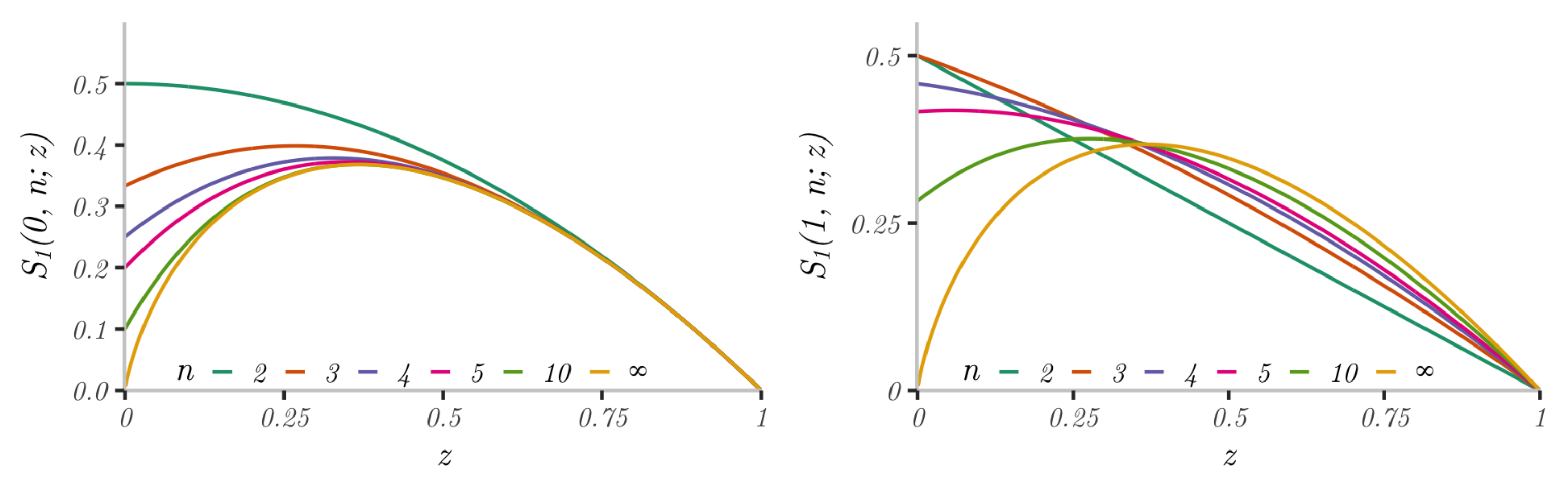Trapping the Ultimate Success

Abstract

We introduce a betting game where the gambler aims to guess the last success epoch in a series of inhomogeneous Bernoulli trials paced randomly in time. At a given stage, the gambler may bet on either the event that no further successes occur, or the event that exactly one success is yet to occur, or may choose any proper range of future times (a trap). When a trap is chosen, the gambler wins if the last success epoch is the only one that falls in the trap. The game is closely related to the sequential decision problem of maximising the probability of stopping on the last success. We use this connection to analyse the best-choice problem with random arrivals generated by a Pólya-Lundberg process.

1. Introduction

Suppose a series of inhomogeneous Bernoulli trials, with a given profile of success probabilities $\mathit{p}=(p_k,k\ge 1)$, is paced randomly in time by some independent point process. As the outcomes and epochs of the first $k\ge 0$ trials become known at some time t, the gambler is asked to bet on the time of the last success. The gambler is allowed to choose either a $\mathtt{bygone}$ action, a $\mathtt{next}$ action, or a proper subset of future times called trap. The gambler wins with $\mathtt{bygone}$ if no further successes occur, and with $\mathtt{next}$ if exactly one success occurs after time t. In the case a trapping action is chosen, the gambler wins if the last success epoch is isolated by the trap from the other success epochs.

Motivation to study this game stems from connections to the best-choice problems with random arrivals [1,2,3,4,5,6,7,8,9] and the random records model [10,11]. A prototype problem of this kind involves a sequence of rankable items arriving by a Poisson process with a finite horizon, where the $k^{\mathrm{th}}$ arrival is relatively the best (a record) with probability $p_k=1/k$. The optimisation task is to maximise the probability of selecting the overall best item (the last record) using a non-anticipating stopping strategy. Cowan and Zabczyk [5] showed that the optimal strategy is myopic, which means that the decision to stop on a particular record arrival only depends on whether the winning chance with $\mathtt{bygone}$ exceeds that with $\mathtt{next}$. They also determined the critical cut-offs of the optimal strategy and studied some asymptotics. Similar results have been obtained for the best-choice problem with some other pacing processes [1,4,7,9]. In this context, trapping can be employed to test optimality of the myopic strategy, which fails if in some situations the action $\mathtt{bygone}$ outperforms $\mathtt{next}$ but a trapping action is better still. Simple trapping strategies are easy to evaluate and provide insight into the occurrence of records.

Regarding the pacing point process, we shall assume that it is mixed binomial [12]. This setting covers, in particular, the wide class of mixed Poisson processes. In essence, this pacing process is characterised by the prior distribution $\pi$ of the total number of trials, and some background continuous distribution to spread the epochs of the trials in an i.i.d. manner. Without loss of generality, the distribution will be assumed uniform; hence, given the number of trials, they are scattered in time like the uniform order statistics on $[0,1]$. We enrich the model with a natural size parameter by letting $\pi$ vary within a family of power series distributions.

The most obvious instance of a trapping action amounts to leaving some fraction of time to isolate the last success. We call this trapping action the z-strategy, with a parameter designating the proportion of time getting skipped (as compared to the real-time cut-off in the name of the familiar ‘$1/e$-strategy’ of the best choice [13,14]). The overall optimality of the class of z-strategies among all trapping actions will be explored for a fixed and a random number of trials. For the problem of stopping on the last success, the optimality of the myopic strategy will be shown to hold if the sequence of its cut-offs is decreasing and interlacing with another set of critical points of z-strategies.

Then we specialise to the best-choice problem driven by a Pólya-Lundberg pacing process, when the number of trials follows a logarithmic series distribution. In different terms, the model was introduced by Bruss and Yor [15]. Bruss and Rogers [4] recently observed that the strategy stopping at the first record after time threshold $1/e$ is not optimal. We present a more detailed analysis; in particular, we use a curious property of certain hypergeometric functions to show that the cut-offs of the myopic strategy are increasing, hence the monotone case of optimal stopping [16] does not hold. Simulation suggests, however, that the myopic strategy is very close to optimality, both in terms of the cut-offs and the winning probability. A better approximation to optimality is achieved by the strategy that stops as soon as $\mathtt{bygone}$ becomes more beneficial than trapping with a z-strategy.

Viewed inside a bigger picture, the log-series prior appears as the edge $\nu =0$ instance of the random records model with negative binomial distribution $\mathrm{NB}(\nu ,q)$ of the number of trials. It is known that for $\nu =1$, corresponding to the geometric prior, all cut-offs coincide [17,18], while for integer $\nu >1$ they are decreasing [7]. In [19], we show that for $0<\nu <1$ the myopic strategy is not optimal, with the pattern of cut-offs as in the log-series case treated here.

2. Setting the Scene

2.1. The Probability Model

Let $\pi$ be a power series distribution

$$\begin{array}{c}\hfill {\pi }_n=c\left(q\right)w_n{q}^n,n\ge 0,\end{array}$$

(1)

$$\mathrm{with}\mathrm{weights}{w}_0\ge 0,w_n>0\mathrm{for}n\ge 1$$

and scale parameter $q>0$ varying within the interval of convergence of ${\sum }_n{w}_n{q}^n$.

The associated mixed binomial process $(N_t,t\in [0,1])$ is an orderly counting process with the uniform order statistics property. The process can also be seen as a time inhomogeneous pure-birth process, with a transition rate expressible through the generating function of $\left(w_n\right)$, see [20].

Conditionally on $N_t=k$:

(i)

The epochs of the trials within $[0,t]$ and $(t,1]$ are independent;

(ii)

The posterior distribution of the number of trials yet to occur is a power series distribution

$$\pi \left(j\right|t,k):=\mathbb{P}(N_1-N_t=j|N_t=k)=f_k\left(x\right)\left(\genfrac{}{}{0pt}{}{k+j}{j}\right)w_{k+j}{x}^j,j\ge 0,$$

(2)

with scale variable

$$x:=(1-t)q$$

(3)

and a normalisation function $f_k\left(x\right)$.

(iii)

$\left(N_{t+s/(1-t)}-N_t,s\in [0,1]\right)$ is a mixed binomial process on $[0,1]$, with the number of trials distributed according to (2).

The conditioning relation (2) appears in many statistical problems related to censored or partially observable data.

In principle, instead of considering a family of distributions for $\left(N_t\right)$ with parameter q, we could deal with one counting process on the x-scale. We prefer not to adhere to this viewpoint, as the ‘real time’ variable is more intuitive. Nevertheless, we will use (3) to switch back and forth between t and x, as x is better suitable for power series work.

Let $=(p_k,k\ge 1)$ be a profile of success probabilities. We assume that

$$0\le p_1\le 1,0\le p_k<1\mathrm{for}k>1\mathrm{and}\sum _{k=1}^{\infty }{p}_k=\infty .$$

The $k^{\mathrm{th}}$ trial, which is occurring at index/epoch k, is a success with probability $p_k$, independently of other trials and the pacing process. Thus, the point process of success epochs is obtained from $\left(N_t\right)$ by thinning out the $k^{\mathrm{th}}$ point with probability $1-p_k$. Taken by itself, the process counting the success epochs is typically intractable [10]. A notable exception is the random records model ($p_k=1/k$) with the geometric prior $\pi$, when the process is Poisson [1].

We shall identify state $(t,k)$ with the event $N_t=k$. The notation ${(t,k)}^{\circ }$ will be used to denote the event that the $k^{\mathrm{th}}$ trial epoch is t and the outcome is a success. If there is at least one success, the sequence of successes ${(t_i,k_i)}^{\circ }$ increases in both components.

2.2. The Trapping Game and Stopping Problem

A single episode of the trapping game refers to the generic state $(t,k)$. The gambler plays either $\mathtt{next}$ or $\mathtt{bygone}$, or chooses a proper subset of the interval $(t,1]$. The trap $[t+z(1-t),1]$, for $0<z<1$, will be called z-strategy; this action leaves a $(1-z)$ portion of the remaining time to isolate the last success epoch from other successes.

Let ${\mathcal{F}}_t$ be the sigma-algebra generated by the epochs and outcomes of trials on $[0,t]$. Under stopping strategy $\tau$, we mean a random variable taking values in $[0,1]$ and adapted to the filtration $({\mathcal{F}}_t,t\in [0,1])$. The performance of $\tau$ is assessed by the probability of the event that ${(\tau ,N_{\tau })}^{\circ }$ is the last success state.

We call a stopping strategy Markovian if in the event $\tau \ge t$ a decision to stop or to continue in state ${(t,k)}^{\circ }$ does not depend on the trials before time t. The general theory [21] implies existence of the optimal stopping strategy and that it can be found within the class of Markovian strategies.

Conditional on ${\mathcal{F}}_t$, the probability that ${(t,k)}^{\circ }$ is the last success equals the winning probability with $\mathtt{bygone}$, while the probability that ${(t,k)}^{\circ }$ is the penultimate success equals the winning probability with $\mathtt{next}$. If for every $(t,k)$, where $\mathtt{bygone}$ is at least as good as $\mathtt{next}$, also every state $(t^{\prime },k^{\prime })\in [t,1]\times \{k,k+1,\cdots \}$ has this property, then the optimal stopping problem is monotone [21].

Define the myopic stopping strategy ${\tau }^{*}$ to be the first record ${(t,k)}^{\circ }$, if any, such that $\mathtt{bygone}$ is at least as beneficial as $\mathtt{next}$. In the monotone case the myopic strategy is optimal among all stopping strategies.

Suppose for each $k\ge 1$ there exists a cut-off time $a_k$ such that the action $\mathtt{bygone}$ is at least as good as $\mathtt{next}$ precisely for $t\in [a_k,1]$. Then ${\tau }^{*}$ coincides with the time of the first success ${(t,k)}^{\circ }$ satisfying $t\ge a_k$ (or ${\tau }^{*}=1$ if there is no such trial). The problem is monotone, hence ${\tau }^{*}$ is optimal if the cut-offs are non-increasing, that is $a_1\ge a_2\ge \cdots$.

3. The Game with Fixed Number of Trials

In this section, we assess the outcomes of actions in state $(t,k)$ conditioned on the total number of trials $n>k$. This can be interpreted as the game of an informed gambler who knows n but not the outcomes of unseen trials $k+1,\cdots ,n$. The time t is not important and a comparison of $\mathtt{bygone}$ with $\mathtt{next}$ is tantamount to the discrete-time optimal stopping at the last success [22,23]. The best action will be shown to coincide with a z-strategy provided $\mathtt{next}$ beats $\mathtt{bygone}$.

3.1. $\mathtt{bygone}$ vs. $\mathtt{next}$

The number of successes in trials $k+1,\cdots ,n$ has probability generating function

$$\lambda \mapsto \prod _{m=k+1}^n(1-p_m+p_m\lambda )=\left(1+\lambda \sum _{i=k+1}^n\frac{p_i}{1-p_i}\right)\prod _{m=k+1}^n(1-p_m)+O\left({\lambda }^2\right).$$

From this expansion, the probability of no success is

$$s_0(k+1,n):=\prod _{m=k+1}^n(1-p_m),$$

and the probability of exactly one success is

$$s_1(k+1,n):=\sum _{i=k+1}^n\frac{p_i}{1-p_i}\prod _{m=k+1}^n(1-p_m)=s_0(k+1,n)\sum _{i=k+1}^n\frac{p_i}{1-p_i}.$$

There is an obvious recursion

$$s_1(k,n)=(1-p_k)s_1(k+1,n)+p_k{s}_0(k+1,n),$$

which we can write as

$$\begin{array}{ccc}\hfill s_1(k,n)-s_1(k+1,n)& =& p_k\{s_0(k+1,n)-s_1(k+1,n)\}\hfill \\ & =& p_k{s}_0(k+1,n)\left(1-\sum _{i=k+1}^n\frac{p_i}{1-p_i}\right).\hfill \end{array}$$

(4)

Note that the sequence,

$$\begin{array}{c}\hfill 1-\sum _{i=k+1}^n\frac{p_i}{1-p_i},0\le k\le n-1,\end{array}$$

(5)

has the sign pattern

$$-,\cdots ,-,\ge 0,+,\cdots ,+,$$

and let $k^{*}$ be the index value where the sign changes from negative. It follows that:

(i)

$s_1(·,n)$ is unimodal with maximum at $k^{*}$;

(ii)

at $k^{*}$ bygone becomes at least as good as next;

(iii)

$k^{*}$ is non-decreasing in n.

Each $A\subset \{1,\cdots ,n\}$ corresponds to a stopping strategy in the discrete time problem [22,23]. We say that A wins if the index of the last success falls in A while no other index of success does.

Lemma 1.

Among all $A\subset \{1,\cdots ,n\}$, the set $A^{*}:=\{k^{*}+1,\cdots ,n\}$ wins with the maximal probability.

Proof. 

Clearly, $n\in A$ is necessary for A to be optimal. By induction, suppose we have shown that $\{k+1,\cdots ,n\}\subset A$. Including k adds to said probability

$$c{p}_k\{s_0(k+1,n)-s_1(k+1)\},$$

where $c\ge 0$ depends on $A\cap \{1,\cdots ,k-1\}$ only. However, this is non-negative precisely for $k\ge k^{*}$.    □

The next lemma improves upon Theorem 3.1 of [24] by offering a weaker condition for monotonicity.

Lemma 2.

For $k^{*}=k^{*}\left(n\right)$, if $p_{k^{*}+1}\ge p_{n+1}$ then ${max}_k{s}_1(k,n)\ge {max}_k{s}_1(k,n+1)$.

Proof. 

It is readily checked that the maximum value of $s_1(·,n+1)$ is achieved at either $k^{*}$ or $k^{*}+1$.

Firstly, compare the winning probability of $A^{*}$ for n trials with that of $B:=\{k^{*}+1,\cdots ,n+1\}$ for $n+1$ trials. A difference results from the event that the ${(n+1)}^{\mathrm{st}}$ trial is a success, and the number of successes among trials $k^{*}+1,\cdots ,n$ does not exceed 1. Hence the difference of winning probabilities is

$$(s_1(k^{*}+1,n)-s_0(k^{*}+1,n))p_{n+1}=\left(1-\sum _{i=k^{*}+1}^n\frac{p_i}{1-p_i}\right)s_0(k^{*}+1,n)\ge 0.$$

Secondly, compare $A^{*}$ with the other possible maximiser, $C:=\{k^{*}+2,\cdots ,n,n+1\}$. The difference of winning probabilities of $A^{*}$ in the setting with n trials and C with $(n+1)$ trials has four components:

(a)

$p_{k^{*}+1}{s}_0(k^{*}+2,n)(1-p_{n+1})$, equal the probability that ${(k^{*}+1)}^{\mathrm{st}}$ trial is a success, $A^{*}$ wins while C loses,

(b)

$(1-p_{k^{*}+1}{s}_1(k^{*}+2,n)p_{n+1}$, equal the probability that ${(k^{*}+1)}^{\mathrm{st}}$ trial is a failure, $A^{*}$ wins while C loses,

(c)

$p_{k^{*}+1}{s}_1(k^{*}+2,n)(1-p_{n+1})$, equal the probability that ${(k^{*}+1)}^{\mathrm{st}}$ trial is a success, $A^{*}$ loses while C wins,

(d)

$(1-p_{k^{*}+1})s_0(k^{*}+2,n)p_{n+1}$, equal the probability that ${(k^{*}+1)}^{\mathrm{st}}$ trial is a failure, $A^{*}$ loses while C wins.

After simplification, (a) + (b) − (c) − (d) becomes

$$\left(1-\sum _{i=k^{*}+2}^n\frac{p_i}{1-p_i}\right)(p_{k^{*}+1}-p_{n+1}),$$

which has the same sign as $p_{k^{*}+1}-p_{n+1}$ because the first factor is non-negative by the optimality of $A^{*}$.    □

3.2. z-Strategies

For n fixed, the winning probability of a z-strategy in state $(t,k)$ does not depend on t and is given by a Bernstein polynomial in $z\in [0,1]$,

$$\begin{array}{c}\hfill S_1(k,n;z):=\sum _{j=0}^{n-k-1}\left(\genfrac{}{}{0pt}{}{n-k}{j}\right)z^j{(1-z)}^{n-k-j}{s}_1(k+j+1,n).\end{array}$$

(6)

In particular, $S_1(k,n;0)=s_1(k+1,n)$ is the probability to win with $\mathtt{next}$. Similarly,

$$\begin{array}{c}\hfill S_0(k,n;z):=\sum _{j=0}^{n-k}\left(\genfrac{}{}{0pt}{}{n-k}{j}\right)z^j{(1-z)}^{n-k-j}{s}_0(k+j+1,n)\end{array}$$

is the probability that none of the successes occurs in the time interval $(t+z(1-t),1]$, so $S_0(k,n;0)=s_0(k+1,n)$ equals the probability to win with $\mathtt{bygone}$.

Note that $s_0(k+1,n)=S_0(k,n;0)$ and $s_1(k+1,n)=S_1(k,n;0)$. From (i) and (ii) above

$$k\ge k^{*}⟺S_0(k,n;0)\ge S_1(k,n;0)⟹S_1(k,n;0)=\underset{z}{max}{S}_1(k,n;z).$$

(7)

This is also valid for the maximum taken over all trapping actions.

From the unimodality of $s_1(·,n)$ and the shape-preserving properties of the Bernstein polynomials (see [25], Theorem 3.3), it follows that (6) is unimodal. Thus, either the maximum is at 0 and $\mathtt{next}$ beats all z-strategies, or there exists a unique optimal z-strategy. Next result stating that the optimum can be understood in a strong sense is a continuous-time counterpart of Lemma 1.

Theorem 1.

If $S_0(k,n;0)<S_1(k,n;0)$ then the optimal trapping action is a z-strategy with threshold determined as the unique maximiser of $S_1(k,n;·)$.

Proof. 

By a change of variables we reduce the claim to the case $(t,k)=(0,0)$. There is certainly a final interval that belongs to the optimal trap, because close to the end of the time, the probability of two or more successes is of order $o(1-t)$. Now, suppose $[z,1]$ belongs to the trap and we are assessing if the length element $[z-\mathrm{d}z,z]$ is worth including. The change of the winning probability due to the inclusion is a multiple of

$$\begin{array}{ccc}\hfill \sum _{j=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{j-1}\right)z^{j-1}{(1-z)}^{n-j}{p}_j\{s_0(j+1,n)-s_1(j+1,n)\}nh+o\left(h\right)& =& \\ \hfill {(1-z)}^n\sum _{j=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{j-1}\right){\left(\frac{z}{1-z}\right)}^j{p}_k\{s_0(j+1,n)-s_1(j+1,n)\}nh+o\left(h\right),\end{array}$$

(8)

with some positive factor depending on the structure of the trap within $[0,z-h]$. By (4), in the variable $z/(1-z)$ the polynomial $\sum (\cdots )$ has at most one variation of sign in the coefficients. Applying Descartes’ rule of signs, we see that the polynomial has at most one positive root. This implies that the optimal trap is a final interval with the cut-off coinciding with the root, or $[0,1]$ (action $\mathtt{next}$) if there are no roots.

It remains to check that the root, if any, coincides with the maximiser of

$$S_1(0,n;z)=\sum _{j=0}^n\left(\genfrac{}{}{0pt}{}{n}{j}\right)z^j{(1-z)}^{n-j}{s}_1(j+1,n).$$

Indeed, we have for the derivative using (4)

$$\begin{array}{c}\hfill D_z{S}_1(0,n;z)=\\ \hfill \sum _{j=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{j-1}\right)n{z}^{j-1}{(1-z)}^{n-j}{s}_1(j+1,n)-\sum _{j=0}^{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{j}\right)n{z}^j{(1-z)}^{n-j-1}{s}_1(j+1,n)\\ \hfill =\sum _{k=1}^n(\cdots )-\sum _{k=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)n{z}^{k-1}{(1-z)}^{n-k}{s}_1(k,n)\\ \hfill =\sum _{k=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)n{z}^{k-1}{(1-z)}^{n-k}\{s_1(k+1,n)-s_1(k,n)\}\\ \hfill =\sum _{k=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)n{z}^{k-1}{(1-z)}^{n-k}{p}_k\{s_1(k+1,n)-s_0(k+1,n)\},\end{array}$$

which is the negative of the polynomial in (8). This provides the desired conclusion.    □

3.3. Examples

The best-choice problem is related to the profile $p_k=1/k$. The associated Bernstein polynomials satisfy

$$S_1(k,n;z)\to -zlogz,n\to \infty ,$$

where the convergence is uniform. Both maximiser and the maximum value converge to $1/e$ as $n\to \infty$

The case $k=0$ was studied in much detail [13,14,17,26]. The winning probability of z-strategy can be alternatively written as a Taylor polynomial

$$S_1(0,n;z)=1-z-\sum _{j=2}^n\frac{{(1-z)}^j}{j(j-1)},$$

which decreases pointwise to $z\mapsto -zlogz$ as n increases (see Figure 1). The maximisers increase monotonically to $1/e$ and also ${max}_z{S}_1(0,n;z)\downarrow 1/e.$ These facts underlie the minimax property that the $1/e$-strategy ensures winning probability of at least $1/e$ for every $n\ge 1$.

The nice monotonicity properties do not extend to $k>0$, the minimax value is below $1/e$ and the $1/e$-strategy is not minimax. This is already seen in the case $k=1$, where the Bernstein polynomials become

$$\begin{array}{ccc}\hfill S_1(1,n;z)& =& \frac{n-1}{n}-\sum _{j=2}^{n-1}\frac{(n-j){(1-z)}^j}{nj(j-1)}\hfill \\ & =& S_1(0,n;z)+\sum _{j=1}^{n-1}\frac{{(1-z)}^{j+1}}{nj}-\frac{(1-z)}{n}.\hfill \end{array}$$

The first formula is derived by conditioning on the highest rank j of trials that occur before the threshold of z-strategy.

The more general profile

$$p_k=\frac{\theta }{\theta +k-1},k\ge 1,$$

(9)

with parameter $\theta >0$, plays a central role in the combinatorial structures related to the Ewens sampling formula for random partitions [27]. The term Karamata–Stirling law was coined in [28] for the distribution of the number of successes with these probabilities. The number of successes in trials $k+1,\cdots ,n$ has probability generating function

$$\lambda \mapsto \frac{{(k+\theta \lambda )}_{n-k}}{{(k+\theta )}_{n-k}}.$$

As $n\to \infty$, $S_1(k,n;z)\to -\theta z^{\theta }logz$. The maximum values still converge to $1/e$ but the maximisers approach $e^{-1/\theta }$. The shapes vary considerably with $\theta$, see Figure 2. For $\theta$ large, the minimax winning probability is close to zero.

4. Random Number of Trials: $\mathbf{z}$-Strategies

We proceed with the continuous time setting, assuming $\mathit{p}$ and $\pi$ are given. In state $(t,k)$, the probability of isolating the last success by means of a z-strategy is a convex mixture of the Bernstein polynomials:

$$\begin{array}{c}\hfill {\mathcal{S}}_1(t,k;z):=\sum _{j=1}^{\infty }\pi \left(j\right|t,k)\sum _{i=0}^{j-1}\left(\genfrac{}{}{0pt}{}{j}{i}\right)z^i{(1-z)}^{j-1}{s}_1(k+i+1,k+j).\end{array}$$

(10)

The $z=0$ instance,

$${\mathcal{S}}_1(t,k;0)=\sum _{j=1}^{\infty }\pi \left(j\right|t,k)s_1(k+1,k+j),$$

is the probability to win with $\mathtt{next}$, and ${\mathcal{S}}_1(t,k;1)=0.$ Similarly, the probability that none of the successes are trapped by the z-strategy is:

$$\begin{array}{c}\hfill {\mathcal{S}}_0(t,k;z):=\sum _{j=0}^{\infty }\pi \left(j\right|t,k)\sum _{i=0}^{j-1}\left(\genfrac{}{}{0pt}{}{j}{i}\right)z^i{(1-z)}^{j-1}{s}_0(k+i+1,k+j),\end{array}$$

and ${\mathcal{S}}_0(t,k;0)$ is the probability to win with $\mathtt{bygone}$.

Being a convex mixture of unimodal functions, ${\mathcal{S}}_1(t,k;·)$ itself need not be unimodal. Accordingly, the optimal trap need not be a final interval. It may rather include a few disjoint intervals akin to ‘islands’ in the discrete time best-choice problems [29].

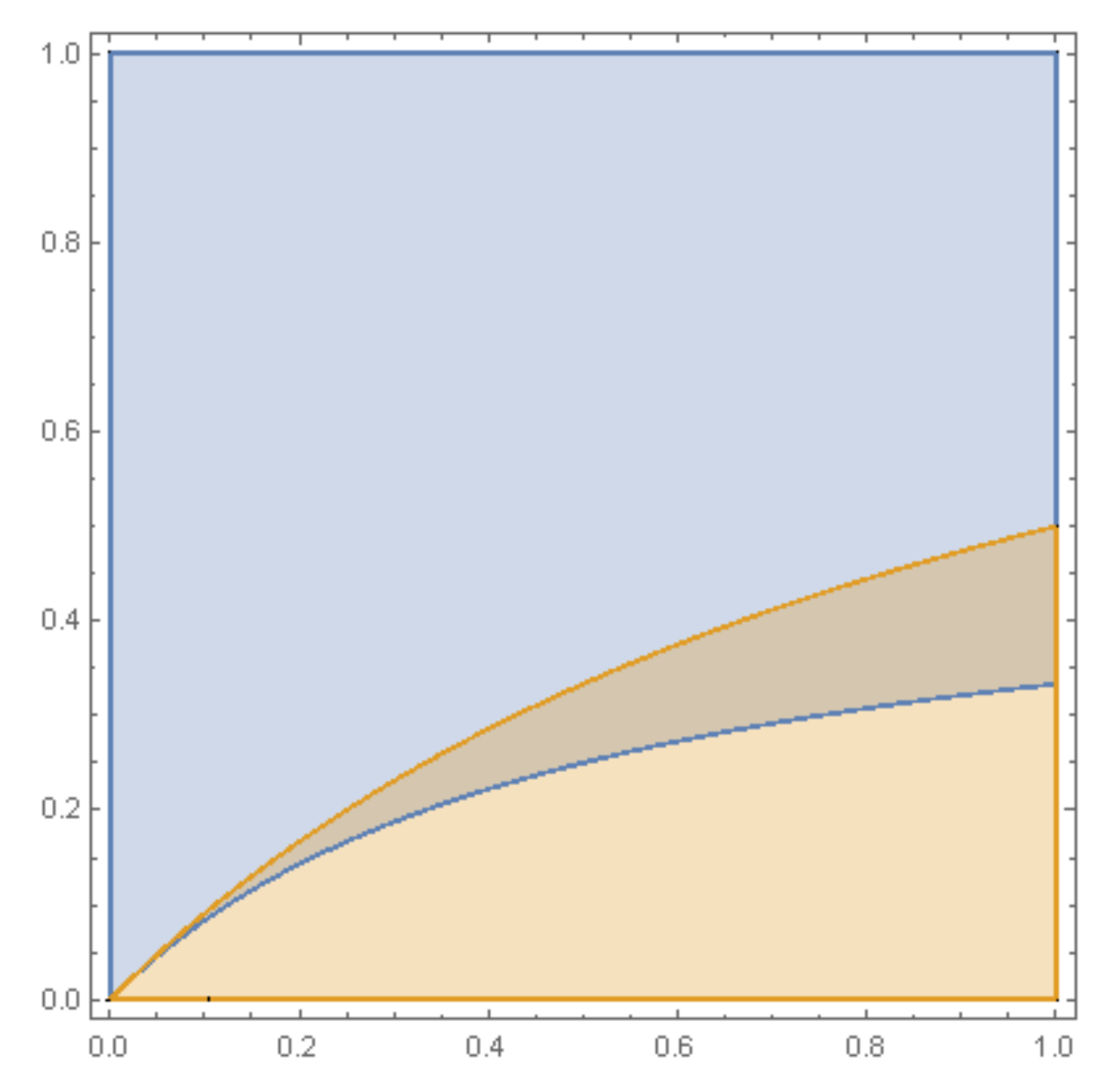
Concavity is a simple condition to ensure unimodality. We say that $s_1(·,n)$ is concave if for every $n\ge 1$ the second difference in the first variable is non-positive.

Theorem 2.

Suppose $s_1(·,n)$ is concave. Then ${\mathcal{S}}_1(t,k;·)$ is unimodal with maximum at some $z^{*}$. If $z^{*}\in (0,1)$ then for $z=z^{*}$ the z-strategy is optimal among all trapping actions, and if $z^{*}=0$ then $\mathtt{next}$ outperforms every trapping action.

Proof. 

By the shape-preserving properties of Bernstein polynomials [25], the internal sum in (10) is a concave function in z, therefore the mixture ${\mathcal{S}}_1(t,k;·)$ is also concave hence unimodal. The maximum is attained at 0 if $D_z{\mathcal{S}}_1(t,k;0)\le 0$, and $z^{*}>0$ otherwise. The overall optimality follows from the unimodality as in Theorem 1.    □

The concavity is easy to express in terms of $\mathit{p}$ explicitly. The second difference in the variable k of the probability generating function

$$\lambda \mapsto \prod _{j=k}^n(1-p_j+\lambda p_j)$$

becomes

$$\{(1-p_k+\lambda p_k)(1-p_{k+1}+\lambda p_{k+1})-2(1-p_{k+1}+\lambda p_{k+1})+1\}\prod _{j=k+2}^n(1-p_j+\lambda p_j).$$

Computing $D_{\lambda }$ at $\lambda =0$ yields the second difference of $s_1(·,n)$

$$(p_k-2p_k{p}_{k+1}-p_{k+1})+(p_k{p}_{k+1}-p_k+p_{k+1})\sum _{j=k+2}^n\frac{p_j}{1-p_j}.$$

(11)

From this, a sufficient condition for the concavity of $s_1(·,n)$ is

$$p_k-2p_k{p}_{k+1}-p_{k+1}\le 0,p_k{p}_{k+1}-p_k+p_{k+1}\le 0,k\ge 1.$$

(12)

Notably, (12) ensures unimodality for arbitrary $\pi$ and only involves two consecutive success probabilities. The price to pay for the simplicity is that the condition is restrictive, as seen in Figure 3.

For the profile (9), straight calculation shows that (11) is non-positive, hence $s_1(·,n)$ is concave, iff

$$\frac{1}{2}\le \theta \le 1.$$

This is only a half range, but it includes two most important for application cases $\theta =1$ and $\theta =1/2$.

5. Tests for the Monotone Case of Optimal Stopping

Using (2) and (3), we can cast the winning probabilities with actions $\mathtt{bygone},\mathtt{next}$ and a z-strategy as:

$$\begin{array}{ccc}\hfill {\mathcal{S}}_0(t,k;0)& =& f_k\left(x\right)P_k\left(x\right),\hfill \\ \hfill {\mathcal{S}}_1(t,k;0)& =& f_k\left(x\right)Q_k\left(x\right),\hfill \\ \hfill {\mathcal{S}}_1(t,k;z)& =& f_k\left(x\right)R_k(x,z),\hfill \end{array}$$

(13)

where $x=q(1-t)$ and

$$\begin{array}{ccc}\hfill P_k\left(x\right)& :=& \sum _{j=0}^{\infty }\left(\genfrac{}{}{0pt}{}{k+j}{j}\right)w_{k+j}{x}^j{s}_0(k+1,k+j),\hfill \\ \hfill Q_k\left(x\right)& :=& \sum _{j=1}^{\infty }\left(\genfrac{}{}{0pt}{}{k+j}{j}\right)w_{k+j}{x}^j{s}_1(k+1,k+j),\hfill \\ \hfill R_k(x,z)& :=& \sum _{j=1}^{\infty }\left(\genfrac{}{}{0pt}{}{k+j}{j}\right)w_{k+j}{x}^j\sum _{i=0}^{j-1}\left(\genfrac{}{}{0pt}{}{j}{i}\right)z^i{(1-z)}^{j-i}{s}_1(k+i+1,k+j).\hfill \end{array}$$

Thus, $Q_k\left(x\right)=R_k(x,0)$. We are looking next at some critical points for the trapping game and the optimal stopping problem.

Lemma 3.

Equation $P_k\left(x\right)=Q_k\left(x\right)$ has at most one root ${\alpha }_k>0$, for every $k\ge 1$.

Proof. 

Coefficients of the series $P_k\left(x\right)-Q_k\left(x\right)$ have at most one change of sign from + to −, hence Descartes’ rule of signs for power series [30] entails that there is at most one positive root.    □

We set ${\alpha }_k=\infty$ if the root does not exist. Define the cut-off

$$a_k={\left(1-\frac{{\alpha }_k}{q}\right)}_{+}.$$

This is the earliest time when $\mathtt{bygone}$ becomes at least as good as $\mathtt{next}$. Keep in mind that if the sequence $\left({\alpha }_k\right)$ is monotone, then $\left(a_k\right)$ is also monotone but with the monotonicity direction reversed. The monotone case of optimal stopping holds for every q, hence ${\tau }^{*}$ is optimal, if ${\alpha }_k\uparrow$.

Example 1.

In the paradigmatic case $p_k=1/k$ and the geometric prior with $w_n=1$, we have

$$s_0(k+1,n)=\frac{k}{n},s_1(k+1,n)=\frac{k}{n}\sum _{j=k+1}^n\frac{1}{j-1},$$

and explicitly computable power series

$$P_k\left(x\right)=\frac{1}{{(1-x)}^k},Q_k\left(x\right)=\frac{-log(1-x)}{{(1-x)}^k}.$$

The equation $P_k\left(x\right)=Q_k\left(x\right)$ yields identical roots ${\alpha }_k=1-1/e$ and coinciding cut-offs $a_k={(1-(1-e^{-1})/q)}_{+}$. Thus, ${\tau }^{*}$ stops at the first success trial after a time threshold. See [1,7,17,18,19] for details on this remarkable case.

Lemma 4.

Equation $D_z{R}_k(x,0)=0$ has at most one root ${\beta }_k>0$, for every $k\ge 0$. If the root exists, then ${\beta }_k\le {\alpha }_{k+1}$.

Proof. 

We follow the argument in Lemma 3. The derivative at $z=0$ is

$$D_z{R}_k(x,0)=p_{k+1}\sum _{j=1}^{\infty }\left(\genfrac{}{}{0pt}{}{k+j}{j}\right)w_{k+j}j{x}^j\{s_0(k+2,k+j)-s_1(k+2,k+j)\},$$

which has at most one change of sign for $x\ge 0$, and then from + to −. Furthermore,

$$\begin{array}{ccc}\hfill D_z{R}_k(x,0)& \ge & p_{k+1}\sum _{j=1}^{\infty }\left(\genfrac{}{}{0pt}{}{k+j}{j}\right)w_{k+j}{x}^j\{s_0(k+2,k+j)-s_1(k+2,k+j)\}\hfill \\ & =& p_{k+1}\{P_{k+1}\left(x\right)-Q_{k+1}\left(x\right)\}.\hfill \end{array}$$

This follows by comparing the series and noting that the weights at positive terms in $D_z$ are higher.    □

If there is no finite root, we set ${\beta }_k=\infty$. Let

$$b_k:={\left(1-\frac{{\beta }_k}{q}\right)}_{+}.$$

We have $D_z{R}_k(q(1-t),0)<0$ for $t\in (b_k,1]$, and $b_k\ge a_{k+1}$ by Lemma 4. Thus, $b_k$ is the earliest time when the action $\mathtt{next}$ at index k cannot be improved by a z-strategy with small enough z.

To summarise the above: for $t<a_k$ action $\mathtt{next}$ is better than $\mathtt{bygone}$, and tor $t<b_k$ a trapping strategy is better than next.

Theorem 3.

The optimal stopping problem belongs to the monotone case (for every admissible q) if and only if ${\alpha }_1\le {\alpha }_2\le \cdots .$ In that case we have the interlacing pattern of roots

$$\cdots \le {\alpha }_k\le {\beta }_k\le {\alpha }_{k+1}\le {\beta }_{k+1}\le \cdots .$$

(14)

Proof. 

We argue in probabilistic terms. The bivariate sequence of success epochs ${(t,k)}^{\circ }$ is an increasing Markov chain. The monotone case of optimal stopping occurs iff the set of states where $\mathtt{bygone}$ outperforms $\mathtt{next}$ is closed, which holds iff this is an upper subset with respect to the partial order in $[0,1]\times \{1,2,\cdots \}$. The latter property amounts to the monotonicity condition ${\alpha }_k\uparrow$.

By Lemma 3, the inequality ${\alpha }_k\le {\beta }_{k+1}$ always holds. In the monotone case, if in some state ${(t,k)}^{\circ }$ the actions bygone and next are equally good, then trapping cannot improve upon these by optimality of the myopic strategy. In the analytic terms, the above translates as the inequality ${\beta }_k\le {\alpha }_k$.    □

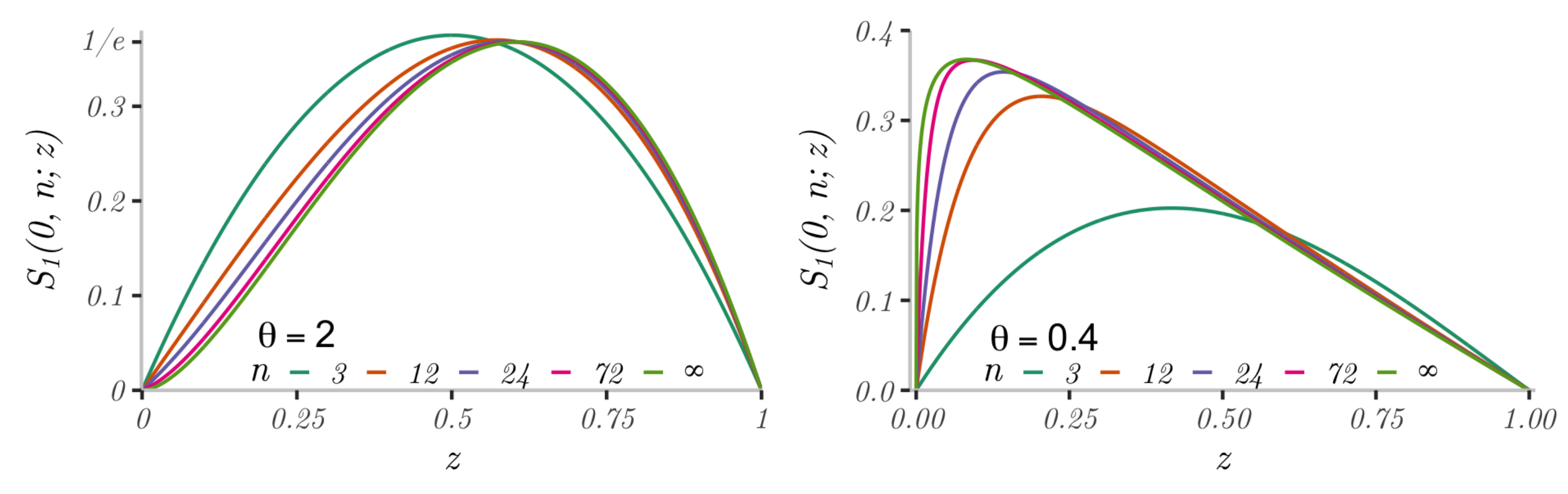
6. The Best-Choice Problem under the Log-Series Prior

In this section we consider the random records model with the classic profile $p_k=1/k$, and a pacing process with the logarithmic series prior

$${\pi }_n=c\left(q\right)\frac{q^n}{n},n\ge 1,$$

(15)

(so ${\pi }_0=0$), where $0<q<1$ and $c\left(q\right)={|log(1-q)|}^{-1}$. See [31] for Poisson mixture representations of $\pi$. The function ${\mathcal{S}}_1(t,k;·)$ is concave, hence by Theorem 2 it is sufficient to consider z-strategies.

Let $T_1$ be the time of the first trial.

Lemma 5.

Under the logarithmic series prior (15) the pacing process has the following features:

(i)

The time of the first trial $T_1$ has probability density function

$$t\mapsto \frac{c\left(q\right)q}{1-(1-t)q},t\in [0,1].$$

(ii)

$(N_t,t\in [0,1])$ is a Pólya-Lundberg birth process with transition rates

$$\begin{array}{c}\hfill \mathbb{P}(N_{t+\mathrm{d}t}-N_t=1|N_t=k)=\begin{array}{c}\hfill \frac{c\left(\right(1-t\left)q\right)q}{1-(1-t)q},k=0,\end{array}\\ \hfill \frac{k}{t+q^{-1}-1},k\ge 1.\end{array}$$

(iii)

Given $N_t=k$, the posterior distribution $\pi (·|t,k)$ of $N_1-N_t$ is $\mathrm{NB}(k,(1-t\left)q\right).$ In particular, conditionally on $T_1=t_1$, the posterior distribution is geometric with the ‘failure’ probability $(1-t_1)q$.

Proof. 

Assertion (i) follows from

$$\mathbb{P}(T_1>t)=\mathbb{P}(N_t=0)=\sum _{n=1}^{\infty }\frac{c\left(q\right)q^n{(1-t)}^n}{n},$$

and (iii) from the identity

$$\left(\genfrac{}{}{0pt}{}{k+j}{j}\right)\frac{x^j}{k+j}=\left(\genfrac{}{}{0pt}{}{k+j-1}{j}\right)\frac{x^j}{k}$$

underlying the formula for $\pi \left(j\right|t,k)$ in terms of $x=(1-t)q$. □

In view of part (ii), we will use $\mathrm{NB}(0,q)$ to denote the log-series prior (15).

6.1. Hypergeometrics

The power series of interest can be expressed via the Gaussian hypergeometric function

$$F(a,b;c;x):=\sum _{j=0}^{\infty }\frac{{\left(a\right)}_j{\left(b\right)}_j}{{\left(c\right)}_j}\frac{x^j}{j!}.$$

Recall the differentiation formula

$$D_{x}F(a,b;c,x)=\frac{ab}{c}F(a+1,b+1;c+1,x),$$

the parameter transformation formula

$$F(a,b;c;x)={(1-x)}^{c-a-b}F(c-a,c-b;c;x),$$

and Euler’s integral representation for $c>b>0$

$$F(a,b;c;x)=\frac{\Gamma \left(c\right)}{\Gamma \left(b\right)\Gamma (c-b)}{\int }_0^1\frac{y^{b-1}{(1-y)}^{c-b-1}\mathrm{d}y}{{(1-xy)}^a}.$$

The probability generating function for the number of successes following state $(t,k)$, for $k\ge 1$, is given by a hypergeometric function:

$$\begin{array}{ccc}\hfill \lambda \mapsto {(1-x)}^k\sum _{j=0}^{\infty }\left(\genfrac{}{}{0pt}{}{k+j-1}{j}\right)x^j\frac{{(k+\lambda )}_j}{{(k+1)}_j}& =& \\ \hfill {(1-x)}^k\sum _{j=0}^{\infty }\frac{{\left(k\right)}_j{(k+\lambda )}_j}{{(k+1)}_j}\frac{x^j}{j!}& =& \\ \hfill {(1-x)}^{k}F(k+\lambda ,k;k+1;x).\end{array}$$

Expanding at $\lambda =0$ we identify two basic power series as:

$$\begin{array}{ccc}\hfill P_k\left(x\right)& =& k^{-1}F(k,k;k+1;x),\hfill \\ \hfill Q_k\left(x\right)& =& k^{-1}{D}_{a}F(k,k;k+1;x),\hfill \end{array}$$

where as before $x=(1-t)q\in [0,1]$ and $D_a$ is the derivative in the first parameter. The differentiation formula implies backward recursions:

$$\begin{array}{ccc}\hfill D_x{P}_k\left(x\right)& =& k{P}_{k+1}\left(x\right),\hfill \\ \hfill D_x{Q}_k\left(x\right)& =& P_{k+1}\left(x\right)+k{Q}_{k+1}\left(x\right).\hfill \end{array}$$

(16)

The normalisation function for probabilities (14) is $f_k\left(x\right)=k{(1-x)}^k$ for $k\ge 1$, and $f_0\left(x\right)={|log(1-x)|}^{-1}$. Applying the transformation formula yields $P_k\left(x\right)={(1-x)}^{1-k}F(1,1;k+1,x),$ hence, we may write the winning probability with $\mathtt{bygone}$ as the series

$$\begin{array}{c}\hfill {\mathcal{S}}_0(t,k;0)=(1-x)\sum _{j=0}^{\infty }\frac{j!x^j}{{(k+1)}_j},x=(1-t)q.\end{array}$$

It is readily seen that, as k increases, this function decreases to $1-x$. This result was already observed in [18] using a probabilistic argument. The convergence to $1-x$ relates to the fact that for large k, the point process of record epochs approaches a Poisson process.

For $R_k(x,z)$, we derive an integral formula. Consider first the case $k\ge 1$. The probability generating function of the number of record epochs following $(t,k)$ and falling in the final interval $[t+z(1-t),1]$ has probability generating function

$$\begin{array}{ccc}\hfill \lambda \mapsto {(1-x)}^k\sum _{j=0}^{\infty }\left(\genfrac{}{}{0pt}{}{k+j-1}{j}\right)x^j\sum _{i=0}^j\left(\genfrac{}{}{0pt}{}{j}{i}\right)z^i{(1-z)}^{j-i}\frac{{(k+i+\lambda )}_{j-i}}{{(k+i+1)}_{j-i}}& =& \\ \hfill {(1-x)}^k\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{k+i-1}{i}\right){\left(xz\right)}^{i}F(k+i+\lambda ,k+i,k+i+1;x-xz)& =& \\ \hfill k{(1-x)}^k\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{k+i}{i}\right){\left(xz\right)}^i{\int }_0^1\frac{y^{k+i-1}\mathrm{d}y}{{(1-xy+xyz)}^{k+i+\lambda }}& =& \\ \hfill k{(1-x)}^k{\int }_0^1\frac{y^{k-1}{(1-xy+xyz)}^{1-\lambda }\mathrm{d}y}{{(1-xy)}^{k+1}}.\end{array}$$

Differentiating at $\lambda =0$ yields ${\mathcal{S}}_1(k,t;z)$, which is the same as $k{(1-x)}^k{R}_k(x,z)$ for $x=(1-t)q$, whence

$$R_k(x,z)={\int }_0^1\frac{y^{k-1}(1-xy+xyz)|log(1-xy+xyz)|\mathrm{d}y}{{(1-xy)}^{k+1}}.$$

(17)

For $k=0$, a similar calculation with log-series weights NB$(0,x)$ gives

$$R_0(x,z)={\int }_0^1\frac{(1-xy+xyz)log(1-xy+xyz)}{y(1-xy)}\mathrm{d}y.$$

6.2. The Myopic Strategy

The positive root obtained by equating

$$P_1\left(x\right)=\frac{|log(1-x\left)\right|}{x}\mathrm{and}{Q}_1\left(x\right)=\frac{{|log(1-x)|}^2}{2x}$$

is ${\alpha }_1=1-e^{-2}=0.864665\cdots$. On the other hand, solving $D_z{R}_1(x,0)=0$ yields a smaller value ${\beta }_1=0.756004\cdots$, hence the interlacing condition of Theorem 3 fails for $k=1$. Translating in terms of the best-choice problem, this means that ${\tau }^{*}$ stops at the first trial if this occurs before $a_1={(1-{\alpha }_1/q)}_{+}$, but a z-strategy will be more beneficial for a bigger range of times $t\le b_1={(1-{\beta }_1/q)}_{+}$. Therefore, at least for $q>{\beta }_1$, it is not optimal to stop at the first trial before $b_1$ and the myopic strategy can be beaten.

The root ${\alpha }_2:=0.755984\cdots$ is found by equating

$$\begin{array}{c}\hfill P_2\left(x\right)=\frac{2(x-L+xL)}{(1-x)x^2}\mathrm{and}{Q}_2\left(x\right)=\frac{-2x+2L-L^2+x{L}^2}{(1-x)x^2},\end{array}$$

where for shorthand $L:=-log(1-x)$. Formulas become more complicated for larger k.

We see that ${\alpha }_1>{\alpha }_2$, which suggests monotonicity of the whole sequence. To show this, pass to the quotient and re-define the root ${\alpha }_k$ as a unique solution on $[0,1)$ to

$$\frac{Q_k\left(x\right)}{P_k\left(x\right)}=1⟺\frac{D_{a}F(k,k;k+1;x)}{F(k,k;k+1;x)}=1,$$

(18)

where $D_a$ acts in the first parameter. As x increases from 0 to 1, this logarithmic derivative runs from 0 to ∞.

Lemma 6.

The logarithmic derivative (18) increases in k, hence the sequence of roots ${\alpha }_k$ is strictly decreasing.

Proof. 

Euler’s integral specialises as:

$$F(k+\lambda ,k;k+1;x)=k{\int }_0^1\frac{y^{k-1}}{{(1-xy)}^{k+\lambda }}\mathrm{d}y.$$

Expanding in parameter at $\lambda =0$ gives the integral representations

$$\begin{array}{c}\hfill P_k\left(x\right)={\int }_0^1\frac{y^{k-1}}{{(1-xy)}^k}\mathrm{d}y,Q_k\left(x\right)={\int }_0^1\frac{y^{k-1}|log(1-xy)|}{{(1-xy)}^k}\mathrm{d}y.\end{array}$$

From these formulas,

$$\begin{array}{cc}\hfill Q_k\left(x\right)P_{k+1}\left(x\right)& {\displaystyle ={\int }_0^1\frac{y^{k-1}|log(1-xy)|}{{(1-xy)}^k}\mathrm{d}y{\int }_0^1\frac{z^k}{{(1-xz)}^{k+1}}\mathrm{d}z}\\ & {\displaystyle ={\int }_0^1{\int }_0^1\frac{y^{k-1}{z}^{k-1}|log(1-xy)|}{{(1-xy)}^k{(1-xz)}^k}\frac{z}{(1-xz)}\mathrm{d}y\mathrm{d}z.}\end{array}$$

By the same kind of argument, a similar formula is obtained for $Q_{k+1}\left(x\right)P_k\left(x\right)$. Splitting the integration domain, and using symmetries of the integrand yields for $x\in [0,1)$

$$\begin{array}{ccc}\hfill Q_k\left(x\right)P_{k+1}\left(x\right)-Q_{k+1}\left(x\right)P_k\left(x\right)& =& \\ \hfill {\int }_0^1{\int }_0^1\frac{y^{k-1}{z}^{k-1}|log(1-xy)|}{{(1-xy)}^{k+1}{(1-xz)}^{k+1}}\left(z-y\right)\mathrm{d}y\mathrm{d}z& =& \\ \hfill \int \underset{0<y<z<1}{\int }\frac{y^{k-1}{z}^{k-1}}{{(1-xy)}^{k+1}{(1-xz)}^{k+1}}log\left(\frac{1-xz}{1-xy}\right)\left(z-y\right)\mathrm{d}y\mathrm{d}z& <& 0,\hfill \end{array}$$

which implies the asserted monotonicity. □

Figure 4 shows some shapes of $f_k\left(x\right)P_k\left(x\right)$ and $f_k\left(x\right)Q_k\left(x\right)$ for $k=1,2,3$.

The log-series distribution weights satisfy $w_{n+1}/w_n\uparrow 1$. Comparison with the geometric distribution, as in [19], in combination with the lemma give ${\alpha }_k\downarrow (1-1/e)$ as $k\to \infty$. The same limit has been shown for analogous roots in the best-choice problem with the negative binomial prior $\mathrm{NB}(\nu ,q)$ for integer $\nu \ge 1$; however, the monotonicity direction in that setting is different [7].

To summarise findings of this section, we have:

Theorem 4.

The monotone case of optimal stopping does not hold. The myopic strategy ${\tau }^{*}$ is not optimal and has the following features:

(i)

for $q>1-1/e$, the cut-offs of ${\tau }^{*}$ satisfy $a_k\uparrow 1-(1-1/e)/q$;

(ii)

for $t\ge {(1-(1-1/e)/q)}_{+}$, $\mathtt{bygone}$ is the optimal action for every ${(t,k)}^{\circ }$;

(iii)

for times as in (ii), the myopic strategy coincides with the optimal stopping strategy (in the event ${\tau }^{*}\ge t$).

6.3. Optimality and Bounds

For state $(t,k)$ and $x=q(1-t)$, define the continuation value $V_k\left(x\right)$ to be the maximum probability of the best choice, as achievable by stopping strategies starting in the state. By the optimality principle, the overall optimal stopping strategy, starting from $(0,0)$, stops at the first record ${(t,k)}^{\circ }$ satisfying $k{(1-x)}^k{P}_k\left(x\right)\ge V_k\left(x\right)$.

Given $N_t=k$, let $T_{k+1}$ be the next trial epoch (or 1 in the event $N_1=k$). Similar to the argument in Lemma 5, we find that the random variable $(1-T_{k+1})/(1-t)$ has density

$$y\mapsto \frac{kx{(1-x)}^k}{{(1-x+xy)}^{k+1}},y\in (0,1].$$

By the ${(k+1)}^{\mathrm{st}}$ trial, the optimal stopping strategy stops if this is a record and $\mathtt{bygone}$ is more beneficial than the optimal continuation, hence integrating out $T_{k+1}$ we obtain

$$V_k\left(x\right)={\int }_0^1\left[\frac{1}{k+1}max\{{(1-y)}^{k+1}{P}_{k+1}\left(y\right),V_{k+1}\left(y\right)\}+\frac{k}{k+1}{V}_{k+1}\left(y\right)\right]\frac{kx{(1-x)}^k\mathrm{d}y}{{(1-x+xy)}^{k+1}}.$$

This has the equivalent differential form for $k\ge 1$,

$$(1-x)D_x{V}_k\left(x\right)=\frac{k}{k+1}{\left({(1-x)}^{k+1}{P}_{k+1}\left(x\right)-V_{k+1}\left(x\right)\right)}_{+}+k\{V_{k+1}\left(x\right)-V_k\left(x\right))\}.$$

(19)

For the special instance $k=0$, integrating out the variable $T_1$ gives

$$V_0\left(x\right)={\int }_0^{1}max((1-y)P_1\left(y\right),V_1\left(y\right))\frac{\mathrm{d}y}{(1-x+xy)|log(1-x\left)\right|},$$

or, in the differential form with initial conditions $V_0\left(0\right)=1$ and $V_k\left(0\right)=0,\mathrm{for}k\ge 1$

$$(1-x)|log(1-x)|D_x{V}_0\left(x\right)=max\{(1-x)P_1\left(x\right),V_1\left(x\right)\}-V_0\left(x\right).$$

(20)

By Corollary 4, the continuation value coincides with the winning probability of $\mathtt{next}$ in a segment of the range; therefore:

$$\begin{array}{c}\hfill V_k\left(x\right)=k{(1-x)}^k{Q}_k\left(x\right),\mathrm{for}0\le x\le 1-1/e,k\ge 0.\end{array}$$

(21)

As a check, for $k\ge 1$ let ${\widehat{V}}_k\left(x\right):=k^{-1}{(1-x)}^{-k}{V}_k\left(x\right)$. With this change of variable, (19) simplifies as

$$D_x{\widehat{V}}_k\left(x\right)={(P_{k+1}\left(x\right)-{\widehat{V}}_{k+1}\left(x\right))}_{+}+(k+1){\widehat{V}}_{k+1}\left(x\right).$$

For x in the range where $P_{k+1}\left(x\right)-{\widehat{V}}_{k+1}\left(x\right)\ge 0$, this becomes the recursion (16).

Outside the range covered by (21), Equations (19) and (20) should be complemented by a ‘$k=\infty$’ boundary condition

$$\underset{k\to \infty }{lim}{V}_k\left(x\right)=\left\{\begin{array}{c}1/e,\mathrm{for}1-1/e\le x\le 1,\hfill \\ -(1-x)log(1-x),\mathrm{for}0\le x\le 1-1/e.\hfill \end{array}\right.$$

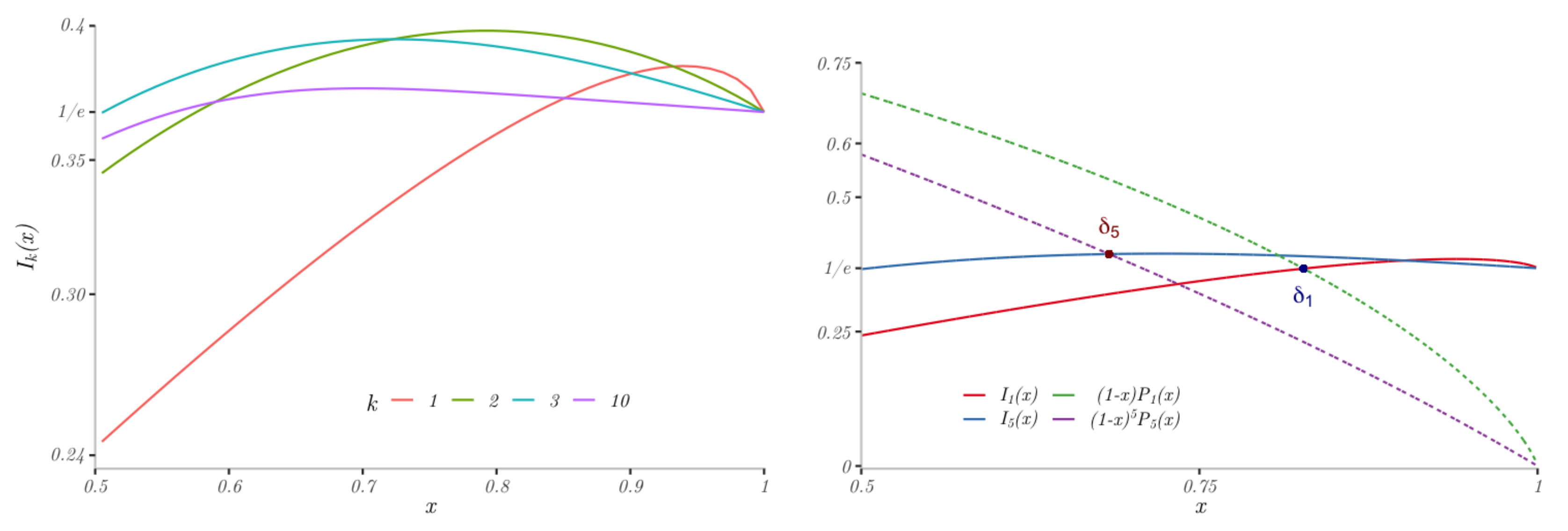
Figure 5 shows stop, continuation and z-strategy curves for $k=1,2$ and 3. The numerical simulation suggests that the equation $k{(1-x)}^k{P}_k\left(x\right)=V_k\left(x\right),k\ge 1$ has a unique solution ${\gamma }_k$ and that the critical points increase with k, so the optimal stopping strategy is similar to the myopic. These critical points have lower bounds ${\delta }_k$ defined as the solution to $k{(1-x)}^k{P}_k\left(x\right)=I_k\left(x\right)$ and upper bounds ${\rho }_k$ defined as the critical points where $\mathtt{bygone}$ is the same as the z-strategy.

To approximate the continuation value in the range $1-1/e<x<1$, we simulated some easier computable bounds

$$k{(1-x)}^k{Q}_k\le k{(1-x)}^k\underset{z}{max}{R}_k(x,z)\le V_k\left(x\right)<I_k\left(x\right).$$

The upper information bound $I_k\left(x\right)$ (see Figure 6) is the winning probability of an informed gambler who in state $(t,k)$ (with $x=q(1-t)$) knows the total number of trials $N_1$, as in Section 3. Two lower bounds stem from the comparison with the myopic and z-strategies. The points ${\beta }_k$ computed for $k\le 10$ all satisfy ${\beta }_k<{\alpha }_k$, and so the first relation turns equality for $0\le x\le {\beta }_k$. Therefore, the critical points satisfy

$${\delta }_k<{\gamma }_k<{\rho }_k\le {\alpha }_k.$$

The results of computation are presented in Figure 5 and

Table 1. Critical points: ${\alpha }_k$: Solution to $P_k\left(x\right)=Q_k\left(x\right)$, ${\beta }_k$: Solution to $D_z{R}_k(x,z)=0$, ${\gamma }_k$: Solution to $k{(1-x)}^k{P}_k\left(x\right)=V_k\left(x\right)$, ${\delta }_k$: Solution to $k{(1-x)}^k{P}_k\left(x\right)=I_k\left(x\right)$, ${\rho }_k$: Solution to $P_k\left(x\right)={max}_z{R}_k(x,z)$.

k	${\mathit{\beta }}_{\mathit{k}}$	${\mathit{\delta }}_{\mathit{k}}$	${\mathit{\gamma }}_{\mathit{k}}$	${\mathit{\rho }}_{\mathit{k}}$	${\mathit{\alpha }}_{\mathit{k}}$
1	0.756004	0.826893	0.849635	0.850335	0.864665
2	0.714616	0.718332	0.753621	0.753727	0.755984
3	0.693549	0.683295	0.713957	0.713995	0.714596
4	0.680931	0.668986	0.693275	0.693311	0.693529
5	0.672567	0.661520	0.680687	0.680814	0.680911
6	0.666632	0.656902	0.672194	0.672499	0.672547
7	0.662206	0.653656	0.665900	0.666584	0.666611
8	0.658782	0.651188	0.661005	0.662169	0.662186
9	0.656055	0.649234	0.657108	0.658751	0.658761
10	0.653833	0.647653	0.653911	0.656028	0.656034

,

Table 2. Winning probability and bounds for k = 1.

x	$(1-\mathit{x}){\mathit{P}}_1\left(\mathit{x}\right)$	$(1-\mathit{x}){\mathit{Q}}_1\left(\mathit{x}\right)$	$(1-\mathit{x}){max}_{\mathit{z}}{\mathit{R}}_1(\mathit{x},\mathit{z})$	${\mathit{V}}_1\left(\mathit{x}\right)$	${\mathit{I}}_1\left(\mathit{x}\right)$
0.60	0.6109	0.2799	0.2799	0.2799	0.2864
0.65	0.5653	0.2967	0.2967	0.2967	0.3069
0.70	0.5160	0.3106	0.3106	0.3106	0.3262
0.75	0.4621	0.3203	0.3203	0.3204	0.3439
0.80	0.4024	0.3238	0.3269	0.3275	0.3597
0.85	0.3348	0.3176	0.3342	0.3354	0.3728
0.90	0.2558	0.2945	0.3428	0.3446	0.3821
0.95	0.1577	0.2362	0.3532	0.3555	0.3848
0.995	0.0266	0.0705	0.3659	0.3667	0.3731

,

Table 3. Winning probability and bounds for k = 2.

x	$2{(1-\mathit{x})}^2{\mathit{P}}_2\left(\mathit{x}\right)$	$2{(1-\mathit{x})}^2{\mathit{Q}}_2\left(\mathit{x}\right)$	$2{(1-\mathit{x})}^2{max}_{\mathit{z}}{\mathit{R}}_2(\mathit{x},\mathit{z})$	${\mathit{V}}_2\left(\mathit{x}\right)$	${\mathit{I}}_2\left(\mathit{x}\right)$
0.60	0.5189	0.3297	0.3297	0.3297	0.3743
0.65	0.4682	0.3429	0.3429	0.3429	0.3850
0.70	0.4149	0.3509	0.3509	0.3509	0.3926
0.75	0.3586	0.3521	0.3541	0.3543	0.3970
0.80	0.2988	0.3440	0.3570	0.3575	0.3981
0.85	0.2348	0.3227	0.3600	0.3608	0.3960
0.90	0.1654	0.2809	0.3630	0.3643	0.3903
0.95	0.0887	0.2018	0.3659	0.3674	0.3811
0.995	0.0098	0.0428	0.3678	0.3679	0.3694

and

Table 4. Winning probability and bounds for k = 3.

x	$3{(1-\mathit{x})}^3{\mathit{P}}_3\left(\mathit{x}\right)$	$3{(1-\mathit{x})}^3{\mathit{Q}}_3\left(\mathit{x}\right)$	$3{(1-\mathit{x})}^3{max}_{\mathit{z}}{\mathit{R}}_3(\mathit{x},\mathit{z})$	${\mathit{V}}_3\left(\mathit{x}\right)$	${\mathit{I}}_3\left(\mathit{x}\right)$
0.60	0.4811	0.3460	0.3460	0.3460	0.3869
0.65	0.4296	0.3562	0.3562	0.3562	0.3923
0.70	0.3762	0.3603	0.3604	0.3605	0.3947
0.75	0.3207	0.3568	0.3620	0.3622	0.3946
0.80	0.2629	0.3431	0.3635	0.3640	0.3923
0.85	0.2026	0.3155	0.3649	0.3660	0.3881
0.90	0.1391	0.2674	0.3663	0.3679	0.3824
0.95	0.0719	0.1846	0.3673	0.3685	0.3755
0.995	0.0075	0.0359	0.3679	0.3679	0.3687

. The data show excellent performance of the strategy that by the first trial chooses between stopping and proceeding with a z-strategy.