The Development of Log Aesthetic Patch and Its Projection onto the Plane

Abstract

In this work, we introduce a new type of surface called the Log Aesthetic Patch (LAP). This surface is an extension of the Coons surface patch, in which the four boundary curves are either planar or spatial Log Aesthetic Curves (LACs). To identify its versatility, we approximated the hyperbolic paraboloid to LAP using the information of lines of curvature (LoC). The outer part of the LoCs, which play a role as the boundary of the hyperbolic paraboloid, is replaced with LACs before constructing the LAP. Since LoCs are essential in shipbuilding for hot and cold bending processes, we investigated the LAP in terms of the LoC’s curvature, derivative of curvature, torsion, and Logarithmic Curvature Graph (LCG). The numerical results indicate that the LoCs for both surfaces possess monotonic curvatures. An advantage of LAP approximation over its original hyperbolic paraboloid is that the LoCs of LAP can be approximated to LACs, and hence the first derivative of curvatures for LoCs are monotonic, whereas they are non-monotonic for the hyperbolic paraboloid. This confirms that the LAP produced is indeed of high quality. Lastly, we project the LAP onto a plane using geodesic curvature to create strips that can be pasted together, mimicking hot and cold bending processes in the shipbuilding industry.

1. Introduction

The introduction of Bezier curves and surfaces representation was a significant breakthrough of Computer Aided Geometric Design (CAGD), which was later extended to B-spline representation [1,2]. Eventually, B-splines and NURBS became the de facto standard for computer graphics packages, computer-aided design (CAD), and computer-aided manufacturing (CAM) [3]. The complex form of curvature of these curves, which are not suitable for direct manufacturing, led to the introduction of a variety of efficient fairing algorithms to reduce the oscillation in the curvature profile of these curves [4,5,6]. However, Cornu spirals, or clothoids, are members of spiral curves that have monotonic curvature profiles by nature [7,8,9].

The Log Aesthetic Curve (LAC) is a type of curve that possesses a monotonic curvature profile, hence suiting the aesthetic design environment. The research on LACs has been active since Miura [10] introduced a linear Logarithmic Curvature Graph (LCG) as its fundamental equation. The LAC equation can be used to represent various spirals, e.g., clothoid, logarithmic spiral, circle involute, and Nielsen’s spiral. LCG can also be used as a shape interrogation tool to investigate the characteristics of arbitrary curves [11]. Yoshida and Saito [12] developed a method of drawing and controlling LACs alternatively using a bisection method; hence, it can be shaped using control points, similar to Bezier curves. Moreover, Yoshida et al. [13] also introduced an algorithm to interactively control the Log Aesthetic Space Curve (LASC), which has a linear LCG as well as a linear Logarithmic Torsion Graph (LTG).

There are numerous works on developing surfaces using the LAC. In 2012, Ziatdinov [14] implemented the generalized version of LAC as a profile curve to generate a surface of revolution called a superspiraloid. Inoue et al. [15] developed an algorithm that used the LAC as a profile curve to generate a log aesthetic curved surface using the virtual reality (VR) technique. Furthermore, the LAC has also been used to design bi-cubic B-spline surfaces [16]. The fundamental equation of the LAC can also be used as a digital filter to smooth any arbitrary surfaces [17]. The latest work is to investigate the characteristics of LoCs for Log Aesthetic (LA) surfaces of revolution and LA swept surfaces on GPU [18].

Surface modeling is a basic mathematical method for forming surfaces in CAD applications. The NURBS surface is the de facto surface for the CAD environment and is built on the basis of control points, knots, degrees, and weights [19]. Designers can interactively draw NURBS surfaces by controlling these variables. Meanwhile, the Coons surface patch is a parametric surface consisting of four boundary curves, which are connected like a closed fence [20]. This surface has been widely used, as it interpolates four boundary curves. The advantage of Coons patch is that designers require only four boundary curves to design a surface rather than controlling each control point or weight to draw the desired surface; hence, it has widely been used for patching holes. Examples of works include the implementation of the Coons patch for image interpolation [21] and automotive design [22].

A ship hull must be a smooth streamlined surface that satisfies hydrodynamic properties such as pressure and frictional and wave resistances [23]. Hence, designing a ship hull that involves bending thick plates is one of the top priorities in shipbuilding. Fukano et al. [24] proposed a point-based shape monitoring method for bent plates of a large storage tank. The plates used to construct the storage tank are similar to those used in the shipbuilding industry and are very thick and difficult to bend. Note that a typical ship hull is built of 200–300 thick, doubly curved plates that are more than 1 cm thick [25]. Fukano et al.’s [24] method is time-consuming, as the process requires laser scanning to extract the desired points on the plate, identifying the differences, plate bending, and repeating the process until the desired shape is formed. To fabricate each doubly curved plate, the engineers are required to bend each planar plate along the lines of curvature (LoC) using the cold and hot bending techniques. Cold bending is performed by pressing along the LoC with a smaller curvature magnitude, which causes the plate to bend along the LoC with a larger curvature magnitude [25]. Then, hot bending is applied by implementing local heat treatment along the LoC with a larger curvature magnitude on the plate, causing the plate to bend along the LoC with a smaller curvature magnitude. In other words, the plates used in shipbuilding can be formed by applying these two processes.

An LoC is a curve on a surface whose tangent is in the principal direction. A principal direction is a tangent direction that has either a maximum or a minimum surface of the normal curvature. Takezawa et al. [26] proposed a method of using LoCs to shape the doubly curved plates used in shipbuilding. In 2014, Joo et al. [25] proposed an algorithm for computing LoCs on parametric surfaces as well as to derive its curvature and torsion. They further showed that these LoCs may aid in designing ship hulls. The authors also provided an algorithm for using geodesic curvature to develop a surface using LoCs by projecting them onto a plane, as shown in Section 3.1. In 2019, Takezawa et al. [23] proposed an interactive method to control LoCs on a doubly curved surface. They smoothed the experiment surfaces by implementing smoothed directions on the LoCs instead of using true principal directions. Recently, Takezawa et al. [27] proposed a fabrication method for unfolding generalized principal patches to design carbon fiber reinforced plastic automobile parts and marine propeller blades.

In 2021, Gobithaasan et al. [18] applied LACs to draw LA surfaces of revolution and LA swept surfaces, and the LoCs of these surfaces are indeed the LAC itself. This motivated us to design free-from surfaces by applying LACs or LASCs as boundary curves for the Coons patch. In this paper, we use LACs or LASCs to form a Coons-like patch, denoted as the Log Aesthetic Patch, or LAP in short. Next, we approximated the hyperbolic paraboloid using the LAP and analyzed the characteristics of LoCs on the resulting LAP. Finally, we employed an algorithm to project the LAP onto a plane for the fabrication mimicking the shipbuilding process.

The rest of the paper is arranged as follows. Section 2, Section 3 and Section 4 describe the literature review of this work; Section 2 introduces the LAC and LASC; Section 3 reviews the differential geometry of the surface and the development of the surface onto a plane; and Section 4 describes the fundamental equation of the Coons patch. Section 5 describes the development of the LAP and presents a numerical example with the development of a surface by mapping onto a plane before finally elaborating on the conclusion.

2. LAC and LASC

This section describes the general equations of the LAC and LASC.

$$\log \left(\rho \frac{ds}{d\rho }\right)=\alpha \log \left(\rho \right)+C_1,$$

(1)

$$\log \left(\mu \frac{ds}{d\mu }\right)=\beta \log \left(\mu \right)+C_2,$$

(2)

Equation (1) represents the LCG as a linear function, where $\alpha$ is the slope of LCG, $s$ is the arc length of the curve, $\rho$ is the radius of curvature, and $C_1$ is a constant [12]. Equation (2) represents the LTG function, where $\beta$ is the slope of LTG, $s$ is the arc length of a curve, $\mu$ is the radius of torsion and $C_2$ is a constant [13]. If we differentiate and simplify Equations (1) and (2), we obtain:

$$\frac{ds}{d\rho }=\frac{{\rho }^{\alpha -1}}{\mathsf{\Lambda }},$$

(3)

$$\frac{ds}{d\mu }=\frac{{\mu }^{\beta -1}}{\mathsf{\Omega }},$$

(4)

where $\mathsf{\Lambda }=e^{-C_1}$ and $\mathsf{\Omega }=e^{-C_2}$ are shape parameters. Integrating Equations (3) and (4) yields:

$$\rho =\{\begin{array}{cc}{\rho }_0{e}^{\mathsf{\Lambda }\mathrm{s}}& if \alpha =0\\ {\left({\rho }_0{}^{\alpha }+\mathsf{\Lambda }\alpha \mathrm{s}\right)}^{\frac{1}{\alpha }}& otherwise\end{array},$$

(5)

$$\mu =\{\begin{array}{cc}{\mu }_0{e}^{\mathsf{\Omega }\mathrm{s}}& if \beta =0\\ {\left({\mu }_0{}^{\alpha }+\mathsf{\Omega }\beta \mathrm{s}\right)}^{\frac{1}{\beta }}& otherwise\end{array},$$

(6)

where ${\rho }_0$ is the initial radius of curvature and ${\mu }_0$ is the initial radius of torsion. It is important to note that Yoshida et al. [13] set ${\mu }_0=\nu$. Hence, the curvature and torsion of a curve are shown below:

$$\kappa =\{\begin{array}{cc}\frac{1}{{\rho }_0{e}^{\mathsf{\Lambda }\mathrm{s}}}& ,\alpha =0,\\ {\left({\rho }_0{}^{\alpha }+\mathsf{\Lambda }\alpha \mathrm{s}\right)}^{-\frac{1}{\alpha }}& ,otherwise\end{array}$$

(7)

$$\tau \left(s\right)=\{\begin{array}{cc}\frac{1}{{\mu }_0{e}^{\mathsf{\Omega }\mathrm{s}}}& if \beta =0\\ {\left({\upsilon }^{\beta }+\mathsf{\Omega }\beta \mathrm{s}\right)}^{-\frac{1}{\beta }}& otherwise\end{array}$$

(8)

We can substitute Equation (3) to $\frac{d\theta }{ds}=\frac{1}{\rho }$, where $\theta$ is the tangential angle [12], to obtain:

$$\frac{d\theta }{ds}\frac{ds}{d\rho }=\frac{d\theta }{d\rho }=\frac{1}{\rho }\frac{{\rho }^{\alpha -1}}{\rho \mathsf{\Lambda }}=\frac{{\rho }^{\alpha -2}}{\mathsf{\Lambda }}$$

(9)

Integrating Equation (9) yields:

$$\rho =\{\begin{array}{cc}{\rho }_0{e}^{\mathsf{\Lambda }\theta }& if \alpha =1\\ {\left({\rho }_0{}^{\alpha -1}+\mathsf{\Lambda }\left(\alpha -1\right)\theta \right)}^{\frac{1}{\alpha -1}}& otherwise\end{array}$$

(10)

Let $C\left(s\right)=\left(x\left(s\right),y\left(s\right),z\left(s\right)\right)$ be an arc length of the parameterized space curve; $\mathit{t}\left(s\right)$ is the unit tangent vector, $\mathit{n}\left(s\right)$ is the unit normal vector, and $\mathit{b}\left(s\right)$ is the unit binormal vector. The Frenet–Serret formulas in terms of arc length parameterized can be represented as follows:

$$\begin{gathered} {\mathit{t}}^{\prime }\left(s\right)=\kappa \left(s\right)\mathit{n}\left(s\right) \\ {\mathit{n}}^{\prime }\left(s\right)=-\kappa \left(s\right)\mathit{t}\left(s\right)+\tau \left(s\right)\mathit{b}\left(s\right) \\ {\mathit{b}}^{\prime }\left(s\right)=-\tau \left(s\right)\mathit{n}\left(s\right) \end{gathered}$$

(11)

Assume that $\phi \left(u\right)=\frac{ds}{du}$; the Frenet–Serret formula in terms of the parameter $u$ is defined as [28]:

$$\begin{gathered} \dot{\mathit{t}}\left(u\right)=\phi \left(u\right)\kappa \left(u\right)\mathit{n}\left(u\right) \\ \dot{\mathit{n}}\left(u\right)=\phi \left(u\right)\left(-\kappa \left(u\right)\mathit{t}\left(u\right)+\tau \left(u\right)\mathit{b}\left(u\right)\right) \\ \dot{\mathit{b}}\left(u\right)=-\phi \left(u\right)\tau \left(u\right)\mathit{n}\left(u\right) \end{gathered}$$

(12)

The LASC is a curve in three-dimensional space that can be drawn by applying curvature (Equation (7)) and torsion (Equation (8)) to Equation (11). Since the LAC is a curve in two-dimensional space, we can draw this curve by applying curvature (Equation (7)) and assigning torsion, $\tau \left(s\right)=0$, in Equation (11). The details on how the LAC and LASC can be drawn and controlled interactively are fully discussed in [12,13].

3. Lines of Curvature

Let a parametric surface $R\left(u,v\right)=\left(x\left(u,v\right),y\left(u,v\right),z\left(u,v\right)\right)$; the first and second fundamental equation of the surface are [25,29]:

$$\mathrm{I}\left(u,v\right)=E{\dot{u}}^2+2F\dot{u}\dot{v}+G{\dot{v}}^2,$$

(13)

$$\mathrm{II}\left(u,v\right)=L{\dot{u}}^2+2M\dot{u}\dot{v}+N{\dot{v}}^2,$$

(14)

where $E=R_u.R_u$, $F=R_u.R_v$, $G=R_v.R_v$, $L=\mathrm{N}.R_{uu}$, $M=\mathrm{N}.R_{uv}$, $N=\mathrm{N}.R_{vv}$, $\mathrm{N}=\frac{R_u\times R_v}{\left|R_u\times R_v\right|}$, $\dot{u}=\frac{du}{dt}$, and $\dot{v}=\frac{dv}{dt}$. Equations (15)–(17) represent the Gaussian curvature, mean curvature, and principle curvature, respectively.

$$K=\frac{LN-M^2}{EG-F^2},$$

(15)

$$H=\frac{EN+GL-2FM}{2\left(EG-F^2\right)},$$

(16)

$${\kappa }_p=H\pm \sqrt{H^2-K}.$$

(17)

By solving the following initial value problems numerically, the LoC on a surface can be computed as [25]:

$$u^{\prime }\left(s\right)=\frac{dt}{ds}\times \dot{u}\left(t\right)=\{\begin{array}{cc}\eta \left(M-{\kappa }_{p}F\right)& \left|L-{\kappa }_{p}E\right|\ge \left|N-{\kappa }_{p}G\right|\\ \mu \left(N-{\kappa }_{p}G\right)& \left|L-{\kappa }_{p}E\right|<\left|N-{\kappa }_{p}G\right|\end{array},$$

(18)

$$v^{\prime }\left(s\right)=\frac{dt}{ds}\times \dot{v}\left(t\right)=\{\begin{array}{cc}-\eta \left(L-{\kappa }_{p}E\right)& \left|L-{\kappa }_{p}E\right|\ge \left|N-{\kappa }_{p}G\right|\\ -\mu \left(M-{\kappa }_{p}F\right)& \left|L-{\kappa }_{p}E\right|<\left|N-{\kappa }_{p}G\right|\end{array},$$

(19)

where the non-zero factor ($\eta$ and $\mu$) can be obtained by normalizing the first fundamental equation, as shown below:

$$\frac{dt}{ds}=\frac{\pm 1}{\sqrt{E\dot{u}{\left(t\right)}^2+2F\dot{u}\left(t\right)\dot{v}\left(t\right)+G\dot{v}{\left(t\right)}^2}}.$$

(20)

The sign of $\frac{dt}{ds}$ can be determined from Equation (20) [29]. LoCs can be generated by solving initial value problems (Equations (18) and (19)) using various types of numerical approaches, such as the Runge–Kutta method.

Let $c\left(s\right)=R\left(u\left(s\right),v\left(s\right)\right)$ represent a curve on a surface; the derivatives of the curve on the surface can be obtained using the chain rule as follows [25]:

$$c^{\prime }\left(s\right)=R_u{u}^{\prime }+R_v{v}^{\prime }.$$

(21)

$$c^{″}\left(s\right)=R_{uu}{u^{\prime }}^2+2R_{uv}{u}^{\prime }{v}^{\prime }+R_{vv}{v^{\prime }}^2+R_u{u}^{″}+R_v{v}^{″}.$$

(22)

$$\begin{gathered} c^{‴}\left(s\right)=R_{uuu}{u^{\prime }}^3+3R_{uuv}{u^{\prime }}^2{v}^{\prime }+3R_{uvv}{u}^{\prime }{v^{\prime }}^2+R_{vvv}{v^{\prime }}^3+R_v{v}^{‴}+R_u{u}^{‴}+ \\ 3\left(R_{uu}{u}^{\prime }{u}^{″}+R_{uv}\left(u^{\prime }{v}^{″}+u^{″}{v}^{\prime }\right)+R_{vv}{v}^{\prime }{v}^{″}\right). \end{gathered}$$

(23)

In 2014, Joo et al. [25] proposed a novel method to compute the curvature and torsion of LoCs. Equation (24) represents the proposed method for computing $u^{″}$, $v^{″}$, and the geodesic curvature, ${\kappa }_g$.

$$\left[\begin{array}{c}{v}^{″}\\ v^{″}\\ {\kappa }_g\end{array}\right]={\left[\begin{array}{ccc}E& F& -\left(U·R_u\right)\\ F& G& -\left(U·R_v\right)\\ -\dot{v}\left(t\right)& \dot{u}\left(t\right)& 0\end{array}\right]}^{-1}\left[\begin{array}{c}-\left({\gamma }_1·R_u\right)\\ -\left({\gamma }_1·R_v\right)\\ {\delta }_1\end{array}\right],$$

(24)

where

$$U=\mathrm{N}\times t,$$

$${\gamma }_1=R_{uu}{u^{\prime }}^2+2R_{uv}{u}^{\prime }{v}^{\prime }+R_{vv}{v^{\prime }}^2,$$

$$\dot{v}\left(t\right)=\{\begin{array}{cc}-\left(L-{\kappa }_{p}E\right)& if \left|L-{\kappa }_{p}E\right|\ge \left|N-{\kappa }_{p}G\right|\\ -\left(M-{\kappa }_{p}F\right)& if \left|L-{\kappa }_{p}E\right|<\left|N-{\kappa }_{p}G\right|\end{array},$$

$$\dot{u}\left(t\right)=\{\begin{array}{cc}M-{\kappa }_{p}F& if \left|L-{\kappa }_{p}E\right|\ge \left|N-{\kappa }_{p}G\right|\\ N-{\kappa }_{p}G& if \left|L-{\kappa }_{p}E\right|<\left|N-{\kappa }_{p}G\right|\end{array},$$

$${\delta }_1=\{\begin{array}{cc}-\left(L^{\prime }-{{\kappa }^{\prime }}_{p}E-{\kappa }_p{E}^{\prime }\right)u^{\prime }-\left(M^{\prime }-{{\kappa }^{\prime }}_{p}F-{\kappa }_p{F}^{\prime }\right)v^{\prime }& if \left|L-{\kappa }_{p}E\right|\ge \left|N-{\kappa }_{p}G\right|\\ -\left(M^{\prime }-{{\kappa }^{\prime }}_{p}F-{\kappa }_p{F}^{\prime }\right)u^{\prime }-\left(N^{\prime }-{{\kappa }^{\prime }}_{p}G-{\kappa }_p{G}^{\prime }\right)v^{\prime }& if \left|L-{\kappa }_{p}E\right|<\left|N-{\kappa }_{p}G\right|\end{array}$$

The curvature of the LoC can be calculated using principal curvature and geodesic curvature, as shown below:

$$\kappa =\sqrt{{\kappa }_p{}^2+{\kappa }_g{}^2}.$$

(25)

Note that the classical method for computing geodesic curvature is given by [25]:

$${\kappa }_g=\left({\mathsf{\Gamma }}_{11}^2{\left(\frac{du}{ds}\right)}^3+\left(2{\mathsf{\Gamma }}_{12}^2-{\mathsf{\Gamma }}_{11}^1\right){\left(\frac{du}{ds}\right)}^2\frac{dv}{ds}+\left({\mathsf{\Gamma }}_{22}^2-2{\mathsf{\Gamma }}_{12}^1\right)\frac{du}{ds}{\left(\frac{dv}{ds}\right)}^2-{\mathsf{\Gamma }}_{22}^1{\left(\frac{dv}{ds}\right)}^3+\frac{du}{ds}\frac{d^{2}v}{d{s}^2}-\frac{d^{2}u}{d{s}^2}\frac{dv}{ds}\right)\sqrt{EG-F^2}.$$

(26)

where ${\mathsf{\Gamma }}_{11}^1=\frac{G\frac{dE}{du}-2F\frac{dF}{du}+F\frac{dE}{dv}}{2\left(EG-F^2\right)}$, ${\mathsf{\Gamma }}_{11}^1=\frac{G\frac{dE}{du}-2F\frac{dF}{du}+F\frac{dE}{dv}}{2\left(EG-F^2\right)}$, ${\mathsf{\Gamma }}_{12}^1=\frac{G\frac{dE}{dv}-F\frac{dG}{du}}{2\left(EG-F^2\right)}$, ${\mathsf{\Gamma }}_{22}^1=\frac{2G\frac{dF}{dv}-G\frac{dG}{du}-F\frac{dG}{dv}}{2\left(EG-F^2\right)}$, ${\mathsf{\Gamma }}_{11}^2=\frac{2E\frac{dF}{du}-E\frac{dE}{dv}-F\frac{dE}{du}}{2\left(EG-F^2\right)}$, ${\mathsf{\Gamma }}_{12}^2=\frac{E\frac{dG}{du}-F\frac{dE}{dv}}{2\left(EG-F^2\right)}$, and ${\mathsf{\Gamma }}_{22}^2=\frac{E\frac{dG}{dv}-2F\frac{dF}{dv}+F\frac{dG}{du}}{2\left(EG-F^2\right)}$.

The torsion and first derivative of LoC curvature on a surface can be computed using the equation below:

$$\left[\begin{array}{c}{u}^{‴}\\ \begin{array}{c}{v}^{‴}\\ \begin{array}{c}{\kappa }^{\prime }\\ \tau \end{array}\end{array}\end{array}\right]={\left[\begin{array}{cccc}E& F& -\left(\mathit{n}·R_u\right)& -\kappa \left(\mathit{b}·R_u\right)\\ F& G& -\left(\mathit{n}·R_v\right)& -\kappa \left(\mathit{b}·R_v\right)\\ \left(\mathit{n}·R_u\right)& \left(\mathit{n}·R_v\right)& -1& 0\\ -\dot{v}\left(t\right)& \dot{u}\left(t\right)& 0& 0\end{array}\right]}^{-1}\left[\begin{array}{c}-\left({\gamma }_2·R_u\right)-{\kappa }^2\left(\mathit{t}·R_u\right)\\ \begin{array}{c}-\left({\gamma }_2·R_v\right)-{\kappa }^2\left(\mathit{t}·R_v\right)\\ \begin{array}{c}-\left(\mathit{n}·{\gamma }_2\right)\\ {\delta }_2\end{array}\end{array}\end{array}\right]$$

(27)

where

$$\mathit{t}=c^{\prime }\left(s\right),$$

$$\mathit{n}=\frac{c^{″}\left(s\right)}{\kappa },$$

$$\mathit{b}=\mathit{t}\times \mathit{n}=\frac{{\mathit{c}}^{\prime }\left(s\right)\times c^{″}\left(s\right)}{\kappa },$$

$${\gamma }_2=R_{uuu}{u^{\prime }}^3+3R_{uuv}{u^{\prime }}^2{v}^{\prime }+3R_{uvv}{u}^{\prime }{v^{\prime }}^2+R_{vvv}{v^{\prime }}^3+3\left(R_{uu}{u}^{\prime }{u}^{″}+R_{uv}\left(u^{\prime }{v}^{″}+u^{″}{v}^{\prime }\right)+R_{vv}{v}^{\prime }{v}^{″}\right),$$

$${\delta }_2=\{\begin{array}{cc}-\left(\begin{array}{c}2\left(L^{\prime }-{{\kappa }^{\prime }}_{p}E-{\kappa }_p{E}^{\prime }\right)u^{″}+2w\left(M^{\prime }-{{\kappa }^{\prime }}_{p}F-{\kappa }_p{F}^{\prime }\right)v^{″}\\ +\left(L^{″}-{{\kappa }^{″}}_{p}E-2{{\kappa }^{\prime }}_p{E}^{\prime }-{\kappa }_p{E}^{″}\right)u^{\prime }+\\ \left(M^{″}-{{\kappa }^{″}}_{p}F-2{{\kappa }^{\prime }}_p{F}^{\prime }-{\kappa }_p{F}^{″}\right)v^{\prime }\end{array}\right)& if \left|L-{\kappa }_{p}E\right|\ge \left|N-{\kappa }_{p}G\right| \\ -\left(\begin{array}{c}2\left(M^{\prime }-{{\kappa }^{\prime }}_{p}F-{\kappa }_p{F}^{\prime }\right)u^{″}+2w\left(N^{\prime }-{{\kappa }^{\prime }}_{p}G-{\kappa }_p{G}^{\prime }\right)v^{″}\\ +\left(M^{″}-{{\kappa }^{″}}_{p}F-2{{\kappa }^{\prime }}_p{F}^{\prime }-{\kappa }_p{F}^{″}\right)u^{\prime }+\\ \left(N^{″}-{{\kappa }^{″}}_{p}G-2{{\kappa }^{\prime }}_p{G}^{\prime }-{\kappa }_p{G}^{″}\right)v^{\prime }\end{array}\right)& if \left|L-{\kappa }_{p}E\right|<\left|N-{\kappa }_{p}G\right| \end{array}$$

Further details of LoCs can be obtained from [25] and references therein.

3.1. The Projection of a Surface onto a Plane

Geodesic curvature is an important tool for developing a surface on a plane. Joo et al. [25] proposed six steps to project a surface onto a plane as follows:

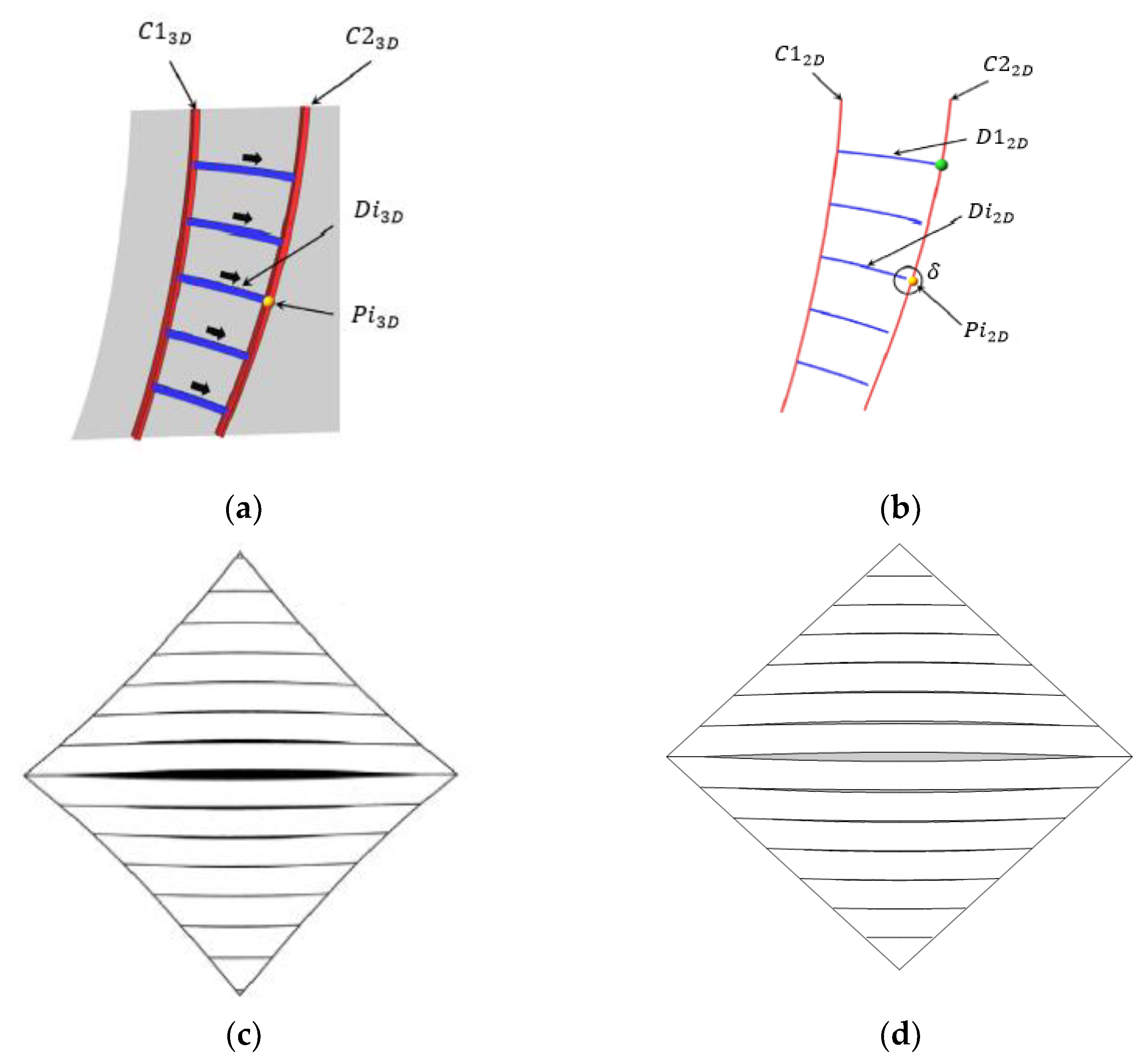
• Generate two LoCs with larger curvature magnitude named $\mathrm{C}{1}_{3D}$ and $\mathrm{C}{2}_{3D}$ along the surface (refer to Figure 1a).
• Generate $n$ number of LoCs with smaller curvature magnitude (named $\mathrm{D}{i}_{3D}$, $i=1,\dots ,n$), starting from $\mathrm{C}{1}_{3D}$ and stopping at $\mathrm{C}{2}_{3D}$. The stopping points on $\mathrm{C}{2}_{3D}$ are labelled as $\mathrm{P}{i}_{3D}$, $i=1,\dots ,n$.
• Project $\mathrm{C}{1}_{3D}$ and $\mathrm{D}{i}_{3D}$ onto a plane isometrically, and represent them as $\mathrm{C}{1}_{2D}$ and $\mathrm{D}{i}_{2D}$. Note that the starting angles of $\mathrm{D}{i}_{2D}$ from $\mathrm{C}{1}_{2D}$ are ${90}^{\circ }$ (refer to Figure 1b).
• Transform $\mathrm{C}{2}_{3D}$ onto a plane isometrically from the end point of $\mathrm{D}{j}_{2D}$ with an angle of ${90}^{\circ }$, and represent it as $\mathrm{C}2j_{2D}$. The corresponding points of $\mathrm{P}{i}_{3D}$ on $\mathrm{C}2j_{2D}$ are indicated as $\mathrm{P}{i}_{2D}$.
• Compute the sum of gaps ${\mathsf{\delta }}_{ij}$ between the endpoints of $\mathrm{D}{j}_{2D}$ and $\mathrm{P}{i}_{2D}$ where ${\mathsf{\delta }}_j={{\displaystyle \sum }}^{}{\mathsf{\delta }}_{ij}$.
• Select the connection $j$ with minimum ${\mathsf{\delta }}_j$.

A curve on a surface can be projected onto a plane by applying geodesic curvature along the curve to the Frenet–Serret formula ${\mathit{t}}^{\prime }={\kappa }_g\mathit{n}$. The plane curve is calculated using the classic Runge–Kutta method to solve the Frenet–Serret formula by assigning the torsion as 0. For an example, we used Joo et al.’s [25] method to reconstruct the hyperbolic paraboloid onto a plane, as shown in Figure 1. Figure 1c is the planar hyperbolic paraboloid by [25], while Figure 1d is the planar hyperbolic paraboloid computed on GPU using Mathematica.

3.2. Efficient LoC Computation

This paper used CUDA programming to perform LoC calculations on GPU. Mathematica 11.0 was used to compute the performance metrics of CPU and GPU. Hence, we computed the significant error of LoCs on the hyperbolic paraboloid in CPU and GPU to validate our method. The significant error of the LoC computation is $3.869\times {10}^{-7}$ (all the function types are “Float”). If we change all the function types to “Double”, the significant error is reduced to $6.02988\times {10}^{-16}$. Readers are referred to [18] for the details of LA surface’s LoC computation using GPU, where the computation time is greatly reduced.

4. Coons Patch

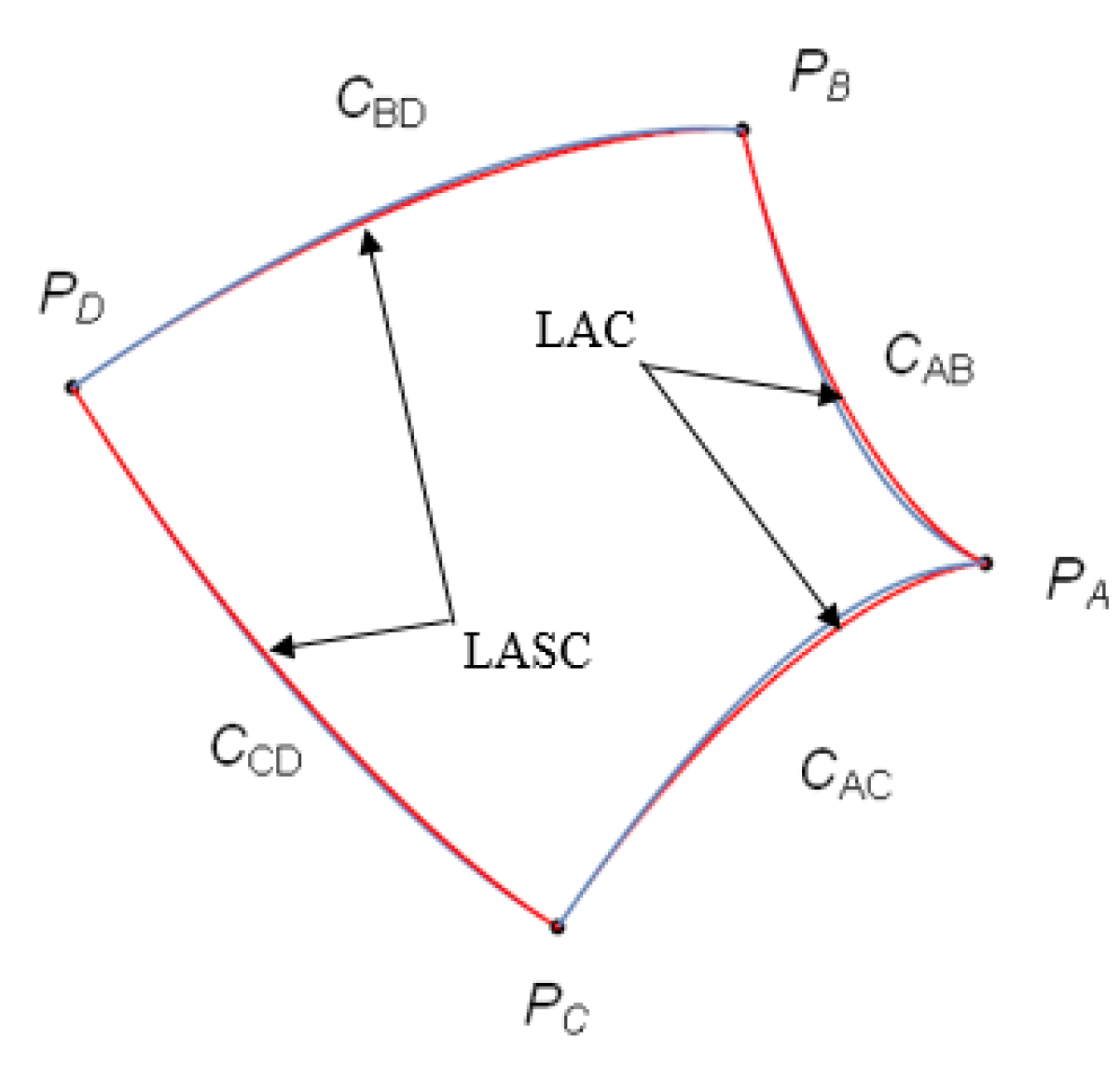
Assume that the four parametric curves defined in $c_0\left(u\right)$,$c_1\left(u\right)$,$d_0\left(v\right)$, and $d_1\left(v\right)$ meet at four end points, where $c_0\left(0\right)=d_0\left(0\right)$, $c_1\left(0\right)=d_0\left(1\right)$, $c_0\left(1\right)=d_1\left(0\right)$ and $c_1\left(1\right)=d_1\left(1\right)$. Three surfaces are defined by linear interpolation [20]:

$$L_c\left(u,v\right)=\left(1-v\right)c_0\left(u\right)+v{c}_1\left(u\right),$$

(28)

$$L_d\left(u,v\right)=\left(1-u\right)d_0\left(v\right)+u{d}_1\left(v\right),$$

(29)

$$L_b\left(u,v\right)=\left(1-u\right)\left(1-v\right)c_0\left(0\right)+u\left(1-v\right)c_0\left(1\right)+\left(1-u\right)v{c}_1\left(0\right)+uv{c}_1\left(1\right).$$

(30)

A bilinear Coons patch $CP\left(u,v\right)$ is defined over the parameter domain containing the unit square (u, v) ∈ [0,1] × [0,1]:

$$CP\left(u,v\right)=L_c\left(u,v\right)+L_d\left(u,v\right)-L_b\left(u,v\right).$$

(31)

In this paper, we defined the Log Aesthetic Patch (LAP) as a surface using Equations (28)–(31) with four parametric curves either in the form of LAC or LASC. To show its versatility, we approximated the hyperbolic paraboloid using LAP by replacing the LoCs of the hyperbolic paraboloid with LACs/LASCs. This approach is in line with Joo et al.’s [25] idea, where they considered LoCs the boundaries of a developable surface. The first step is to replace the four connected LoCs of the hyperbolic paraboloid with LACs or LASCs, depending on the type of boundary curves we are dealing with. On the basis of these four boundary curves, an LAP surface is constructed using the Coons patch equations, as stated in (28)–(31). 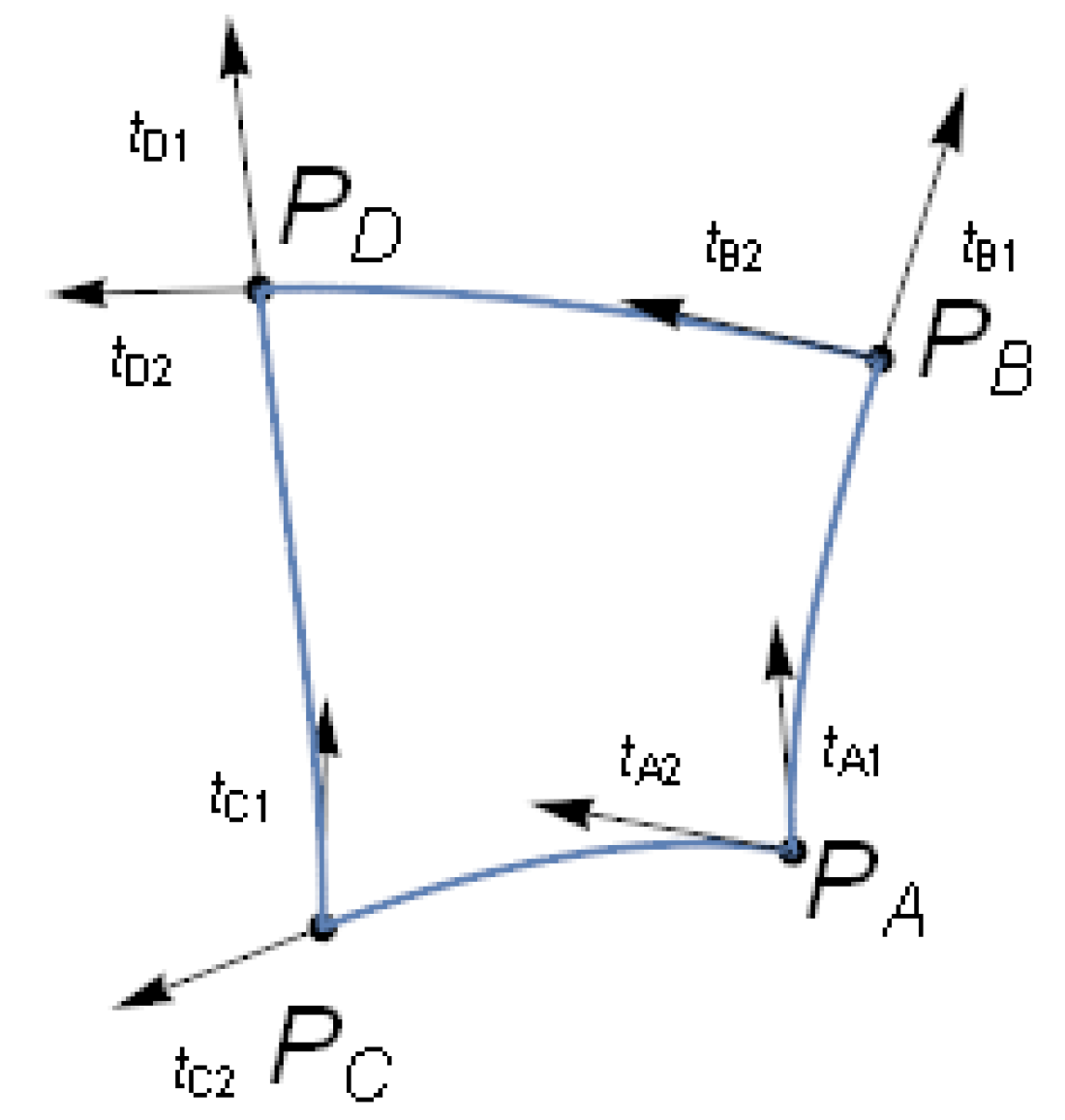In the first step, we obtain four LoCs from a hyperbolic paraboloid, which are connected like a closed fence, as shown in Figure 2.

Next, we calculated the four endpoints (the intersection of LoCs) and their maximum and minimum principal direction with their corresponding vectors. Then, LACs or LASCs were generated using two endpoints and their respective tangent vector (maximum or minimum principal direction). Using the given LAC or LASC shape parameters ($\alpha ,\beta ,{\rho }_0$, and $\mathsf{\Omega }$), we could compute the LAC/LASC that meets the constraints using the bisection method [12] and the modified Nelder and Mead downhill simplex method [13]. We then scaled the LACs and converted them back to the position of the point shown in Figure 3.

Note that the red curves are LAC and LASC segments, while the blue curves are original LoCs on the hyperbolic paraboloid. The transformed unit tangent, normal, and binormal vectors at the initial point are named ${\mathit{t}}_s\left(s_0\right)$, ${\mathit{n}}_s\left(s_0\right)$, and ${\mathit{b}}_s\left(s_0\right)$, respectively. The subscript $s$ indicates that the vector is in terms of arc length, and the scaling ratio of LAC/LASC is denoted as $m$.

The Coons patch requires two general parameters to shape the surface, which are rendered in the parameter domain (u, v) ∈ [0,1] × [0,1]. Hence, we must reparametrize the curvature of LAC, the torsion of LASC, and the Frenet–Serret formula in terms of the arc length parameter to the general parameters $u$ or $v$. Let the arc length $s=u{S}_T$; then we have $\phi \left(u\right)=\frac{ds}{du}=S_T$, where $S_T$ is total arc length. Next, by applying $s=u{S}_T$ into Equations (7) and (8), we obtain the curvature of the LAC and the torsion of the LASC as well as their derivatives in terms of parameter $u$:

$$\kappa \left(u\right)=\{\begin{array}{cc}\frac{1}{{\rho }_0{e}^{\mathsf{\Lambda }u{S}_T}}& \alpha =0\\ {\left({\rho }_0{}^{\alpha }+\mathsf{\Lambda }\alpha u{S}_T\right)}^{-\frac{1}{\alpha }}& otherwise\end{array},$$

(32)

$$\dot{\kappa }\left(u\right)=\{\begin{array}{cc}\frac{-\mathsf{\Lambda }{S}_T}{{\rho }_0{e}^{\mathsf{\Lambda }u{S}_T}}& \alpha =0\\ -\mathsf{\Lambda }{S}_T{\left({\rho }_0{}^{\alpha }+\mathsf{\Lambda }\alpha u{S}_T\right)}^{-\left(1+\frac{1}{\alpha }\right)}& otherwise\end{array},$$

(33)

$$\ddot{\kappa }\left(u\right)=\{\begin{array}{cc}\frac{{\left(\mathsf{\Lambda }{S}_T\right)}^2}{{\rho }_0{e}^{\mathsf{\Lambda }u{S}_T}}& \alpha =0\\ \left(1+\alpha \right){\left(\mathsf{\Lambda }{S}_T\right)}^2{\left({\rho }_0{}^{\alpha }+\mathsf{\Lambda }\alpha u{S}_T\right)}^{-\left(2+\frac{1}{\alpha }\right)}& otherwise\end{array},$$

(34)

$$\tau \left(u\right)=\{\begin{array}{cc}\frac{1}{{\mu }_0{e}^{\mathsf{\Omega }u{S}_T}}& \beta =0\\ {\left({\upsilon }^{\beta }+\mathsf{\Omega }\beta u{S}_T\right)}^{-\frac{1}{\beta }}& otherwise\end{array},$$

(35)

$$\dot{\tau }\left(u\right)=\{\begin{array}{cc}\frac{-\mathsf{\Omega }{S}_T}{{\mu }_0{e}^{\mathsf{\Omega }u{S}_T}}& \beta =0\\ -\mathsf{\Omega }{S}_T{\left({\upsilon }^{\beta }+\mathsf{\Omega }\beta u{S}_T\right)}^{-\left(1+\frac{1}{\beta }\right)}& otherwise\end{array}.$$

(36)

The Frenet–Serret formula of the LAC/LASC in terms of parameter $u$ is as follows:

$${\mathit{t}}_u\left(0\right)=S_T\left(m{\mathit{t}}_s\left(s_0\right)\right),$$

(37)

$${\mathit{n}}_u\left(0\right)=S_T\left(m{\mathit{n}}_s\left(s_0\right)\right),$$

(38)

$${\mathit{b}}_u\left(0\right)=S_T\left(m{\mathit{b}}_s\left(s_0\right)\right),$$

(39)

$${\dot{\mathit{t}}}_u\left(u\right)=S_T\left(\kappa \left(u\right){\mathit{n}}_u\left(u\right)\right),$$

(40)

$${\dot{\mathit{n}}}_u\left(u\right)=S_T\left(-\kappa \left(u\right){\mathit{t}}_u\left(u\right)+\tau \left(u\right){\mathit{b}}_u\left(u\right)\right),$$

(41)

$${\dot{\mathit{b}}}_u\left(u\right)=S_T\left(-\tau \left(u\right){\mathit{n}}_u\left(u\right)\right).$$

(42)

Thus, by solving the initial value problems using the classical Runge–Kutta method, the LAC and LASC segments shown in Figure 3 can be computed. Finally, an LAP can be drawn based on these four curves.

4.1. Numerical Example

The details of Figure 2 are given as $P_A=\left\{0,0,0\right\}$, $P_B=\left\{-0.70773,0,0.50088\right\}$, $P_C=\left\{0,-0.70773,-0.50088\right\}$, $P_D=\left\{-1.00131,-1.00131,0\right\}$, ${\mathit{t}}_{A1}=\left\{-1,0,0\right\}$, ${\mathit{t}}_{A2}=\left\{0,-1,0\right\}$, ${\mathit{t}}_{B1}=\left\{-0.57701,0,0.81673\right\}$, ${\mathit{t}}_{B2}=\left\{0,-1,0\right\}$, ${\mathit{t}}_{C1}=\left\{-1,0,0\right\}$, ${\mathit{t}}_{C2}=\left\{0,-0.57701,-0.81673\right\}$, ${\mathit{t}}_{D1}=\left\{-0.66647,-0.33353,0.66676\right\}$, and ${\mathit{t}}_{D2}=\left\{-0.33353,-0.66647,-0.66676\right\}$ respectively. Hence, the above information was used to find the appropriate LAC and LASC segments to replace the original LoCs of the hyperbolic paraboloid. Note that the curves from $P_A$ to $P_B$ and $P_A$ to $P_C$ are planar curves. Hence, we replaced these two curves with LACs. On the other hand, the curves from $P_B$ to $P_D$ and $P_C$ to $P_D$ are space curves. In fact, these two curves can be originated from two disjoint surfaces. For numerical illustration, we replaced these space curves with LASCs. According to [18], the LoCs of LA swept surfaces have the same monotonic curvature profile when the path curve and profile curve are both LACs with ${\alpha }_{LAC}=2$. Therefore, for the LAC, we set ${\alpha }_{LAC}=2$ and the initial radius of curvature ${\rho }_0{}_{LAC}=1$ for the entire curve finding process. For the LASC, we set ${\alpha }_{LAC}=2$, ${\beta }_{LASC}=2$, ${\mathsf{\Omega }}_{LASC}=1$, and the initial radius of curvature ${\rho }_0{}_{LASC}=1$ for the entire curve-finding process as well. The curvature of the LAC and the torsion of the LASC were inserted into the Frenet–Serret formula and numerically solved using the classical Runge–Kutta method. The initial value of the unit tangent, normal, and binormal vectors were set as $\left\{1,0,0\right\}$, $\left\{0,0,1\right\}$, and $\left\{0,1,0\right\}$, respectively, and the initial coordinate was at the origin $\left\{0,0,0\right\}$.

For the LAC, we set torsion $\tau =0$ in the Frenet–Serret formula, and the curvature of the LAC can be obtained from Equation (7). Then, we used the bisection method to compute the parameter ${\mathsf{\Lambda }}_{LAC}$ and the arc length ${\mathrm{s}}_{LAC}$. The tolerance of this method was set to ${10}^{-15}.$ For the LASC, the curvature and torsion of the LASC can be obtained from Equations (7) and (8), respectively. The bisection method was used to compute the arc length ${\mathrm{s}}_{LASC}$, and the modified Nelder and Mead downhill simplex method was used to compute the parameters ${\mathsf{\Lambda }}_{LASC}$ and ${\upsilon }_{LASC}$. The tolerance of these two methods was set to${10}^{-15}$ and ${10}^{-14}$, respectively. Finally, we fit the LAC segments with the shape parameter ${\mathsf{\Lambda }}_{LAC}=12.71843$ and the arc length ${\mathrm{s}}_{LAC}=6.76436$, satisfying the constraints of $P_A$ to $P_B$ and $P_A$ to $P_C$. Meanwhile, the LASC segment with parameters ${\mathsf{\Lambda }}_{LASC}=6.28525$, ${\upsilon }_{LASC}=7.30313$, and arc length ${\mathrm{s}}_{LASC}=3.10842$ satisfied the constraints of $P_B$ to $P_D$ and $P_C$ to $P_D$. In order to simplify labels, we named the LAC or LASC from $P_A$ to $P_B$ as $C_{AB}$, $P_A$ to $P_C$ as $C_{AC}$, $P_B$ to $P_D$ as $C_{BD}$, and $P_C$ to $P_D$ as $C_{CD}$. The scaling ratios $m_{AB}$, $m_{AC}$, $m_{BD}$, and $m_{CD}$ for the curves $C_{AB}$, $C_{AC}$, $C_{BD}$, and $C_{CD}$ are $m_{AB}=m_{AC}=0.13192$ and $m_{BD}=m_{CD}=0.38164$, respectively. Because the curves are scaled, their vectors must be scaled as well. During the reverse transformation, we also transformed its tangent, normal, and binormal vectors at the origin to the original position. The scaled LAC and LASC segments that met the constraints are shown in Figure 3.

Table 1. The properties for each curve segment.

Curve	Frenet–Serret Equations
$C_{AB}$	$C_{AB}\left(0\right)=P_A$  ${\mathit{t}}_{AB}\left(0\right)=S_{AB}{m}_{AB}{\mathit{t}}_s\left(s_0\right)=S_{AB}{m}_{AB}\left\{-1,0,0\right\}$ ${\mathit{n}}_{AB}\left(0\right)=S_{AB}{m}_{AB}{\mathit{n}}_s\left(s_0\right)=S_{AB}{m}_{AB}\left\{0,0,1\right\}$ ${\mathit{b}}_{AB}\left(0\right)=S_{AB}{m}_{AB}{\mathit{b}}_s\left(s_0\right)=S_{AB}{m}_{AB}\left\{0,1,0\right\}$ ${\dot{\mathit{t}}}_{AB}\left(u\right)=S_{AB}\left({\kappa }_{AB}\left(u\right){\mathit{n}}_{AB}\left(u\right)\right)$ ${\dot{\mathit{n}}}_{AB}\left(u\right)=S_{AB}\left(-{\kappa }_{AB}\left(u\right){\mathit{t}}_{AB}\left(u\right)\right)$ ${\dot{\mathit{b}}}_{AB}\left(u\right)=0$
$C_{AC}$	$C_{AC}\left(0\right)=P_A$ ${\mathit{t}}_{AC}\left(0\right)=S_{AC}{m}_{AC}{\mathit{t}}_s\left(s_0\right)=S_{AC}{m}_{AC}\left\{0,-1,0\right\}$ ${\mathit{n}}_{AC}\left(0\right)=S_{AC}{m}_{AC}{\mathit{n}}_s\left(s_0\right)=S_{AC}{m}_{AC}\left\{0,0,-1\right\}$ ${\mathit{b}}_{AC}\left(0\right)=S_{AC}{m}_{AC}{\mathit{b}}_s\left(s_0\right)=S_{AC}{m}_{AC}\left\{1,0,0\right\}$ ${\dot{\mathit{t}}}_{AC}\left(v\right)=S_{AC}\left({\kappa }_{AC}\left(v\right){\mathit{n}}_{AC}\left(v\right)\right)$ ${\dot{\mathit{n}}}_{AC}\left(v\right)=S_{AC}\left(-{\kappa }_{AC}\left(v\right){\mathit{t}}_{AC}\left(v\right)\right)$ ${\dot{\mathit{b}}}_{AC}\left(v\right)=0$
$C_{BD}$	$C_{BD}\left(0\right)=P_B$ ${\mathit{t}}_{BD}\left(0\right)=S_{BD}{m}_{BD}{\mathit{t}}_s\left(s_0\right)=S_{BD}{m}_{BD}\left\{0,-1,0\right\}$ ${\mathit{n}}_{BD}\left(0\right)=S_{BD}{m}_{BD}{\mathit{n}}_s\left(s_0\right)=S_{BD}{m}_{BD}\left\{-0.59306,0,-0.80516\right\}$ ${\mathit{b}}_{BD}\left(0\right)=S_{BD}{m}_{BD}{\mathit{b}}_s\left(s_0\right)=S_{BD}{m}_{BD}\left\{0.80516,0,-0.59306\right\}$ ${\dot{\mathit{t}}}_{BD}\left(v\right)=S_{BD}\left({\kappa }_{BD}\left(v\right){\mathit{n}}_{BD}\left(v\right)\right)$ ${\dot{\mathit{n}}}_{BD}\left(v\right)=S_{BD}\left(-{\kappa }_{BD}\left(v\right){\mathit{t}}_{BD}\left(v\right)+{\tau }_{BD}\left(v\right){\mathit{b}}_{BD}\left(v\right)\right)$ ${\dot{\mathit{b}}}_{BD}\left(v\right)=S_{BD}\left(-{\tau }_{BD}\left(v\right){\mathit{n}}_{BD}\left(v\right)\right)$
$C_{CD}$	$C_{CD}\left(0\right)=P_C$ ${\mathit{t}}_{CD}\left(0\right)=S_{CD}{m}_{CD}{\mathit{t}}_s\left(s_0\right)=S_{CD}{m}_{CD}\left\{-1,0,0\right\}$ ${\mathit{n}}_{CD}\left(0\right)=S_{CD}{m}_{CD}{\mathit{n}}_s\left(s_0\right)=S_{CD}{m}_{CD}\left\{0,-0.59306,0.80516\right\}$ ${\mathit{b}}_{CD}\left(0\right)=S_{CD}{m}_{CD}{\mathit{b}}_s\left(s_0\right)=S_{CD}{m}_{CD}\left\{0,0.80516,0.59306\right\}$ ${\dot{\mathit{t}}}_{CD}\left(u\right)=S_{CD}\left({\kappa }_{CD}\left(u\right){\mathit{n}}_{CD}\left(u\right)\right)$ ${\dot{\mathit{n}}}_{CD}\left(u\right)=S_{CD}\left(-{\kappa }_{CD}\left(u\right){\mathit{t}}_{CD}\left(u\right)+{\tau }_{CD}\left(u\right){\mathit{b}}_{CD}\left(u\right)\right)$ ${\dot{\mathit{b}}}_{CD}\left(u\right)=S_{CD}\left(-{\tau }_{CD}\left(u\right){\mathit{n}}_{CD}\left(u\right)\right)$

Note that $S_{AB}=6.76436$, $S_{AC}=6.76436$, $S_{BD}=3.10842$, and $S_{CD}=3.10842$ are the total arc lengths of each curve. In addition, the curvature $\kappa$ and torsion $\tau$ in terms of parameters $u$ or $v$ can be obtained from Equations (32) and (35), respectively.

shows the Frenet–Serret equations for each curve as well as their transformed unit tangent, normal, and binormal vectors.

Next, the general equation for the LAP is shown in Section 4. We implement four LA equations (LACs and LASCs) into the Coons patch equations as follows:

$$L_{c\_LA}\left(u,v\right)=\left(1-v\right)C_{AB}\left(u\right)+v{C}_{CD}\left(u\right),$$

(43)

$$L_{d\_LA}\left(u,v\right)=\left(1-u\right)C_{AC}\left(v\right)+u{C}_{BD}\left(v\right),$$

(44)

$$L_{b\_LA}\left(u,v\right)=\left(1-u\right)\left(1-v\right)C_{AB}\left(0\right)+u\left(1-v\right)C_{AB}\left(1\right)+\left(1-u\right)v{C}_{CD}\left(0\right)+uv{C}_{CD}\left(1\right),$$

(45)

$$LAP\left(u,v\right)=L_{c\_LA}\left(u,v\right)+L_{d\_LA}\left(u,v\right)-L_{b\_LA}\left(u,v\right).$$

(46)

Hence, an LAP can be drawn using Equation (46). Figure 4a,b represents hyperbolic paraboloid and LAP, respectively. Figure 4c shows the combination of both surfaces. The zebra map on LAP shown in Figure 4d shows that it is a smooth surface.

4.2. LoCs on Surfaces

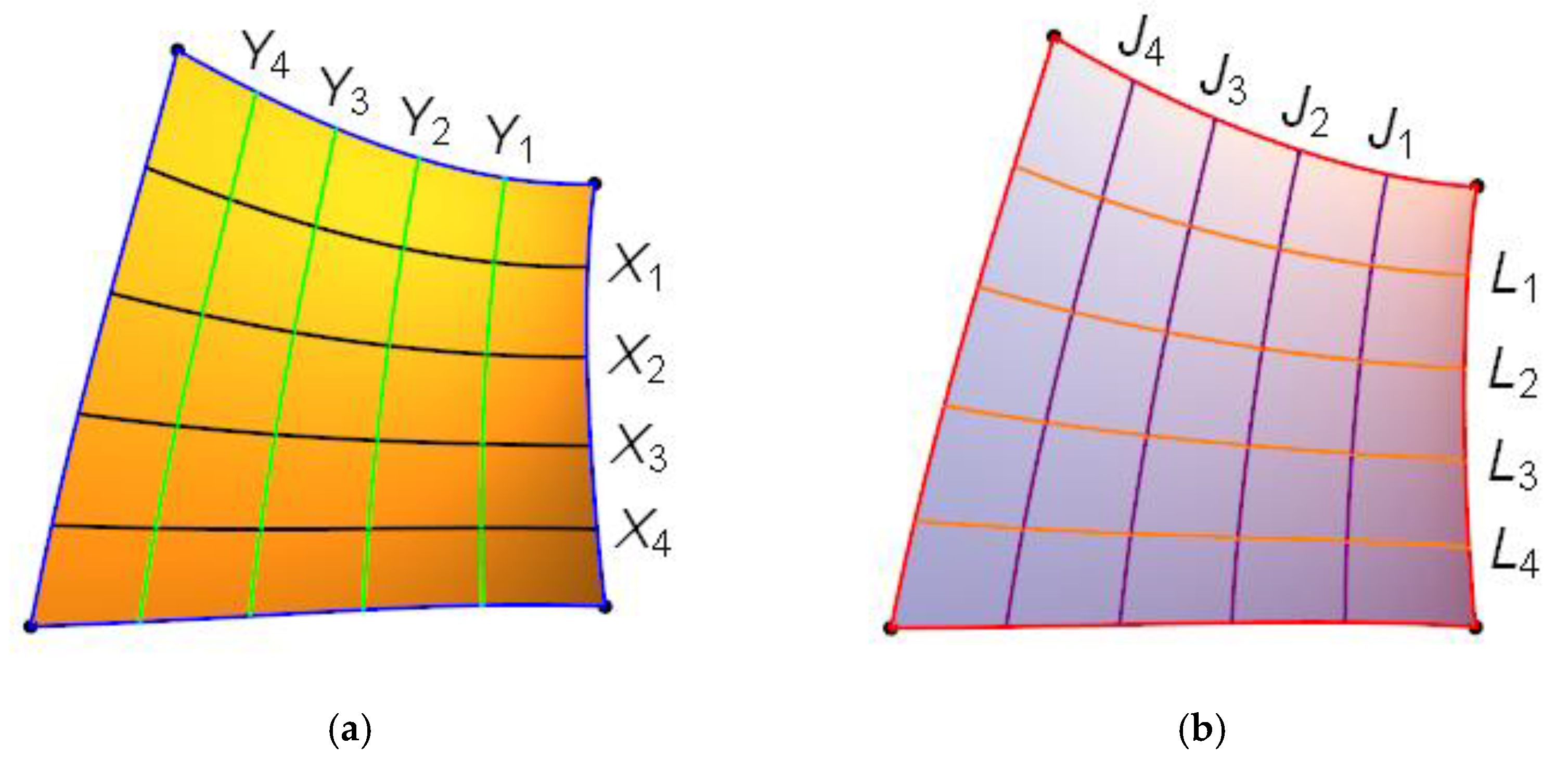
In this subsection, the properties of LoCs on the hyperbolic paraboloid and its approximated LAP are compared. Figure 5 displays the LoCs on the hyperbolic paraboloid and the approximated LAP.

The green curves labeled as Y₁, Y₂, Y_3, and Y₄ and the black curves labeled as X₁, X₂, X₃, and X₄ are LoCs on the hyperbolic paraboloid, whereas the blue curves are the boundaries and the LoCs of the original surface. The orange curves labeled as L₁, L₂, L₃, and L₄ and purple curves labeled as J₁, J₂, J₃, and J₄ are the LoCs on the approximated LAP, while the red curves are the boundaries of the surface.

Even though they are visually similar, we found that the curvature profile of LoCs on LAP is different than the hyperbolic paraboloid, as shown in Figure 6. Although the curvatures of LoCs on both surfaces were monotonically decreasing, the derivative of the curvature profile of the approximated LAP was improved from non-monotonic to monotonic. However, there was not much improvement on the torsion of LoCs, but it was apparent that all the computed LoCs on approximated LAPs were indeed LACs. We can clearly see that their LCGs approximate a line with gradient 2, illustrated with a red line in Figure 6. This outcome is in line with the original setting, in which we used ${\alpha }_{LAC}=2$ to generate the boundary curves.

4.3. Surface Projection onto a Plane

Joo et al. [25] mapped a surface onto a plane by implementing geodesic curvature along the LoC as the curvature of the curve on the plane. Since the boundary curve of the approximated LAP is not the LoC of the surface, the geodesic curvature of the boundary curve must be computed. The geodesic curvature of the boundary curve can be calculated using the fact that $\frac{du}{ds}=\frac{d^{2}u}{d{s}^2}=0$ or $\frac{dv}{ds}=\frac{d^{2}v}{d{s}^2}=0$. By applying $\frac{dv}{ds}=\frac{d^{2}v}{d{s}^2}=0$ (for curves $C_{AB}$ and $C_{CD}$) or $\frac{du}{ds}=\frac{d^{2}u}{d{s}^2}=0$ (for curves $C_{AC}$ and $C_{BD}$) into Equation (26), the geodesic curvature equation of the boundary curves are shown below:

$${\kappa }_g=\{\begin{array}{cc}\left({\mathsf{\Gamma }}_{11}^2{\left(\frac{du}{ds}\right)}^3\right)\sqrt{EG-F^2}& if \frac{dv}{ds}=\frac{d^{2}v}{d{s}^2}=0\\ \left(-{\mathsf{\Gamma }}_{22}^1{\left(\frac{dv}{ds}\right)}^3\right)\sqrt{EG-F^2}& if \frac{du}{ds}=\frac{d^{2}u}{d{s}^2}=0\end{array}.$$

(47)

At $\frac{du}{ds}=\frac{d^{2}u}{d{s}^2}=0$, the geodesic curvature of curve $C_{AB}$ can be computed by applying $v=0$, while $v=1$ is used for curve $C_{CD}$. The geodesic curvature of curve $C_{AC}$ can be calculated by setting $u=0$, while $u=1$ is used for curve $C_{BD}$ at $\frac{dv}{ds}=\frac{d^{2}v}{d{s}^2}=0$. Contrarily, the geodesic curvature of the LoC can be computed using Equation (24). By solving the Frenet–Serret formula, ${\mathit{t}}^{\prime }=\kappa \mathit{n}$ (where $\mathit{n}=\mathit{t}\times \left\{0,0,1\right\}$, $\kappa ={\kappa }_g$ and $\tau =0$), the LoC can be mapped onto a plane [25].

The following Algorithm 1 is the algorithm for mapping an LAP onto a plane.

Algorithm 1: Mapping LAP onto a plane for fabrication

INPUT: 1, G1 data: Endpoints of boundary curves ($P_A$, $P_B$, $P_C$, $P_D$) and its tangent direction ($t_{A1}$, $t_{A2}$, $t_{B1}$, $t_{B2}$, $t_{C1}$, $t_{C2}$, $t_{D2}$, and $t_{D2}$), 2, LAC and LASC shape parameters: $\alpha ,\beta ,{\rho }_0,\mathsf{\Omega }$; 3. $tol={10}^{-15}$ (by default) Begin Step 1 Compute the boundary curves from the given G1 data: If the LoC between two endpoints is a planar curve, the shape parameter $\mathsf{\Lambda }$ and the arc length $\mathrm{s}$ of the LAC must be computed. The bisection method is used to compute shape parameter $\mathsf{\Lambda }$ and arc length $\mathrm{s}$ of LAC as presented by Yoshida and Saito [12]. Then, scale and transform the generated LAC to the original position. If the LoC between two endpoints is a space curve, shape parameter $\mathsf{\Lambda }$, $\nu$, and arc length $\mathrm{s}$ of LASC must be computed. The bisection method and the modified Nelder and Meaddownhill simplex method are used to compute the shape parameter $\mathsf{\Lambda }$, $\nu$, and arc length $\mathrm{s}$ of hteLASC, as demonstrated by Yoshida et al. [13]. Finally, scale and transform the generated LASC to the original position. Step 2 On the basis of the four generated LAC/LASCs boundaries, an LAP can be generated using Equation (31). Step 3 Compute the two LoCs, denoted as $\mathrm{C}{1}_{3D}$ and $\mathrm{C}{2}_{3D}$, and the boundary curves, denoted as $\mathrm{B}{1}_{3D}$, as shown in Figure 1a. Then, compute the intersection point’s position of LoCs and the boundary curve. Step 4 Generate $n$number of LoCs orthogonal to $\mathrm{C}{1}_{3D}$ and $\mathrm{C}{2}_{3D}$ (denoted as $\mathrm{D}{i}_{3D}$, $i=1,\dots ,n$) that start from $\mathrm{C}{1}_{3D}$ and stop at $\mathrm{C}{2}_{3D}$, as shown in Figure 1b. The stopping points on $\mathrm{C}{2}_{3D}$ are denoted as $\mathrm{P}{i}_{3D}$, $i=1,\dots ,n$. Step 5 Compute the geodesic curvature along the LoCs and boundary curves. Step 6 Draw the boundary curve onto a plane isometrically using its geodesic curvature, which is denoted as $\mathrm{B}{1}_{2D}$ (refer to Figure 7a). Step 7 $\mathrm{On} \mathrm{the} \mathrm{basis} \mathrm{of} \mathrm{the} \mathrm{position} \mathrm{of} \mathrm{the} \mathrm{intersection} \mathrm{point} \mathrm{in} \mathrm{step} 4, \mathrm{C}{1}_{3D}$ and $\mathrm{C}{2}_{3D}$ are developed onto a plane isometrically (denoted as $\mathrm{C}{1}_{2D}$ and $\mathrm{C}{2}_{2D}$ as shown in Figure 7a) from a specific point on the boundary curve $\mathrm{B}{1}_{2D}$. Note that the starting angles of $\mathrm{C}{1}_{2D}$ and $\mathrm{C}{2}_{2D}$ from $\mathrm{B}{1}_{2D}$ are ${90}^{\circ }$. Step 8 On the basis of the geodesic curvature of $\mathrm{D}{i}_{3D}$ and their stopping points $\mathrm{P}{i}_{3D}$, 2D LoCs $\mathrm{D}{i}_{2D}$ and their stopping points $\mathrm{P}{i}_{2D}$ are computed starting from specific points on $\mathrm{C}{1}_{2D}$. Then, join the stopping points $\mathrm{P}{i}_{2D}$ to form a curve ${\mathrm{P}}_{2D}$. Step 9 Develop the second 3D boundary curve $\mathrm{B}{2}_{3D}$ (Figure 7c) onto a plane isometrically from a specific point on curve $\mathrm{C}{1}_{2D}$ and denote it as $\mathrm{B}{2}_{2D}$ (Figure 7a). Note that the starting angle of $\mathrm{B}{2}_{2D}$ from $\mathrm{C}{1}_{2D}$ is ${90}^{\circ }$. The length of $\mathrm{B}{2}_{2D}$ depends on the length of $\mathrm{B}{2}_{3D}$, starting at a point on $\mathrm{C}{1}_{3D}$ and stopping at a point on $\mathrm{C}{2}_{3D}$. Step 10 Repeat steps 4 to 9 until all the desired curves are projected onto a plane. Step 11 Cut along the line and stick the boundaries together to create the desired LAP surface.

A simple overview of the planar curves generated by the algorithm for the approximated LAP of the hyperbolic paraboloid is shown in Figure 7. Figure 7c also shows the visualization of LoCs (purple) and boundary curves (red). The LAP surface is fabricated using paper by cutting and pasting the boundaries of the plane surface, as shown in Figure 7d. Finally, Figure 7e shows a close-up of the LoC, ${\mathrm{J}}_3$, which is twisted and uniformly curves along the line. The complete implementation of the CUDA coding in Mathematica for this paper is readily available on GitHub [30].

Figure 7. An example of the fabrication process of approximated hyperbolic paraboloid using LAP: (a) development of LoCs onto a plane; (b) development of LAP with gaps; (c) approximated LAP with LoCs (purple) and boundary curves (red); (d) fabricated surface using a paper; (e) close-up view of the LoC J₃.

Figure 7. An example of the fabrication process of approximated hyperbolic paraboloid using LAP: (a) development of LoCs onto a plane; (b) development of LAP with gaps; (c) approximated LAP with LoCs (purple) and boundary curves (red); (d) fabricated surface using a paper; (e) close-up view of the LoC J₃.

5. Conclusions and Future Work

In this work, we proposed the development of the Log Aesthetic Patch (LAP) using the LAC and LASC as its boundary curves. To show its applicability, we used a hyperbolic paraboloid as a numerical example and approximated it with LAP by applying LACs and LASCs as the boundaries of the surface replacing its LoC boundaries. In comparison, the curvature profile of all the LoCs and its derivatives on the approximated LAP are always monotonic, indicating smoothness of a higher degree. The final section showed an algorithm for LAP projection onto a plane.

Our future work includes implementing this technique to steel plate fabrication in shipbuilding and investigating the generation of other types of LA surfaces.