Approximations of Fuzzy Numbers by Using r-s Piecewise Linear Fuzzy Numbers Based on Weighted Metric
Abstract
:1. Introduction
2. Basic Definitions and Notations
3. The Approximations of Membership Functions
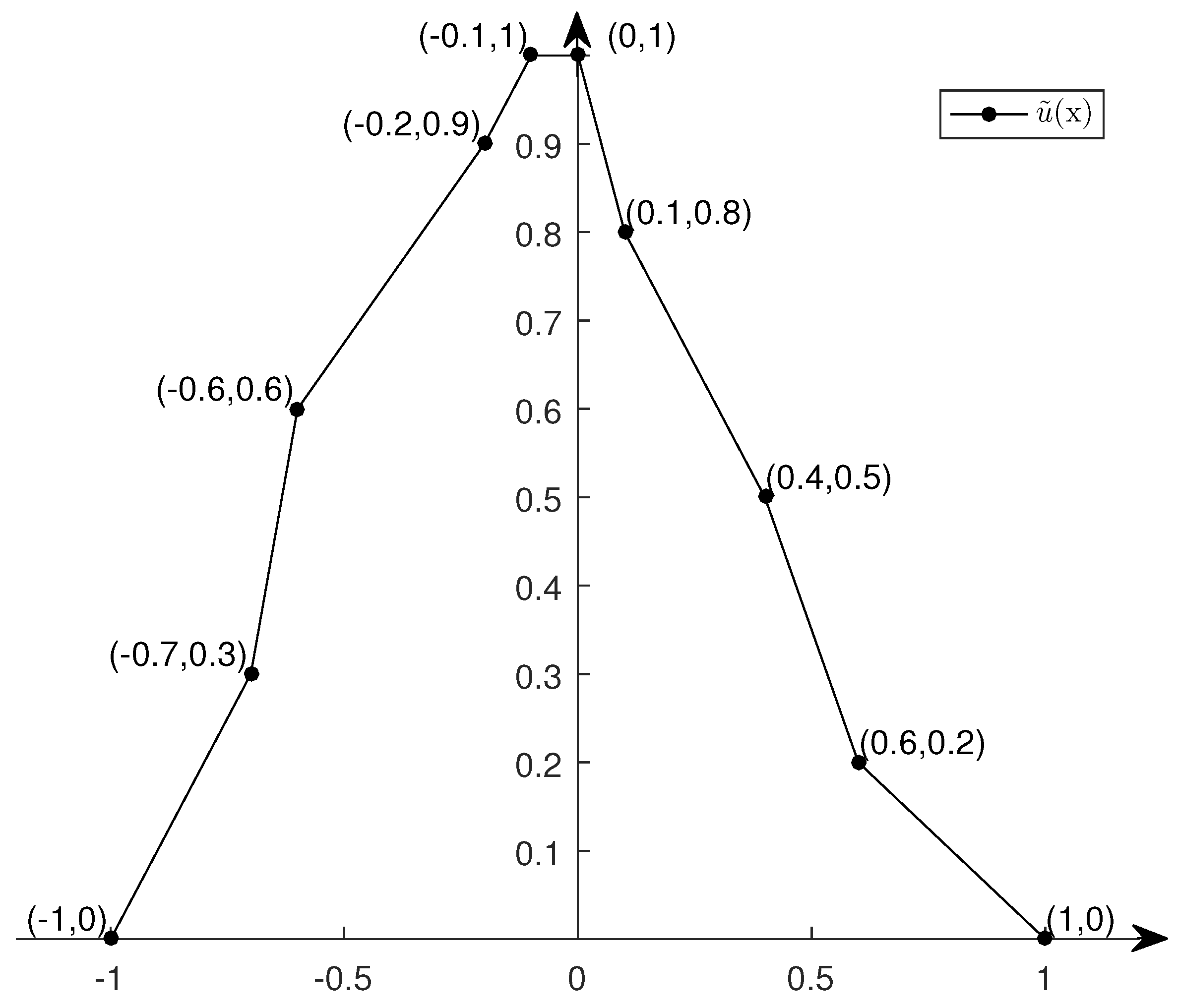
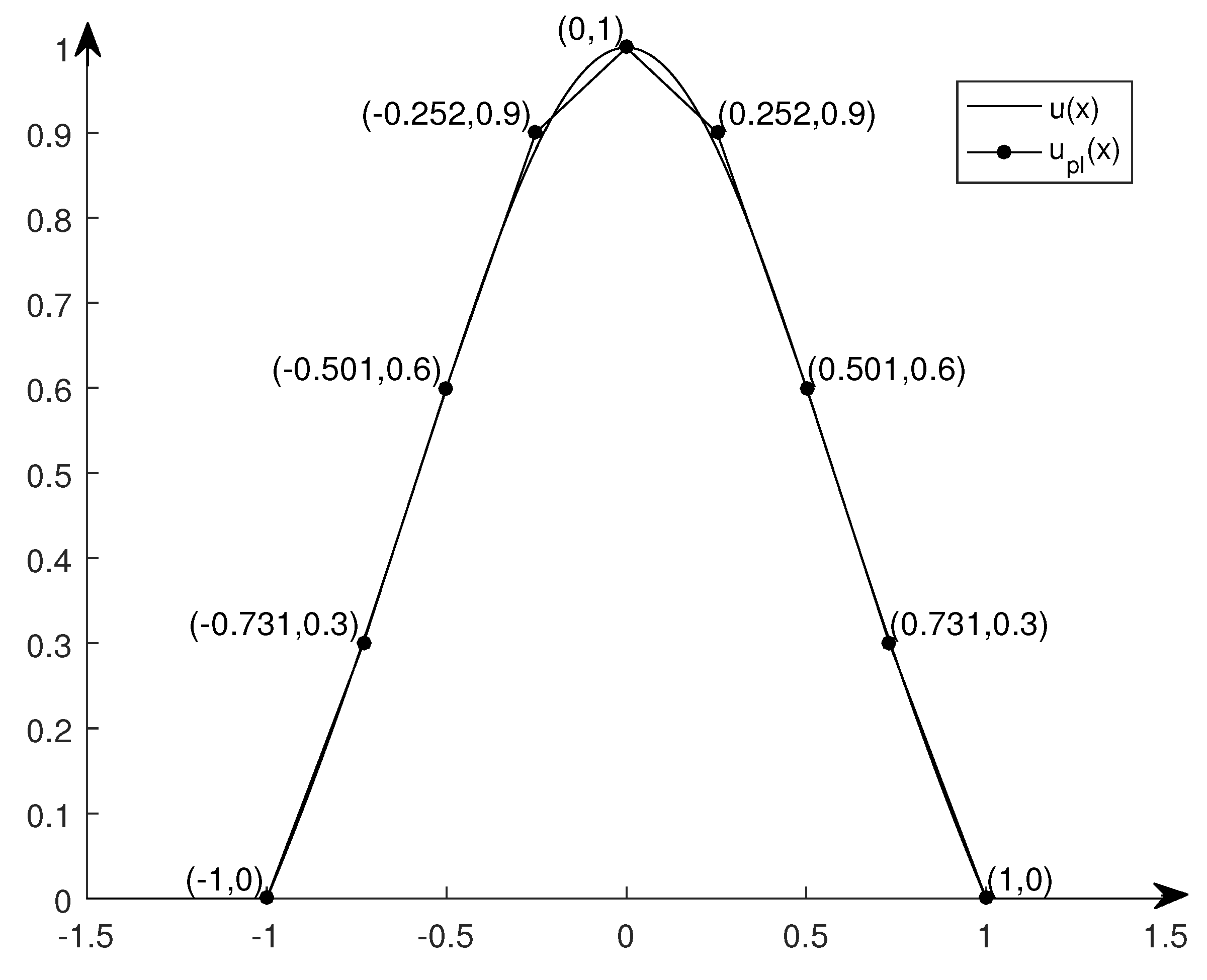
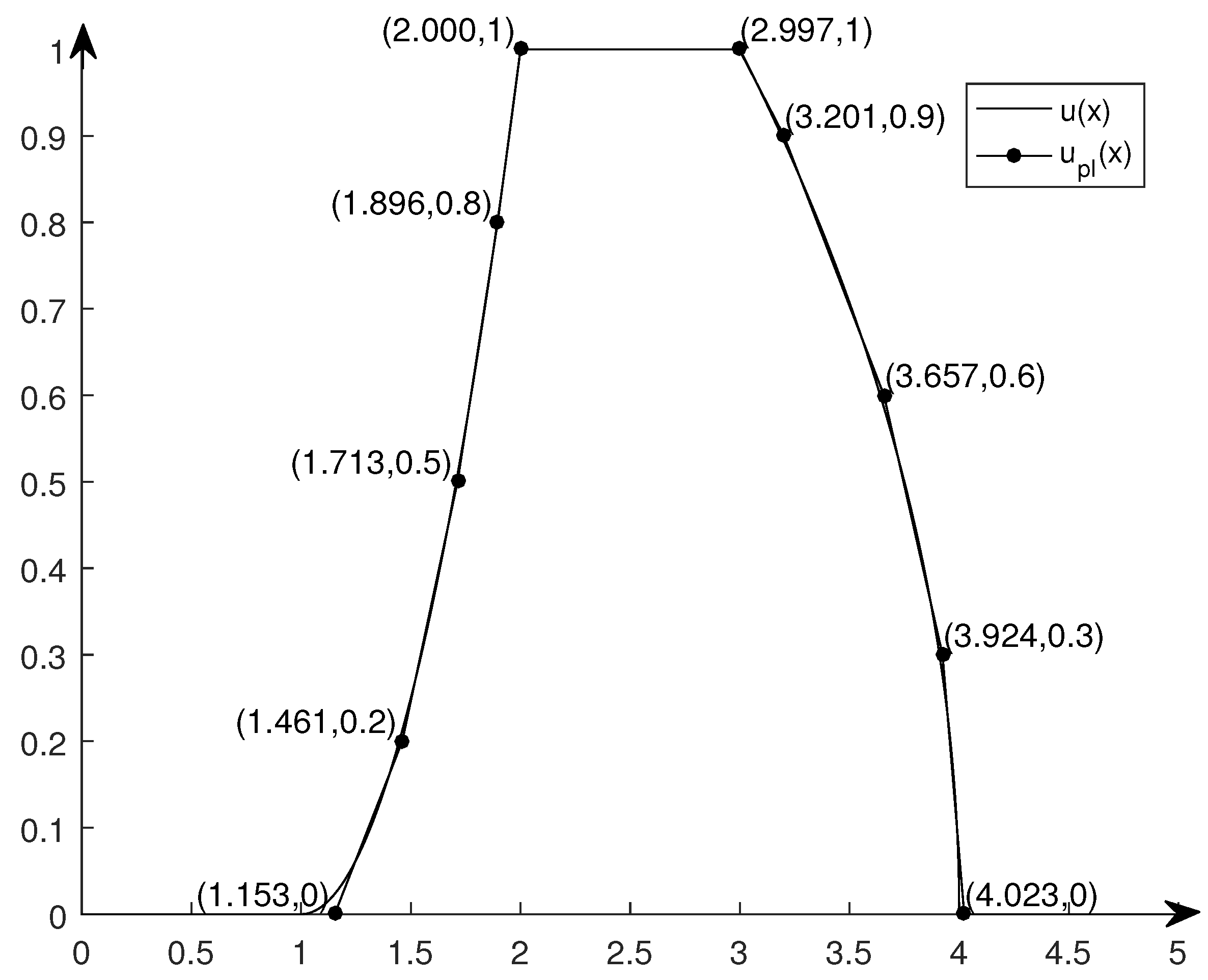
4. Examples and Comparisons of Some Approximation Methods
5. Conclusions and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Treanţǎ, S. On a class of constrained interval-valued optimization problems governed by mechanical work cost functionals. J. Optim. Theory Appl. 2021, 188, 913–924. [Google Scholar] [CrossRef]
- Guo, Y.; Ye, G.; Liu, W.; Zhao, D.; Treanţǎ, S. Optimality conditions and duality for a class of generalized convex interval-valued optimization problems. Mathematics 2021, 9, 2979. [Google Scholar] [CrossRef]
- Fu, Y.; Xiao, H.; Lee, L.H.; Huang, M. Stochastic optimization using grey wolf optimization with optimal computing budget allocation. Appl. Soft. Comput. 2021, 103, 107154. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, M.; Zhang, W.; Zhuang, X. Fuzzy optimization model for electric vehicle routing problem with time windows and recharging stations. Expert Syst. Appl. 2020, 145, 113123. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Ambrin, R.; Ibrar, M.; Delasen, M.; Rabbi, I.; Khan, A. Extended TOPSIS method for supplier selection under picture hesitant fuzzy environment using linguistic variables. J. Math. 2021, 2021, 6652586. [Google Scholar] [CrossRef]
- Mahmood, T.; Ali, Z. Entropy measure and TOPSIS method based on correlation coefficient using complex q-rung orthopair fuzzy information and its application to multi-attribute decision making. Soft Comput. 2021, 25, 1249–1275. [Google Scholar] [CrossRef]
- Ibrahim, H.Z.; Al-shami, T.M.; Elbarbary, O.G. (3,2)-Fuzzy sets and their applications to topology and optimal choices. Comput. Intell. Neurosci. 2021, 2021, 1272266. [Google Scholar] [CrossRef]
- Atef, M.; Ali, M.I.; Al-shami, T.M. Fuzzy soft covering-based multi-granulation fuzzy rough sets and their applications. Comput. Appl. Math. 2021, 40, 115. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wan, L.; Zhang, B. Topological structures induced by L-fuzzifying approximation operators. Iran. J. Fuzzy Syst. 2021, 18, 141–154. [Google Scholar]
- Coroianu, L.; Stefanini, L. General approximation of fuzzy numbers by F-transform. Fuzzy Sets Syst. 2016, 288, 46–74. [Google Scholar] [CrossRef]
- Huang, H.; Wu, C.; Xie, J.; Zhang, D. Approximation of fuzzy numbers using the convolution method. Fuzzy Sets Syst. 2017, 310, 14–46. [Google Scholar] [CrossRef]
- Yeh, C.T.; Chu, H.M. Approximations by LR-type fuzzy numbers. Fuzzy Sets Syst. 2014, 257, 23–40. [Google Scholar] [CrossRef]
- Chanas, S. On the interval approximation of a fuzzy number. Fuzzy Sets Syst. 2001, 122, 353–356. [Google Scholar] [CrossRef]
- Grzegorzewski, P. On the interval approximation of fuzzy numbers. Commun. Comput. Inf. Sci. 2012, 299, 59–68. [Google Scholar]
- Grzegorzewski, P. Nearest interval approximation of a fuzzy number. Fuzzy Sets Syst. 2002, 130, 321–330. [Google Scholar] [CrossRef]
- Ban, A.I.; Coroianu, L. Symmetric triangular approximations of fuzzy numbers under a general condition and properties. Soft Comput. 2016, 20, 1249–1261. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hajjari, T. Weighted trapezoidal approximation-preserving cores of a fuzzy number. Comput. Math. Appl. 2010, 59, 3066–3077. [Google Scholar] [CrossRef] [Green Version]
- Khastan, A.; Moradi, Z. Width invariant approximation of fuzzy numbers. Iran. J. Fuzzy Syst. 2016, 13, 111–130. [Google Scholar]
- Coroianu, L.; Gagolewski, M.; Grzegorzewski, P. Nearest piecewise linear approximation of fuzzy numbers. Fuzzy Sets Syst. 2013, 233, 26–51. [Google Scholar] [CrossRef]
- Coroianu, L.; Gagolewski, M.; Grzegorzewski, P. Piecewise linear approximation of fuzzy numbers: Algorithms, arithmetic operations and stability of characteristics. Soft Comput. 2019, 23, 9491–9505. [Google Scholar] [CrossRef]
- Wang, G.; Shen, C.; Wang, Y. Approximation of fuzzy numbers by using multi-knots piecewise linear fuzzy numbers. J. Intell. Fuzzy Syst. 2020, 39, 3597–3615. [Google Scholar] [CrossRef]
- Grzegorzewski, P. Metrics and orders in space of fuzzy numbers. Fuzzy Sets Syst. 1998, 97, 83–94. [Google Scholar] [CrossRef]
- Zeng, W.; Li, H. Weighted triangular approximation of fuzzy numbers. Int. J. Approx. Reason. 2007, 46, 137–150. [Google Scholar] [CrossRef] [Green Version]
- Taussky, O. A recurring theorem on determinants. Am. Math. Mon. 1949, 56, 672–676. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, H.; Wang, G. Approximations of Fuzzy Numbers by Using r-s Piecewise Linear Fuzzy Numbers Based on Weighted Metric. Mathematics 2022, 10, 145. https://doi.org/10.3390/math10010145
Lv H, Wang G. Approximations of Fuzzy Numbers by Using r-s Piecewise Linear Fuzzy Numbers Based on Weighted Metric. Mathematics. 2022; 10(1):145. https://doi.org/10.3390/math10010145
Chicago/Turabian StyleLv, Haojie, and Guixiang Wang. 2022. "Approximations of Fuzzy Numbers by Using r-s Piecewise Linear Fuzzy Numbers Based on Weighted Metric" Mathematics 10, no. 1: 145. https://doi.org/10.3390/math10010145
APA StyleLv, H., & Wang, G. (2022). Approximations of Fuzzy Numbers by Using r-s Piecewise Linear Fuzzy Numbers Based on Weighted Metric. Mathematics, 10(1), 145. https://doi.org/10.3390/math10010145





