Enhancing Student Motivation in Secondary School Mathematics Courses: A Methodological Approach
Abstract
1. Introduction
2. Literature Review
3. Methodology
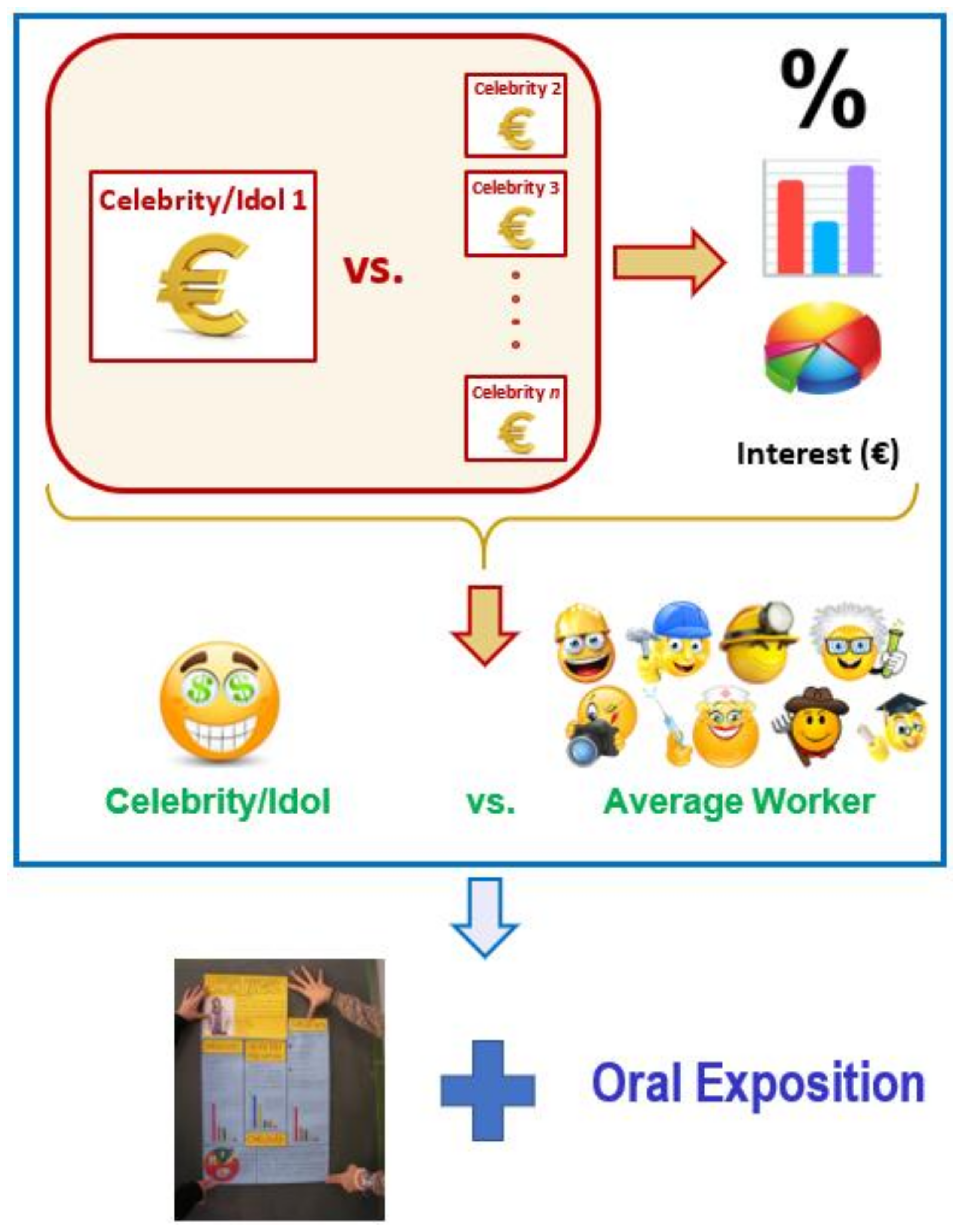
- (a)
- Students must calculate the total amount earned by the selected celebrity per year, per month, per day, per hour, per minute, and per second (taking into account the huge amounts earned by certain celebrities, these values are still big even for the two last cases, i.e., per minute or per second).
- (b)
- To compare, as a percentage, how much money the selected celebrity earns with the amount of money earned by the celebrities selected by other groups and with the average salary of a Spanish worker. This allows students to develop transversal skills, e.g., identifying social inequalities and social unfairness, which can help them to reflect on what is more important in life.
- (c)
- To establish bar and pie charts with the data obtained in the previous step. This aspect is especially important because all secondary school science textbooks contain many such diagrams [35]. In this way, the differences between each of the celebrities selected by all of the groups can be visually observed.
- (d)
- To evaluate the bank interest that each celebrity would receive from one year’s salary by working with compound interest. This topic is covered in the third course of Spanish compulsory secondary education (14-year-old students). The results show that certain celebrities would earn more monthly from a fixed-term deposit in the bank than an average Spanish worker would from his/her work.
- (e)
- To design a poster (A1–A2 size) with an original organization of all of the content produced in the previous steps, selecting appropriate sizes of elements (letters, spaces, plots, etc.) that ensure everything can be correctly seen and aligning margins correctly. This task requires greater effort than students might think, and it represents an important challenge of learning the importance of measuring and estimating the size of each section in the poster. In Figure 2, an example of the posters made by secondary school students during the development of this methodology is shown.
- (f)
- Presentations and debate about the developed work, thereby developing oral and exposition skills (and reinforcing the mathematical learning at the same time [36]).

- The methodology was applied during four academic courses (from 2011/2012 to 2014/2015) in different Spanish High Schools.
- The experimental group was composed of 134 students enrolled in the first three courses of Spanish compulsory secondary education (i.e., from 12 to 14 years old). At this education level, students have not decided yet their academic path (technical/science or social/humanities). Thus, students with a high variety of particular personal interests are together in the same classroom.
- All the Spanish High Schools where these educational experiences were applied were public centers. There, students of middle-class families attend classes (the annual gross income of the middle class in Spain is around 26,500 € [38]).
4. Findings
4.1. Teaching Observations
4.2. Students’ Opinions
5. Discussion
6. Limitations of the Present Study and Suggestions for Future Research
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lampert, M. Knowing, doing, and teaching multiplication. Cognit. Instruct. 1990, 3, 305–342. [Google Scholar] [CrossRef]
- Reeves, P.M.; Pun, W.H.; Chung, K.S. Influence of teacher collaboration on job satisfaction and student achievement. Teach. Teach. Educ. 2017, 67, 227–236. [Google Scholar] [CrossRef]
- Langer-Osuna, J.M. Productive disruptions: Rethinking the role of off-task interactions in collaborative mathematics learning. Educ. Sci. 2018, 8, 87. [Google Scholar] [CrossRef]
- Méndez, I.; Cerezo, F. Grade repetition rate in secondary education and associated risk factors. Educ. XX1 2018, 21, 41–62. [Google Scholar] [CrossRef]
- Saglam, Y.; Türker, B.; Umay, A. Geometry anxiety scale for secondary school students. Proc. Soc. Behav. Sci. 2011, 15, 966–970. [Google Scholar] [CrossRef][Green Version]
- Tarver, T. The retention rate of students of mathematics education. Proc. Soc. Behav. Sci. 2015, 177, 256–259. [Google Scholar] [CrossRef]
- Taylor, P. Teach the mathematics of mathematicians. Educ. Sci. 2018, 8, 56. [Google Scholar] [CrossRef]
- Trninic, D.; Wagner, R.; Kapur, M. Rethinking failure in mathematics education: A historical appeal. Think. Skills Creat. 2018, 30, 76–89. [Google Scholar] [CrossRef]
- Çiftçi, S.K. Effects of secondary school students’ perceptions of mathematics education quality on mathematics anxiety and achievement. Educ. Sci. Theory Pract. 2015, 15, 1487–1501. [Google Scholar] [CrossRef]
- Hill, F.; Mammarella, I.C.; Devine, A.; Caviola, S.; Passolunghi, M.C.; Szűcs, D. Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learn. Individ. Differ. 2016, 48, 45–53. [Google Scholar] [CrossRef]
- Kukk, A.; Rajalaane, R.; Rei, M.L.; Piht, S. Parents opinions on homework in the II stage of primary school (Estonian example). Proc. Soc. Behav. Sci. 2015, 171, 134–144. [Google Scholar] [CrossRef]
- Hagger, M.S.; Sultan, S.; Hardcastle, S.J.; Chatzisarantis, N.L.D. Perceived autonomy support and autonomous motivation toward mathematics activities in educational and out-of-school contexts is related to mathematics homework behavior and attainment. Contemp. Educ. Psychol. 2015, 41, 111–123. [Google Scholar] [CrossRef]
- Baki, A.; Çatlıoglu, H.; Costu, S.; Birgin, O. Conceptions of high school students about mathematical connections to the real-life. Proc. Soc. Behav. Sci. 2009, 1, 1402–1407. [Google Scholar] [CrossRef]
- Hernandez-Martinez, P.; Pampaka, M. “I Did Use to Like Maths…”: Emotional changes toward mathematics during secondary school education. In Understanding Emotions in Mathematical Thinking and Learning; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Jankvist, U.T.; Niss, M. Counteracting destructive student misconceptions of Mathematics. Educ. Sci. 2018, 8, 53. [Google Scholar] [CrossRef]
- Taştan, S.B.; Mousavi-Davoudi, S.M.; Masalimova, A.R.; Bersanov, A.S.; Kurbanov, R.A.; Boiarchuk, A.V.; Pavlushin, A.A. The impacts of teacher’s efficacy and motivation on student’s academic achievement in science education among secondary and high school students. EURASIA J. Math. Sci. Technol. Educ. 2018, 14, 2353–2366. [Google Scholar] [CrossRef]
- González-DeHass, A.R.; Furner, J.M.; Vásquez-Colina, M.D.; Morris, J.D. Pre-service elementary teachers’ achievement goals and their relationship to math anxiety. Learn. Individ. Differ. 2017, 60, 40–45. [Google Scholar] [CrossRef]
- Chris Bradford, C.; Braaten, M. Teacher evaluation and the demoralization of teachers. Teach. Teach. Educ. 2018, 75, 49–59. [Google Scholar] [CrossRef]
- Verschaffel, L.; Depaepe, F.; de Corte, E. Mathematics Education. Int. Encycl. Soc. Behav. Sci. 2015, 14, 816–821. [Google Scholar] [CrossRef]
- Guerrero, G.; Ayala, A.; Mateu, J.; Casades, L.; Alamán, X. Integrating virtual worlds with tangible user interfaces for teaching Mathematics: A pilot study. Sensors 2016, 16, 1775. [Google Scholar] [CrossRef] [PubMed]
- Altanis, I.; Retalis, S.; Petropoulou, O. Systematic design and rapid development of motion-based touchless games for enhancing students’ thinking skills. Educ. Sci. 2018, 8, 18. [Google Scholar] [CrossRef]
- Vidermanova, K.; Vallo, D. Practical geometry tasks as a method for teaching active learning in geometry. Proc. Soc. Behav. Sci. 2015, 191, 1796–1800. [Google Scholar] [CrossRef][Green Version]
- Berlinski, S.; Busso, M. Challenges in educational reform: An experiment on active learning in mathematics. Econ. Lett. 2017, 156, 172–175. [Google Scholar] [CrossRef]
- Briz, A.; Serrano, A. Learning mathematics through the R programming language in secondary education. Educ. Mater. 2018, 30, 133–162. [Google Scholar] [CrossRef]
- Gasco, J.; Villarroel, J.D. Algebraic problem solving and learning strategies in compulsory secondary education. Proc. Soc. Behav. Sci. 2012, 46, 612–616. [Google Scholar] [CrossRef][Green Version]
- Kyaruzi, F.; Strijbos, J.W.; Ufer, S.; Brown, G.T.L. Teacher AfL perceptions and feedback practices in mathematics education among secondary schools in Tanzania. Stud. Educ. Eval. 2018, 59, 1–9. [Google Scholar] [CrossRef]
- Costu, S.; Aydın, S.; Filiz, M. Students’ conceptions about browser-game-based learning in mathematics education: TTNetvitamin case. Proc. Soc. Behav. Sci. 2009, 1, 1848–1852. [Google Scholar] [CrossRef][Green Version]
- Benton, L.; Saunders, P.; Kalas, I.; Hoyles, C.; Noss, R. Designing for learning mathematics through programming: A case study of pupils engaging with place value. Int. J. Child-Comput. Interact. 2018, 16, 68–76. [Google Scholar] [CrossRef]
- Mamolo, A. Perceptions of social issues as contexts for secondary mathematics. J. Math. Behav. 2018, 51, 28–40. [Google Scholar] [CrossRef]
- Hunt, J.; Westenskow, A.; Moyer-Packenham, P.S. Variations of reasoning in equal sharing of children who experience low achievement in mathematics: Competence in context. Educ. Sci. 2017, 7, 37. [Google Scholar] [CrossRef]
- Clark, K.R. The effects of the flipped model of instruction on student engagement and performance in the secondary mathematics classroom. J. Educ. Online 2015, 12, 91–115. [Google Scholar] [CrossRef]
- Bhagat, K.K.; Chang, C.N.; Chang, C.Y. The impact of the flipped classroom on mathematics concept learning in high school. J. Educ. Technol. Soc. 2016, 19, 134–142. [Google Scholar]
- Smith, K.A. Cooperative learning: Making “groupwork” work. In New Directions for Teaching and Learning; Wiley: Hoboken, NJ, USA, 1996; Volume 67, pp. 71–82. [Google Scholar] [CrossRef]
- Vergara, D. An educational experience of cooperative learning in the university. Una experiencia educativa de aprendizaje cooperativo en la universidad. Rev. Curric. Form. Profr. 2012, 16, 339–354. (In Spanish) [Google Scholar]
- Liu, Y.; Treagust, D.F. Content analysis of diagrams in secondary school science textbooks. In Critical Analysis of Science Textbooks; Khine, M., Ed.; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Stylianides, A.J. Secondary students’ proof constructions in mathematics: The role of written versus oral mode of argument representation. Rev. Educ. 2019, 7, 156–182. [Google Scholar] [CrossRef]
- Joutsenlahti, J.; Perkkilä, P. Sustainability development in mathematics education—A case study of what kind of meanings do prospective class teachers find for the mathematical symbol “2/3”? Sustainability 2019, 11, 457. [Google Scholar] [CrossRef]
- Dementiev, A. Spain vs. Portugal: The turbulent past and the complicated present. Iberoam. Notes 2018, 2, 14–21, (In Spanish and Russian). [Google Scholar]
- Skinner, E.A.; Belmont, M.J. Motivation in the classroom: Reciprocal effects of teacher behavior and student engagement across the school year. J. Educ. Psychol. 1993, 85, 571–581. [Google Scholar] [CrossRef]
- Gatz, J.; Kelly, A.M. Afterschool school triathlon training for 11- to 14-year old girls: Influences on academic motivation and achievement. Health Educ. J. 2018, 77, 156–168. [Google Scholar] [CrossRef]
- Parhiala, P.; Torppa, M.; Vasalampi, K.; Eklund, K.; Poikkeus, A.M.; Aroa, T. Profiles of school motivation and emotional well-being among adolescents: Associations with math and reading performance. Learn. Individ. Differ. 2018, 61, 196–204. [Google Scholar] [CrossRef]
- Rieche, H.; Leuders, T.; Renkl, A. If a student thinks, “I’m not a math person”, do preservice teachers notice? Eur. J. Sci. Math. Educ. 2019, 7, 32–49. [Google Scholar]
- Opdecam, E.; Everaert, P. Seven disagreements about cooperative learning. Account. Educ. 2018, 27, 223–233. [Google Scholar] [CrossRef]
- Weinberger, Y.; Shonfeld, M. Students’ willingness to practice collaborative learning. Teach. Educ. 2018. [Google Scholar] [CrossRef]
- Kastberg, S.E.; Long, R.; Lynch-Davis, K.; D’Ambrosio, B.S. “Draw what you see” transcending the mathematics classroom. In Interdisciplinary Mathematics Education; ICME-13 Monographs; Doig, B., Williams, J., Swanson, D., Borromeo Ferri, R., Drake, P., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Orcos, L.; Hernandez-Carrera, R.M.; Espigares, M.J.; Magrenan, A.A. The Kumon method: Its importance in the improvement on the teaching and learning of mathematics from the first levels of early childhood and Primary Education. Mathematics 2019, 7, 109. [Google Scholar] [CrossRef]
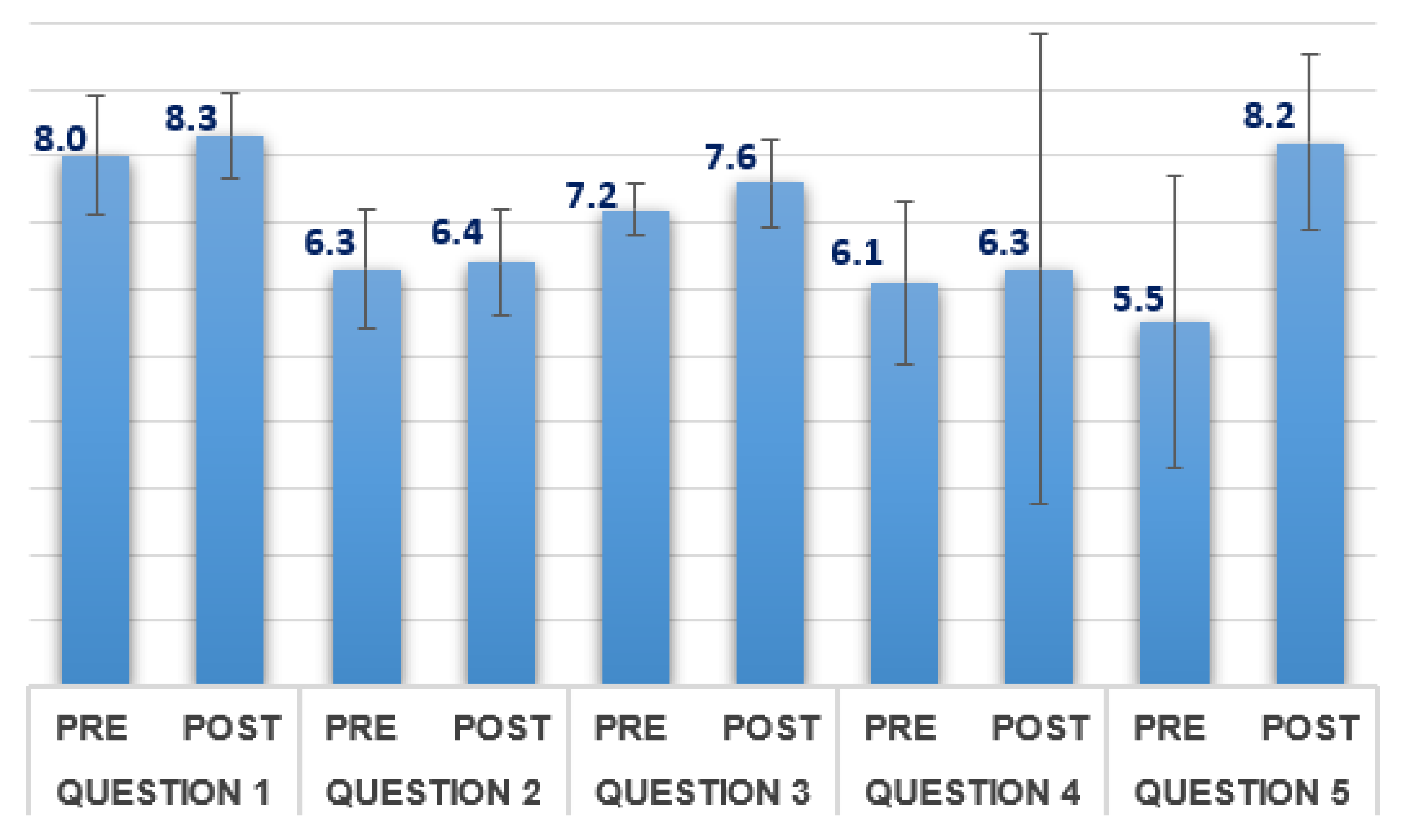
| Question Number | Pre-Test | Post-Test |
|---|---|---|
| 1 | Do you believe that the Mathematics subject is useful in real life? Rate from 1 to 10 your answer | Do you believe that the Mathematics subject is useful in real life? Rate from 1 to 10 your answer |
| 2 | Do you like the Mathematics subject? Rate from 1 to 10 your answer | Do you like the Mathematics subject? Rate from 1 to 10 your answer |
| 3 | Do you think that you will like the new methodology? Rate from 1 to 10 your answer | Have you enjoyed the new methodology? Rate from 1 to 10 your answer |
| 4 | Do you consider that the methodology will help you to learn percentages and bar and pie charts? Rate from 1 to 10 your answer | Do you consider that the methodology helped you to learn percentages and bar and pie charts? Rate from 1 to 10 your answer |
| 5 | Do you consider that making an oral presentation will help you to better understand what is learnt? Rate from 1 to 10 your answer | Do you consider that making an oral presentation helped you to better understand what you learnt? Rate from 1 to 10 your answer |
| 6 | Do you prefer the new methodology or a conventional class? | Do you prefer the new methodology or a conventional class? |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vergara, D.; Fernández, M.L.; Lorenzo, M. Enhancing Student Motivation in Secondary School Mathematics Courses: A Methodological Approach. Educ. Sci. 2019, 9, 83. https://doi.org/10.3390/educsci9020083
Vergara D, Fernández ML, Lorenzo M. Enhancing Student Motivation in Secondary School Mathematics Courses: A Methodological Approach. Education Sciences. 2019; 9(2):83. https://doi.org/10.3390/educsci9020083
Chicago/Turabian StyleVergara, Diego, María Luz Fernández, and Miguel Lorenzo. 2019. "Enhancing Student Motivation in Secondary School Mathematics Courses: A Methodological Approach" Education Sciences 9, no. 2: 83. https://doi.org/10.3390/educsci9020083
APA StyleVergara, D., Fernández, M. L., & Lorenzo, M. (2019). Enhancing Student Motivation in Secondary School Mathematics Courses: A Methodological Approach. Education Sciences, 9(2), 83. https://doi.org/10.3390/educsci9020083






