Insights Chinese Primary Mathematics Teachers Gained into their Students’ Learning from Using Classroom Assessment Techniques
Abstract
:1. Introduction
1.1. Assessment in the Hands of Teachers
1.2. Assessment Techniques
1.3. A New Approach to Assessment in Mathematics Education in China
1.4. The Present Study
2. Methods
2.1. Participants
2.2. Multiplication of Two-Digit Numbers
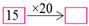 and
and 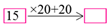 , in which the students are required to fill in the empty frames.
, in which the students are required to fill in the empty frames.2.3. CATs for Assessing Multiplication of Two-Digit Numbers
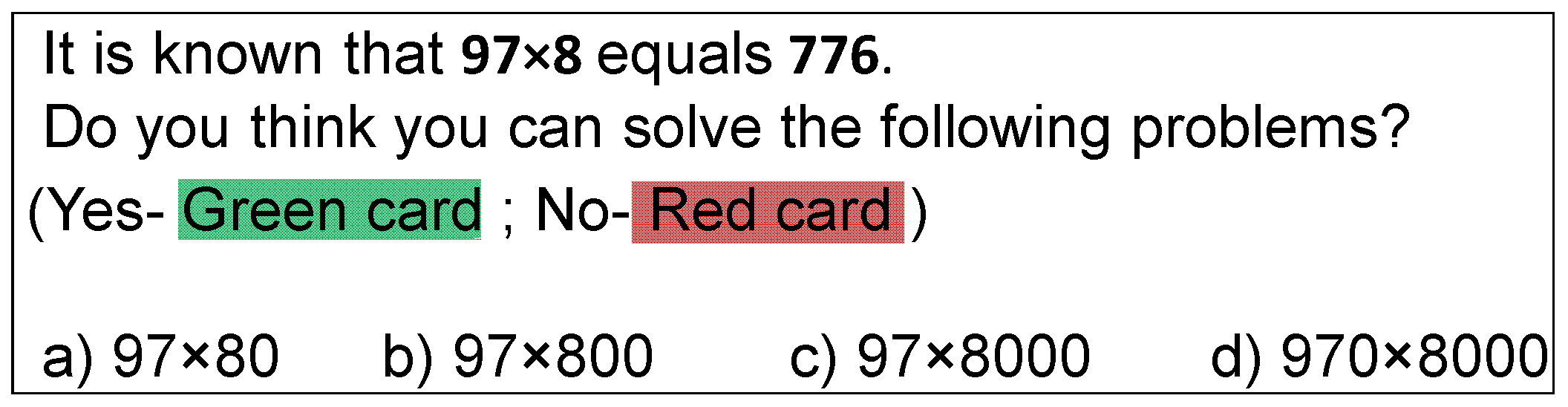
2.3.1. CAT-1: Family Problems
2.3.2. CAT-3: Breaking down a Multiplication
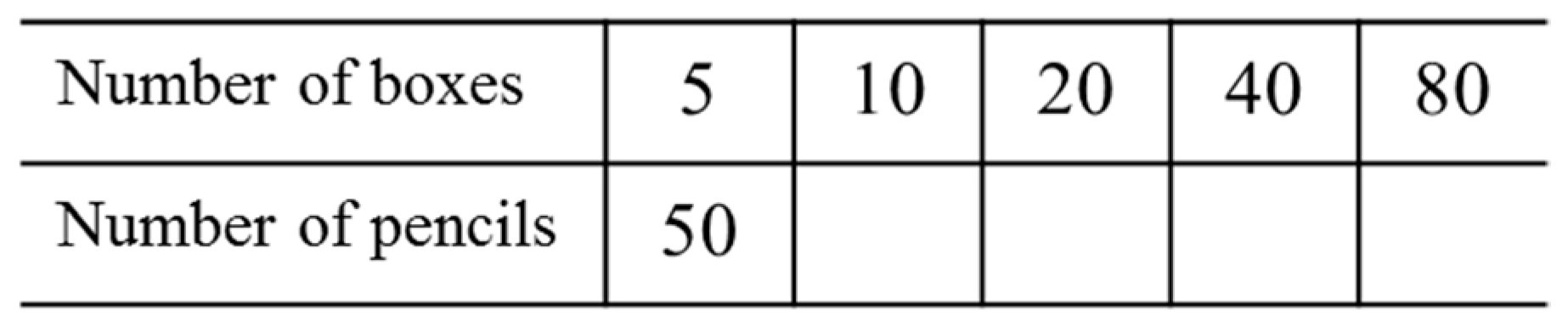
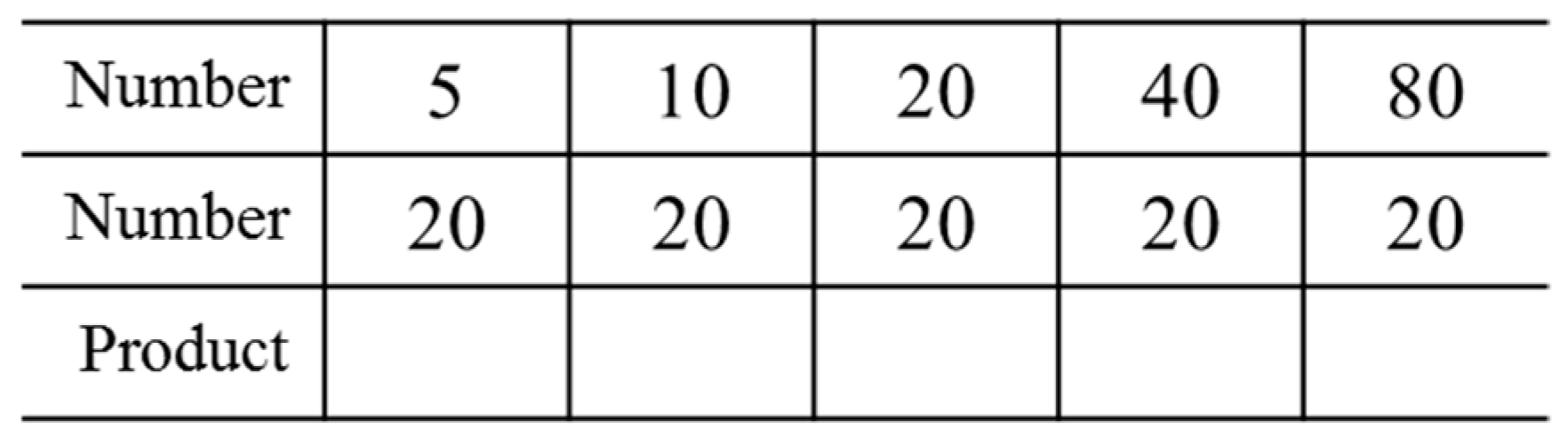
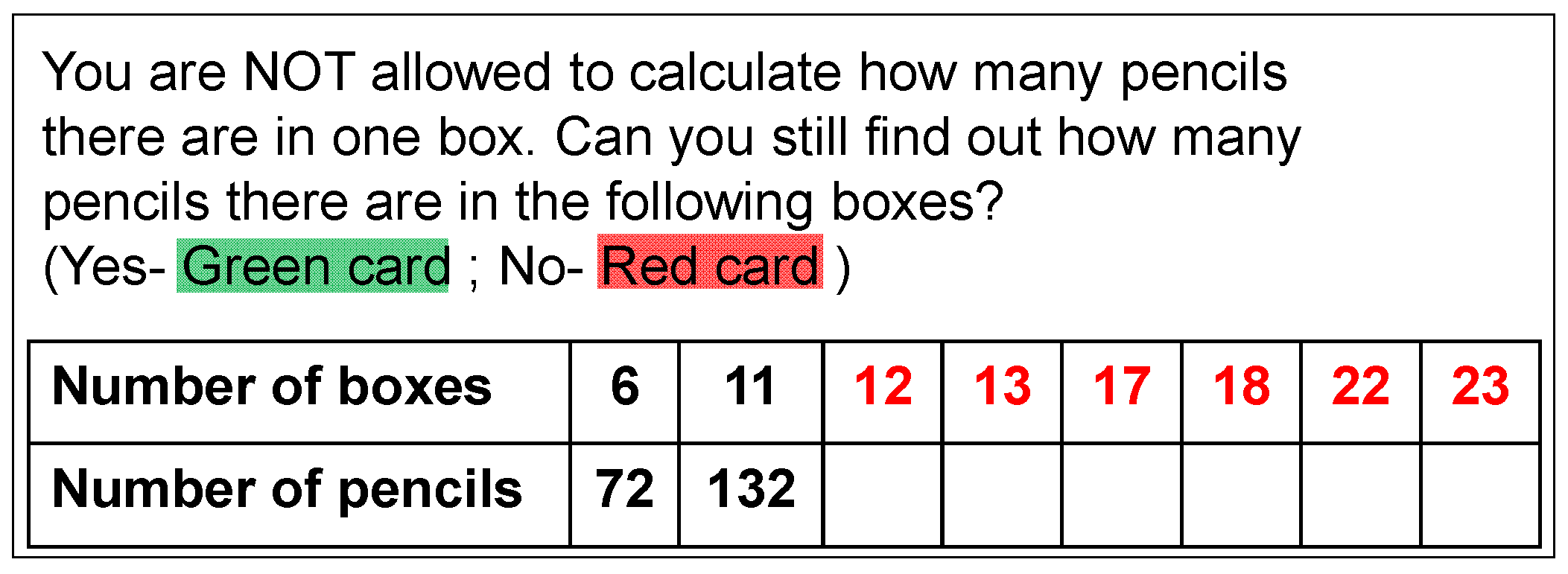
2.3.3. CAT-4: Completing the Ratio Table
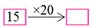 are followed by
are followed by 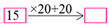 , and there is an opportunity to discuss that this is equal to 16 × 20. This way of reasoning about the ratio table is in any case explicitly promoted in CAT-4 and can provide teachers with extra information about their students’ understanding of the ratio aspect of multiplication.
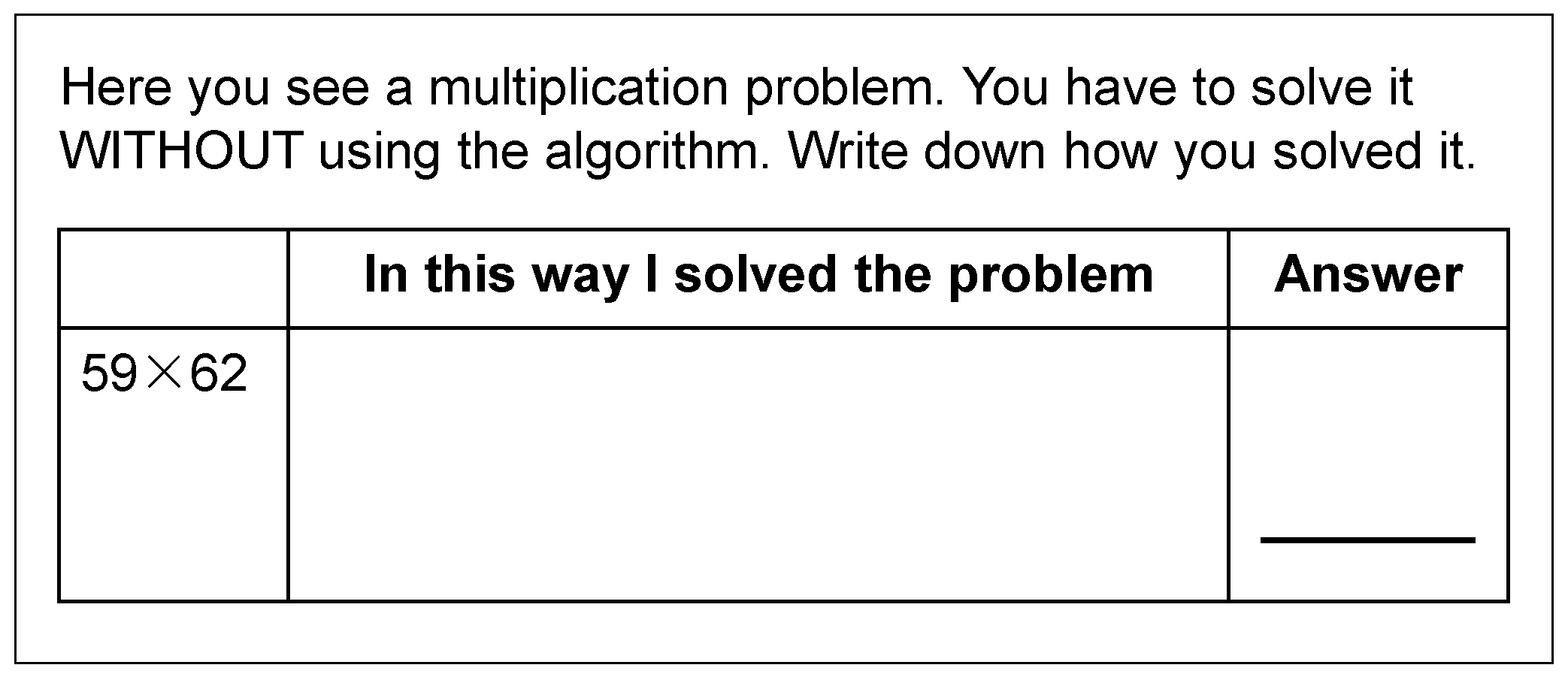
, and there is an opportunity to discuss that this is equal to 16 × 20. This way of reasoning about the ratio table is in any case explicitly promoted in CAT-4 and can provide teachers with extra information about their students’ understanding of the ratio aspect of multiplication.2.3.4. CAT-8: Solving Problems without Algorithm
2.4. Teacher Training
2.5. Data Collection
2.6. Data Analysis
- Referring to the mathematical content the CAT is supposed to assess. For this, teachers can use their own words or give a clear description of the purpose of the CAT by using (partly) the wording that appeared in the teacher guide. However, this criterion is not met when teachers only refer to the CAT in general terms not mentioning the mathematics assessed.
- Providing specific information about students. This includes mentioning the proportion of students showing a particular performance on the assessed content or describing the difficulties students encountered with this content.
- Describing the novelty of the gained information about students. This means that teachers learn something “new”, “unexpected”, “surprising”, or “that was not known before” about students’ understanding of the assessed content.
- Explaining an instructional adaptation matching the findings from the CAT. Such an instructional adaptation has to correspond to the information about the assessed content as revealed by using the CAT; general phrases such as “providing additional exercises” or “give extra instruction” are not sufficient.
3. Results
3.1. Teachers Gaining Insights from Using the CATs
3.2. Four Examples of Teachers Gaining Insights from Using CATs
3.2.1. Insights from Using CAT-1: Family Problems.
3.2.2. Insights from Using CAT-3: Breaking down a Multiplication
3.2.3. Insights from Using CAT-4: Completing the Ratio Table
3.2.4. Insights from Using CAT-8: Solving Problems without Algorithm
4. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Title | Format | Example | Purpose |
|---|---|---|---|
| Family problems (CAT-1) | Red/Green cards |  | Assessing whether students can recognize analogous problems and are aware of the relationship among the results of these problems |
| How many approximately? (CAT-2) | Red/Green cards |  | Assessing whether students can find the approximate average of a series of numbers |
| Breaking down a multiplication (CAT-3) | Worksheet |  | Assessing whether students understand how the multiplication algorithm works |
| Completing the ratio table (CAT-4) | Red/Green cards |  | Assessing whether students can make use of the ratio table by reasoning horizontally |
| Bigger or smaller? (CAT-5) | Red/Green cards |  | Assessing whether students can estimate the product by reasoning |
| Quick check of answers (CAT-6) | Red/Green cards |  | Assessing whether students can quickly check the correctness of the result of multiplication problems without performing the algorithm |
| Fruit language (CAT-7) | Worksheet | 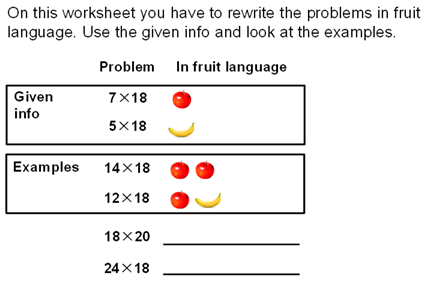 | Assessing whether students can use the associative and distributive property of multiplication to restructure a multiplication problem |
| Solving problems without using the algorithm (CAT-8) | Worksheet |  | Assessing whether students have a deep understanding of the multiplication operation and whether they have, instead of the algorithm, other strategies available to solve multiplication problems |
References
- Shavelson, R.J. The Basic Teaching Skill: Decision Making (R & D Memorandum No.104); Stanford University: Stanford, CA, USA, 1973. [Google Scholar]
- Parkes, J. Reliability in classroom assessment. In Sage Handbook of Research on Classroom Assessment; McMillan, J.H., Ed.; Corwin Press: Thousand Oaks, CA, USA, 2013; pp. 107–123. Available online: http://sci-hub.tw/10.4135/9781452218649.n7 (accessed on 11 March 2019).
- Harlen, W. Assessment of Learning; Sage: London, UK, 2007; Available online: http://sci-hub.tw/10.4135/9781446214695 (accessed on 11 March 2019).
- Shepard, L.A.; Penuel, W.R.; Pellegrino, J.W. Using learning and motivation theories to coherently link formative assessment, grading practices, and large-scale assessment. Educ. Meas. Issues Pract. 2018, 37(1), 21–34. [Google Scholar] [CrossRef]
- Black, P.; Wiliam, D. Assessment and classroom learning. Assess. Educ. Princ. Policy Pract. 1998, 5, 7–74. [Google Scholar] [CrossRef]
- Brookhart, S.M. Classroom assessment: Tensions and intersections in theory and practice. Teach. Coll. Rec. 2004, 106, 429–458. [Google Scholar] [CrossRef]
- De Lange, J. Framework for Classroom Assessment in Mathematics; NICLA; WCER: Madison, WI, USA, 1999. [Google Scholar]
- Shepard, L.A. The role of assessment in a learning culture. Educ. Res. 2000, 29(7), 4–14. [Google Scholar] [CrossRef]
- Stiggins, R.; Chappuis, J. Using student-involved classroom assessment to close achievement gaps. Theory Pract. 2005, 44(1), 11–18. [Google Scholar] [CrossRef]
- Wiliam, D. Keeping learning on track: Classroom assessment and the regulation of learning. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Ed.; Information Age Publishing: Greenwich, UK, 2007; pp. 1053–1098. [Google Scholar]
- Schoenfeld, A.H. Summative and formative assessments in mathematics supporting the goals of the common core standards. Theory Pract. 2015, 54, 183–194. [Google Scholar] [CrossRef]
- Lin, P.J. Conceptualizing teachers’ understanding of students’ mathematical learning by using assessment tasks. Int. J. Sci. Math. Educ. 2006, 4, 545–580. [Google Scholar] [CrossRef]
- Panizzon, D.; Pegg, J. Assessment practices: Empowering mathematics and science teachers in rural secondary schools to enhance student learning. Int. J. Sci. Math. Educ. 2008, 6, 417–436. [Google Scholar] [CrossRef]
- Gallego-Arrufat, M.J.; Dandis, M. Rubrics in a secondary mathematics class. Int. Electron. J. Math. Educ. 2014, 9, 73–82. [Google Scholar]
- Jin, H.; Wong, K.Y. Mapping conceptual understanding of algebraic concepts: An exploratory investigation involving grade 8 Chinese students. Int. J. Sci. Math. Educ. 2015, 13, 683–703. [Google Scholar] [CrossRef]
- Leahy, S.; Lyon, C.; Thompson, M.; Wiliam, D. Classroom assessment: Minute-by minute and day by day. Educ. Leadersh. 2005, 63(3), 18–24. [Google Scholar]
- Andersson, C.; Palm, T. The impact of formative assessment on student achievement: A study of the effects of changes to classroom practice after a comprehensive professional development programme. Learn. Instr. 2017, 49, 92–102. [Google Scholar] [CrossRef]
- Keeley, P.; Tobey, C.R. Mathematics Formative Assessment: 75 Practical Strategies for Linking Assessment, Instruction, and Learning; Corwin Press: Thousand Oaks, CA, USA, 2011. [Google Scholar]
- Veldhuis, M.; Van den Heuvel-Panhuizen, M. Supporting primary school teachers’ classroom assessment in mathematics education: Effects on student achievement. Math. Educ. Res. J. 2019. Available online: https://link.springer.com/article/10.1007/s13394-019-00270-5 (accessed on 3 June 2019).
- Wiliam, D. Embedded Formative Assessment; Solution Tree: Bloomington, IN, USA, 2011. [Google Scholar]
- Wylie, E.C.; Lyon, C.J. The fidelity of formative assessment implementation: Issues of breadth and quality. Assess. Educ. Princ. Policy Pract. 2015, 22, 140–160. [Google Scholar] [CrossRef]
- James, M.; McCormick, R. Teachers learning how to learn. Teach. Teach. Educ. 2009, 25, 973–982. [Google Scholar] [CrossRef]
- Phelan, J.; Choi, K.; Niemi, D.N.; Vendlinski, T.; Baker, E.L.; Herman, J. The effects of POWERSOURCE© assessments on middle-school students’ math performance. Assess. Educ. Princ. Policy Pract. 2012, 19, 211–230. [Google Scholar] [CrossRef]
- Davidson, A.; Herbert, S.; Bragg, L.A. Supporting elementary teachers’ planning and assessing of mathematical reasoning. Int. J. Sci. Math. Educ. 2018. [Google Scholar] [CrossRef]
- Martino, A.M.; Maher, C.A. Teacher questioning to promote justification and generalization in mathematics: What research practice has taught us. J. Math. Behav. 1999, 18, 53–78. [Google Scholar] [CrossRef]
- Heritage, M.; Heritage, J. Teacher questioning: The epicenter of instruction and assessment. Appl. Meas. Educ. 2013, 26, 176–190. [Google Scholar] [CrossRef]
- Zhang, D.; Lee, P.Y. Examination culture and mathematics teaching. In Proceedings of the ICMI–China Regional Conference of Mathematical Education, Beijing, China, 5–8 August 1991. [Google Scholar]
- Li, Y. Purpose, function and types of mathematics assessment in China. ZDM 2000, 32, 192–200. [Google Scholar] [CrossRef]
- Ministry of Education of the People’s Republic of China (MoE). Jichu jiaoyu kecheng Gaige Gangyao (Shixing) [Curriculum Reform Outline of Basic Education (Trial Version)]. Available online: http://old.moe.gov.cn/publicfiles/business/htmlfiles/moe/s8001/201404/167343.html (accessed on 11 March 2019).
- Ministry of Education of the People’s Republic of China (MoE). Quanrizhi Yiwu Jiaoyu Shuxue Kecheng Biaozhun (Shiyangao); [Mathematics Curriculum Standards of Nine-Year Compulsory Education (Trial Version)]; Beijing Normal University Press: Beijing, China, 2001.
- Ministry of Education of the People’s Republic of China (MoE). Yiwu jiaoyu shuxue kecheng biaozhun (2011 nian ban) [Mathematics Curriculum Standards of Nine-Year Compulsory Education (2011 Version)]. Available online: http://ncct.moe.edu.cn/2014/curriculumPolicy_1115/3175.html (accessed on 11 March 2019).
- Cai, J.; Wang, T. Conceptions of effective mathematics teaching within a cultural context: Perspectives of teachers from China and the United States. J. Math. Teach. Educ. 2010, 13, 265–287. [Google Scholar] [CrossRef]
- Cai, J.; Ding, M.; Wang, T. How do exemplary Chinese and U.S. mathematics teachers view instructional coherence? Educ. Stud. Math. 2014, 85, 265–280. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, W.; Cai, J. Understanding students’ mathematical thinking for effective teaching: A comparison between expert and nonexpert Chinese elementary mathematics teachers. Eurasia J. Math. Sci. Technol. Educ. 2018, 14, 213–224. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Kulm, G. Mathematics teachers’ practices and thinking in lesson plan development: A case of teaching fraction division. ZDM 2009, 41, 717–731. [Google Scholar] [CrossRef]
- Liu, J. Xiaoxue Dinianji Shuxue Jiaokeshu Zhong De Xiti Yanjiu—Jiyu Zhongguo Xinjiapo Jiaokeshu Bijiao De Shijiao; [Study in Mathematics Textbook Tasks for Lower Grades in Primary School—From the Perspective of Comparison Between Textbooks in China and that in Singapore]. Master’s Thesis, Northeast Normal University, Changchun, China, 2012. [Google Scholar]
- Gu, F.; Gu, L. Characterizing mathematics teaching research specialists’ mentoring in the context of Chinese lesson study. ZDM 2016, 48, 441–454. [Google Scholar] [CrossRef]
- Zhao, X.; Van den Heuvel-Panhuizen, M.; Veldhuis, M. Chinese primary school mathematics teachers’ assessment profiles: Findings from a large-scale questionnaire survey. Int. J. Sci. Math. Educ. 2018, 16, 1387–1407. [Google Scholar] [CrossRef]
- Zhao, X.; Van den Heuvel-Panhuizen, M.; Veldhuis, M. Teachers’ use of classroom assessment techniques in primary mathematics education—an explorative study with six Chinese teachers. Int. J. STEM Educ. 2016, 3, 19. [Google Scholar] [CrossRef]
- Jiangsu Phoenix Education Publishing House. Sujiaoban Jiaokeshu; (Xiaoxue Shuxue Sannianji Xiace) [Sujiaoban Textbook (Mathematics Textbook for Grade 3 in Primary Education, Volume 2)]; Jiangsu Phoenix Education Publishing House: Nanjing, China, 2014. [Google Scholar]
- Heritage, M.; Kim, J.; Vendlinski, T.; Herman, J. From evidence to action: A seamless process in formative assessment? Educ. Meas. Issues Pract. 2009, 28(3), 24–31. [Google Scholar] [CrossRef]
- Veldhuis, M.; van den Heuvel-Panhuizen, M. Primary school teachers’ assessment profiles in mathematics 718 education. PLoS ONE 2014, 9, e86817. [Google Scholar] [CrossRef]

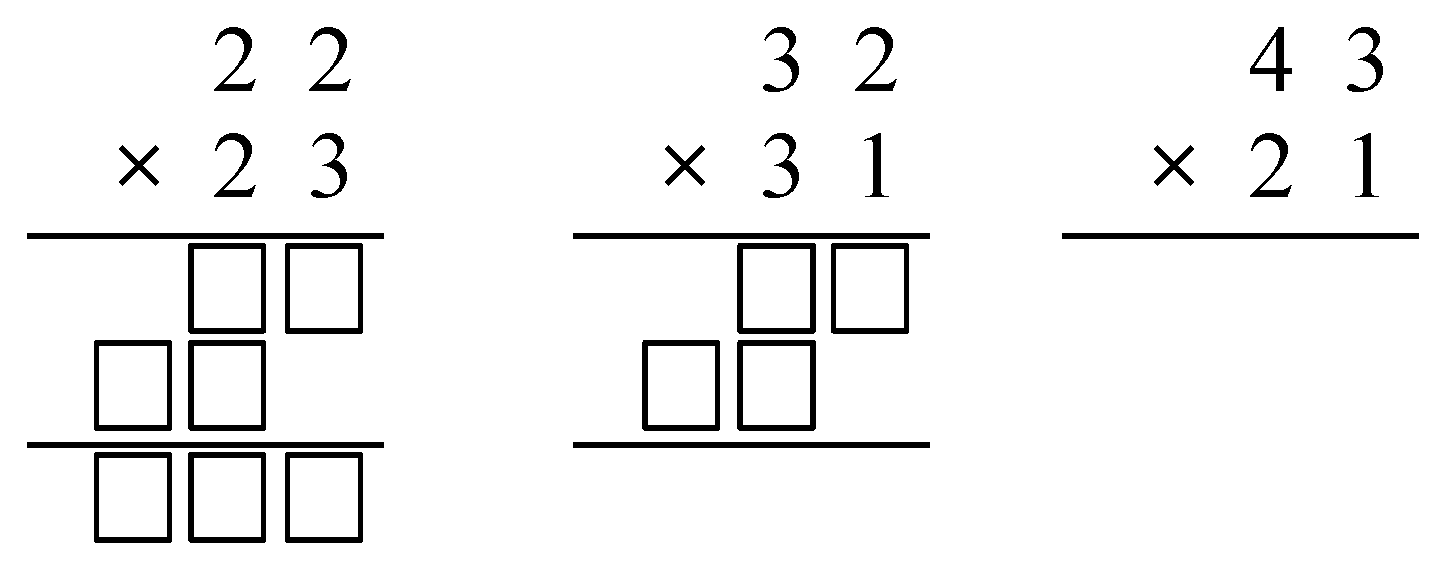
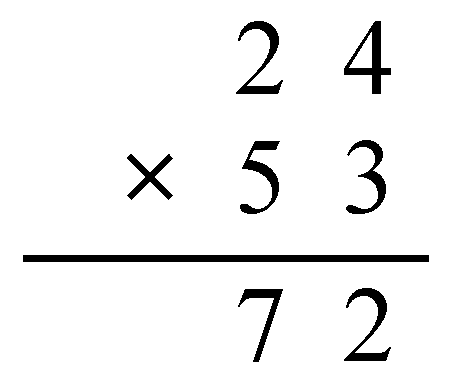

| Example of Teacher’s Response | Criterion Met | Having Gained Insights |
|---|---|---|
| Example 1: Teacher S14 “In my expectation, the vast majority of the students can find the correct answer without being disturbed by the increasing number of zeroes. However, the reality is that students felt difficult when the numbers became bigger and bigger [II, III]. Therefore, it illustrated that the students were not flexible enough when solving by mental calculation the problem with multiples of 10 [I]. Also, it means that the students lack the ability of reasoning and generalization [I].” | I, II, III | Yes |
| Example 2: Teacher S09 “The students could not recognize such analogous problems very well [I]. Most students showed their cards based on their ‘gut feeling’ [II]. Only a small proportion of the students could find the rule [II]. As the number of zeroes increased, the accuracy went down [II].” | I, II | Yes |
| Example 3: Teacher S04 “Most of the students could give the answer quickly, but some individual students need help [II].” | II | No |
| Example 4: Teacher S10 “This CAT helps the students to extend the boundary of knowledge. The difficulty level is appropriate. The students showed strong interests when doing the CAT. In general, the CAT is helpful to extend students’ knowledge and to improve their initiatives.” | [no criterion applicable] | No |
| Insight | Teacher | CAT | Total of ✓ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 7 | 2 | 5 | 6 | 3 | 8 | |||
| High | H01 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 7 | |
| Insight | H02 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 6 | ||
| H03 | ✓ | ✓ | ✓ | ✓ | ✓ | 5 | ||||
| H04 | ✓ | ✓ | ✓ | ✓ | ✓ | 5 | ||||
| H05 | ✓ | ✓ | ✓ | ✓ | ✓ | 5 | ||||
| Some | S01 | ✓ | ✓ | ✓ | 3 | |||||
| Insight | S02 | ✓ | ✓ | ✓ | 3 | |||||
| S03 | ✓ | ✓ | ✓ | 3 | ||||||
| S04 | ✓ | ✓ | ✓ | 3 | ||||||
| S05 | ✓ | ✓ | ✓ | 3 | ||||||
| S06 | ✓ | ✓ | ✓ | 3 | ||||||
| S07 | ✓ | ✓ | 2 | |||||||
| S08 | ✓ | ✓ | 2 | |||||||
| S09 | ✓ | ✓ | 2 | |||||||
| S10 | ✓ | 1 | ||||||||
| S11 | ✓ | 1 | ||||||||
| S12 | ✓ | 1 | ||||||||
| S13 | ✓ | 1 | ||||||||
| S14 | ✓ | 1 | ||||||||
| No | N01 | 0 | ||||||||
| Insight | N02 | 0 | ||||||||
| N03 | 0 | |||||||||
| N04 | 0 | |||||||||
| N05 | 0 | |||||||||
| N06 | 0 | |||||||||
| Total of ✓ | 5 | 5 | 5 | 6 | 8 | 8 | 9 | 11 | 57 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; van den Heuvel-Panhuizen, M.; Veldhuis, M. Insights Chinese Primary Mathematics Teachers Gained into their Students’ Learning from Using Classroom Assessment Techniques. Educ. Sci. 2019, 9, 150. https://doi.org/10.3390/educsci9020150
Zhao X, van den Heuvel-Panhuizen M, Veldhuis M. Insights Chinese Primary Mathematics Teachers Gained into their Students’ Learning from Using Classroom Assessment Techniques. Education Sciences. 2019; 9(2):150. https://doi.org/10.3390/educsci9020150
Chicago/Turabian StyleZhao, Xiaoyan, Marja van den Heuvel-Panhuizen, and Michiel Veldhuis. 2019. "Insights Chinese Primary Mathematics Teachers Gained into their Students’ Learning from Using Classroom Assessment Techniques" Education Sciences 9, no. 2: 150. https://doi.org/10.3390/educsci9020150
APA StyleZhao, X., van den Heuvel-Panhuizen, M., & Veldhuis, M. (2019). Insights Chinese Primary Mathematics Teachers Gained into their Students’ Learning from Using Classroom Assessment Techniques. Education Sciences, 9(2), 150. https://doi.org/10.3390/educsci9020150






