EduSciFIT: A Computer-Based Blended and Scaffolding Toolbox to Support Numerical Concepts for Flipped Science Education
Abstract
1. Introduction
1.1. Computer-Based Learning Environment
1.2. Blended and Scaffolding Learning
1.3. Flipped Classroom
1.4. Research Objective and Process
2. Materials and Methods
2.1. Educational Framework
2.2. Toolbox Description, EduSciFIT
2.3. Survey Modeling and Description
3. Results and Discussion
3.1. Experimental Data Inputs
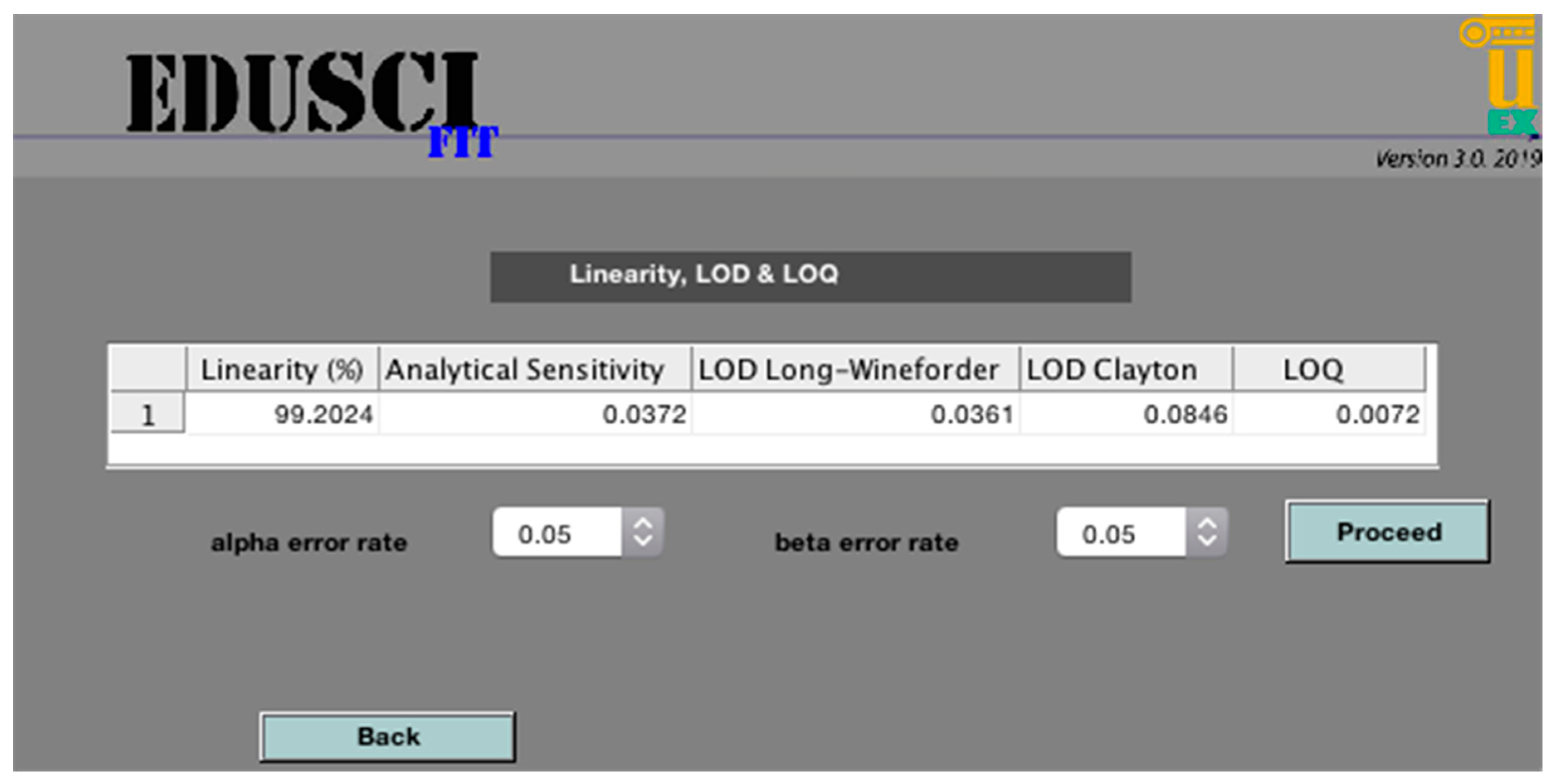
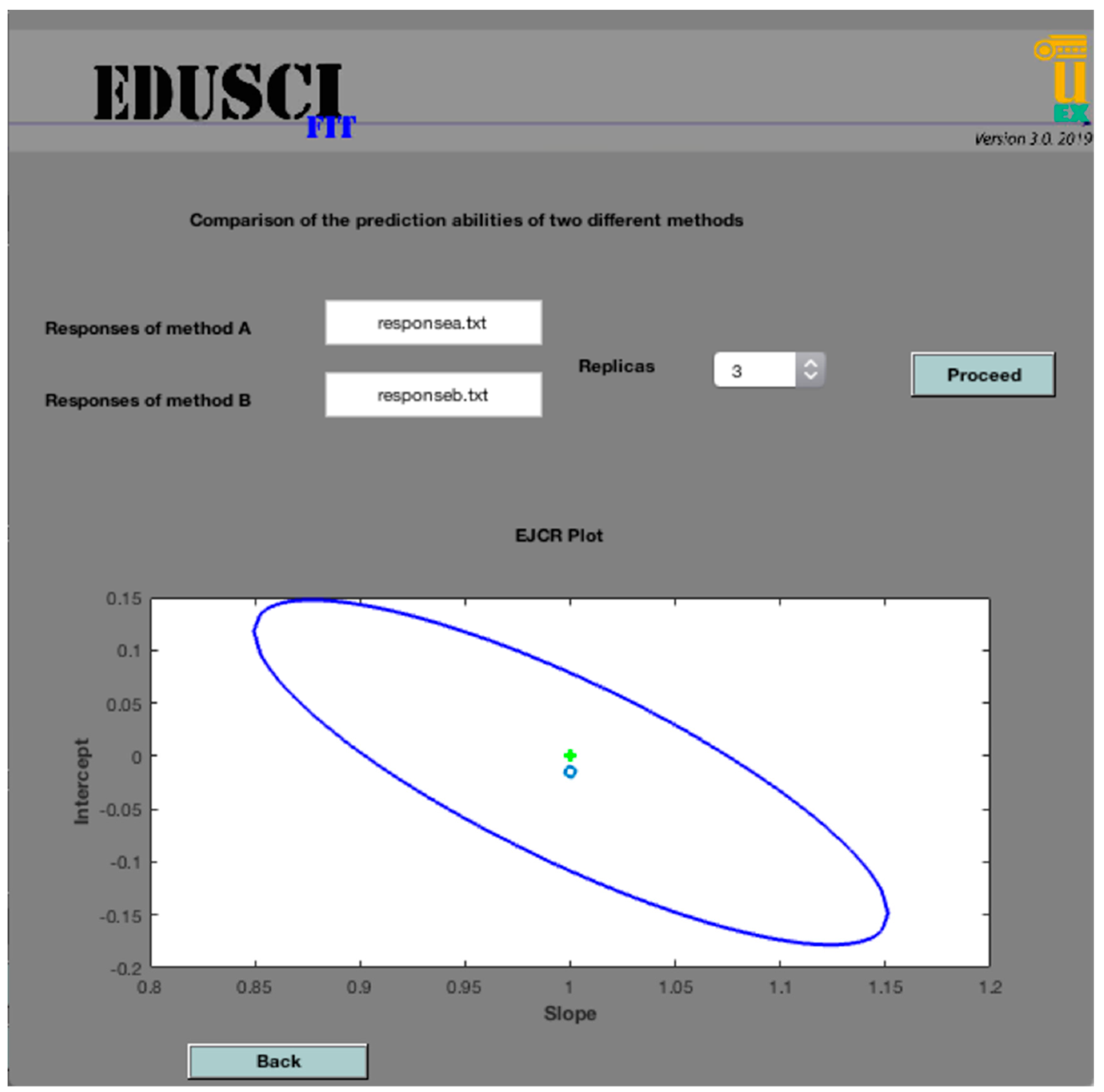
3.2. Quality of the Numerical and Analytical Method
3.3. Numerical and Analytical Tests
3.4. Survey Analysis, Results, and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Linn, M.C.; Clark, D.; Slotta, J.D. WISE design for knowledge integration. Sci. Educ. 2003, 87, 517–538. [Google Scholar] [CrossRef]
- Roschelle, J.M.; Pea, R.D.; Hoadley, C.M.; Gordin, D.N.; Means, B.M. Changing how and what children learn in school with computer-based technologies. Future Child 2000, 10, 76–101. [Google Scholar] [CrossRef]
- González-Gómez, G.; Jeong, J.S.; Airado Rodríguez, D.; Cañada-Cañada, F. Performance and perception in the flipped learning model: An initial approach to evaluate the effectiveness of a new teaching methodology in a general science classroom. J. Sci. Educ. Technol. 2016, 25, 450–459. [Google Scholar] [CrossRef]
- Kuiper, E.; Volman, M.; Terwel, J. Developing Web literacy in collaborative inquiry activities. Comput. Educ. 2009, 52, 668–680. [Google Scholar] [CrossRef]
- González-Gómez, D.; Airado Rodríguez, D.; Cañada-Cañada, F.; Jeong, J.S. A comprehensive application to assist in acid−base titration self-learning: An approach for high school and undergraduate students. J. Chem. Educ. 2015, 92, 855–863. [Google Scholar] [CrossRef]
- Steyn, M.D.V.; Alexander, P.M.; Röhm, D. CAL for first year analytical chemistry by distance education. Comput. Educ. 1996, 27, 95–101. [Google Scholar]
- Cingi, C.C. Computer aided education. Procedia Soc. Behav. Sci. 2013, 103, 220–229. [Google Scholar] [CrossRef][Green Version]
- Heck, B.S.; Poindexter, S.E.; Garcia, R. Integrating the web into traditional teaching methods. In Proceedings of the American Control Conference, Chicago, IL, USA, 28–30 June 2000. [Google Scholar]
- Jeong, J.S.; Ramírez-Góomez, Á. Development of a web graphic model with fuzzy-Decision-Making Trial and Evaluation Laboratory/Multi-Criteria-Spatial Decision Support System (F-DEMATEL/MC-SDSS) for sustainable planning and construction of rural housings. J. Clean. Prod. 2018, 199, 584–592. [Google Scholar] [CrossRef]
- Jeong, J.S.; González-Gómez, D.; Cañada-Cañada, F. The study of flipped-classroom for pre-service science teachers. Educ. Sci. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Espinosa Manasilla, A.; Muñoz de la Peña, A.; Cañada Cañada, F.; Bohoyo Gil, D.; Gonzalez Gómez, D. Analytical chemistry computational experiments. An educational kenetic study using Matlab programming. Chem. Educ. 2007, 12, 190–195. [Google Scholar]
- Jeong, J.S.; González-Gómez, D.; Cañada-Cañada, F.; Gallego-Picó, A.; Carlos Bravo, J. Effects of active learning methodologies on the students’ emotions, self-efficacy beliefs and learning outcomes in a science distance learning course. J. Technol. Sci. Educ. 2019, 9, 217–227. [Google Scholar] [CrossRef]
- Jeong, J.S.; González-Gómez, D.; Cañada-Cañada, F. Students’ perceptions and emotions toward learning in a flipped general science classroom. J. Sci. Educ. Technol. 2016, 25, 747–758. [Google Scholar] [CrossRef]
- Sánchez-Martín, J.; Zamora-Polo, F.; Moreno-Losada, J.; Parejo-Ayuso, J.P. Innovative education tools for developing ethical skills in university science lessons. The case of the moral cross dilemma. Ramon Llull J. Appl. Ethics 2017, 8, 225–245. [Google Scholar]
- Larreamendy-Joerns, J.; Leinhardt, G. Going the distance with online education. Rev. Educ. Res. 2006, 76, 567–605. [Google Scholar] [CrossRef]
- Tallent-Runnels, M.K.; Thomas, J.A.; Lan, W.Y.; Cooper, S.; Ahern, T.C.; Shaw, S.M. Teaching courses online: A review of the research. Rev. Educ. Res. 2006, 76, 93–135. [Google Scholar] [CrossRef]
- Stockwell, B.R.; Stockwell, M.S.; Cennamo, M.; Jiang, E. Blended learning improves science education. Cell 2015, 162, 933–936. [Google Scholar] [CrossRef] [PubMed]
- Vygotsky, L. Mind in Society; Harvard University Press: London, UK, 1978. [Google Scholar]
- Harrison, N. Using the interactive whiteboard to scaffold a metalanguage: Teaching higher order thinking skills in preservice teacher education. Austral. J. Educ. Technol. 2013, 29, 54–65. [Google Scholar] [CrossRef]
- González-Gómez, D.; Jeong, J.S.; Cañada-Cañada, F.; Gallego Picó, A. La enseñanza de contenidos científicos a través de un modelo «Flipped»: Propuesta de instrucción para estudiantes del Grado de Educación Primaria. Enseñanzade las Ciencias 2017, 35, 71–87. [Google Scholar]
- Jeong, J.S.; Ramírez-Gómez, Á.; González-Gómez, D. A web-based scaffolding-learning tool for design students’ sustainable spatial planning. Archit. Eng. Des. Manag. 2017, 13, 262–277. [Google Scholar] [CrossRef]
- Oosterhof, A.; Conrad, R.M.; Ely, D.P. Assessing Learners Online; Pearson: New York, NY, USA, 2008. [Google Scholar]
- Zawilinski, L.M.; Richard, K.A.; Henry, L.A. Inverting instruction in literacy methods courses: Making learning more active and personalized. J. Adolesc. Adult Lit. 2016, 59, 695–708. [Google Scholar] [CrossRef]
- Butt, A. Student views on the use of a flipped classroom approach: Evidence from Australia. Bus. Educ. Acredit. 2014, 6, 33–43. [Google Scholar]
- Tucker, B. The Flipped classroom. Online instruction at home frees class for learning. Educ. Next 2012, 12, 82–83. [Google Scholar]
- Munir, M.T.; Baroutian, S.; Young, B.R.; Carter, S. Flipped classroom with cooperative learning as a cornerstone. Educ. Chem. Eng. 2018, 23, 25–33. [Google Scholar] [CrossRef]
- Hill, J.R.; Song, L.; West, R.E. Social learning theory and web-based learning environments: A review of research and discussion of implications. Am. J. Distance Educ. 2009, 23, 88–103. [Google Scholar] [CrossRef]
- Tourón, J.; Santiago, R. Flipped learning model and the development of talent at school. Rev. Educ. 2015, 368, 33–65. [Google Scholar]
- Moraros, J.; Islam, A.; Yu, S.; Banow, R.; Schindelka, B. Flipping for success: Evaluating the effectiveness of a novel teaching approach in a graduate level setting. BMC Med. Educ. 2015, 15, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, H.; Lamina, M. Implementing flipped classroom that used an intelligent tutoring system into learning process. Comput. Educ. 2018, 124, 62–76. [Google Scholar] [CrossRef]
- Bull, G.; Ferster, B.; Kjellstrom, W. Inventing the flipped classroom. Learn. Technol. 2012, 40, 10–11. [Google Scholar]
- Strayer, J.F. How learning in an inverted classroom influences cooperation, innovation and task orientation. Learn. Environ. Res. 2012, 15, 171–193. [Google Scholar] [CrossRef]
- Rutten, N.; van Joolingen, W.R.; van der Veen, J.T. The learning effects of computer simulations in science education. Comput. Educ. 2012, 58, 136–153. [Google Scholar] [CrossRef]
- Massart, D.L.; Vandeginste, B.G.M.; Buydens, L.M.C.; De Jong, S.; Lewi, P.J.; Smeyers-Verbeke, J. Handbook of Chemometrics and Qualimetrics: Part A; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Miller, N.J.; Miller, J.C. Statistics and Chemometrics for Analytical Chemistry; Prentice Hall: London, UK, 2000. [Google Scholar]




| Item | Course | |
|---|---|---|
| Male | 65% | |
| Female | 35% | |
| Age (years) | 21 | |
| Grade Point Average (GPA) | 6.95 | |
| Educational Background | Social Science | 63% |
| Science | 18% | |
| Arts | 5% | |
| Technology | 3% | |
| Others | 11% | |
| Equation | Function |
|---|---|
| Regression line slope in unweighted fit | |
| Regression line standard error in unweighted fit | |
| Standard deviation slope in unweighted fit | |
| Intercept Standard deviation in unweighted fit | |
| Standard deviation prediction in unweighted fit | |
| Regression line slope in weighted fit | |
| Regression standard error in weighted fit | |
| Intercept standard deviation in weighted fit | |
| Intercept standard deviation in weighted fit | |
| Prediction standard deviation of in weighted fit |
| Five-Point Likert Scale | Screens | |||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | ||
| 5 | Very likely | 45% | 33% | 29% | 39% | 34% |
| 4 | Likely | 41% | 42% | 38% | 44% | 43% |
| 3 | Not likely, not unlikely | 10% | 10% | 15% | 9% | 10% |
| 2 | Unlikely | 1% | 7% | 6% | 3% | 6% |
| 1 | Very unlikely | 1% | 5% | 6% | 3% | 4% |
| 0 | Do not know/blank | 2% | 3% | 6% | 2% | 3% |
| Overall evaluation | 4.22 | 3.82 | 3.68 | 4.07 | 3.88 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Gómez, D.; Jeong, J.S. EduSciFIT: A Computer-Based Blended and Scaffolding Toolbox to Support Numerical Concepts for Flipped Science Education. Educ. Sci. 2019, 9, 116. https://doi.org/10.3390/educsci9020116
González-Gómez D, Jeong JS. EduSciFIT: A Computer-Based Blended and Scaffolding Toolbox to Support Numerical Concepts for Flipped Science Education. Education Sciences. 2019; 9(2):116. https://doi.org/10.3390/educsci9020116
Chicago/Turabian StyleGonzález-Gómez, David, and Jin Su Jeong. 2019. "EduSciFIT: A Computer-Based Blended and Scaffolding Toolbox to Support Numerical Concepts for Flipped Science Education" Education Sciences 9, no. 2: 116. https://doi.org/10.3390/educsci9020116
APA StyleGonzález-Gómez, D., & Jeong, J. S. (2019). EduSciFIT: A Computer-Based Blended and Scaffolding Toolbox to Support Numerical Concepts for Flipped Science Education. Education Sciences, 9(2), 116. https://doi.org/10.3390/educsci9020116






