Experimental Equipment to Develop Teaching of the Concept Viscosity

Abstract

Some of the subjects have complex concepts, which are currently taught using deductive methods in the first years of University Degree. However, the experience shows the results obtained from students’ learning goals were quite low. Therefore, the use of inductive method is a crucial factor to improve students’ learning results and re-thinking the way to teach in basic subject of Engineering Bachelor Degree. One example is the subject called Fluid Mechanics, which is present in many Bachelor Degrees. This matter has abstract concepts, which are normally taught by traditional methods. This type of teaching makes difficult to be understood by the student. This research proposes an inductive methodology to work the viscosity concept using an activity. In this test, the student has to carry out some measurements with different fluids using a simple measurement device while they participated actively in the learning.

1. Introduction

If the learning process is analysed inside a University environment, particularly in Engineering Bachelor Degree, there are some problems. One of the main problems is the complexity of numerous concepts in some subjects, which are taught in the first courses such as Mathematics, Physics or Fluid Mechanics [1,2]. Currently, this complexity is bigger in the subjects, which use traditional methods. In these methods, the theoretical concepts are taught by the professor and the student has to assimilate it (e.g., master class, lectures, and exercises). This learning causes the students are neither receptive nor motivated to study. Therefore, they do not reach the learning objectives, which are considered by the teaching guide of the subject. Consequently, the use of the active learning methods in which the students participle actively in the development of the learning is recommendable. These methods are based on experimentation (e.g., playing learning, project-based learning, role activities) and they are a possible solution to improve the students’ learning. Active learning, collaborative learning, cooperative learning and problem-based learning are active methodologies that use traditional activities partially, but the students learn participating in the learning process actively. A deep review and discussion of these methods was considered by [3]. Therefore, they should be applied to facilitate the understanding of the student at different cognitive levels (lower order thinking skills (LOTS) and higher order thinking skills (HOTS)). Viscosity, which is taught in Fluid Mechanics is one of those theoretical concepts.

The object of this research is to show a simple activity in which different experiment measurements are developed by students, improving the understanding of the concept of fluid viscosity. The knowledge is acquired by students through activities methodologies, particularly using experiential learning and combining with mathematical equations. The consideration of experimental and the use of mathematics theory allow students to increase the acquisition of competences [4,5]. Besides, they can propose physical models to explain the different viscous nature of various fluids. Therefore, this practice could be implemented in the subject of the Fluids Mechanics in any Bachelor Degree where the matter is taught. If this activity is developed, the students would be given better opportunities to learn the viscosity concept and to analyse its properties using a simple apparatus, which is described. This apparatus could be reproduced in any lab and it can operate with common materials such as water, ketchup or cornstarch. Besides, the research shows the possibility to evaluate the transversal competence ‘CT-13.-Specific instrumentation’, which is included in the project ‘Plan Estrátegico 2015–2020’. This plan is currently being developed by Universitat Politècnica València (UPV). The UPV plan tries to implement these competences inside of the student’s curriculum since the transversal competences increase the significance in the pupil’s training joined to specific competences. This project tries to evaluate the learning objective using a descriptor replacing traditional methods [2]. This competence develops student’s thinking skills and the way he/she behaves trying to solve or analyse a case study.

The aim of this research is to develop an instrument, which can be used by students to assimilate the viscosity concept, combining the experimental learning and the use of the theoretical equations, which are commonly teaching by traditional methods. The objective is to analyse the fluid nature that is, the measurement of the viscosity value is not goal of this research. To measure it, there are many instruments that were previously enumerated and they obtain values more exact. The methodology was applied in a group of students who were studying Engineering Bachelor Degrees related to the Fluid Mechanics topics. Therefore, re-thinking the way to teach better the concept of viscosity and its influence on the fluid behaviour is the objective of the authors. It was the origin to propose the development of a new viscometer. The use of this device was suggested as an activity to help students visualize the viscosity phenomenon and understand the viscosity variations as a function of the fluid nature as well as temperature.

The manuscript has four different sections. Firstly, the introduction describes the research topic. The second section contains the description of the materials and methods. The third section of this paper shows the experimental results obtained by the students. Finally, the manuscript enumerates the main conclusions and applications of this research.

2. The Viscosity in the Engineering Curricula. Re-Thinking as the Professor Teaches this Crucial Concept in Fluid Mechanics

2.1. The Viscosity. How Is It Taught? Looking for Alternatives to Improve the Student´S Learning Process

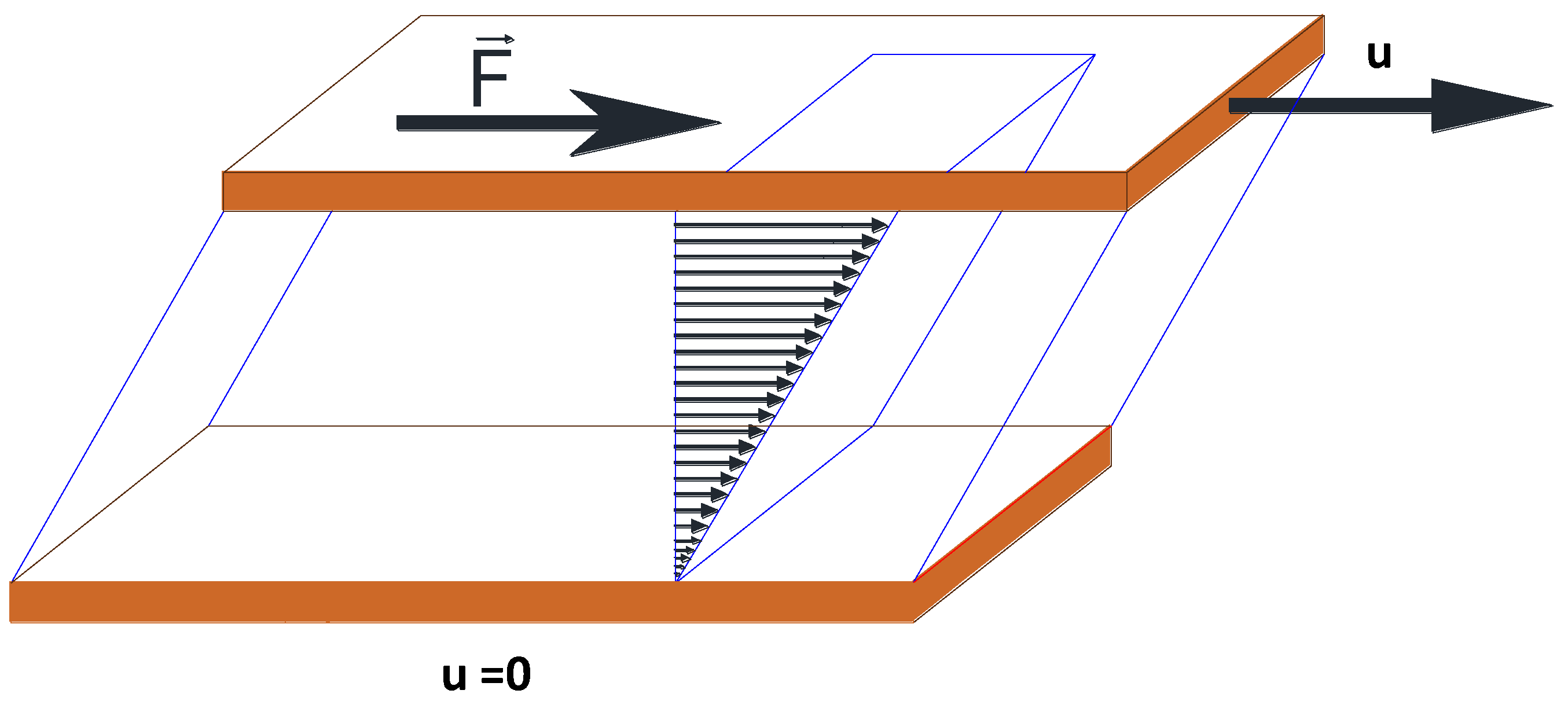
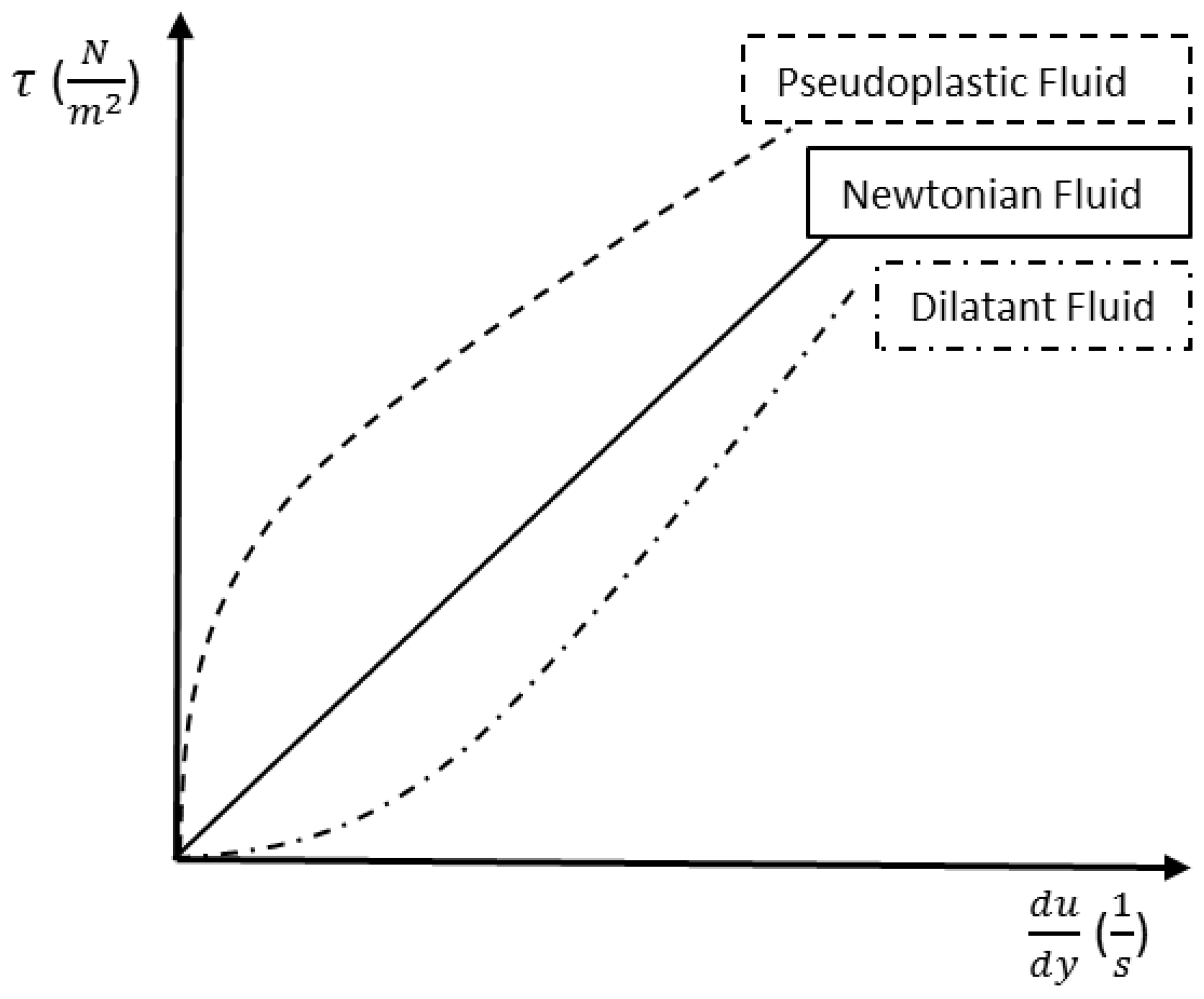
2.1.1. The Concept of the Viscosity. What Is It? What Is Its Equation That Defines the Fluid Behaviour?

The viscosity is a fluid property, which leads to the existence of shear forces within the fluid and to resistance when the fluid is in contact with a solid boundary. According to Newton [3], the viscosity is directly proportional (Equation (1)) between applied shear and velocities gradient in a fluid. The fluid is a substance, which experiences a continual deformation when a shear is applied over it [6]. The viscosity effect can be observed through in laminar Couette flow. In this experiment, a rectangular portion of a fluid (i.e., the fluid is confined between two sheets) is subjected to shear using a surface in which a parallel force is applied upon. This force is aligned with the free surface direction. When this force is applied, a velocity gradient is generated in the fluid (Figure 1). This force generated a uniform gradient in which the fluid velocity varies between zero and u. The value zero is for the particles, which are in contact with the lower sheet. The value u is for the particles in contact with the upper sheet. The velocity in the sheet is equal to fluid particle’s velocity in contact with it due to adhesion condition. This fluid property is defined by the Equation (1), according to Newton’s assumption.

$$\tau =\mu \frac{du}{dy}$$

(1)

where τ is the shear; μ is the viscosity, and du/dy is the wall-normal gradient of the wall-parallel velocity.

2.1.2. The Viscosity. How Is It Taught? Looking for Alternatives to Improve the Student´s Learning Process

The Viscosity and Its Traditional Learning

When the viscosity concept is described by using traditional methods, the lesson is generally divided into three parts: concept, type of fluids, and apparatus to measure the property. These concepts are taught using a master class. This type of teaching is a lesson where someone who is an expert at something advises a group of students, using deductive methods. In this type of teaching, the professor teaches concepts, principles, theorems and/or equations during a limited time (normally two or three hours) while the student has to extract the different conclusions and learn the concepts taught by the professor. Once, the theory is taught, the students carry out experimental practices. Along these sessions, the students can check the theoretical concept that were developed in class using commercial viscometers. This type of learning is called cognitive learning and it is not recommended when the student has not yet assimilated the concepts, principles or equations.

The knowledge of the concepts and properties of the viscosity using traditional methods are focused on the following learning objectives. These learning goals are crucial for students’ learning in the first unit of the subject of Fluid Mechanics.

The main learning objectives were:

• To understand the concept of the viscosity and the equation that defines it;
• To analyze the viscosity variation according to fluid nature;
• To analyze the viscosity variation according to temperature.

The viscosity is a fluid property, which is similar to friction between solids surfaces. The fluid characteristic mainly depends on: the molecular weight of solute; pressure; suspended matter; and temperature [7]. The cohesion level of the fluid varies according to: (i) physical nature (i.e., liquid or gas), (ii) the relationship between viscosity and concentration of solute is usually direct when the temperature is constant, increasing with the concentration. Otherwise, the viscosity is practically invariable when the pressure varies and the fluid property is inversely proportional to temperature changes.

The viscosity establishes an important classification of the fluids according to their nature. If the viscosity keeps its value constant when the velocity gradient varies, the fluid is defined as Newtonian fluid (e.g., water, oils or glycerine). Otherwise, if the viscosity changes when the velocity gradient is modified, the fluid is denominated as non-Newtonian fluid. This can be classified as: (i) pseudoplastic or Bingham (shear-thinning fluids, or even ketchup); or (ii) dilatant fluid (shear-thickening fluids which increase viscosity at higher rates; e.g., the uncooked paste with water and cornstarch). Figure 2 shows shear stress as a function of strain rate (i.e., Newtonian, pseudoplastic, or dilatant flow). The types of non-Newtonian fluids are completed with the plastic (also called Bingham) and pseudoplastic fluid with yield point.

Equation (1) is a particular case of the power law. Independently of nature fluid, the power law defines the viscosity of the fluid, being established by the Equation (2) [8]:

$$\tau =K{(\frac{du}{dy})}^{n-1}$$

(2)

where K is the consistency index, and n is the flow behaviour index. If n is smaller than one, the fluid is pseudoplastic, therefore the viscosity decreases when the velocity gradient is increased (e.g., fruit juices, sauces). If n exponent is higher than one, the fluid is called dilatant. This type of fluid is less common (e.g., uncooked paste with water and cornstarch, blood) and the viscosity increases when the velocity gradient is increased. If n value is one, the fluid is Newtonian. If the rheological properties of the fluid are determined to develop models in different temperature, according to [9,10], the Equation (2) can be written as expression (3):

$${\mu }_{ap}=K{(\dot{\gamma })}^{n-1}{e}^{T/T_0}$$

(3)

where $\dot{\gamma }$ is the shear rate, T₀ is the reference temperature, and T is the temperature fluid.

If the viscosity value is determined, its determination must be done with an appropriate apparatus, which is related to nature fluid. This measurement devices can be classified into three types: capillary, rotational, and mobile.

Capillary type: this type of viscometer is probably the most used to determine the viscosity, which is measured considering the average circulating flow through a tube as well as the applied pressure. The Hagen-Poiseuille’s equation is used to determine the viscosity value [11,12]. These devices are useful to measure great types of fluids. American Society for Testing Materials (ASTM) describe the experimental measure procedure as a function of the considered fluid. The capillary viscometer can be classified in: (i) glass capillary viscometer, which is used to measure Newtonian fluid, (ii) cup viscometer (this type is also called orifice viscometer) and (iii) extrusion viscometer (this is also named piston viscometer). Ostwald viscometer is the basic design of this glass capillary viscometer. Cannon-Fenske, Ubbelohde, FitzSimons, SIL, Atlantic, Zeitfuchs are another similar viscometer [13]. A singular capillary viscometer is the tube of viscometry, which is used to measure the viscosity of suspensions [14]. The cup viscometers are used to measure the fluid properties in the manufacture, process and different applications of dies, paints, and adhesives. Cup viscometers (e.g., Ford, Zahm, Shell, Saybolt, and Furol) are simple and non-expensive rapid methodological devices that are widely used in quality control of Newtonian or near-Newtonian liquids where extreme accuracy is not needed [7]. In this case, the viscosity cannot be determined using the Hagen-Poiseuille equation because the flow analysis is more complex, and the consideration of the emptied time is necessary as parameter to measure the fluency (e.g., Saybolt seconds, Ford seconds). This viscometer type should not be used with non-Newtonian fluid. Finally, the piston viscometer is used to measure the viscosity of fluids very viscous such as molten polymers. This viscometer is made up using a reservoir, which contains the fluid to measure, which is connected to capillary. The fluid crosses the capillary by the force applied due to some sort of piston action.

Rotational type: this type of viscometers is made up by two parts, separated by the fluid to analyse. Depending on the viscometer type, these parts can be: two cylinders (coaxial rotational viscometer), two plates (parallel plates viscometer), and a surface and cone (cone-plate viscometer). In all cases, one of the parts is mobile and the other is fixed. The movement of cylinder, plate or cone generates a shear stress, being determined the viscosity as function of the applied torque to mobile element, rotational speed, radius of the cylinder, plate, or cone; and length of the cylinder or cone. The most famous rotational viscometer is Couette viscometer [15]. The detailed analysis of the equations is shown for coaxial rotational viscometer [16] and for cone-plate and parallel plate viscometer [17].

Mobile type: this type of viscometers operates by the mobility of a mobile part (e.g., sphere, disc, bubble) inside of the fluid that the viscosity is aim to determine. The most famous viscometer of this type is falling-ball viscometer. In this viscometer, the fall time of a sphere is measured to determine the viscosity of the fluid by Stokes equation. The designed viscometer which is described and tested in this research is classified in this type [18].

Looking for Alternatives to Improve the Learning Results by Changing Traditional Methods

When these complex concepts are taught, the inductive learning is more recommended. It is because the student learns the concept, equations or principles through experimental cases [4,5]. The development of experimental tests allows students to assimilate the theory better and reach the learning results at a greater degree. As a final stage, the formulation is deduced for the definition of viscosity. This particular case intends to improve the learning results related to viscosity using an experimental device in which the students firstly check the different behaviour of the fluids as a function of nature, and later, they can assimilate the theoretical expression and concept that command the fluid nature.

The use of the experimentation in different fluids allows students to understand the viscosity concept using easy tools as well as the viscosity variation when the fluid and/or the temperature change.

2.2. Materials and Methods

Previously, to make the proposed viscometer, a group of students proposed the new educational viscometer assisted by the authors of this contribution. The main design constraints of the apparatus were its easy application as well as the obtaining of intuitive results. The obtained values and their analysis will encourage future students to understand the behaviour of the different fluids as a function of their nature. The use of this advice allows students to get an inductive learning, in which the knowledge is provided by experimental activities, reducing the master class hours.

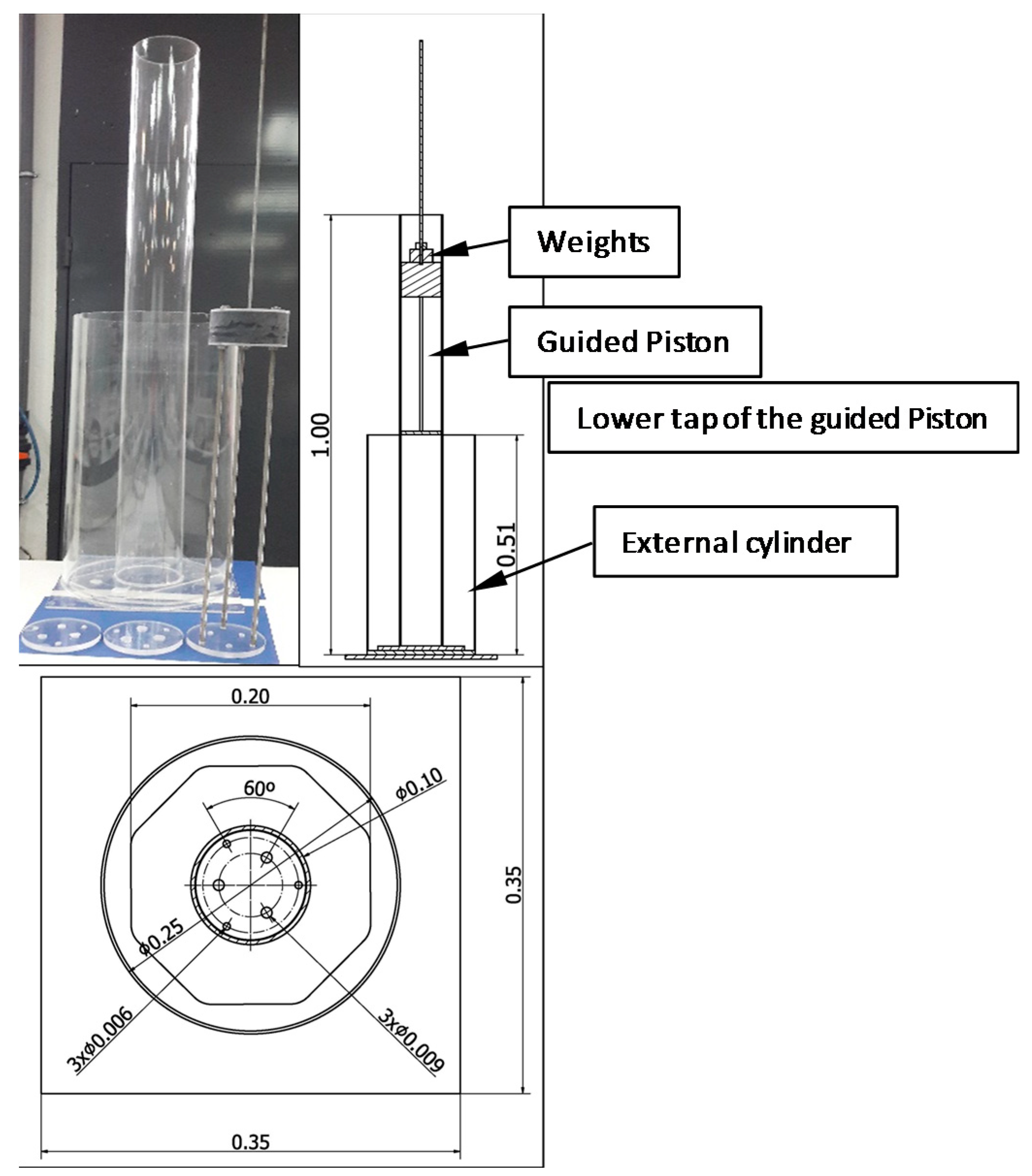
2.2.1. Materials. Apparatus Designed

The viscometer was designed and built by four independent elements (Figure 3): (a) one calibrated cylinder with the inner diameter of 0.092 m and the total height of 1m. The calibrated volume was 6.64 × 10⁻³ m³. The primary function of this element was to contain the tested fluid; (b) guided piston, which was made up of two covers. The diameter was near the inner diameter of the element (a). The lower tap had three holes which had an inner diameter of 9 × 10⁻³ m each one. This cover was connected to the upper tap by three screw bars. The length was 0.5 m. The upper tap whose inner diameter was equal to lower upper guides to lower tap. This is to ensure the parallel and lineal displacement of the lower tap through the cylinder. (c) series of eight calibrated weights to put in the piston and to increase the applied force to the fluid. (d) cylinder with an inner diameter of 0.49 m and a height of 0.50 m. The function of this external cylinder was to maintain the temperature of the inner calibrated cylinder (a). This cylinder will be full of water, which could be at different temperatures using one electrical resistance.

The operating of the viscometer was easy. Firstly, the fluid was introduced into the cylinder (a) until the flow level reached a height of 0.43 m. Once the cylinder contained the fluid, the piston was introduced into the cylinder (a). The initial position of the piston was established just above the open surface of the fluid. When the piston was in the initial position considering the selected weight, the piston was left free and was moved by gravity. With the piston in movement, the fluid crossed the lower tap through of the holes, stopping when the piston reached the bottom of the cylinder. In this final position, all fluid was located above of lower tap of the piston. As the measurement had to be repeated, the operator moved the piston to the initial position.

2.2.2. Work Methodology of the Experimental Practice

The objective of this experimentation was the students differentiated the nature of fluids through their behaviour on the device measurement. It was of paramount importance to propose them a methodological strategy to proceed and they were an active part of their learning process about this physical concept of viscosity. Therefore, the proposed methodology for the experimental practice was described in the following points:

(1)

Fluid selection: In this first step, the student selected the fluid according to the proposed fluids by the professors. If the fluid was a mixture of different matters, the mixture was made in this step (e.g., the uncooked paste with water and cornstarch). Once the fluid was prepared to be used, the fluid was introduced into in the cylinder, activating the heating to keep the temperature constant during the experiment;

(2)

Weights selection: The weights were selected depending on the type of the fluid, since each fluid needs a different value of shear stress (e.g., when the uncooked pate with water and cornstarch is tested needs more weight than water. In the study case, the eight calibrated weights were proposed to be used. The weights (W), which units are kilograms (kg), were 0.130 (W1), 0.129 (W2), 0.130 (W3), 0.259 (W4), 0.536 (W5), 0.534 (W6), 1.074 (W7), 1.043 (W8), and 0.509 (Weight WP). WP corresponded with the piston weight. W1, W2 and W3 are approximately equal to increase the flexibility in the applied force by the piston in the different tests.

The selected weight established the shear stress, which depended on the weight and cylindrical surface of the orifices (A). This stress was defined by the Equation (4):

$$\tau =\frac{WT}{A}$$

(4)

where WT is the total weight of the piston (own piston weight (WP) plus all considered weights) in N; A is the total cylindrical surface of the orifices in m², which was defined by Equation (5):

$$A=N2\pi rh$$

(5)

where N is the number of orifices; r is the radius of the orifice in m, and h is the thickness of the tap in m.

(3)

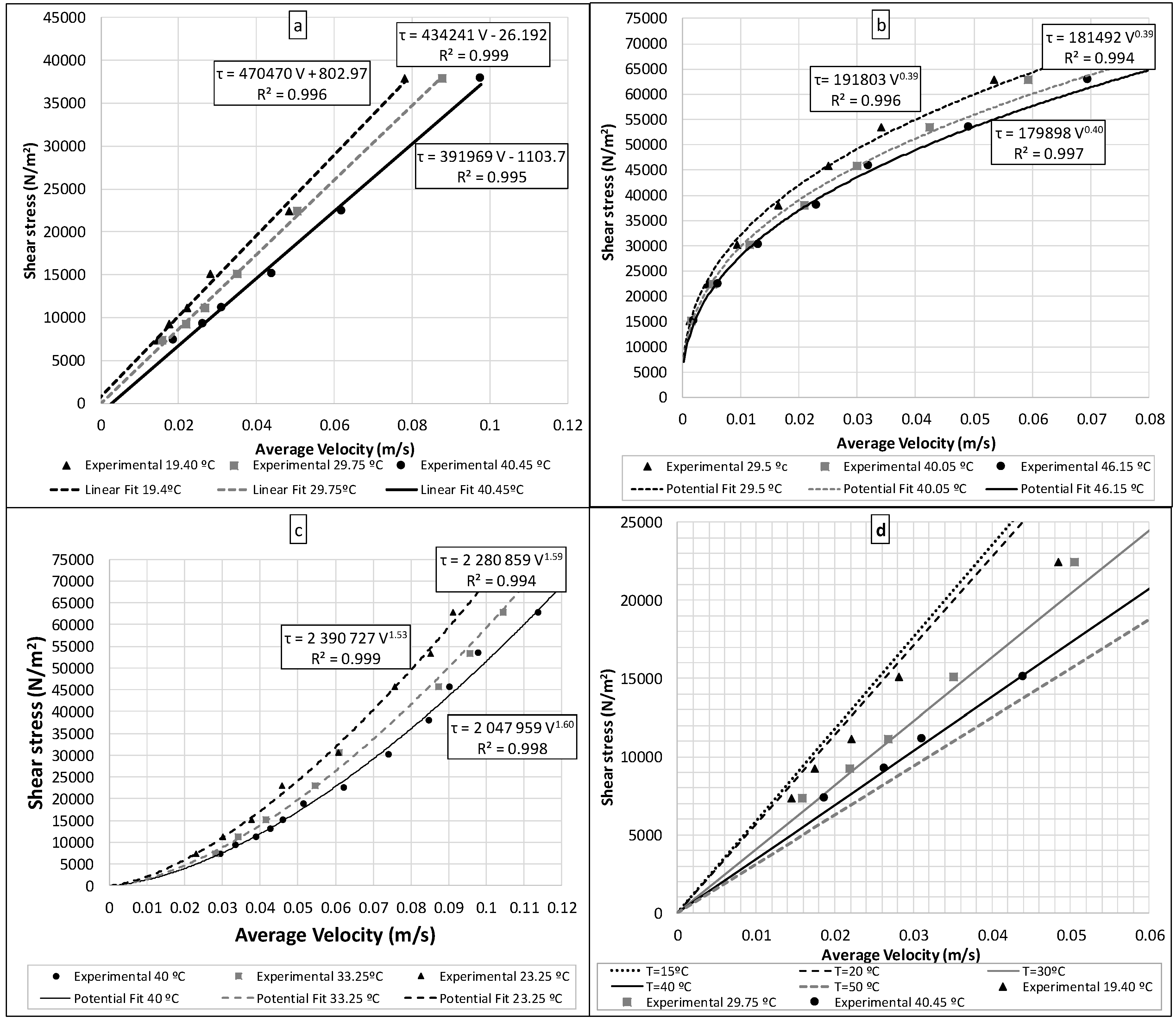
Test development: Each analysed fluid was tested under different temperatures (e.g., 20, 30, and 40 °C) and weights (minimum five weights were selected according to tested fluid). For each stage (one fluid and temperature constant), three repetitions were carried out. The time was measured in each repetition and test. Once the data were known, these were managed to determine the average fall velocity (V) and shear stress (τ). When these data were calculated, the experimental results could be drawn, looking at trend line of the fluid (e.g., linear or expotential) and determining its nature;

(4)

Guarantee of uniform temperature: The temperature was remained constant to obtain reliable results. This condition was reached through of an immersion bath where the viscometer was introduced. The temperature was remained uniform since two resistances were connected and one temperature sounder measured the temperature value, guaranteeing the uniform value along the test;

(5)

Determination of viscosity: the use of the viscometer allowed students to determine the absolute viscosity of the tested fluid using the Newton’s equation. If the determination of these values must be calculated, the viscometer had previously been corrected considering the introduction of a geometrical parameter (GP). GP was a coefficient, which was inherent to viscometer and it was related to the manufacturing process. Considering GP, the absolute viscosity was defined using Equation (6):

$${\mu }_e=GP\frac{\tau }{V}$$

(6)

3. Results

The described results showed an example of the obtained experimental results by the students. These pupils studied the subject Fluids Mechanics, in the second course of Mechanical Engineering Bachelor’s Degree. There were one hundred students between 19 and 25 years old. They studied the subject during the academic year 2016/2017.

The tested fluids by the students were water, ketchup, and uncooked paste with water and cornstarch. Their average densities were: 995.71 kg/m³; 1140.16 kg/m³; and 1466.19 kg/m³, respectively, when the temperature was 30 °C.

The development of the described methodology enabled to characterize the different tested fluids. Furthermore, it helped students to understand the fluid behaviour depending on its nature and velocity. The minimum developed tests were fifty-four in each fluid (minimum six test with three repetitions at each tested temperature). The tested temperatures were 19.40 °C, 29.75 °C, and 40.45 °C for the water. When the ketchup was tested, sixty-three tests were done, being the tested temperature 29.50 °C, 40.50 °C, and 46.15 °C. Finally, one hundred seventeen tests were developed for the water-cornstarch mixture for the three temperatures (23.25 °C, 33.25 °C, and 40.00 °C).

Figure 4a–c show the relation between shear stress and velocity in the different developed tests for each fluid, which were obtained by the students. All figures showed the behaviour of each fluid with a good coefficient fit (R² is above 0.99 in all cases). Figure 4a shows water’s Newtonian condition as well as the viscosity reduction when the temperature increases. This decrease can be observed in the lessening of the slope of the straight line, which crossed near frame’s origin.

Similar results were obtained in the tests with ketchup (Figure 4b). The developed experimental viscometer established the pseudoplastic condition of the ketchup with the obtained result (τ vs. V pairs data). As water case, the reduction of the viscosity can be observed when the temperature was increased. The fit showed the exponent value was smaller than one as it was described in Equation (2). The obtained experimental data showed the pseudoplastic condition. The viscosity reduced when the velocity gradient was increased. Figure 4c shows the results for the water-cornstarch mixture. In this case, the viscometer defined the dilatant condition of the fluid, showing the potential fit an exponent greater than one. Also for dilatant fluid, the viscometer was perfectly able to determine the nature fluid, increasing the viscosity value when the gradient velocity increases. This non-Newtonian’s behaviour (ketchup and corn starch) was perfectly sensed in the developed tests. This visibility in the behaviour helped the user (students, who carried out the practice) to understand the concept of viscosity.

Figure 4a–c contain the effect of temperature variation. These figures show the proportionality between shear force and velocity with the dynamic viscosity. Figure 4d shows the theoretical expressions for different values of temperature (e.g., 15 °C, 20 °C, 30 °C, 40, and 50 °C), considering the temperature effect on the viscosity.

Finally, the students compared the experimentally obtained values in the water tests with the obtained theoretical expressions for the temperature equal to 19.4 °C, 29.75 °C, and 40.45 °C. This comparison was developed, considering the average value of the regression constant (K) (average value of the slope for each tested temperature in the water) as well a temperature of 20 °C. Figure 4d shows an accurate fit between experimental values and theoretical expressions. This fit enabled to estimate the viscosity of the water for different temperatures. The presented fit can be improved when students increase the number of tests for different temperatures. The increase of test numbers will improve the knowledge of constant value (K). The same way, these equations can also be developed for both non-Newtonians fluids (i.e., ketchup and cornstarch). Finally, the corrector value (GP; Equation (6)) of the viscometer was determined for the water. Average GP was calculated from experimental results, considering a temperature equal to 40.45 °C. The average GP was 1.79 × 10⁻⁹ m. Once, this parameter was determined for the temperatures 29.75 and 40.45 °C, the dynamic viscosity can be determined using Equation (6) and experimental data.

The obtained average dynamic viscosity value was 77.9 × 10⁻⁵ kg/ms, which had an average error of 5.65% compared with the real dynamic viscosity for the temperature of 30 °C (79.7 × 10⁻⁵ kg/ms [6]). When the viscosity value was determined for a temperature of 20°C, the value was 93.6 × 10⁻⁵ kg/ms. The average error was 6.53% if the experimental viscosity was compared with real dynamic viscosity value for the temperature of 20 °C (100.5 × 10⁻⁵ kg/ms [6]).

This activity proposed interesting learning results, the usefulness of the viscometer to support active methodologies in class of Fluid Mechanics as a complement to the master class were verified both experimentally and by numerous evidences. The simplicity and promptness in the proposed tests enabled the introduction of this experience to encourage the students to be more active and participative during the learning. This activation was promoted by the experimentation of different fluids through the use of the viscometer, using common fluids such as water, ketchup, or cornstarch mixture. The visualization and the fundamental parallel analysis (following the described methodology) to determine the fluid viscosity as well as the representation of the experimental data allowed the students to internalize the concept and the variables on which the viscosity depends (e.g., temperature, shear stress, velocity).

4. Conclusions and Future Applications

The development of this didactical experience caused two positive results. On the one hand, the students worked the transversal competences of teamwork. They practised thinking, designed specific instrumental, and assembled the viscometer with the help of the professors. This design was created to help the teaching staff to re-think the way to teach the first unit of Fluid Mechanics’ matter, particularly, the viscosity as well as its properties. The design and assembly of the apparatus joined to the development of the tests checked the appropriate behaviour of the viscometer in the characterization of fluid nature. The results showed the apparatus was able to define the type of fluid: Newtonian, or non-Newtonian (pseudoplastic or dilatant), showing to students the main concepts related to the viscosity by experimental evidence.

A work methodology was proposed to develop the experimental practice, which was designed by the professor in charge of the subject. This methodology enables to reproduce the experimental tests in any subject of Fluid Mechanics and courses. The use of this simple viscometer enabled to determine the fluid nature. The experimental results were fitted as a function of fluid’s nature, presenting all regression coefficient values upper than 0.99 (Figure 4a–c). In all cases, the viscometer was sensible to the variation of the temperature. Besides, the experimental dynamic viscosity was estimated for different temperatures of the water. Low error values were obtained when the results are compared with published values in the bibliography.

Future researches will be focused on checking if the use of this apparatus can improve the learning results in the students of Bachelor Degree. Normally, these students have difficulty to understand abstract concepts. These concepts can be understand better if the students develop empirical activities. Currently, the use of this viscometer has been using in the subject ‘Fluid Mechanics’ that is taught in the second course of Mechanical Engineering Bachelor Degree in the Universitat Politècnica of Valencia. The observed results are encouraging and it is living up the development of the viscosity concept. The future work line is to develop simple apparatus that can be used by the students, improving the learning results and introducing the transversal competences in the students’ curricula. Although this research is to show an experimental equipment to develop teaching of the concept viscosity, a first survey were carried out to identify that method the participants would prefer to be taught through. The results showed that the inductive way of teaching was prioritized, since complex concepts were learnt in a natural way. This practice motivated students to continue their learning, synthesizing the contents of the subject, thus reducing the abandonment rate. The innovation improvements will be published in future research related to the improvement of the learning goal.