Productive Disruptions: Rethinking the Role of Off-Task Interactions in Collaborative Mathematics Learning

Abstract

This paper confronts the myth that all off-task interactions in mathematics classrooms is detrimental to learning. To do so, this paper first explores links between participation, learning, and identity in mathematics education research that points to the importance of positional resources. Positional resources are related to identity processes and carry central functions that regulate learning and doing mathematics together. The paper then frames off-task behavior as an important positional resource in collaborative mathematics learning environments. With these ideas in mind, the paper then closes with new questions for research.

1. Introduction

Myths are stories we share over time and in community that serve to illuminate worldviews. Several myths exist about what it means to do and learn mathematics, many of which constrain possibilities for teaching and learning [1]. This paper explores a myth that has dominated assumptions about learning mathematics with others; that off-task behavior in classrooms is detrimental to learning. As Wagner and Herbel-Eisenmann state,

“changing the stories (or myths) told about mathematics is necessary for changing the way mathematics is done and the way it is taught. We emphasize the need for change to combat the sense of repression often associated with mathematics.”

[2], (p. 2).

The vision of learning and doing mathematics with others includes notions of strict focus and attention to the task at hand. Part of what fuels this myth, as it plays out in mathematics in particular, is that learning and doing mathematics with others can evoke an Enlightenment-era vision of disembodied rational minds, engaged in the search for universal truth. This vision centers reason as the primary source of authority, where inductive and deductive logics enable new insights and give rise to a long-lasting and still held faith in the human capacity to attain objective knowledge that transcends even humanity. The idea that bringing in disruptions or distractions to the table could be productive simply does not ring true.

This paper explores the idea that off-task participation has an important role to play in collaborative mathematics classrooms. To do so, I first explore extant research in mathematics education, grounded in sociocultural/situative frameworks (i.e., [3]) to argue that the emphasis on mathematics forms of talk has helped obscure inquiry into other forms of participation and their functions for productive collaborative mathematics activity. I then bring in a smaller set of new work that draws on positioning theory (and similar approaches) to expand our understanding of the relations between participation, identity, and learning posited by situative theories of learning. From a positioning perspective, described further below, interactions serve as identity resources that can be leveraged to navigate access to learning opportunities and other important group dynamics. This expanded view of learning and doing mathematics together is then applied to the case of collaborative problem solving, and, in particular, the kinds of on-task and off-task talk students engage in while doing mathematics together. I recast the oft-maligned role of off-task interactions as central to and supportive of learning mathematics together. I close with the implications of confronting this myth for new research.

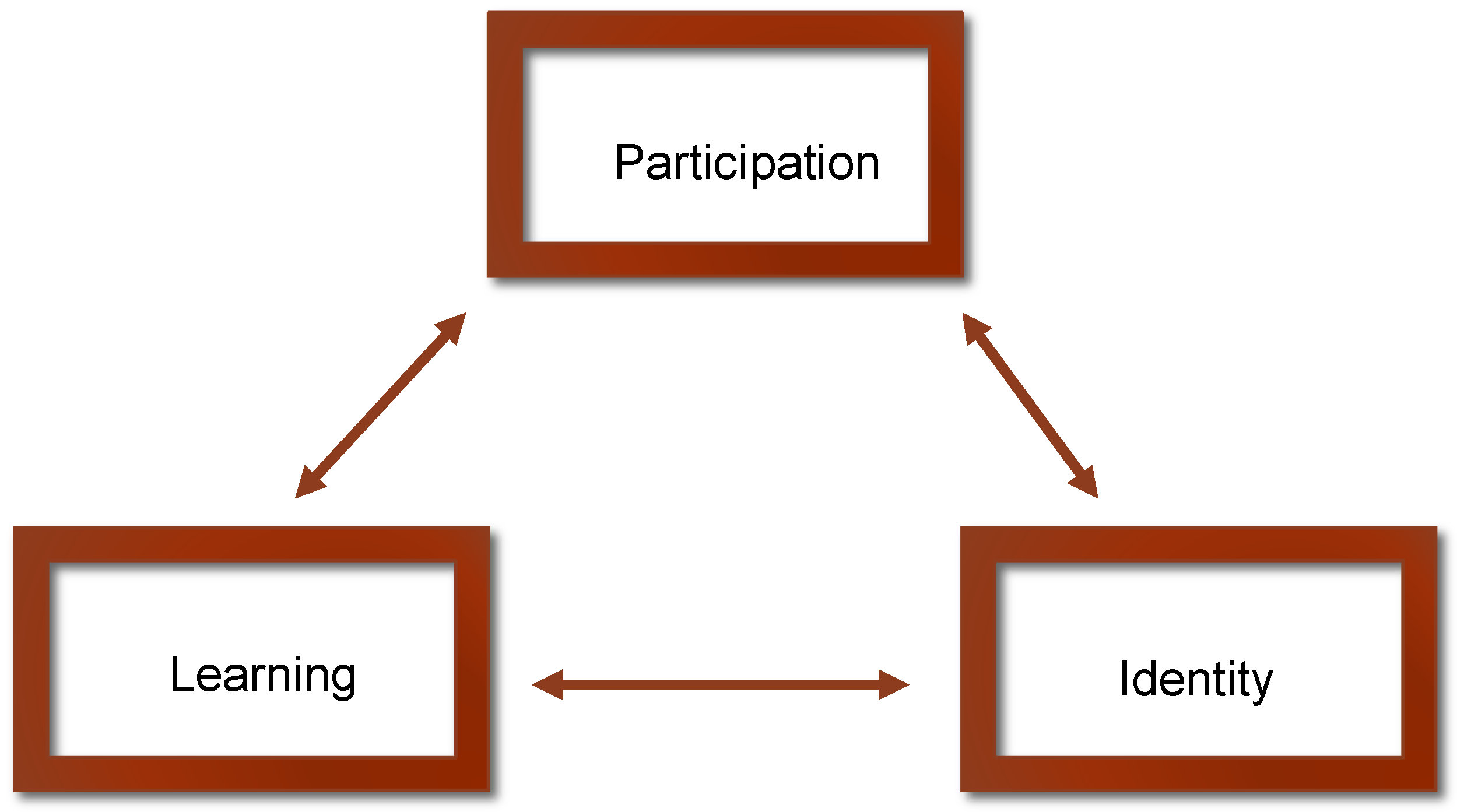
2. Participation, Identity, and Learning in Collaborative Mathematics

Much of mathematics education research draws on situative theories of learning, which assert that participation, learning, and identity are tightly interconnected in mathematical activity (see Figure 1). While identity-related processes are conceptualized as fundamental to both participation and learning, it has been relatively de-emphasized in extant research.

2.1. Links between Participation and Learning

Much of math education research focuses on the link between participation and learning (see Figure 2), whether participation in mathematics with others or individually with a particular task. Because this body of work is interested in participation related to mathematics in particular, off-task participation is often ignored. Rather, the focus tends to specifically be on mathematics forms of language and participation, and the ways those forms are connected to conceptual development [4,5,6,7]. Even sociocultural and situative perspectives, which center the social origins of learning, nevertheless privilege forms of participation explicitly related to mathematical reasoning, such as explaining ideas, asking for or offering help, or making conjectures [8,9,10,11]. Overall, the vast majority of mathematics education research has focused exclusively on the links between participation and learning, especially particular forms of participation, like verbalizing one’s thinking, and particular learning opportunities, like reflecting on a mathematical idea. Because this work has often looked for what is specifically mathematical about student interactions and classroom participation, the productive functions of off-task participation have not been explored.

2.2. Links to Identity

The potential role of off-task participation becomes a bit clearer when additionally considering the links to identity (see Figure 1). From a situative perspective, identity, like learning, is framed as constructed through social interaction within particular activities. Within mathematics education research, connections to identity are most typically elaborated through the use of positioning theory ([12]; cf. 1) and similar approaches that emphasize the interactional, negotiated, and emergent nature of becoming (e.g., [13,14]). In this paper, I focus on positioning theory in particular in order to illuminate core ideas. Through positioning theory, we see that students do not simply “bring themselves” to learning in an abstract sense; rather, students construct themselves and others discursively through mathematics activity [15]. Positioning is ‘identity in interaction’. As the studies below make clear, identity-related processes connect to learning and doing mathematics by orienting individuals toward one another and the task in particular ways. Further, students negotiate these processes by drawing on positional resources, which are made available discursively through interaction and, in particular, through the storylines brought to bear on activity that make particular identities possible. In the sections below, I detail these resources and how they act upon collaborative dynamics in consequential ways. I then argue that, because off-task interactions disrupt on-task dynamics by making new storylines and new identities possible, such interactions can play an important role in shifting dynamics to support not only more inclusive, but also more generative mathematics collaborative learning.

2.2.1. Identity-in-Interaction: A Focus on Positioning Theory

Positioning theory rests on the constructs of positioning, positions or positional identities, and storylines [12]. The most basic unit is the act of positioning, an interactional moment where claims about a person are asserted or revealed. For example, the statement, “Ask Joey. He’s in charge,” positions Joey with authority, as someone with the right to manage and lead others. These acts can be accepted, as when others agree with the statement about Joey or otherwise act as if he were in charge, or they can be rejected or altered. For instance, Joey could assert, “I’m not in charge! Don’t ask me!” or others could state, “Joey, in charge? Yeah, that’ll be the day.” Bids for particular positions, and their rejection or uptake from others, create social realities about individuals in activity that are consequential for participation, authority, and influence [16]. Positional identities develop out of acts of positioning over time as likelihoods that particular individuals will be positioned in particular ways, creating seemingly stable identities. These positional identities carry rights and obligations and, in this sense, represent relations of power between and among individuals. For example, the positional identity of teacher, constructed every day in the classroom through social interaction with students and others, positions the teacher with the right to issue directives to students who are, in turn, positioned with the obligation to obey.

These rights and obligations arise from storylines, which figure particular identities by making acts by individuals interpretable. Wagner & Herbel-Eisenmann note that positioning theory’s conceptualization of storylines resembles the construct of scripts from cognitive psychology [2]. Storylines are also similar to Goffman’s frames and Gumperz’s contextualization cues [17,18]. Broadly, they are the characters and plots of everyday situations, socially constructed across time, that serve as resources for making sense of and acting in the world. Storylines have been relatively understudied in mathematics education research that draws on positioning theory, as the constructs of positioning and positional identities have garnered greater interest cf., [2]. Positioning theory asserts that multiple storylines can be at play during social activity. These storylines can exist at multiple scales [1], including local storylines constructed by teacher and students at the classroom level, as well as broader storylines about gender, race, romance, and friendship [19].

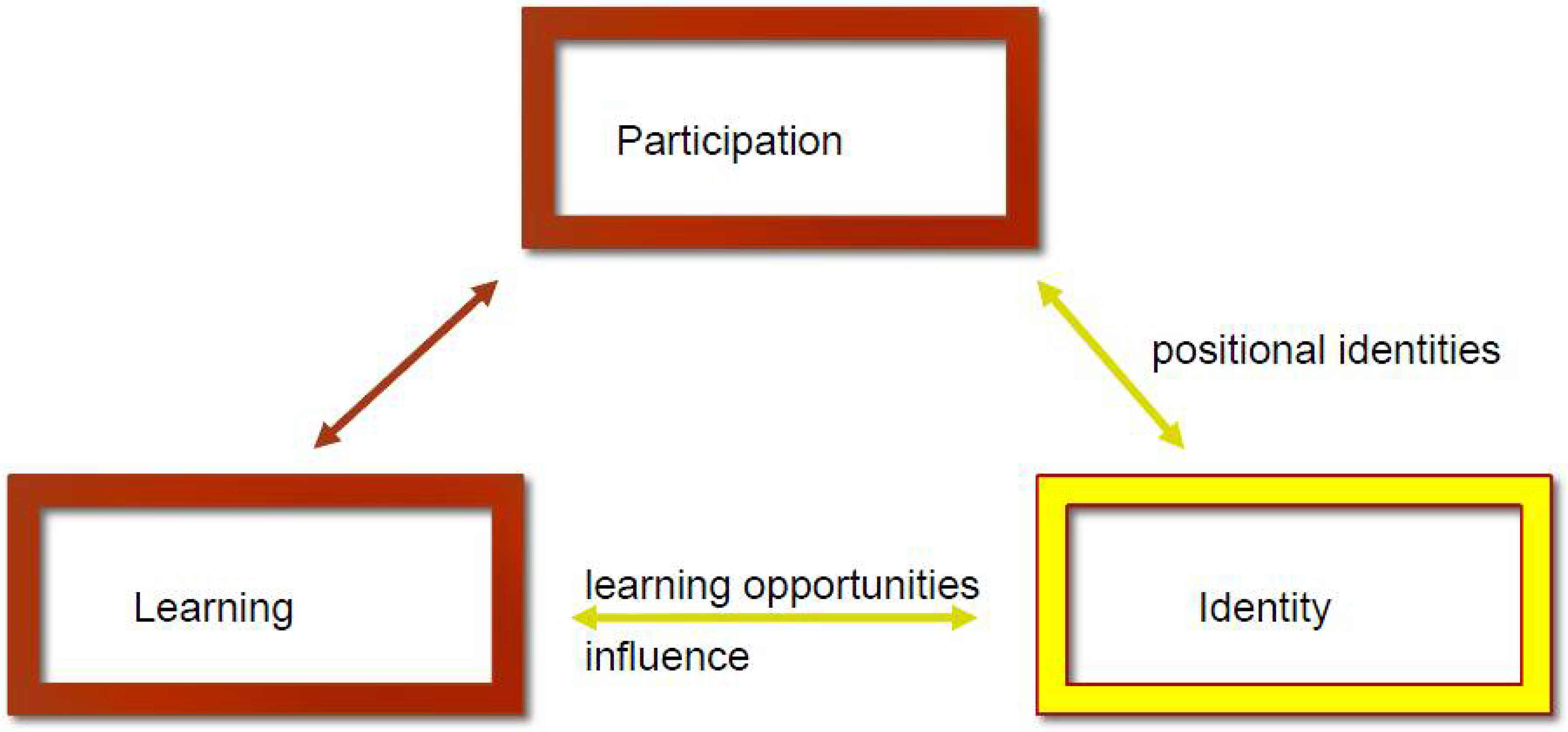
2.2.2. Links between Participation and Identity

Within mathematics education research, this interactional and negotiated approach to examining identity has been applied to understand several aspects of learning and doing mathematics together in classrooms [13,14,20,21,22,23,24,25,26] (See Figure 3). Studies have traced how particular student identities become possible and enacted through participation in classroom activities. Across this small, but growing body of work, researchers have found that students regularly bid for, accept, resist, and reject positional identities as they engage in mathematics together. For example, Anderson examined small group interactions at multiple levels to trace how students became positioned as kinds, influencing how different ways of participating were recognized and valued across interactions [20]. Similarly, Heyd-Metzuyanim examined the discursive construction of an identity of failure in mathematics as it occurred through positional interactions [22]. Across these studies, identities of competence or incompetence are most central. That is, what it means to be a mathematics kind of person is—to be positioned by oneself and others with identities of competence; when classrooms offer multiple kinds of identities of competence through new storylines about what it means to do mathematics (often framed as reform-oriented or Standards-based), more students are able to take them on [27,28,29].

Participation constructs positionality, which in turn, enables or constraints particular forms of participation. Langer-Osuna examined the discursive patterns of two group leaders, Brianna and Kofi, within the same small group over the course of the academic year and found that students’ ability to enact authority affected their patterns of engagement in mathematics activities and their identities as mathematics students [25]. When Brianna’s bids for social authority, in particular the right to issue directives to peers, were routinely rejected, she became increasingly marginalized from the collaborative dynamics. Likewise, when Kofi’s very similar bids for social authority were routinely taken up, he became an increasingly central participant in the group. Further, during interviews, Brianna described a negative shift in identification with mathematics, claiming that she had learned not to “want it [success in mathematics] so much” and to, instead, “pass the stick” of achievement. Kofi, whose bids for authority were taken up, described greater identification with mathematics, claiming to desire more experiences and to enjoy engaging in mathematics problem solving. Both the analysis of students’ interactions and interviews with students show that the two students’ very similar bids for authority were taken up by the same peers differently in ways that were organized by gender. The enactment of social authority by the female student was positioned as “bossy” and taken up as inappropriate by peers, who rejected her bids. However, the similar enactment of social authority to the same peers by the male student was taken up as appropriate and accepted. In interviews, both students offered gendered interpretations of their experiences, with Brianna concluding that “boys don’t listen to girls”.

These findings not only highlight the bi-directional relationship between participation and identity, but the ways in which storylines, in this case about gender and displays of power, organize how individual acts are interpreted. These findings also highlight that these storylines are not always about mathematics, per se, but can invoke multiple social hierarchies found in broader society and recreated in classroom dynamics. This point is echoed by Shah and Leonardo, who found that students drew on racial storylines about mathematical ability, such as “Asians are good at math”, to make sense of their own and their peers’ mathematical experiences [30].

2.2.3. Links between Identity and Learning

Other work has focused on how acts of positioning enable or constrain particular student learning opportunities [31,32,33,34,35,36] (See Figure 3). For example, Wood showed that particular acts of positioning opened or closed mathematics learning opportunities [36]. In particular, when a student was positioned with relatively greater authority (such as being positioned as a “mathematical explainer”), opportunities to engage in important mathematics reasoning was made available. When a student was positioned with relatively demoted authority (such as being positioned as a “menial worker”), the student was unable to access these learning opportunities. These findings tie in with the research above on the links between participation and identity because particular kinds of positional identities—which develop as discursive likelihoods out of acts of positioning over time—can chronically enable or constrain learning opportunities for students in the same classroom, creating a feedback loop leading quickly to failure and marginalization, or even undue influence.

The studies above highlight how positioning theory helps challenge the myth that learning and doing mathematics is agnostic to identity-related processes by clarifying how positional identities are connected to individual learning opportunities. Yet, perhaps more profoundly, positioning theory also stands to challenge the myth that the very construction of mathematical knowledge itself is agnostic to identity-related process. This challenge goes straight to the heart of what it means to do mathematics; that is, the ways in which mathematical ideas are taken up as true.

The idea that the construction of mathematics knowledge is social in origin is not new [37,38]. Across this work is a focus on the spread of ideas as a function of collective mathematical reasoning and, in particular, the construction of shared mathematical meaning. For example, Forman draws on social constructivist theory to argue that the social construction of mathematics knowledge arises from the communicative establishment of mutual understanding or intersubjectivity [37]. These understandings are grounded in mathematical reasoning and argumentation.

Positioning theory brings a lens of relational power to bear on the uptake and spread of mathematics ideas [13,16,21,39]. This becomes clearer through a focus on the social construction of influence during collaborative work. Engle, Langer-Osuna, & McKinney de Royston found that the social construction of influence during student-led discussions emerged out of the negotiation of five kinds of interactions, including interactions around influence itself [16]. The other four kinds of interactions that explain whose ideas become influential are as follows: The first is intellectual authority, defined as interactions during which a student acts, is treated, or evaluated as a credible source of information. Second is intellectual merit, defined as interactions during which a student’s idea is positioned as high quality. This may occur even if, objectively, in a mathematical sense, the idea is incorrect or misleading or proves to not be fruitful. Third is access to the conversational floor, defined as the degree to which a student can initiate turns as desired and complete them without interruption. And lastly is spatial privilege, defined as the degree to which a student is visually attended to and physically oriented to by others when speaking. Engle, Langer-Osuna, McKinney de Royston further posited specific links between these kinds of interactions [16]. For example, negotiations around the merit of an idea and students’ positions of intellectual authority directly linked to influence, regardless of how well argued or even correct the idea was. Students’ position of authority was directly linked to all other kinds of interactions. That is, promotions or demotions in authority predicted access to the interactional space and conversational floor, the evaluation of the merit of the idea, and influence itself. The influence framework resonates with findings from Bishop, who found that positional identities affect who talks and initiates sequences (similar to interactions around the conversational floor) and whose ideas are taken up and publicly recognized (similar to influence) [13]. DeJarnette and González likewise found that students’ positioning moves related to the ways they engaged in the task, including the construction of its final product [21]. Langer-Osuna applied the Influence Framework to a case of two students, Ana and Jerome, who collaboratively solved an open-ended mathematics problem [39]. The case is one where the interactional dynamics around authority affected the uptake of, in this case, largely Ana’s ideas. The normative quality of Ana’s ideas could not explain how she garnered intellectual authority, nor why her ideas were taken up. Rather, the case shows how social forms of authority, specifically the right to issue directives to Jerome, ultimately led to Ana becoming positioned with intellectual authority and influencing the construction of the solution path. In this case, mathematical ideas were taken up as true as a function of social dominance, not shared reasoning.

Taken together, we see that identity-related processes, operationalized as acts of positioning during mathematical activity, are fundamental to the construction and distribution of both individual learning opportunities and student identities, as well as the nature of mathematical discussions and the very construction of mathematics problem solutions. These studies illuminate the discursive mechanisms that link identity to processes of participation and learning and suggest that both storylines, and the positional identities made possible by them, can and do serve as resources to navigate collaborative learning dynamics. In the next section, I apply these logics to the case of off-task participation, arguing that, rather than a problematic form of distraction, such interactions can become productive forms of disruption to existing dynamics, creating new participation pathways for learners.

3. Off-Task Interactions as Positional Resources in Collaborative Mathematics

While on-task participation draws primarily from storylines about schooling and school mathematics (e.g., what a “good student” looks and sounds like, and so on), off-task participation can draw on a broader range of storylines, including those of friendship and popular culture, potentially making a greater range of positional resources available to students to leverage as they interact with one another and the task [19,26,40]. In this sense, off-task interactions are not simply the lack of directly engaging in the mathematical task, but rather the bringing together of multiple storylines, identities, and relations onto the collaborative activity and, as such, may be drawn into the shared regulation of activity.

There’s some precedent to consider this possibility. Sullivan and Wilson found that students used playful talk to negotiate status during collaboration [40]. They draw on Vygotsky who “argued that play arises in young children as a response to desires that cannot be immediately gratified [41]. To cope, children invent imaginary situations…in an effort to fulfill their unrealizable wishes. This behavior is what Vygotsky considered the foundation of play,” [40] (pp. 7–8). In playful talk, students use imaginary situations unavailable in the official collaborative learning activity to position themselves or others as either more or less capable. For example, a student with low status engaged in playful talk to position herself with competence, while a high-status student engaged in playful talk to position others as less competent and, in doing so, maintained his status. These acts of positioning functioned to influence opportunities to learn within the group. They also found that playful talk served to establish and maintain group cohesion and thus achieved higher levels of coordination.

Esmonde and Langer-Osuna found that off-task interactions—which drew on discourses of romance and friendship, which were racialized and gendered—regulated group members’ participation in small group mathematics discussions [19]. Students’ off-task conversations functioned to resist domination by a peer with high academic status, enabling shared intellectual contributions to the mathematics discussion. Off-task conversations supported shared participation in large part because two students who were relatively marginalized from engagement in the mathematics utilized off-task conversations to position themselves with social power, which functioned to resist the third student who had been dominating the mathematical work. That is, off-task interactions offered students the ability to position themselves with relatively greater power than was available through on-task interactions. While on-task interactions drew from school math discourses, off-task interactions primarily drew from discourses of youth popular culture, friendship, and romance. Students utilized these discourses as positional resources, enabling new pathways into the collaboration.

In the example provided above, students drew on storylines beyond the scope of mathematics to manage participation in ways that math talk alone could not do. This demonstrates that students may be able to find relatively more powerful positions, such as positions of competence through storylines not originating with participating in school tasks [36,40]. Langer-Osuna followed a focal student, Terrance, over an academic year as he constructed positional identities of himself as a learner, starting with a resistant identity and shifting to a productive and engaged identity [26]. To do so, Terrance drew on a variety of school-based and out-of-school-based storylines as he engaged with peers in collaborative learning activities. The discourses that organized much of the off-task interactions, such as youth popular culture or the armed forces, offered Terrance positional identities that ultimately supported engagement in mathematical work. Off-task interactions can thus enable new positions by drawing on alternate storylines.

Langer-Osuna, Gargroetzi, Chavez and Munson recently examined the functions of off-task interactions during collaborative mathematics problem solving [42]. The research team analyzed 13 videos of 20 to 30 min collaborative mathematics problem-solving sessions among fourth graders during a classroom unit on place value [43]. Fifty-six instances of off-task participation, such as conversations about games or movies, making play swords out of connecting cubes, or singing a popular song together, were identified and coded for their functions on the collaborative dynamics. The functions of off-task interactions were determined by the shift between the nature of the interactions prior to and subsequent to off-task interactions. For example, at a table of four students working in pairs, a focal student made several bids to engage the second partnership to work as a group of four. His bids were ignored and so he began telling a story about riding his horse in the online game Minecraft and burning down a village. As he did so, the gaze of other students at the table shifted up and toward the focal student, giving him their attention. Upon gaining their attention, he shifted back to the collaborative work, suggesting that they, “put all your tens in here!” His peers took up his suggestion and began to work together, discussing their contributions to the task thus far. This instance of off-task interaction was coded as functioning to recruit others into the collaboration. After several unsuccessful bids to grow a collaboration that would include both his immediate partner and another table mate, the student’s Minecraft story functioned to gain his peers’ attention, in particular their gaze. Once he had their gaze, he again made a bid for collaboration, suggesting they organize their 10 sticks in a basket that he held up. His peers took up his suggestion, thereby enabling him to recruit both girls into a collaboration with him and with each other.

Results of this study found that the majority of off-task instances—59%—function to support the collaborative process [42]. The functions identified that served to grow or sustain the collaboration were: warming up to collaboration, gaining attention, recruiting others into the collaboration, gaining access to the collaboration for self, resisting concentrated authority in the group, and extending the task. Importantly, a fifth of instances served to bring more peers into the collaboration, whether recruiting others or gaining access for one self. These instances typically began after unsuccessful bids to work with others through the task itself. The off-task interactions created new opportunities for the students to engage with one another by disrupting the on-task dynamics and enabling students to either gain traction into and join existing collaborations or recruit peers into interaction through off-task activity, which subsequently shifted back on task, while maintaining the larger collaborative group. These instances typically occurred after a series of successful bids to either join or initiate collaborative work, suggesting that interactional pathways into the collaboration through on-task activity were restricted or more cumbersome. Students often utilized these discourses as positional resources, enabling relatively powerful positions that were otherwise unavailable through on-task interactions.

Why did off-task interactions succeed where on-task bids failed? To examine this question, Langer-Osuna, et al. additionally examined the positional identities made available through the off-task interactions [42]. Specifically, they analyzed a subset of the instances that served to shift the group dynamics by growing or destabilizing the collaboration, as well as the “flops” that bid for shifts but were unsuccessful. These instances were further coded for the storylines invoked, the positional identity made available, and whether the bid was successful for shifting the dynamics. Results showed that when students drew on positional identities that did not afford them relatively greater power, their bids were as likely to be successful as unsuccessful. These positional identities included characters such as “victim” in the storyline of theft and “noodle server” in the storyline of patrons at a restaurant. However, when students positioned themselves powerfully within the storylines-imagined social hierarchies, their bids were nearly always successful. These positional identities included “warrior” in the storyline of conquering villages, and “maker” in the storyline of genius inventing. These findings suggest the possibility that off-task interactions functioned to support collaborative learning because students were better able to negotiate positions of power that drew from storylines beyond school mathematics and enabled access to their peers, resources, and the collaboration itself.

4. Discussion

Herbel-Eisenmann, et al. call on mathematics education researchers to “intervene to shift these storylines and positionings and to have greater impact on policy, practice, and public perception in the future” [1], (p. 103). In particular, they argue that researchers “need to identify and better understand historical, current, and pervasive storylines about mathematics education research (p. 110).” To this end, this paper offer a counter-story that can be theoretically and empirically fruitful for mathematics educators, that is, that identity is inherent to learning and doing mathematics together in classrooms and, as such, positional resources, including those made available during off-task interactions, merit serious attention by the field.

Though mathematics education research literature has historically and primarily focused on classroom talk that is explicitly mathematical in form, new work points to mathematics problem solving as social negotiations, including positional negotiations that serve to make claims about individuals in relation to mathematics activity. These negotiations partly determine who participates and in what ways, as well as what mathematical ideas are taken as true by the group. As such, interactions during collaborative mathematics problem solving serve not only as cognitive resources for shared thinking, but also as identity resources that can be leveraged to navigate access to learning opportunities and other important group dynamics. These functions of talk can draw on discourses beyond mathematics, per se. Indeed, off-task interactions can have the potential to offer a broader range of identity resources than made available strictly through on-task interactions.

With these ideas in mind, several new questions arise. What kinds of storylines are potentially productive, and how might teachers prime or otherwise make available such storylines for students? Rather than whether off-task participation is good or bad for learning, we might ask, when and in what ways is off-task participation beneficial or detrimental to learning and doing mathematics together? Further, how might classrooms be designed in ways that resist problematic and powerful storylines, such as racialized and gendered storylines about mathematics ability or enacting authority? Just as research in mathematics education has become increasingly interested in and concerned about the role of identity in mathematics teaching and learning, so, too, must teachers and teacher educators. How might we support teachers in noticing and effectively responding to student collaborative dynamics? When should teachers intervene and when should they step back and allow off-task talk to co-occur with on-task activity?