Against the Odds: Insights from a Statistician with Dyscalculia
Abstract
1. Introduction
“We don’t say people with dyslexia will never learn to read, so we shouldn’t say that people with dyscalculia can never learn to do math.”(Dylan; second author)
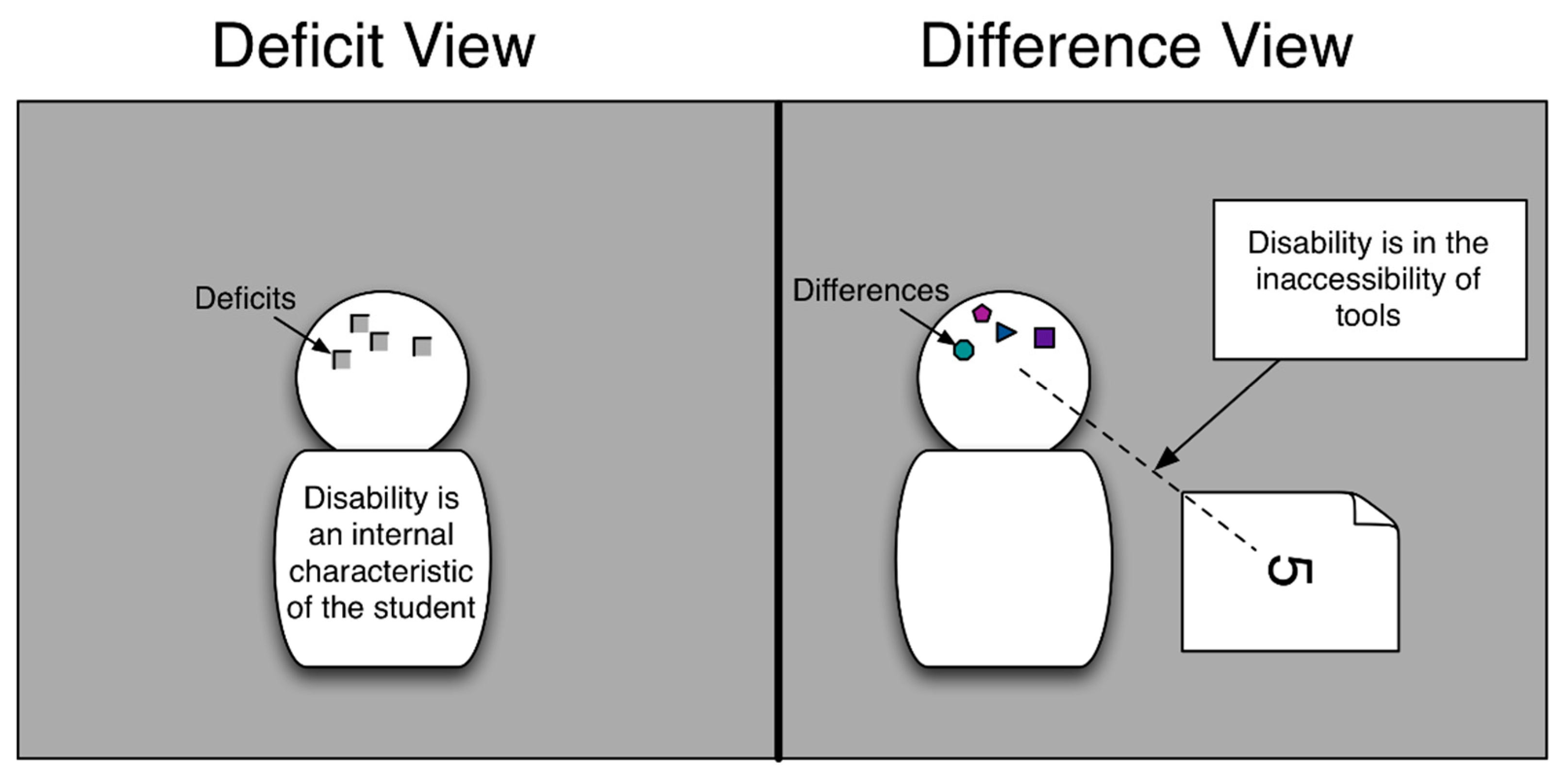
- Dyscalculia results from inherent cognitive deficits within the individual;
- Students with dyscalculia cannot learn or do higher-level mathematics.
- Students must master the “basics” to succeed in higher-level mathematics;
- Speed and efficiency are important to succeed in mathematics.
1.1. Understanding Dyscalculia as Difference
1.2. Emancipatory Research Approach
1.3. Role of the Researchers
2. Methods
3. Results
3.1. Overview of Dylan’s Issues of Access, Tools, and Compensatory Strategies
- Graph paper (4 squares per inch) to help her align and space her notation;
- Mechanical pencils to ensure a consistently sized lead thickness;
- A retractable eraser to enable her to erase precisely; and
- Colored pens to color code her notes and help her track various symbols and elements.
- Rewriting in words—she translated mathematical symbols into words (e.g., 3 as “three”);
- Creating a dictionary—she created an internally consistent and differentiated way of writing each mathematical symbol so it had only one meaning and was not perceptually confused with other symbols;
- Rewriting for consistency—she rewrote problems in a consistent form to make use of space to maintain clarity about her solution process;
- Consistent solution process—she developed and used consistent solution processes to solve particular kinds of problems; and
- Grounding the abstract—she grounded her understanding of values and mathematics concepts in real-world examples.
3.1.1. Rewriting in Words
Dylan: “I am stronger with language, so this is a thing that I did when I was a kid. And then I actually started doing it—it came up more in my higher level math classes. If I have like five plus three equals eight [writes 5 + 3 = 8; see Figure 2], I actually do really well with language. [writes out “five plus three equals eight”]”.
Dylan: “This is calculus, but you can see it illustrated with this notation [writes f(x) = x + 4x3; see Figure 2] this notation, the way people say this is “f of x” which is also terrible. It’s the function of x equals this [as writing “function of x = x + 4x3; see Figure 2]. This little notation here [points to f(x)] would throw me off really badly in my classes, because f times x? No, it’s a notation that is basically applying this function to the variable x. I would sometimes write out something like this [writes bracket underneath “function of x”] right underneath whatever it was and again, this is really verbose, [but] it might be helpful.”
3.1.2. Creating a Dictionary
Dylan: “There is the lower-case x and the upper-case x, and God forbid you rotate it and it looks like a plus. Coming up with some distinct way so that I know what my variable means and then the language that I associate with the way that looks right.”
Dylan: “So I would be taking two math courses in the same semester and one would use an “r” for one meaning and one would use an “r” for another meaning. I would have to do a lower-case r for that class and an upper-case r for this class.”
3.1.3. Rewriting with Consistency
Dylan: “Another thing I do is, although I could have started working off your problem, I won’t. I’ll rewrite it in my own handwriting. One, because I’m familiar with my handwriting. And two, because it forces me to rewrite the problem again, so I know what I’m solving.”
Dylan: “So let’s say we have the problem 4x times 3 equals 5 [writes 4x • 3 = 5; see Figure 5]. If I saw this written down, I will actually rewrite it like this [writes 4x(3) = 5; see Figure 5], so parentheses are used as multiplication. I come up with a really consistent form of notation, so it’s unambiguous.”
Dylan: “Division [writes , see Figure 6] is typically taught like this to younger students. I despise this symbol, because I’m not sure what is acting on what. Long division is a little easier [writes long division sign to right of ; see Figure 6]; however, long division, once you start doing square roots [writes square root sign below long division sign; see Figure 6], so I actually use the fraction symbol [draws fraction bar; see Figure 6].”
3.1.4. Consistent Solution Process
- Converting all fractions to a common base or language (i.e., denominator);
- Showing all steps of her solution process;
- Pulling out like terms (e.g., negatives or variables);
- Distributing first to get rid of parentheses to simplify the problem;
- Using her “abcd” method for solving fraction division problems (i.e., ); and
- Solving problems as inverse operations.
Dylan: “So this is the classic thing, that I see these two numbers and they aren’t in the same language. I would immediately try to get these into the same common denominator so I can try to understand them. And that’s where I have my cross multiplying thing that goes on [draws arrow between the denominator of each fraction and the numerator and denominator of the other fraction; see Figure 7], one of those little rules. So three times four, to get them into the same base is 12. So now I will have twelve on the bottom for both of them [writes /12 and /12], and to get this 4 times 3 is 12, 4 times 1 is 4 [writes 4]. And 3 times 4 is 12 and 3 times 1 is 3 [writes 3]. And now I can actually compare these two numbers [writes >]. The three is smaller and now I can rewrite them [writes 1/3 > 1/4].”
Dylan: “I’m a big proponent of writing out every single step including anything that is intermediate even if it seems redundant. If I have [writes 12x + 5 - 3 = 6; see Figure 8] and I wanted to solve for x. This is actually a good one. I’ll just go through it with my steps of how I would do it, so you can see the way I think through problems. So, the first thing that I immediately see is that I want to start combining things that are similar. I use the word language a lot so these guys [points to 5 and 3] speak in the same language, because they are just numbers, this one [points to 12x] has a variable attached to it so it’s speaking in a different language, there is one that is just a number [points to 6]. So, I’ll start with the language that these guys are speaking. So, I’ll rewrite twelve x [writes 12x] because I’m not going to do anything to it. Plus [writes +] I’m not doing anything to. Um, five minus three, now I’ve got 2 [writes 2 =]. I’m not doing anything to the 6 [writes 6]. Now I want to get rid of this two because it speaks the same language as the 6. So I need to, and this is where my colors come in. So, I’m going to minus 2 from this side [writes −2] and minus 2 from this side [writes -2]. And sometimes I’ll rewrite this out [writes 12x + 2 − 2 = 6 − 2]. So, now I’m leaving the 12x alone [writes 12x], two minus two is zero [writes +0]. This is one of the steps I may or may not do depending upon how much I have going on. Six minus two is 4. [writes 4]. Now I can get rid of my plus 0, since it doesn’t do anything 12x = 4 [writes 12x = 4]. I’ve got to get this 12 somehow over here, so I can isolate this x by itself. I know I can divide by 12 [writes /12] and divide by 12 [writes /12]. 12 divided by 12 is 1. One x equals four-twelfths [writes 1x = 4/12]. This [pointing to 1] is redundant because 1 times x is just x. [writes x = 4/12] I can go further and simplify that, but I don’t think I’ll do that right now.”
3.1.5. Grounding the Abstract
Dylan: “The reason why it’s funny that I did statistics, but it makes a lot of sense, is that if I could take one of these concepts and apply it to something that was actually tangible to me, so like the percentage of people that are over the age of 55 that have a landline phone, if I come up with these stories or narratives, then I could actually recall how to do an operation, but I had to have some sort of narrative that was actually based in the real world.”
Dylan: “Sometimes I would google “real life examples of blah blah blah” because even if it wasn’t that exact problem, all the sudden if I could connect to that—Oh! That’s why I need to know this. I really struggled with math when I was like “why are we learning this?”
3.2. Structural Barriers
Dylan: “The math department is very unaccommodating. People in math tend to have an attitude of, if you can do it then great, if you can’t, then you’re just not meant to be. Which is ridiculous, because it’s not acceptable to not be able to read, so I don’t know how it’s acceptable to not be able to do math. I got told that I should probably drop out of Berkeley and reapply the next semester into a different degree program. At this point I was a junior in college. Which is not really possible, it’s like, no I’m committed.”
Dylan: “The way I was able to get through was brute force. I had this professor, and she said there are two kinds of mathematicians: those that are smarter than everyone else, and those that work harder. And so I worked harder. I took classes multiple times, I created this incredible library of stuff, I have this really specific system of how I write and rewrite… In order to learn a basic concept, I would attack it from every angle until something stuck. So it was just brute force, and working harder than everyone else. Which is frustrating, right? Because you are being asked to do a phenomenal amount more work than anyone else in this class has to do and it would be really lovely if we just lived in a world where we were given lots of options of all these different ways of learning this one particular concept. And unfortunately, right now you have to cultivate all these different ways yourself.”
Dylan: “When I’m learning something, I try to remove myself really quick, and go learn why would I ever do this, what are the definitions of all these terms, then come up with my note taking system for how I’m going to do it, then I can dive into the subject. Needless to say, this is why I had to take so many classes in college a couple times.”
Dylan: “It’s really really unfortunate to me, I think that, in mathematics, it’s not just that you understand the concept. It’s not just that you can get a correct answer, you also have to do it in a certain amount of time, which inevitably is like this really bizarre artificial constraint. Especially now that I’ve worked in industry at as a data analyst. And yes, I had time constraints, I had to get a report done in this amount of time or whatnot. It’s nothing like sitting down for a test and you have 60 min to do this insane page of stuff and this huge mental dump, where these kinds of rewriting things would really become problematic, I would just flat out run out of time. I would have to either not rewrite things and inevitably make mistakes or rewrite things and not finish exams. I would have to make calculated decisions at the beginning of exams.”
Dylan: “I had grad students—one in particular, I think it was multivariate calculus—he would write on the top of my assignments “please shorten steps” or whatever because he has to grade x numbers of assignments and he hated how verbose mine were.”
3.3. Instructional Recommendations
- Identify issues of access, particularly in notation. Dylan often assessed this by asking students to write out all numerals and mathematical symbols they knew. She noted if students inverted numbers (e.g., wrote 18 as 81), misread numbers (e.g., reading 6 as a 9), or confused operators (e.g., solved subtraction as addition). She would discuss any issues of perceptual similarity and suggest the student change the form of their notation or use graph paper or color to space and organize their notation sufficiently.
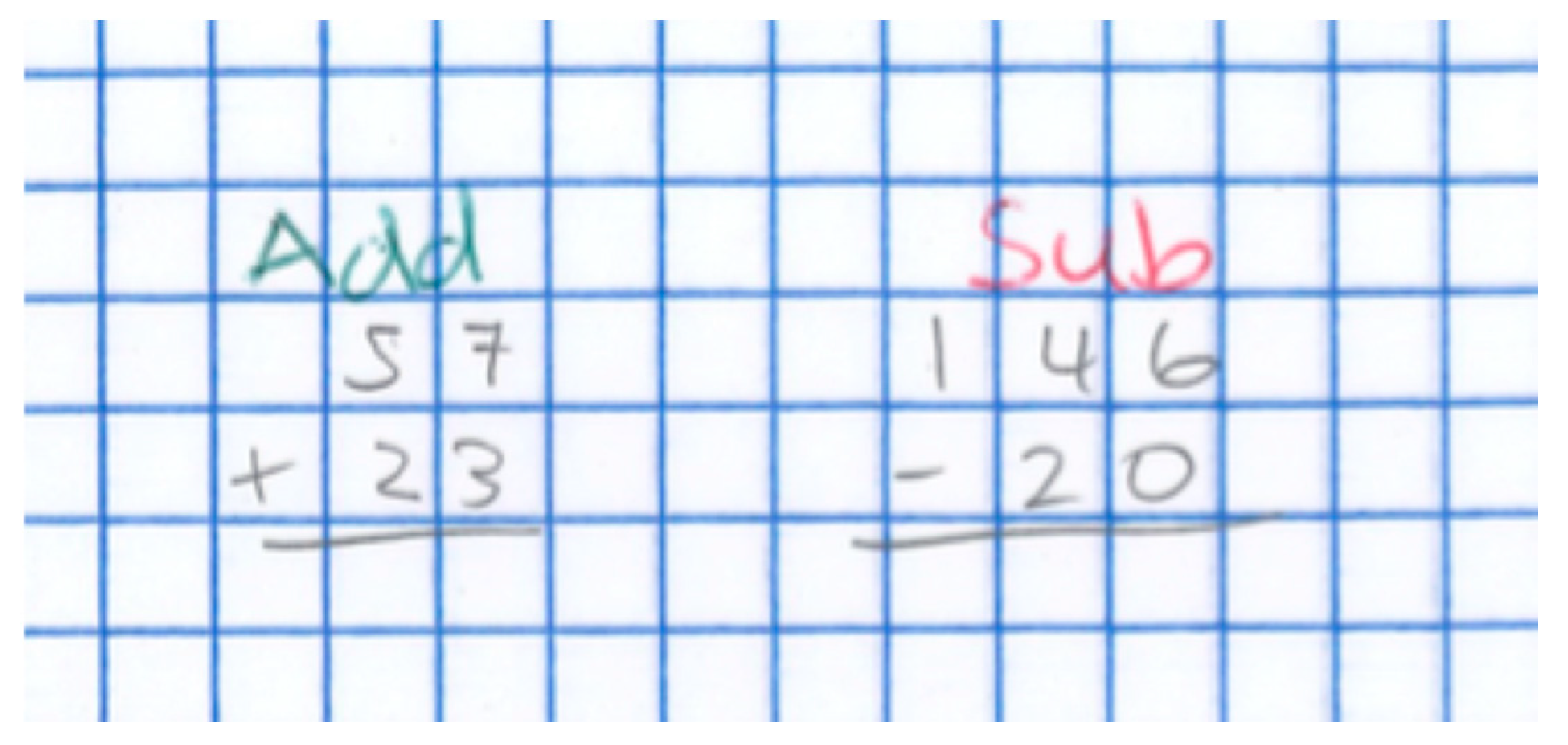
- Identify and build on the student’s strengths. Dylan asked students to explain their areas of strengths (e.g., language, organization) and would use this to think about how to support their understanding of mathematics. For example, she might have a student label their addition and subtraction problems with “add” or “sub” (see Figure 10) to help them attend to the difference in the operator symbol.
- Connect the mathematics to something meaningful. Dylan recommended always contextualizing mathematics in terms of something that was concrete for the student, either physical manipulatives or real world contexts.
- Teach and allow for multiple solution paths. Dylan recommended teaching multiple ways to understand a concept and multiple problem solving approaches. The value of a particular approach should be determined by whether it enables the student to make sense of the mathematics, rather than whether it is efficient (e.g., standard algorithms).
- Give student agency over reflecting and determining what works for them. Dylan was careful not to generalize from her own experiences and repeatedly emphasized the importance of students figuring out what systems would work for them.
4. Discussion
4.1. Countering the Myth: Dyscalculia Results from Inherent Cognitive Deficits
4.2. Countering the Myth: Students with Dyscalculia Cannot Learn Higher Level Mathematics
4.3. Countering the Myth: Students Must Master the “Basics” to Succeed
4.4. Countering the Myth: Speed and Efficiency Are Important
4.5. Removing Structural Barriers
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lewis, K.E.; Lynn, D.M. An insider’s view of a mathematics learning disability: Compensating to gain access to fractions. Investig. Math. Learn. 2018, in press. [Google Scholar] [CrossRef]
- Lewis, K.E.; Lynn, D.M. Access through compensation: Emancipatory view of a mathematics learning disability. Cognit. Instruct. in press.
- Shalev, R.S. Prevalence of developmental dyscalculia. In Why is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities; Berch, D.B., Mazzocco, M.M.M., Eds.; Paul, H. Brookes: Baltimore, MD, USA, 2007; pp. 49–60. [Google Scholar]
- Devine, A.; Hill, F.; Carey, E.; Szűcs, D. Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. J. Educ. Psychol. 2018, 110, 431–444. [Google Scholar] [CrossRef]
- Butterworth, B. Foundational numerical capacities and the origins of dyscalculia. Trends Cogn. Sci. 2010, 14, 534–541. [Google Scholar] [CrossRef] [PubMed]
- Desoete, A.; Ceulemans, A.; De Weerdt, F.; Pieters, S. Can we predict mathematical learning disabilities from symbolic and non-symbolic comparison tasks in kindergarten? Findings from a longitudinal study. Br. J. Educ. Psychol. 2012, 82, 64–81. [Google Scholar] [CrossRef] [PubMed]
- Butterworth, B.; Varma, S.; Laurillard, D. Dyscalculia: From brain to education. Science 2011, 332, 1049–1053. [Google Scholar] [CrossRef] [PubMed]
- Mazzocco, M.M.M.; Devlin, K.T.; McKenney, S.J. Is it a fact? Timed arithmetic performance of children with mathematical learning disabilities (MLD) varies as a function of how MLD is defined. Dev. Neuropsychol. 2008, 33, 318–344. [Google Scholar] [CrossRef] [PubMed]
- Mazzocco, M.M.M.; Myers, G.F.; Lewis, K.E.; Hanich, L.B.; Murphy, M.M. Limited knowledge of fraction representations differentiates middle school students with mathematics learning disability (dyscalculia) versus low mathematics achievement. J. Exp. Child Psychol. 2013, 115, 371–387. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.M.; Mazzocco, M.M.M.; Hanich, L.B.; Early, M.C. Cognitive characteristics of children with mathematics learning disability (MLD) vary as a function of the cutoff criterion used to define MLD. J. Learn. Disabil. 2007, 40, 458–478. [Google Scholar] [CrossRef] [PubMed]
- Geary, D.C. Mathematical disabilities: Reflections on cognitive, neuropsychological, and genetic components. Learn. Individ. Differ. 2010, 20, 130–133. [Google Scholar] [CrossRef] [PubMed]
- Geary, D.C.; Hoard, M.K.; Bailey, D.H. Fact Retrieval Deficits in Low Achieving Children and Children with Mathematical Learning Disability. J. Learn. Disabil. 2012, 45, 291–307. [Google Scholar] [CrossRef] [PubMed]
- Lewis, K.E.; Fisher, M.B. Taking stock of 40 years of research on mathematical learning disability: Methodological issues and future directions. J. Res. Math. Educ. 2016, 47, 338–371. [Google Scholar] [CrossRef]
- Swanson, H.L. Cognitive Aspects of Math Disabilities. In Why is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities; Berch, D.B., Mazzocco, M.M.M., Eds.; Paul H Brookes Publishing: Baltimore, MD, USA, 2007; pp. 133–146. ISBN 978-1-55766-864-6. [Google Scholar]
- Oliver, M. Changing the social relations of research production? Disabil. Handicap Soc. 1992, 7, 101–114. [Google Scholar] [CrossRef]
- Vygotsky, L.S. Introduction: Fundamentals problems of defectology. In The Collected Works of L. S. Vygotsky, Volume 2: The Fundamentals of Defectology; Rieber, R.W., Carton, A.S., Eds.; Plenum Press: London, NY, USA, 1929; ISBN 0-306-42442-8. [Google Scholar]
- Thaler, L.; Arnott, S.R.; Goodale, M.A. Neural correlates of natural human echolocation in early and late blind echolocation experts. PLoS ONE 2011, 6, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Mercer, G. From critique to practice: Emancipatory disability research. In Implementing the Social Model of Disability: Theory and Research; Barnes, C., Mercer, G., Eds.; The Disability Press: Leeds, UK, 2004; pp. 118–137. [Google Scholar]
- Barnes, C. “Emancipatory disability research”: Project or process? J. Res. Spec. Educ. Needs 2002, 2, 1–8. [Google Scholar] [CrossRef]
- Stone, E.; Priestley, M. Parasites, pawns and partners: Disability research and the role of non-disabled researchers. Br. J. Sociol. 1996, 47, 699–716. [Google Scholar] [CrossRef] [PubMed]
- Moser Opitz, E.; Freesemann, O.; Prediger, S.; Grob, U.; Matull, I.; Hußmann, S. Remediation for students with mathematics difficulties: An intervention study in middle schools. J. Learn. Disabil. 2017, 50, 724–736. [Google Scholar] [CrossRef] [PubMed]
- Jackson, K.; Gibbons, L.; Sharpe, C.J. Teachers’ views of students’ mathematical capabilities: Challenges and possibilities for ambitious reform. Teach. Coll. Rec. 2017, 119, 1–43. [Google Scholar]
- Wilhelm, A.G.; Munter, C.; Jackson, K. Examining relations between teachers’ explanations of sources of students’ difficulty in mathematics and students’ opportunities to learn. Elem. Sch. J. 2017, 117, 345–370. [Google Scholar] [CrossRef]
- Silva, E.; White, T. Pathways to Improvement: Using Psychological Strategies to Help College Students Master Developmental Math; Carnegie Foundation: Stanford, CA, USA, 2013. [Google Scholar]
- Geary, D.C.; Bow-Thomas, C.C.; Yao, Y. Counting knowledge and skill in cognitive addition: A comparison of normal and mathematically disabled children. J. Exp. Child Psychol. 1992, 54, 372–391. [Google Scholar] [CrossRef]
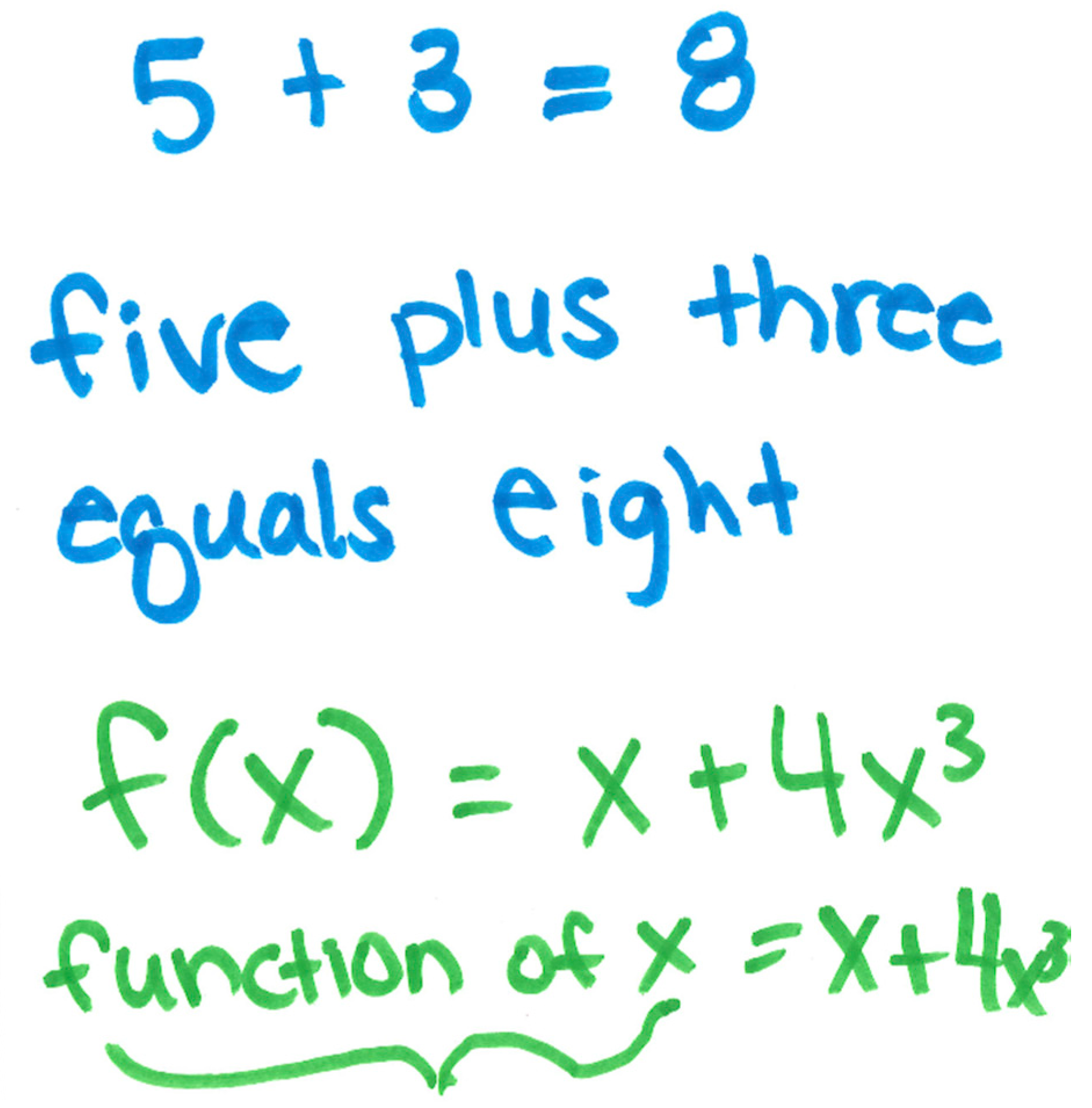
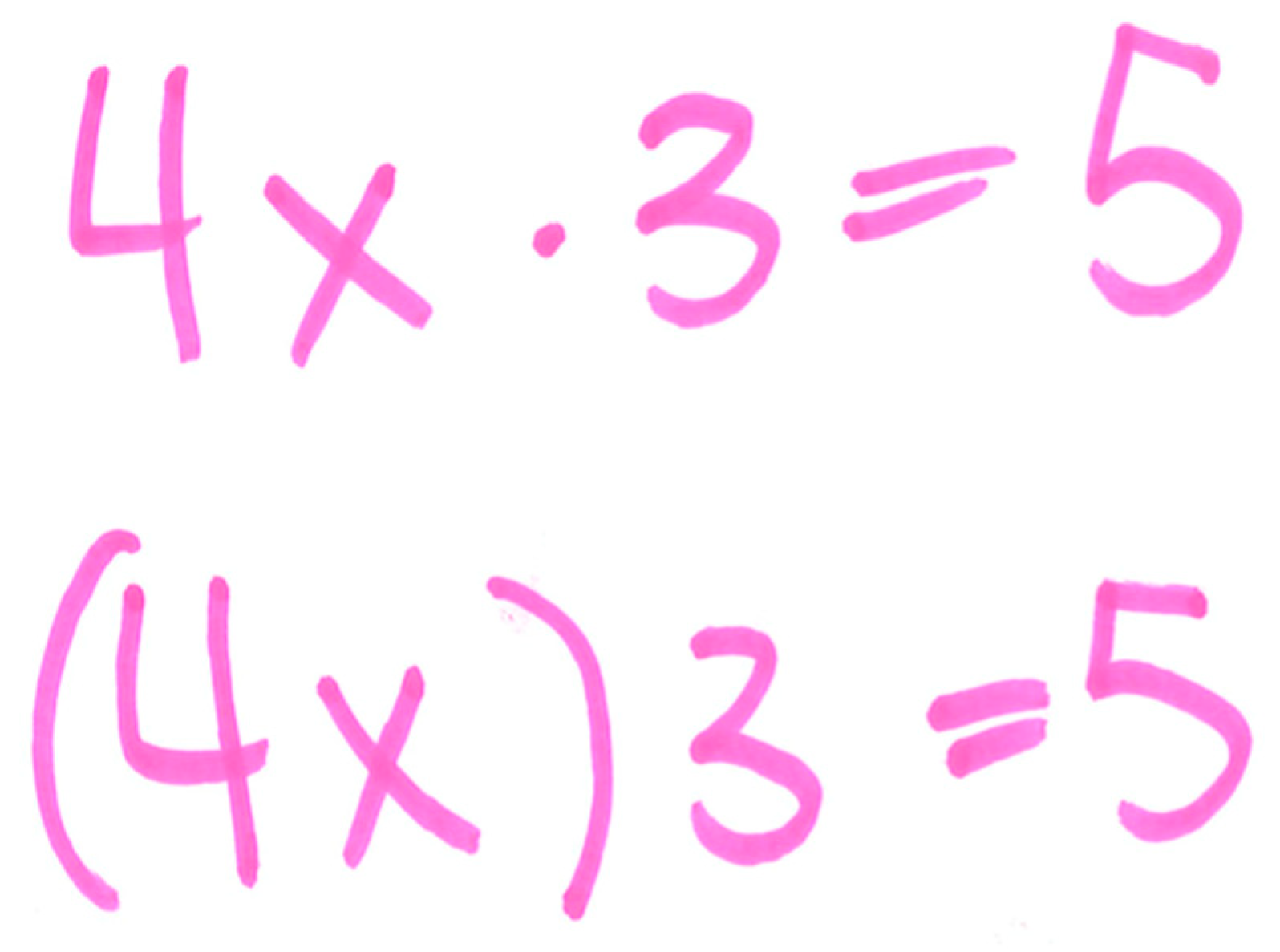

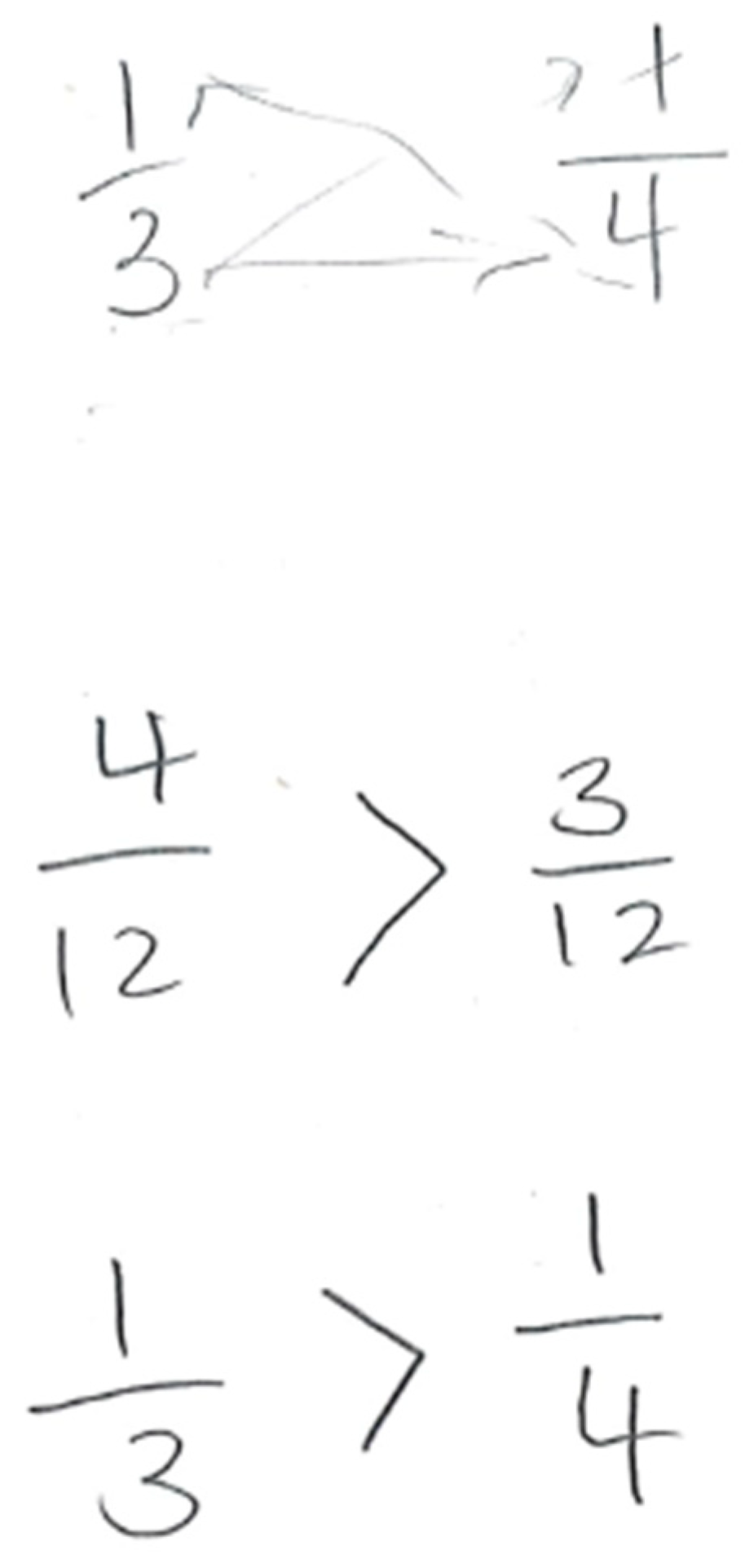
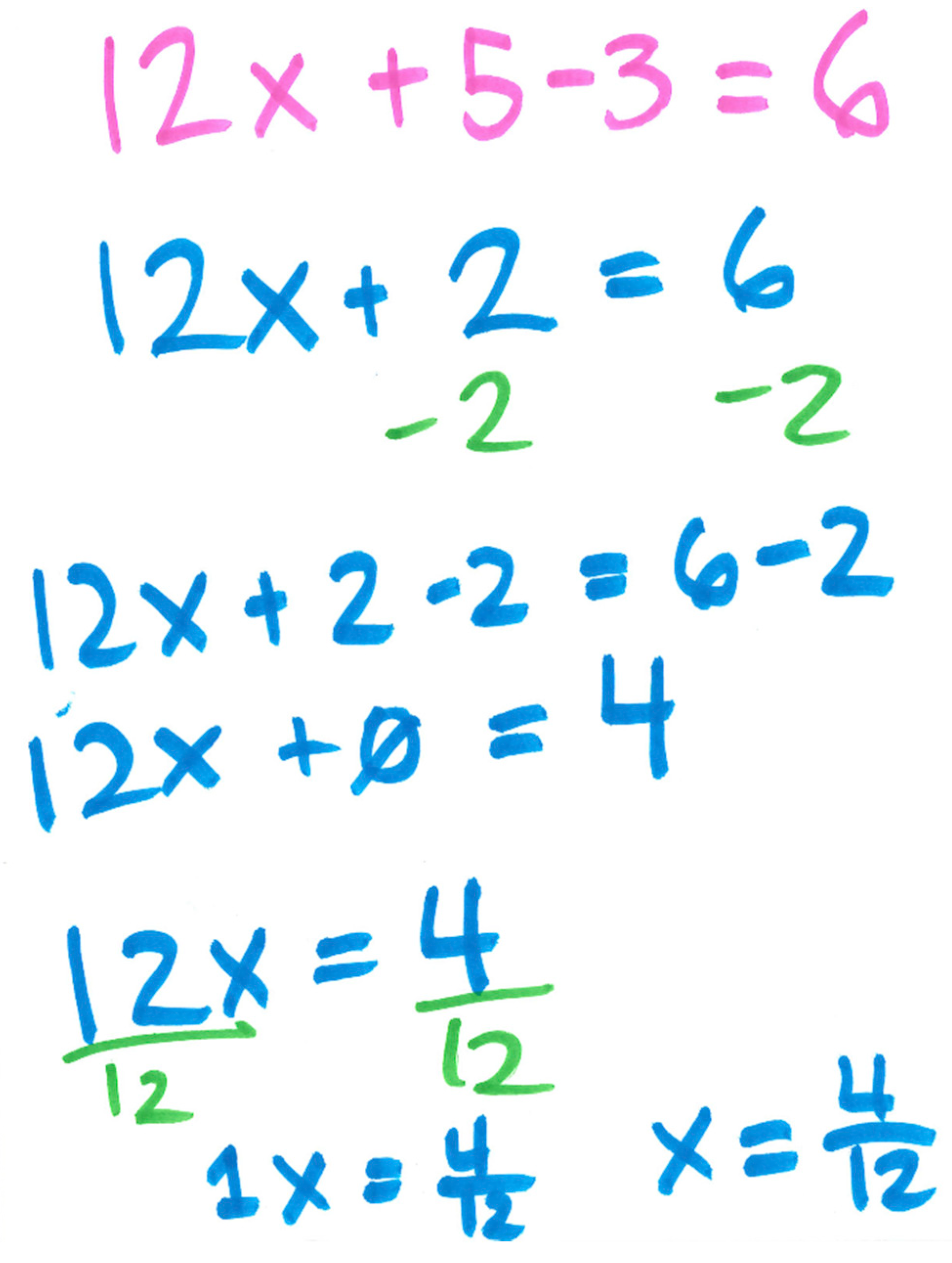

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewis, K.E.; Lynn, D.M. Against the Odds: Insights from a Statistician with Dyscalculia. Educ. Sci. 2018, 8, 63. https://doi.org/10.3390/educsci8020063
Lewis KE, Lynn DM. Against the Odds: Insights from a Statistician with Dyscalculia. Education Sciences. 2018; 8(2):63. https://doi.org/10.3390/educsci8020063
Chicago/Turabian StyleLewis, Katherine E., and Dylan M. Lynn. 2018. "Against the Odds: Insights from a Statistician with Dyscalculia" Education Sciences 8, no. 2: 63. https://doi.org/10.3390/educsci8020063
APA StyleLewis, K. E., & Lynn, D. M. (2018). Against the Odds: Insights from a Statistician with Dyscalculia. Education Sciences, 8(2), 63. https://doi.org/10.3390/educsci8020063



