Problem-Based Learning (PBL) and Student Interest in STEM Careers: The Roles of Motivation and Ability Beliefs
Abstract
:1. Introduction
1.1. The Importance of Increasing Interest in STEM Careers for All Students
1.2. Inclusive STEM High Schools
1.3. The PBL Experience
1.4. Students’ Beliefs about Ability, Interest and Intrinsic Motivation in STEM
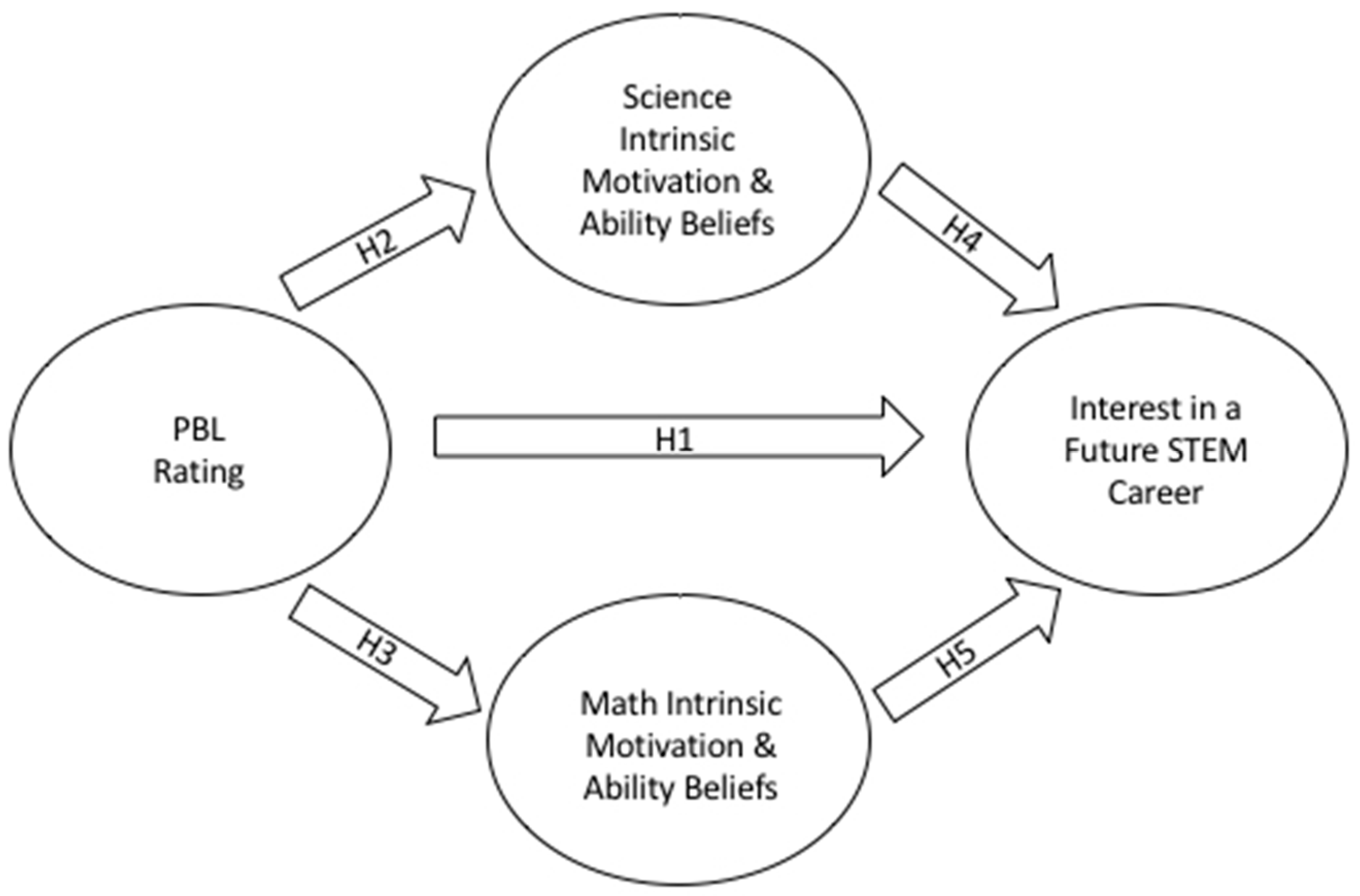
1.5. The Current Study
2. Materials and Methods
2.1. Procedure
2.2. Participants
2.3. Measures
2.3.1. Perceptions of PBL
2.3.2. Interest in a Future STEM Career (IFSTEMC)
2.3.3. Ability Beliefs
2.3.3.1. Science Ability Beliefs
2.3.3.2. Math Ability Beliefs
2.3.4. Intrinsic Motivation
2.3.4.1. Science Intrinsic Motivation
2.3.4.2. Math Intrinsic Motivation
2.3.5. Additional Covariates
2.3.5.1. General Intrinsic Motivation for Schoolwork
2.3.5.2. General Ability Beliefs for Schoolwork
2.3.5.3. Attitudes toward School
2.3.5.4. School, Grade, Race/Ethnicity, Gender
2.4. Analysis
2.4.1. Multivariate Regression Analyses
2.4.2. Mediation Analyses
3. Results
3.1. PBL and Interest in a Future STEM Career
3.2. PBL and STEM Intrinsic Motivation and Ability Beliefs
3.3. STEM Intrinsic Motivation, Ability Beliefs and Interest in a Future STEM Career
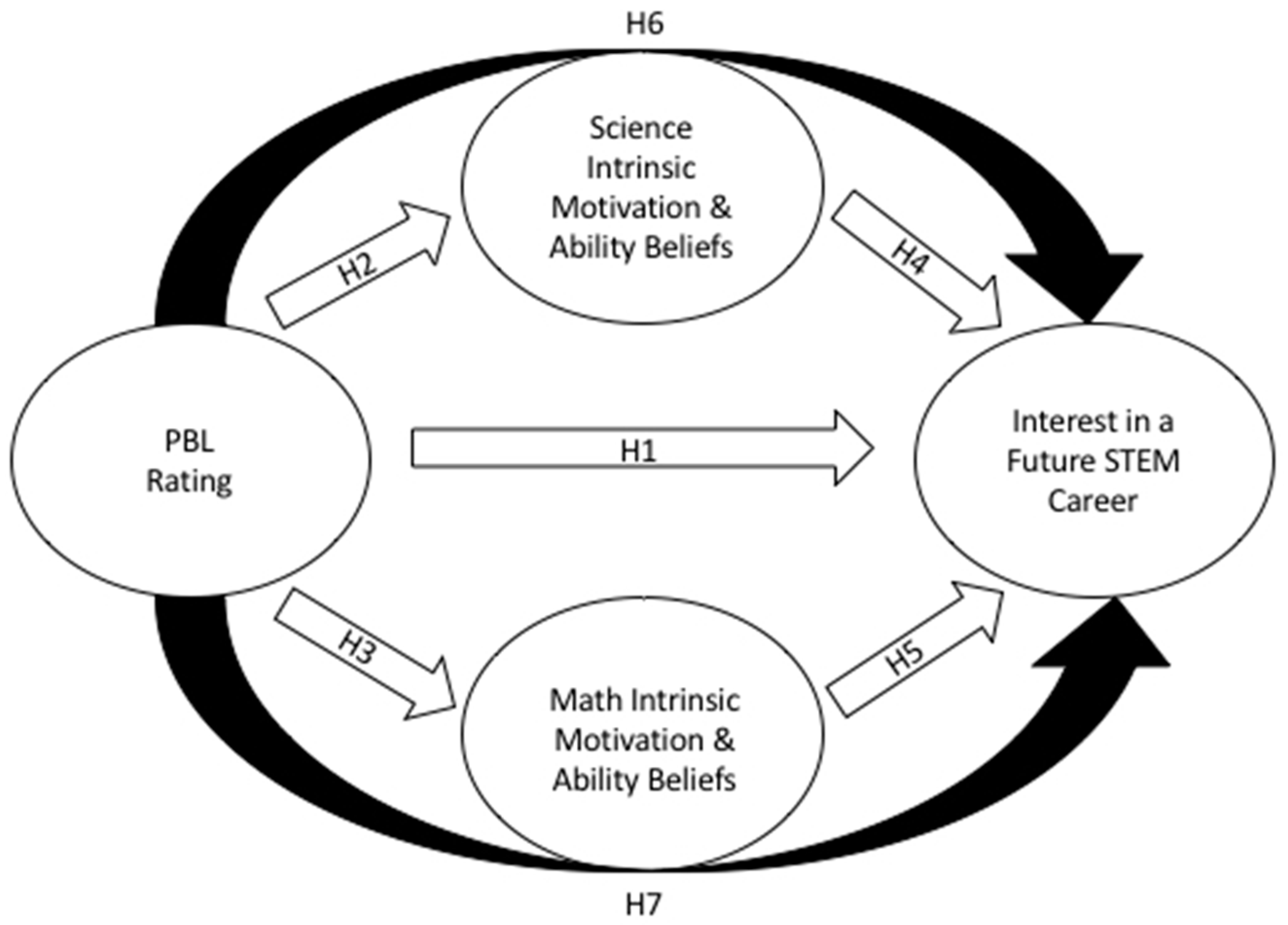
3.4. Mediation Model
3.5. Direct Effect of PBL Career Content on IFSTEMC
3.6. Race and Gender
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Science Board. Science and Engineering Indicators 2016; NSB-2016-1; National Science Foundation: Arlington, VA, USA, 2016.
- United States Department of Labor. The STEM Workforce Challenge: The Role of the Public Workforce System in a National Solution for a Competitive Science, Technology, Engineering and Mathematics (STEM) Workforce; United States Department of Labor: Washington, DC, USA, 2007.
- Committee on STEM Education National Science and Technology Council. Federal Science, Technology, Engineering and Mathematics (STEM) Education: 5-Year Strategic Plan; Committee on STEM Education National Science and Technology Council: Washington, DC, USA, 2013. Available online: http://www.whitehouse.gov/sites/default/files/microsites/ostp/stem_stratplan_2013.pdf (accessed on 10 April 2017).
- Savery, J.R. Overview of problem-based learning: Definitions and distinctions. Interdiscip. J. Probl. Based Learn. 2006, 1, 8–20. [Google Scholar] [CrossRef]
- About BIE. Available online: http://www.bie.org/about/about_bie (accessed on 10 April 2017).
- Lent, R.W.; Brown, S.D.; Hackett, G. Toward a unifying social cognitive theory of career and academic interest, choice and performance. J. Vocat. Behav. 1994, 45, 79–122. [Google Scholar] [CrossRef]
- Holdren, J.; Lander, E.; Varmus, H. Prepare and Inspire: K-12 Science, Technology, Engineering and Math (STEM) Education for America’s Future; Executive Office of the President, The President’s Council of Advisors on Science and Technology: Washington, DC, USA, 2010. [Google Scholar]
- National Research Council. Successful STEM Education: A Workshop Summary; The National Academies Press: Washington, DC, USA, 2011. [Google Scholar]
- National Research Council. A Framework for K-12 Science Education: Practices, Crosscutting Concepts and Core Ideas; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
- Organization for Economic Co-Operation and Development (OECD). Country Note: Key Findings from PISA 2015 for the United States; OECD Publishing: Paris, France, 2016; Available online: https://www.oecd.org/pisa/pisa-2015-United-States.pdf (accessed on 10 April 2017).
- U.S. Department of Education Office for Civil Rights. 2013–2014 Civil Rights Data Collection: A First Look: Key Data Highlights on Equity and Opportunity Gaps in Our Nation’s Public Schools; U.S. Department of Education Office for Civil Rights: Washington, DC, USA, 2016.
- Wang, X. Why students choose stem majors: Motivation, high school learning and postsecondary context of support. Am. Educ. Res. J. 2013, 50, 1081–1121. [Google Scholar] [CrossRef]
- Bettinger, E. To be or not to be: Major choices in budding scientists. In American Universities in a Global Market; University of Chicago Press: Chicago, IL, USA, 2010; pp. 69–98. [Google Scholar]
- National Science Foundation. Table 2–8. Intention of Freshmen to Major in S&E Fields, by Race or Ethnicity and Sex: 2012; National Science Foundation: Washington, DC, USA, 2012. Available online: https://www.nsf.gov/statistics/wmpd/2013/pdf/tab2-8_updated_2014_05.pdf (accessed on 10 April 2017).
- Lowell, B.L.; Salzman, H.; Bernstein, H. Steady as she goes? Three generations of students through the science and engineering pipeline. In Proceedings of the Annual Meetings of the Association for Public Policy Analysis and Management, Washington, DC, USA, 7 November 2009. [Google Scholar]
- Hidi, S.; Renninger, K.A. The four-phase model of interest development. Educ. Psychol. 2006, 41, 111–127. [Google Scholar] [CrossRef]
- Maltese, A.V.; Tai, R.H. Pipeline persistence: Examining the association of educational experiences with earned degrees in stem among U.S. Students. Sci. Educ. 2011, 95, 877–907. [Google Scholar] [CrossRef]
- U.S. Congress Joint Economic Committee. STEM Education: Preparing for the Jobs of the Future; U.S. Congress Joint Economic Committee: Washington, DC, USA, 2012.
- White House Office of Science and Technology Policy. Progress Report on Coordinating Federal Science, Technology, Engineering and Mathematics (STEM) Education; White House Office of Science and Technology Policy: Washington, DC, USA, 2014. Available online: https://obamawhitehouse.archives.gov/sites/default/files/microsites/ostp/stem_ed_budget_supplement_fy16-march-2015.pdf (accessed on 10 April 2017).
- Subotnik, R.F.; Tai, R.H.; Almarode, J. Study of the Impact of Selective SMT High Schools: Reflections on Learners Gifted and Motivated in Science and Mathematics; The National Academies: Washington, DC, USA, 2011. [Google Scholar]
- Community for Advancing Discovery Research in Education. (n.d.). STEM Smart Brief: Specialized STEM Secondary Schools. Available online: http://successfulstemeducation.org/sites/successfulstemeducation.org/files/Specialized%20STEM%20Secondary%20Schools_FINAL_0.pdf (accessed on 10 April 2017).
- Lynch, S.J.; Behrend, T.; Burton, E.P.; Means, B. Inclusive Stem-Focused High Schools: Stem Education Policy and Opportunity Structures; Annual Conference of National Association for Research in Science Teaching (NARST): Rio Grande, Puerto Rico, 2013. [Google Scholar]
- Scott, C.E. A Comparative Case Study of the Characteristics of Science, Technology, Engineering and Mathematics (STEM) Focused High Schools. Ph.D. Thesis, George Mason University, Fairfax, VA, USA, 2009. [Google Scholar]
- Young, V.M.; House, A.; Wang, H.; Singleton, C.; Klopfenstein, K. Inclusive Stem Schools: Early Promise in Texas and Unanswered Questions; Workshop on Successful STEM Education in K-12 Schools, National Academies: Washington, DC, USA, 2011. [Google Scholar]
- LaForce, M.; Noble, E.; King, H.; Century, J.; Blackwell, C.; Holt, S.; Ibrahim, A.; Loo, S. The eight essential elements of inclusive STEM high schools. Int. J. STEM Educ. 2016, 3, 21. [Google Scholar] [CrossRef]
- Means, B.; Confrey, J.; House, A.; Bhanot, R. STEM High Schools: Specialized Science Technology Engineering and Mathematics Secondary Schools in the U.S.; SRI Project P17858; SRI International: Menlo Park, CA, USA, 2008. [Google Scholar]
- Bicer, A.; Navruz, B.; Capraro, R.M.; Capraro, M.M.; Oner, T.; Boedeker, P. STEM schools vs. Non-STEM schools: Comparing students’ mathematics growth rate on high-stakes test performance. Int. J. New Trends Educ. Their Implic. 2015, 6, 138–150. [Google Scholar]
- Hansen, M. Characteristics of schools successful in stem: Evidence from two states’ longitudinal data. J. Educ. Res. 2014, 107, 374–391. [Google Scholar] [CrossRef]
- Lavertu, S.; Gnagey, J. The Impact of Ohio STEM High Schools on Student Achievement; Ohio Education Research Center at the Ohio State University: Columbus, OH, USA, 2015. [Google Scholar]
- Means, B.; Wang, H.; Young, V.; Peters, V.L.; Lynch, S.J. STEM-focused high schools as a strategy for enhancing readiness for postsecondary stem programs. J. Res. Sci. Teach. 2016, 53, 709–736. [Google Scholar] [CrossRef]
- Subotnik, R.F.; Tai, R.H.; Almarode, J.; Crowe, E. What are the value-added contributions of selective secondary schools of mathematics, science and technology? Preliminary analyses from a U.S. national research study. Talent Dev. Excell. 2013, 5, 87–97. [Google Scholar]
- Wiswall, M.; Stiefel, L.; Schwartz, A.E.; Boccardo, J. Does attending a stem high school improve student performance? Evidence from New York City. Econ. Educ. Rev. 2014, 40, 93–105. [Google Scholar] [CrossRef]
- Means, B.; House, A.; Young, V.; Wang, H.; Lynch, S. Expanding access to stem-focused education: What are the effects? In Proceedings of the 86th NARST Annual Conference, National Association for Research in Science Teaching, Rio Grande, Puerto Rico, 6–9 April 2013. [Google Scholar]
- Goodwin, B.; Hein, H. STEM schools produce mixed results. Educ. Leadersh. 2015, 72, 84–85. [Google Scholar]
- Buck Institute for Education. Gold Standard PBL: Essential Project Design Elements; Buck Institute for Education: Novato, CA, USA, 2015; Available online: http://www.bie.org/object/document/gold_standard_pbl_essential_project_design_elements# (accessed on 10 April 2017).
- Barrows, H.S. A taxonomy of problem-based learning methods. Med. Educ. 1986, 20, 481–486. [Google Scholar] [CrossRef] [PubMed]
- Hmelo-Silver, C.E. Problem-based learning: What and how do students learn? Educ. Psychol. Rev. 2004, 16, 235–266. [Google Scholar] [CrossRef]
- Hung, W. Theory to reality: A few issues in implementing problem-based learning. Educ. Technol. Res. Dev. 2011, 59, 529–552. [Google Scholar] [CrossRef]
- Harden, R.M.; Davis, M.H. The continuum of problem-based learning. Med. Teach. 1998, 20, 317–322. [Google Scholar]
- Barrows, H.S. Problem-based learning in medicine and beyond: A brief overview. New Dir. Teach. Learn. 1996, 68, 3–12. [Google Scholar] [CrossRef]
- Baran, M.; Maskan, A. The effect of project-based learning on pre-service physics teachers electrostatic achievements. Cypriot J. Educ. Sci. 2010, 5, 243–257. [Google Scholar]
- Cerezo, N. Problem-based learning in the middle school: A research case study of the perceptions of at-risk females. RMLE Online 2015, 27, 1–13. [Google Scholar] [CrossRef]
- Massa, N.; Dischino, M.; Donnelly, J.; Hanes, F. Problem-based learning in photonics technology education: Assessing student learning. In Proceedings of the 11th Education and Training in Optics and Photonics, Wales, UK, 5–7 June 2009; Optical Society of America: Washington, DC, USA, 2009. [Google Scholar]
- Mergendoller, J.R.; Maxwell, N.L.; Bellisimo, Y. The effectiveness of problem-based instruction: A comparative study of instructional methods and student characteristics. Interdiscip. J. Probl. Based Learn. 2006, 1. [Google Scholar] [CrossRef]
- Bell, S. Project-based learning for the 21st century: Skills for the future. Clear. House J. Educ. Strateg. Issues Ideas 2010, 83, 39–43. [Google Scholar] [CrossRef]
- Albanese, M.A.; Mitchell, S. Problem-based learning: A review of literature on its outcomes and implementation issues. Acad. Med. 1993, 68, 52–81. [Google Scholar] [CrossRef] [PubMed]
- Ertmer, P.A.; Schlosser, S.; Clase, K.; Adedokun, O. The grand challenge: Helping teachers learn/teach cutting-edge science via a pbl approach. Interdiscip. J. Probl. Based Learn. 2014, 8. [Google Scholar] [CrossRef]
- Dominguez, C.; Jamie, A. Database design learning: A project-based approach organized through a course management system. Comput. Educ. 2010, 55, 1312–1320. [Google Scholar] [CrossRef]
- Allen, D.E.; Duch, B.J.; Groh, S.E. The power of problem-based learning in teaching introductory science courses. New Dir. Teach. Learn. 1996, 1996, 43–52. [Google Scholar] [CrossRef]
- Lou, S.-J.; Shih, R.-C.; Ray Diez, C.; Tseng, K.-H. The impact of problem-based learning strategies on stem knowledge integration and attitudes: An exploratory study among female Taiwanese senior high school students. Int. J. Technol. Des. Educ. 2010, 21, 195–215. [Google Scholar] [CrossRef]
- Norman, G.R.; Schmidt, H.G. Effectiveness of problem-based learning curricula: Theory, practice and paper darts. Med. Educ. 2000, 34, 721–728. [Google Scholar] [CrossRef] [PubMed]
- Ravitz, J.; Hixson, N.; English, M.; Mergendoller, J. Using Project Based Learning to Teach 21st Century Skills: Findings from a Statewide Initiative; American Educational Research Association Conference: Vancouver, BC, Canada, 2012; Available online: http://www.bie.org/research/study/PBL_21CS_WV (accessed on 10 April 2017).
- Organisation for Economic Co-Operation and Development. Programme for International Assessment (PISA) Results from PISA 2012: United States Country Note; Organisation for Economic Co-Operation and Development (OECD): Paris, France, 2012; Available online: http://www.oecd.org/unitedstates/PISA-2012-results-US.pdf (accessed on 10 April 2017).
- Eccles, J.S.; Wigfield, A. Motivational beliefs, values and goals. Annu. Rev. Psychol. 2002, 53, 109–132. [Google Scholar] [CrossRef] [PubMed]
- Fortus, D. Attending to affect. J. Res. Sci. Teach. 2014, 51, 821–835. [Google Scholar] [CrossRef]
- Ryan, R.M.; Deci, E.L. Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemp. Educ. Psychol. 2000, 25, 54–67. [Google Scholar] [CrossRef] [PubMed]
- Wigfield, A.; Eccles, J.S. Expectancy-value theory of achievement motivation. Contemp. Educ. Psychol. 2000, 25, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Bandura, A. Self-Efficacy: The Exercise of Control; Macmillan: London, UK, 1997. [Google Scholar]
- Weiner, B. An attributional theory of achievement motivation and emotion. Psychol. Rev. 1985, 92, 548–573. [Google Scholar] [CrossRef] [PubMed]
- Deci, E.L.; Ryan, R.M. The general causality orientations scale: Self-determination in personality. J. Res. Personal. 1985, 19, 109–134. [Google Scholar] [CrossRef]
- Greene, B.A.; Miller, R.B. Influences on achievement: Goals, perceived ability and cognitive engagement. Contemp. Educ. Psychol. 1996, 21, 181–192. [Google Scholar] [CrossRef]
- Miller, R.B.; Greene, B.A.; Montalvo, G.P.; Ravindran, B.; Nichols, J.D. Engagement in academic work: The role of learning goals, future consequences, pleasing others and perceived ability. Contemp. Educ. Psychol. 1996, 21, 388–422. [Google Scholar] [CrossRef] [PubMed]
- Dowey, A.L. Attitudes, Interests and Perceived Self-Efficacy toward Science of Middle School Minority Female Students: Considerations for Their Low Achievement and Participation in Stem Disciplines. Ph.D. Thesis, University of California, San Diego, CA, USA, 2013. [Google Scholar]
- Zimbardo, P.G.; Boyd, J.N. Putting time in perspective: A valid, reliable individual-differences metric. In Time Perspective Theory; Review, Research and Application: Essays in Honor of Philip G. Zimbardo; Stolarski, M., Fieulaine, N., van Beek, W., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 17–55. [Google Scholar]
- Osborne, J.; Simon, S.; Collins, S. Attitudes towards science: A review of the literature and its implications. Int. J. Sci. Educ. 2003, 25, 1049–1079. [Google Scholar] [CrossRef]
- Lent, R.W.; Lopez, F.G.; Bieschke, K.J. Predicting mathematics-related choice and success behaviors: Test of an expanded social cognitive model. J. Vocat. Behav. 1993, 42, 223–236. [Google Scholar] [CrossRef]
- Bandura, A. Social Foundation of Thought and Action: A Social-Cognitive View; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Bong, M.; Skaalvik, E.M. Academic self-concept and self-efficacy: How different are they really? Educ. Psychol. Rev. 2003, 15, 1–40. [Google Scholar] [CrossRef]
- Degenhart, S.H.; Wingenbach, G.J.; Dooley, K.E.; Lindner, J.R.; Mowen, D.L.; Johnson, L. Middle school students’ attitudes toward pursuing careers in science, technology, engineering and math. NACTA J. 2007, 51, 52–59. [Google Scholar]
- Mau, W.-C. Factors that influence persistence in science and engineering career aspirations. Career Dev. Q. 2003, 51, 234–243. [Google Scholar] [CrossRef]
- Pajares, F. Gender difference in mathematics self-efficacy beliefs. In Gender Differences in Mathematics: An Integrative Psychological Approach; Gallagher, A.M., Kaufman, J.C., Eds.; Cambridge University Press: New York, NY, USA, 2005; pp. 294–315. [Google Scholar]
- Tai, R.H.; Liu, C.Q.; Maltese, A.V.; Fan, X. Planning early for careers in science. Science 2006, 312, 1143–1144. [Google Scholar] [CrossRef] [PubMed]
- Bandura, A. Perceived self-efficacy in cognitive development and functioning. Educ. Psychol. 1993, 28, 117–148. [Google Scholar] [CrossRef]
- Lent, R.W.; Lopez, F.G.; Bieschke, K.J. Mathematics self-efficacy: Sources and relation to science-based career choice. J. Couns. Psychol. 1991, 38, 424–430. [Google Scholar] [CrossRef]
- Simpkins, S.D.; Davis-Kean, P.E.; Eccles, J.S. Math and science motivation: A longitudinal examination of the links between choices and beliefs. Dev. Psychol. 2006, 42, 70–83. [Google Scholar] [CrossRef] [PubMed]
- Stevens, T.; Olivarez, A.; Lan, W.Y.; Tallent-Runnels, M.K. Role of mathematics self-efficacy and motivation in mathematics performance across ethnicity. J. Educ. Res. 2004, 97, 208–222. [Google Scholar] [CrossRef]
- Marsh, H.W.; Walker, R.; Debus, R. Subject-specific components of academic self-concept and self-efficacy. Contemp. Educ. Psychol. 1991, 16, 331–345. [Google Scholar] [CrossRef]
- Berk, L.J.; Muret-Wagstaff, S.L.; Goyal, R.; Joyal, J.A.; Gordon, J.A.; Faux, R.; Oriol, N.E. Inspiring careers in stem and healthcare fields through medical simulation embedded in high school science education. Adv. Physiol. Educ. 2014, 38, 210–215. [Google Scholar] [CrossRef] [PubMed]
- Harada, V.H.; Kirio, C.; Yamamoto, S. Project-based learning: Rigor and relevance in high schools. In School Library Management, 7th ed.; Dickinson, G.K., Repman, J., Eds.; Linworth: Santa Barbara, CA, USA, 2015; pp. 157–160. [Google Scholar]
- Jacques, L.A. What does project-based learning (pbl) look like in the mathematics classroom? Am. J. Educ. Res. 2017, 5, 428–433. [Google Scholar]
- Schettino, C. A framework for problem-based learning: Teaching mathematics with a relational problem-based pedagogy. Interdiscip. J. Probl. Based Learn. 2016, 10. [Google Scholar] [CrossRef]
- Munshi, F.M.; El Zayat, S.A.; Dolmans, D.H. Development and utility of a questionnaire to evaluate the quality of PBL problems. South East Asian J. Med. Educ. 2008, 2, 34. [Google Scholar]
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Cattell, R.B. The scree test for the number of factors. Multivar. Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef] [PubMed]
- Ledesma, R.D.; Valero-Mora, P. Determining the number of factors to retain in efa: An easy-to-use computer program for carrying out parallel analysis. Pract. Assess. Res. Eval. 2007, 12, 1–11. [Google Scholar]
- Horn, J.L. A rationale and test for the number of factors in factor analysis. Psychometrika 1965, 30, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Kabacoff, R. Determining the dimensionality of data: A sas macro for parallel analysis. In Proceedings of the 28th Annual Meeting of SAS Users Group International, Seattle, WA, USA, 30 March–2 April 2003. [Google Scholar]
- Çokluk, Ö.; Koçak, D. Using horn’s parallel analysis method in exploratory factor analysis for determining the number of factors. Educ. Sci. Theory Pract. 2016, 16, 537–551. [Google Scholar] [CrossRef]
- Hoover-Dempsey, K.V.; Sandler, H.M. Final Performance Report for OERI Grant # r305t010673: The Social Context of Parental Involvement: A Path to Enhanced Achievement; Project Monitor, Institute of Educational Sciences, U.S. Department of Education: Washington, DC, USA, 2005. [Google Scholar]
- Patrick, H.; Ryan, A.M.; Kaplan, A. Early adolescents’ perceptions of the classroom social environment, motivational beliefs and engagement. J. Educ. Psychol. 2007, 99, 83–98. [Google Scholar] [CrossRef]
- Germann, P.J. Development of the attitude toward science in school assessment and its use to investigate the relationship between science achievement and attitude toward science in school. J. Res. Sci. Teach. 1988, 25, 689–703. [Google Scholar] [CrossRef]
- Suhr, D.D. Exploratory or Confirmatory Factor Analysis; SAS Institute: Cary, NC, USA, 2006. [Google Scholar]
- Palmieri, P.A.; Fitzgerald, L.F. Confirmatory factor analysis of posttraumatic stress symptoms in sexually harassed women. J. Trauma. Stress 2005, 18, 657–666. [Google Scholar] [CrossRef] [PubMed]
- Browne, M.W.; Cudeck, R. Single sample cross-validation indices for covariance structures. Multivar. Behav. Res. 1989, 24, 445–455. [Google Scholar] [CrossRef] [PubMed]
- Bentler, P.M.; Bonett, D.G. Significance tests and goodness of fit in the analysis of covariance structures. Psychol. Bull. 1980, 88, 588–606. [Google Scholar] [CrossRef]
- Hu, L.T.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. Multidiscip. J. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Chen, G.; Gully, S.M.; Eden, D. Validation of a new general self-efficacy scale. Organ. Res. Methods 2001, 4, 62–83. [Google Scholar] [CrossRef]
- Sobel, M.E. Asymptotic confidence intervals for indirect effects in structural equation models. Sociol. Methodol. 1982, 13, 290–312. [Google Scholar] [CrossRef]
- Kenny, D.A. Mediation. 2016. Available online: http://davidakenny.net/cm/mediate.htm (accessed on 10 April 2017).
- MacKinnon, D.P.; Warsi, G.; Dwyer, J.H. A simulation study of mediated effect measures. Multivar. Behav. Res. 1995, 30, 41–62. [Google Scholar] [CrossRef] [PubMed]
- Bollen, K.A.; Stine, R. Direct and indirect effects: Classical and bootstrap estimates of variability. Sociol. Methodol. 1990, 115–140. [Google Scholar] [CrossRef]
- Preacher, K.J.; Hayes, A.F. SPSS and SAS procedures for estimating indirect effects in simple mediation models. Behav. Res. Methods 2004, 36, 717–731. [Google Scholar] [CrossRef]
- Preacher, K.J.; Leonardelli, G.J. Calculation for the Sobel Test: An Interactive Calculation Tool for Mediation Tests. 2001. Available online: http://quantpsy.org/sobel/sobel.htm (accessed on 10 April 2017).
- Martel, M.O.; Dolman, A.J.; Edwards, R.R.; Jamison, R.N.; Wasan, A.D. The association between negative affect and prescription opioid misuse in patients with chronic pain: The mediating role of opioid craving. J. Pain 2014, 15, 90–100. [Google Scholar] [CrossRef] [PubMed]
- Duffy, R.D.; Allan, B.A.; Dik, B.J. The presence of a calling and academic satisfaction: Examining potential mediators. J. Vocat. Behav. 2011, 79, 74–80. [Google Scholar] [CrossRef]
- Hayes, A.F. SPSS MEDIATE Macro Syntax Reference, updated 6 October 2014. Available online: http://afhayes.com/public/mediate.pdf (accessed on 10 April 2017).
- Bender, R.; Lange, S. Multiple test procedures other than bonferroni’s deserve wider use. Br. Med. J. 1999, 318, 600. [Google Scholar] [CrossRef]
- Parsons, J.E.; Adler, T.; Meece, J.L. Sex differences in achievement: A test of alternate theories. J. Personal. Soc. Psychol. 1984, 46, 26–43. [Google Scholar] [CrossRef]
- Miller, A. Tips for Using Project-Based Learning to Teach Math Standards [Blog Post]. 2011. Available online: https://www.edutopia.org/blog/project-based-learning-math-standards (accessed on 10 April 2017).
| Item | How Often Is the Following True? |
|---|---|
| 1 | PBL projects get students to discuss ideas in class. |
| 2 | PBL projects do a good job of getting students to do research to look for background information. |
| 3 | PBL projects draw from multiple courses or subjects. |
| 4 | PBL projects are interesting and fun. |
| 5 | PBL projects are relevant to students’ daily lives. |
| 6 | PBL projects give students a chance to think about future careers. |
| 7 | PBL projects help students to better understand current events and/or environmental issues. |
| 8 | PBL projects draw on things students have learned previously. |
| 9 | PBL projects require students to apply knowledge learned in the classroom to a real-life event. |
| 10 | PBL projects are central to the curriculum. |
| 11 | PBL projects require a thorough process of inquiry, knowledge building and resolution. |
| 12 | PBL projects are more student-led than teacher-led. |
| Factor | Actual | Simulated |
|---|---|---|
| 1 | 8.133 | 1.072 |
| 2 | 0.744 | 1.054 |
| 3 | 0.555 | 1.040 |
| 4 | 0.424 | 1.027 |
| 5 | 0.354 | 1.015 |
| Discipline | Model | EFA | Parallel Analysis | CFA Chi-Square | RMSEA | CFI | NNFI | AGFI |
|---|---|---|---|---|---|---|---|---|
| Science | ||||||||
| Two Factor (AB & IM as unique constructs) | Moderately supported | Supported | p < 0.001 (Supported) | 0.085 (Not supported) | 0.987 (Supported) | 0.987 (Supported) | 0.933 (Supported) | |
| One Factor (AB & IM as one construct) | Moderately supported | Not supported | p < 0.001 (Supported) | 0.307 (Not supported) | 0.807 (Not supported) | 0.715 (Not supported) | 0.321 (Not supported) | |
| Math | ||||||||
| Two Factor (AB & IM as unique constructs) | Moderately supported | Not supported | p < 0.001 (Supported) | 0.093 (Not supported) | 0.984 (Supported) | 0.973 (Supported) | 0.919 (Supported) | |
| One Factor (AB & IM as one construct) | Moderately supported | Supported | p < 0.001 (Supported) | 0.295 (Not supported) | 0.818 (Not supported) | 0.732 (Not supported) | 0.355 (Not supported) |
| Hypothesis | Independent Variable | Dependent Variable | Coefficient | p-Value | Semi-Partial Correlation | Total Model Adjusted R2 |
|---|---|---|---|---|---|---|
| 1 | Problem-Based Learning Rating (PBL) | Interest in Future STEM Career | 0.05 | 0.007 * | 0.0001 | 0.45 |
| 2 | Science Intrinsic Motivation | 0.04 | 0.005 * | 0.006 | 0.55 | |
| 2 | Science Ability Beliefs | 0.03 | 0.006 * | 0.005 | 0.64 | |
| 3 | Math Intrinsic Motivation | −0.03 | 0.06 | 0.0008 | 0.62 | |
| 3 | Math Ability Beliefs | 0.02 | 0.15 | 0.00005 | 0.67 | |
| 4 | Science Ability Beliefs | Interest in Future STEM Career (IFSTEMC) | 0.27 | <0.001 ** | 0.028 | 0.45 |
| 4 | Science Intrinsic Motivation | 0.23 | <0.001 ** | 0.09 | 0.45 | |
| 5 | Math Intrinsic Motivation | 0.16 | <0.001 ** | 0.04 | 0.45 | |
| 5 | Math Ability Beliefs | 0.10 | <0.001 ** | 0.002 | 0.45 |
| Indirect Effect of PBL on IFSTEMC through: | Effect | Lower Bound (LLCI) | Upper Bound (ULCI) | Significance | |
|---|---|---|---|---|---|
| Science Intrinsic Motivation | 0.024 | 0.0140 | 0.0363 | Significant | |
| Science Ability Beliefs | 0.029 | 0.0181 | 0.0415 | Significant | |
| Math Intrinsic Motivation | −0.0048 | −0.0128 | 0.0019 | Non-Significant | |
| Math Ability Beliefs | 0.0002 | −0.0032 | 0.0040 | Non-Significant |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
LaForce, M.; Noble, E.; Blackwell, C. Problem-Based Learning (PBL) and Student Interest in STEM Careers: The Roles of Motivation and Ability Beliefs. Educ. Sci. 2017, 7, 92. https://doi.org/10.3390/educsci7040092
LaForce M, Noble E, Blackwell C. Problem-Based Learning (PBL) and Student Interest in STEM Careers: The Roles of Motivation and Ability Beliefs. Education Sciences. 2017; 7(4):92. https://doi.org/10.3390/educsci7040092
Chicago/Turabian StyleLaForce, Melanie, Elizabeth Noble, and Courtney Blackwell. 2017. "Problem-Based Learning (PBL) and Student Interest in STEM Careers: The Roles of Motivation and Ability Beliefs" Education Sciences 7, no. 4: 92. https://doi.org/10.3390/educsci7040092
APA StyleLaForce, M., Noble, E., & Blackwell, C. (2017). Problem-Based Learning (PBL) and Student Interest in STEM Careers: The Roles of Motivation and Ability Beliefs. Education Sciences, 7(4), 92. https://doi.org/10.3390/educsci7040092





