Engaging Elementary Students in the Creative Process of Mathematizing Their World through Mathematical Modeling
Abstract
:1. Introduction
2. Background
- (1)
- How can phases of mathematical modeling as a process serve as a venue for exhibiting students’ critical 21st century skills?
- (2)
- What were some effective pedagogical practices teachers used as they implemented mathematical modeling with elementary students and how did these promote students’ 21st century skills?
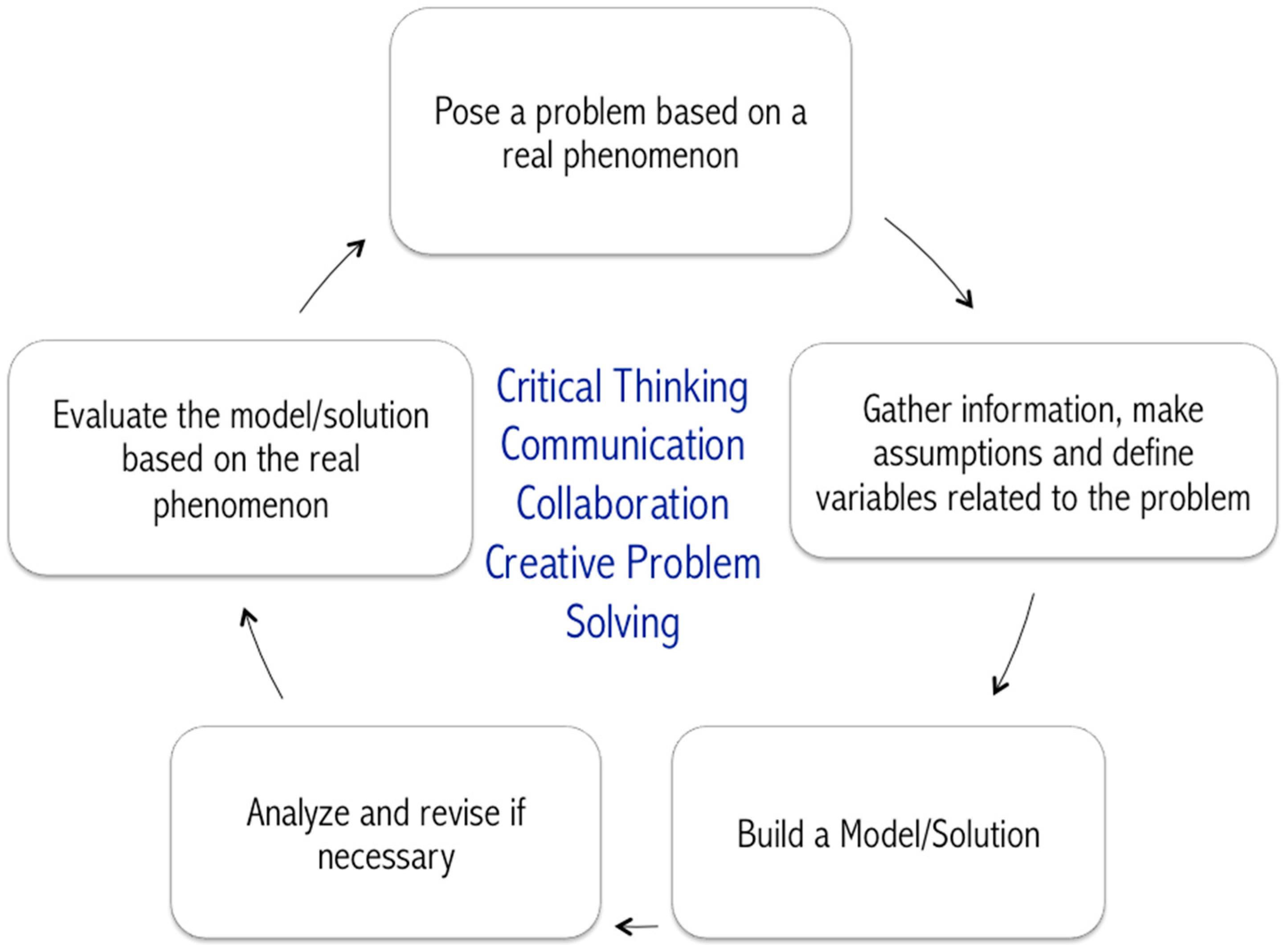
3. Materials and Methods
3.1. Design
3.2. Participants
3.3. Context
3.4. Data Collection
3.5. Data Analysis
4. Results
4.1. Critical 21st Century Skills Elicited as Students Engaged in MM Task 1: Touring a City
4.1.1. Critical Thinking and Problem Solving
- What is our budget?
- What mode of transportation can we use to get there?
- What mode of transportation can we use while we are there?
- What sites do we want to see in this city?
- What sites can we skip while there?
- Figure out the price of food depending on how much people eat, that led to the question of:
- What is the relation between the price of food and the number of people eating the food?
- Figure out the price of transportation depending on the time of year and place, that led to the question of,
- What is the best way to get to the destination? Considering choices between driving a car, taking a train, subway or plane. How will traffic be accounted for?
- Considering how weather could be a factor when planning a trip.
- Our family is going to need ____ budget for sightseeing.
- Our family will need to travel ____ miles to get to all the sites.
- Does our answer/solution make sense?
- How does our answer compare to the problem?
- Is there another solution we could look at?
- What are the strengths of our model? Where could our model use some improvements?
- Are there any factors or ideas we haven’t considered?
4.1.2. Creativity and Innovation
One student thought they had all their variables accounted for but when explaining his model to another student realized, “I forgot to include all the time my Dad takes when taking his pictures! He always takes so many and we all complain about how much time it takes.” The students then worked together to help the student add in “Picture Taking Time” to their model. As students took their models and considered the reality of the problems solving capability they often found themselves revising their thought processes and hence their model. One of the incidents that helped students see the need for revising the model occurred when students took their planning sheet home over the weekend. After sharing their proposal with their parents several students found that they needed to adjust the number of family members going, or that the attractions picked were not appropriate for younger siblings. This became a natural launching point for the discussion of revising their model.
4.1.3. Communication and Collaboration
4.2. Critical 21st Century Skills Elicited as Students Engaged in MM Task 2: In Opening a School Store
4.2.1. Critical Thinking and Problem Solving
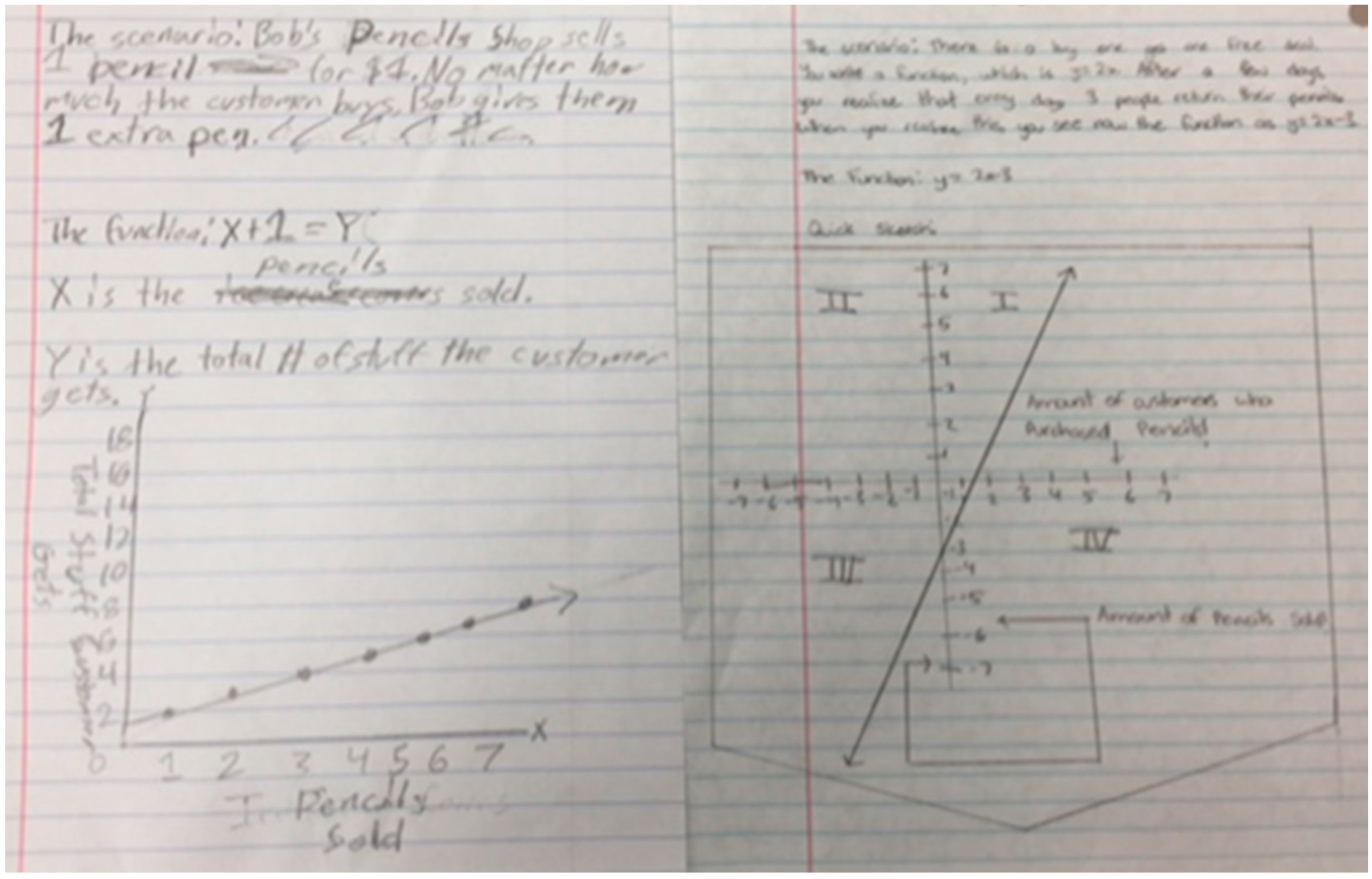
- What items should we sell at our store?
- How should we price our items?
- What will our profit be? What should we do with the profit?
- What hours should the store be open?
- Where should the store be located?
- How will we staff the store?
- Where will we store our inventory and keep it secure?
[P]lanned a status-of-the-school-store conversation with the entire ‘company’, with the goal of firming up a timeline for provisioning, advertising, and opening. The data crunching challenges will come up, so I will challenge the entire class to think about how we could expedite the process. My hope is that one option that’s thrown out is narrowing the sample space by taking a random sampling from each grade level. But, I want that to come from them (knowing that I will need to teach them the correct terminology). And, if the class thinks that using a random sampling is prudent, I’m even wondering if validity will come up, with someone suggesting that we take several random samplings, crunch the data, then compare results.
- Carla:
- “They don’t like these pencils. The mechanical ones are way cooler, so they don’t even consider buying the graphite ones.”
- Dan:
- “I think they’re too expensive for a boring old graphite pencil!”
- Teacher:
- “Talk to us about your thinking, Dan”
- Class:
- “Yea, maybe they do cost a little too much!”
- Carla:
- “But it’s more than that—customers just aren’t interested in them. We need to really push them.”
- Jake:
- “Yea, I’m thinking a combination of dropping the price and making people WANT to buy them is what we need to do.”
4.2.2. Creativity and Innovation
You got to define your problem, you have to narrow it down...so what are we really asking? What’s our goal here? What are the constraints? And so it’s a natural problem solving process so by putting it up there. It’s just a good anchor for the kids, like today it was a wonderful way to reiterate the point I was making that would take them through college to really figure out that it is, you don’t just come up with a solution and your problem is solved. It’s messy.
And another one and another one, so by having that visual it’s continuing to help them be ok with the messiness of multiple iterations of going back to the drawing board and failure even, we’ve had failure in some of the things that we try but that’s all ok because if we know that if it just swings back and forth.
That is really by giving them something they are accountable for...that they all had to think about what they would put in a survey. They had to have a poster and they had to include... I’m just asking for a deliverable, so just asking for something so ok you guys are all going to be thinking about how would you survey to find out and so they took thought to that or another day, the day that you were here, I asked them just to project for a week and I knew they would all be talking about.
4.2.3. Communication and Collaboration
4.3. Effective Pedagogical Practices Teachers Used in Enacting Mathematical Modeling with Elementary Students: Modeling Mathematics Pedagogical Practices
4.3.1. Finding the “Sweet Spot” along the Continuum of Openness and Providing Focus for the Learning
Their reality is not in a lot of the problems that textbooks give them. Their reality is not in a lot of things we try to hand them anymore and so it does take time for us to learn more about our kids and it does take time for us to figure out what are students are interested in and what their lives consist of, and what are their real challenges. My students have real challenges this summer of figuring out where they want to go and a lot of them have real challenges of trying to convince their parents to take them but if they can come up with an amazing opportunity to explain hey mom and dad we can do this in an entire day, it’s only going to cost us $250 or maybe even less and figure out the budget and explain to them how budgeting even less is even better and being able to help them understand. It’s a lot easier for them to relate to this as 8- and 9-year-olds because this is their world.
VA, DC, MD area6:30 a.m. to 11:59 p.m.Budget—$250FoodTravel at least see 3 different sites, must have at least two mealsAdmissions to museums
My questioning was intentional. I anticipated where I thought the discussion might go and prepared worksheets to help the students organize their thoughts. I gave students time to come up with the ideas themselves instead of telling them. Students need structure even though the task is open-ended. Each day I would tell them, for example, how much time we would be spending on math that day. I provided structure while maintaining open-endedness by providing students with worksheets, I’ll call them worksheets even though they’re not really traditional worksheets, to help them organize their thoughts. I did this when they were working on the surveys and I had them use the last portion of the math class to predict what would happen during the first week the store was open. I directed them to use math to predict what would happen. Similarly, I provided them with a “worksheet” asking them to suggest 3 business moves to move the ‘dead’ stock, show all of the math for each business move, and graph their results.(Alice’s reflective memo)
4.3.2. Seizing “Teachable Moments” and Having Curricular Knowledge
Entry 1: Create a budget sheetDon’t introduce it right away but let them see what it is.Create google excel budget sheet for third round to useEntry 2: Make a list of visitor websites, train and travel websitesRelook at the guiding questionsCome up w/ reflection sheet for studentsEntry 3: Mini goals for each dayWorking independently given time to collaborate idea share in pairsEntry 4: Define My Problem—Determining my city and list of possible attractions aka “MY Best”Getting around: Distance and cost of travel (review opportunity cost)Having Fun: Cost of attractions, Cost of foodBudget Day: organize information intoFinal Calculations and result sharing(Excerpt from Lisa’s daily log)
It’s just going to depend on where they are going with it, definitely, and that’s the best part with mathematical modeling for a teacher because it really gives you that part of teaching back that you really like about teaching when you are able to say ok this is an opportunity for me as a teacher to really listen to my students to hear what they are thinking and then being able to take those teachable moments and turn them back around and say ok let’s stop here and look at what types of questions you are asking or not asking and trying to derive that.—Lisa’s Interview
It is important for teachers to know their curriculum. They don’t need to be very experienced teachers to do mathematical modeling but, as long as they know what lies ahead and what they will need to cover, mathematical modeling will work for them. I think teachers with just a year or two of experience can do mathematical modeling. Mathematical modeling is open-ended so you never know exactly where the problem-solving will lead but if you know your curriculum you recognize the possibilities when they arise. The math may not develop in the same order as the pacing guide but that’s alright because it will get covered.—Alice’s Memo
4.3.3. Use of Mathematical Modeling Process Tools and Student-Generated Artifacts to Thoughtfully Orchestrations the MM Process and Mathematical Discourse
I mean again they have all their data and stats I have to teach and we even saw a quick mini lesson and you saw another quick review this morning that’s all happened just peppered here or there and they are just taking it well beyond and they are just looking at the statistics they are looking at the idea of random sampling and that stuff is well beyond and they’ll never forget any of it because they need it they want it they are motivated the math hasn’t been done onto them they are filling up the math.—Alice’s Interview
So I’m sure in any modeling situation you know these messier modeling scenarios I think any teacher is going to see “Oh my gosh these guys need this math but these guys are doing that but I really want them all to see it” so you’ve got some decisions to make and sometimes if it’s a review or math they’ve learned earlier than simply in the sharing out and stuff you hang in the room with just that intentional opportunity to give their status and kind of explain what they were doing then everybody ends up engaging or it could be as extreme as dropping everything for a day and say “oh my gosh these guys are using spreadsheets you’ve got to see what they are doing” and experience the magic everybody!—Alice’s Interview
4.4. Pedagogical Moves that Promoted Students’ 21st Century Skills
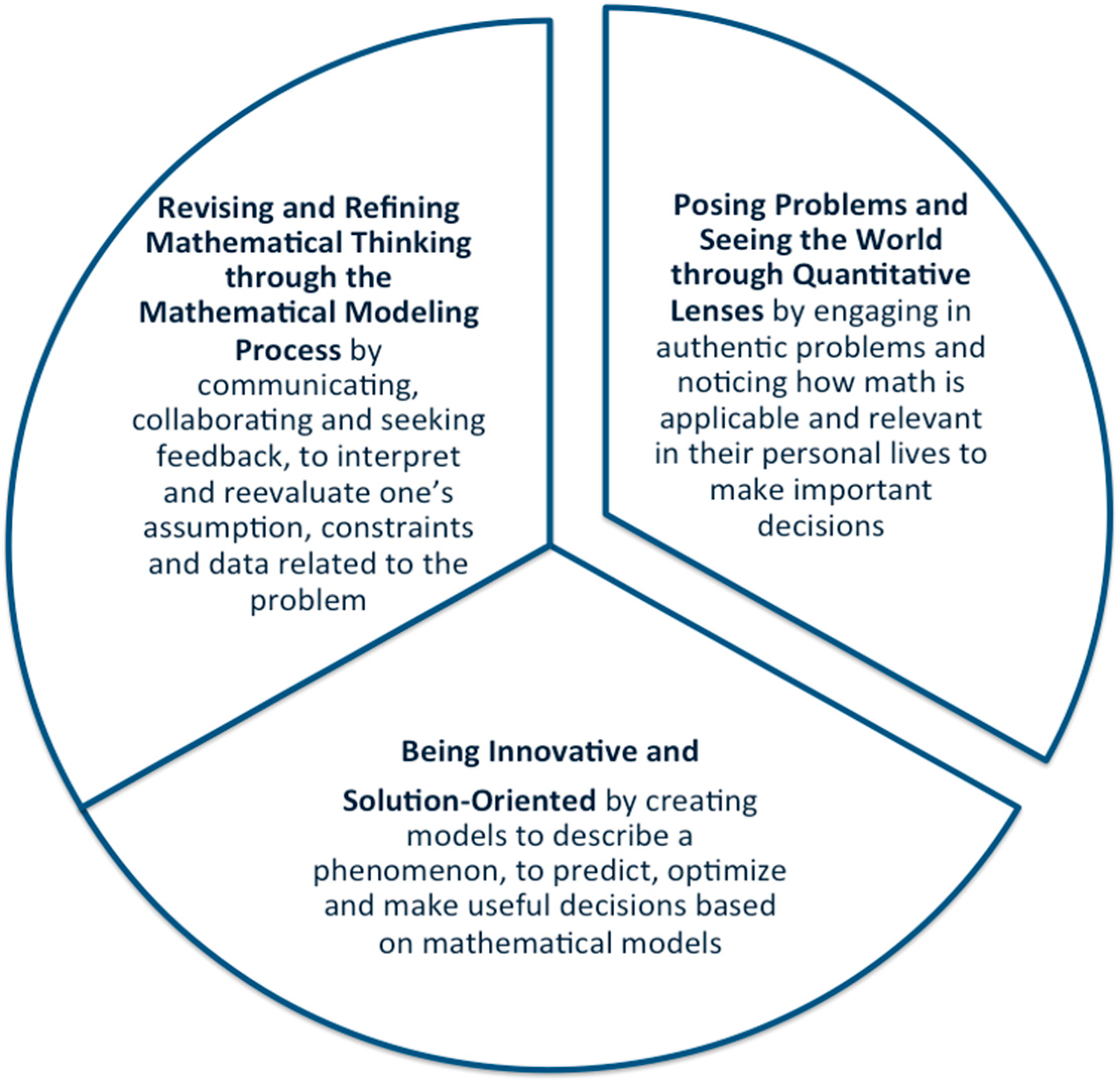
5. Discussion
- Confidence in dealing with complexity;
- Persistence in working with difficult problems;
- Tolerance and ability to deal with open ended problem;
- The ability to communicate and work with others to achieve a common goal or solution
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gravemeijer, K.; Stephan, M.; Julie, C.; Lin, F.-L.; Ohtani, M. What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 2017, 15, 105–123. [Google Scholar] [CrossRef]
- Wolfram, C. Teaching Kids Real Math with Computers. Youtube, Uploaded by TedTalks. 15 November 2010. Available online: https://www.youtube.com/watch?v=60OVlfAUPJg (accessed on 15 January 2017).
- English, L.D.; Charles, K.L.; Cudmore, D.H. Students’ statistical reasoning during a data modelling program. In Proceedings of the 24th Conference of the International Group for the Psychology of Mathematics Education, Hiroshima, Japan, 23–27 July 2000; Nakahara, T., Koyama, M., Eds.; pp. 265–272. [Google Scholar]
- Greer, B. Statistical thinking and learning. Math. Think. Learn. 2000, 2, 1–9. [Google Scholar] [CrossRef]
- Lajoie, S.P. Reflection on Statistics: Learning, Teaching and Assessment in Grades K-12; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1998; ISBN 978-0805819724. [Google Scholar]
- Cirillo, M.; Pelesko, J.; Felton-Koestler, M.; Rubel, L. Perspectives on modeling in school mathematics. In Mathematical Modeling and Modeling Mathematics; Hirsch, C.R., Roth, A.R., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2016; pp. 3–16. ISBN 978-0-87353-973-9. [Google Scholar]
- Garfunkel, S.A.; Montgomery, M. (Eds.) GAIMME: Guidelines for Assessment & Instruction in Mathematical Modeling Education; Consortium for Mathematics and Its Applications [COMAP, Inc.]: Bedford, MA, USA; Society for Industrial and Applied Mathematics [SIAM]: Philadelphia, PA, USA, 2016; Available online: http://www.siam.org/reports/gaimme-full_color_for_online_viewing.pdf (accessed on 15 January 2017).
- Blum, W.; Ferri, R.B. Advancing the teaching of mathematical modeling: Research-based concepts and examples. In Mathematical Modeling and Modeling Mathematics; Hirsch, C.R., McDuffie, A.R., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2016; pp. 65–76. ISBN 978-0-87353-973-9. [Google Scholar]
- Blum, W.; Ferri, R.B. Mathematical modeling. Can it be taught and learnt? J. Math. Mod. Appl. 2009, 1, 45–58. [Google Scholar]
- P21 Partnership for 21st Century Learning. Available online: http://www.p21.org/ (accessed on 15 February 2017).
- Stake, R. The Art of Case Study Research; Sage Publications: Thousand Oaks, CA, USA, 1995; ISBN 978-0803957671. [Google Scholar]
- Patton, M. Qualitative Research and Evaluation Methods, 4th ed.; Sage Publications: Thousand Oaks, CA, USA, 2015; ISBN 978-1-4129-7212-3. [Google Scholar]
- Rogers, E.M. Diffusion of Innovations, 5th ed.; Free Press: New York, NY, USA, 2003; ISBN 978-0743222099. [Google Scholar]
- Saldaña, J. The Coding Manual for Qualitative Researchers, 3rd ed.; Sage Publications: Los Angeles, CA, USA, 2016; ISBN 978-1473902497. [Google Scholar]
- Dedoose Version 6.2.7. Available online: http://www.dedoose.com/ (accessed on 1 October 2016).
- Angelides, P. The development of an efficient technique for collecting and analyzing qualitative data: The analysis of critical incidents. Int. J. Qual. Stud. Educ. 2001, 14, 429–442. [Google Scholar] [CrossRef]
- Hill, C.E.; Thompson, B.J.; Nutt Williams, E. A guide to conducting consensual qualitative research. Couns. Psychol. 1997, 25, 517–572. [Google Scholar] [CrossRef]
- Blanton, M.L.; Kaput, J.J. Developing elementary teachers’: “Algebra eyes and ears”. Teach. Child. Math. 2003, 10, 70–78. [Google Scholar]
- Blanton, M.L.; Kaput, J.J. Characterizing a classroom practice that promotes algebraic reasoning. J. Res. Math. Educ. 2005, 36, 412–446. [Google Scholar]





|
| Mathematical Modeling | Teaching Practices for Mathematical Modeling | Opportunities for Students to Engage in 21st Century Skills |
|---|---|---|
| Pose a problem | Teachers presenting an engaging phenomenon that elicits mathematical modeling. Teachers helping students problematize the situation by considering what problems students might want to pose related to this phenomenon. | As students posed problems relevant to the phenomenon at hand, they brainstormed which encouraged divergent thinking and creativity. |
| Make assumption/define variable | Teachers determining the appropriate degree of openness and constraints that students would consider. To focus on the important mathematics, the teachers asked what students knew/would they need to know, using a Know, Want, and, Learned (KWL) chart. What assumptions will students make to define this problem? How will students solve this problem? | Students used critical thinking as they made choices while formulating their problem, making assumptions and defining the variables. What kinds of choices need to be made to mathematize this problem? What are the quantities to be considered related to the problem at hands? How are these quantities related to one another? |
| Build a model | Teachers anticipating potential pathways for mathematical thinking and asking what mathematics students would need in order to approach a solution or build a model. Will the mathematical topics be ones they know and can apply or will the mathematics be above their current learning goals? | Students were able to apply the math they know to solve real-world problem and make a connection to important applications. Students were exposed to mathematics that were at a higher level but in context and this peaked their interest in learning challenging mathematics. |
| Analyze model | Teachers actively monitoring the mathematical modeling process and selecting mathematical ideas for students to present to peers for feedback and to test their model against others’ model. | Students were given the opportunity to justify their reasoning and use numbers, models and words to explain their solution. |
| Evaluate and refine the model | Teachers providing time and space for students to revise and refine their thinking while learning from one another, critiquing, appreciating peers’ solutions, and refining their own math thinking in the process. | Students used the feedback to ask: What can I change based on what I learned from evaluating my model along with my peers’ solution? |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suh, J.M.; Matson, K.; Seshaiyer, P. Engaging Elementary Students in the Creative Process of Mathematizing Their World through Mathematical Modeling. Educ. Sci. 2017, 7, 62. https://doi.org/10.3390/educsci7020062
Suh JM, Matson K, Seshaiyer P. Engaging Elementary Students in the Creative Process of Mathematizing Their World through Mathematical Modeling. Education Sciences. 2017; 7(2):62. https://doi.org/10.3390/educsci7020062
Chicago/Turabian StyleSuh, Jennifer M., Kathleen Matson, and Padmanabhan Seshaiyer. 2017. "Engaging Elementary Students in the Creative Process of Mathematizing Their World through Mathematical Modeling" Education Sciences 7, no. 2: 62. https://doi.org/10.3390/educsci7020062
APA StyleSuh, J. M., Matson, K., & Seshaiyer, P. (2017). Engaging Elementary Students in the Creative Process of Mathematizing Their World through Mathematical Modeling. Education Sciences, 7(2), 62. https://doi.org/10.3390/educsci7020062






