Using Grounded Theory to Extend Existing PCK Framework at the Secondary Level
Abstract
:1. Introduction
(3) Teachers need to be aware of what each and every student is thinking and knowing, to construct meaning and meaningful experiences in light of this knowledge, and have proficient knowledge and understanding of their content to provide meaningful and appropriate feedback…; (4) Teachers need to know the learning intentions and success criteria of their lessons, know how well they are attaining these criteria for all students, and know where to go next…; (5) Teachers need to move from the single idea to multiple ideas, and to relate and then extend these ideas [so that their students can] construct and reconstruct their knowledge and ideas [which is critical for success].[1] (pp. 238–239)
2. Theoretical Framework
2.1. Applicablity of the Existing Frameworks for Capturing the Knowledge Needed for Teaching and the Choice of the Content Focus
2.2. Research Question
3. Materials and Methods
3.1. Participants
3.2. Instruments
3.3. The Methodological Challenges of This Mixed Methods Approach
4. Data Analysis and Results
4.1. How Were the Different Data Combined in Grounded Theory
- Identified our substantive area—teaching geometry; population consisted of the 39 intermediate/secondary school teachers;
- Collected both qualitative and quantitative data;
- Open coded the data as we collected them, so that the core category and the main concern become apparent;
- Wrote memos throughout the entire process;
- Conducted selective coding and theoretical sampling starting from a subset of seven marker cases; once that the core category and main concern were recognized; open coding would stop and selective coding—coding only for the core category and related categories—would begin;
- Further sampling from the raw data from 39 teachers was directed by the developing theory and used to saturate the core category and related categories;
- After our categories became saturated, we sorted our memos and found the Theoretical Codes which best organized our substantive codes;
- When we felt that the theory was well formed, we read the literature and integrated it with our theory through selective coding;
- As a result, we isolated the following five dimensions of PCK: (1) content knowledge (e.g., knowledge of geometry); (2) knowledge of student challenges and understandings; (3) knowledge of appropriate diagnostic questions; (4) pedagogical knowledge (i.e., knowledge of appropriate instructional strategies, including use of manipulatives and technology); and (5) knowledge of possible extensions (designed to deepen students’ understanding of the problem; e.g., knowledge of geometric extensions); and
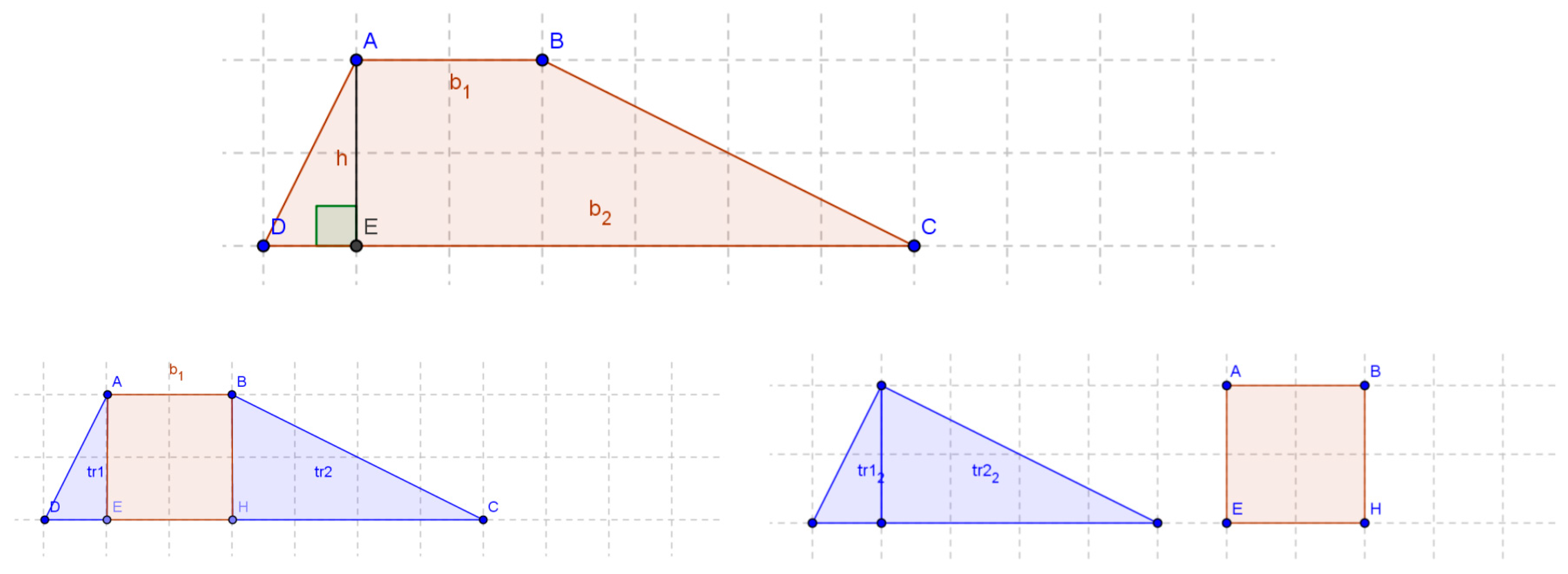
- Wrote our theory—which meant that we created the rubrics for identifying specific characteristics of different levels of teachers’ PCK. These rubrics were result of modifications in Stages 6–9, when we refined them to achieve differentiation between levels 0–4 of teacher competencies levels (4 being the highest; adequate for an expert Geometry teacher). This was the main contribution to better understanding the nature of educator’s mathematics content knowledge and extending the existing frameworks for PCK in/for teaching mathematics at the secondary level. Table 1 and Table 2 contain excerpts from the rubric used to identify teachers’ knowledge of student challenges and conceptions at Level 4 and Level 1. For this dimension, we identified 15 sub-components (A–O), and based on their presence/absence in teacher data, we were able to identify the level of teacher’s knowledge of student challenges and understandings. Each participant received an average score based on responses to questions (b) and (c) on the six PCK items (e.g., one item presented Scott’s approach in developing a trapezoid formula).
…every trapezoid cannot be broken into two right triangles and a rectangle. [A, see Table 1] Scott’s method would not work for a right trapezoid because there wouldn’t be a second triangle to recompose into one larger triangle. Of course, a right trapezoid could be decomposed into one rectangle and one triangle…. Scott’s method also wouldn’t work for trapezoids whose parallel sides do not overlap… because a rectangle wouldn’t be constructed.Scott is limited by his experience with trapezoids. If he believes that his method will work for all trapezoids, then he’s only considering trapezoids that look like the typical isosceles trapezoid. [B, see Table 1] He may be at Level 1 in van Hiele if he doesn’t understand the variety of shapes can still fall under the same categories. [D, see Table 1]Scott did not spend enough time manipulating quadrilaterals. He is probably used to being presented with trapezoids that all look similar, such as the one he used to derive an area formula. Scott is possibly more comfortable with rectangles and triangles, which is why he focuses on the properties of those shapes instead of the properties of trapezoids. [F, see Table 1]
4.2. Identification of Results
- i
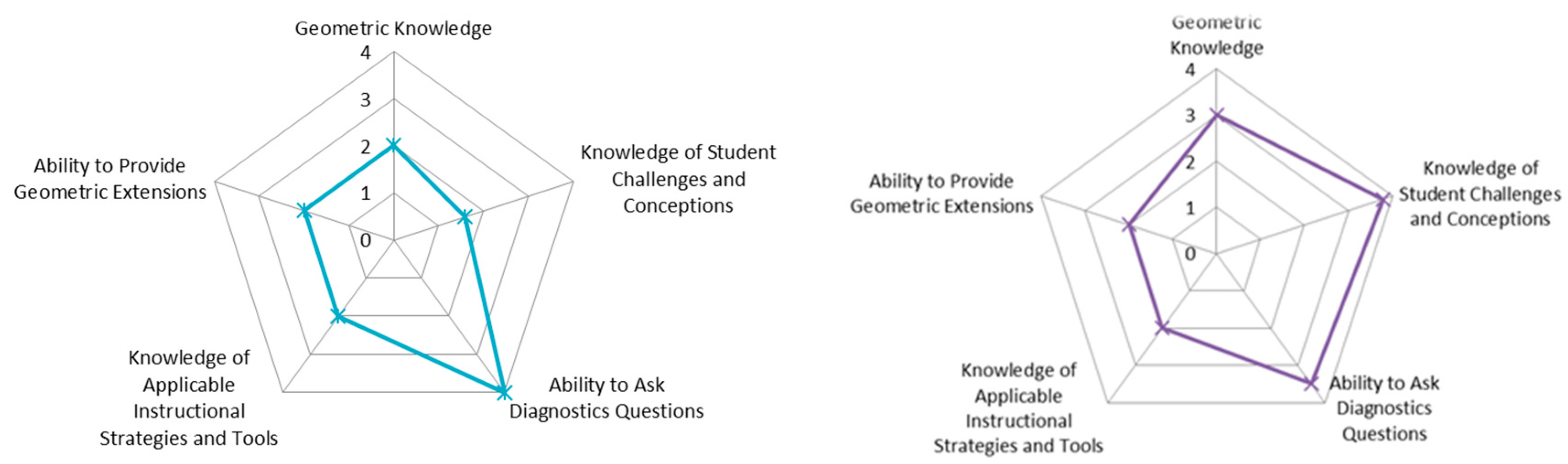
- Teachers’ PCK profiles are distinct. The distinct teacher profiles using the PCK instrument and the developed rubrics were generated for each teacher. Representation of the PCK profile for two of our marker cases—Peter and Sally, both experienced secondary school teachers, are presented in Figure 1.
- ii
- Dimensions of teachers’ PCK may be affected by their teaching practice and education [17]. Teachers’ “geometric knowledge” appeared stable, as it was mainly developed during teacher education programs, while the “knowledge of applicable instructional strategies and tools” as well as “knowledge of student challenges and conceptions” appeared dynamic and situated in teaching practice.
- iii
- Teachers need to develop strategies for creating opportunities for all students to learn. Our participants had fewer problems with recognizing that a student’s approach is limited and that it points to some misconception, then when they were given a mathematically correct approach for developing the area of trapezoid formula. In the latter cases, most of the participants were not able to provide convincing scenarios of how to facilitate further student thinking and help them to extend their approach.
- iv
- Teachers’ individual characteristics, such as their attitudes, values with respect to mathematics teaching, and motivations affect their PCK. Our participants differed in how they described the main responsibility of the geometry teacher (e.g., creating a learner-centered vs. teacher-centered environment).
4.3. Study Limitations
5. Discussion
- Methodological: By choosing a mixed methods approach to measure multiple facets of PCK, our work forms an important counterpart to unidimensional large scale studies on PCK. This might take the larger education community discussion on measuring PCK to a next level. By providing details about the sample and the context we allow other researchers “to assess the fittingness or transferability of the findings” [27] (p. 433).
- Thematic: Our focus on one specific PCK topic, namely geometry of trapezoids can be seen as a counterpart to a large number of PCK studies that try to measure an overall PCK. The teacher’s PCK is contextual [9] and may be different for every topic s/he teaches. Determining this would require using the PCK tool on a larger sample of participants, which may be addressed in another study. In addition, by measuring PCK in geometry, we attend to a domain that has not received much attention in current PCK studies. We propose that the PCK instruments should be designed as “probes” around the topics commonly taught by a targeted group of teachers (e.g., middle school). If the researchers put their efforts into developing such probes, the research community will be more adept to critically examine them, and those that pass the examination, will be more likely to be implemented.
- Connected to practice: Online exemplars and rubrics that we created may be used when planning differentiated professional development activities or for self-assessment purposes [9].
Author Contributions
Conflicts of Interest
Appendix A. Exemplars of Holly’s and Scott’s Work from the PCK Instrument. Both Represent the Cases Decomposing, but Holly’s Approach is Generalizable, while Scott’s Presents Special (Non-Generalizable) Case
Appendix A.1. ITEM Holly
- Based on the diagram above (see Figure A1), describe Holly’s thinking. If she were to complete the formal derivation of the area formula in her diagrams, would her method work for any trapezoid? Why, or why not?
- If her approach presents a misunderstanding, what underlying geometric misconception(s) or misunderstanding(s) might lead her to the error presented in this item?
- If Holly’s approach presents misconception or misunderstanding, how might she have developed the misconception(s)?
- What further question(s) might you ask Holly to understand her thinking?
- What instructional strategies and/or tasks would you use during the next instructional period to address Holly’s misconception(s) (if any presented)? Why?
- If applicable, how would you use technology or manipulatives to address her misconception or misunderstanding?
- How would you extend this problem to help Holly further develop her understanding of the area of a trapezoid?

Appendix A.2. ITEM Scott
- Based on the diagram above (see Figure A2), describe Scott’s thinking. If he were to complete the formal derivation of the area formula using his diagrams, would his method work for any trapezoid? Why, or why not?
- If Scott’s approach presents a misunderstanding, what underlying geometric misconception(s) or misunderstanding(s) might lead him to the error presented in this item?
- If Scott’s approach presents a misconception or misunderstanding, how might he have developed the misconception(s)?
- What further question(s) might you ask Scott to understand his thinking?
- What instructional strategies and/or tasks would you use during the next instructional period to address Scott’s misconception(s) (if any presented)? Why?
- If applicable, how would you use technology or manipulatives to address Scott’s misconception or misunderstanding?
- How would you extend this problem to help Scott further develop his understanding of the area of a trapezoid?
Appendix B. Detailed Timeline of Methodological Steps Taken in This Study
References
- Hattie, J. Visible Learning: A Synthesis of over 800 Meta-Analyses Relating to Achievement; Routledge: New York, NY, USA, 2009. [Google Scholar]
- Ontario Ministry of Education. Achieving Excellence: A Renewed Vision for Education in Ontario. Available online: http://www.edu.gov.on.ca/eng/about/renewedVision.pdf (accessed on 10 January 2017).
- National Council of Teachers of Mathematics. Principles to Actions. Available online: www.nctm.org/PtA/ (accessed on 10 January 2017).
- OECD (Organization for Economic Co-operation and Development). Are the New Millennium Learners Making the Grade? Technology Use and Educational Performance in PISA 2006; OECD Publishing: Paris, France, 2006; Available online: www.oecd.org/edu/ceri/45053490.pdf (accessed on 10 January 2017).
- Borko, H.; Jacobs, J.; Eiteljorg, E.; Pittman, M.E. Video as a tool for fostering productive discussions in mathematics professional development. Teach. Teach. Educ. 2008, 24, 417–436. [Google Scholar] [CrossRef]
- Usiskin, Z. Teachers’ mathematics: A collection of content deserving to be a field. Math. Educ. 2001, 6, 86–98. [Google Scholar]
- Ontario Ministry of Education. Report: A Forum for Action, Effective Practices in Mathematics Education, Toronto, Ontario, 11–12 December 2013. Available online: http://thelearningexchange.ca/wp-content/uploads/2013/12/math-forum-report_final_april7-1.pdf (accessed on 10 January 2017).
- Sinclair, N. Research Paper Prepared for a Forum for Action: Effective Practices in Mathematics Education, Toronto, Ontario, 11–12 December 2013. Available online: https://mathforum1314.files.wordpress.com/2014/01/dr-nathalie-sinclair-research-paper-math-forum-2013.pdf (accessed on 10 January 2017).
- Manizade, A.G.; Martinovic, D. Developing interactive instrument for measuring teachers’ professionally situated knowledge in geometry and measurement. In International Perspectives on Teaching and Learning Mathematics with Virtual Manipulatives; Moyer-Packenham, P., Ed.; Springer: Cham, Switzerland, 2016; pp. 323–342. [Google Scholar]
- Shulman, L.S. Knowledge and teaching: Foundations of new reforms. Harv. Educ. Rev. 1987, 57, 1–23. [Google Scholar] [CrossRef]
- Hill, H.; Sleep, L.; Lewis, J.; Ball, D. Assessing teachers’ mathematical knowledge: What knowledge matters and what evidence counts. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Jr., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 111–156. [Google Scholar]
- Hill, H.C.; Ball, D.L.; Schilling, S.G. Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. J. Res. Math. Educ. 2008, 39, 374–400. [Google Scholar]
- University of Louisville. Diagnostics Mathematics Assessment for Middle School Teachers. Available online: http://louisville.edu/education/centers/crmstd/diag-math-assess-middle (accessed on 5 January 2017).
- Depaepe, F.; Verschaffel, L.; Kelchtermans, G. Pedagogical content knowledge: A systematic review of the way in which the concept has pervaded mathematics educational research. Teach. Teach. Educ. 2013, 34, 12–25. [Google Scholar] [CrossRef]
- Selling, S.K.; Garcia, N.; Ball, D.L. What does it take to develop assessments of mathematical knowledge for teaching?: Unpacking the mathematical work of teaching. Math. Enthus. 2016, 13, 35–51. [Google Scholar]
- Howell, H.; Lai, Y.; Phelps, G.; Croft, A. Assessing Mathematical Knowledge for Teaching Beyond Conventional Mathematical Knowledge: Do Elementary Models Extend? 2016. Available online: https://doi.org/10.13140/RG.2.2.14058.31680 (accessed on 5 January 2017).
- Kaiser, G.; Blömeke, S.; Busse, A.; Döhrmann, M.; König, J. Professional knowledge of (prospective) mathematics teachers—its structure and development. In Proceedings of the PME 38 & PME-NA 36 (V. 1), Vancouver, BC, Canada, 15–20 July 2014; Liljedahl, P., Nicol, C., Oesterle, S., Allan, D., Eds.; PME: Vancouver, BC, Canada, 2014. [Google Scholar]
- Manizade, A.G.; Mason, M.M. Using Delphi methodology to design assessments of teachers’ pedagogical content knowledge. Educ. Stud. Math. 2011, 76, 183–207. [Google Scholar] [CrossRef]
- Manizade, A.G.; Mason, M.M. Developing the area of a trapezoid. Math. Teach. 2014, 107, 508–514. [Google Scholar] [CrossRef]
- Clarke, D.; Hollingsworth, H. Elaborating a model of teacher professional growth. Teach. Teacher Educ. 2002, 18, 947–967. [Google Scholar] [CrossRef]
- Hollingsworth, H. Teacher Professional Growth: A Study of Primary Teachers Involved in Mathematics Professional Development. Ph.D. Thesis, Deakin University, Victoria, Australia, 1999. [Google Scholar]
- Charmaz, K. Constructing Grounded Theory, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2014. [Google Scholar]
- Strauss, A.L.; Corbin, J. Basics of Qualitative Research: Grounded Theory Procedures and Techniques; Sage Publications: Newbury Park, CA, USA, 1990. [Google Scholar]
- University of Chicago. Van Hiele Levels and Achievement in Secondary School Geometry: Appendix B. Zalman Usiskin: Chicago, IL. Available online: ucsmp.uchicago.edu/resources/van_hiele_levels.pdf (accessed on 5 January 2017).
- Martinovic, D.; Manizade, A.G. Teachers Evaluating Dissections as an Approach to Calculating Area of Trapezoid: Exploring the Role of Technology. In Proceedings of the 5th North American GeoGebra Conference: Explorative Learning with Technology, Toronto, ON, Canada, 21–22 November 2014; Martinovic, D., Karadag, K., McDougall, D., Eds.; University of Toronto: Toronto, ON, Canada, 2014; pp. 44–50. [Google Scholar]
- Junker, B.; Weisberg, Y.; Matsumura, L.C.; Crosson, A.; Wolf, M.K.; Levison, A.; Resnick, L. Overview of the Instructional Quality Assessment; CSE Technical Report 671; Center for the Study of Evaluation National Center for Research on Evaluation, Standards, and Student Testing (CRESST); University of California: Los Angeles, VA, USA, 2006; Available online: https://www.cse.ucla.edu/products/reports/r671.pdf (accessed on 5 January 2017).
- Chiovitti, R.F.; Piran, N. Rigour and grounded theory research. J. Adv. Nurs. 2003, 44, 427–435. [Google Scholar] [CrossRef] [PubMed]
- Tiainen, T.; Koivunen, E.-R. Exploring forms of triangulation to facilitate collaborative research practice: Reflections from a multidisciplinary research group. J. Res. Pract. 2006, 2, M2. Available online: http://jrp.icaap.org/index.php/jrp/article/view/29/61 (accessed on 5 January 2017).
- Gellert, U.; Becerra Hernández, R.; Chapman, O. Research methods in mathematics teacher education. In Third International Handbook of Mathematics Education; Clements, M.A.K., Bishop, A.J., Keitel, C., Kilpatrick, J., Leung, F.K.S., Eds.; Springer Science & Business Media: New York, NY, USA, 2013; Volume 27, pp. 431–457. [Google Scholar]
- Lincoln, Y.S.; Guba, E.G. Naturalistic Inquiry; Sage Publications: Beverly Hills, CA, USA, 1985. [Google Scholar]
- Gall, M.D.; Gall, J.P.; Borg, W.R. Educational Research: An Introduction; Pearson Education: Boston, MA, USA, 2007. [Google Scholar]
- Jackson, P.W. The Way Teaching Is; National Education Association: Washington, DC, USA, 1996; pp. 7–27. Available online: http://files.eric.ed.gov/fulltext/ED028110.pdf (accessed on 5 January 2017).
| Teacher is able to identify A and (B or C) and (D or E) and F *: |
|---|
|
| Teacher’s Response Covers G and (H or I) *: |
|---|
|
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinovic, D.; Manizade, A.G. Using Grounded Theory to Extend Existing PCK Framework at the Secondary Level. Educ. Sci. 2017, 7, 60. https://doi.org/10.3390/educsci7020060
Martinovic D, Manizade AG. Using Grounded Theory to Extend Existing PCK Framework at the Secondary Level. Education Sciences. 2017; 7(2):60. https://doi.org/10.3390/educsci7020060
Chicago/Turabian StyleMartinovic, Dragana, and Agida G. Manizade. 2017. "Using Grounded Theory to Extend Existing PCK Framework at the Secondary Level" Education Sciences 7, no. 2: 60. https://doi.org/10.3390/educsci7020060
APA StyleMartinovic, D., & Manizade, A. G. (2017). Using Grounded Theory to Extend Existing PCK Framework at the Secondary Level. Education Sciences, 7(2), 60. https://doi.org/10.3390/educsci7020060





