Abstract
This paper examines the experiences of two elementary teachers’ implementation of mathematical modeling in their classrooms and how the enactment by the teachers and the engagement by students exhibited their creativity, critical thinking, collaboration and communication skills. In particular, we explore the questions: (1) How can phases of mathematical modeling as a process serve as a venue for exhibiting students’ critical 21st century skills? (2) What were some effective pedagogical practices teachers used as they implemented mathematical modeling with elementary students and how did these promote students’ 21st century skills? We propose that mathematical modeling provides space for teachers and students to have a collective experience through the iterative process of making sense of and building knowledge of important mathematical ideas while engaging in the critical 21st century skills necessary in our complex modern world.
1. Introduction
Over the years, the cycle of student learning has shifted from students as consumers of information to students as creators of information. Integral to this paradigm shift is the important role of developing the 21st century skills and mathematical proficiency of each and every learner. This requires proficiency in communication, creativity, critical thinking, and collaboration to solve big, complex and non-routine real-world problems. In a recent special Science, Technology, Engineering, and Mathematics (STEM) education article, What Mathematics Education May Prepare Students for the Society of the Future, Gravemeijer et al. [1] posed questions about what mathematical proficiency means in today’s world and what shifts need to be made in both content and pedagogy to prepare students for 21st century skills and mathematical reasoning. They called for the development of 21st century skills, conceptual understanding of mathematics, and attending to the mathematics that prepare students for the workplace and have practical relevance outside of school. Wolfram [2] states that the mathematics involved in the real world requires: recognizing where mathematics is applicable; translating practical problems into mathematical problems; and interpreting and evaluating the outcomes. Developing these essential skills to solve problems can be nurtured as early as elementary grades, by providing students with opportunities to engage in solving authentic real-world problems within their world. The associated student reasoning often involves posing problems, generating data, quantifying information, representing solutions and communicating results [3,4,5]. In this paper, we will share how mathematical modeling provided a unique opportunity to engage elementary level students in this creative process of mathematizing their world.
2. Background
Mathematical modeling has gained the attention of researchers and educators with the release of the Common Core State Standards in Mathematics (CCSSM) Standard for Mathematical Practice 4 (SMP4): Model with Mathematics. Though SMP4 is intended to cut across grades K–12, mathematical modeling is not highlighted in connection with the K–8 content standards and thus teachers’ understanding of mathematical modeling is not supported [6]. Mathematical Modeling can be easily confused with other uses of the words, such as models and modeling, in mathematics education. Modeling can be viewed as physical modeling (e.g., the use of manipulatives), mental modeling (e.g., student viewing a concept such as negative numbers as a balance), or the modeling of thinking (demonstrations of procedures or strategies). Thus, it is important to define what mathematical modeling is and what it is not.
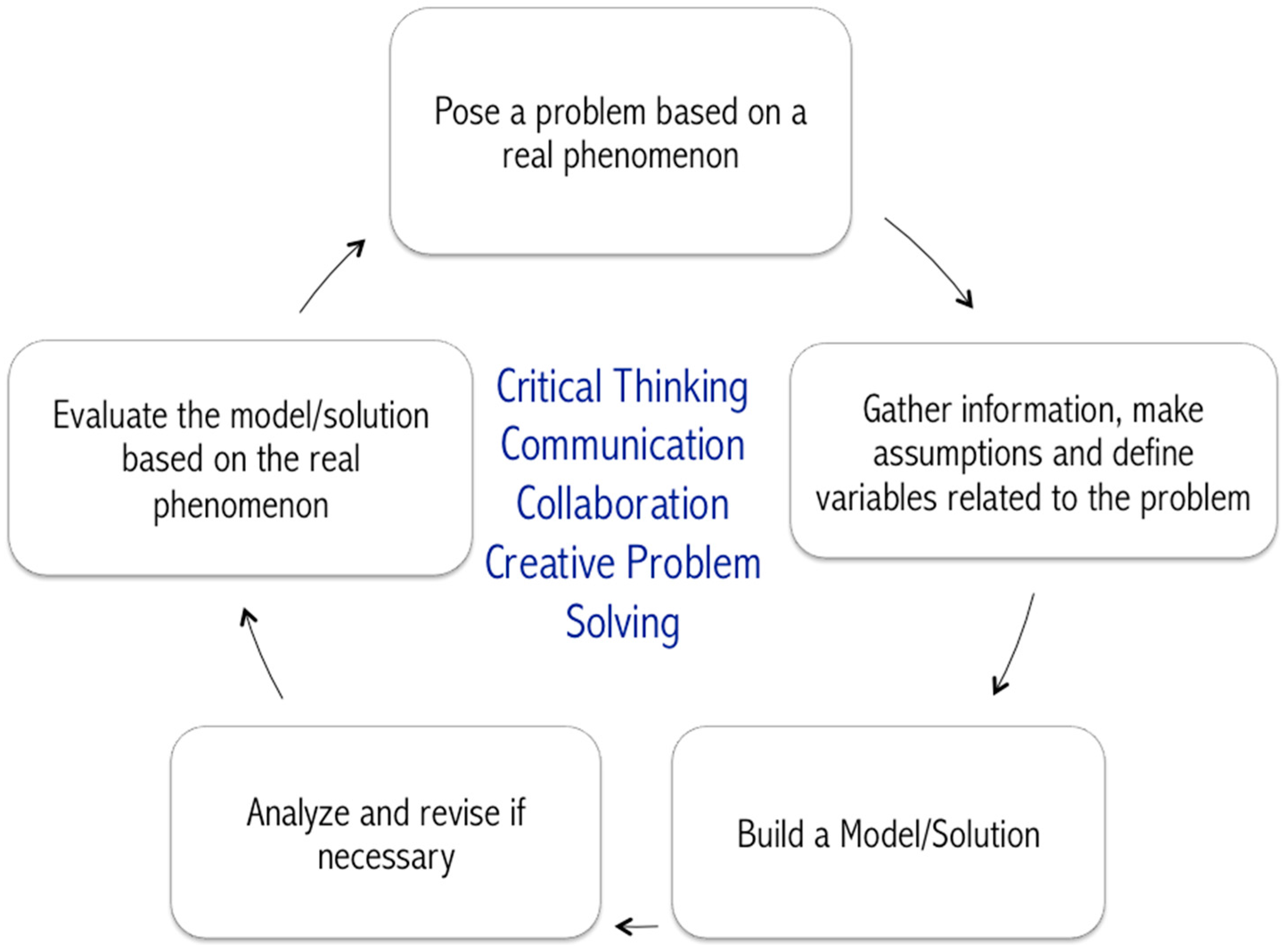
Mathematical modeling is, “a process that uses mathematics to represent, analyze, make predictions or otherwise provide insight into the real-world phenomena” [7] (p. 8, the Guidelines for Assessment & Instruction in Mathematical Modeling Education, GAIMME report). Mathematical modeling “denotes the process of translating, in both directions, between mathematics and the extra-mathematical world” [8] (p. 65). Similar to the GAIMME report, we see mathematical modeling as an iterative problem solving process that includes posing authentic, open-ended problems, making assumptions, identifying constraints and variables, building mathematical solutions and, finally, analyzing and interpreting these solutions. It is iterative because once the initial solution is tested and translated back to the real world, revisions usually need to be made and the process continued until a satisfactory solution is reached and can be justified (see Figure 1). This iterative process not only helps to validate the model but also helps to optimize the method and the process in the context of the real-world problem.
Figure 1.
Promoting the 21st century skills at the core of the mathematical modeling process.
Mathematical modeling is a critical part of mathematics education that moves students beyond solving traditional textbook problems that use a predetermined procedural approach to arrive at a single correct answer. Unlike traditional textbook problems, mathematical modeling tasks can be solved in multiple ways and have more than one answer. Often, students work collaboratively to pose and solve authentic problems, creating conditions that foster the 21st century skills of critical thinking and problem solving, creativity and innovation, and collaboration and communication. In addition, the relevance of mathematical modeling tasks motivates students to learn mathematics and promotes deep comprehension and retention of their learning [9].
We propose that mathematical modeling is a critical mathematical process and a habit of the mind that every student needs to be successful in the 21st century. In our research, we examined how introducing mathematical modeling in the elementary grades provided opportunities for students to engage in three of the essential 21st century skills as identified by the Partnership for 21st Century Skills [10] described in Table 1. We explored the following research questions:

Table 1.
Description of 21st century skills in math [10] (p. 5).
- (1)
- How can phases of mathematical modeling as a process serve as a venue for exhibiting students’ critical 21st century skills?
- (2)
- What were some effective pedagogical practices teachers used as they implemented mathematical modeling with elementary students and how did these promote students’ 21st century skills?
3. Materials and Methods
3.1. Design
A qualitative approach was used involving an exploratory case study with two participants [11]. We were interested in gaining insights into how teachers’ implementation of mathematical modeling promoted students use of 21st century skills. We were not looking to do a detailed study of the individual teachers as that would entail separate case studies. Instead, our unit of analysis was the similarities and differences across the two teachers’ experiences in implementing MM. The boundaries of the case were determined by place, time and event. Participants were in-service, K–6, mathematics teachers, in a large mid-Atlantic school district, involved in a professional development (PD) initiative focused on mathematical modeling, between August 2015 and June 2016.
3.2. Participants
The selection of the two participants was purposeful and criterion-based [12]. We selected two mathematics teachers from our PD who demonstrated an understanding of mathematical modeling that was consistent with the project goals. In implementing mathematical modeling tasks in their classrooms, our participants demonstrated fidelity to the real-life, authentic, problem posing and solving, open-ended, student-driven, iterative nature of MM. Both of our participants implemented several mathematical modeling tasks across the course of the school year and both confirmed their decision to continue using this innovation in their classroom [13]. Our participants were in-service mathematics teachers, in a large mid-Atlantic school district, involved in our professional development (PD) initiative focused on mathematical modeling, between August and November 2015. Both elected to participate in a Teacher Research Study Group (TRSG), following our PD, between January and June 2016. Lisa, a third grade teacher, had 5 years of teaching experience at the time of our study. She had a class of 29 students with diverse learning needs ranging from gifted, to some identified as twice exceptional with the identification of gifted, and special education needs including two students with individualized education programs (IEPs) and two students with 504s plans (plans that list the accommodations a school will supply so that a student with a disability has equal access to the general education curriculum). In Lisa’s school, 33% of the students participated in a free or reduced-cost lunch program. Alice was an experienced teacher with 28 years of experience and taught a sixth grade advanced academics program class. In total, 7% of the students in Alice’s school participated in a free or reduced-cost lunch program. The selection criteria for the teachers provided us with the best opportunity to learn about teaching practices related to supporting mathematical modeling and the engagement of 21st century skills in the elementary grades. While the other four teachers in our TRSG were also viable candidates for this study, our participants were selected because of their careful documentation of implementing MM in their classrooms and because we had more opportunities to visit their classrooms and correspond with these teachers than with the other TRSG members.
3.3. Context
The two teachers in our study were part of a group of twenty-four elementary teachers participating in a PD program focused on mathematical modeling. The first part of the PD immersed the teachers in mathematical modeling during a week-long summer PD institute to experience first-hand the cycle of mathematical modeling and improve their content-specific knowledge of mathematical modeling. The second part included collaborative coaching and a lesson study to support teachers’ needs as they implemented mathematical modeling materials and strategies in their classrooms. Teachers in the PD program presented their experiences at a local symposium following the completion of the lesson study. Following the PD, a group of six teachers, including our two participants, elected to participate in a six-month teacher research study group (TRSG) examining the implementation of MM in their classrooms. The PD was part of a larger three-year research project that seeks to research and evaluate the effects of PD in mathematical modeling for elementary grades mathematics teachers. This portion of the study took place during Year 1 and Year 2 of the project.
3.4. Data Collection
Data sources included semi-structured interviews with teachers before, during and after their mathematical modeling lessons across the PD and TRSG, field notes from classroom observations, researcher memos, teacher’s annotated lesson plans and reflections, student artifacts, and personal correspondence. All interviews were audio-recorded and transcribed for analysis.
3.5. Data Analysis
To examine our research questions, we began with an exploratory coding method to help us understand and explain how mathematical modeling elicited and promoted students’ 21st century skills. Each of the interview transcripts was examined using a provisional coding system, a “start list of researcher-generated codes based on what preparatory investigation suggest might appear” [14] (p. 165). For our first research question, we applied the descriptions of the 21st century skills as tentative labels as the data was initially reviewed [10], and coded the key words, phrases and specific episodes where teachers described students’ use of critical thinking skills specifically linked to the MM process as MM critical thinking, students’ use of creativity skills specifically linked to the MM process as MM creativity, and students’ use of communication and collaboration specifically linked to the MM process as MM communication and collaboration. These provisional codes were applied to the interview transcriptions and field notes in order to better understand how the teachers viewed mathematical modeling as providing opportunities for the development of these critical 21st century skills [14]. Provisional coding helped us initiate the data analysis through identifying significantly similar themes between the two participants [14]. Due to the emergent nature of qualitative research, we did not limit ourselves to these provisional codes, but were open to where the data led and noted the similarities between the two participants. This allowed us to write a full, rich description of the phenomenon. To identify pedagogical moves used by teachers as they implemented MM tasks, we used process coding [14]. Process coding “uses gerunds exclusively to connote action in the data—both simple observable activity and more general conceptual action” [14] (p. 11).
Researchers individually coded the teacher interview transcript data and field memos twice, first using our provisional codes (21st century skills) and second, using process coding to identify teaching practices. Coding was done with Dedoose, an internet-based data management tool [15]. After individually coding, we compared our codes in order to agree on our observations of teacher moves and critical incidents [16] that elicited 21st century skills. Similar to Angelides [16] (p. 431), we define critical incidents as, “not necessarily sensational events involving a lot of tension. Rather they may be minor incidents, small everyday events that happen in every school and in every classroom. Their criticality is based on the justification, the significance, and the meaning given to them”. We used consensual qualitative analysis to come to a common understanding about our interpretations of the data [17]. Here, consensus about understanding the data relied on, “mutual respect, equal involvement, and shared power” [17] (p. 523). Teachers’ annotated lesson plans, reflections and students’ artifacts were used to help us develop a more comprehensive understanding of the phenomenon.
The two mathematical modeling tasks observed for this study were a third grade lesson, Touring a City and a sixth grade lesson, Opening a School Store. Descriptions of each task are presented below. Both tasks took place over extended periods of time; Touring a City spanned about two weeks and Opening a School Store took place over several months. The two tasks allowed us to document how the mathematical modeling tasks afforded opportunities for students to engage in 21st century skills and opportunities for teachers to demonstrate effective pedagogical moves to engage their students.
4. Results
We discuss our results based on our research questions using the specific mathematical modeling tasks implemented in each teacher’s classroom. First, with the main goal of student learning of mathematics at the forefront, we observed how teachers described mathematical modeling as a process that exhibited 21st century skills. Specifically, teachers saw that the mathematical modeling tasks necessitated student engagement in critical thinking and problem solving, creativity and innovation, and collaboration and communication. For coherence, we discuss each teacher’s task separately to provide a sense of the emerging student skills throughout the mathematical modeling cycle. Second, we looked across the two tasks to explore the mathematical pedagogies used by teachers as they implemented mathematical modeling tasks with elementary students and we present how these pedagogical moves promoted students’ 21st century skills.
4.1. Critical 21st Century Skills Elicited as Students Engaged in MM Task 1: Touring a City
For the lesson, Touring a City, Lisa gave her students the following task: Your family is going on vacation this summer. What is the best way to get your family to visit this city in only one day? Constraints given to the students were: a $250 family budget, timeline of one day from 6:30 a.m. to 11:59 p.m., the chosen city must be within a three state area, they must see three different tourist sites, and must eat at least two meals.
4.1.1. Critical Thinking and Problem Solving
Students brainstormed some destinations first as a whole class and then in small groups. In order to provide examples of student engagement in critical thinking and problem solving, we include five segments of the mathematical modeling process and describe the way in which they prompted the use of 21st century skills. The segments are: (1) Defining the task by posing a mathematics problem; (2) Considering the variables; (3) Building a solution; (4) Creating a generalized model; and (5) Evaluating the “best” trip.
(1) Defining the task—As students became excited about the project, the teacher asked students to consider what sorts of mathematical thoughts and ideas would be important to the planning process. Students offered problems that this proposal posed such as:
- What is our budget?
- What mode of transportation can we use to get there?
- What mode of transportation can we use while we are there?
- What sites do we want to see in this city?
- What sites can we skip while there?
(2) Considering the variables—in order to delve more deeply into the problem at hand, students needed to think about some variables to consider such as the destinations, distance, food and transportation, time to visit, and schedule of activities. This required some logistics and planning. Students needed to make choices and construct arguments to defend their choices for the destination. Students needed to apply the math they knew to solve the problem and ask for assistance if they needed to apply math that they had not learned.
- Figure out the price of food depending on how much people eat, that led to the question of:
- What is the relation between the price of food and the number of people eating the food?
- Figure out the price of transportation depending on the time of year and place, that led to the question of,
- What is the best way to get to the destination? Considering choices between driving a car, taking a train, subway or plane. How will traffic be accounted for?
- Considering how weather could be a factor when planning a trip.
(3) Building a solution—The teacher offered verbal cues by asking students to articulate the decisions that would help build their model. She provided sentence structures such as the following to provide, in her own words, “students with some parameters to determine whether their choice is feasible or if they would have to make another choice”.
- Our family is going to need ____ budget for sightseeing.
- Our family will need to travel ____ miles to get to all the sites.
As students listened to and evaluated others’ reasoning, they offered feedback for improvements and corrections, with supporting arguments.
- Does our answer/solution make sense?
- How does our answer compare to the problem?
- Is there another solution we could look at?
- What are the strengths of our model? Where could our model use some improvements?
- Are there any factors or ideas we haven’t considered?
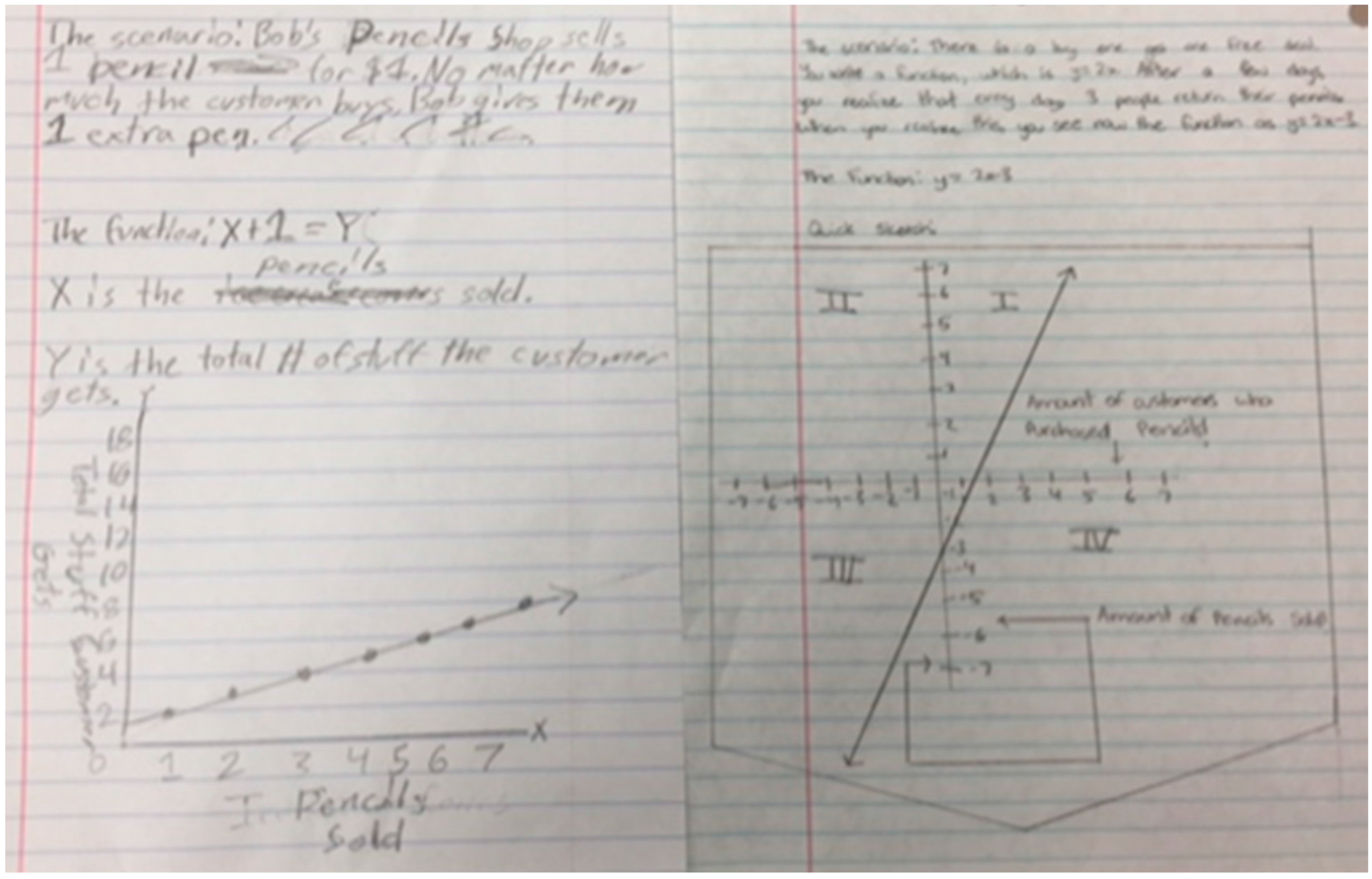
Students learned from mistakes, and made repeated attempts at solving problems. As students compared different ways students approached that mathematical problems, they started to see some efficient and innovative solutions, such as not having to write their destination names in full words but as D1, D2, D3. Eventually, these creative shortcuts and patterns led the class to an opportune lesson in algebra and using variables (See Figure 2). In order to support her students in the MM process, Lisa found it helpful to provide her third graders with an organizational tool to keep track of their choices.
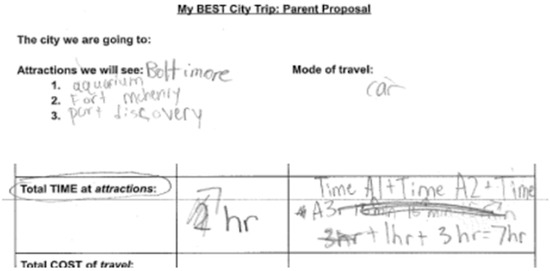
Figure 2.
Keeping track of planning the best trip using a table that led to a lesson on spreadsheets.
(4) Creating a generalized model—A teaching episode that was marked as innovative for the third grade class was a class session where they discovered a “new” technology tool to keep track of their expenditure and the use of a “variable”. Initially, students created lists, tables, organized and some “not-so” organized list of cost of the venue, travel time and mileage. Having multiple variables to this math modeling task gives a great lesson on using an organized table. Capitalizing on this opportunity, the third grade teacher made a decision to introduce spreadsheets and variables. This led to an interesting discovery about the power of technology.
(5) Critiquing and defending their “best” trip—one of the most important stages of math modeling is the evaluation stage where students critique their model. This was a perfect opportunity to have students share their mathematics solution and get feedback. In defending their best trip, students had an opportunity to offer their rationale for why their trip was the best. Some cited that their trip was the best because it was the most economical and fun, the closest and fun, and the most entertaining for all age groups. These criteria led to a great discussion with the teacher about using ranking model as a way to determine the “best” under different circumstances.
4.1.2. Creativity and Innovation
The Partnership for 21st Century Learning [10] describes creativity and innovation in mathematics taking place as students “listen to and evaluate others’ reasoning and offer improvements and corrections with supporting arguments.” Creativity and innovation in mathematics includes listening to feedback, learning from mistakes and making repeated attempts at solving problems [10]. Reflecting on her students’ demonstration of these skills, Lisa commented,
One student thought they had all their variables accounted for but when explaining his model to another student realized, “I forgot to include all the time my Dad takes when taking his pictures! He always takes so many and we all complain about how much time it takes.” The students then worked together to help the student add in “Picture Taking Time” to their model. As students took their models and considered the reality of the problems solving capability they often found themselves revising their thought processes and hence their model. One of the incidents that helped students see the need for revising the model occurred when students took their planning sheet home over the weekend. After sharing their proposal with their parents several students found that they needed to adjust the number of family members going, or that the attractions picked were not appropriate for younger siblings. This became a natural launching point for the discussion of revising their model.
4.1.3. Communication and Collaboration
Critiquing one’s mathematical model is challenging for students and is a skill that they need to develop. Lisa asked her students to engage in critiquing their models by asking them to compare and contrast their solution to planning their family trip. By communicating and talking about the similarity and differences, students could see that although the venue was different, many had to calculate admissions fees (zoo, amusement parks, museums, etc.) They noticed that some had general admissions while others had to calculate different fees for child and adult.
By identifying these variables, students worked together to generate an emergent model for planning the trip: Cost of admissions fee + Cost of parking + Cost of Food + Cost of Gas = Cost of Trip. Communicating and collaborating on this task allowed the students to notice that different trips all had commonalities and a generalized model could be used to calculate the cost of the trip.
4.2. Critical 21st Century Skills Elicited as Students Engaged in MM Task 2: In Opening a School Store
To launch her mathematical modeling task, Alice asked her students, “How can we have a positive impact on our grade level, school, and/or community?” Students brainstormed ideas and identified projects that could be solved with mathematics (Designated in Figure 3 with “M”).

Figure 3.
Students brainstorm how they can help their community and identify which problems could be solved with math.
One of the initiatives identified by students—opening a school store—became one of the overarching mathematical modeling tasks Alice posed to her students. The process of opening and running their school store provided the students with many rich opportunities for engaging in 21st century skills while learning and applying mathematics. Within the context the school store task, we highlight the challenges encountered by Alice’s students and Alice’s description of how solving these mathematical modeling tasks elicited student’s 21st century skills.
4.2.1. Critical Thinking and Problem Solving
In order to provide examples of student engagement in critical thinking and problem solving in, we include five segments and describe the way in which they prompted the use of 21st century skills. The segments are: (1) Defining the task; (2) Processing survey data; (3) Predicting sales; (4) Determining pricing; and (5) Moving dead stock.
(1) Defining the task—Once the overarching task was defined, student brainstormed as a whole class to identify what they needed to know in order to open their store. This process engaged them in looking for a logical structure to address their problem. As they grappled with where to begin, students identified the following questions through a whole class discussion:
- What items should we sell at our store?
- How should we price our items?
- What will our profit be? What should we do with the profit?
- What hours should the store be open?
- Where should the store be located?
- How will we staff the store?
- Where will we store our inventory and keep it secure?
At first glance, not all of these questions appeared to lead to mathematical thinking but through familiarity with the curriculum, Alice was able to guide her students to focus on questions that would access meaningful mathematics and lead to critical thinking and problem solving. Alice commented, “with the realization that there will be a lot of data collection involved in setting up and running our school store, we sidetracked to see how many types of graphs we could name, and brainstormed for how each type might reflect school store data”.
(2) Processing survey data—After listing ideas of items they would like to sell at their school store, students realized they needed to know what their “customers” would be interested in buying. They worked together to develop and send out a school-wide survey to identify the most desirable items for their store. Over 600 surveys were returned and students were overwhelmed by the amount of data they had collected. Alice noted, “We are still working on it. The marketing group has their hands full with 600 kids’ worth of survey data... They still aren’t open to ‘outsourcing’ data crunchers, and, we haven’t had much time for them to get a lot done.” In order to address the large amount of data and move the project forward, Alice noted she:
[P]lanned a status-of-the-school-store conversation with the entire ‘company’, with the goal of firming up a timeline for provisioning, advertising, and opening. The data crunching challenges will come up, so I will challenge the entire class to think about how we could expedite the process. My hope is that one option that’s thrown out is narrowing the sample space by taking a random sampling from each grade level. But, I want that to come from them (knowing that I will need to teach them the correct terminology). And, if the class thinks that using a random sampling is prudent, I’m even wondering if validity will come up, with someone suggesting that we take several random samplings, crunch the data, then compare results.
The way Alice’s students met this challenge demonstrated perseverance in problem solving. Importantly, the students also began developing the statistical skills needed to understand large amounts of data. They organically discovered through mathematical modeling that big data is messy and without the means to analyze it, it is useless.
(3) Predicting sales—While waiting for the survey results, the teacher asked her students to “predict the first week sales.” In order to make predictions, students made assumptions about how they would stock their store, researched wholesale costs, determined unit costs, estimated retail prices and evaluated various profit scenarios. Students were able to identify and ask significant questions about mathematics as they moved between defining the problem to making assumptions and mathematizing a solution. Through this mini-task, students were able to make sense of applied mathematics and explain and justify the mathematical choices they made—an important component of critical thinking and problem-solving skills.
(4) Determining Prices—Another episode highlighting critical thinking and problem solving was related to students pricing their inventory. After setting the store prices, students received negative feedback from the other sixth graders about how expensive things were. The feedback prompted a discussion amongst the store “departments” about the balance between profit and affordability. Students decided to revise and reprint their price lists, order forms, and marketing signage resulting in an initial model for opening the store.
(5) Moving dead stock—The initial opening of the store was a great success. After being open for a week, the store sold out of many items and closed to reorder stock and to assess the store model. As a class, students discussed what worked well and what needed improvement. Two particular dilemmas, that developed into mini-mathematical modeling tasks were identified: (a) how to reduce the customer line rate in order to expedite traffic flow issues and students being late to class; and (b) how to move dead stock. Solving both of these dilemmas required the use of meaningful mathematics.
This dialogue shows how Alice’s students engaged in the problem posing phase of the mathematical modeling cycle and demonstrated critical thinking and problem solving and creativity to address the issue of moving dead stock:
- Carla:
- “They don’t like these pencils. The mechanical ones are way cooler, so they don’t even consider buying the graphite ones.”
- Dan:
- “I think they’re too expensive for a boring old graphite pencil!”
- Teacher:
- “Talk to us about your thinking, Dan”
Dan continued by elaborating on his comparison of the cost of the mechanical pencil and graphite one to show that they were charging too much for something much less sophisticated.
- Class:
- “Yea, maybe they do cost a little too much!”
- Carla:
- “But it’s more than that—customers just aren’t interested in them. We need to really push them.”
- Jake:
- “Yea, I’m thinking a combination of dropping the price and making people WANT to buy them is what we need to do.”
Throughout this rich discourse, students were making assumptions, realizing constraints, and defining the variables. Figure 4 lists the student-generated thoughts during class discussion for each of these processes. After this discussion, students were ready to develop plans to move the dead stock.

Figure 4.
Student assumptions, constraints and variables for addressing ‘dead stock’.
Students worked in triads to develop solutions and create profit projections based on their ideas for solving the dilemma of the dead stock. They discovered that their profit projection tables were tables of values that could be represented with linear functions. They realized that graphing their predictions would allow them to select which triad’s plan was optimal for moving the dead stock. Students were able to defend their assumptions and choices, analyze each other’s proposals, and agree on the best approach to moving their dead stock. Figure 5 below shows the graphs students created to present their triad’s plan to the rest of the class. In addition to creating a graph of a linear function from their table of values, students wrote equations for their functions, and discussed the significance of the y-intercept for their specific situation.
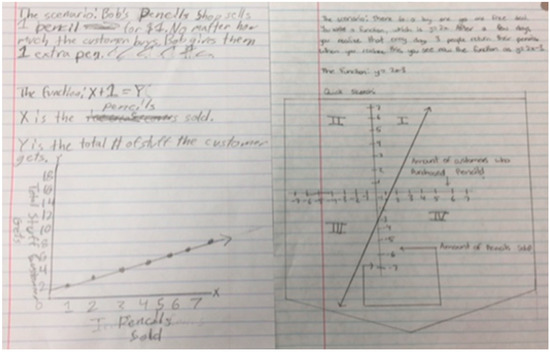
Figure 5.
Student created graphs of a linear function to compare their proposals to get rid of dead stock.
4.2.2. Creativity and Innovation
The open-ended nature of mathematical modeling tasks offered plenty of opportunity for students to be creative. On multiple occasions, Alice referred to the MM process as a creative endeavor involving iterations and sometimes failure, that was part of the creative mess. She emphasized that the MM cycle provided an organizational structure—we refer to it as “order in chaos: structure in the creative mess in MM”—for her students to systematically solve a relevant problem.
You got to define your problem, you have to narrow it down...so what are we really asking? What’s our goal here? What are the constraints? And so it’s a natural problem solving process so by putting it up there. It’s just a good anchor for the kids, like today it was a wonderful way to reiterate the point I was making that would take them through college to really figure out that it is, you don’t just come up with a solution and your problem is solved. It’s messy.
And another one and another one, so by having that visual it’s continuing to help them be ok with the messiness of multiple iterations of going back to the drawing board and failure even, we’ve had failure in some of the things that we try but that’s all ok because if we know that if it just swings back and forth.
We saw this in Alice’s classroom as students determined that a school-wide survey would be the best way to choose how to stock their store, and as they developed final survey questions. This was also evident when, after students realized the scope of the task they had set out to do, they resolved to create different departments in order to efficiently proceed with opening their school store. They created the following departments: Marketing, Merchandise, Accounting, Sales/Personnel, Security/Storage, and Customer Service. As they made these decisions, they listened to and evaluated others’ reasoning.
Creativity and innovation in mathematics involves comparing different ways of approaching mathematical problems and finding innovative solutions ([10], p. 5). After operating their store for one week, the class evaluated what was working well and where there was opportunity for improvement, coming up with a list of problems they needed to fix. We highlight two problems identified by students that demonstrated creativity and innovation in mathematics: (a) Long wait-time; and (b) How to handle dead stock.
For the “long wait-time” problem, students considered how to improve wait-time in the store line by listening to and evaluating their classmates’ ideas. After exchanging various views, they decided that they would post prices at the end of the line and have students preselect items to purchase before arriving at the cashier. Mathematically, they had to test how this would impact the wait-time. Students positioned themselves with timers and used a sample group of clients to determine how long it would take to get through the line with the new method. Once they determined rate/flow of customers under the new system and compared it to the original rate, then decided to make the change. Figure 6 shows the constraints discussed by students in addressing this dilemma and their initial recording of the line rate under their new system. This segment illustrated creativity and innovation in mathematics as students looked for patterns that suggested creative shortcuts and made generalizations from patterns they observed in repeated calculations.

Figure 6.
Solving wait-time dilemma, constraints and initial rate measurements.
For the problem of “How to handle dead stock”, we also observed creativity and innovation in mathematics as students pondered different ideas for dealing with their dead stock dilemma. As mentioned above, the dead stock problem was an issue identified by the students. Students came up with a variety of ideas including a price drop, a buy-one-get-one free (BOGO), and a give-away-with-purchase plan. As discussed above, they presented their proposals to each other by graphically representing their predicted sales. After listening to and evaluating each other’s mathematical reasoning, students selected the BOGO option. By discovering fresh insights and communicating them to others in this process, students had the opportunity to understand that mathematics is a creative endeavor that builds on previous knowledge.
Alice used the word “messy” six times during one of her interviews to refer to the open-ended nature of the MM tasks and the creative process that is necessary to progress through the phases of MM. In her use of the word “messy”, Alice referred to the disorderly nature of the authentic, real-world MM problems that differentiates them from the straightforward, procedural problems often found in textbooks. When asked, how did you make sure the students focused on the mathematics? Alice responded,
That is really by giving them something they are accountable for...that they all had to think about what they would put in a survey. They had to have a poster and they had to include... I’m just asking for a deliverable, so just asking for something so ok you guys are all going to be thinking about how would you survey to find out and so they took thought to that or another day, the day that you were here, I asked them just to project for a week and I knew they would all be talking about.
She continued on and said that she required “some accountability, some recording, some deliverable.” To focus her students on using meaningful mathematics, Alice gave her students a MM process tool as shown in Figure 7. While allowing the MM process to develop organically in the classroom, at times, Alice used these MM process tool to take advantage of a rich mathematics opportunity. The following tool provided students opportunity to use creativity and maintain the openness of the task, while allowing to focus on building a model to predict sales. Students were asked to develop three business move to address the deadstock issue—while focusing on using mathematics to justify and explain their choices. We note that for elementary students, teachers’ support and guidance provided a rich opportunity for students to discover how mathematics can be used to make decisions among the creative choices faced in a real-life situation or phenomena.

Figure 7.
Mathematical modeling process tool.
4.2.3. Communication and Collaboration
In developing a final survey, students made assumptions about what items students might be interested in, what would sell, and possible profit margins. While waiting for the survey results, the teacher asked students to, “predict the first week sales”. Students gathered 600 survey responses in order to determine what goods they should stock in the store. Students used the cost of the store’s inventory to set initial prices of their stock and estimate profit. Students listened to each other’s ideas as they brainstormed ideas for tasks and came to a consensus. They worked in small groups to develop marketing surveys for their school store. The groups compared their drafts and crafted a final survey that was administered to all students and teachers in the elementary school.
Students created a method to measure the customer line rate and worked together to gather data from a sample group of clients to determine the average rate for clients to complete a transaction. They used this rate/flow information to revise their system and provide customers with order forms and price lists before reaching the cashier in order to expedite the transaction time. As we observed students working together during the Opening a Store project, we noted that they were respectful of each other, asking thoughtful questions of their classmates and affirming the ideas of others.
4.3. Effective Pedagogical Practices Teachers Used in Enacting Mathematical Modeling with Elementary Students: Modeling Mathematics Pedagogical Practices
As we analyzed our data across both teachers, three main themes related to effective pedagogical practices for mathematical modeling emerged. These themes were finding the “sweet spot” along the continuum of openness and providing a focus for learning, seizing “teachable moments” by having deep curricular knowledge, and the ability to use MM tools and artifacts to thoughtfully orchestrate MM process and mathematical discourse. We provide specific examples of how the two teachers in our case study demonstrated these practices.
4.3.1. Finding the “Sweet Spot” along the Continuum of Openness and Providing Focus for the Learning
Lisa, the teacher who led the math modeling task, touring the city, kept a design log and an annotated lesson plan as she designed the project. She was aware that textbook problems were too closed and that mathematical modeling would open up students to problem solving that would be of interest to them.
Their reality is not in a lot of the problems that textbooks give them. Their reality is not in a lot of things we try to hand them anymore and so it does take time for us to learn more about our kids and it does take time for us to figure out what are students are interested in and what their lives consist of, and what are their real challenges. My students have real challenges this summer of figuring out where they want to go and a lot of them have real challenges of trying to convince their parents to take them but if they can come up with an amazing opportunity to explain hey mom and dad we can do this in an entire day, it’s only going to cost us $250 or maybe even less and figure out the budget and explain to them how budgeting even less is even better and being able to help them understand. It’s a lot easier for them to relate to this as 8- and 9-year-olds because this is their world.
In this excerpt she talks about the importance of knowing her students and their interest. She provided some parameters for the mathematical modeling problem by creating some constraints to focus on the learning while keeping the task personally relevant.
Her lesson notes stated “How to limit”
VA, DC, MD area6:30 a.m. to 11:59 p.m.Budget—$250FoodTravel at least see 3 different sites, must have at least two mealsAdmissions to museums
She anticipated the possible models that this task would elicit as she wrote in her note, “Production—(a) Distance (b) Budget (c) Time (d) Traffic”. She thought through how she would engage each individual student and encourage collaboration. She wrote, “Brainstorm individually and then group by common interest on a piece of paper.”
In Alice’s mathematical modeling task, opening a school store, she created ways to be open and give students ownership while using questioning and a “worksheet” to keep them focused on the mathematics.
My questioning was intentional. I anticipated where I thought the discussion might go and prepared worksheets to help the students organize their thoughts. I gave students time to come up with the ideas themselves instead of telling them. Students need structure even though the task is open-ended. Each day I would tell them, for example, how much time we would be spending on math that day. I provided structure while maintaining open-endedness by providing students with worksheets, I’ll call them worksheets even though they’re not really traditional worksheets, to help them organize their thoughts. I did this when they were working on the surveys and I had them use the last portion of the math class to predict what would happen during the first week the store was open. I directed them to use math to predict what would happen. Similarly, I provided them with a “worksheet” asking them to suggest 3 business moves to move the ‘dead’ stock, show all of the math for each business move, and graph their results.(Alice’s reflective memo)
Both teachers shared the ways in which mathematical modeling engaged their students and also reflected on how they attended to diverse learners with special needs. Lisa shared, “I tried to figure out how to scaffold this for special needs students, because special needs students really struggle with broad ideas and not knowing where to go with them. So the next thing that I did was I thought through the steps that I was asking them to do.” She shared how she conferenced with the individual student to set goals each day, “So every day we highlighted the goal for that day.” Alice also reflected on reaching each and every student by sharing, “I have one or two this year that really had a hard time engaging. Tony is one example. What I try to do with him is give him special tasks related to the project that he can work on and then refer to those as often as possible.” This individualized learning allowed these individual students access to the MM task as well as a way to contribute their work to the larger group project.
4.3.2. Seizing “Teachable Moments” and Having Curricular Knowledge
Having deep curricular knowledge allowed for Alice and Lisa to capitalize on emerging opportunities to develop students’ mathematical understanding. Lisa found opportunities to seize “teachable moments” and many of these teachable moments were taken up because she looked for these opportunities and made note of it throughout the implementation of the MM unit.
In her daily log, she wrote:
Entry 1: Create a budget sheetDon’t introduce it right away but let them see what it is.Create google excel budget sheet for third round to useEntry 2: Make a list of visitor websites, train and travel websitesRelook at the guiding questionsCome up w/ reflection sheet for studentsEntry 3: Mini goals for each dayWorking independently given time to collaborate idea share in pairsEntry 4: Define My Problem—Determining my city and list of possible attractions aka “MY Best”Getting around: Distance and cost of travel (review opportunity cost)Having Fun: Cost of attractions, Cost of foodBudget Day: organize information intoFinal Calculations and result sharing(Excerpt from Lisa’s daily log)
In one of her interviews, Lisa noted how listening to her students grapple with this MM task provided her with these “teachable moments”.
It’s just going to depend on where they are going with it, definitely, and that’s the best part with mathematical modeling for a teacher because it really gives you that part of teaching back that you really like about teaching when you are able to say ok this is an opportunity for me as a teacher to really listen to my students to hear what they are thinking and then being able to take those teachable moments and turn them back around and say ok let’s stop here and look at what types of questions you are asking or not asking and trying to derive that.—Lisa’s Interview
In Alice’s memo, she reflected on the need for deep curricular knowledge. She provided a rationale that because MM is set in a real world problem with its complexity and open-endedness, there is a lot of uncertainty encountered by both teachers and students. In order for teachers to navigate through the context and seize math opportunities, knowing what lies ahead and what needs to be covered in the curriculum is important.
It is important for teachers to know their curriculum. They don’t need to be very experienced teachers to do mathematical modeling but, as long as they know what lies ahead and what they will need to cover, mathematical modeling will work for them. I think teachers with just a year or two of experience can do mathematical modeling. Mathematical modeling is open-ended so you never know exactly where the problem-solving will lead but if you know your curriculum you recognize the possibilities when they arise. The math may not develop in the same order as the pacing guide but that’s alright because it will get covered.—Alice’s Memo
4.3.3. Use of Mathematical Modeling Process Tools and Student-Generated Artifacts to Thoughtfully Orchestrations the MM Process and Mathematical Discourse
Mathematical modeling afforded opportunities for teachers to use student artifacts as pedagogical tools to push the mathematics agenda forward. For example, Lisa used a student’s work shown in Figure 2 to move the students to consider algebraic thinking. She noticed that one of the students was able to articulate that the time for the trip involved adding the time spent at attraction site 1, 2 and 3. She took the opportunity to do what we called a “catch and release”, an opportunity to bring pause in the modeling process to zoom into an important mathematical idea. Alice used student-created graphs of a linear function (Figure 5) for the class to analyze and evaluate the different proposals to get rid of dead stock and vote on an agreed upon solution. Both Lisa and Alice used records of student thinking to revisit key mathematics concepts that they heard as they monitored the class working in groups. In this way, Alice stated she was able to bring up important mathematical conversations.
I mean again they have all their data and stats I have to teach and we even saw a quick mini lesson and you saw another quick review this morning that’s all happened just peppered here or there and they are just taking it well beyond and they are just looking at the statistics they are looking at the idea of random sampling and that stuff is well beyond and they’ll never forget any of it because they need it they want it they are motivated the math hasn’t been done onto them they are filling up the math.—Alice’s Interview
She recounted one episode where she was able to ask one group to share an important mathematical idea to the entire class,
So I’m sure in any modeling situation you know these messier modeling scenarios I think any teacher is going to see “Oh my gosh these guys need this math but these guys are doing that but I really want them all to see it” so you’ve got some decisions to make and sometimes if it’s a review or math they’ve learned earlier than simply in the sharing out and stuff you hang in the room with just that intentional opportunity to give their status and kind of explain what they were doing then everybody ends up engaging or it could be as extreme as dropping everything for a day and say “oh my gosh these guys are using spreadsheets you’ve got to see what they are doing” and experience the magic everybody!—Alice’s Interview
Both teachers used student generated artifacts as well as teacher-created materials that we referred to as MM process tools that helped elementary students focus on the MM process. For example, a retrospective analysis showed that the brainstorming poster shown in Figure 3 from Alice’s class helped focus students to pose an authentic mathematical modeling problem. Figure 2 from Lisa’s class helped students understand how to use the different variables such as time and cost that influenced their mathematical model for their best family trip. Figure 7 illustrated a tool used to get students to build a model for getting rid of their deadstock at their store. All of these tools were designed by the teachers as they moved their students organically through the process of mathematical modeling.
4.4. Pedagogical Moves that Promoted Students’ 21st Century Skills
For our second research question, we focused on identifying specific pedagogical moves that elicited students’ engagement in 21st century skills. The analysis of the two teachers’ interviews and observational memos revealed notable teaching practices which emerged during the different phases of the MM processes. These effective practices and teacher moves promoted the opportunities for students to engage in 21st century skills (see Table 1). The most notable practices were, first, how we saw the teachers presenting an engaging phenomenon that elicited mathematical modeling and helping problematize the situation by asking, what is a problem we want to tackle related to this phenomenon? Both teachers kept the problem real and personally relatable to the students. Second, the teachers were artful in determining the appropriate degree of openness and constraints to place around the mathematical modeling problem. The parameters allowed the mathematics agenda to proceed without getting into the weeds or skimming the surface of the important mathematical opportunities that presented themselves. Third, the teachers were intentional and thoughtful in anticipating potential pathways for mathematical thinking and asking what mathematics will students need to get a solution or build a model? Fourth, teachers were actively monitoring the mathematical modeling process and selecting mathematical ideas for students to present to peers for feedback and looking for opportunities to refine their thinking by questioning their assumptions. Finally, through the iteration of mathematical solutions, we observed teachers providing time and space for students to discover the essence of mathematical modeling which was the process of refining mathematical models and solutions based on important quantities and relationships among quantities (See Table 2).

Table 2.
Teaching practices for MM and 21st century skills elicited during a MM cycle.
5. Discussion
The 21st century skills of critical thinking and problem solving permeated both MM tasks. To begin with, for both tasks, students had to determine what they knew and what they needed to know in order to proceed through the mathematical modeling cycle. As they brainstormed what they needed to know, students had to critically determine how they would gather the needed information and how they would use this information to come up with a realistic solution to their problems. Furthermore, they had to identify what would change and what would stay the same, thus defining variables for their model. Critical thinking and problem solving were also promoted as students explained their ideas, justified their choices, and, based on their assumptions, determined the best solution to their problem. Creativity was a natural part of the mathematical modeling tasks and developed through a combination of individual thinking, whole class discussion and primarily working together in small groups. This structure meant that in order to develop a solution, students needed to collaborate and communicate with their peers. These results support the GAIMME report assertion that, “the Partnership 21’s 21st century skills of creativity and innovation, critical thinking and problem solving, communication and collaboration are all accessible via modeling.” [7] (p. 23), for students in grades K–8.
Our study illustrates the role of mathematical modeling tasks in engaging elementary students’ 21st century skills and helping students learn meaningful mathematics—two important goals proposed by Gravemeijer et al. [1] to prepare students for society and the future. Our observations presented evidence of students integrating conceptual understanding with the learning of procedures, an approach that differs from the traditional, more procedural way of teaching. Students developed and discussed mathematical ideas of their own, shared different strategies for solving the same problem, performed analysis and critiqued each other's approaches, discovered relationships among the quantities of interest and explained by providing rational justification of their solution strategies. For a teacher, the MM process allowed them to encourage their students experience of open-ended real world problems. This in turn helped students to construct mathematical meaning for themselves and supported them in becoming more mathematically proficient.
Through the mathematical modeling process, we observed the how students engaged in 21st century learning skills. The process also supported the emergence of what we called the mathematical modeling dispositions.
- Confidence in dealing with complexity;
- Persistence in working with difficult problems;
- Tolerance and ability to deal with open ended problem;
- The ability to communicate and work with others to achieve a common goal or solution
In our study, mathematical modeling activities that were effective in elementary grades have been ones that were situated in contexts that were meaningful, relevant and relatable to the students. The task’s connection to students’ world brought immediate ownership and engagement, unlike exercises on a worksheet. Early mathematical modeling tasks tended to be descriptive models where students used quantities to describe a situation or phenomenon while with advanced levels, some mathematical modeling tasks used predictive models to forecast what might happen within a situation, which offered opportunities for the young modelers to use the mathematics they know and seek the need to learn higher level mathematics which provides links for future learning goals. The process of mathematical modeling was iterative and it offered students opportunities to revise their model and refine their mathematical thinking. Mathematical modeling tasks, as shared by the two teachers in our case study, were “group-worthy tasks” in that they had complexity and had potential for collaboration work. The nature of the group activity also pushed students to share their diverse ideas using visible thinking strategies with words, pictures, number which lead to building a model.
These important student practices did not occur without intentionality on the teacher’s part. Our case study shows that the two teachers exhibited specific pedagogical expertise that facilitated student learning. It was through finding the “sweet spot” along the continuum of openness and providing focus for the learning, seizing “teachable moments” and having curricular knowledge, using of mathematical modeling tools and artifacts, and thoughtful orchestrations of mathematical practices that teachers supported their students’ learning. Specific teaching competencies we observed for mathematical modeling included: (a) problematizing the situation by asking, what is a problem we want to tackle related to this phenomenon; (b) determining the appropriate degree of openness and constraints to place around the MM problem; (c) anticipating potential pathways for mathematical thinking and asking what mathematics students would need to get a solution or building a model; (d) monitoring the mathematical modeling process by selecting mathematical ideas for students to present to peers for feedback and to refine their thinking by questioning their assumptions; and finally; (e) providing time and space for students to discover the essence of mathematical modeling.
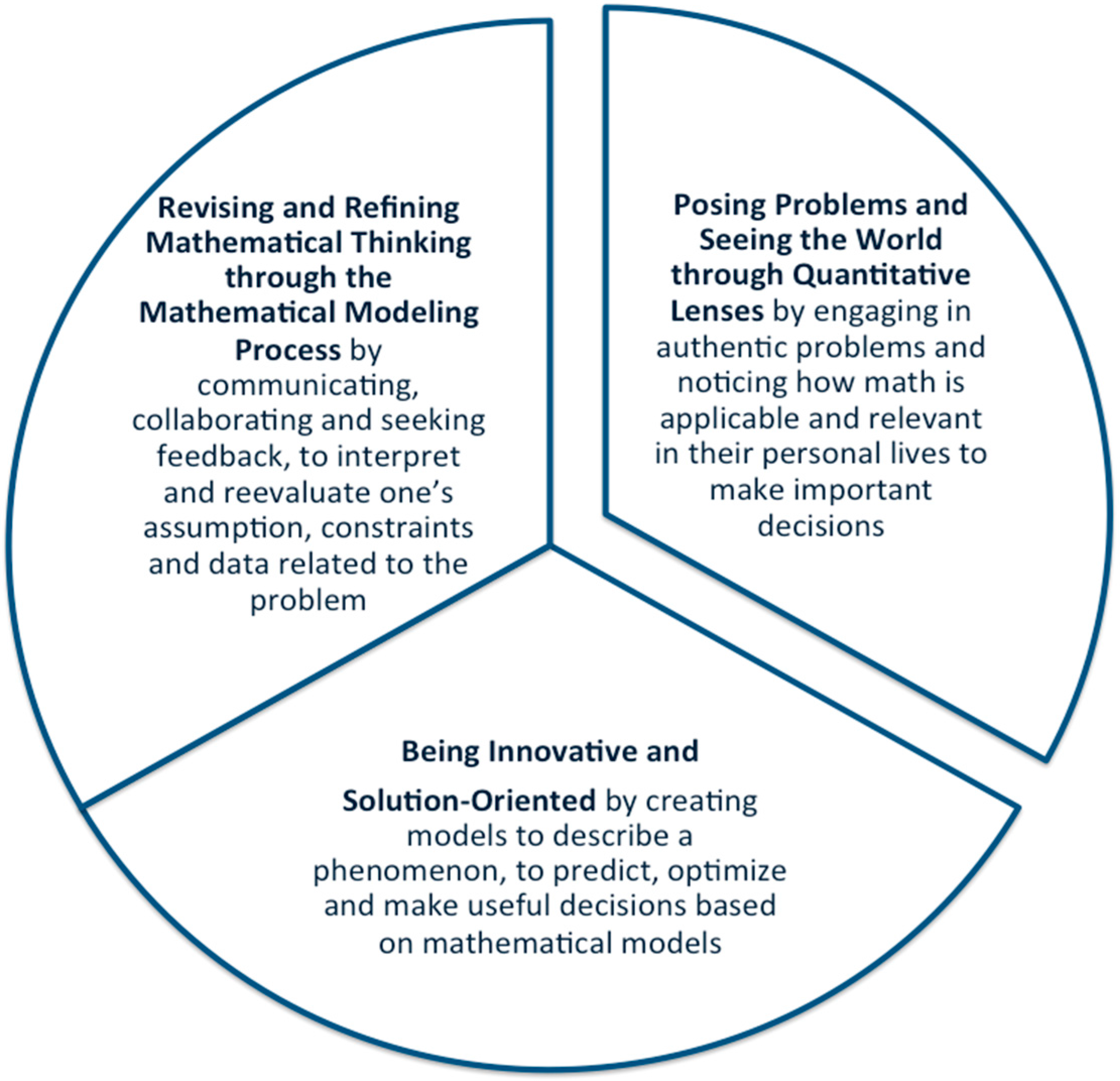
More than a decade ago, Blanton and Kaput [18,19] called for elementary teachers to “algebraify” their curriculum and provided teachers with strategies for identifying and creating opportunities for students to engage in algebraic thinking by developing their algebraic “eyes and ears”. This referred to teachers being attentive to connecting algebra across their K–6 curriculum and finding opportunities to engaging students in algebraic reasoning in “planned and spontaneous” algebraic teachable moments. Similarly, we propose in our study that elementary teachers can create opportunities for students to engage in mathematical modeling that can promote 21st century skills as early as elementary grades. We saw how students engaged in these skills and practices and learned how teachers intentionally planned and sometimes took up on spontaneous “teachable MM moments” while engaged in authentic problem solving. Mathematical modeling in the early grades may look differently than what high school mathematical modeling may look like. Yet, educators might consider how mathematical modeling may advance across the learning progression and how developing a habit of mind for mathematical modeling at an early grade may provide students more access to being ready for the complexity of the problems we face in our modern world. We offer the following framework (see Figure 8) for developing the mathematical modeling habits of mind to help educators develop early mathematical modelers in the ways that our two teachers did in our study. The three interrelated habits of mind that we noticed teachers and students developing in these two classrooms were: (1) posing MM problems and seeing the world through quantitative lenses; (2) becoming solution oriented by thinking about the “best” solution (optimizing), or predicting or projecting the sales at the school store, (predictive), and describing a situation in mathematical terms to make decisions based on data (descriptive); and (3) developing the habit of iterating, going back to the drawing board, to revise and refine their model. This process in mathematics is not common in a traditional classroom when there is one correct answer. Through mathematical modeling, students experienced how their mathematical solution can be revised when they changed their assumption, like the cost of the trip changed when they added another destination or the travel time changed due to traffic considerations and students saw how mathematical thinking and solutions could be refined.
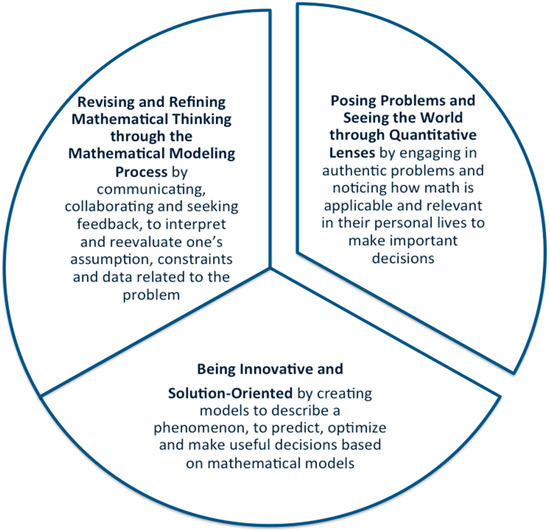
Figure 8.
Developing mathematical modeling of habits of mind.
Our study raises several issues for future research, such as the ways teachers can use the iterative process of mathematical modeling to help focus students on revising and refining their mathematical thinking; worthwhile mathematical modeling tasks for early mathematical modelers; how teachers can manage groups to build each and every students’ sense of agency towards mathematics; how teachers can capitalize on student artifacts produced during mathematical modeling process to assess the process of mathematical modeling; and how teachers can develop their pedagogical expertise in facilitating the open-ended nature of mathematical modeling tasks while maintaining the rigor of the mathematics and student-centered learning. The outcome of this study demonstrates the importance of exposing students to mathematical modeling in the elementary grades, as it provides opportunities for children to appreciate mathematics as a creative endeavor that is useful and relevant and a process that involves an iterative cycle of refinement of mathematical ideas using critical thinking and problem solving, and collaboration and communication.
Acknowledgments
This project was funded by the National Science Foundation Sponsored STEM-C Program (NSF-1441024).
Author Contributions
Each of the authors contributed to the paper equally.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gravemeijer, K.; Stephan, M.; Julie, C.; Lin, F.-L.; Ohtani, M. What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 2017, 15, 105–123. [Google Scholar] [CrossRef]
- Wolfram, C. Teaching Kids Real Math with Computers. Youtube, Uploaded by TedTalks. 15 November 2010. Available online: https://www.youtube.com/watch?v=60OVlfAUPJg (accessed on 15 January 2017).
- English, L.D.; Charles, K.L.; Cudmore, D.H. Students’ statistical reasoning during a data modelling program. In Proceedings of the 24th Conference of the International Group for the Psychology of Mathematics Education, Hiroshima, Japan, 23–27 July 2000; Nakahara, T., Koyama, M., Eds.; pp. 265–272. [Google Scholar]
- Greer, B. Statistical thinking and learning. Math. Think. Learn. 2000, 2, 1–9. [Google Scholar] [CrossRef]
- Lajoie, S.P. Reflection on Statistics: Learning, Teaching and Assessment in Grades K-12; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1998; ISBN 978-0805819724. [Google Scholar]
- Cirillo, M.; Pelesko, J.; Felton-Koestler, M.; Rubel, L. Perspectives on modeling in school mathematics. In Mathematical Modeling and Modeling Mathematics; Hirsch, C.R., Roth, A.R., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2016; pp. 3–16. ISBN 978-0-87353-973-9. [Google Scholar]
- Garfunkel, S.A.; Montgomery, M. (Eds.) GAIMME: Guidelines for Assessment & Instruction in Mathematical Modeling Education; Consortium for Mathematics and Its Applications [COMAP, Inc.]: Bedford, MA, USA; Society for Industrial and Applied Mathematics [SIAM]: Philadelphia, PA, USA, 2016; Available online: http://www.siam.org/reports/gaimme-full_color_for_online_viewing.pdf (accessed on 15 January 2017).
- Blum, W.; Ferri, R.B. Advancing the teaching of mathematical modeling: Research-based concepts and examples. In Mathematical Modeling and Modeling Mathematics; Hirsch, C.R., McDuffie, A.R., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2016; pp. 65–76. ISBN 978-0-87353-973-9. [Google Scholar]
- Blum, W.; Ferri, R.B. Mathematical modeling. Can it be taught and learnt? J. Math. Mod. Appl. 2009, 1, 45–58. [Google Scholar]
- P21 Partnership for 21st Century Learning. Available online: http://www.p21.org/ (accessed on 15 February 2017).
- Stake, R. The Art of Case Study Research; Sage Publications: Thousand Oaks, CA, USA, 1995; ISBN 978-0803957671. [Google Scholar]
- Patton, M. Qualitative Research and Evaluation Methods, 4th ed.; Sage Publications: Thousand Oaks, CA, USA, 2015; ISBN 978-1-4129-7212-3. [Google Scholar]
- Rogers, E.M. Diffusion of Innovations, 5th ed.; Free Press: New York, NY, USA, 2003; ISBN 978-0743222099. [Google Scholar]
- Saldaña, J. The Coding Manual for Qualitative Researchers, 3rd ed.; Sage Publications: Los Angeles, CA, USA, 2016; ISBN 978-1473902497. [Google Scholar]
- Dedoose Version 6.2.7. Available online: http://www.dedoose.com/ (accessed on 1 October 2016).
- Angelides, P. The development of an efficient technique for collecting and analyzing qualitative data: The analysis of critical incidents. Int. J. Qual. Stud. Educ. 2001, 14, 429–442. [Google Scholar] [CrossRef]
- Hill, C.E.; Thompson, B.J.; Nutt Williams, E. A guide to conducting consensual qualitative research. Couns. Psychol. 1997, 25, 517–572. [Google Scholar] [CrossRef]
- Blanton, M.L.; Kaput, J.J. Developing elementary teachers’: “Algebra eyes and ears”. Teach. Child. Math. 2003, 10, 70–78. [Google Scholar]
- Blanton, M.L.; Kaput, J.J. Characterizing a classroom practice that promotes algebraic reasoning. J. Res. Math. Educ. 2005, 36, 412–446. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).