Abstract
This paper addresses two critical issues in mathematics education, the need: (a) to understand the nature of educator’s subject matter knowledge and pedagogical content knowledge; and (b) to find ways to measure them. It stems from a mixed-methods study designed to inspect the secondary mathematics teachers’ pedagogical content knowledge (PCK) related to the area of a trapezoid, a common topic in intermediate/secondary school classes. Based on the provided exemplars of student work, in-service teachers were invited to propose possible ways for addressing perceived difficulties of students and provide extensions. Using a Grounded Theory approach, we identified themes in our data and incorporated them with existing conceptualizations of knowledge for teaching secondary level mathematics, and developed rubrics that allow discriminating different levels of teachers’ PCK. In this paper, we describe the process of developing the rubrics, and propose ways to: (a) extend the existing frameworks for PCK in/for teaching mathematics at the secondary level; and (b) measure multiple facets of PCK in order to design technology-based professional development for mathematics teachers.
1. Introduction
Researchers agree that teachers can significantly and positively influence student learning outcomes, especially if they use particular teaching methods (e.g., based on problem solving or peer collaboration), and also if they expect much of their students and have good relationship with them; in other words, “what teachers DO matters” [1] (p. 22, emphasis in original). As a message coming from his synthesis of over 800 meta-analyses related to student achievement, John Hattie suggests that teachers should “spend more time and energy understanding learning through the eyes of students” (p. 241), which involves careful observation and reflection to understand both the personal and objective learning experiences of students. Out of Hattie’s six “signposts towards excellence in education” (p. 238), we find the following three most relevant to our work presented in this paper:
(3) Teachers need to be aware of what each and every student is thinking and knowing, to construct meaning and meaningful experiences in light of this knowledge, and have proficient knowledge and understanding of their content to provide meaningful and appropriate feedback…; (4) Teachers need to know the learning intentions and success criteria of their lessons, know how well they are attaining these criteria for all students, and know where to go next…; (5) Teachers need to move from the single idea to multiple ideas, and to relate and then extend these ideas [so that their students can] construct and reconstruct their knowledge and ideas [which is critical for success].[1] (pp. 238–239)
Now that government agencies and teacher organizations pay particular attention to success of mathematics students [2,3,4], there are increased expectations for mathematics teachers to be more observant and reactive to their students’ current mathematical thinking and understanding (e.g., [5]), so that they can be proactive and use it for instructional decision-making during and when planning lessons. While the researchers and practitioners seem to agree that what teachers do in the classroom matters, there is no consensus if what teachers know matters and in which way it may matter. For example, Hattie [1] states that it is hard to find conclusive evidence that teacher subject matter knowledge is important, although he posits that there must be “an interaction between teaching competence and need for high levels of knowledge in the subject” (p. 127). However, Zalman Usiskin [6] is more direct when asserting that, “A mathematics teacher needs to know mathematics” (p. 86), and Alex Lawson [7] calls for action stating that, “Teachers’ lack of mathematical content knowledge and mathematical pedagogical knowledge is one of the most central issues we face in effective mathematics instruction” (p. 12). This is the first critical issue that we address in this paper, especially from the point of developing tools to measure teachers’ subject matter knowledge and pedagogical content knowledge, and potentially using this information to guide and plan professional learning (both formal and informal).
As researchers in technology applications in mathematics education, we also work on identifying challenges that teachers face when choosing appropriate software applications for teaching a specific mathematics topic. Although there is a wide variety of technology applications that are currently available to mathematics teachers, they do not relate to mathematical concepts in the same way. Nathalie Sinclair [8] highlights that it does not help that curriculum documents keep using general terms, such as “digital technologies” and “dynamic geometry software,” as if they all equally well and in the same way address mathematical concepts. Sinclair asserts that despite mentioning technology, curriculum documents “continue to be written for a default paper and-pencil toolset, [making it] very difficult for teachers to see how they can develop concepts using other tools” (such as different software and hardware; n. p.). This is the second critical issue that we address here, as in our study we developed the tools to measure different types of teachers’ knowledge in electronic form [9]. In [9], we proposed that designing online, interactive, dynamic, short, scenario-based instruments would allow mathematics educators to gather information needed to customize professional development according to mathematics teachers’ individual needs, and even use them in self-assessment.
2. Theoretical Framework
There exist different theoretical frameworks for describing knowledge needed for teaching mathematics in schools. Building on Lee Shulman’s [10] seminal work in this area and his conceptualization of pedagogical content knowledge (PCK), there seems to be an agreement that the knowledge of mathematics and the knowledge of teaching are different, and that both are important for mathematics teachers to have. Shulman considered PCK a distinguishing factor between “the understanding of the content specialist from that of the pedagogue” (p. 8). Hill, Sleep, Lewis and Ball [11] warn education researchers to not confuse the quality of teacher’s mathematics instruction with the quality of mathematics in that instruction. In an effort to measure mathematics teachers’ PCK, different research groups developed their own instruments, each with their own strengths and limitations (e.g., [12,13]). For example, the well-known Mathematical Knowledge for Teaching (MKT) framework by Ball et al. was intended to empirically validate PCK [14]. Depaepe, Verschaffel, and Kelchtermans [14] discuss some deficiencies of the model, such as difficulty in delineating subcomponents of the MKT, and its focus on mainly cognitive aspects of teachers’ knowledge (such that could be tested and are independent of the context in which the teacher teaches). In their most recent work, the MKT research team turned to adding more items that would potentially allow for specialized knowledge of mathematics teaching to be measured [15]. Recent attempts have been made to validate the MKT extension into the secondary domain [16], and these attempts still have to undergo piloting on the larger sample. The variances in theoretical frameworks and the instruments reflect the differences in highlighting aspects of the PCK [17].
2.1. Applicablity of the Existing Frameworks for Capturing the Knowledge Needed for Teaching and the Choice of the Content Focus
In their recent paper, Depaepe, Verschaffel, and Kelchtermans [14] presented results of a systematic search for PCK studies reported in the databases ERIC, PsycInfo and Web of Science. Overall, they reviewed 60 articles to identify the way PCK was conceptualized and (empirically) studied in mathematics education research. They found two perspectives on teachers’ PCK: cognitive (i.e., the knowledge needed for teaching mathematics) and situated cognitive (i.e., dynamic knowledge that is created through the practice of teaching and is recognized in teacher’s actions). Depaepe et al. further listed eight components of PCK, which includes the knowledge of: (1) students’ (mis)conceptions and difficulties; (2) instructional strategies; (3) mathematical tasks and cognitive demands; (4) educational ends; (5) curriculum and media; (6) context; (7) content; and (8) pedagogy [14] (p. 15). The authors identified fractions as the popular topic in the PCK studies that focused on elementary school teachers, and algebra, along with functions, as popular topics in the PCK research at the secondary level. Depaepe et al. identified four shortcomings of the strictly cognitive approaches to measuring PCK: (a,b) professional development may not be adequate as it is separated from both the classroom and the socio-historical contexts; (c) it may not be clear how the components of the PCK interact during one’s teaching; and (d) affective aspects of teaching may be missing. While the situated cognitive perspective on teachers’ PCK deals with the stated deficiencies of the purely cognitive model, it has its own deficiencies, such as lack of generalizability because of its overreliance on the small samples research [14]. Depaepe et al. suggest that researchers “clearly state their position in the conceptualization and operationalization of PCK” and “triangulate classroom observations with, for instance, […] stimulated recall in which teachers can document their choices and justifications” (p. 23). In our study we integrated both cognitive and situated cognitive perspectives, because while they each have their own weaknesses [14], when unified, they provide an important insight into teachers’ PCK. A fuller description of this integration is provided in the methodology section of this paper.
2.2. Research Question
One of our research questions, namely, “What is the nature of the secondary mathematics teachers’ PCK related to the area of a trapezoid?” was addressed both theoretically and empirically [9]. Initial conceptualization of the PCK related to the area of a trapezoid came from [18] and consisted of: (a) knowledge of subject specific difficulties and common misconceptions; (b) knowledge of useful representations of the content; (c) knowledge of developmental levels; (d) knowledge of connections among “big math ideas”; and (e) understanding of appropriateness, of student’s proof, justification or mathematical discourse. Through the further literature review and analysis of data we have revised these initial categories.
Our ultimate goal was to tackle a practical question of, “How to measure PCK in this domain?” which addressed the issue of finding a suitable method for measuring and comparing knowledge for teaching mathematics at the secondary level.
3. Materials and Methods
In designing this study, we decided to use one mathematical discipline (i.e., geometry) and within geometry, one topic that fits the middle school and high school curriculum (i.e., the area of trapezoid, where trapezoid is defined as a quadrilateral with exactly one pair of parallel sides). This decision presents another critical issue, this time in mathematics education research, as it opens discussion regarding a choice of the study focus, especially: (a) what are the reasoning and underlying assumptions made by the authors when selecting the [geometric] topic of the study; and (b) how it [the topic] affects the interpretive and validity arguments in relation to this study’s findings.
This study is also building on the previous work related to design of the instruments for measuring PCK done by Manizade and Mason [18], and teachers’ reasoning about area of trapezoid [19]. It outlines a program for future researchers to follow the development of new PCK tools in other mathematical disciplines and topics; rather than having a single tool measuring overall PCK, we posit that the tools should be highly tailored.
We view teacher professional learning as continual, non-linear and recursive, regardless if it is seen as the development of knowledge or of practice [20]. Because the teachers’ growth is individualistic, complex, and gradual [21], it made sense to conduct a study over one whole year (including a semester course, classroom observations and development of instruments and rubrics) with multiple data sources; it also supported our goal of developing an instrument that will measure teacher’s knowledge before the professional development commenced. After all, if each teacher’s starting point is unique and complex, we assume that the professional development of the type “one size fits all” would not work. Having a narrow disciplinary focus also agreed with an exploratory nature of a Grounded Theory method [22,23]. In our decision, we were encouraged by Clarke and Hollingsworth’s [20] findings that through reflection and enactment “of something a teacher knows, believes or has experienced” (p. 951), “aspect of teachers’ knowledge and practice may promote subsequent growth in other areas” (such as that change in knowledge, beliefs and attitudes may affect teacher practice or vice versa, p. 951). To provide multiple entry points to our participants-practicing teachers, we have deliberately selected a topic with which all of them were familiar.
3.1. Participants
Volunteer participants in this study were secondary in-service teachers (N = 39) who had experience teaching at the intermediate/secondary level. They were recruited from a pool of the practicing teachers who were voluntarily participating in the professional development program designed for mathematics teachers in the state of Virginia.
Data collection was conducted during a five-month period using different means (see Instrumentation section), followed by at-work observations of select teachers after completion of the initial data collection. In preparation for the use of Grounded Theory to design the rubrics for evaluation of teachers’ PCK, the data collection started by implementing the PCK instrument. In this instrument, after discussing different ways to calculate the area of a trapezoid and to develop a general formula, all 39 participants were provided with nine exemplars of student solutions (some correct and some with mathematical limitations), accompanied with prompts to evaluate and interpret “student” work (two exemplars from the Trapezoid PCK Instrument are provided in Appendix A). These examples were developed using the sample of three types of approaches [19] for developing area of a trapezoid formula (i.e., decomposing, using transformational geometry, and enclosing the trapezoid). By focusing on the development of an area of trapezoid formula, we could relate concepts that were created in lower grades (i.e., the concept of area and corresponding units of measurement, areas of triangles and quadrilaterals, geometric transformations, congruence, similar triangles, parallel lines and angle relations, heights of parallelograms and triangles, etc.) to capture the knowledge needed for teaching at the secondary level. We assumed secondary school teachers would be comfortable with these concepts and would likely engage in pedagogical analysis of student sample approaches for deriving the area of a trapezoid.
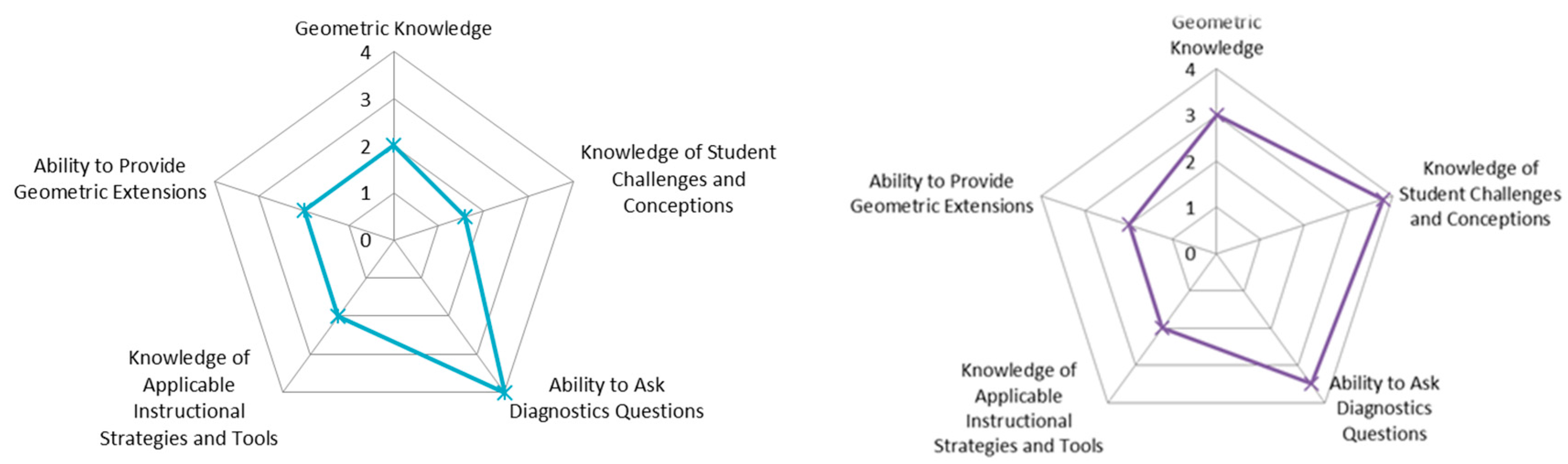
Based on their scores on the van Hiele geometry test [24], we purposefully selected a subset of seven participants for whom we conducted complete data analysis to create the draft rubrics. Among them, there were one case each at Levels 1 and 4 of geometry content knowledge, two cases at Level 2, and three cases at Level 3. This provided us with participants with a range of geometry knowledge which presented our starting point in creating their PCK profiles (see Figure 1).
Figure 1.
Representation of Peter’s and Sally’s PCK along the five dimensions (levels from 0 to 4).
Based on demographic information about the teachers’ years of experience in teaching Geometry and teaching in general, in our subset we had three novice teachers (those who were within the first 4 years of their teaching career), two semi-experienced teachers (those who have taught between 5 and 9 years, but had limited exposure to teaching Geometry), and two experienced teachers (those who have taught for ≥10 years including teaching Geometry). This allowed us to consider potential connections between teachers’ PCK, and their teaching experience and education.
After drafting the PCK rubrics and creating PCK profiles of seven selected cases, we returned to the rest of the 39 participants and implemented the rubrics on their Trapezoid PCK instrument data to see how these data would force the rubrics to change. The same process was repeated with several other cohorts of participants, and the complete results of this multi-year study will be presented in another publication.
3.2. Instruments
These dimensions of PCK were identified and measured after using the six data collection methods: (1) a van Hiele test [24], to determine each teacher’s developmental level in Geometry (this test contains 25 multiple choice items, where each of five van Heile levels is measured by five items; since our participants were in-service teachers, we used a stricter, 4 of 5 correct criterion); (2) a Trapezoid Questionnaire pre-test that we developed to measure teachers’ knowledge of the area of trapezoid concept (it contains six open-ended questions regarding defining trapezoid, and teaching area of trapezoid and developing its formula); (3) a Trapezoid PCK instrument with nine exemplars of student solutions (adapted from [18,19])—these exemplars contained illustrations created in GeoGebra, accompanied with questionnaires asking teachers to interpret student work, rate the appropriateness, clarity, sophistication, and limitations of student strategies [25], and propose possible ways to address student misconceptions and difficulties (see Appendix A); (4) teachers’ reflections on their perceived PCK learning in this process (where in less than 800 words they described their experience, as a teacher and a learner, with the trapezoid activity); (5) teachers’ demographic survey, where we recorded their gender, school grades taught, years of teaching experience, and years of teaching geometry; and (6) follow-up classroom observations using Instructional Quality Assessment Classroom Observation Tool (IQA, [26]), where we observed instructional practice of purposefully selected teachers and validated previous findings.
Validity and reliability of the instruments used in the study (i.e., the van Hiele test [24]; IQA [26]; and part of a PCK instrument) have been established and reported in the literature. Other surveys that we developed for this study went through multiple rounds of peer review (five mathematics education researchers have reviewed the instruments three times each). Using the Grounded Theory [22] approach, we developed rubrics to measure teachers’ PCK related to geometry topics and triangulated different sources of data to create a PCK profile for each selected teacher. Grounded Theory was suitable for its flexible and yet systematic inductive approach to creating hypotheses based on data. It is flexible as it allows for use of: (a) different data (e.g., data from interviews, observations, and experiments); (b) mixing of research methods (qualitative and quantitative); and (c) additional data collection and sampling, when its iterative nature requires. It offers “a set of general principles, guidelines, strategies and heuristic devices rather than formulaic prescriptions” (p. 3). Since the researchers apply the Grounded Theory strategies in their own way, they need to describe methodology in detail, attesting that they adhered to its core analytic tenets (i.e., theoretical sampling and constant comparison). Following Charmaz’s constructivist approach to Grounded Theory, researchers’ perspectives and background affect how the data are interpreted and the process involves construction of a theory, rather than its discovery. One of the authors was the instructor in the course and had first-hand familiarity with the topic and the participants. The data collection for this study was approved by the university’s IRB office.
3.3. The Methodological Challenges of This Mixed Methods Approach
The major methodological challenge was to develop a study that would achieve somewhat conflicting goals: to have data collection embedded into the course work (i.e., the study participants were also students in the course); to collect substantial amount of data without over-burdening and disengaging participants; to develop the research-related activities that would not diverge from the course objectives (e.g., have focus on geometry; propose activities that participants would relate to professional development); to keep the research processes separate from the course assessment—to protect participants and support their genuine involvement in the study; and to recruit teacher volunteers with specific profiles for classroom observations. Another challenge was in working with a substantive amount of data, going back to the data that we already analyzed and analyzing them again every time we modified our rubrics (to make sure that the new version of the rubric was consistent to what we saw in data), and resolving our occasional differences in opinions during data analysis and interpretation of findings.
To deal with a first challenge, and aligned with a Grounded Theory approach, we collected some baseline data at the start of the study, and throughout the study continued to develop and use the instruments which could deepen our understanding of the secondary mathematics teachers’ PCK related to the area of a trapezoid. The fact that our participants were all the in-service teachers who volunteered to take professional development courses, meaning they intended to improve their practice, was aligned with our research problem. In addition, the literature that informed this study was readily available since the teachers’ PCK presents a recurring and recognized challenge for teacher education (see [10]). During the study, our instruments’ questions and rubrics were revised to be more clear and non-repetitive, and the number of participants were considered appropriate for a mixed method study [27]. We implemented a multitude of measures to explore teachers’ PCK. Our multiple forms of triangulation included using multiple data sources, methods, theories, and two researchers [28]. With this approach, we intended to overcome the weaknesses and biases of the single method, single-analyst, and single-theory studies.
After we adapted the PCK instrument from [18], we also had two member checking sessions with three other mathematics education colleagues, to get their feedback and check the face validity of the adapted version of the instrument (the mathematical content focus of the adapted instrument has changed, although the PCK questions remained same). That way we made sure that in their professional opinion the adapted instrument still measures what we think it should measure. To deal with a second challenge, we collected data on a whole sample (N = 39), but used quantitative findings to select a subset of seven participants, so that we had representative cases at different levels of content knowledge (0–4, as determined by the participants’ course marks and their results on the van Hiele test [24]). Only qualitative data from the subset were used in developing teacher profiles and initial rubrics. A detailed timeline of this research [22] is provided in Appendix B. It describes a year-long process of iterative data collection and analysis, where the two of us made comparisons between data, codes, and categories to develop a conceptual understanding of how the PCK in geometry could be measured. After developing each rubric level, we scrutinized it through our discussions and by adding additional data, until we were satisfied with changes. When developing teacher profiles, we consulted literature and conducted observations of their teaching to confirm our findings and obtain some quotes from the classroom situations.
4. Data Analysis and Results
Our choice of the Grounded Theory method does not mean that we started our research totally “theoryless” or because we were skeptical “of the usefulness of the theories that have been generated in the field” [29] (p. 333); on the contrary, the previously developed theories of PCK were part of our theoretical and conceptual framework, and we could see their main aspects emerging from our data.
4.1. How Were the Different Data Combined in Grounded Theory
Researchers who are conducting grounded theory research are advised by Lincoln and Guba [30] to explain their inquiry process when developing a theory. This process enabled us to develop a theory about how teacher’s content knowledge about the area of trapezoid interacts with their pedagogical knowledge, and how such interaction could be enhanced. During the methodological stages (see [22]), we:
- Identified our substantive area—teaching geometry; population consisted of the 39 intermediate/secondary school teachers;
- Collected both qualitative and quantitative data;
- Open coded the data as we collected them, so that the core category and the main concern become apparent;
- Wrote memos throughout the entire process;
- Conducted selective coding and theoretical sampling starting from a subset of seven marker cases; once that the core category and main concern were recognized; open coding would stop and selective coding—coding only for the core category and related categories—would begin;
- Further sampling from the raw data from 39 teachers was directed by the developing theory and used to saturate the core category and related categories;
- After our categories became saturated, we sorted our memos and found the Theoretical Codes which best organized our substantive codes;
- When we felt that the theory was well formed, we read the literature and integrated it with our theory through selective coding;
- As a result, we isolated the following five dimensions of PCK: (1) content knowledge (e.g., knowledge of geometry); (2) knowledge of student challenges and understandings; (3) knowledge of appropriate diagnostic questions; (4) pedagogical knowledge (i.e., knowledge of appropriate instructional strategies, including use of manipulatives and technology); and (5) knowledge of possible extensions (designed to deepen students’ understanding of the problem; e.g., knowledge of geometric extensions); and
- Wrote our theory—which meant that we created the rubrics for identifying specific characteristics of different levels of teachers’ PCK. These rubrics were result of modifications in Stages 6–9, when we refined them to achieve differentiation between levels 0–4 of teacher competencies levels (4 being the highest; adequate for an expert Geometry teacher). This was the main contribution to better understanding the nature of educator’s mathematics content knowledge and extending the existing frameworks for PCK in/for teaching mathematics at the secondary level. Table 1 and Table 2 contain excerpts from the rubric used to identify teachers’ knowledge of student challenges and conceptions at Level 4 and Level 1. For this dimension, we identified 15 sub-components (A–O), and based on their presence/absence in teacher data, we were able to identify the level of teacher’s knowledge of student challenges and understandings. Each participant received an average score based on responses to questions (b) and (c) on the six PCK items (e.g., one item presented Scott’s approach in developing a trapezoid formula).
 Table 1. Rubric used to evaluate teacher’s knowledge of student challenges and conceptions, Level 4.
Table 1. Rubric used to evaluate teacher’s knowledge of student challenges and conceptions, Level 4. Table 2. Rubric used to evaluate teacher’s knowledge of student challenges and conceptions, Level 1.
Table 2. Rubric used to evaluate teacher’s knowledge of student challenges and conceptions, Level 1.
While inspecting an item that contains Scott’s approach, one participant for whom we will use fictional name Sally, wrote:
…every trapezoid cannot be broken into two right triangles and a rectangle. [A, see Table 1] Scott’s method would not work for a right trapezoid because there wouldn’t be a second triangle to recompose into one larger triangle. Of course, a right trapezoid could be decomposed into one rectangle and one triangle…. Scott’s method also wouldn’t work for trapezoids whose parallel sides do not overlap… because a rectangle wouldn’t be constructed.Scott is limited by his experience with trapezoids. If he believes that his method will work for all trapezoids, then he’s only considering trapezoids that look like the typical isosceles trapezoid. [B, see Table 1] He may be at Level 1 in van Hiele if he doesn’t understand the variety of shapes can still fall under the same categories. [D, see Table 1]Scott did not spend enough time manipulating quadrilaterals. He is probably used to being presented with trapezoids that all look similar, such as the one he used to derive an area formula. Scott is possibly more comfortable with rectangles and triangles, which is why he focuses on the properties of those shapes instead of the properties of trapezoids. [F, see Table 1]
Sally received Level 4 on this item, as her answer covered A and B and D and F rubric entries (see Table 1). However, since Sally did not teach Geometry, we did not schedule observations of her teaching.
When asked to describe Scott’s thinking, one participant wrote: “While his method works for his particular trapezoid, it would not work for every trapezoid. His diagram implies that he believes that every trapezoid can be partitioned into one square and two smaller right triangles that can be translate to form into one large triangle. While he is correct in his logic pertaining to the triangles, not every trapezoid can be partitioned to contain a square and two triangles. Instead, he needs to approach a more general trapezoid and use the fact that every trapezoid can be partitioned into a rectangle and two triangles.” Because of the limitation in the teacher’s understanding of the trapezoid concept (I, see Table 2), according to the rubric, this answer was evaluated as Level 1.
4.2. Identification of Results
Through the processes described in this paper, we created a substantive theory, because it emerged, “from the study of a phenomenon situated within one particular situational context” [23] (p. 174). Through convergence, we confirmed our findings, and created instruments and rubrics that would be straightforward and easy to use for future analysts. This theory will be presented in a different paper, as the focus of this paper is to discuss the grounded theory as a method appropriate in developing such instruments and rubrics for measuring teachers PCK. Some of our findings in the project are briefly summarized under the following four themes.
- i
- Teachers’ PCK profiles are distinct. The distinct teacher profiles using the PCK instrument and the developed rubrics were generated for each teacher. Representation of the PCK profile for two of our marker cases—Peter and Sally, both experienced secondary school teachers, are presented in Figure 1.
Peter knew how to ask diagnostic questions; in fact, this was his strongest PCK attribute. For example, while he was given an exemplar containing Scott’s approach, Peter was asked, “d. What further question(s) might you ask to understand Scott’s thinking?” He answered, “I would ask ‘would this method work on every type of trapezoid?’ and ‘what is your formula for calculating the area of a trapezoid?”. These and other Peter’s responses regarding diagnostic questions were at Level 4. However, he did not know what to do with students’ answers, as he was lacking in other dimensions of PCK.
When answering question “(b) If Scott’s approach presents a misunderstanding, what underlying geometric misconception(s) or misunderstanding(s) might lead Scott to the error presented in this item?”, Peter wrote, “The misunderstanding is that his method will not work for most other types of trapezoids. His method works well for isosceles and right-angled trapezoids. In addition, although he might be able to present a formula for calculating the area of the given trapezoid, his formula would not work for other trapezoids.”
Regarding question “(c) If Scott’s approach presents a misconception or misunderstanding, how might he have developed the misconception(s)?”, Peter added: “He would have developed the misconception by believing that he was given a trapezoid at random then his method would work for all trapezoids. Perhaps he does not recognize the special nature of the given trapezoid, and he might think all trapezoids can be decomposed into a square and two right triangles.” Due to the lack of depth of his responses on questions (b) and (c) on all of the items of the PCK instrument, as measured by the rubric partially presented in Table 1 and Table 2, the average of Peter’s scores on questions related to teacher’s knowledge of common student challenges on six items was 1.6.
In addition, during the observation of his teaching, Peter was focused on having a controlled, teacher-centered environment (“[when I taught trapezoids] I just gave them the formula and told them how to plug in the numbers. I also explained how the first part of the formula gives the length of the median.”), that is efficient and orderly (e.g., “With the stress and time constraints of high stakes testing, I often don’t allow my students to do much exploration on their own because it often leads to chaos and a lot of wasted time”), which runs “as a well-oiled machine.” During one of the classroom observations, Peter proudly announced to the observer that he is incorporating small group activities in his classroom. Although the students were placed in small groups during the observation, Peter presented a traditional lecture followed by the handouts with practice problems. The group work was not implemented in this lesson.
We concluded that Peter’s teaching perspective and attitude were consistent with his profile in Figure 1 where he scored low on every attribute except for asking diagnostic questions. Observational notes of his teaching confirmed what we saw in his profile—Peter may be relying on a traditional teaching format to cover up the deficiencies in both content knowledge and most aspects of PCK.
- ii
- Dimensions of teachers’ PCK may be affected by their teaching practice and education [17]. Teachers’ “geometric knowledge” appeared stable, as it was mainly developed during teacher education programs, while the “knowledge of applicable instructional strategies and tools” as well as “knowledge of student challenges and conceptions” appeared dynamic and situated in teaching practice.
Teaching experience had the strongest negative correlation with the Knowledge of Applicable Instructional Strategies and Tools (r = −0.74, N = 7) and with the Ability to Provide Geometric Extensions (r = −0.67). The weakest correlation was between years of teaching experience and Geometric Knowledge (r = −0.09), which is in accordance with [17] notion that mathematical knowledge (ability to think mathematically and to solve mathematical problems with respect to a specific content idea) at the end of the teacher education program and four years after its completion remain stable. Without the intent to make general conclusions based on a small sample, these observations may be informative for future work.
- iii
- Teachers need to develop strategies for creating opportunities for all students to learn. Our participants had fewer problems with recognizing that a student’s approach is limited and that it points to some misconception, then when they were given a mathematically correct approach for developing the area of trapezoid formula. In the latter cases, most of the participants were not able to provide convincing scenarios of how to facilitate further student thinking and help them to extend their approach.
For example, Holly’s approach to developing an area of trapezoid is generalizable, while Scott’s is limited (special case, see Appendix A). One teacher wrote after being presented with Scott’s approach: “I would not introduce any new strategies during the instructional period simply because I do not believe there is any misconception or misunderstanding presented in this approach.” Regarding Holly’s approach, most teachers did not offer any extension. While acknowledging that Holly’s approach does not present a misunderstanding, one teacher wrote: “Holly should spend time with other types of trapezoids to refine her approach.”
- iv
- Teachers’ individual characteristics, such as their attitudes, values with respect to mathematics teaching, and motivations affect their PCK. Our participants differed in how they described the main responsibility of the geometry teacher (e.g., creating a learner-centered vs. teacher-centered environment).
We recorded differences in considering all mathematics topics as opportunities for learning vs. perceiving some topics as a “waste of time”; in accepting their students (and themselves) as capable of learning through experimentation vs. using rigid approaches to teaching (in an attempt “not to confuse the students”). For example, one teacher commented on Scott’s non-generalizable approach: “This is a very simple technique to find the area of many trapezoids, and one most students should be able to visualize,” while she found generalizable cases working for all trapezoids, “but… very confusing.” Teachers differed in their awareness that all instructional strategies have limitations vs. accepting all strategies at face-value; and, in presenting a range of perspectives related to affordances of technology (e.g., those helpful for developing concepts vs. unreliable or difficult to master) [25].
4.3. Study Limitations
The limitations of the study include the following: (1) potential generalizations based on statistical analysis completed in the study are limited due to sample size; (2) the sample of teachers chosen for observation was a convenience sample (only two teachers taught geometry in that period); (3) as researchers we have a social constructivist perspective, which may have affected our research design; and (4) we also recognize limitations of the research method and in our implementation of it. For example, we did not follow Glaser’s advice to first develop a theory and then conduct a literature review [31]. Simply put, educator’s knowledge for teaching mathematics is a mature research area and as mathematics educators, we followed it for years. However, researchers agree that its research is far from being completed, as different existing PCK frameworks demonstrate. We also felt that instead of creating long, multiple-choice tests, we could propose a selection of carefully chosen commonly taught mathematics domains and developing instruments that will identify a teacher’s developmental level in those areas. In that view, we felt that being informed about the field is an advantage, rather than a limitation, so we conducted literature review throughout the study.
5. Discussion
We started this paper with acknowledging that what teachers do [1] and what teachers know is important [6,7]. Through our study, we addressed several critical issues in mathematics education, the need to find ways to measure teachers’ subject matter knowledge and pedagogical content knowledge in order to use this information to guide and plan professional development. Contribution of our work to developing methods for measuring, assessing, evaluating and comparing knowledge for teaching mathematics at the secondary level is critical and multidimensional. It is:
- Methodological: By choosing a mixed methods approach to measure multiple facets of PCK, our work forms an important counterpart to unidimensional large scale studies on PCK. This might take the larger education community discussion on measuring PCK to a next level. By providing details about the sample and the context we allow other researchers “to assess the fittingness or transferability of the findings” [27] (p. 433).
- Thematic: Our focus on one specific PCK topic, namely geometry of trapezoids can be seen as a counterpart to a large number of PCK studies that try to measure an overall PCK. The teacher’s PCK is contextual [9] and may be different for every topic s/he teaches. Determining this would require using the PCK tool on a larger sample of participants, which may be addressed in another study. In addition, by measuring PCK in geometry, we attend to a domain that has not received much attention in current PCK studies. We propose that the PCK instruments should be designed as “probes” around the topics commonly taught by a targeted group of teachers (e.g., middle school). If the researchers put their efforts into developing such probes, the research community will be more adept to critically examine them, and those that pass the examination, will be more likely to be implemented.
- Connected to practice: Online exemplars and rubrics that we created may be used when planning differentiated professional development activities or for self-assessment purposes [9].
It is understandable that different mathematics topics require different apparatuses to teach them; for example, one would teach continuous mathematics differently from discrete mathematics. However, the approach that we used in this study is relevant for all mathematics domains. We believe that developing a positive disposition towards teaching secondary school mathematics (i.e., implementing, measuring, and improving all five dimensions of PCK identified in our study) could be achieved by using a concept from any prior level—primary, as well as intermediate/secondary.
While our research continues with two new classes of in-service teachers each year, we managed to establish strong connections between our findings and the existing theoretical frameworks, which we also extended. We hope that other researchers, practitioners, and administrators will find our contribution useful and inspirational for researching PCK in other areas of mathematics.
Author Contributions
Dragana Martinovic and Agida G. Manizade conceived and designed the study; Agida G. Manizade performed data collection; and Dragana Martinovic and Agida G. Manizade analyzed the data and collaborated on writing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Exemplars of Holly’s and Scott’s Work from the PCK Instrument. Both Represent the Cases Decomposing, but Holly’s Approach is Generalizable, while Scott’s Presents Special (Non-Generalizable) Case
Appendix A.1. ITEM Holly
When presented with the task of developing a formula for the area of any trapezoid in her high school geometry class, Holly developed the diagrams as a strategy for deriving the formula for the area of a trapezoid described by the sketches below. She sketched line BE parallel to the line AD in the trapezoid. This way she constructed a parallelogram ABED and a triangle BCE. Then she calculated the area of this parallelogram ABED and the area of the triangle BCE. She added these areas to find the area of the trapezoid ABCD.
- Based on the diagram above (see Figure A1), describe Holly’s thinking. If she were to complete the formal derivation of the area formula in her diagrams, would her method work for any trapezoid? Why, or why not?
- If her approach presents a misunderstanding, what underlying geometric misconception(s) or misunderstanding(s) might lead her to the error presented in this item?
- If Holly’s approach presents misconception or misunderstanding, how might she have developed the misconception(s)?
- What further question(s) might you ask Holly to understand her thinking?
- What instructional strategies and/or tasks would you use during the next instructional period to address Holly’s misconception(s) (if any presented)? Why?
- If applicable, how would you use technology or manipulatives to address her misconception or misunderstanding?
- How would you extend this problem to help Holly further develop her understanding of the area of a trapezoid?

Figure A1.
Holly’s diagram.
Figure A1.
Holly’s diagram.

Appendix A.2. ITEM Scott
When presented with the task of developing a formula for the area of any trapezoid in his high school geometry class, Scott developed the diagrams as a strategy for deriving the formula for the area of a trapezoid described by the sketches below. He decomposed a trapezoid into a square and two right triangles. Then he combined the right triangles, creating a new triangle. Finally, he calculated the area of this triangle and added it to the area of the decomposed square to find the area of the original trapezoid.
- Based on the diagram above (see Figure A2), describe Scott’s thinking. If he were to complete the formal derivation of the area formula using his diagrams, would his method work for any trapezoid? Why, or why not?
- If Scott’s approach presents a misunderstanding, what underlying geometric misconception(s) or misunderstanding(s) might lead him to the error presented in this item?
- If Scott’s approach presents a misconception or misunderstanding, how might he have developed the misconception(s)?
- What further question(s) might you ask Scott to understand his thinking?
- What instructional strategies and/or tasks would you use during the next instructional period to address Scott’s misconception(s) (if any presented)? Why?
- If applicable, how would you use technology or manipulatives to address Scott’s misconception or misunderstanding?
- How would you extend this problem to help Scott further develop his understanding of the area of a trapezoid?
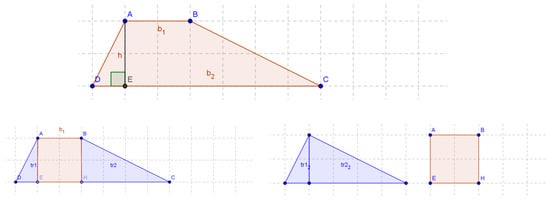
Figure A2.
Scott’s diagram.
Figure A2.
Scott’s diagram.
Appendix B. Detailed Timeline of Methodological Steps Taken in This Study
February: For coding of the geometry content knowledge for the area of a trapezoid, we adopted the IQA instrument rubric [26]; for each participant, we individually evaluated and compared our assessment of their answers to the (a) question on the first five exemplars from the Trapezoid PCK Instrument (i.e., “(a) Based on the diagram above, describe [student]’s thinking. If [s/he] were to complete the formal derivation of the area formula in [her/his] diagrams, would [her/his] method work for any trapezoid? Why, or why not?”). We examined our individual scores and identified scores that did not match. During the peer debriefing sessions, we adjusted our rubric to develop consistent scoring for the participants’ responses and reached consensus on scoring them. We then completed the process for the other three exemplars. Based on the average scores per teacher and their ranking, we selected four marker cases for this study, one for each level (1–4). From the start, we wrote memos to record nascent ideas, document what prompted us to make data-gathering decisions and initial sampling, and note development of theoretical categories.
March: Individually, we developed rubrics for evaluation of (b) and (c) sections for each exemplar (i.e., “(b) If […]’s approach presents a mathematical limitation, what kind of thinking might lead [her/him] to the limitation presented in this item?” and “(c) If [student]’s approach presents a mathematical limitation, how might [s/he] have developed it?”). The rubrics were based on research literature of developmental levels in Geometry, such as discussed by van Hiele and Piaget. We then focused on two main mathematics concepts in the rubrics—those of trapezoid and area, compared and modified our rubrics to reach consensus, and used the newly developed rubric to complete scoring of sections (b) and (c) for the first five exemplars provided by marker cases. Further, we discussed possible changes in the instrument for clarity purposes. These changes acknowledged the breath and richness of teachers’ responses to exemplars, and required that in order to be highly ranked, their responses should recognize students’ developmental level on the van Hiele scale with respect to the area concept and the trapezoid concept.
April: Memo-writing helped us to “flag incomplete categories and gaps in [our] analysis”; it prompted us “to predict where and how [we] can find needed data to fill such gaps and to saturate categories” [22] (p. 199, italics in original). Aligned with the logic of theoretical sampling, we decided to add new marker cases to illuminate our categories. Based on the average scores per teacher and our consensus of their ordering according to the coding, we added two more marker cases, for the total of six. Using rubric for sections (b) and (c), we compared our individual analyses for exemplars 1 and 5 (which presented two non-generalizable approaches which used an enclosing trapezoid technique) for marker cases, reached consensus, and made changes in the rubric. We then completed analyses for the marker cases on exemplars 3 and 6 (which presented two generalizable approaches, one using an enclosing trapezoid and the other using a decomposing trapezoid strategy).
June: We looked at the rubric for sub-questions (b) and (c), and agreed on what works and what should be changed. Then, we completed analysis for exemplars 1, 3, 5, and 6 for marker cases. After considering our marker cases’ data and re-examining them, we decided to add one more marker case, to expose our theoretical interpretation to more empirical inspection [22]. We then created an initial version of a rubric for sub-question “(d) What further question(s) might you ask [student] to understand [student’s] thinking?”
Next, we discussed grouping of sub-questions into two clusters, the first cluster representing Pre-Active Behaviors [32] and consisting of sub-questions (e), (f), and (g) (i.e., “(e) What instructional strategies and/or tasks would you use during the next instructional period to address [student]’s challenge(s) (if any presented)? Why?”; “(f) If applicable, how would you use technology or manipulatives to address [student]’s challenge(s)?”; “(g) How would you extend this problem to help [student] further develop [her/his] understanding of the area of a trapezoid?”). These questions were related to Pre-Active Behaviors because they addressed planning, thinking how to deal with learning and behavioral issues with students, and assessment outside the classroom, in other words, things that teacher does before and after school or during recess.
Sub-questions (b) and (c) were considered as describing Interactive Behaviors [32], since they relate to what happens when teacher is with students (in our case the participants used these sub-questions to think about the mathematics task). After inspecting Pre-Active Behaviors, we decided to look into (d) separately, or in combination with (b) and (c). We checked participants’ answers under (d), to see if we are finding the evidence that one can be mathematically weak but pedagogically strong. Then we completed analyses for the marker cases on all items for sub-question (d), went over the current version of rubric for (d), and suggested modifications to better discriminate between marker cases. After modifying the rubric by evaluating marker cases’ responses and seeing how many responses address characteristics in sub-questions (a)–(g), we made decision on how to split the levels in the rubric. Going back and forth with creation of the rubrics, looking into the literature and exploring data through that lens, revising the rubrics iteratively, treating data analysis and collection simultaneously—were aligned with the emergent nature of the Grounded Theory method.
July: We finalized the rubric for sub-question (d) and analyzed exemplars 1, 3, 5, and 6 for seven marker cases. After creating a draft rubric for sub-questions (e), (f), and (g), we consulted the IQA rubrics [26] to see if they could be somehow utilized. We identified the IQA RUBRIC 1: Potential of the Task, as relevant for (e); and IQA RUBRIC 2: Implementation of the Task, as relevant for both (f) and (g). Then we looked for and read the articles related to the theoretical framework of our project, and completed the rubrics for sub-questions (e), (f), and (g). This stage ended with compilation of data from marker cases for exemplars 1, 3, 5, 6 for (e) and (f), and exemplars 1–9 for (g).
August: We completed analyses of marker cases for sub-questions (e), (f), and (g) using developed rubrics and identified five dimensions of PCK—namely, geometric knowledge (a), knowledge of student challenges and conceptions (b) and (c); ability to ask diagnostics questions (d); knowledge of applicable instructional strategies and tools (e)–(f); and ability to extend understanding of geometric problem (g). We then created profiles for marker cases. With this research phase, we completed the steps of theoretical sorting, diagraming, and integrating [22].
September: We contacted marker cases to schedule observations of those participants who were teaching Geometry. To complete our analysis, we checked reflections of marker cases to identify their individual characteristics, such as attitudes, perspectives, and motivations. We then analyzed the marker cases’ answers to the question, “Given that all of these students were in the same class you taught, what level 1–4 would you assign to each response [using the criteria of: (a) math appropriateness (suitability to generate expected outcome/formula for the area of any trapezoid), (b) clarity (how clear/unambiguous is this student’s strategy/approach), (c) sophistication (how sophisticated/complex is the student’s approach), and (d) limitations (how limited is this approach)]” [25]. Then we adjusted the profiles, calculated correlations, and created demographics summaries. Using the IQA rubrics [26], the course instructor completed two in-school observations for each teacher.
Throughout October–January 2015: We created qualitative descriptions of the observed lessons illustrated with additional artifacts gathered during the lessons (e.g., pictures, screenshots, etc.). To allow for easy use of the Trapezoid PCK instrument, we created online, dynamic, version of its six representative exemplars and looked into the reliability and validity of the instrument. Reliability was addressed in a multi-rater agreement. All exemplars’ data were first separately evaluated by each author, after which any disagreement was discussed and resolved. Face validity of the Trapezoid PCK instrument was achieved before the data collection commenced, through the multiple rounds of peer review, and a content validity through analysis of items by two authors, both experts in the field. Finally, we agreed upon the new labels for the categories (e.g., focus on why vs. how; explorative/exploration vs. formulaic approach), and selected representative quotes for our report.
References
- Hattie, J. Visible Learning: A Synthesis of over 800 Meta-Analyses Relating to Achievement; Routledge: New York, NY, USA, 2009. [Google Scholar]
- Ontario Ministry of Education. Achieving Excellence: A Renewed Vision for Education in Ontario. Available online: http://www.edu.gov.on.ca/eng/about/renewedVision.pdf (accessed on 10 January 2017).
- National Council of Teachers of Mathematics. Principles to Actions. Available online: www.nctm.org/PtA/ (accessed on 10 January 2017).
- OECD (Organization for Economic Co-operation and Development). Are the New Millennium Learners Making the Grade? Technology Use and Educational Performance in PISA 2006; OECD Publishing: Paris, France, 2006; Available online: www.oecd.org/edu/ceri/45053490.pdf (accessed on 10 January 2017).
- Borko, H.; Jacobs, J.; Eiteljorg, E.; Pittman, M.E. Video as a tool for fostering productive discussions in mathematics professional development. Teach. Teach. Educ. 2008, 24, 417–436. [Google Scholar] [CrossRef]
- Usiskin, Z. Teachers’ mathematics: A collection of content deserving to be a field. Math. Educ. 2001, 6, 86–98. [Google Scholar]
- Ontario Ministry of Education. Report: A Forum for Action, Effective Practices in Mathematics Education, Toronto, Ontario, 11–12 December 2013. Available online: http://thelearningexchange.ca/wp-content/uploads/2013/12/math-forum-report_final_april7-1.pdf (accessed on 10 January 2017).
- Sinclair, N. Research Paper Prepared for a Forum for Action: Effective Practices in Mathematics Education, Toronto, Ontario, 11–12 December 2013. Available online: https://mathforum1314.files.wordpress.com/2014/01/dr-nathalie-sinclair-research-paper-math-forum-2013.pdf (accessed on 10 January 2017).
- Manizade, A.G.; Martinovic, D. Developing interactive instrument for measuring teachers’ professionally situated knowledge in geometry and measurement. In International Perspectives on Teaching and Learning Mathematics with Virtual Manipulatives; Moyer-Packenham, P., Ed.; Springer: Cham, Switzerland, 2016; pp. 323–342. [Google Scholar]
- Shulman, L.S. Knowledge and teaching: Foundations of new reforms. Harv. Educ. Rev. 1987, 57, 1–23. [Google Scholar] [CrossRef]
- Hill, H.; Sleep, L.; Lewis, J.; Ball, D. Assessing teachers’ mathematical knowledge: What knowledge matters and what evidence counts. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Jr., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 111–156. [Google Scholar]
- Hill, H.C.; Ball, D.L.; Schilling, S.G. Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. J. Res. Math. Educ. 2008, 39, 374–400. [Google Scholar]
- University of Louisville. Diagnostics Mathematics Assessment for Middle School Teachers. Available online: http://louisville.edu/education/centers/crmstd/diag-math-assess-middle (accessed on 5 January 2017).
- Depaepe, F.; Verschaffel, L.; Kelchtermans, G. Pedagogical content knowledge: A systematic review of the way in which the concept has pervaded mathematics educational research. Teach. Teach. Educ. 2013, 34, 12–25. [Google Scholar] [CrossRef]
- Selling, S.K.; Garcia, N.; Ball, D.L. What does it take to develop assessments of mathematical knowledge for teaching?: Unpacking the mathematical work of teaching. Math. Enthus. 2016, 13, 35–51. [Google Scholar]
- Howell, H.; Lai, Y.; Phelps, G.; Croft, A. Assessing Mathematical Knowledge for Teaching Beyond Conventional Mathematical Knowledge: Do Elementary Models Extend? 2016. Available online: https://doi.org/10.13140/RG.2.2.14058.31680 (accessed on 5 January 2017).
- Kaiser, G.; Blömeke, S.; Busse, A.; Döhrmann, M.; König, J. Professional knowledge of (prospective) mathematics teachers—its structure and development. In Proceedings of the PME 38 & PME-NA 36 (V. 1), Vancouver, BC, Canada, 15–20 July 2014; Liljedahl, P., Nicol, C., Oesterle, S., Allan, D., Eds.; PME: Vancouver, BC, Canada, 2014. [Google Scholar]
- Manizade, A.G.; Mason, M.M. Using Delphi methodology to design assessments of teachers’ pedagogical content knowledge. Educ. Stud. Math. 2011, 76, 183–207. [Google Scholar] [CrossRef]
- Manizade, A.G.; Mason, M.M. Developing the area of a trapezoid. Math. Teach. 2014, 107, 508–514. [Google Scholar] [CrossRef]
- Clarke, D.; Hollingsworth, H. Elaborating a model of teacher professional growth. Teach. Teacher Educ. 2002, 18, 947–967. [Google Scholar] [CrossRef]
- Hollingsworth, H. Teacher Professional Growth: A Study of Primary Teachers Involved in Mathematics Professional Development. Ph.D. Thesis, Deakin University, Victoria, Australia, 1999. [Google Scholar]
- Charmaz, K. Constructing Grounded Theory, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2014. [Google Scholar]
- Strauss, A.L.; Corbin, J. Basics of Qualitative Research: Grounded Theory Procedures and Techniques; Sage Publications: Newbury Park, CA, USA, 1990. [Google Scholar]
- University of Chicago. Van Hiele Levels and Achievement in Secondary School Geometry: Appendix B. Zalman Usiskin: Chicago, IL. Available online: ucsmp.uchicago.edu/resources/van_hiele_levels.pdf (accessed on 5 January 2017).
- Martinovic, D.; Manizade, A.G. Teachers Evaluating Dissections as an Approach to Calculating Area of Trapezoid: Exploring the Role of Technology. In Proceedings of the 5th North American GeoGebra Conference: Explorative Learning with Technology, Toronto, ON, Canada, 21–22 November 2014; Martinovic, D., Karadag, K., McDougall, D., Eds.; University of Toronto: Toronto, ON, Canada, 2014; pp. 44–50. [Google Scholar]
- Junker, B.; Weisberg, Y.; Matsumura, L.C.; Crosson, A.; Wolf, M.K.; Levison, A.; Resnick, L. Overview of the Instructional Quality Assessment; CSE Technical Report 671; Center for the Study of Evaluation National Center for Research on Evaluation, Standards, and Student Testing (CRESST); University of California: Los Angeles, VA, USA, 2006; Available online: https://www.cse.ucla.edu/products/reports/r671.pdf (accessed on 5 January 2017).
- Chiovitti, R.F.; Piran, N. Rigour and grounded theory research. J. Adv. Nurs. 2003, 44, 427–435. [Google Scholar] [CrossRef] [PubMed]
- Tiainen, T.; Koivunen, E.-R. Exploring forms of triangulation to facilitate collaborative research practice: Reflections from a multidisciplinary research group. J. Res. Pract. 2006, 2, M2. Available online: http://jrp.icaap.org/index.php/jrp/article/view/29/61 (accessed on 5 January 2017).
- Gellert, U.; Becerra Hernández, R.; Chapman, O. Research methods in mathematics teacher education. In Third International Handbook of Mathematics Education; Clements, M.A.K., Bishop, A.J., Keitel, C., Kilpatrick, J., Leung, F.K.S., Eds.; Springer Science & Business Media: New York, NY, USA, 2013; Volume 27, pp. 431–457. [Google Scholar]
- Lincoln, Y.S.; Guba, E.G. Naturalistic Inquiry; Sage Publications: Beverly Hills, CA, USA, 1985. [Google Scholar]
- Gall, M.D.; Gall, J.P.; Borg, W.R. Educational Research: An Introduction; Pearson Education: Boston, MA, USA, 2007. [Google Scholar]
- Jackson, P.W. The Way Teaching Is; National Education Association: Washington, DC, USA, 1996; pp. 7–27. Available online: http://files.eric.ed.gov/fulltext/ED028110.pdf (accessed on 5 January 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).