Abstract
This research discusses a single case study of a first-grade Latino English Learner (EL) student, Allen (pseudonym), from a larger inquiry-based intervention on inversion and mental reversibility development. The purpose of this case study was to develop a better understanding of the relationship between Allen’s English language proficiency and his ability to solve inversion and compensation mathematics tasks. The integration of multiple paradigms confronting radical constructivism and sociocultural theory of learning via culturally relevant pedagogy provided us with a multi-faceted set of perspectives in understanding the interconnection between Allen’s cultural and linguistic background and his development of algebraic reasoning. Through conceptual and retrospective analyses, we found that Allen’s language features are highly correlated with the development of his thinking strategies and his ability to solve mathematics tasks. Implications of this study include the development of teaching strategies that address critical issues in mathematics, such as the individual differences of learners, specifically ELs from Latino background. We suggest further research is needed in the field of language acquisition and access to STEM related concepts.
1. Introduction
Today at least 350 different languages are spoken by students in U.S. schools [1]. Speakers of other languages have been historically categorized through different labels in the U.S. education system, such as students with Limited English Speaking Ability (LESA), Limited English Proficient students (LEP), English Language Learners (ELLs), and English Learners (ELs). For the purposes of this study and the statistics presented in this paper, English Learners are defined as persons for whom English is not their primary language [2]. Although ELs can have a variety of primary languages, approximately 80 percent of ELs in the U.S. are Spanish speakers from Hispanic heritage cultures (i.e., Hispanic) [1,3]. Hispanic is the term officially adopted by the U.S. Census Bureau to classify students who are from Latin American roots. Even though we argue that this is an imposed definition, based on the use of Spanish as primary language of communication, we will keep the Hispanic definition when reporting demographic data from the U.S. Census Bureau. At the same time, we will use the term Latino when referring to Allen’s (pseudonym) cultural heritage because this term better describes his Latin American roots. Allen is a first-grade English Learner (EL) student and the focus participant for this case study.
In 2015, the average mathematics scores of Hispanic students was 18 points below White students in fourth-grade, and 22 points below White students in eighth-grade [4]. Although the difference between Hispanic and White students does not directly compare EL students to White students, the high percentage of ELs that are Hispanic indicates a cause for concern for ELs in Mathematics. In the same year, the achievement gap in mathematics between non-ELs and ELs was 25 points in fourth-grade and 38 points in eighth-grade [4]. These discrepancies between ELs and non-ELs further indicate ELs’ unequal access to mathematics achievement success and note a critical issue in education.
The purpose of this paper was to better understand factors that may contribute to the problem of ELs’ unequal access to mathematics achievement. Specifically, we were interested in how English language proficiency levels and cultural or linguistic differences may affect ELs’ mathematics achievement in algebraic reasoning. Thus, this study used a single case study design to analyze how different factors may have affected one Latino EL’s (Allen) mathematics achievement. Details pertaining to this problem, and factors that may contribute to it, are presented in the next section.
1.1. Problem Statement
The U.S. is home to a number of students from different ethnicities and with different levels of proficiency with the English language. Coley [5] suggests that these students may have difficulty accessing classroom instruction due to a lack of critical home experiences, delineating a critical issue in mathematics education. Ginsburg and Pappas [6] found that children from low Socioeconomic Status (SES) homes struggled when engaging in a type of mental activity necessary for latter success in algebraic reasoning described as mental reversibility (i.e., 2 + 7 = 9 is inversely related to 9 − 7 = 2). Findings from their study suggest that students from low-SES homes are missing some critical experiences that may support the development of this activity in early elementary school and evidence a critical need to support students with several characteristics (described as co-factors) (i.e., household where English is not the first language, race, household income) that might prevent them from succeeding in school mathematics. Two-thirds of ELs (i.e., students receiving extra English language instruction in school) come from low-income families [4], indicating that EL status may be a prominent co-factor of low SES. Allen is one of these students. Ultimately, without addressing this critical issue of equal access to early algebraic reasoning in mathematics education, our society’s STEM-oriented fields will continue to be underrepresented by diverse individuals, limiting our society’s ability to address multi-faceted social concerns in future generations [7,8]. This case study seeks to address part of this critical issue in mathematics education by considering how one EL first-grade student is able to access and learn critical foundations in Algebra by developing language features through tasks that elicit early forms of mental reversibility.
In hopes of closing these aforementioned discrepancies, the National Mathematics Advisory Panel [9] suggested elementary educators focus their instructional practices on three critical algebraic foundations to promote all students’ opportunities for success in latter Algebra courses and support STEM oriented careers. One of these critical algebraic foundations is fluency with whole numbers, which encapsulates: (a) (de)composition of number, (b) basic operations on number, and (c) operational properties of number [9]. Coupled with this suggestion and the findings from Ginsburg and Pappas [6], we focused this particular study on the design of effective fluency of whole number tasks at the early elementary grade levels for ELs who are struggling in mathematics (based upon participants’ standardized achievement on TEMA tests). We focused on whole numbers because we consider mental reversibility an underlying mental activity that students would need to rely on for latter success in fluency with inverse operations of whole numbers, a critical area of Algebra.
We define mental reversibility as the individual’s underlying mental actions that allow a person to understand the relationship of an action and its effect [10]. Individuals describing operatively inverse relationships (whereby one operation undoes the effect of another, e.g., 4 + x = 7 and 7 – 4 = x) or compensation between numbers (whereby an operation returns to an equivalent state, e.g., x + 3 = 7 + 4) rely on mental reversibility [10,11,12].
We want all our students to have opportunities to construct reversible actions when acting on a mathematical object (i.e., whole numbers) so they can construct critical foundations for Algebra. With this goal in mind, we considered the role of English language in the development of mental reversibility. While we know about the aforementioned achievement gaps between these different student populations and areas in mathematics that we should focus on, we do not yet know how mental reversibility develops in young children, what role languages play in these children’s ability to access these mathematical concepts, nor how these intervention tasks could best be designed to ensure equitable access. Thus, in this case study, we investigated how one Latino EL first-grade student, Allen, changed his counting, grouping, and strategy development when engaging in mental reversibility tasks over time. Specifically, our research questions were twofold:
- How did Allen’s culturally embedded mathematics perception and his English language proficiency level interplay with his ability to solve inversion and compensation mathematics tasks?
- Considering Allen’s cultural and linguistic differences, how can educators facilitate the development of algebraic reasoning and address individual differences of ELs like him?
To answer these questions, we researched about the multisemiotic nature (multiple modalities) of mathematics [13,14], focusing on the mathematics register—including vocabulary, word problems, and syntax—and its connection to the development of mental reversibility in ELs like Allen.
In the next sections, we define the inversion and compensation mathematics tasks that were the focus of this study and offer a review of literature and theories about mathematics register and its connection with linguistic and culturally relevant pedagogy, to address the development of mathematics strategies we observed in Allen, a Latino EL first-grade student.
1.2. Literature Review
We reviewed the literature to better understand current research relative to mental reversibility. Specifically, we looked at research on inversion and compensations tasks in earlier grades similar to those used in the design of this study and how these tasks relate to Algebra concepts in elementary school. We also reviewed the literature to better understand current research relative to mathematics register and how ELs gain access or are limited in mathematics tasks. We found three main themes, which encapsulate this review. First, we contextualized our research through the definitions of early algebra and mental reversibility, which provide the background to understand Allen’s performance in these tasks during our study. Second, we reviewed how cultural and societal perceptions about mathematics affect student’s thinking and learning. Third, we considered how mathematics register and the language of school mathematics may have played a role in Allen’s achievements in this study. Finally, we provide concluding remarks to connect these three main research fields together, on which we built our conceptual framework and situated our methods and analyses for this study.
1.2.1. Early Algebra and Mental Reversibility
Mental reversibility was initially defined broadly by Piaget as structurally understanding the operations to allow for reversible actions (as cited by [15]). Inversion is one of the simpler forms of mental reversibility (e.g., understanding how subtraction inversely relates to addition), but Hackenberg [16] argues that an individual’s ability to solve inversion tasks may not be relying on true mental reversibility. Thus, Hackenberg suggests that individuals would be required to solve both inversion and compensation tasks (i.e., understanding how to bring an equal state between two relations) when relying on mental reversibility.
Common misconceptions students experience when initially solving inversion tasks come from their inability to coordinate operations with numbers when solving inversion problems [17]. For example, students either generalize that all inverse relations use the same number and return to the original state (i.e., 4 + 5 − 5 = 4) or operations were skipped or changed in their strategies [17]. Also, young students struggle to comprehend relational terms (e.g., more, less, and the same) when solving inversion tasks [18]. To support early forms of algebraic development and support students’ coordination of operations and numbers and use of relational terms, findings suggest that students begin with additive and subtraction experiences with simple expressions before students are required to combine multiple operations and numbers in more comprehensive expressions [19].
Younger children have not typically been given compensation tasks. Hackenberg [16] notes that some older children are able to engage in inversion tasks and compensation tasks. Essentially, inversion tasks only require students to reverse their operational reasoning, whereas compensation tasks require students to understand the operational structure of the problem, as these problems do not indicate a starting and ending point [16]. Thus, for a student to solve compensation tasks he or she would need to construct relational structures of the operations and numbers coordinated, which is more difficult than simply reversing the order of an additive or subtractive operation.
In Algebra, the interdependent relationship between mathematics and language requires students to translate everyday language to algebraic expressions, and then back again to explain their reasoning or understanding. Recent findings suggest that young students are capable of constructing algebraic generalizations, paying attention to the explicit language and use of conjectures in solving operation problems [19,20,21,22]. Students as young as preschool-age have been found capable of transitioning their everyday experiences to mathematical experiences when developing an additive-subtractive inversion principle [19].
Similar findings from Carraher, Schliemann, Brizuela, and Earnest’s [20] study, with second-grade through fourth-grade students, suggest that students drew from familiar experiences to develop an early awareness to negative integers. Blanton, Brizuela, Gardiner, Sawrey, and Newman-Owens [21] found that students enrolled in second-grade could attend to co-varying relationships if they began in kindergarten generalizing from familiar contexts and with only one variation in a quantity before transitioning towards more abstract situations and with co-varying quantities.
These studies show that educators need to more explicitly bridge empirical generalizations around young students’ use of conjectures towards abstract generalizations [22]. Therefore, ELs lacking “typical” experiences and necessary English language levels of proficiency in which to access school Algebra may be limited when developing abstract generalizations about mathematics relationships. This is an important point related to the research in this paper, because the authors hope to contribute to the research on algebraic development by looking at how an EL’s algebraic development may compare to a typical algebraic development and how mental reversibility may develop from empirical experiences and transition towards abstract experiences with young children.
1.2.2. Cultural Perceptions in Mathematics
A study by Bush and Ohio University [23] found five cultural factors that affect mathematics: (a) societal influences; (b) parent attitudes, values, and beliefs; (c) teacher attitudes, values, and beliefs; (d) student perceptions and beliefs; and (e) language. A common thread through these factors is the beliefs and perceptions in mathematics developed in the student’s personal background. We adapted these five main factors to the purpose of this study, and considered them while engaging in compensation and inversion tasks with Allen.
One social and cultural perception about mathematics is that it is a “universal language”. There is a misperception that mathematics is based only on a language of numbers and symbols [24]. Although mathematics may seem to be number-based, there is the underlying cultural element of mathematics [25] that suggests individuals’ reliance upon language and culture needs to be considered when designing mathematics pedagogy.
Another common perception about mathematics is that student experience with numbers and equations in mathematics is the only key factor in accessing mathematics understandings. This is not true. The discrepancy between student performance on verbally formatted problems and numerically formatted problems strongly suggests that verbal factors contribute towards students’ success in solving word problems. Hence, students’ language background relates to their performance on mathematics word problems [26]. Although students who are ELs come to school with varying degrees of numerical and verbal experiences that foster their mathematics abilities, they face many obstacles that affect their ability to access their mathematics understandings [27].
One such obstacle is constructing interactions between numerical and verbal experiences. Lager [28] explains that students’ mathematics reasoning and their ability to abstract their mathematics understandings are based upon their ability to construct relationships between their mathematics and language understandings. For instance, students’ understanding of mathematical relationships between concrete experiences, semi-concrete graphical illustrations, abstract symbolic representations, verbal language, and written expressions of mathematical ideas are more capable of developing abstract conceptual understandings in mathematics.
When students solve word problems that connect to their own life experiences, they are able to build many of these relationships. For example, when students are asked to count candies in a jar, students would need to be familiar with the context of candy in a jar so they can attach it to an experience when verbally describing their results and developing abstract mathematics concepts. Through these types of word problems, students can develop mathematical concepts, as students’ specific working mathematical knowledge and ability to abstract this knowledge through English language develops when word problems are set in meaningful contexts [27].
Culturally responsive teachers connect mathematical concepts by connecting contexts with students’ experiences and cultures [29,30,31,32], as we will further argue through our conceptual framework. This connection between home and school languages and cultures could include, but is not limited to, introducing contexts in mathematic word problems that are culture specific to students through the use of media (e.g., images or videos) or by exchanging unfamiliar contexts with a context that is more relevant to the students’ personal or cultural experiences. Mathematics problems that are culturally relevant help students better understand the structure and relationships of the problems, which increases the chances of student success [33,34,35].
1.2.3. Mathematics Register and the Language of School Mathematics for ELs
As discussed above, language is a key factor in developing an abstract, conceptual understanding of mathematics [28]. One of the challenges for ELs in learning mathematics language is that it is acquired quite often in school and not through social, conversational interactions [24]. While ELs in early elementary grades are working on expanding their first language and English language competence, at the same time they are introduced to a completely new language, which is the language of school mathematics. In school, ELs are exposed to mathematics concepts and to verbal descriptions of them, which require the acquisition of a new set of linguistic competences.
When ELs are required to read a mathematics prompt, they experience two different language challenges: first, they culturally mediate mathematics via their interpretations of the mathematics terms in order to develop a more comprehensible and familiar vocabulary [28]; second, they interpret numbers and words to identify and/or develop effective strategies when solving a problem. Adding to the challenge is the fact that the reading level of mathematics texts are often higher than the intended grade level, even though the mathematical concepts themselves are developmentally appropriate [36].
Moreover, ELs’ development of domain specific vocabulary and syntax may also hinder reading comprehension of word problems. These aspects of the mathematics register present several challenges due to the complexities of the English language. One complexity is the existence of multiple meanings for mathematic vocabulary and multiple terms that mean the same thing [37,38]. For example, “add them up,” “the sum,” “the total,” “in all,” and “altogether” are phrases used in reference to the addition operation, but these are not terms used in everyday language. In Algebra, “less than” can be used to mean x < 5, as in “a number less than 5” or x − 5, as in “5 less than a number.” The complexity of such mathematical terms can lead ELs to create a logical, yet incorrect, solution path which may lead to further misunderstandings or misconceptions [28]. In addition, it is important to consider that students may lack basic mathematics concepts in their first language or they may have already developed mathematics misconceptions in their first language that can cause confusion [25,39,40]. In order to reduce confusion caused by multiple mathematics language registers and increase conceptual understating, connections should be made between terms or expressions in both languages [41].
The structure of word problems may also create language issues for ELs. For example, there are three structural types of quantity unknown problems for addition and subtractions: (a) result unknown (e.g., 8 + 4 = x, 12 − 4 = x); (b) change unknown (e.g., 8 + x = 12, 12 − x = 8); and (c) start unknown (e.g., x + 4 = 12, x − 4 = 8) [42]. Result unknown problems can be referred to as the computational form of the equation because the unknown quantity is isolated, which increases efficiency in problem solving strategy [33,42]. Artut [43] found that children made more mistakes with start unknown problems than result unknown. When interpreting these findings, Artut [43] proposed that children may have failed in start-unknown problems because they could not determine the initial count of objects with direct modeling strategies. Using inversion properties, students can rewrite change or start unknown problems in equivalent computational forms. For example, the start unknown problem x + 4 = 12 can be changed to the equivalent inversion equation 12 − 4 = x. Reading comprehension issues in word problems may affect ELs’ ability to infer the structural problem type or hinder flexibility in creating equivalent computational forms [37,42].
The complexity of the mathematics register clearly emerges in the articulation of word problems, and in the vocabulary and syntax choices that characterize mathematics texts, which may further explain ELs’ inability to perform at the same level as their English-speaking peers when solving mathematics problems. One possible solution to language issues in word problems is for teachers to be more linguistically responsive [44,45]. Linguistically responsive teachers are cognitively aware of the language or linguistic diversity of their students and advocate practices that support ELs [44]. Previewing mathematics prompts to avoid misunderstandings due to language is one example of being linguistically responsive. Another example is by using “you language” (e.g., you are given 8 apples, rather than Eric is given 8 apples). Artut [43] found that using “you language” in word problems helped guide preschool children to correct answers. This is particularly important in this study, as we sought to explore how language becomes a critical factor for ELs’ ability to access mathematics concepts and how the attempts of the teacher-researcher (the third author) to be linguistically responsive affected learning outcomes. Hence, the interaction between language, culture, and mathematics was a critical consideration in this study.
1.2.4. Summary of Literature Review
Considering the three main fields of research (early algebra and mental reversibility, cultural perceptions in mathematics, and mathematics register and the language of school mathematics for ELs) presented in this literature review, integrating mathematics and language teaching is the key to promote developmentally appropriate practice for ELs in mathematics assessment and instruction and to increase performances of ELs’ mathematics achievement [46,47,48,49]. Unfortunately, the integration of mathematics and language registers is not incorporated in most classrooms due to the fact that the majority of students and teachers in the U.S. are non-ELs [28] or lack appropriate training in ESL strategies. Thus, this is a critical area for reform in U.S. schools.
There are three fundamental areas in which reform in mathematics and language registers should take place: curriculum design, assessment, and staff development [50]. This study seeks to address how teachers can integrate curriculum reform within their own classrooms, which may directly impact the student experience. We discussed in the literature review the importance for and the means to integrate mathematics register and algebraic tasks (e.g., inversion tasks, compensation tasks) into linguistically and culturally relevant pedagogy. In integrating these, we would anticipate ELs having more means to access and solve inversion and compensation tasks, and more means for ELs to abstract the mathematical concepts through their use of language.
Numerous empirical works [30,31,32,33,34,35,42,44] support the integration of mathematics and language teaching and argue for the development of culturally and linguistically responsive pedagogy. However, few have considered how students may develop algebraic reasoning through these forms of pedagogy. Thus, this study seeks to contribute to the literature by examining how one Latino EL first-grade student engages in compensation and inversion tasks during after school mathematics intervention.
1.3. Conceptual Framework
For this particular case study, we drew explicitly from a blend of two paradigms: The Radical Constructivist Paradigm [51], to explain Allen’s cognitive changes when learning mathematics, and the Sociocultural Paradigm [52], to explain Culturally Relevant Pedagogy [53] when designing a mathematics intervention for an EL. In this section, we will explain these paradigms and related theories. We will also clarify how we integrated these paradigms and theories into our methods, task design, and analyses.
1.3.1. Radical Constructivist Paradigm
Aspects of Allen’s psychological understanding are described through the Radical Constructivist lens. Essentially, when researchers utilize the Radical Constructivist paradigm, they frame their work within the assumption that mathematics knowledge is actively constructed through engagement with mathematical concepts. Further, each individual’s construction of his or her mathematical concepts informs his or her own unique mathematical reality, which can be quite different from another individual’s mathematical reality.
There is a relationship between the role of concepts and their re-presentations (i.e., the means in which an individual’s mathematical concepts are represented) through linguistic interactions [51]. Von Glasersfeld [51] proposed that an individual’s psychological understanding of a concept is coordinated between compatible sound-image (e.g., the phonetic transcription [‘wʌn] and the graphic representation of the number “1” correspond to the concept of “one”) and re-presentation of a specific word or mathematical concept. For instance, if children hear the word “rhinoceros” they may consider a grey animal with a horn on its head, who lives in Africa. The concept of “rhinoceros” is a result of an association between the re-presentation brought forward by the child and the word “rhinoceros.” It should be noted that the re-presentation of the animal could have been formed by experience, images, or a vicarious description [51]. Students who are ELs may not have associations between a perceived sound and a concept, which would prevent them from bringing forth a re-presentation. In this case study, we investigated associations between a first-grade EL’s mathematics concepts and language development by analyzing Allen’s re-presentations and words used when engaging with compensation and inversion tasks.
1.3.2. Sociocultural Theory of Learning and Culturally Relevant Pedagogy
The second paradigm from which we drew when framing this study is the sociocultural paradigm, as we utilized Culturally Relevant Pedagogy when designing tasks and analyzing student interactions with these tasks. Lev Vygotsky [52] best described the sociocultural approach as mathematical learning to be the function of culture (i.e., social life and human social activity). Social interest is a natural instinct in human beings, who from early childhood years begin to seek contact with other people [54]. Adler underlined the importance of social interest in all “tasks” or periods of life and suggested a holistic approach when understanding the human being. Ladson-Billings, as cited in [55] (p. 62), defined culturally relevant pedagogy as “an approach to teaching and learning that empowers students intellectually, socially, emotionally, and politically by using cultural referents to impart knowledge, skills, and attitudes.”
For our research, we considered how an EL’s natural, cultural, and linguistic social activity sphere interacted with his ability to solve inversion and compensation tasks. We analyzed how ELs might better access inversion and compensation tasks through culturally relevant pedagogy, by adapting the teaching approach to use cultural referents and identifying how the changes affected learning knowledge, skills, and attitude.
1.3.3. Blending the Radical Constructivist and Sociocultural Paradigms: An Emergent Perspective
Based on the sociocultural paradigm, the social context of educational tasks plays a prominent role in learning. Applying the sociocultural paradigm to mathematics education, the social and cultural background in which the inquiry-based intervention was performed were considered a crucial factor in holistically evaluating a Latino EL’s response to the algebraic tasks [56]. In other words, it is essential to reflect on a Latino EL’s interaction with other social agents such as classmates, parents, educators, and members of the local community, thus avoiding approaching the individual in isolation [57,58]. It is also critical to consider how these social agents are affecting each student’s own mathematical realities through the Radical Constructivist lens.
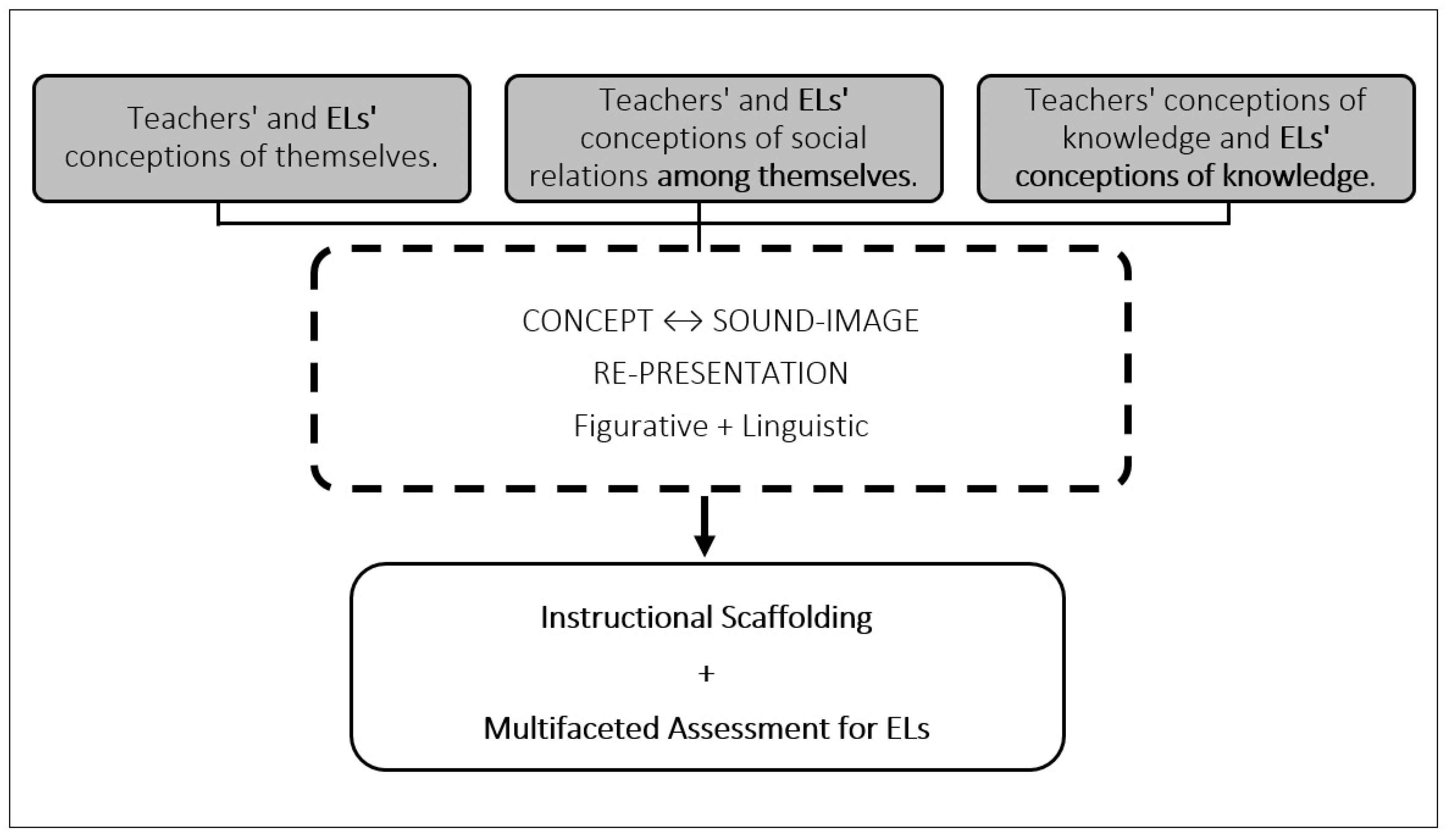
In the attempt to blend the Radical Constructivist paradigm, and the Sociocultural paradigm, we considered how the association between mathematics concepts and sound-image interact with three main areas in which culturally relevant educators demonstrate pedagogical understanding of: (a) conceptions of themselves and others, (b) conceptions of social relations, and (c) conceptions of knowledge (see Figure 1).
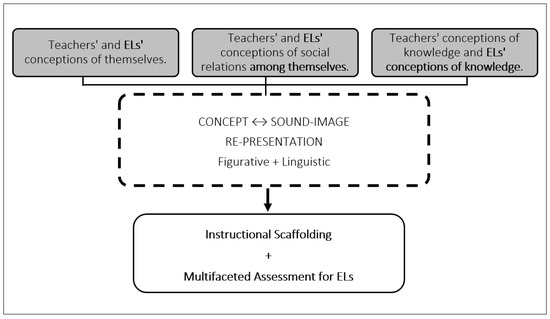
Figure 1.
Sociocultural Constructivist English Learner (EL) Intervention Framework. A theoretical framework for mathematics intervention with ELs, adapted and integrated from Von Glasersfeld [51] and Grant and Ladson-Billings [55].
To visually represent our theoretical framework as seen in Figure 1, we started with the consideration of the three main areas in which culturally relevant educators demonstrate broad pedagogical understanding during mathematics interventions: (a) teachers’ conceptions of themselves and others (teachers understand that learning happens in a community); (b) teachers’ conceptions of social relations (teachers are aware of the connections between themselves and ELs and between ELs and their peers); and (c) teachers’ conceptions of knowledge (teachers facilitate learning through multifaceted means and assessments) [55]. These are each represented as the plain text within each of the grey boxes in Figure 1. We expanded these teachers’ conceptions within the cultural relevant pedagogy to include the experiences of ELs, as indicated by the bold text included in the three grey boxes.
Von Glasersfeld’s [51] radical constructionist paradigm, in which an individual’s conception of knowledge is constructed by the re-presentation of concepts based upon sound-image, is delineated within the dash line box. The black connector in Figure 1 shows that the teachers’ and ELs’ conception of themselves, social relations, and knowledge will filter and integrate the re-presentation of concepts and sound-image. We argue that this re-presentation (in the dashed box) is connected to both teachers’ and ELs’ conceptions of themselves, social relations, and knowledge. Through this consideration, teachers would be able to offer instructional scaffolding opportunities for ELs learning and, consequently, multifaceted forms of assessment, validating multiple forms of students’ expression and understanding, as seen in the bottom box of Figure 1.
In this blend of the Radical Constructivist paradigm and Culturally Relevant Pedagogy, culturally relevant teachers would inquire within their own knowledge acquisition process, understand that their knowledge is not static (i.e., may be different than an EL’s and may change in time), and for this reason must viewed critically [55]. In this way, educators will be able to incorporate ELs’ perspective and provide opportunity for ELs to develop their own knowledge system and see assessment as a way to show their mastery of particular concepts (e.g., compensation and inversion tasks) instead of just a number on their records.
2. Materials and Methods
In this section, we provide a brief overview of the methods applied in this case study, which is part of a larger study. The larger study included 11 students enrolled in kindergarten to second-grade in an elementary school in the West Mountain Region of the United States and was approved by the Utah State University Institutional Review Board (protocol number irb-6849, 22 July 2015). The students were purposefully chosen and participated in five concurrent teaching experiment groups throughout an academic term [59]. This larger study aimed to establish and measure the key defining characteristics of tasks meant to promote children’s construction of mental reversibility. Throughout the teaching experiments, students participated in no more than 28 sessions. As part of the on-going analysis of the 11 participants, we advanced questions regarding the development of one first-grade student, Allen. In particular, we were interested in the interplay between Allen’s culturally embedded mathematics perception and his English language proficiency level when determining his ability to access and solve problems during the teaching experiment sessions.
2.1. Participants
Allen is a Latino student enrolled in a first-grade classroom (in Spanish nouns have genders, therefore, with Latino we refer to a male student and with Latina to a female student from Latin American heritage). He was six years and four months old at the onset of the study. Based on the federal criteria for students who qualify for free or reduced lunch and Allen’s family income range and household size, we categorized Allen as coming from a home designated as low-SES. Becka is a Latina student enrolled in a first-grade classroom. She was also six years and four months old at the onset of the study. Based on the same criteria mentioned above, Becka also came from a home designated as low-SES. Both Allen’s and Becka’s families indicated on a school demographic form that they spoke primarily Spanish at home, which categorized them as ELs. Allen and Becka both received EL services at school daily, prevalently through pull out intervention model. Allen and Becka’s teachers did not indicate the students’ English proficiency level.
After the screening interview, we determined that Allen and Becka were able to count nine items sufficiently and Allen used his fingers to attempt to find a missing addend during an inversion task. Becka quickly gave an inaccurate solution for the missing addend task and justified that she “saw it” when asked how she knew this answer to be true. Further, it seemed that Allen and Becka were able to subitize up to 10 items, but depended heavily upon “known” patterned items [60]. Based on Allen and Becka’s similar age, use of strategies, and demographic information, we chose both students to work together. Due to Becka’s inconsistent attendance, we chose to focus this study primarily on Allen’s strategy development relative to changes in tasks.
2.2. Research Design
This is a case study, which we understand as “the empirical study of human activity” [61] (p. 454) to evidence Allen’s relatively–in comparisons with his
peers- equal access to mathematical concept development through a change in his use of strategy. Initially, Allen was purposefully chosen to be part of the larger study as a result of his participation in three screening interviews. Analyses of these interview findings indicated that: (a) he was not capable of relying on inverse operations abstractly when solving problems and explaining his reasoning, but evidenced early strategies that allowed him to solve additive inverse problems; (b) his standardized score in the Test of Early Mathematics Ability (TEMA-3) [62] was in the cut-off range from 70 to 95 (his score was 84) [59]. The TEMA-3 is a norm-referenced test designed to measure mathematics ability levels for children between the ages of 3 years 0 months and 8 years 11 months [62]. Standardized scores and percentile rankings from the TEMA-3 were used, as these scores control for age. TEMA-3 standardized scores have a mean of 100 with a standard deviation of 15. This standardized assessment provided us a measure in which to categorize students as “struggling” in mathematics.
For this case study, we collected quantitative and qualitative data, in the form of: (a) participant observation during the teaching experiment sessions; (b) field notes, collected at the end of the teaching experiment sessions and watching the videos of Allen’s sessions; (c) student interviews, collected three times during the study (screening interviews, midterms, and final interviews); and (d) TEMA-3 scores. Through this data, we explored Allen’s learning of key characteristics. The quantitative data (the TEMA-3 scores and the statistics from the coding sessions) will be described qualitatively for this case study, as our focus was on the insight provided through an in-depth qualitative analysis of Allen’s responses. In this sense, we did not compare Allen’s TEMA-3 scores with the results obtained by other students in the larger intervention study, but rather analyzed each occurrence (e.g., Allen could not count down from 10 to 1) in its specific context (e.g., the language used to ask Allen to count down from 10 to 1).
In each interview and teaching experiment session, we used two video cameras and one audio recorder to record Allen’s verbal and empirical responses. During the first interview, Allen was asked to perform subitizing tasks used in MacDonald and Wilkins’ [60] teaching experiment sessions to determine how perceptual activity may relate to Allen’s number understanding and early operational thinking. The second interview included counting tasks modeled after Steffe and Cobb’s [63] teaching experiment tasks to determine flexible manners, in which children use counting when understanding number. The third interview included the TEMA-3 [62] to determine Allen’s standardized mathematics ability level. Allen participated in 23 teaching experiment sessions over the course of one academic term. He engaged with tasks that were designed to elicit counting and subitizing with the objective to solve inversion and compensation tasks.
2.2.1. Teaching Experiment Sessions
The purpose of using a teaching experiment is to build a second-order thinking model of a student’s learning from our interpretations of their interactions with mathematics tasks [64]. A second-order thinking model depicts a researcher’s inferred perspective of a student’s mathematical reality. This reality is based on the mathematical concepts and activity that the students used in previous tasks to build towards subsequent strategy use and development in later tasks. This methodology was chosen because it aligned with the Radical Constructivist paradigm this study was grounded in. Allen’s interactions with task design features were observed by a “witness” (a graduate researcher) in each session who interrupted ineffective interactions by asking questions to help Allen reflect on his responses or a peer’s responses. The teacher-researcher” (the third author) engaged the students with the tasks and essentially led the sessions. Allen participated in 23 teaching experiment sessions with Becka. For each teaching experiment session, the teacher-researcher and the witness worked semiweekly for about 15–20 minute after school with Allen and Becka.
2.2.2. Tasks
During each teaching experiment session, Allen engaged in subitizing [60], counting [63], inversion [65], and/or compensation activity [66]. Subitizing and counting activities were elicited to indicate early development of mental reversibility that may relate to later abstract development of mental reversibility [60,63]. Thus, tasks that elicited these types of activity were utilized to better understand how multiple modalities may allow students equal access to mental reversibility development. The numbers used in these tasks were chosen in accordance with each student’s conceptual analysis with simple (de)composition tasks.
To elicit each of these four types of activity (e.g., subitizing, counting, inversion, and compensation), variations of tasks were utilized. As analyses informed the research team of changes in Allen’s responses, they also informed the need for slight changes in task designs. Thus, the tasks were developed at the onset of the study, but changes to these tasks were made to provoke changes in Allen’s second-order thinking model. The changes made to the tasks were in response to an analysis of Allen’s responses during the sessions and after the sessions. Essentially, when Allen relied on re-presentations (i.e., fingers, drawings, movement of counters, language) we considered how these re-presentations could inform us of Allen’s mathematical understandings and the degree of abstraction relative to these understandings. This also informed us of social conceptions of himself as a student of mathematics and the relative norms established around these conceptions. Throughout the conceptual analyses and retrospective analyses meetings, the first and third author would meet bi-weekly to discuss these possible social norms and mathematical understandings. The teacher-researcher changed tasks as a result of these meetings and forms of analyses so that language and context of the tasks were more culturally relevant (i.e., closely aligned with Allen’s language and home experiences).
Allen and Becka engaged in subitizing, addition, subtraction, identity, negation, inversion [18], and compensation tasks. For the purpose of this study we recall Clement’s [67] (p. 400) definition of subitizing, as the act of “instantly seeing how many,” or the ability of “direct perceptual apprehension of the numerosity of a group”. Tasks varied by context, number, visibility of counters, and whether parts relative to the whole were discussed with Allen and Becka sequentially or concurrently. More addition, subtraction, and compensation tasks were used with Allen to build from a +1/−1 type of reasoning towards more abstract inversion thinking. For this paper, only two tasks will be discussed (compensation and inversion tasks).
2.3. Analytical Procedures
We started the analysis using Maxqda 12 software, a management program for qualitative data analysis. Maxqda 12 is a Window-based software for categorization of themes and managing data. We used Maxda 12 because its user-friendly interface allowed us to code video and audio segments of the data, establish new in vivo codes, and visualize the interceptions between different codes. Maxqda 12 also allowed the research team to code the data and organize it into themes and patterns that were collectively shared.
The data was organized in a logical and useful way according to these three main categories:
(a) the TEMA scores PDF files; (b) the interviews video files; and (c) the teaching sessions video files. We explored the data through conceptual and retrospective analysis guidelines. We began the interpretation by using an open coding technique, which allowed us to consider “all potentials and possibilities contained within them” [68] (p. 160). An eclectic coding [69] was employed in our second cycle of coding. We synthesized the variety and number of codes into a more unified scheme. Through the different cycles of coding and member checking phases, we identified three main emerging themes: (a) teaching strategies; (b) language features; and (c) thinking strategies. We looked at the subcodes connected with three main themes and further analyzed and synthesized them. We used the statistic of subcode function in Maxqda 12 to verify and visualize the frequency and the percentage of occurrence of the three main themes, and their relations.
2.3.1. Conceptual Analyses
When analyzing the video footage from each session, we described what students might understand based upon the various strategies they employ [70]. To accomplish this goal, we engaged in conceptual analysis where, through analysis of observed student responses, we inferred mental operations Allen may be using and/or developing [51]. Our approach is particularly relevant when considering the semantic connection between Allen’s constructed algebraic operations, graphical re-presentations, and descriptive re-presentations. Throughout this conceptual analysis, we paid close attention as to how his responses suggested development of certain mathematics concepts. We also examined Allen’s descriptions in Spanish and English where he referred to his formal schooling experiences when engaging with tasks.
2.3.2. Retrospective Analysis
We complemented our conceptual analysis procedure with retrospective analysis to better understand overarching trends in Allen’s use of strategies and inferred cognitive changes. In a retrospective analysis, researchers conduct a historical analysis of video records, meaning they look at how the experiential models of students’ mathematical thinking change over time [71]. While we used conceptual analysis to analyze Allen’s responses between tasks and sessions, we used retrospective analysis to analyze the changes that occurred over longer periods of time and at the conclusion of the study [71]. Three times throughout the study, all the authors of the research team engaged in coding both transcriptions of Allen’s responses and organized them in an excel sheet. The excel sheet format was utilized to determine relationships between Allen’s responses and task characteristics. In the first retrospective analysis session, the research team brought open codes to the meeting and categorically grouped these to determine larger categories. In the second retrospective analysis session, qualitative data were reviewed and discussed relative to categorical codes and student responses. Further, codes were color coded to determine changes between sophisticated activity (i.e., “counting to”) to more rudimentary activity (i.e., “counting all”) and vice versa.
We also used retrospective analysis to analyze the interconnection between Allen’s and researchers’ personal, social, and knowledge conceptions [55]. Changes in Allen’s learning and re-presentation were considered in light of researcher changes in task language and context. These changes in colors were used to help the research team focus on specific shifts in our second-order thinking model for Allen relative to culturally relevant pedagogical changes. In the final retrospective analysis session, the first author revisited all of the video data that she found to be of interest relative to Allen’s use of language, re-presentations, and conceptual material.
2.4. Limitations
For the purpose of this research, we focused on one specific participant of a larger study. This provided us insight to an in-depth set of questions regarding Allen’s access to mathematical concepts throughout the course of the study. However, as a general limitation of a case study, the results cannot be generalized to the rest of the participants of the larger study, nor to the wider population of EL students in the school [72].
Other limitations to the study can be the researcher’s own subjective feelings and positionality. The first author approached this study as a Sicilian-Italian, first generation college student, female, multilingual (Italian, Spanish, and English) and multicultural recent graduate in Curriculum and Instruction, with specialization in cultural studies and bilingual education. She brought to this research project her experience teaching, tutoring, and observing K-12 students in Italy and in the United States for the past 15 years. The second author approached this study as a white, female doctoral student in Mathematics Curriculum and Instruction. She brought to this research project 15 years of experience in teaching, tutoring, observing, and task development as an English as a Second Language (ESL) endorsed elementary teacher in low SES (Title One) schools with large Latino EL populations. The third author approached this study as a white, female, early childhood mathematics researcher and educator. She brought to this research project 17 years of experience in teaching, tutoring, coaching, and observing elementary school students and teachers as a classroom teacher and instructional specialist working in fully inclusive school settings. Furthermore, her previous research, investigating cognitive mechanisms (e.g., subitizing) early childhood children utilize when developing number and operational understandings informed her perspective when working with students. Shifts in these perspectives stemmed from her reflection upon her students’ ability to access mathematical concepts via her use of language. We acknowledged our different backgrounds and we consider our personal, social, and knowledge conceptions [55] while we interpreted the data of this mathematics intervention study.
We also acknowledge the difficulty to replicate this study, which could be time consuming [72]. In order to answer these potential threats to the validity of the study, we acknowledged the researchers’ positionality, used multiple theoretical lenses when informing our design and analysis, and used member checking during all phases of data collection and analysis. In addition, we recurred to the use of Maxqda 12 software to build a coding platform that could be used as a term of comparison for the larger study and for future specific case studies on ELs in mathematics research.
3. Results
In retrospective analysis, we learned that the term “language” was an open code identified by each member of our team as a crucial concept in our interpretation of the data. Therefore, we decided to focus further on the code “language” making it our key category and consider the connections between this code and the correspondent subcodes. Through the Code-Subcode-Segments Model function we checked the frequencies of intersections between Language Features and various subcodes. We found out that Language Features was in use more often in connection with the subcode Phrasal Verbs. Hence, it emerged that among the different language features the use of specific phrasal verbs represented a crucial element that interplayed with Allen’s ability to solve inversion and compensation mathematics tasks. Using structural coding [69] we considered the connection between the Language Features and another subcode, Culturally Embedded Mathematics Perception, in relation to our specific research question. Due to its relevance, we considered phrasal verbs and culturally embedded mathematics perception emergent subcategories. We assigned different colors to the Culturally Embedded Mathematics Perception subcode to monitor the code-co-occurrence with the Phrasal Verbs category. The following examples illustrate where Cultural References and Linguistics Features interplayed with Allen’s ability to solve the mathematics task.
3.1. Examples of Task Design that Prevented Allen Equal Access to Mathematical Concepts
In the first example, which is a transcript section from Allen’s first screening interview, the student was asked to count backwards starting from ten. This task came directly from a TEMA-3 [62] assessment item.
- Teacher-Researcher:
- Remember how rocket ships count off? How they count backwards like that?
- Allen:
- [shakes his head to indicate he does not understand]
- Teacher-Researcher:
- Like three-two-one blast off!
- Allen:
- [nodding].
- Teacher-Researcher:
- Yah? Can you do that when you start at ten for me?
- Allen:
- [seems disengaged, he plays with his chair and seems not to understand what he has been asked to do].
- Teacher-Researcher:
- Like ten, nine, …
- Allen:
- I can’t do.
- Teacher-Researcher:
- you can do that; can you try?
- Allen:
- Nope!
(Student’s interview, PRE_03ScreeningInterview_part2_1, minute 03:07–03:31)
The teacher-researcher’s reference to rocket ships counting down before blasting off did not seem to align with Allen’s past experiences which seemed to prevent him from understanding what was expected of him. A visual re-presentation of the example may have helped Allen to connect the concept to his sound-image of a rocket ship or a different cultural context may have helped Allen understand the premise of the backwards-counting task.
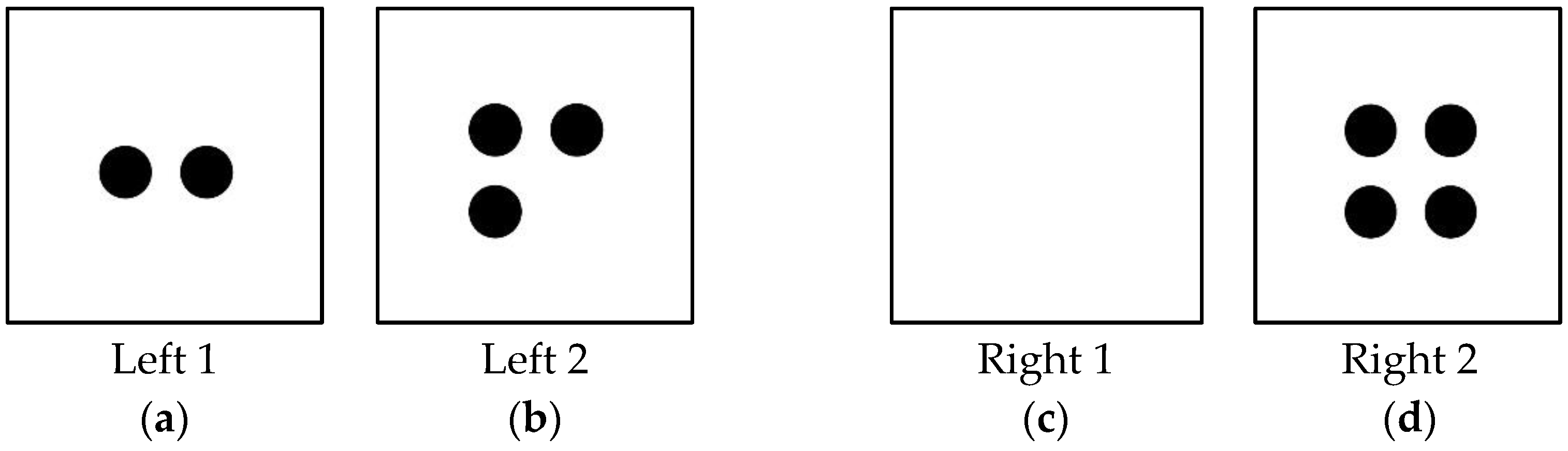
In the second example—a transcript from Allen’s tenth session—Allen is given a compensation task to solve. In this excerpt, the Cultural References and Phrasal Verbs seemed to play a decisive role in Allen’s ability to solve this problem. The teacher-researcher introduced the compensation task and gave Allen four pieces of paper with some counters on them (see Figure 2). Underlined words are meant to highlight the teacher-researcher and witness’s use of phrasal verbs. Phrasal verbs are verbal constructions formed by one verb and one preposition. The word altogether is in italics because we observed that Allen was not familiar with its meaning at the beginning of the study, but he began to use it by the end of the study.
- Teacher-Researcher:
- We are going to do a balance activity today.
- Allen:
- What’s balance?
- Teacher-Researcher:
- Did you ever put weights on a balance scale? And when you put more weights on one side, it dips down and the other one goes up? [While talking, the teacher-researcher opened up her arms mimicking a balance scale with her hands. She moved her left hand down while moving her right hand up as they were the two parts of a balance scale].
- Allen:
- [shakes his head to indicate he does not understand]
- Teacher-Researcher:
- Did you ever do that, Allen?
- Allen:
- No! [shakes his head]
- Teacher-Researcher:
- We are going to pretend that these papers (see Figure 2) are like that.
(Teaching Sessions, Allen_1_19_16a, minute 0:49–1:12)
- Allen:
- Um, six?
- Teacher-Researcher:
- You think a six should go here? So, six and four is in one hand, and three and two is in the other hand. Are they balanced?
- Allen:
- [shakes head to indicate “no”]
- Teacher-Researcher:
- No. What could we put here [points to Figure 2c] to make four and something balance with three and two.
- Allen:
- [holds his hands up like a balance scale] uh,
- Witness:
- Which one is more right now?
- Allen:
- Think you put two right here [points to Figure 2c].
- Teacher-Researcher:
- You think two, how come? What tells you that two should go there? Did you see that somewhere else?
- Allen:
- Um, [shakes head to indicate “no”].
- Allen:
- Six.
- Teacher-Researcher:
- Six? What do I have on this side [points to Figure 2a,b]?
- Allen:
- Two.
- Teacher-Researcher:
- No, on this side of the scale [points to Figure 2a,b]?
- Allen:
- Oh, five.
- Teacher-Researcher:
- Five. Ok, where do you see two on this side of the scale?
- Allen:
- [points to the two counters on Figure 2a]
- Teacher-Researcher:
- Ok, so we matched these two [points to a and c], they would be equal, wouldn’t they? Right, are these two [points to Figure 2b,d] equal though?
- Allen:
- [shakes head to indicate “no”]
- Teacher-Researcher:
- No. So, what can we do to make these two equal?
- Allen:
- Take one off. Take one away… [Indicating which counters by pointing to Figure 2d]
- Teacher-Researcher:
- Ok, well let me tell you this, watch. If I take one away, I cannot take it off altogether I have to put it over here. Now, are these two matched?
- Allen:
- [shakes head to indicate “no”]
(Teaching Sessions, Allen_1_19_16a, minute 1:52–5:43)
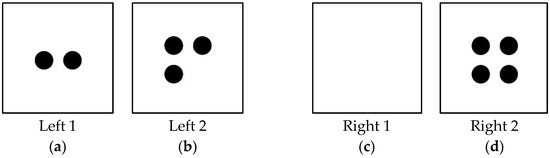
Figure 2.
Four pieces of paper used in the equation task.
Allen demonstrated difficulties in engaging in the activity due to the cultural reference of a balance scale. The teacher-researcher attempted to help Allen visualize a scale through motions, however he was not able to understand the concept of a balanced scale until a verbal description of quantities such as “more” and “equal” were introduced. This verbal description may have helped Allen re-present the concept in terms he was familiar with, thus facilitating understanding [51]. An understanding of the cultural reference alone did not help Allen complete the task in which he spent a significant time accessing the mathematical concepts intended in the task. This is consistent with the research that both language and mathematical understanding play a role in comprehension of word problems [18,21,24,31].
Phrasal verbs are particularly common in spoken English language; however, they constitute one of the most complex elements of the English language for ELs [73,74]. The use of phrasal verbs (underlined portions of the transcripts) at the end of the intervention period may have interfered in the exchange of information with Allen. When Allen used the phrasal verbs “take off” and “take away”, he used them both to mean “remove”. If we apply this definition to the teacher-researcher’s response, the result is a contradiction of “I remove one, I can’t remove one”. In this case, it is proposed that the use of cognate verbs (e.g., English “remove”/Spanish “remover”; English “cancel”/Spanish “cancelar”; etc.) in addition to the phrasal verbs (e.g., take off, take away) might have been able to provide Allen with equal access to the mathematical concepts and allow him the ability to connect these concepts with different English and Spanish verbal expressions [73,74]. Thus, we considered our use of phrasal verbs as a contributing factor to Allen’s ability to access the mathematics in the tasks and changed the language features we used in our task designs.
3.2. Examples of Task Design that Allowed Allen Equal Access to Mathematical Concepts
Through our initial retrospective analysis, we recognized the aforementioned concerns with our use of cultural context and language, and modified our task design to allow Allen access to mathematical concepts. For instance, we replaced questions and prompts in phrasal verb form (e.g., How many you take off? How many altogether?) with questions and prompts that used more direct or cognate verbs (e.g., How many you remove? How many total?). Furthermore, we changed the context of many of the tasks to align with Allen’s own cultural experiences. For example, after asking Allen about the activities he does with his family to celebrate birthdays, we found out that he was familiar with the cultural experience of filling and breaking a piñata. In the discussion with Allen, the teacher-researcher also asked Allen and Becka what shape their favorite piñata would be. From these conversations, one of the inversion tasks was changed; Allen was asked how many candies were in a Unicorn shaped piñata before more candies were added. The change in cultural reference may have helped Allen to understand the structural form of this start unknown word problem [42]. A compensation task was changed so that Allen was asked an equal sharing question with cupcakes on trays, a cultural reference he was familiar with, as we found out while engaging in a dialogue about his family’s cooking habits and birthday parties he had attended outside of school. The latter task changed and Allen’s interaction with these types of tasks is described in more detail in the following excerpt.
In this excerpt, Allen is in his fourth and final task for this session. This task was designed to provoke attention to the differences between the groups, not the differences between the total sets of counters by providing a difference of only one or two counters in subsets of groups. For example, in this task, Allen has eight cupcakes on one side of his mat and six cupcakes on the other. Becka’s cupcake mat has seven cupcakes, which is one more and one less than either side of Allen’s mat. The students are told that Becka needs more cupcakes so they have the same number of cupcakes. In earlier tasks, Allen has struggled to use Becka’s strategy of totaling the number of cupcakes for each student and then adding up from the smaller to the larger total in order to find the number of missing cupcakes. We used double-sided counters, featuring red on one side and yellow on the other. Allen begins to solve this by counting counters and then loses track of his counting, prompting him to begin counting all counters again. Thus, to help him re-establish the total counters in each side, the teacher-researcher restates the problem below.
- Teacher-Researcher:
- This is eight [points to counters on one side of the mat in front of Allen] and six [points to the counters on the other side of the mat in front of Allen]. You [indicating to Becka] have seven [points to counters on one side of the mat in front of Becka] and you need some more over here [points to the empty space on the other side of the mat in front of Becka].
- Allen:
- [counts the seven counters on one side of the mat in front of Becka] put one here and … [points to the empty side if the mat in front of Becka]. [Counts the counters on the mat in front of him].
- Becka:
- Eight—no we need eight. We need eight, Allen!
- Teacher-Researcher:
- What do you think [points to Allen]? You said put one here…
- Becka:
- It doesn’t make sense.
- Allen:
- [Places one counter on the empty side of the mat. Then, places a second counter on the same side of the mat. Looks at the mat in front of him and seems to nod a bit as if counting.] What’s altogether here?
- Teacher-Researcher:
- I am not telling you that. I am telling you have eight and six.
- Allen:
- [Counts the counters on both sides of the mat in front of him before looking at the counters on the mat in front of Becka. Places five more counters on the side of the mat in front of Becka so there is a total of seven counters on each side of the mat in front of Becka. When Allen initially places the final counter on the mat he turns it over so it is yellow and then turns it back over so it is red like the other six counters on this side of the mat] Got it…got it… got it…got it.
(Teaching Sessions, Allen_4_12_16d, minute 12:46–13:41)
Upon review of this excerpt, it seems that Allen was attempting to use the differences between the groups at first, as he counted the seven and then he stated “put one here” before counting the other part. This strategy was more difficult, as Allen would need to consider the operational structure in a non-directional manner [16]. However, Allen then switched to count the total in the larger group (the mat in front of Allen) and counted on from the smaller group (the mat in front of Becka). This strategy was quite typical relative to the literature on algebraic reasoning development, as it seemed Allen was able to access the task additively before inversely considering the relations on both cupcake trays [19]. Regardless, these new strategies Allen was developing evidences of changes in his ability to access multiple reasoning strategies elicited through access of the mathematical concepts in the task. This shift in how Allen is both utilizing mathematical language and accessing the mathematical concepts suggests the changes made to the tasks to be more culturally relevant were effective, thus supporting the idea that teachers need to be culturally relevant in their mathematics instruction and intervention [29,30,31,32,33,34,35].
3.3. Teaching Strategies, Language Features, and Thinking Strategies
In subsequent retrospective analyses, we used the statistic of subcode function in Maxqda 12, to calculate and visualize the frequency and percentage of occurrence within the three main emerging themes: (a) teaching strategies; (b) language features; and (c) student thinking strategies. Intersecting the statistics of subcodes with qualitative analyses, we reported each main code and subcode statistic qualitatively, we grouped the subcodes in categories, and we interpreted the results to determine more in-depth forms of how teaching strategies, language features of tasks, and Allen’s thinking strategies interacted. In the following sections, we discuss the three themes and the interaction between them.
3.3.1. Teaching Strategies
We identified four types of teaching strategies during the mathematics intervention with Allen:
- Explaining Thinking (31%): teaching strategies that focus on “asking the students to explain thinking” and “teachers suggesting answer/strategies”.
- Naming Tasks (24%): teaching strategy that focuses on relating possible solutions to the name associated with the task.
- Using instructions (24%): teaching strategies regarding giving instructions on how to complete a task. These instructions were either differentiated (directly connected with the task and explained as such to the student) or implicit (implied).
- Asking questions (19%): teaching strategies that include asking questions that were general in nature (e.g., how many do you see altogether?) or specific in nature (e.g., where do you see two on this side of the scale?).
A total of 77 uses of a teaching strategy were coded over the course of Allen’s 28 teaching sessions. The most frequent teaching strategies used in the study are: asking Allen to explain his thinking, naming tasks, and using differentiated instructions and general questions. To deliberately explore and develop the most effective tasks for Allen’s algebraic development when enacting these teaching strategies, we addressed Allen’s individual differences in mathematics register, cultural experiences, and English language proficiency. We then considered how these teaching strategies and changes in tasks interacted with Allen’s algebraic development.
3.3.2. Language Features
We observed that the language features that influenced Allen’s mathematics development can be described through three main categories:
- Vocabulary (35%): synonyms, literal translations from primary language, and unknown words.
- Syntax (33%): phrasal verbs, prepositions, question structure, and subject pronouns.
- Culture (31%): cultural and contextual influences in story problems.
Considering the incidence of each language feature, we found that vocabulary is the language feature that affected Allen’s mathematics development the most (35%). In particular, synonyms, literal translations from primary language, and unknown words were influential with regard to vocabulary (e.g., altogether, equal, share fairly). Syntax was influential when phrasal verbs, prepositions, question structure, and subject pronouns were introduced during a task (e.g., take off, take away, take out, spill over, slide over, polling down, check out, pull off, pull down, brought over, turn around, hold on). Culture was determinant when within cultural influence, perception and story problems interplayed with Allen’s ability to solve mathematics tasks (e.g., the references to the rocket ship and the use of the piñata). Following the principles of culturally relevant pedagogy, we questioned the linguistic and cultural assumptions [75] we used in the mathematics interventions that could have prevented Allen from performing compensation and inversion tasks.
3.3.3. Allen’s Thinking Strategies
Allen’s thinking strategies, observed during the sessions with Allen, concern three main forms of re-presentations: Manipulatives (44%), Verbal (35%), and Visual (21%). These findings suggest that the use of manipulatives has the most influence (44%) on the development of thinking strategies during mathematics interventions. The most relevant manipulative strategy we observed is the use of fingers to count and to explain the rationale to solve the task. Verbal strategies were spoken strategies or actions by Allen. The most recurrent verbal strategies were: explaining thinking, rephrasing the questions and the possible answers, and the use of counting as a mnemonic action. For the visual category, we observed an extensive use of counters to represent Allen’s use of patterns, shapes, or actions, rather than as a counting mechanism.
3.4. Connections Between Teaching Strategies, Language Features, and Student Thinking Strategies
From a thorough consideration of our research questions in connection with the data emerging from the statistics of subcode, we observed that all three main themes of the analysis (i.e., teaching strategies, language features, and Allen’s thinking strategies) related to Allen’s ability to engage with the mathematics and solve inversion and compensation tasks. In order to better understand the connections or relationships between each of the themes, such as teaching strategies that may have prompted Allen’s development of language or thinking strategies, we considered and analyzed the co-occurrence of these themes.
For this purpose, we used two Maxqda 12 features. First, we ran the code relation browser. Through the code relation browser, we were able to visualize how often overlapping codes occurred, which allowed us to consider relationships between the three main codes: teaching strategies, language features, and student thinking strategies. The code relation browser computed the number of intersections of the codes. From the code relation browser, we found that the segments in which these three main codes intersections are represented by the following subcodes: suggesting answer/strategies, using differentiated instructions, asking to explain thinking, naming tasks, using implicit instructions, phrasal verbs, counting with fingers and counters, and explaining thinking.
The results we obtained through the code relation browser, were confirmed through the co-occurrence model function in Maxqda 12, which clarified the nature of these intersections between the three emerging themes. Teaching Strategies and Thinking Strategies are interconnected through Language Features, and in particular through the linking subcodes, listed in order of relevance (in terms of frequencies of intersections between the three emerging themes): verbal student thinking strategies (35); explaining teaching strategies (24); syntax language features (20); and manipulative student thinking strategies (20).
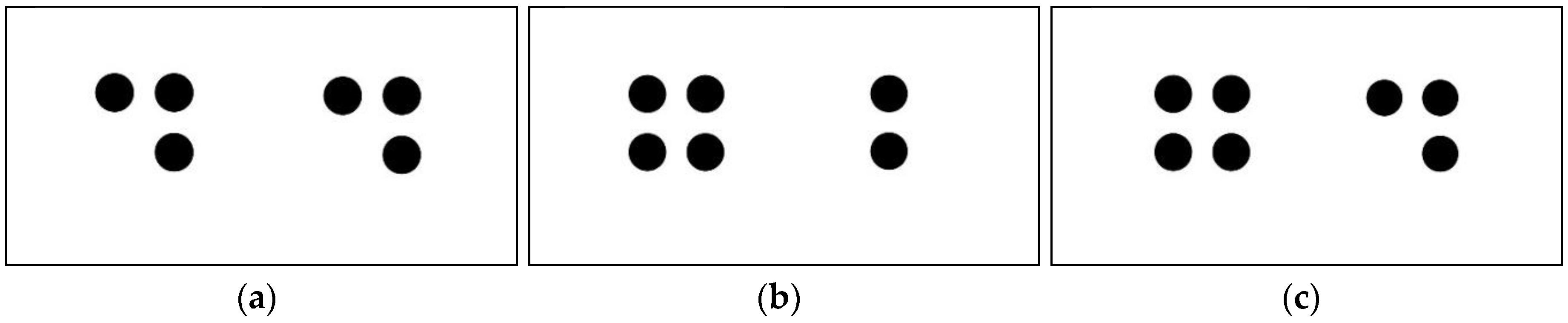
To focus our analyses of these results, we discuss the interconnections between only the top three subcodes listed above. Our findings suggest a strong connection between the emerging themes “explaining teaching strategies” and “verbal student thinking strategies”. This was evident when Allen adopted the teacher-researcher’s language and when the teacher-researcher provided Allen connections between his verbal strategies. For example, during one of the teaching sessions that targeted subitizing, the teacher-researcher hid counters under a mat (see Figure 3a). Then she quickly lifted up the paper and showed the mat to Allen, while asking “how many counters there were under the paper?”
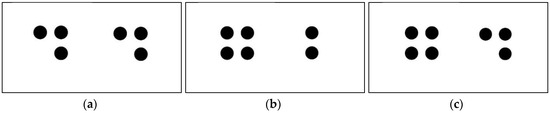
Figure 3.
Amount and position of counters as showed by the teacher-researcher to Allen during a subitizing task: (a) the teacher-researcher hid three counters on the left and three on the right side of the mat; (b) the teacher-researcher hid four counters on the left and two on the right side of the mat; (c) the teacher-researcher hid four counters on the left and three on the right side of the mat.
The teacher-researcher repeated the task (Figure 3b). Allen answered correctly by stating “six” for both task a and b. The third time this task was given to Allen (Figure 3c), the teacher-researcher asked Allen to complete the task by asking “how many counters there were under the paper” and then to explain his thinking.
- Teacher-Researcher:
- So, tell me what these groups told you “about seven”.
- Allen:
- [looked distracted]
- Allen:
- [pause, looking at the mat] I saw the four and the three, when you put altogether makes seven.
(Teaching Sessions, Allen_3_3_16b minutes 3:36–4:15)
From this excerpt, it seems that Allen is incorporating the teaching suggestion in his thinking strategy and reflected on his past explanation and reasoning. From this teaching strategy Allen was better able to elaborate upon his initial explanation. He also used the word altogether, which he learned through the teaching sessions, to help explain his operations. Other similar transcriptions of video footages seemed to also illustrate Allen’s tendency to adopt the teacher-researcher’s suggestion as part of his thinking strategies. In other cases, when he did not incorporate the teacher-researcher’s suggestions in part of his thinking strategy, he responded by simply agreeing with the teacher-researcher. Quite often, teaching strategies such as the use of differentiated instruction and suggesting answers occurred at the end of the task, as a sort of explanation or confirmation of Allen’s use of strategy.
The connections between teaching strategies, language features, and student thinking strategies confirm that the social and cultural background in which we performed the inquiry-based intervention became a crucial factor in determining Allen’s response to the algebraic tasks [56]. This indicates that an EL’s responses during mathematics intervention and instruction need to be considered holistically. In other words, it is essential to reflect on an EL’s interaction with other social agents such as classmates, parents, educators, and members of the local community, thus avoiding approaching the individual in isolation [57,58].
4. Discussion and Conclusions
The purpose of this case study was to focus on the relationship between ELs’ language proficiency and their ability to solve inversion and compensation mathematics tasks. We focused on Allen, one first-grade Latino EL, who participated in a larger inquiry-based intervention focusing on inversion and mental reversibility. Our research was twofold: first, we intended to inquire in which way Allen’s culturally embedded mathematics perception and his English language proficiency level interplayed with his ability to solve inversion and compensation tasks; second, considering Allen’s cultural and linguistically differences, we investigated how educators can facilitate the development of algebraic reasoning and address individual differences of learners like him. Answering our two main research questions we found that:
- Allen’s culturally embedded mathematics perception and his English language proficiency level both interfere with his ability to solve inversion and compensation tasks. Findings to this study suggest that Allen’s language proficiency level is closely connected with his ability to solve mathematics tasks and to develop thinking strategies.
- In order to facilitate the development of algebraic reasoning and address individual differences of learners, educators need to consider students’ cultural and linguistic differences and implement strategies in their instruction that support these differences.
In particular, we found that language features were a connector between teacher-researcher teaching and Allen’s thinking strategies. Our results indicate that Language Features that the teacher-researcher utilized informed her teaching and task design and then (dis)allowed Allen opportunities to engage and develop particular thinking strategies during the intervention. For example, the reference to the rocket ship did not serve as a contextual model according to which Allen could perform backward counting from ten to one. In addition, the use of the phrasal verb “count off” mislead Allen on the task he was asked to complete. However, the reference to the “piñata” problem helped Allen to solve inversion tasks, thanks to his cultural experience related to this social life event.
The use of different language features, especially phrasal verbs and vocabulary, influenced the way the teacher-researcher and witness suggested answers and strategies, asked Allen to explain his thoughts, named tasks, and gave implicit and differentiated instructions during the sessions. In the same way, these language features influenced Allen’s ability to engage with the mathematical concepts and the degree of abstract strategy development when explaining his thinking (i.e., rely on finger counting, visual representations, and counters). Finally, connecting these language features to multiple forms of re-presentations seemed to afford Allen an opportunity to construct multi-dimensional means to access mathematics concepts. For example, when Allen used the phrasal verbs “take off” and “take away,” he used them both to mean “remove.” Therefore, the use of a more descriptive verb such as “remove” instead of “take off” afforded Allen access to the instruction to complete the task.
These findings, suggesting language features as a means to provide Allen access to these algebraic tasks, echo findings from Carraher et al.’s [22] study. Essentially, Carraher et al. [22] found that student developed conjectures as a mean to provide students explicit statements of mathematical relationships. Furthermore, Carraher et al. [22] stated that without these conjectures in place, students would not transition from empirical generalizations to abstract generalizations. With Allen, we found that language features allowed Allen access to his own experiences and language when attending to and conjecturing about empirical generalizations.
In our conceptual framework, we theorized the integration of the Radical Constructivist paradigm and the Sociocultural paradigm, with particular attention to the contribution that culturally relevant pedagogy can provide to make inversion and compensation mathematics tasks to ELs. We argued that in the case of Allen, the association between his concepts and his sound-image was mediated by language features and sociocultural experiences. Therefore, his re-presentation of concepts depended on both figurative and linguistic features that were integrated through instructional scaffolding [13,14]. The findings of our case study supported our theoretical stance and provided practical examples that could help culturally relevant educators to provide opportunity for ELs to develop their own knowledge system and have a more equal access to the language and the tasks of school mathematics.
In this sense, the findings suggest that teachers should be linguistically responsive [42,43] by considering the language of instruction (e.g., use of phrasal verbs, vocabulary, sentence structure, questions used in mathematical tasks). They should also be culturally responsive [44,45,46,47] to their students’ sociocultural background (e.g., math problems built upon students’ experiences, use of visual aids) when teaching and assessing students’ skills to solve inversion and compensation mathematics tasks. For example, teachers can use visual aids to better explain tasks and use a more descriptive language (e.g., use the image of a rocket ship and model its function). In situations, teachers may need to modify the language of the task without altering mathematical challenge of the task [28,33,41,42,44,45]. In order to be both linguistically and culturally responsive, teachers will need to get to know their ELs’ personal cultural and background story so they can incorporate that knowledge regularly in lesson planning and enactment of mathematics tasks. In addition, teachers need to consider their own positionality and thinking skills (e.g., teacher’s socio-cultural background, their own thinking strategies, how they learned to solve compensation and inversion tasks, etc.). Finally, teachers need to inquire within their own knowledge acquisition process, understand that their knowledge is not static, and for this reason must be viewed critically. In this way, educators will be able to provide opportunities for ELs to develop their own knowledge system through instructional scaffolding and multifaceted task development.
In conclusion, although the findings of this study are limited to Allen’s case study, they imply that educators’ following up with precise validation of students’ use of language and development of strategies, modification of language during instruction to support student comprehension, and tasks aligned with students’ cultural experiences would be beneficial to students’ mathematics achievement when solving compensation and inversion tasks. An implication of this study is that the strategies we observed at the beginning of the mathematics intervention session can increase the student’s self-awareness of the specific situation and self-efficacy to succeed accomplishing the task in later sessions. An additional implication worth noting is how students’ self-awareness and self-efficacy may influence motivation when engaging with these tasks. Quite often EL students are given interventions grounded in rudimentary tasks that limit their ability to reason in sophisticated manners. These findings suggest ELs are capable of more sophisticated early algebraic tasks which may close achievement gaps. We encourage more research in the field of mathematics and ELs, in order to further contribute to the development of instructional practices that can provide a more equal access to the language and the tasks of school mathematics for ELs.
Acknowledgments
This case study research did not receive any funding. The authors did not received funds for covering the costs to publish in open access. This case study is part of a larger inquiry-based intervention study on inversion and mental reversibility, which received internal funds from the Office of Research and Graduate Studies at Utah State University. The authors want to recognize the support that the graduate student who served as witness during the teaching sessions, and all members of the larger study, M. Jill Ashby and Cathy Maahs-Fladung, provided in terms of preliminary analysis, open codes analysis, and member checking during the preliminary developmental phases of this case study research. The authors also want to thank the teachers and administrators who supported the development and implementation of the larger study. Finally, the authors would like to thank the anonymous reviewers for their helpful and constructive comments that greatly contributed to improving this manuscript.
Author Contributions
Beth L. MacDonald conceived, designed, and performed the experiments; Marialuisa Di Stefano performed the data analysis through Maxqda 12; Kristy Litster contributed to the data analysis and the interpretation of the data, provided review of literature and other sources needed to the development of the conceptual framework; the first author wrote the preliminary and the final draft of the paper, while the second and the third authors significantly contributed to its development and editing phase.
Conflicts of Interest
The authors declare no conflict of interest. The sponsor, which funded the larger inquiry-based intervention study on inversion and mental reversibility, had no role in the design of the case study research that is the object of this publication; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- U.S. Department of Education, National Center for Education Statistics. State Nonfiscal Survey of Public Elementary and Secondary Education. Digest of Education Statistics 2015. Available online: https://nces.ed.gov/programs/coe/indicator_cge.asp (accessed on 16 March 2017).
- The Glossary of Education Reform. Hidden Curriculum. Available online: http://edglossary.org/english-language-learner/ (accessed on 13 March 2017).
- National Education Association. English Language Learners Face Unique Challenges. Available online: http://www.nea.org/assets/docs/HE/ELL_Policy_Brief_Fall_08_(2).pdf (accessed on 13 March 2017).
- Snyder, T.D.; De Brey, C.; Dillow, S.A. Digest of Education Statistics 2014; National Center for Education Statistics, Institute of Education Sciences, U.S. Department of Education: Washington, DC, USA, 2016.
- Coley, R.J. An Uneven Start: Indicators of Inequality in School Readiness. Policy Information Report 2002. Available online: https://www.ets.org/Media/Research/pdf/PICUNEVENSTART.pdf (accessed on 16 March 2017).
- Ginsburg, H.P.; Pappas, S. SES, ethnic, and gender differences in young children’s informal addition and subtraction: A clinical interview investigation. J. Appl. Dev. Psychol. 2004, 25, 171–192. [Google Scholar] [CrossRef]
- Bradley, R.H.; Corwyn, R.F. Socioeconomic status and child development. Annu. Rev. Psychol. 2002, 53, 371–399. [Google Scholar] [CrossRef] [PubMed]
- Marx, S. (Ed.) Qualitative Research in STEM: Studies of Equity, Access, and Innovation; Routledge: New York, NY, USA, 2016. [Google Scholar]
- National Mathematics Advisory Panel. Foundations for Success: The Final Report of the National Mathematics Advisory Panel; US Department of Education, 2008. Available online: https://www2.ed.gov/about/bdscomm/list/mathpanel/report/final-report.pdf (accessed on 16 March 2017).
- Piaget, J. The Child’s Conception of Number; WW Norton: New York, NY, USA, 1965. [Google Scholar]
- Hackenberg, A.J. Construction of Algebraic Reasoning and Mathematical Caring Relations. Ph.D. Thesis, University of Georgia, Athens, GA, USA, 2005. [Google Scholar]
- Simon, M.A.; Placa, N.; Avitzur, A. Participatory and anticipatory stages of mathematical concept learning: Further empirical and theoretical development. J. Res. Math. Educ. 2016, 47, 63–93. [Google Scholar] [CrossRef]
- O’Halloran, K.L. Multimodal discourse analysis. In Companion to Discourse; Hyland, K., Paltridge, B., Eds.; Continuum: New York, NY, USA, 2011; pp. 120–137. [Google Scholar]
- O’Halloran, K.L. The semantic hyperspace: Accumulating mathematical knowledge across semiotic resources and modalities. In Disciplinarity: Functional Linguistic and Sociological Perspectives; Christie, F., Maton, K., Eds.; Continuum: London, UK; New York, NY, USA, 2010; pp. 217–236. [Google Scholar]
- Norton, A.; Boyce, S. Provoking the construction of a structure for coordinating n + 1 levels of units. J. Math. Behav. 2015, 40, 211–232. [Google Scholar] [CrossRef]
- Hackenberg, A.J. Students’ reasoning with reversible multiplicative relationships. Cognit. Instr. 2010, 28, 383–432. [Google Scholar] [CrossRef]
- Klein, J.S.; Bisanz, J. Preschoolers doing arithmetic: The concepts are willing but the working memory is weak. Can. J. Exp. Psychol. 2000, 54, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Donaldson, M.; Balfour, G. Less is more. Br. J. Psychol. 1968, 59, 461–471. [Google Scholar] [CrossRef]
- Baroody, A.J.; Lai, M. Preschoolers’ understanding of the addition—Subtraction inverse principle: A Taiwanese sample. Math. Think. Learn. 2007, 9, 131–171. [Google Scholar] [CrossRef]
- Carraher, D.W.; Schliemann, A.D.; Brizuela, B.M.; Earnest, D. Arithmetic and Algebra in early mathematics education. J. Res. Math. Educ. 2006, 37, 87–115. [Google Scholar]
- Blanton, M.; Brizuela, B.; Gardiner, A.; Sawrey, K.; Newman-Owens, A. A learning trajectory in six-year-olds’ thinking about generalizing algebraic relationships in functions. J. Res. Math. Educ. 2015, 46, 511–558. [Google Scholar] [CrossRef]
- Carraher, D.W.; Martinez, M.V.; Schliemann, A.D. Early algebra and mathematical generalization. Math. Educ. 2008, 40, 3–22. [Google Scholar] [CrossRef]
- Bush, W.S.; Ohio Univ, A.M. Bridging the Gap between Culture and Mathematics: The Appalachian Perspective. Occasional Paper 2003. Available online: http://www.eric.ed.gov/contentdelivery/servlet/ERICServlet?accno=ED478244 (accessed on 14 January 2017).
- Janzen, J. Teaching English language learners in the content areas. Rev. Educ. Res. 2008, 78, 1010–1038. [Google Scholar] [CrossRef]
- Sistla, M.; Feng, J. More than numbers: Teaching ELLs mathematics language in primary grades. In Proceedings of the Chinese American Educational Research & Development Association Annual Conference, Philadelphia, PA, USA, 2–3 April 2014. [Google Scholar]
- Abedi, J.; Lord, C. The language factor in mathematics tests. Appl. Meas. Educ. 2001, 14, 219–234. [Google Scholar] [CrossRef]
- Solano-Flores, G.; Trumbull, E. Examining language in context: The need for new research and practice paradigms in the testing of English-language learners. Educ. Res. 2003, 32, 3–13. [Google Scholar] [CrossRef]
- Lager, C. Types of mathematics-language reading interaction that unnecessarily hinder Algebra learning and assessment. Read. Psychol. 2006, 27, 165–204. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.; Amaro-Jiménez, C. Teaching English language learners (ELLs) mathematics in early childhood. Child. Educ. 2011, 87, 253–260. Available online: http://search.proquest.com/docview/866565276?accountid=12382 (accessed on 14 January 2017). [CrossRef]
- Artiles, A.J.; Trent, S.C.; Hoffman-Kipp, P.; López-Torres, L. From individual acquisition to cultural-historical practices in multicultural teacher education. Remedial Spec. Educ. 2000, 21, 79–120. [Google Scholar] [CrossRef]
- Gay, G. Culturally responsive teaching in special education for ethnically diverse students: Setting the stage. Int. J. Qual. Stud. Educ. 2002, 15, 613–629. [Google Scholar] [CrossRef]
- Villegas, A.M.; Lucas, T. Preparing culturally responsive teachers rethinking the curriculum. J. Teach. Educ. 2002, 53, 20–32. [Google Scholar] [CrossRef]
- Outhred, L.; Sardelich, S. A problem is something you do not want to have: Problem solving by kindergartners. Teach. Child. Math 2008, 12, 146–154. [Google Scholar]
- Lowrie, T. Young children posing problems: The influence of teacher intervention on the type of problems children pose. Math. Educ. Res. J. 2002, 14, 87–98. [Google Scholar] [CrossRef]
- Monroe, E.; Panchyshyn, R. Helping children with words in word problems. Aust. Prim. Math. Classr. 2005, 10, 27–29. [Google Scholar]
- Brennan, A.D.; Dunlap, W.P. What are the prime factors of reading Mathematics? Read. Improv. 1985, 22, 152–159. [Google Scholar]
- Jan, S.; Rodrigues, S. Students’ difficulties in comprehending mathematical word problems in language learning contexts. Int. Res. 2012, 1, 151–160. [Google Scholar]
- Baumann, J.; Graves, M. What is academic vocabulary? J. Adolesc. Adult Lit. 2010, 54, 4–12. [Google Scholar] [CrossRef]
- Ganesh, T.G.; Middleton, J.A. Challenges in linguistically and culturally diverse elementary settings with math instruction using learning technologies. Urban Rev. 2006, 38, 101–143. [Google Scholar] [CrossRef]
- Lee, H.; Jung, W.S. Limited-English-proficient (LEP) students and mathematics understanding. Math. Teach. Middle Sch. 2004, 9, 269–272. [Google Scholar]
- Khisty, L.L. Making inequality: Issues of language and meanings in mathematics teaching with Hispanic students. In New Directions for Equity in Mathematics Education; Secada, W., Fennema, E., Adajian, L., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 279–297. [Google Scholar]
- Van de Walle, J.A.; Karp, K.S.; Bay-Williams, J.M.; Wray, J. Elementary and Middle School Mathematics: Teaching Developmentally, 9th ed.; Pearson Education: Boston, MA, USA, 2016. [Google Scholar]
- Artut, P.D. Preschool children’s skills in solving mathematical word problems. Educ. Res. Rev. 2015, 10, 2539–2549. [Google Scholar]
- Lucas, T.; Villegas, A.M.; Freedson-Gonzalez, M. Linguistically responsive teacher education preparing classroom teachers to teach English language learners. J. Teach. Educ. 2008, 59, 361–373. [Google Scholar] [CrossRef]
- Oviedo, G.C.B. Comprehending algebra word problems in the first and second languages. In Proceedings of the 4th International Symposium on Bilingualism, Arizona State University, Tempe, AZ, USA, 30 April–3 May 2003; Cohen, J., McAlister, K.L., Rolstad, K., MacSwan, J., Eds.; Cascadilla Press: Somerville, MA, USA, 2005; pp. 267–295. [Google Scholar]
- Kang, H.W.; Pham, K.T. From 1 to Z: Integrating math and language learning. In Proceedings of the Annual Meeting of English to Speakers of Other Languages, Long Beach, CA, USA, 28 March–1 April 1995. [Google Scholar]
- Iliev, N.; D’Angelo, F. Teaching mathematics through multicultural literature. Teach. Child. Math. 2014, 20, 452–457. [Google Scholar]
- Pimm, D. Speaking Mathematically: Communication in Mathematics Classrooms; Routledge and Kegan Paul: London, UK, 1987. [Google Scholar]
- Silver, E.A.; Smith, M.S. Building discourse communities in mathematics classrooms. In Communication in Mathematics, K-12 and Beyond; Elliott, P., Ed.; National Council of Teacher of Mathematics: Reston, VA, USA, 1996; pp. 20–28. [Google Scholar]
- Buchanan, K.; Helman, M. Reforming Mathematics Instruction for ESL Literacy Students. NCBE Progr. Inf. Guide Ser. 1993, 15, 1–19. Available online: http://www.ncela.us/files/rcd/BE019270/PIG15.pdf (accessed on 14 January 2017).
- Von Glasersfeld, E. Radical Constructivism: A Way of Knowing and Learning. Studies in Mathematics Education Series: 6; Falmer Press, Taylor & Francis Inc.: Bristol, PA, USA, 1995. [Google Scholar]
- Vygotsky, L.S. The genesis of higher mental functions. In The concept of Activity in Soviet Psychology; Wertsch, J.V., Ed.; Sharpe: Armonk, NY, USA, 1981; pp. 144–188. [Google Scholar]
- Ladson-Billings, G. Toward a theory of culturally relevant pedagogy. Am. Educ. Res. J. 1995, 32, 465–491. [Google Scholar] [CrossRef]
- Adler, A. Social Interest; Oneworld Publications Limited: London, UK, 1998. [Google Scholar]
- Grant, C.A.; Ladson-Billings, G. Dictionary of Multicultural Education; The Oryx Press: Phoenix, AZ, USA, 1997. [Google Scholar]
- Cobb, P.; Yackel, E. Constructivist, emergent, and sociocultural perspectives in the context of developmental research. Educ. Psychol. 1996, 31, 175–190. [Google Scholar] [CrossRef]
- Di Stefano, M. New perspective for global education and language immersion class. In Acquiring Lingua Franca of the Modern Time. Current Issues and Strategies in ESL Studies; Polyudova, E., Ed.; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2014; pp. 33–57. [Google Scholar]
- Renshaw, P. The sociocultural theory of teaching and learning: Implications for the curriculum in the Australian context. In Proceedings of the Annual Conference of the Australian Association for Research in Education, Deakin University, Geelong, Victoria, Australia, November 1992. [Google Scholar]
- MacDonald, B.L.; Ashby, M.J.; Litster, K.; Di Stefano, M.; Maahs-Fladung, C. Mental Reversibility Tasks in Early Elementary: Interventions for Struggling Students. 2017; in preparation. [Google Scholar]
- MacDonald, B.L.; Wilkins, J.L.M. Seven types of subitizing activity characterizing young children’s mental activity. In Qualitative Research in STEM; Marx, S., Ed.; Routledge: New York, NY, USA, 2016; pp. 256–286. [Google Scholar]
- Stake, R.E. Qualitative Case Studies. In The Sage Handbook of Qualitative Research; Denzin, N.K., Lincoln, Y.S., Eds.; Sage Publications, Inc.: Thousand Oaks, CA, USA, 2005. [Google Scholar]
- Ginsburg, H.P.; Baroody, A.J. Test of Early Mathematics Ability-Third Edition; Pro Ed.: Austin, TX, USA, 2003. [Google Scholar]
- Steffe, L.P.; Cobb, P. Construction of Arithmetical Meanings and Strategies; Springer-Verlag, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Steffe, L.P.; Thompson, P.W. Teaching experiment methodology: Underlying principles and essential elements. In Handbook of Research Design in Mathematics and Science Education; Kelly, A., Lesh, R., Eds.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2000; pp. 267–306. [Google Scholar]
- Baroody, A.J. The developmental foundations of number and operation sense. In Proceedings of the National Science Foundation conference on Learning and Education: Building Knowledge, Understanding Its Implications, Arlington, VA, USA, May 2002. [Google Scholar]
- Flavell, J.H. The Developmental Psychology of Jean Piaget; Ardent Media: New York, NY, USA, 1963. [Google Scholar]
- Clements, D.H. Subitizing: What is it? Why teach it? Teach. Child. Math. 1999, 5, 400–405. [Google Scholar]
- Corbin, J.; Strauss, A. Basics of Qualitative Research: Techniques and Procedures for Developing Grounded Theory, 3rd ed.; Sage: Thousand Oaks, CA, USA, 2008. [Google Scholar]
- Saldaña, J. The Coding Manual for Qualitative Researchers; Sage: Thousand Oaks, CA, USA, 2009. [Google Scholar]
- Thompson, P.W. Conceptual analysis of mathematical ideas: Some spadework at the foundation of mathematics education. Proc. Jt. Meet. PME 2008, 32, 31–49. [Google Scholar]
- Steffe, L.P.; Ulrich, C. The constructivist teaching experiment. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- McLeod, S. Social Identity Theory. Simply Psychology, 2008. Available online: http://www.simplypsychology.org/case-study.html (accessed on 18 October 2016).
- Marashi, H.; Maherinia, E. The effect of teaching phrasal verbs through pictures on EFL learners’ active application of phrasal verbs in speaking. J. Engl. Lang. Teach. 2011, 1, 37–44. [Google Scholar]
- Sjoholm, K. The Influence of Crosslinguistic, Semantic, and Input Factors on the Acquisition of English Phrasal Verbs: A Comparison between Finnish and Swedish Learners at an Intermediate and Advanced Level. 1995. Available online: https://eric.ed.gov/?id=ED390305 (accessed on 13 March 2017).
- Ramirez, O.; McCollough, C.A.; Diaz, Z. Creating a model of acceptance: Preservice teachers interact with non-English-speaking Latino parents using culturally relevant mathematics and science activities at family learning events. Sch. Sci. Math. 2016, 116, 43–54. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).