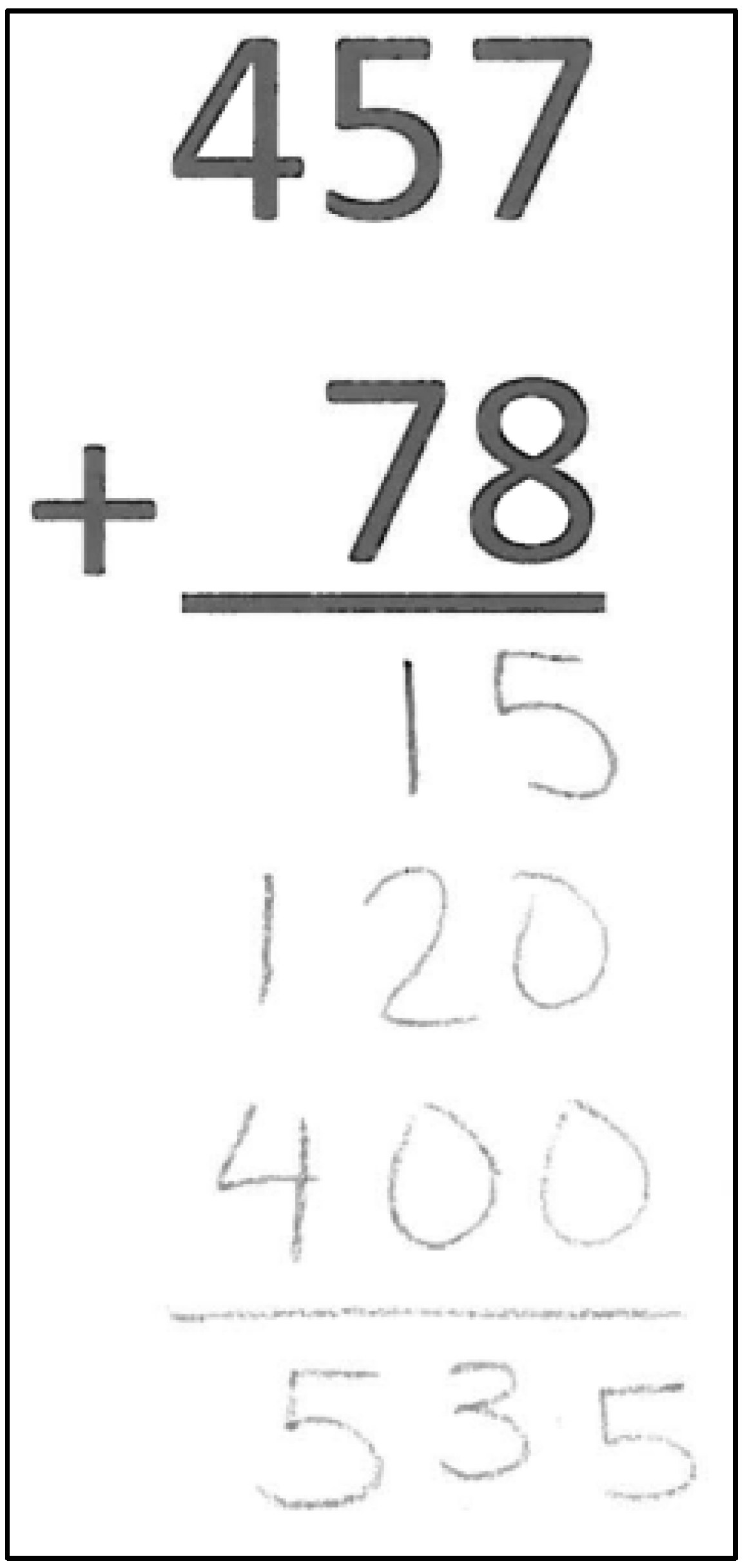1. Introduction
Manipulatives are concrete objects that are commonly used in elementary classrooms to make mathematical ideas tangible. Typically, manipulatives are intended to represent specific mathematical concepts. Base-ten blocks, for example, are blocks specially configured to represent the denominations in the decimal number system (i.e., ones, tens, hundreds, and so on). Ones are represented with single blocks, tens are represented as ten such blocks attached together to form a stick, and a group of 100 is represented as ten such sticks attached together. Together, the blocks are considered a “proportional” model because their physical sizes reflect the factor of 10 that differentiates one denomination from the one above and below it. Base-ten blocks are very popular in North American classrooms; they are used to help children “see” and operate on foundational concepts in the decimal number system, such as place value and regrouping. Teachers often use manipulatives to ground students’ conceptual understanding in mathematics before abstract notation, such as written numerals, is introduced (Clements, 1999; Uttal, Scudder & DeLoache, 1997) [
1,
2].
Despite their popularity, manipulatives do not always result in desired educational objectives. Although their value is apparent on the surface, recent research has demonstrated that the conditions under which students learn and apply knowledge with manipulatives is complex and as yet, not well understood (McNeil & Jarvin, 2007) [
3]. Moreover, because manipulatives are ubiquitous in North American mathematics classrooms in the early elementary years, and because teachers often have an unquestioning faith in their benefits for student learning (e.g., Moyer, 2001) [
4], the study of how manipulatives are best used in mathematics instruction is a critical issue in education. Even if elementary teachers were aware that manipulatives are not a guarantee for student learning, the research is almost silent on specific ways to guide their practice with concrete external representations.
It is in this context that the present study emerged. Research evidence points to the benefits of manipulatives under specific conditions, including the instructional context, the prior knowledge of the student, and the learning objectives (Laski, Jor’dan, Daoust & Murray, 2015; Marley & Carbonneau, 2014; McNeil & Jarvin, 2007; Trespalacios, 2010) [
3,
5,
6,
7]. The focus of our research is on the instructional context, specifically on lesson sequencing and instructional guidance. There is evidence to suggest that the order in which different types of mathematical representations—concrete and otherwise—are presented to students during instruction is predictive of students’ learning of mathematical concepts. Presenting concrete instantiations before abstract ones can be beneficial (e.g., Fyfe, McNeil, Son & Goldstone, 2014) [
8], for example, but the question of representational sequencing has led to inconclusive results on the whole (e.g., Rittle-Johnson & Koedinger, 2009) [
9]. Lending clarity to the issue of representational sequencing for elementary students’ mathematics learning was a primary objective of our study.
Another factor at the centre of this research is how much instructional guidance is needed to assist students in making the conceptual connection between concrete representations and their corresponding abstract ones. Manipulatives and their intended abstract referents can be considered “pedagogical analogies” (English, 2004) [
10]: They differ on superficial features, but thinking mathematically about the two systems consists of mapping a common conceptual structure from one to the other (Richland, Stigler, & Holyoak, 2012) [
11]. The literature on analogical reasoning has routinely demonstrated that inducing the conceptual structure is considerably more likely when prompts and explanations are provided than when students are left to their own devices (Alfieri, Nokes-Malach & Schunn, 2014; Gick & Holyoak, 1983) [
12,
13].
In the present study, we focus our attention on the individual and interactive effects of representational sequencing and instructional guidance on second-graders’ conceptual understanding of place value and regrouping concepts. A considerable body of research has focused on students’ use of representations—e.g., diagrams, pictures, abstract symbols—in mathematics and science (Belenky & Schalk, 2014; Schraw, McCrudden & Robinson, 2013; Verschaffel, De Corte, de Jong & Elen, 2010) [
14,
15,
16]. Because manipulatives can also be seen as representations (McNeil & Jarvin, 2007; Uttal et al., 1997 [
2,
3]), we hypothesized that the instructional principles that have emerged from the research on representations more broadly would also apply to children’s mathematics learning with manipulatives. Examining instructional factors such as sequencing and guidance can inform classroom practice with manipulatives, an approach to mathematics teaching that is too often left unchallenged (McNeil & Jarvin, 2007) [
3].
1.1. Representational Sequencing in Instruction
In the literature, the term “concrete” has been used to refer to representations that are tied to (or “grounded in”) the immediate context of the task. In contrast, the term “abstract” has typically referred to representations that do not embody elements of the context and can be considered “idealized” because they do not resemble their referents (Belenky & Schalk, 2014; Schnotz, Baadte, Müller & Rasch, 2010) [
14,
17]. According to a number of pedagogical theories, concrete representations are best presented before abstract ones for optimal learning outcomes (Freudenthal, 1991; Hoong, Kin & Pien, 2015) [
18,
19]. To the extent that there is agreement on how “concrete” and “abstract” are operationalized, there is empirical evidence to support these theoretical accounts. Goldstone and Son (2005) [
20], for example, found that when concrete representations were presented before abstract ones in a computer simulation of complex systems, transfer performance was superior to when abstract representations were presented first. In another study, Braithwaite and Goldstone (2013) [
21] found that when both concrete and abstract solutions to combinatorics problems were presented to students, a concrete-first sequence was found to be more effective than abstract-first or concrete only conditions. Finally, Scheiter, Gerjets, Huk, Imhof, and Kammerer (2009) [
22] found that undergraduate biology students had superior learning outcomes when they viewed realistic (i.e., concrete) videos of cell mitosis before abstract diagrams of the same processes than when they viewed realistic depictions only.
Similarly, McNeil and Fyfe’s (2012) [
23] work supports a “concreteness fading” approach, where the level of concreteness is gradually faded away toward more abstract, or generic, instantiations of concepts and principles. A review by Fyfe et al. (2014) [
8] demonstrates that the preponderance of evidence supports a concrete-to-abstract sequence in mathematics instruction. Concrete or otherwise “grounded” representations (see Belenky & Schalk, 2014) [
14] can activate prior knowledge, which in turn can support the interpretation of subsequently presented abstract symbols, which by themselves are less transparent and as such more difficult to interpret (Fyfe et al., 2014; Koedinger & Nathan, 2004) [
8,
24].
A closer examination of the research literature suggests, however, that the issue of representational sequencing remains an open question (Belenky & Schalk, 2014) [
14]. Some scholars have argued that under certain conditions, concrete representations are best presented
after abstract representations. Abstract representations do not resemble their referents (Schnotz et al., 2010) [
17] and are devoid of superficial features that may distract the learner from abstracting the underlying principle or concept (Kaminski, Sloutsky & Heckler, 2013; McNeil, Uttal, Jarvin & Sternberg, 2009) [
25,
26]. Presenting abstract representations first can reduce cognitive load and allow the learner to focus on important conceptual principles before introducing contextual elements later (van Merriënboer & Sluijsmans, 2009) [
27]. Johnson, Reisslein, and Reisslein (2014) [
28] found that when abstract representations of electrical circuits were presented before diagrams with real-world representations (e.g., those that included depictions of home wiring and lamps), engineering students demonstrated superior problem-solving performance compared to those who received the representations in reverse order. The knowledge targeted by Johnson et al. (2014) [
28] was procedural and not declarative or conceptual (e.g., Goldstone & Son, 2005; Scheiter et al., 2009) [
20,
22], which may in part explain the discrepancies in the literature on representational sequencing. Nevertheless, no clear picture emerges from the literature on effective ways to sequence mathematical representations in the early grades.
In yet other research, the benefits of alternating, or “iterating”, abstract and concrete representations have been demonstrated. Based on the development of conceptual and procedural knowledge (for a recent review, see Rittle-Johnson & Schneider, 2015) [
29], Rittle-Johnson and Koedinger (2009) [
9] compared the effects of lesson sequence on sixth-graders’ conceptual knowledge of place value and procedural knowledge in decimal arithmetic. Compared to a group who received all concepts lessons before the procedures lessons (“blocked” sequence), iterative sequencing resulted in better learning and transfer of procedural knowledge, but no difference was found between conditions on the transfer of place value concepts. The authors urged researchers to test the effects of iterative sequencing against both concepts-first and procedures-first orders, the latter not being included in their study.
Consistent with these findings, Li, Cohen and Koedinger (2013) [
30] programmed a machine-learning system, SimStudent, to solve different types of problems in three areas: fractions, equation solving, and stoichiometry. The authors found that SimStudent proposed a greater number of appropriate problem solving moves when it solved different problem types in alternating sequence than in blocked sequence. The problem types that were presented in varying order differed on a number of dimensions (e.g., problem difficulty, equation form), but not by level of concreteness, which compromises the ability to make fair comparisons across studies. In another study that focused on representation type specifically, Rau, Aleven, and Rummel (2010) [
31] found greater benefits for a blocked sequence: presenting several problems (as many as 36) involving the same type of representation before moving to problems involving another type of representation. The authors compared the impact of iterating pictorial representations to blocked presentations of fractions models (i.e., pie chart, number line, and set model) on fifth- and sixth-graders’ representational knowledge. The results revealed superior performance when the students solved problems presented in the largest blocks relative to iterative practice. Thus, the existing research comparing iterative to blocked presentations fails to provide a clearer understanding of representational sequencing, which is one of the goals of the present study.
In sum, the research shows that the concrete-to-abstract sequence has the most empirical support, particularly when what is targeted is conceptual or declarative knowledge. The studies comparing different representational sequences have been difficult to compare, however, because of differences in outcomes measures, differences in the nature of the tasks used in the instructional interventions, and differences in the experimental conditions being compared—that is, few studies directly compared abstract first, concrete first, and iterative orders to each other. Moreover, sequencing by itself may not tell the whole story; as suggested by Fyfe et al. (2014) [
8], effective forms of sequencing (i.e., concreteness fading) may replace the need for explicit instructional support, but other, less beneficial, sequences may require it. As such, research on the potential moderating effects of instructional guidance may serve to shed light on the inconclusive results in the representational sequencing literature.
1.2. Instructional Guidance
Students benefit from instructional guidance on noticing structural similarities between analogous problems or representations (Alfieri et al., 2014; Richland & McDonough, 2010) [
12,
32]. In their cross-cultural comparison of mathematics teaching, Richland, Zur and Holyoak (2007) [
33] found that teachers from high-performing countries use analogous examples often, but also use specific techniques to encourage structural mapping, such as hand gestures between representations and spatial layouts to make any similarities apparent. Student performance can be enhanced when instructors verbally encourage students to notice the structural similarities between two analogous problems: Such encouragements may take the form of prompts that encourage comparison (e.g., Nagarajan & Hmelo-Silver, 2006) [
34], or they may be more directed, including explicit explanations of the underlying concept or principle that ties the two cases together (Alfieri et al., 2014; Kaminski et al., 2013) [
12,
25]. Young learners also have lower levels of prior knowledge relative to their older peers, which in part explains their struggle to notice structural similarities and engage in mapping processes that lead to relevant schema induction (English, 2004; Vendetti, Matlen, Richland & Bunge, 2015) [
10,
35].
In mathematics specifically, children rarely make conceptual connections between representations on their own (English, 1997; Osana, Przednowek, Cooperman & Adrien, 2013; Resnick & Omanson, 1987) [
36,
37,
38], which can explain many of the struggles they experience in mathematics (English & Halford, 1995; Uttal, Liu & DeLoache, 2006) [
39,
40]. Children also appear to benefit from instructional guidance on making the connection between concrete instantiations of mathematical concepts (i.e., manipulatives) and the abstract referents they are intended to target (Carbonneau, Marley & Selig, 2013; Osana et al., 2013) [
37,
41]. In a recent study with preschool children, Carbonneau and Marley (2015) [
42] found that children who received explicit explanations of how counters corresponded to their numerical symbols outperformed those students who received no explicit links on measures of procedural and conceptual knowledge and transfer. In another study, Osana et al. (2013) [
37] found that explanations on the conceptual referents for plastic chips (blue = “one” and red = “10”) promoted first-graders’ structural mapping between the manipulatives and their corresponding concepts of quantity. Thus, students appear to benefit from teachers’ guidance on the conceptual connections between analogous situations, including in mathematical contexts, but the role of such guidance under specific representational sequencing conditions is not yet known and forms the primary objective of the present study.
1.3. Present Study
We investigated the individual and interactive effects of two factors – representational sequence and instructional guidance—on second-graders’ conceptual understanding of place value and regrouping concepts. We used base-ten blocks as concrete instantiations of quantity and written notation (e.g., numerals) as their abstract counterparts (Koedinger & Nathan, 2004) [
24]. Students were given the same lessons on the multi-digit addition algorithm, with half of the lessons delivered using the manipulatives and the other half using numerals. The students were assigned to one of three conditions that determined the order in which the lessons were presented: manipulatives-first, symbols-first, and iterative. These three conditions were crossed with an instructional guidance factor with two levels: half of each sequence condition received instructional guidance on the conceptual connection between the manipulatives and the written symbols used in the standard algorithm, and the other half did not.
We predicted that, regardless of lesson sequence, students who received instructional guidance on the conceptual links between the manipulatives and the corresponding symbolic representations would outperform those who did not receive any instructional guidance on transfer tasks designed to assess conceptual understanding of place value and regrouping. This prediction is based on previous research that converges on the benefits of explicit instructional guidance on structural mappings between different representations (Alfieri et al., 2014; Kaminski et al., 2013; Osana et al., 2013) [
12,
25,
37]. We also predicted that instructional guidance would act as a moderator on the effects of representational sequence. Specifically, without instructional guidance, students in the manipulatives-first condition would outperform the students in the other two sequence conditions. As Fyfe et al. (2014) [
8] concluded from their own review, concrete instantiations likely replace explicit explanations when they are presented before abstract ones. With instructional guidance, on the other hand, we predicted that students in all sequence conditions would benefit relative to those in the no-guidance conditions, but that the symbols-first condition would benefit the most because there are few cues in the context that would scaffold the meaning they attribute to the symbols used in the standard algorithm. We predicted that the symbols-first condition would benefit the most from instruction because of the research indicating that idealized external representations are not as effective for learning and immediate performance as those that are “grounded” in representational features that are relevant to the task at hand (Belenky & Schalk, 2014) [
14]. In this study, written symbols are less grounded than base-ten blocks because they do not possess perceptual characteristics that are as manifestly connected to concepts of numeration. These findings thus allowed us to predict that explicit explanations on the underlying conceptual structure of place value and regrouping would assist the students in the symbols-first condition the most.
2. Methods
2.1. Participants
The participants were second-graders from six classrooms in two public suburban elementary schools in Canada. The original sample consisted of 98 students, but data from 11 students were removed for missing the pre-test (one student), missing the first instruction session (six students), missing the second instruction session (three students), and missing both instruction sessions (one student). The final sample consisted of 87 students (39 boys and 48 girls) with an average age of 7.91 years (SD = 0.29).
2.2. Design and Procedure
We used a pre-test–intervention–post-test experimental design for this study. Measuring students’ place value and regrouping knowledge both before and after the intervention allowed us to assess students’ growth in the two domains as a result of the instruction. Including time as a repeated measures factor in the analyses was useful in this context because it provided the most possible information on student growth, namely as a function of the two instructional factors (sequencing and instructional guidance) and irrespective of these factors (i.e., testing for main effects of time).
Using a random number generator, the students within each classroom were randomly assigned to instructional conditions by creating an orthogonal combination of two variables: (a) the sequencing of concrete and abstract representations (manipulatives-first, symbols-first, iterative); and (b) the presence or absence of instructional guidance on the structural similarities between the two representations. This resulted in six sequence-guidance conditions: manipulatives-first with instructional guidance (n = 18), manipulatives-first without guidance (n = 12), symbols-first with guidance (n = 13), symbols-first without guidance (n = 16), iterative presentation with guidance (n = 15) and iterative presentation without guidance (n = 13).
The study consisted of three phases: (a) pre-test; (b) instructional intervention, which took place over two sessions during two mathematics periods; and (c) post-test.
Table 1 presents the mean number of days between study phases, including the time between the two instructional sessions, by condition and across conditions. The first instructional session occurred two to 48 days (
M = 17.4,
SD = 9.5) after the pre-test, and the second session was given 2 to 9 days (
M = 6.4,
SD = 2.2) after the first. The post-test was administered 1 to 19 days (
M = 6.4,
SD = 2.2) after the second session.
Because of constraints inherent in the teachers’ schedules, school activities, and holidays, there was considerable variance in the number of days between the pre-test and the first instructional session, between the two instructional sessions, and between the second instructional session and the post-test. During the time between each phase of the study, the students underwent their regular mathematics curriculum with their teacher. The mean number of days between phases did not differ by condition, however. No significant differences in the mean number of days were found between the pre-test and the first instructional session, F(5, 81) = 0.53, p = 0.75; the first and second instructional sessions, F(5, 81) = 0.13, p = 0.99; and the second instructional session and post-test, F(5, 81) = 0.38, p = 0.86.
The pre-test was administered individually in two sessions over two days, and each session lasted approximately 45 min. On the first day, students’ understanding of place value was assessed through the Conventions of Place Value (CPV) task. On the second day, students’ understanding of regrouping was assessed using four different tasks: the Regrouping Symbols with Blocks (RSB) task, the Regrouping Symbols with Partial Sums (RSPS) task, the Evaluation task with Blocks (EVB), and the Evaluation task with Chips (EVC).
In each instructional session, the students worked in small groups in the classroom with a researcher on addition problems that involved regrouping. The small groups consisted of two to four students and the specific group activities corresponded to the six sequence-guidance conditions. In each session, two different lessons were provided—one with manipulatives and one with written symbols—and each was presented seven times, but with different quantities. Depending on the condition, all 14 lessons were presented in a different sequence, with or without instructional guidance. In each session, all 14 lessons were completed in approximately 45 min.
The post-test tasks were isomorphic versions of those administered at pre-test. All five post-test tasks were administered on the same day, and lasted 51 min on average.
2.3. Instructional Intervention
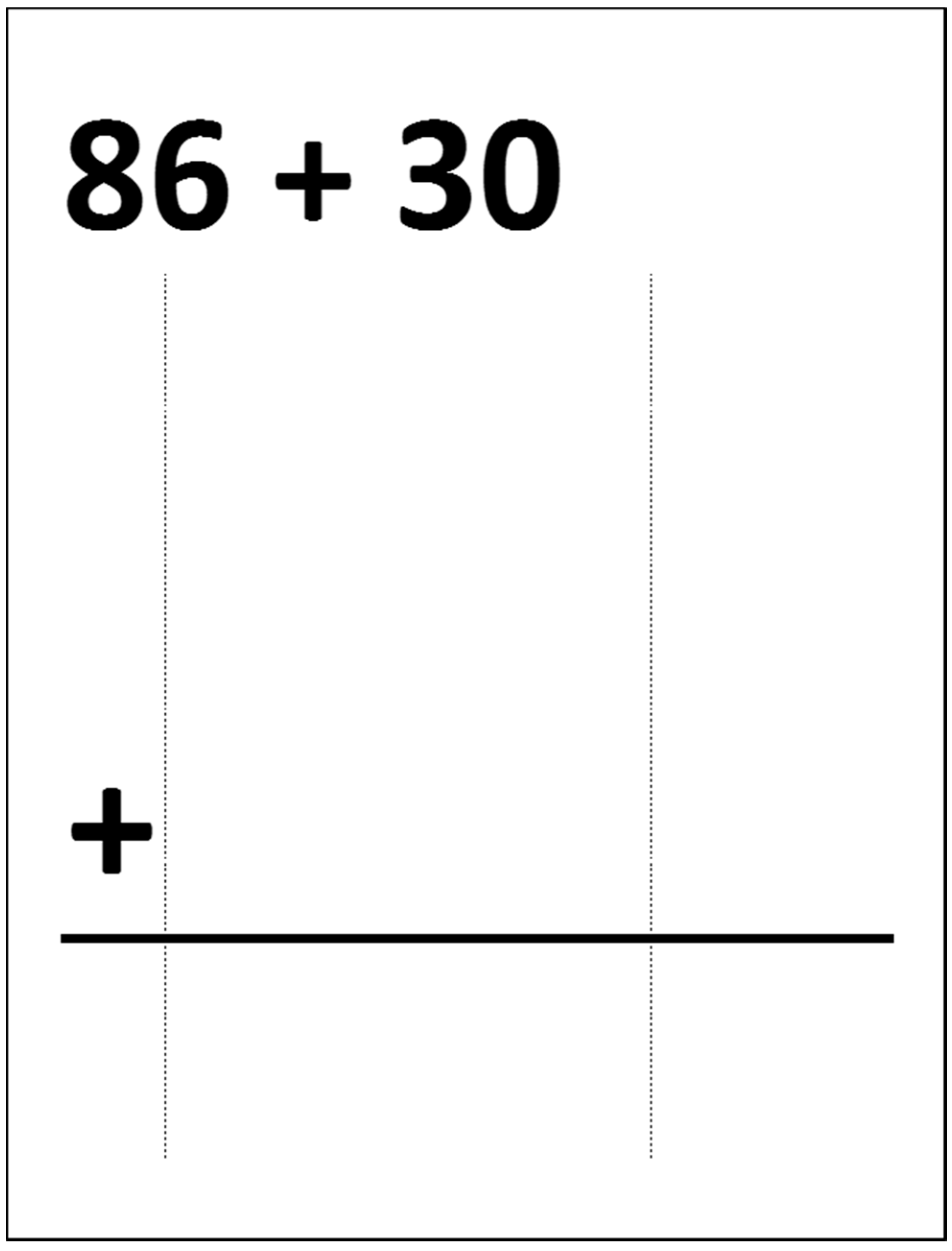
The focus of the instruction was on solving addition problems geared toward the development of place value and regrouping understanding. The first instructional session focused on the following seven addition problems: 59 + 1; 28 + 4; 107 + 6; 226 + 5; 46 + 9; 215 + 7 and 328 + 8, and the second session focused on another seven problems: 98 + 10; 86 + 30; 176 + 50; 353 + 80; 85 + 40; 264 + 70 and 125 + 90. The instructors were trained research assistants who used a specific script for all the lessons in all conditions. In each condition, the instructor provided four demonstrations per session (two for each representation used, manipulatives or written symbols), and the students practiced solving problems with corrective feedback. The explanations, demonstrations, prompts, and corrective feedback statements were kept consistent within each condition and across both instructional sessions.
The instructors guided students in their small groups to solve as many problems as they could in the time allotted. The maximum number of problems that could be solved in each session was 14 because each of the seven problems were solved with manipulatives and also with the standard algorithm (7 problems × 2 representations), but the order of the representations used varied by condition (see
Figure 1). The number of problems completed during each session varied somewhat from group to group. In the first instructional session, the number of problems solved across all 36 small groups (6 classrooms × 6 conditions) ranged from 11 to 14, and the mean number of problems solved across all six conditions ranged from 13.5 and 14. No significant difference in mean number of problems solved was found between conditions,
F(5, 30) = 0.82,
p > 0.05. In the second instructional session, the number of problems solved across all 36 small groups ranged from 10 to 14. The mean number of problems solved in the second session across all six conditions ranged from 13.33 and 14. No significant differences were found between conditions in number of problems solved,
F(5, 30) = 0.88,
p > 0.05.
2.3.1. Manipulatives-First
The top panel of
Figure 1 shows the order in which the problems were solved in the manipulatives-first condition in each instructional session. In each session, all seven problems were first solved with base-ten blocks only. Once all seven were solved, the same problems were solved again, in the same order, using the standard written algorithm only.
To structure the small group activity, the students were each given a 14-page workbook that contained all session problems, with one problem presented horizontally at the top of each page (e.g., “59 + 1”). In the workbook for the manipulatives-first condition, the first seven pages contained a problem written at the top, with nothing else on the page. These pages were used for the seven problems solved with the manipulatives. The next seven pages contained the same problems in the same order, one at the top of each page, but each problem was followed by dotted lines that separated the different place values as scaffolds for performing the standard algorithm (see
Figure 2 for a sample page).
The instructor began each session by demonstrating how to solve the first two problems (in the first session, 59 + 1 and 28 + 4) with base-ten blocks. For each demonstration, the instructor illustrated how to represent the two addends with the blocks and then how to put the two sets of blocks together. When there were 10 ones (or 10 tens, depending on the problem), students were shown how to combine them into one group and trade them for one tens block (or 10 tens blocks for one hundreds block). The instructor then counted the total number of blocks and indicated that this was the answer to the problem. The students then imitated the instructor’s actions with the manipulatives and wrote the answer on the corresponding page in their workbook. Following the demonstrations for the first two problems, the students were each given a set of blocks and used them to solve the remaining five problems on their own, with corrective feedback from the instructor. When a child did not remember what to do next, the instructor stated, “Remember, this is what we do next”, and would then proceed to repeat the same instructions as in the demonstration.
After the seven problems were solved with the manipulatives, the instructor removed all the blocks from view. The remainder of the session involved solving the same seven problems using the standard algorithm using written symbols only. The instructor began by providing demonstrations of how to use the standard algorithm to solve the first two problems (e.g., in the first session, 59 + 1 and 28 + 4). For each demonstration problem, the instructor explained that the first number should be written in the workbook at the top of the corresponding place value grid with one digit per column. The instructor then showed students how to write the second number underneath the first, with the proper digit alignment. Students were then instructed to add numbers in each column, starting with the right-most one. Whenever they had a sum of 10 or bigger, they were told to “write a little 1 in this column above the [digit in the tens or hundreds column]” and to write the other digit below the line. Once they had found the sum of each column, the students wrote the answer again at the top of the page in their workbook.
When the demonstrations of the standard algorithm for the first two problems were completed, the students worked on the remaining five problems on their own, with corrective feedback from the instructor, who ensured they used the standard algorithm that was demonstrated for the first two problems. The instructor provided the same prompts that were used when the problems were solved with the manipulatives if a child did not remember what to do next (e.g., “Remember, this is what we do next”, followed by the same instructions as in the demonstration). No manipulatives were provided as the students executed the standard algorithm. The second session in the manipulatives-first condition followed the same procedure as the first using the next set of seven problems (see
Figure 1).
2.3.2. Symbols-First
The middle panel in
Figure 1 presents the order of the problems in each session of the symbols-first condition. The same procedure as in the manipulatives-first condition was used, but with the order of the manipulative block (i.e., seven problems solved with blocks) and the symbols block (i.e., the same seven problems solved with written symbols) reversed. The students were given the same workbook as those in the manipulatives-first condition, but the first seven pages contained the problems with the place value grid to scaffold the use of the standard algorithm and the next seven pages, used for the problems solved using manipulatives, were blank except for the problem written at the top of the page.
The instructor began each session by demonstrating how to use the standard algorithm for the first two problems (e.g., in the first session, 59 + 1 and 28 + 4). The students imitated the instructor’s use of written symbols to solve each problem. They then solved the remaining five problems on their own with corrective feedback from the instructor. Once the seven problems were completed, the instructor provided the manipulatives to the students. She then demonstrated how to solve the first two problems (e.g., in the first session, 59 + 1 and 28 + 4) using the blocks and the students imitated her actions. The students then solved the remaining five problems on their own, again with the same corrective feedback and prompts from the instructor that were used in the manipulatives-first condition.
2.3.3. Iterative
The bottom panel in
Figure 1 shows the order of the problems solved in the iterative condition. Each problem was solved with the manipulatives first, followed immediately by the solution of the same problem with the standard algorithm, and so on until all seven problems in each session were solved. The workbook provided to the students in the iterative condition consisted of the same pages as the workbooks in the other two conditions, but with alternating pages for the problems solved with manipulatives (blank page with the problem displayed at the top) and the pages for the problems solved with the standard algorithm (with the place value grid).
To begin each session, the instructor provided four demonstrations: the first was to illustrate how to use manipulatives to solve the first problem (59 + 1), which was followed immediately by a demonstration of the solution for the same problem with the standard algorithm. The third demonstration was the solution of the second problem (28 + 4) with manipulatives, followed by the solution to the second problem with the standard algorithm. After the demonstrations, the students solved the remaining problems on their own, each problem first with manipulatives and then with symbols before moving to the next problem. Each time the students solved a problem with manipulatives, the blocks were removed from view and the students then solved the same problem using the standard algorithm. The manipulatives were then returned to the students for the next problem, and so on. The same corrective feedback and prompts as were used in the other two conditions were provided by the instructor where necessary.
2.3.4. Instructional Guidance
The link between the “little 1” and the action of exchanging 10 unit blocks for one tens block (or 10 tens blocks for one hundreds block) was made explicit in the instructional guidance conditions. For students in the manipulatives-first condition, the instructor made the link when each problem was solved using the standard algorithm by referring to the actions performed with the blocks previously for the same problem: “Remember when we were adding numbers with the blocks, and we traded 10 ones for one 10? The little ‘1’ here means the same thing, that we traded 10 ones for one 10.” The same guidance was provided to students in the iterative condition. Each time a problem was solved using the standard algorithm, the instructor explained the connection between the “little 1” in the algorithm and the action with the blocks of composing a group of 10 (or a group of 100) for the same problem solved previously. For students in the symbols-first condition, the instructor made the link whenever any problem was solved with the base-ten blocks by saying, “Remember when we were adding numbers without the blocks, and we added a little ‘1’ at the top of the left column? That little ‘1’ means that we traded 10 ones for one 10, like we’re doing here.” In total, explicit explanations between the concrete and written representations were provided seven times in each session. No explicit links were discussed in the conditions in which there was no instructional guidance.
2.4. Measures
Five tasks were individually administered to all students before and after instruction. The Conventions of Place Value (CPV) task was designed to assess students’ conceptual understanding of place value, and the Regrouping Symbols with Blocks task (RSB), the Regrouping Symbols with Partial Sums task (RSPS), the Evaluation task with Blocks (EVB), and the Evaluation task with Chips (EVC) were designed to assess students’ conceptual understanding of regrouping.
2.4.1. Conventions of Place Value Task
The CPV task was based on Resnick and Omanson (1987) [
38]. In our study, the task was administered individually by a project researcher, who presented 12 two-digit numbers to the students and for each, circled one digit with her finger and asked, “How many things is this worth?” The numbers on the pre-test were (underlined digits indicate the number that was circled by the interviewer) 6
8,
77, 5
3,
29, 3
3,
41, 2
5,
66, 4
2,
38, 1
1,
80, and the numbers on the post-test were 2
7,
44, 6
3,
18, 8
8,
90, 1
6,
55, 6
4,
35, 2
2,
71. The items on the CPV task were novel items because they were not used during instruction. Correct responses were awarded one point, and incorrect responses were awarded 0. The points earned were added to obtain a total score, which could range from 0 to 12.
2.4.2. Regrouping Tasks
In the RSB task, the interviewer presented the student with addition problems solved using the standard algorithm. Students were asked to show with base-ten blocks what the “regrouped one” was worth. On the pre-test, the addition problems were 27 + 5, 192 + 20 and 183 + 45, and on the post-test, they were 63 + 8 and 287 + 40. Students were given one point if they correctly identified the base-ten block that corresponded to the “regrouped 1” and 0 points if they did not. Because the number of items differed at pre-test and at post-test, percent correct scores were calculated and could range from 0 to 1.
In the RSPS task, the interviewer showed students addition problems using the partial sums algorithm in the RSPS task (see
Figure 3 for a sample item). Students were asked to explain in words where each partial sum came from. The addition problems were 17 + 18 and 367 + 56 on the pre-test, and 25 + 29 and 457 + 78 on the post-test. The items on the RSPS task were novel because the partial sums algorithm was not used in the instruction. For each partial sum, students were given one point if they correctly identified where it came from and 0 points if they did not. For the items where two two-digit numbers were added they could get a maximum of two points, and for the items where one three-digit number and one two-digit number were added they could get a maximum of three points. The points earned were summed to obtain a total score that ranged from 0 to 5.
2.4.3. Evaluation Tasks
Two evaluation tasks were administered. Both tasks involved showing students photographs of the start and end of solutions to addition problems with regrouping by a fictitious child using blocks (for the Evaluation with Blocks task, or the EVB task; see Panel a in
Figure 4) or chips (for the Evaluation with Chips task, or the EVC task; see Panel b in
Figure 4). Students were required to indicate whether the solutions were correct or not, and to explain the child’s strategy. For the EVC task, the students were told the quantitative values for the different coloured chips (i.e., green chips were worth 100, red chips were worth 10, and blue chips were worth 1). The addition problems for the EVB task at pre-test were 37 + 4 (correctly solved) and 109 + 6 (incorrectly solved), and at post-test, they were 78 + 5 (incorrectly solved) and 208 + 4 (correctly solved). The addition problems for the EVC task at pre-test were 44 + 9 (incorrectly solved) and 246 + 70 (correctly solved), and 69 + 7 (correctly solved) and 393 + 30 (incorrectly solved) at post-test.
For each item of the EVB and EVC tasks, students were awarded points for identifying whether the addition problem had been solved correctly or not, and they were also given points for their justifications. Specifically, students received 0.5 points if they were accurate in identifying whether the solution presented was correct or not, and they were awarded 0 points if they did not. When students gave a justification explicitly mentioning regrouping, they received two points. When their justifications only involved descriptions of what had been done by the fictitious student or if they demonstrated with blocks how they would solve the addition problem without any mention of regrouping, they were awarded one point. Finally, if students gave no mathematical reasoning in their justification or if they gave an incorrect interpretation, they received 0 points. Scoring both components (identifying correctness and justification) allowed for an overall assessment of the use of regrouping concepts to evaluate another student’s solution to an addition problem. The scores for each item of the EVB and EVC tasks were summed, and total scores for each task could range from 0 to 5.
4. Discussion
We examined the extent to which two factors—the sequencing of concrete and abstract representations and the level of instructional guidance on how the representations are linked—are related to second-graders’ knowledge of place value and regrouping concepts. We provided two different types of lessons to second-graders that involved adding multi-digit numbers. Half of the lessons involved concrete representations (i.e., manipulatives) and the other half involved abstract ones (i.e., numerals). We manipulated the order in which the concrete and abstract representations were presented and also investigated how the level of instructional guidance interacted with the effects of representational sequence.
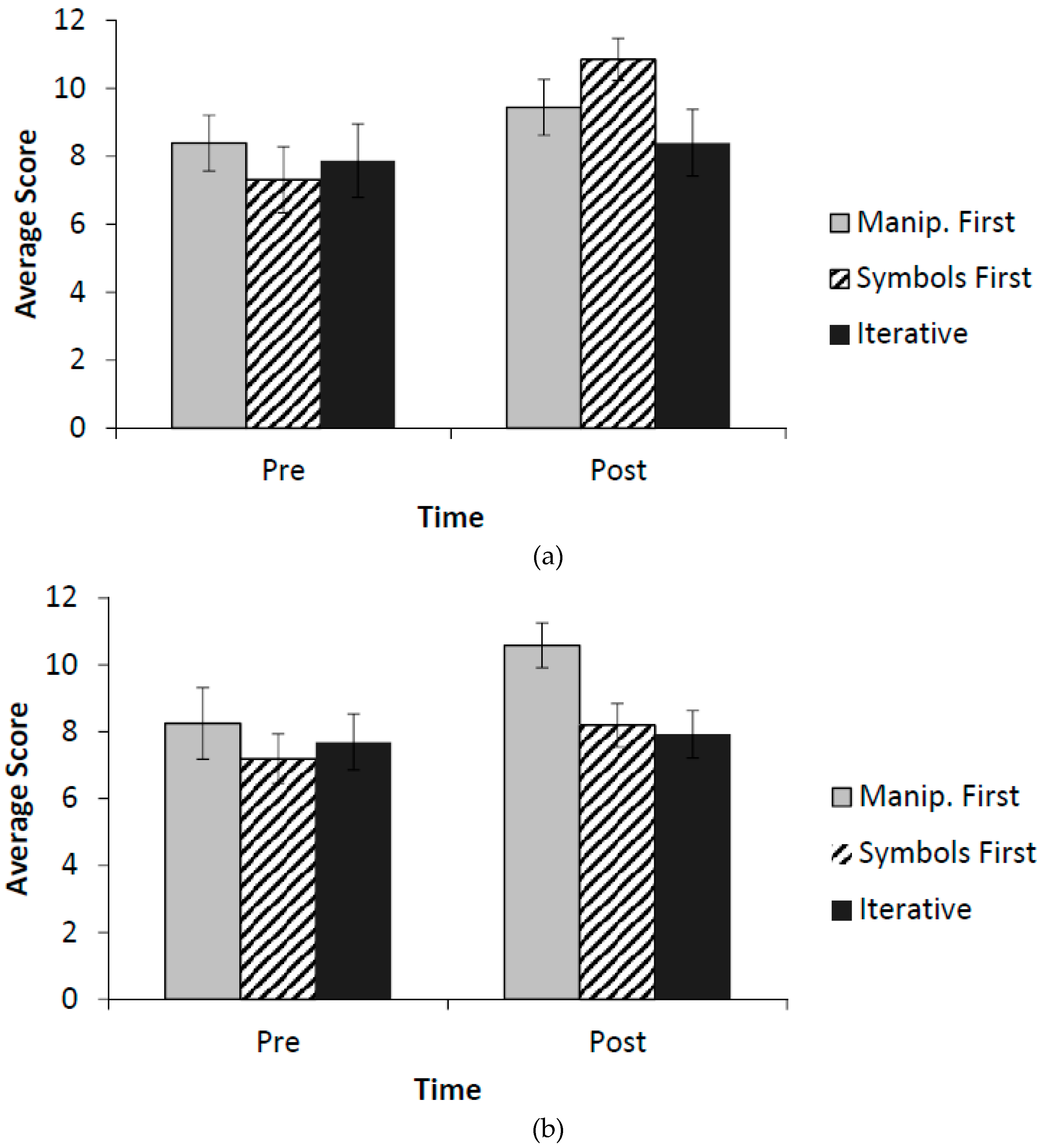
In line with our predictions, the results on the measure of place value knowledge revealed that representational sequencing makes a difference, but the effects are contingent on the level of instructional guidance provided in this study. More specifically, students learned more about place value when they worked with concrete representations before abstract ones, but only when there was no instructional guidance provided on their structural similarities. It is possible, as Fyfe et al. (2014) [
8] speculated, that presenting concrete representations before abstract ones could replace the need for any direct instruction on how the representations are structurally similar (see Canobi, 2009 [
43] for a study showing how problem sequencing can positively impact learning with no explicit instruction). The students may have constructed a grounded understanding of place value concepts from the manipulatives because base-ten blocks are designed to make the proportional relationships between the denominations perceptually evident. This, in turn, may have helped the students to interpret the symbols that were presented subsequently (Fyfe et al., 2014) [
8], circumventing the need for instructional guidance, at least of the type provided in this study.
When the students who worked with base-ten blocks first were given instructional guidance, however, their performance did not improve on the measure of place value knowledge. This result is not what we had expected, as we predicted an effect of instructional guidance regardless of representational sequence. It is possible that the explanations that were provided interfered with the meanings the students had constructed for themselves as they worked with the base-ten blocks. Gravemeijer (2002) [
44] cautioned that teachers’ prescriptions can remove the students as the primary agents of their own understanding, and, more generally, too much emphasis on highly structured procedural treatments of a wide variety of symbols, both abstract and concrete, can result in learning that is mired in the context and disconnected from their meanings, thereby limiting transfer (Belenky & Schalk, 2014; Goldstone & Sakamoto, 2003) [
14,
45].
The only students whose place value knowledge improved when the instructional guidance was provided were those who received lessons with abstract representations before the lessons with the manipulatives. This is consistent with theoretical accounts describing how individuals struggle to create appropriate conceptual knowledge structures for “idealized” (i.e., abstract) representations (Belenky & Schalk, 2014) [
14]. Consistent with this view is the explanation provided by Koedinger and Nathan (2004) [
24], who argued that making sense of algebraic equations requires considerable knowledge of symbols and associated syntax. Such knowledge appears to take longer to develop than knowledge of grounded representations, possibly because abstract symbols, by definition not grounded in any meaningful context, are more difficult to remember, at least initially (Fyfe et al., 2014; Mann, 2014; Marley, Levin & Glenberg, 2010) [
8,
46,
47]. Future research is necessary to test these hypotheses directly with educational materials such as mathematics manipulatives.
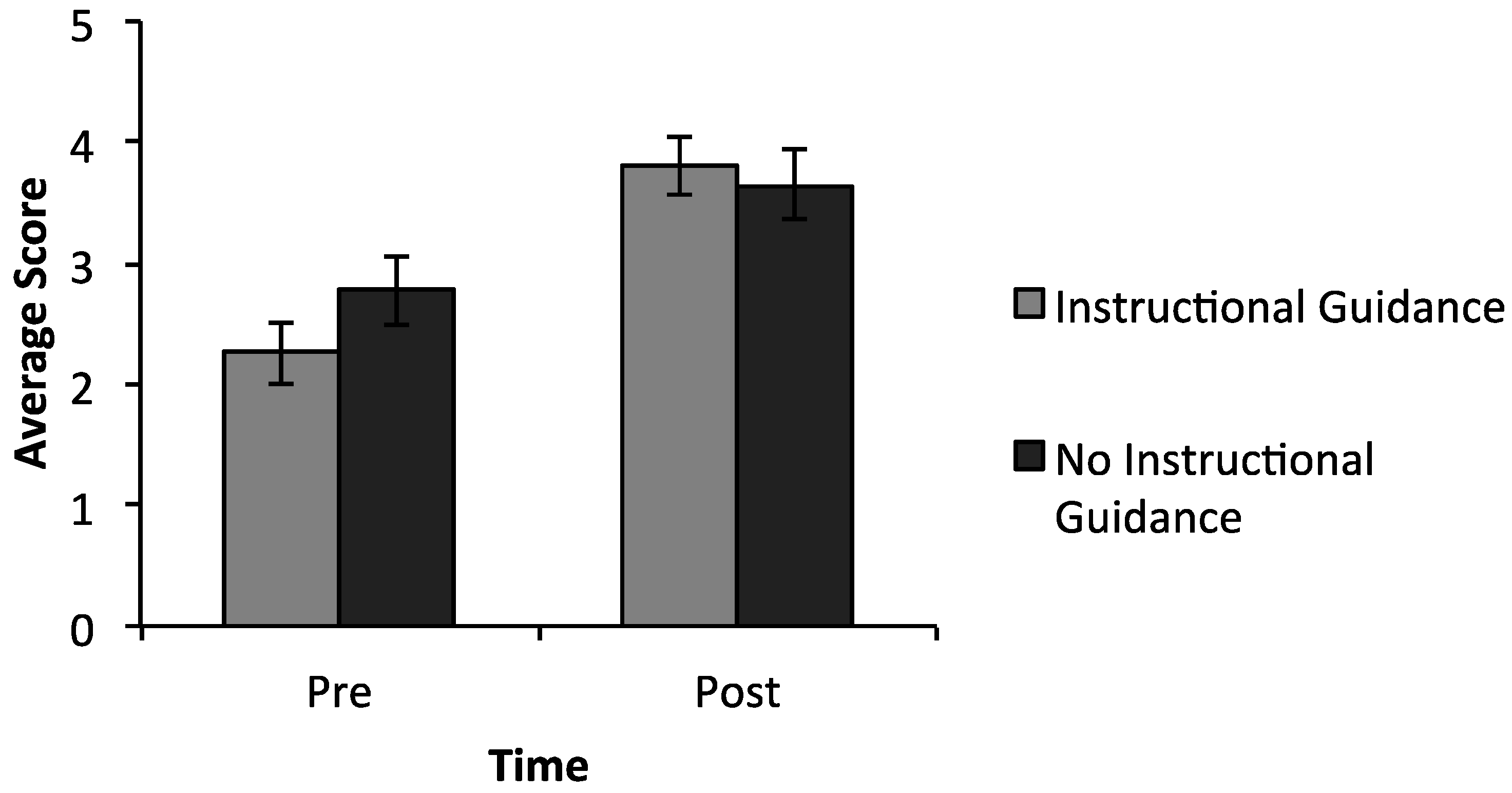
On the two regrouping measures, our predictions regarding the main effect of the instructional guidance as provided in this study were supported. Specifically, irrespective of representational sequence, those students who received instructional guidance on the link between the manipulatives and the written notation improved on their understanding of regrouping relative to those who received no such guidance. These findings are consistent with the literature on analogical reasoning, which has shown that structure mapping, or abstracting the structural similarities between two analogues, is greatly improved when support is provided, whether it is implicit, in the form of prompts or suggestions, or explicit in the form of direct explanations (Alfieri et al., 2014; Vendetti et al., 2015) [
12,
35], as presented in this study. In addition, the findings contribute to the current debate in the literature on optimal ways to use manipulatives in the classroom by suggesting that, at least for regrouping concepts, children benefit from explicit explanations on the meaning of the representations they use in the classroom, regardless of the order in which the materials are presented (see also Carbonneau & Marley, 2015) [
42]. That lesson sequencing mattered for place value and not for regrouping concepts indicates that instructional effects are also contingent on the learning objective in question.
The results also revealed that presenting concrete and abstract representations in alternating order was not effective for any measure regardless of whether instructional guidance was provided. We speculate that presenting two different types of representations in rapid succession, repeated several times, is taxing on students’ cognitive load and inhibits their ability to notice structural commonalities between the two representations. Richland and McDonough (2010) [
32] came to the same conclusion when they found that arranging the solutions to permutation and combination problems side by side (as opposed to sequentially) reduced the strain on participants’ working memory, thereby encouraging them to compare each pair of solutions and notice what was structurally common to both. Similarly, Rittle-Johnson and Star (2007) [
48] found that placing worked examples of algebra problems next to each other, with prompts to compare the two different solution methods, was more effective for procedural knowledge gain and for the generation of multiple solutions than when the problems were placed one after the other on separate pages. The present study should be extended to include a condition where the representations are both kept visible to reduce cognitive load and maximize the likelihood that students would abstract conceptual similarities (see also Richland et al., 2007; Scheiter, Gerjets & Catrambone, 2006) [
33,
49].
Any replication or extension of this research should attend the limitations of the present study. For example, a larger sample would increase statistical power, and confirming the findings in the context of different mathematical domains and with a wide range of mathematical tools would increase generalizability. We also recommend some improvements to the study’s design. For example, better control of the amount of time between study phases would strengthen the conclusions drawn from the data. Furthermore, because the study was conducted in classroom settings, the students were required to follow the regular mathematics curriculum between phases, namely between pre-test and intervention, between the two intervention sessions, and during the time leading to the post-test. The students’ classroom instruction, which likely incorporated a variety of different topics and pedagogical strategies, may have differentially impacted their learning by condition. We therefore recommend, to the extent possible, tighter control of potential confounding variables, such as exposure to mathematics instruction outside the context of the experimental intervention.
Despite these limitations and the need for further research to confirm our findings, the results of the current study can be used to outline preliminary practical guidelines for teachers. First, it appears that presenting manipulatives before written symbols is particularly effective for student learning of place value. In fact, in this context, presenting concrete representations before idealized ones may take the place of direct instruction on the structural mappings between the two representational systems. This said, when teachers use manipulatives to explain mathematical ideas, students need time to work with the objects when solving problems. Removing them and replacing them with more idealized representations (such as written notation) too quickly, even if the manipulatives are brought back later on, appears to hamper students’ connection with the target concepts.
Second, our findings support the notion that when teaching place value, teachers should be discouraged from presenting idealized symbols before more grounded representations, particularly if they are not explicit about how the two representational systems are conceptually connected. Should teachers present, say, written notation before base-ten blocks are introduced, their lessons should incorporate explicit explanations on the structural similarities between the two representations. The results of this research confirm that making explicit structural mappings between representations that vary on their level of “groundedness” is an important recommendation for teachers (e.g., Vendetti et al., 2015) [
35], but also reveal that the recommendation does not apply under all conditions. That is, in educational contexts, appropriate levels of instructional support may depend on other pedagogical factors, such as lesson sequencing.
Clearly, these are tentative recommendations, as further research is needed to replicate and extend the work presented here. Nevertheless, the results of our research suggest that, depending on the learning objective, representational sequencing can make a difference in children’s conceptual understanding of the decimal numeration system. Furthermore, providing direct explanations of the conceptual links between mathematical representations is generally effective, but representational sequencing itself may take the place of explicit pedagogical support for certain learning objectives.