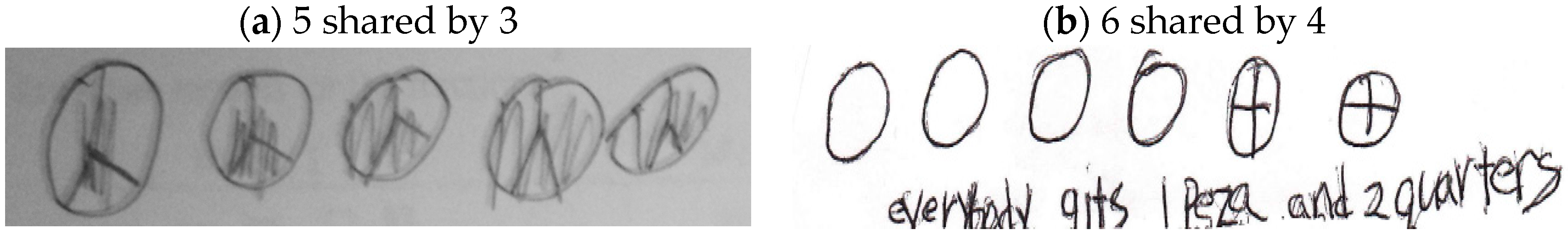1. Introduction
This paper illustrates variations of mathematical reasoning of 43 elementary school children identified as having low achievement in mathematics as evidenced through their problem solving in equal sharing tasks. Addressing this problem is important because illustrating the ways of reasoning these children
do possess (as opposed to describing what they do not know or a level of performance they do not have) can inform the field about the potentially rich mathematics in which these children can engage. Such information can serve as a beginning to conversations concerning how instruction might be leveraged to support these children’s participation and engagement in important mathematics content and practices. As participation in mathematical practices hold implications for children’s later mathematics performance [
1], beginning conversations on how researchers and teachers might support such participation seems essential.
Unfortunately, these conversations stand in sharp contrast to much of the current special education literature base and recommendations for mathematics instruction for children who experience sustained low achievement in mathematics (e.g., see [
2]). Despite the fact that some researchers have long supported the view that children may be, in actuality, disabled by curriculum and school structures (e.g., [
3,
4]) research clearly illustrates that mathematics instruction in classrooms designated for these children has been dominated by explicit instruction and practice computing basic facts [
5,
6]. Moreover, a recent review [
7] of articles researching the mathematics learning of Kindergarten through 12th grade students found significant differences between the mathematical teaching practices used with children with and without sustained low mathematics achievement. Mathematical teaching and learning is informed largely through constructivist and sociocultural perspectives with children without an achievement or learning difference. For children with low achievement or learning differences, mathematical teaching and learning is informed primarily by medical and behavioral perspectives. The research suggests two categories of mathematics learners who “need” different kinds of mathematics [
7]. Consequently, rather than discuss how to increase the participation of these children in mathematics instruction that might work to build powerful mathematics conceptions, current research and policy suggests a replacement of participation with more directive teaching approaches [
8].
We argue that attempts to remediate and “fix” children with procedural training is a poor replacement for supporting children to develop powerful mathematical conceptions [
9]. In fact, if the goal is children’s development of mathematics competence, then such competence involves both procedural fluency
and conceptual understanding, and concepts cannot be imposed onto children [
10]. In this way, we argue that positioning some children as “normal” and others as “deficient” due to arbitrary cut-off scores and then delivering mathematics onto them does little to uncover the knowledge these children
do possess and can build from in the classroom. Instead, we propose that researchers seeking to increase these children’s mathematics competence might begin by uncovering the conceptions that already exist and can be cultivated as children “solve problems that are within [their] reach [while] grappling with key mathematical ideas that are comprehendible but not yet well formed” [
11] (p. 387).
In this study, we begin such a documentation by examining ways of reasoning for 43 children with low achievement as they solved fraction problems. Specifically, we present themes of reasoning evident in children’s partitioning activity in problem contexts not directly taught by the teacher (i.e., equal sharing contexts) over 10 sessions of instruction. Our aim in this work is to continue to challenge a longstanding assumption about the type of mathematics children with low achievement “need” [
2,
8] and their potential as mathematical learners. The following research questions guided our work:
- (1)
What is the fractional reasoning of 43 children with low mathematical achievement as evidenced by their partitioning activity used in equal sharing problems over ten occurrences?
- (2)
What differences, if any, seem apparent in the children’s reasoning from what we know about children without low mathematics achievement?
2. Conceptual Framework
Although there are many ways to capture children’s ways of reasoning with fractions, we used children’s partitioning activity when creating unit fractions, revealed through their problem solving, as a way to frame the current study. Specifically, children’s activity within equal sharing situations—equally sharing some number of the same-sized objects among some number of people, where the result is a fractional quantity—has provided observable evidence of children’s fractional reasoning in previous research [
12,
13,
14,
15,
16]. Additionally, the partitioning activity that children use in these situations is well established as the root of children’s knowledge of fractions [
15]. In this way, children’s work in equal sharing situations provides a window into the ways of reasoning that children do indeed possess. Moreover, equal sharing is an informal analogy not only for fractions, but also for the “big idea” of equal partitioning, which serves as the conceptual basis for partitive and measurement division, measurement, even numbers, and mean averages [
17]. Below, we synthesize prior research on partitioning within equal sharing situations for children who do not experience low performance in mathematics and use it as a conceptual framework for the current study.
3. Children’s Reasoning Revealed in Equal Sharing
Children’s activity within equal sharing situations first appears as representations of acts of partitioning [
12,
13,
14,
15,
18]. Literature suggests that in early experiences with fractions children may see the problem as unsolvable, possibly because they do not yet see wholes as divisible [
14]. For example, when sharing five sticks of licorice equally among four people, some children may begin by adding more whole objects to obtain a whole number result (i.e., add three more sticks such that each person receives one whole stick of licorice) or they may create unequal shares (i.e., give one person two sticks of licorice, [
13]). Empson and her colleagues [
13] refer to this way of reasoning as “no coordination” because the children are attending to either the necessity to make shares equal or the need to share everything (unequally), but not both at the same time.
Children who accept the whole as divisible may begin using a rudimentary knowledge of whole number counting to partition the licorice stick(s) into some number of pieces [
12,
15]. This is to say that children determine the number of pieces they will create within their activity. Steffe and Olive [
15] describe children who might consider the final stick by partitioning it into pieces that are likely unequal; these children may not be all that concerned with sharing the entire licorice stick. In other words, the children do not yet determine the number of parts needed to exhaust the wholes from the onset [
14] and may be in the midst of developing their whole number understanding [
15].
Other children may repeatedly halve the final stick until they have enough parts to deal out to each sharer [
18]. When asked to show only one share, these children may work to make four equal parts but not use the entire stick or they may use the entire stick but not make equal parts [
15]. In each case, children have two goals: to make four equal parts or to use the whole stick, yet they do not know how to coordinate the two goals to exhaust the whole with equal sized parts beyond repeated halving. Thus, they may not yet see the parts in relation to the whole. In fact, for these children, the parts may not be differentiated from the whole. Empson et al. [
13] calls this way of reasoning “non-anticipatory” because, while the student is now attending to both the need to exhaust all items to be shared and make the shares equal, the partitioning and subsequent naming of the fractional quantity produced is not associated with a relation, or coordination, between the number of sharers and the amount being shared.
Over time, children begin to coordinate their two goals of making equal sized parts and exhausting the whole, and their partitioning becomes planned prior to activity. The child begins to use the number of sharers as an a priori plan to create a predetermined number of parts to exhaust the shared items [
13]. Unitizing one whole, the child may eventually plan to cut each stick into four parts [
14]. The mentally-planned partitioning may no longer be an act of counting and is plausibly supported by a developing notion of composite units (i.e., “four” as four units of one and one unit of four). Steffe and Olive [
15] refer to this regular coordination of equal parts within the whole as the first true instance of partitioning. Yet, to the child, the value of the fractional parts remains tied to an empirical representation of a partitioned part out of some contextualized whole [
14,
15]. In other words, the child’s notion of fractions is not yet useful as a quantity.
Children’s notions of unit fractions begin to solidify as they continually coordinate making equal parts with exhausting the whole with larger numbers of sharers and begin to understand that they can repeat one of the parts they created to remake the whole [
15] or other non-unit fractions [e.g., sharing four sticks among six people is (1/6) + (1/6) + (1/6) + (1/6), or (4/6)]. In fact, sustained work in equal sharing situations yields an anticipation of partitioning across wholes [
13,
15]. That is, children may use a developed or developing multiplicative reasoning to spread coordination of parts across the wholes (e.g., in a situation involving four items and six sharers, children might consider a subgroup of two sticks each cut into three parts, then repeat the action so that each of the six sharers receives two-thirds of a stick of licorice). That is, children’s partitioning activity becomes “distributive” [
13].
Despite the depth of information contained in the mathematics education literature on the fractional reasoning of children without low achievement, there is a dearth of similar information on children with low mathematics achievement [
19]. Hackenberg [
19] suggests from her work with six children with low mathematics achievement that their fractional reasoning was consistent with prior research, although the children had not yet developed more sophisticated ways of reasoning that supported a robust knowledge. We hypothesize we may uncover similar results; further, we conjecture that a variance of reasoning will be documented, from early to more advanced ways of considering equal shares.
Our hypothesized result may be viewed by some as reifying what many may consider to be “common sense”. We assert, however, that such results might have important implications in terms of the problem of a continued conceptualization of low achieving students as “different” in terms of their need for specific kinds of teaching and learning experiences and/or detached instructional experiences in school. A description of the participants, data gathering, and analysis procedures follows.
6. Discussion
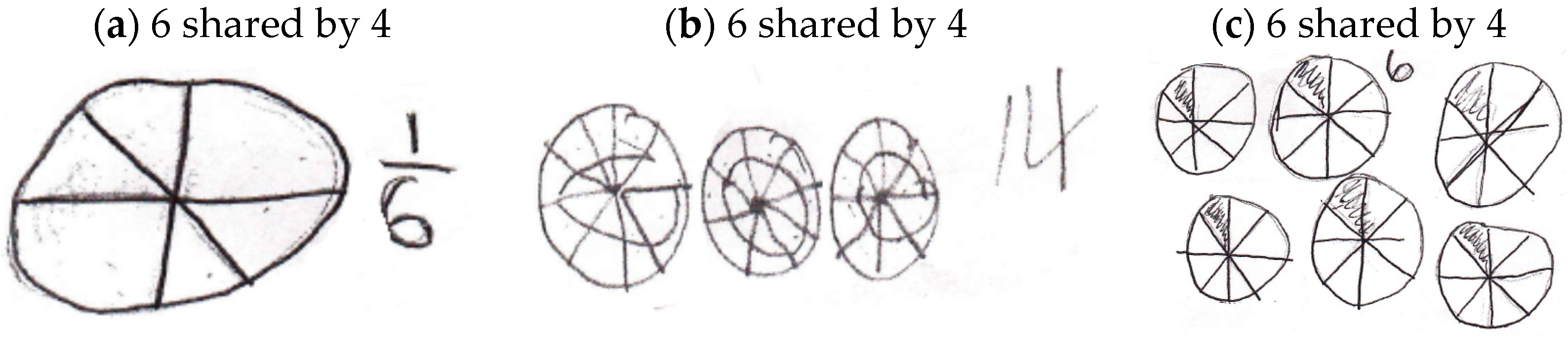
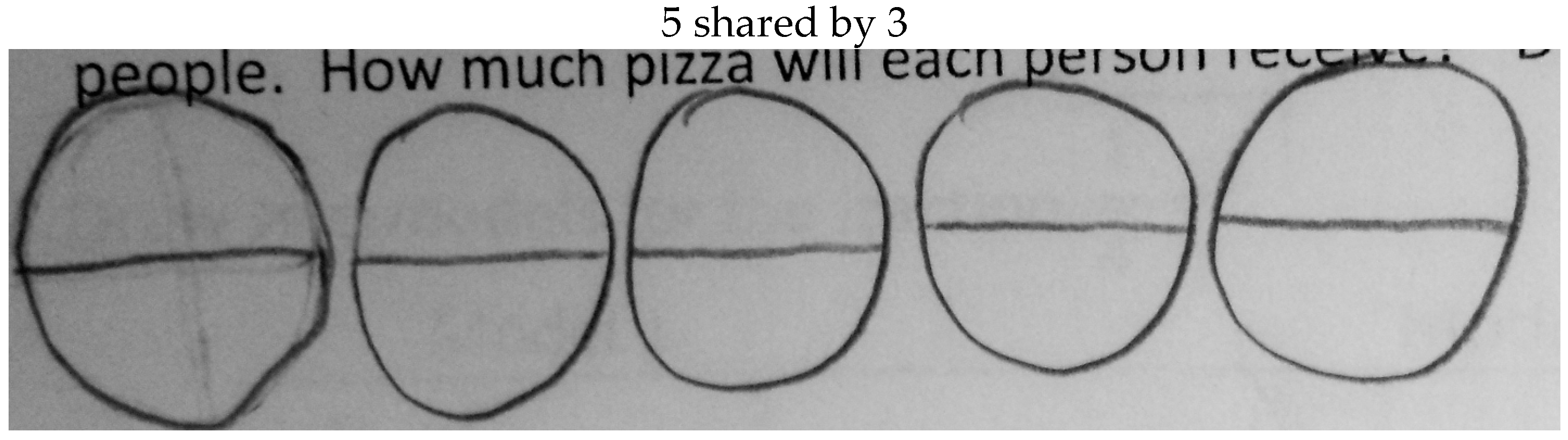
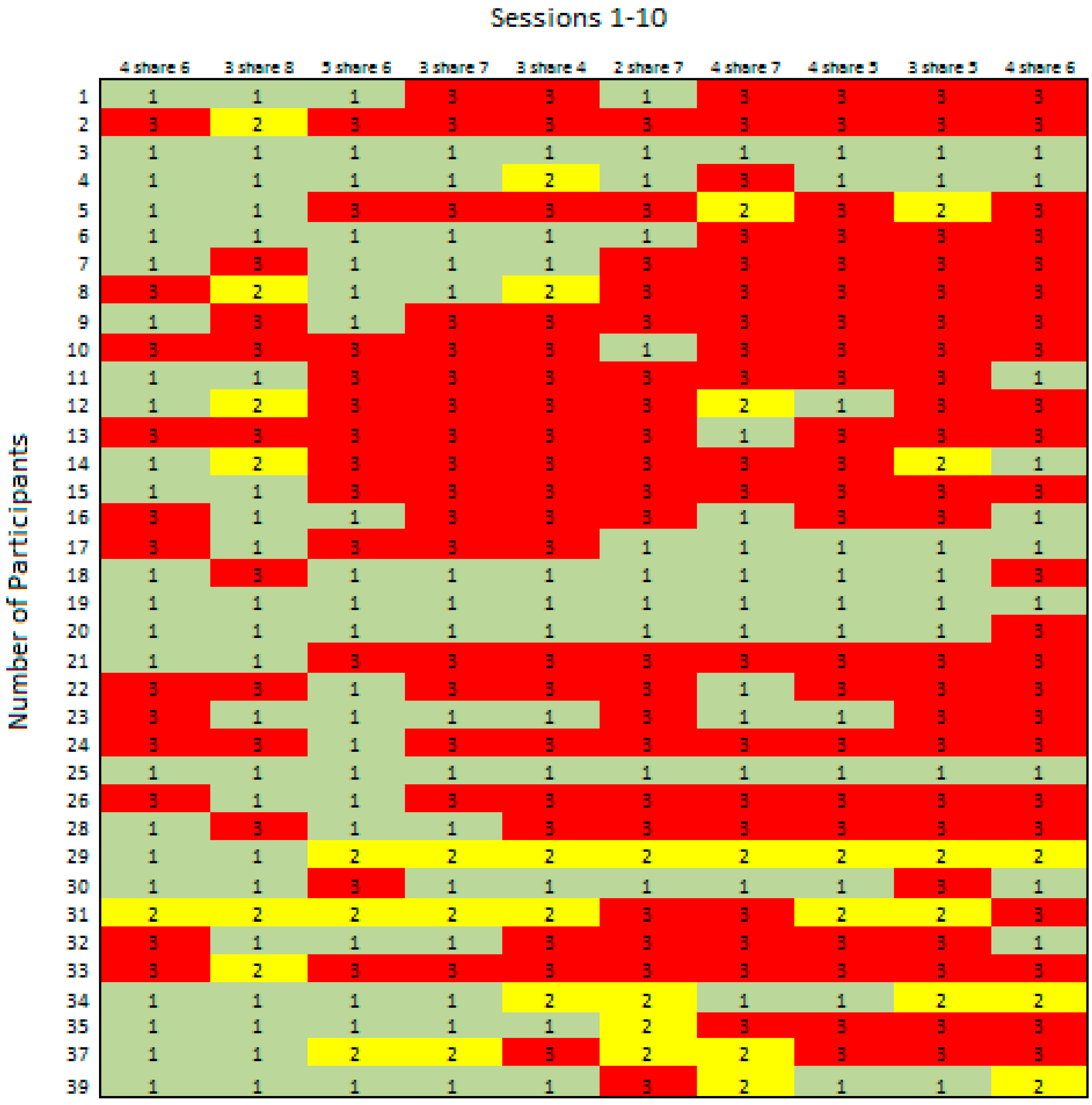
Results of this study revealed three ways of reasoning evidenced in children’s partitioning in equal sharing problems (i.e., “No Linking Between the Number of Objects and/or Parts to the Question Context”, “Partitioning of all Objects into Halves”, “Partitioning of all Objects into the Correct Number of Sharers/Partitioned Leftovers into the Number of Shares”) and evident in children who experience low achievement in mathematics over ten weeks of participation in lessons that did not directly address equal sharing. Trend analyses of the children’s partitioning suggest that children’s ways of thinking through equal sharing tasks varied, showed some change over the course of the sessions, and seemed dependent on the numbers used in the equal sharing problems. Thus, our data do not suggest sequential “levels” with respect to partitioning when looked at as indicators of reasoning, rather, just ways of knowing what exists in the children’s reasoning and that they utilized in equal sharing problems.
Children completed equal sharing problems as part of a daily assessment at the end of each intervention session. Their ways of reasoning provide a window into what conceptions children with low performance in mathematics
do have when immersed in solving problems that supports the
active use of partitioning and subsequent reasoning about the resulting quantity. These were ways of reasoning that the children
already possessed, not a result of a teacher-modeled strategy or thought process. Arguably, the improvement over the sessions was the result of the children
inventing more efficient strategies. Future research with more children who experience low achievement in mathematics solving equal sharing tasks
as the basis for instruction would expand and extend the current findings. Such research might relate fraction symbolism to an equal-sharing analogy (division meaning) of fractions (e.g., 2/3 = two wholes shared equally among three), building on children’s informal knowledge, and naturally connecting to part-whole meanings of fractions [
29]. Furthermore, the research might include a pretest-posttest design with random assignment and a comparison group to test for significant effects of different types of instruction.
The following paragraphs present two main contributions of the current study to the literature: (a) the aspects of the children’s ways of reasoning as “same” and “different” in terms of the children’s label of “low achieving” and (b) the implications of the children’s ways of reasoning in terms of “difference” and the subsequent need for “different” kinds of teaching and learning experiences in school.
6.1. What Did We Learn About Ways of Reasoning for Children Labeled as “Low Achieving”?
Findings from the current study support the notion that most of the children who experienced low performance in fractions in the study used partitioning within equal sharing situations, which is not unlike the performance reported in existing frameworks documenting conceptions of children who were characterized as “typically achieving” [
12,
13,
15,
18] (that is, we add to an existing body of evidence [
30,
31] that, given an opportunity to engage in solving problems and to reason about the results of their own activity, children labeled as “low achieving” evidenced ways of reasoning about fractions and used partitioning in similar ways as children without the label. As noted in past research [
13,
15,
18], the numbers used in the problems seemed to have some effect on children’s partitioning. That is, problems that resulted in making three or five parts across one or more wholes seemed to bring about more difficulty in partitioning than those that did not for many of the assessments. However, as children’s experience with the equal sharing problems increased, ways of reasoning documented in previous research as somewhat more sophisticated [
13,
15] forms of partitioning, were evident. This is evidence that the children’s reasoning in equal sharing problems is not “different” from what we might expect from children who have not been labeled as low achieving.
This is not to say that no differences emerged compared to prior research with children not labeled as low achieving. Namely, some ways of reasoning evident in the children’s partitioning showed that some children did not link the number of sharers in the situation to their plan for partitioning the objects. Children drew an item and partitioned it into the number of items (as opposed the number of sharers) or a seemingly arbitrary number. This finding may be indicative of children who, in their early experiences with sharing situations, pictorially represent the situations (e.g., representations that show only the visual appearance of a problem element) instead of schematically (e.g., representations that show spatial relations among problem parts) [
32]. Yet, these same children evidenced a variety of ways of reasoning over the sessions. Thus, even if we interpret some of the children’s initial depictions of the problem as qualitatively different, the children’s activity and reasoning, leveraged by the equal sharing situations, likely supported advancements in their partitioning plans. Moreover, these data were taken from daily assessments (e.g., static measures of knowing) and not from situations where children interacted with others about the problem situation and their own reasoning. If the children were engaged in instruction that leveraged what they knew and gave opportunities for children to unpack the problem context and engage in discourse about their ways of reasoning, it is likely their thinking would be extended [
33].
6.2. Do Performance Differences Warrant Different Instructional Experiences?
The results of the study hold implications for the type of instruction children labeled as low achieving “need” due to their low mathematical achievement. When working with children, there is often a tendency to use black and white categories to view “knowing” as performance; children’s learning and subsequent conceptions seem to be labeled as either right or wrong. Based on this assessment, children with sustained low achievement are often times given labels of “deficient”, “not ready”, and “unable” [
7,
34,
35] Mathematical knowledge, then, also takes on an altered form and is interpreted for these children as something that needs to be poured in rather than something that already exists [
36], can grow and change, and can be supported and extended in the midst of instruction. In other words, the more children are placed into instructional situations that remove the responsibility for reasoning from the child and place it onto the teacher, the more these children experience an altered means of knowing and learning mathematics in school [
3]. Arguably, such an experience might work to further marginalize and separate these children (e.g., [
37,
38]).
Knowing that children who are labeled as low achieving—a perceived “difference”—evidence ways of reasoning that are similar to those documented among their peers provides a platform from which to explore how to structure mathematics instruction for these children in ways that are currently underutilized. Particularly, children involved in the current study showed ways of knowing and reasoning within their own problem-solving activity that varied with the problem context and in terms of sophistication, just as we would expect from children without low achievement. In this way, the current work challenges the notion that low achieving students simply cannot engage in such problems that leverage their own activity and, thus, need only direct, systematic instruction to learn [
39].
The children involved in the study had two years of regular classroom instruction in fractions that utilized already-partitioned shaded models, vocabulary instruction, and procedural training from which they did not benefit. Arguably, these children were defined as low achieving because they did not perform in an expected way or at an expected rate [
2,
8] from a curriculum that may have been limited in its support of deep fractional understanding [
40]. Although the tradition has shifted in recent years to include concepts along with procedures, the tradition of measuring low achieving children’s “responsiveness” to such models of instruction continues [
2,
8,
33]. Thus, current intervention research in special education focuses on children’s responsiveness to teacher-modeled strategies and not conceptual development within children’s thinking.
The equal share situations children encountered in this study were never directly addressed during the intervention instruction, and children were not given feedback on their solutions to equal sharing problems on the daily assessments. Yet, for the majority of children in the study, a variety of ways of reasoning evidenced through their partitioning were documented. The results of this study suggest that instructional experiences that are based in the child’s activity (e.g., partitioning) are not only beneficial but paramount to children with low achievement to develop their reasoning. We argue that instruction for any child, including children with low achievement, should focus on what the child is able to understand and do mindfully within their own activity and reasoning. Future research might document instruction in fractions for children labeled as low achieving from a problem-solving stance situated within classroom instruction with their peers, documenting how conceptions emerge and can be supported and extended through the children’s activity and reasoning alongside their peers.
7. Conclusions
Framing instruction in a disability studies perspective (e.g., [
3]) that widens instruction from the start so that it is inclusive of diverse ways of knowing might be a way to place competence of all students in context. That is, when someone does not meet an expectation or an assumed “normal way” of doing, we tend to place the problem within the individual and move on. Yet, we question (a) why research and practice defines different ways of reasoning as a problem; and (b) why this “problem” is located
within children. When researchers’ and educators’ notions of “normal” widen, we create spaces for and access to opportunities for diverse perspectives and ideas to be considered, shared, compared, contrasted, and, ultimately, valued. Children with different ways of navigating a mathematics problem may bring forth ways of knowing that, when viewed though a widened conception of “normal”, offers not only a form of access to the mathematics for the child, but also an additional way of viewing the mathematics for other children. Arguably, the mathematics improves, as mathematical knowing and learning becomes enriched and diversified. In this way, we advocate for an increase in research that positions children who experience low performance in mathematics as
capable and decreases in research that positions children as failures and segregates their experiences in school. Instruction should utilize children’s activity as a platform from which to support and extend understanding.