Abstract
This paper presents an effort to revitalize a large introductory engineering course for incoming freshman students that teaches them analytical design through a project-based curriculum. This course was completely transformed from a seminar-based to a project-based course that integrates hands-on experimentation with analytical work. The project is centered on a reconfigurable trebuchet kit that student groups assemble and work to identify design decisions that will maximize projectile launch distance. Challenges include streamlining the project experience for the large enrollment (up to 148 students) with limited contact hours, and helping students fuse hands-on experiences with quantitative engineering analysis. A mixed-methods approach supported the claim that the curriculum improved the students’ engineering judgment and demonstrated to students the value of engineering analysis and mathematical models in practical engineering design. A rigorous statistical analysis of student trebuchet launch performance at different course stages is included. A qualitative assessment of student learning is derived through students’ reflection of their course experience. Comprehensive results comparing students’ design iterations versus algorithmic design optimization iterations provide important insights into student design intuition, paving the way for hybrid design education models that teach students how to combine human design intuition with quantitative design tools to design superior systems.
1. Introduction
Traditional engineering design courses often have relied on happenstance to link theory with practice. Noticing these deficits in student practical engineering design experience, the Department of Industrial and Enterprise Systems Engineering at University of Illinois at Urbana-Champaign decided to revamp its freshman-level engineering course by introducing a project-based curriculum. The premise was that a project-based, hands-on activity that was connected carefully with quantitative engineering analysis would introduce students to the rigors of engineering design practice at an early stage in their engineering career, along with other benefits.
1.1. Project-Based Learning via Trebuchets
Project-Based Learning (PBL) is a teaching method in which students gain knowledge and skills by working for an extended period of time to investigate and respond to an engaging and complex question, problem, or challenge []. Simply put, project-based learning conveys learning through experiences []. PBL curricula are designed in a way in which students work in groups to solve challenging issues that are authentic in nature but based within a curriculum [,].
Over the past several years, the United States has experienced a shortage of qualified engineers. Being cognizant of this fact, the U.S. National Science Foundation (NSF) called for reform in engineering education []. This call for reform included and emphasized project-based learning. PBL encourages self-directed learning that in turn supports life-long learning (which links into the department’s overarching goal). That ultimate goal is to provide students with the required knowledge base and necessary skill set, while also helping students develop attitudes that support becoming efficient and effective engineers.
The PBL authentic approach [] was introduced to the curriculum via a reconfigurable trebuchet kit. A trebuchet is a machine that converts gravitational potential energy to kinetic energy to launch a projectile. These kits and associated curriculum were designed to enhance student engagement, participation, and motivation, which are keys to linking theory to practice in engineering analysis and design. Students were presented with situations that required them to become active learners rather than relying on the rote methods of lecture []. Research has found that implementation of project-based lab activities into engineering design courses help bridge the gap between theory and practice []. Other available research suggests that PBL courses appear to improve retention, student satisfaction, diversity, student learning [], and provide beneficial `soft skill’ development for students [].
Many PBL activities employ open-ended projects that are especially helpful in aiding development of synthesis skills and creative idea generation and exploration. When these open-ended PBL projects include a significant design element they are sometime referred to as design-based learning (DBL). Thus, DBL is a type of project-based learning which involves students engaged in the process of developing, building, and evaluating a product they have designed []. Open-ended projects, however, often are time and resource intensive, may require significant prerequisite coursework to obtain the necessary tools, and often are difficult to connect with rigorous engineering analysis except in capstone or graduate-level projects. More structured projects support streamlined learning activities that are less time and resource intensive but are appropriate for learning objectives that are different from open-ended projects (including integration of analysis). For example, open-ended engineering design projects support learning important elements of design processes, such as problem identification and formulation, design concept generation, trade-off negotiation, and project management. Many argue design is fundamentally open ended []. In cases where students have sufficient technical preparation (e.g., upper-division engineering analysis courses) and ample time is available, open-ended design projects may also provide students with opportunities to learn the important connection between engineering design practice and rigorous engineering analysis. The specific course addressed in this article, however, is a first-year undergraduate engineering course that meets for only one hour per week. Time limitations and lack of deep technical background constrain PBL activities for this type of course. Discovering how engineering analysis supports engineering design practice, however, provides vital context for first-year undergraduates as they begin a sequence of challenging courses in fundamental science and engineering analysis. Given these constraints, how then can educators help beginning students experience the relationship between analysis and engineering practice? Many first-year PBL courses neglect rigorous analytic design in favor of more tangible activities on open-ended design problems (differentiating our approach from classical DBL activities). While these strategies produce valuable learning outcomes, a need exists for integrating analysis into design learning at early stages of education. Our hypothesis here is that a structured PBL curriculum with targeted learning outcomes provides an efficient and engaging learning strategy that addresses the interface between engineering analysis and practice.
The pedagogical approach proposed here aims to help students develop a specific understanding of the synergistic relationship between engineering analysis and practical engineering knowledge and intuition. In the simplest terms, intuition may correspond to simplified mental models or heuristics. It is helpful for an engineer to have good mental models based on experience and practical understanding of engineering systems, but it is also important for them to understand the limitations of these mental models []. Relying solely on intuitive mental models can lead to design fixation especially in case of inexperienced engineers where they may intuitively hold false assumptions about the system being designed, abide by nonexistent limitations, feel overwhelmed or have incomplete or partial information []. The design fixation can be mitigated through design exploration based on rigorous analysis or experimentation which can then feed back into strengthening these mental models and making them more sophisticated or accurate [,,]. One such rigorous strategy is continuous engineering design optimization, which is an important design methodology for many engineering applications []. Introducing students to both intuition-based and quantitative design decision strategies is important, especially early in their engineering education.
The integration of engineering intuition and analysis is referred to in this work as engineering judgment. Although there is no clear definition for engineering judgment in the literature, our definition is based on the approach proposed in Ref. []. Here we define engineering judgment as the ability to utilize simultaneously practical engineering intuition and quantitative engineering analysis to support improved engineering decisions. A primary learning objective is to provide first-year students with a solid foundation for the development of their own engineering judgment, which will be built upon though later coursework. An additional objective is to provide students with a proper perspective on how content in upcoming courses, focused on fundamentals and quantitative analytical tools, relates to finding solutions to real engineering problems. A lean curriculum was developed with targeted learning activities centered on a structured design project. This project involves trebuchet kits that are assembled by students, and that can be reconfigured to change dynamic behavior in complicated ways. Reconfigurable capability provides an opportunity for students to make design decisions without the need to construct one or more physical prototypes from scratch. While there is certainly value in open-ended design and fabrication activities, these are provided in other courses. The focus here is instead on making design decisions supported by quantitative engineering analysis. Students learn to improve their designs through physics-based understanding of the system, and through rational application of modern simulation-based tools. The use of trebuchets in classrooms is certainly not a novel idea. Using trebuchets as a means to understand the relationship between challenging practical design decisions and rigorous analytical tools, however, is.
1.2. Previous Pedagogical Use of Trebuchets
Trebuchets or other projectile-throwing, simple machines are commonly used by educators in PBL activities or for demonstrations. The accessibility of trebuchets permits activities where students at a variety of levels can engage (even beyond engineering and science related courses []). Engineering upperclassmen [,,], engineering freshman [,,], high school students [,], middle school students [], and even K–5 students (as the authors have personally experienced) are all levels of education where trebuchet-based learning activities have played some part.
Many of the reported activities have curricula developed around different learning objectives and trebuchet kits/models not suitable for analytical design activities. Open-ended trebuchet activities and rigorous analytical design exploration do not need to be mutually exclusive activities; however, much of the students’ time during open-ended activities tends to be occupied with important, creative tasks (which are more qualitative in nature) than quantitative exploration of their proposed trebuchet design [,,]. Since teaching analytical design methods is not one of the primary goals of these activities, it is not surprising that only a limited amount of time is spent modeling and perfecting their designs.
Computer models of trebuchets [,] facilitate rapid design iteration through model-based design strategies. Using mathematical optimization tools in conjunction with computer models to identify high-performance designs is an especially powerful strategy [,]. For these efforts to correspond to actual trebuchet design problems, the models and design problems must be based on realistically tunable design variables. For example, adjusting the projectile release angle is convenient from a modeling perspective, but this cannot be adjusted directly on a physical trebuchet. Realistically tunable parameters that influence release angle should be chosen instead as design variables. In addition, computer models can be used jointly with physical trebuchets to demonstrate the value of model-based design when compared to design exploration through physical testing [,].
The variety of trebuchet-based learning activities were shown to achieve a variety of important outcomes, including helping students to connect theoretical course material to realistic engineering design problems [], improving inclination towards continuing in a STEM field [], and improving problem-solving skills []. Here we build on the efforts described in the above literature through the development of a trebuchet-based activity focused on teaching analytical design.
1.3. Transition from Seminar-Based Course
Considering the benefits of PBL, an introductory freshman course, GE 100, was completely redesigned in fall 2012 to help students experience the range of technical topics covered in the department using a single hands-on project, and begin to develop engineering judgment. Before fall 2012, GE 100 was a 1 h, seminar-based course consisting of overview lectures provided by department faculty. While students were exposed to a wealth of important information, the course on the whole did not engage students, and did little to prepare them for the upcoming rigorous curriculum. Each lecture was delivered by a different faculty member with varying levels of engagement and utility for first-year students. The revised course maintained the same session format: 50 min meetings every week for half a semester (eight weeks for a total of 6.7 h). This limited direct contact with the students presented an additional challenge when developing an appropriate course curriculum.
1.4. Curriculum Overview
In the redesigned GE 100 student project groups assemble, design, and test medium-scale trebuchets as part of the project (see Table 1 for the curriculum outline). Reconfigurable trebuchet kits were developed that supported a streamlined yet intensive hands-on experience. Student groups (3–5 students each) followed technical instructions to use hand tools to assemble complete trebuchets from components provided in kits (meetings 1 and 2). Students also learned how to adjust several components, such as pivot location, as a means to influence trebuchet dynamic behavior and projectile range. The reconfigurability of these components is a novel feature of these new kits, and is crucial for the use of these kits in teaching different approaches for engineering design. The design problem presented to students is to determine what is the best setting for four adjustable trebuchet components for maximizing projectile range. This is challenging to solve using intuition alone due to the dimension of the design problem (four correlated design variables), uncertainty in the trebuchet mechanisms and the operating environment (outdoors), and the significant nonlinearity of the overall system.

Table 1.
Curriculum outline.
Early in the course, GE 100 students learn basic design of experiments (DOE) techniques (meeting 2). With this knowledge and some initial intuition stemming from hands-on exploration of the trebuchets, students are then asked to plan out a set of experiments. Each experiment is a distinct trebuchet design (i.e., combination of settings for reconfigurable variables) that the students would like to test physically. The number of physical tests is limited severely because the tests are conducted outdoors during class time, and adjustments must be made between tests. Over the course of several semesters, the trebuchet kits have been refined iteratively to streamline assembly and reduce adjustment time, but the time required to make adjustments still limits the total number of experiments that each project group can perform. During this initial set of experiments, the students have very limited design intuition for the trebuchets, so their experiments are often designed to sample the trebuchet design space broadly (i.e., students use a space-filling experiment design, see Figure 1). During this activity, a handout required students to perform the following activities in order:
- Rank the design variables from 1 to 4 in order of importance;
- Identify variable ranges (min and max) that you would like to test using the physical trebuchet kit for guidance;
- Plan for a budget of eight total experiments with suggestions for space-filling experiments.

Figure 1.
Space-filling Latin Hypercube sampling plan with three variables and eight sample points [].
These tasks provided an introduction to the systematic process of designing experiments.
The first lecture provides an overview of both the course and the department. An introduction to process modeling is also given during this first lecture (meeting 3). A logistics model was created that combines agent-based modeling [] and discrete-event modeling [] to simulate how student groups rotate through trebuchet tests on field days (outdoor test days). Process modeling helps introduce students to some of the department’s courses and core research areas, provides an additional modeling experience beyond physics-based models, and familiarizes students with the field day logistics. The next meeting with the students was the first outdoor field day (meeting 4) where students execute tests specified during the DOE activity, following logistics policies refined using the model.
After the first field day tests, students learn in class about the physics of trebuchets, the basics of simulating nonlinear dynamic systems, and model-based design (meeting 5). This instruction is followed-up with a computer modeling lab where students are introduced to a sophisticated physics-based, multibody dynamic trebuchet model that predicts projectile range as a function of trebuchet design variable values (meeting 6). During this modeling lab project groups use this model to test new design ideas much more rapidly than through physical experiments. Student realize quickly the value of using physics-based models in engineering design. Due to the rapid response from the model, most student groups are able to develop intuition for the influence of design changes and converge on a near-optimal trebuchet design. During this activity, a handout required students to perform the following activities in order:
- Perform three predefined tests and report the distance;
- Answer the following question: “What is a good finger angle when sling length is 26 in and the pivot location is 4 in? Why?” (which is a single variable optimization problem);
- Rank the design variables from 1 to 4 in order of importance (repeat from the DOE activity);
- Plan for a budget of six total experiments for field day #2;
- (optional) Test more designs at home.
A new experiment design is constructed based on the insights gained from the first field day experiments and the computer modeling activity. The new experimental plan is fundamentally different from the first; trebuchet designs to be tested are clustered around the design that was predicted to be optimal during the modeling lab. The purpose of the clustered experimental plan is to account for modeling error and improve the chances of producing the best possible range for a physical trebuchet test. With the new experimental plan, the students then go back out to the test area for a second test launch activity (meeting 7). The student groups largely experience a dramatic improvement in the performance of their trebuchet designs.
The final meeting (8) was devoted to analysis and reflection on the previous seven meetings. This meeting included the following activities:
- Review of both quantitative and qualitative results from all of the project activities, including analysis of experimental results;
- Comparison of variable rankings based on student intuition (before and after the modeling lab);
- Discussion on the effectiveness of the launch day movement policies and comparison with multi-agent modeling results;
- Exploration of a comprehensive data set based on the trebuchet model to more fully understand the trebuchet design problem and the complex tradeoffs involved;
- Discussion on the explicit reasons for why engineering students take math and engineering analysis courses and how these topics are directly useful in engineering practice;
- Asking students their definitions of engineering intuition and judgment, and how course activities influenced their understanding of these ideas;
- Discussion on the value and potential problems with using modeling and simulation in engineering practice;
- Engaging students in a discussion on what they learned about developing a systems perspective for engineering design;
- Review of a variety of strategies for engineering design, including their different levels of analytical rigor, as well as the role of human creativity across all design strategies.
Many of these points are further elaborated in the following sections.
1.5. Learning Objectives
This sequence of activities provides students with first-hand experience that demonstrates the value of mathematical and physics-based knowledge in practical engineering design activities, and also capitalizes on the value of hands-on experiences to deepen student learning. Students gain valuable insights into why it is essential for engineers to learn foundational topics in mathematics and science. It is our objective to provide students at the very beginning of their college education with a solid understanding of how fundamental analysis courses required at early stages of their education provide an important foundation for later design courses, and how these courses will help prepare them to become successful engineers.
In the subsequent sections, we discuss the trebuchet kits used in this curriculum followed by a description of computational model used to explore the design space. Lastly we present the perceived improvement in the students’ engineering judgment outcomes due to the inclusion of this project-based trebuchet activity, supported by the rigorous statistical analysis. Engineering judgment here refers to the ability to utilize simultaneously practical engineering intuition and quantitative engineering analysis to support improved engineering decisions.
2. Reconfigurable Trebuchet Kits
In this section, we describe the design of customized trebuchet kits used by students in this redesigned GE 100 course. The primary motivation for designing these kits in-house was due to unavailability of commercial trebuchet kits that provided the adjustability needed to allow students to make design decisions. A new reconfigurable trebuchet kit was designed that allows continuous adjustments to pivot position, sling length, and finger angle (see Figure 2a). The kits also support one discrete design decision: whether or not wheels are used on the trebuchet base. The kits were designed for durability, ease of use by students (streamlined assembly and adjustments), and ease of fabrication (no specialized equipment required). Engineering drawings, course materials, and software models have been made freely available so that other institutions may use this project as a teaching aid. We now look briefly at some of the design aspects of these trebuchet kits. A number of factors shaped the final design of the trebuchet:
- Reproducibility across trebuchet kits for fair comparisons and use with a computer model;
- Reconfigurable capability to support rapid student adjustment of design variables (under 5 min);
- Streamlined assembly process, enabling most student groups to complete assembly process in less than 40 min given written instructions, components, fasteners, and tools;
- Portability (two college-level students can transport them small distances);
- Durability (multiple years of use, rain/weather protection);
- Reasonable cost (approximately $150 per kit, including all materials, hardware, tools, and manufacturing tools).
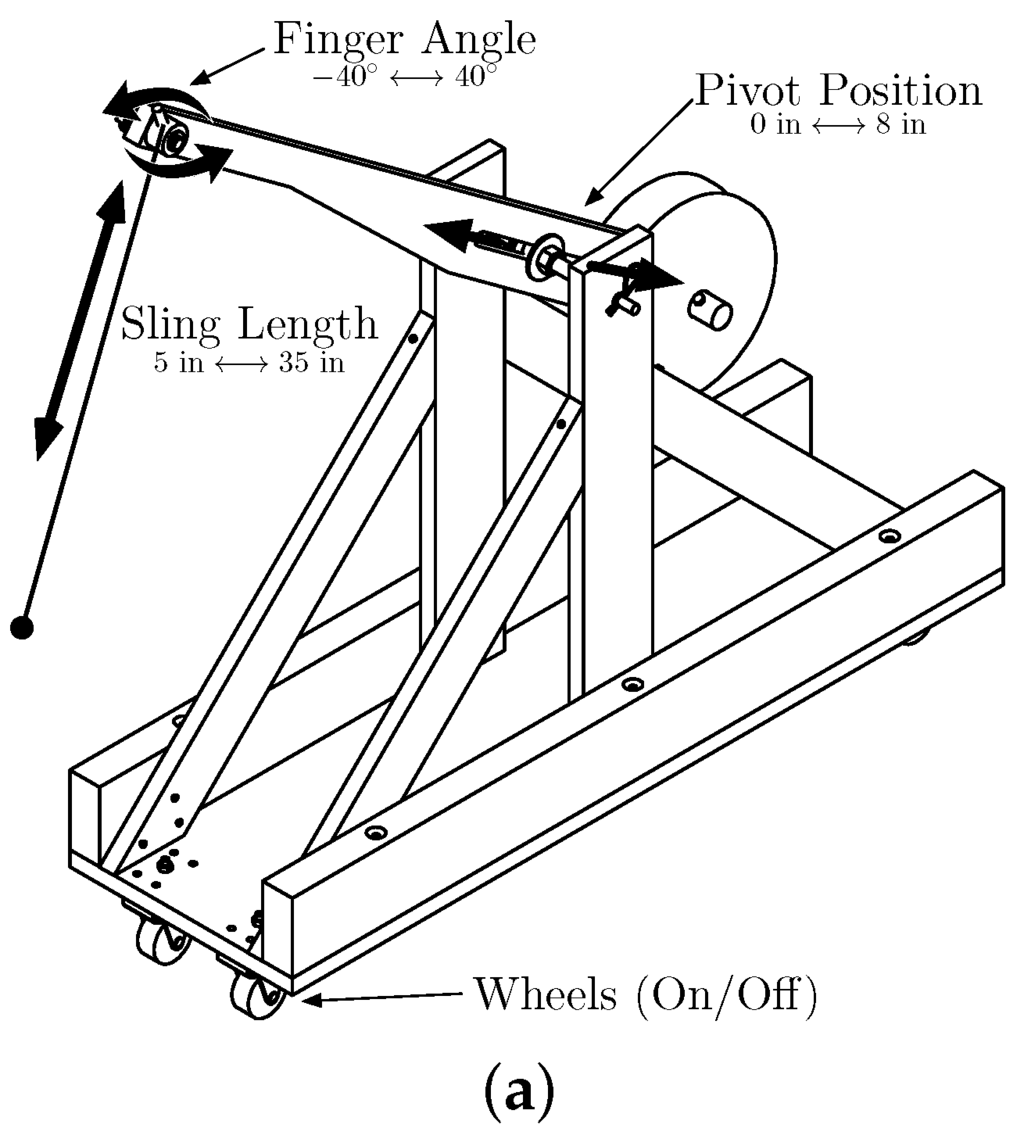
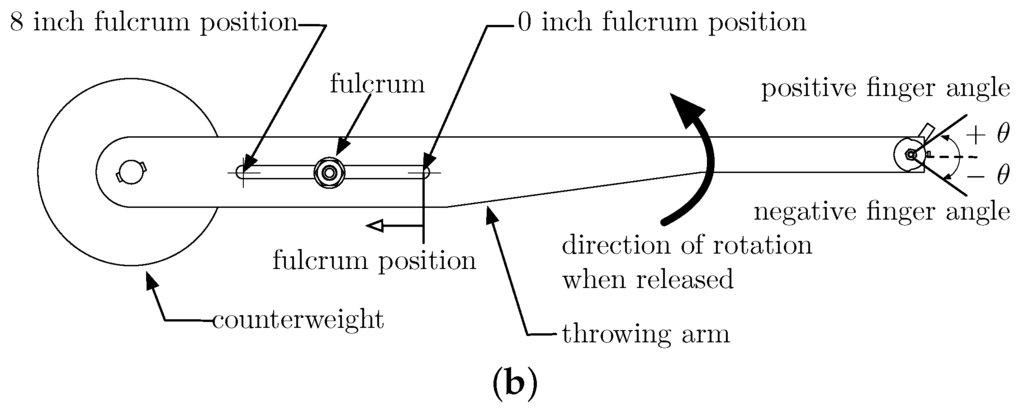
Figure 2.
Reconfigurable trebuchet kit. (a) CAD drawing of trebuchet illustrating the four design variables; (b) measuring conventions for finger angle and pivot position.
A CAD drawing of an assembled trebuchet is shown in Figure 2a. During operation, the user places a soft clay projectile in the pouch at the end of the sling, raises the counterweight to its maximum vertical position, positions the projectile on the base being careful to remove sling slack, and then releases the counterweight to initiate projectile launch. As the weight moves down in curved motion it swings the sling up and forward. One end of the sling is a loop that slid over the “finger”. The finger angle (one of the adjustments) determines the point at which the sling loop slides off the finger, releasing the projectile. The finger angle influences both the launch angle and velocity. Other adjustments also influence the point at which the sling slides off the finger.
Students can make four distinct trebuchet adjustments to influence dynamic behavior and projectile range. These four adjustments (design variables) are detailed in Table 2.

Table 2.
Reconfigurable design variables for trebuchet kits, with lower and upper bound specifications.
The first three design variables are continuous while the fourth is discrete (the design can either have four wheels attached at the base or not). Variable upper and lower bounds were provided to the students to help them understand the range of values that could be used for the continuous design variables. The measuring conventions for and are shown in Figure 2b.
The assembly steps and design variable adjustments require some basic tools. These were provided for each trebuchet kit in the form of a toolbox (see Figure 3(a)). This toolbox contained two nutdrivers, two adjustable wrenches, a hammer, a protractor, and a tape measure. The toolbox also served as storage for the fasteners and smaller parts.

Figure 3.
Photographs of a student toolkit and a trebuchet. (a) toolbox and select tools for assembly and design variable readjustments; (b) assembled trebuchet.
Note that some of the parts are preassembled such as the shoulder (part A in Figure 4) and caster or wheel (part C). Students had a limited amount of time to assemble trebuchet kits in class, so some limited preassembly was used to reduce total assembly time. The students are provided assembly instructions with both a written description and simple drawings that illustrate assembly steps. In addition, a mentor (graduate student or senior undergraduate student) was available if the students had any questions. The six assembly steps are illustrated in Figure 4 and Figure 5.
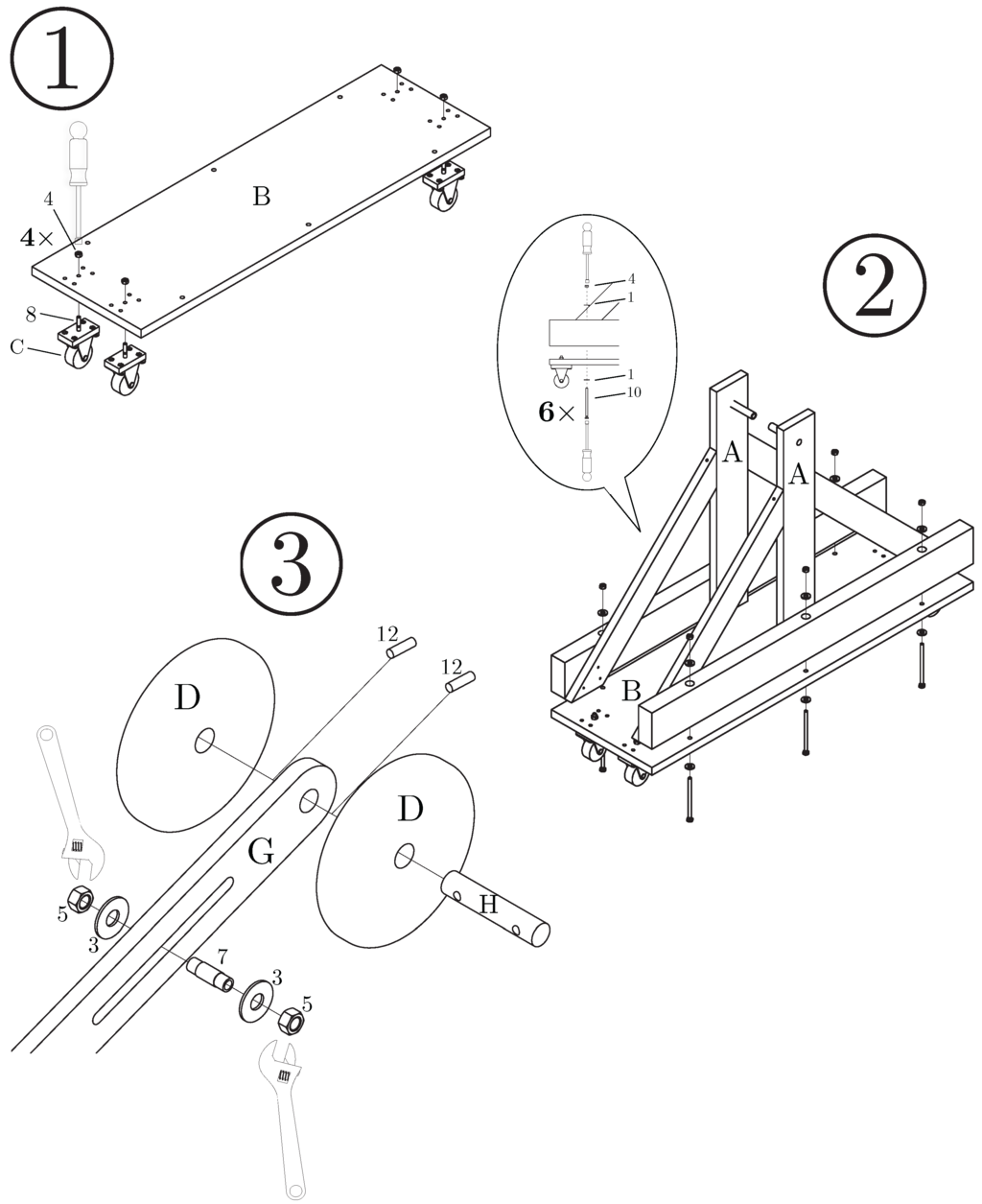
Figure 4.
Drawings illustrating steps 1–3 in the assembly instructions. Step (1) involves fastening of casters to the trebuchet base. Step (2) illustrates attachment of upright shoulders to the base. Step (3) involves assembly of the pivot mechanism and attachment of the counterweights.

Figure 5.
Drawings illustrating steps 3–6 in the assembly instructions. Step (4) illustrates how the finger assembly is to be installed. The throwing arm assembly is then attached to the trebuchet body via the fulcrum in Step (5). Step (6) shows how to attach the sling. The end of the sling cord with a loop is first slid over the finger (part F), and then the other end of the sling is threaded through the clamp mechanism (part E). This clamp mechanism allows rapid adjustment of sling length without the need to untie or tie knots, and also prevents sling cord damage.
Each trebuchet kit has a counterbalance mass consisting of two 10 lbs plates (part D). One of the assembled trebuchets is shown in Figure 3(b). The trebuchet body is approximately 36 inches long, 11 inches wide and 22 inches tall. The throwing arm (without finger) is approximately 36 inches long. The trebuchet parts such as base (part B), shoulders, and throwing arm (part G) are all made of wood. Most wood components are pine, although high-stress components (such as the throwing arm, finger, and main uprights) are oak. The pivot rod (part 6), pins, and fasteners are made of steel. The looping clamp mechanism that simplifies sling length adjustment, and the mounting seats for casters (shown in Figure 6g) were both fabricated via 3D printing (polymer fusion deposition modeling). The 3D printed caster mounting seats streamlined assembly and reduced the time required to switch between with and without wheels configurations. These seats enable assembly with a single large central bolt instead of four machine screws.

Figure 6.
Photographs of trebuchet components.
3. Interactive Computational Models
In this section, we introduce the interactive computational models used in the GE 100 curriculum to help students learn the value of model-based design.
3.1. Design for Maximum Range through Physics-Based Modeling
GE 100 students launch the trebuchets on the field during the first launch activity. They choose their design parameters such as sling length, finger angle and pivot locations, based on intuition stemming from only limited experience with the trebuchets. After the first launch day, students learn at an introductory level the physics of trebuchets, including techniques for simulation of nonlinear dynamic systems. This not only helps them develop deeper physics-based intuition for the influence of design changes on trebuchet behavior, but it also provides a foundational understanding for how sophisticated computational models simulate trebuchet behavior. After learning about trebuchet physics, students complete a modeling lab activity where they are trained in the use of a multibody dynamics trebuchet model. They can then perform rapid design studies by iteratively adjusting design variable values and obtaining projectile range and other results through simulation. Students repeat this process of updating their design based on simulation results until they converge on a design that they are satisfied with. In addition to helping students arrive at a significantly improved design, this modeling lab was also shown to help students improve qualitative understanding and intuition for trebuchet system design.
The physics-based simulation model for trebuchet was developed in MATLAB® and SimMechanicsTM software. The software interface for this simulation model is shown in Figure 7. The goal of providing students with a computer simulation model is to help them experience directly the importance of model-based design in the overall design process. It helps them to develop more accurate intuition through rapid creative exploration of the design space, and demonstrates through experience the value of rapid simulations when striving to solve a design problem quickly [], and to identify better designs than can be achieved through slower physical testing.
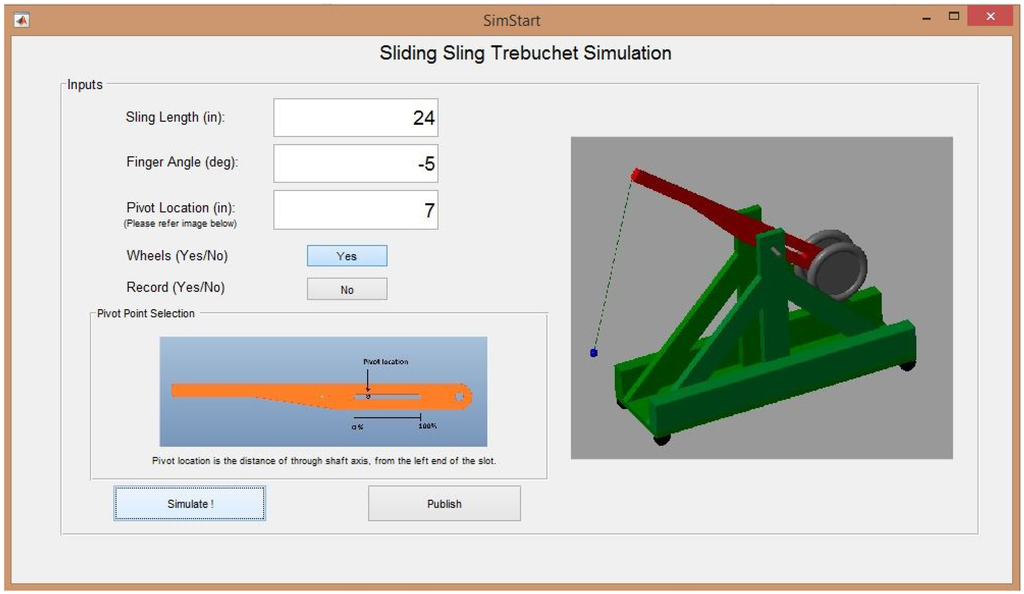
Figure 7.
Graphical user interface for simulation model.
The simulation model is used by students to explore the design space and to discover the relative importance of design variables on improving range. This intuition helps students identify designs quickly that maximize range according to simulated results. The produces two important outputs: (1) predicted throwing range for a given design and the predicted path of projectile as shown in Figure 8; and (2) an animation of trebuchet motion during the sling launch as shown in Figure 7. This rich set of outputs is designed to help students gain insight into how the system behaves, and how design changes influence specific aspects of dynamic behavior.
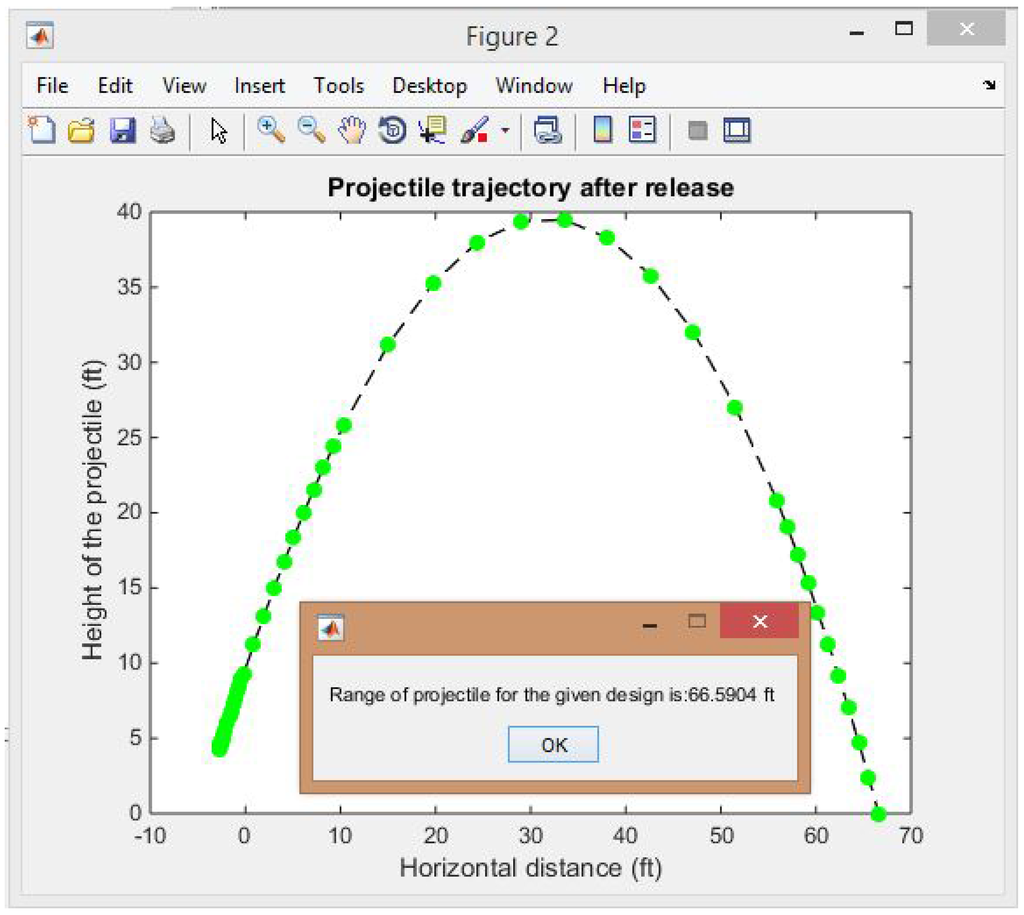
Figure 8.
The range plot pop-up.
While the trebuchet system appears to be mechanically simple, its underlying equations of motion are highly nonlinear due to large-angle rotations of the throwing arm and sling. This system also involves multiple bodies with irregular inertias such as the base, arm, counterbalance weights, wheels, and other components. The governing differential equations for the trebuchet system cannot be solved in closed-form [], so must be solved via numerical simulation. The trebuchet model is further complicated in the case where wheels are attached and the base moves relative to the ground during launch. Another complication is the sliding contact between the projectile and the base (i.e., where it slides before being lifted off and slung forward by the arm). The launch process involve three distinct phases separated by two discrete events: (1) when the projectile lifts off the base; and (2) when the projectile is released. This results in a hybrid dynamic system [] with three phases.
These challenges motivate the use of MATLAB®/SimMechanicsTM. These software tools simplify the process of modeling a complicated multibody dynamic system. Engineers specify the physical properties of the system, and then the equations of motion are constructed internally. These equations are then solved by numerical simulation. Even though a great deal of care is taken to model the trebuchet system in the MATLAB®/SimMechanicsTM with as much as accuracy possible, certain physical aspects cannot be captured with complete accuracy—such as nonlinear friction between mechanical components, air resistance, and minor manufacturing variations across kits. We have ongoing research into these areas to improve the model through computer vision and system identification.
Freshman students did not construct the trebuchet simulation model. This model was developed and refined a priori, and students used it as a tool to explore trebuchet designs, record data, visualize results, and automatically generate results and data reports.
Detailed physics-based models are not only useful for students or engineers seeking to optimally tune an existing reconfigurable system (such as the trebuchet here), but they are also valuable for the development of new reconfigurable systems. For example, it was important in developing the trebuchet kits to ensure that a sufficient level (range) of reconfigurability was provided such that students can explore the desired range of system behavior.
Similarly, this model can be used to identify more narrow ranges of reconfigurability (defined by variable bounds) with the objective of reducing design space size in a way that helps improve the chances that students will identify successful designs. It was found that allowing students to explore the entire range of trebuchet reconfigurability resulted in frustration; significant time was spent exploring unproductive design space regions. A balance must be struck between presenting a solvable problem to students and providing them with a challenging learning activity that will help them develop the desired intuition.
Appropriate ranges for continuous design variables (defined by upper and lower bounds) were identified using the multibody dynamic model. Each of the continuous design variables was varied over a large range of values. This study is shown in Figure 9; individual box plots show the distribution of the range varying the other two continuous design variables. The median range is the central white line, quartile 1 to quartile 2 is shown with a black box, and the range excluding outliers has a thinner black line. Outliers are marked with small red dots. From these studies, we see that the sling length is the most influential of the design variables since the distribution of range is most strongly correlated with the sling length (i.e., large median when ). However, we note that the model seems to break down at around 40 inches for the sling length. Similar conclusions can be drawn for the other two variables. This study was used to identify appropriate values for variable bounds provided to the students in Table 2.
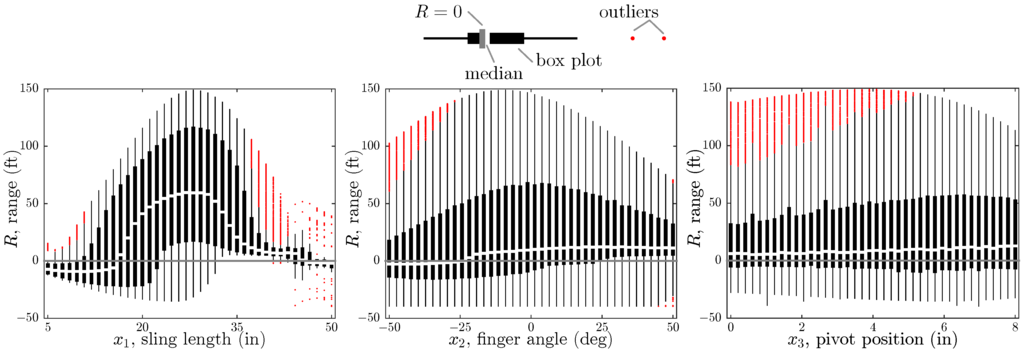
Figure 9.
Sensitivity studies exploring range for each continuous design variable.
Looking at single design variable plots often cannot reveal coupling relationships between design variables. In addition, while it may be simpler to tune a design a single variable at a time, this process may not arrive at a desirable design in an adequate amount of time. Figure 10 reveals the coupling between the sling length and finger angle for two select values of the pivot position. This type of dependence between the range and design variables can make it challenging to arrive at the global optimal design via manual adjustments. Teaching freshman engineering students these principles using a relatively simple problem can help them develop the type of qualitative understanding regarding design variable interaction that is crucial in the development of more complex engineering systems.
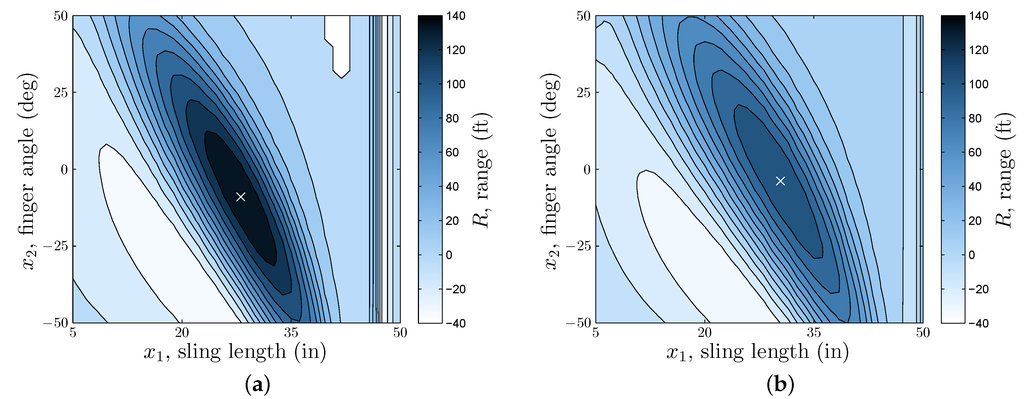
Figure 10.
Coupling between finger angle and sling length for two fixed pivot position values. (a) in; (b) in.
3.2. Process Model for Field Day Logistics
A logistics model was developed that combines agent-based modeling [] and discrete-event modeling [] in AnyLogic® to model the students behavior during the field day activities. This model is introduced to the students before the physics-based SimMechanicsTM model so that the students can get familiar with the field day logistics through the animation demonstrated in Figure 11b, while learning important modeling principles and considerations, such as assumptions, constraints, required data, performance criterion, and protocols.
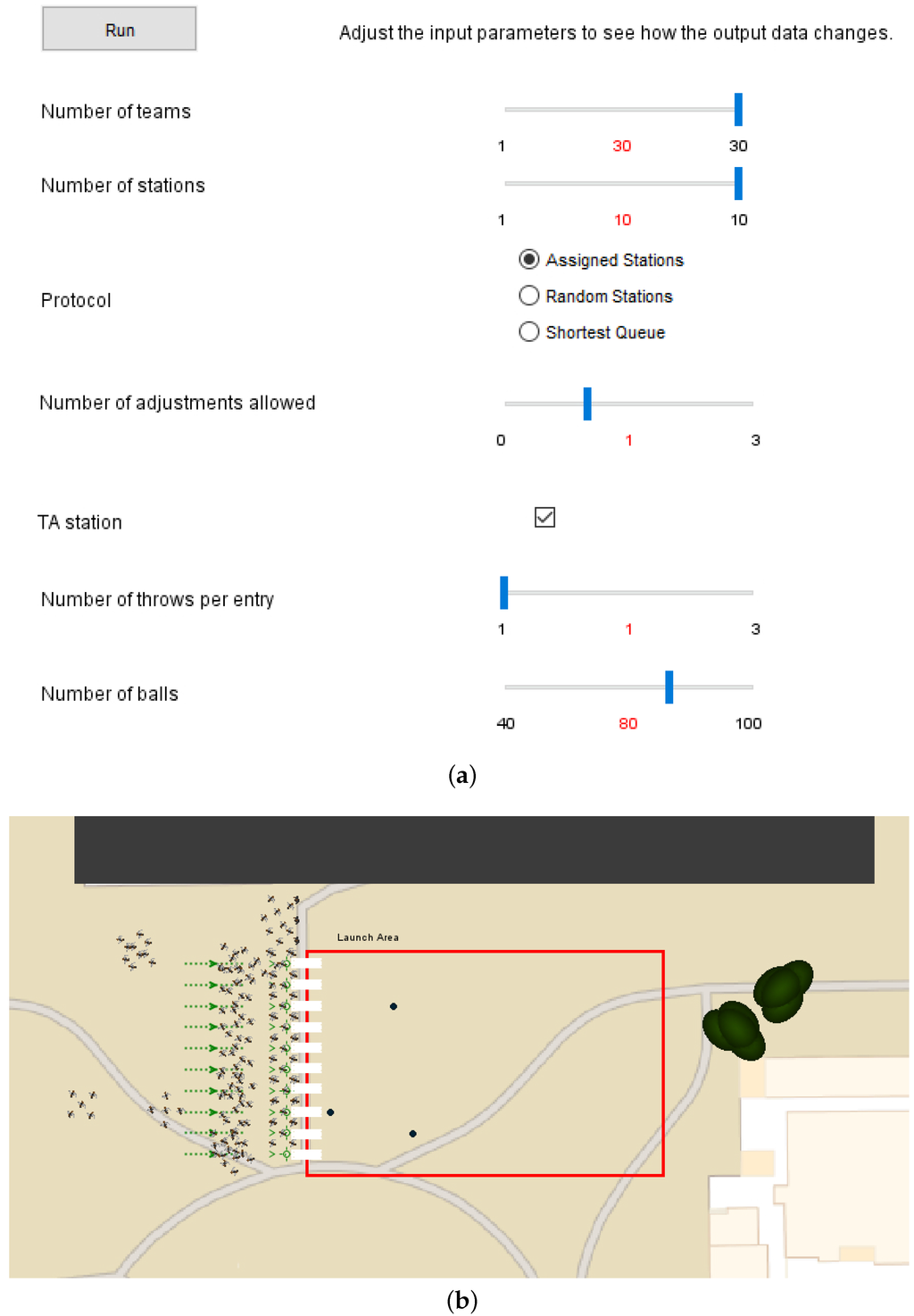
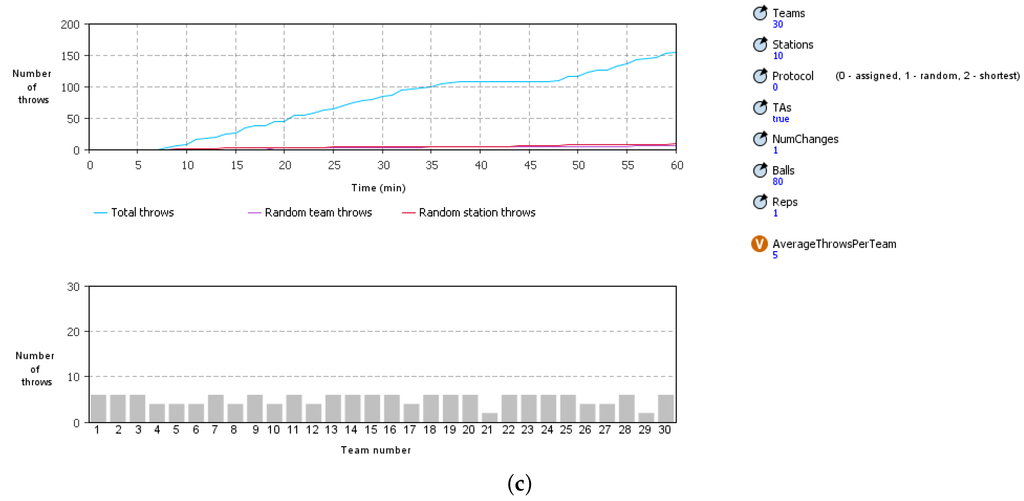
Figure 11.
Field day logistics model built with AnyLogic®. (a) parameter page; (b) screenshot of live animation of the field day logistics model; (c) simulation output page.
Agent-based modeling techniques are used to approximate the movement of students through the launch and staging areas during testing activities. Space limitations constrain the number of student groups that can launch trebuchet projectiles at a time, so many student groups must wait for their turn to test. A discrete-event modeling framework was used to simulate movement through launch queues. Queues fill up based on how the teams decide to join, directions from staff, and other factors. Three different protocols were considered for how the agents (student groups) would interact as they form queue at the launch pads:
- Assigned stations — Each team is assigned a station and they rotate with other teams assigned to the same station;
- Random stations — Teams join a random queue without any thought;
- Shortest queue — When teams are ready, they join a station with the shortest line.
Some other tunable parameters included the number of adjustments allowed on the launch pad and the number of throws per entry (see Figure 11a for the complete list of tunable parameters). Additional constraints considered include the number of throwing stations (i.e., queues, limited due to space constraints), the total amount of class time (50 min), and the limited number of projectiles. When all available projectiles have been launched, the the instructor halts launches and course staff retrieve the projectiles from the field. Some of these constraints were also made tunable so the students could observe their effect on simulation results. A number of different performance criterion available for the students to consider including total number of throws, number of throws for the slowest team, and the number of teams with throws below a certain threshold. Students sought a launch policy that increased the total number of projectile launches, while also striving to fairly distribute tests among project groups.
A large number of parameter values were needed to fully realize an accurate representation of the AnyLogic® model. Model parameter estimation was performed using data obtained during a mock launch day conducted by student volunteers not in the class. Model parameters were estimated from physical tests such as time to adjust specific trebuchet design variables, total time to launch the projectile when on the throwing station, projectile retrieval time for a given number of projectiles and course staff members, and walking speed of the student groups with the trebuchets (which can be determined from the simulation output page in Figure 11c). Under the conditions during fall 2014, it is seen that the assigned station protocol results in the largest total number of throws but with moderate variability in the distribution of throws between groups. The shortest queue had a slightly smaller total number of throws but more uniformity between the groups. The random queue was substantially worse than the other two.
4. Student Improvements in Trebuchet Comprehension and Engineering Judgment
In this section, we provide some results that highlight students’ improvement in trebuchet design comprehension and engineering judgment throughout the course stages. These results are important elements of the mixed-method (triangulation) approach used to determine whether this project-based curriculum was effective at achieving the learning objectives [,]. To that end, we begin with some relevant background information pertaining to the collected data.
4.1. Setup
4.1.1. Participants
The launch data analyzed in this section was obtained from a large group of freshmen engineering students (109 students were enrolled in fall 2014, which is the semester this data was obtained from). The students were divided into four or five member groups resulting in 23 total groups. The facilitators of the course, lab, and launch days consisted of the professor teaching the course, a graduate student TA, and a number of undergraduate and graduate student assistants contributing during modeling labs and launch days.
4.1.2. Instruments and Design—Four Course Activities
The data consists of the information obtained from four course assignments—a DOE activity, model-based design activity (see Section 3.1), and two field day trebuchet launches with physical experiments. The activities were completed in the following order:
DOE → field day #1 → computer modeling lab → field day #2
The DOE exercise consisted of several tasks that culminated in the construction of an experiment plan for the first field day. Task 1 required students to rank the design variables according to perceived influence on projectile range. Task 2 encouraged students to physically adjust all design variables to get an intuitive feel for the trebuchet design and identify the realistic variable bounds. Task 3 required students to practice adjusting the physical components of the trebuchet in a time-efficient manner. The final task, task 4, required students to strategically decide on eight sets of design variables they believed would provide insights and that would lead to a design with maximum launch distance.
During field day #1, the students were tasked with performing a total of eight physical launches using the planned tests from the previous DOE exercise. Throughout the exercise, students made adjustments to the trebuchet settings to explore effects on projectile launch distance. Launch distances were self-reported based on visually determining the distance relative to equally-spaced 10 ft markers. Because certain groups required more time to reconfigure trebuchet settings between launches, not every group completed the eight allotted launches. The total number of launches for field day #1 was 138.
After field day #1 and a lecture on trebuchet physics and simulation, the model-based design lab activity helped students experience the value of physics-based modeling and simulation in the design process. Since the students had already completed a few physical experiments with the trebuchet on field day #1, they were able to appreciate the ability to test many more designs in a short time span using a physics-based computer model. Students were instructed in computer model use, including how to input different design variable values into the trebuchet model and how to run the simulation to obtain the predicted projectile trajectory and launch distance. The model also included sophisticated animation capabilities that helped the students visualize how exactly the trebuchet moved for each candidate design. Students could move forward and backward in time with these animations with precise control to examine trebuchet dynamics very accurately. In the course of these studies students sought a design with maximum projectile range. During this process, they also developed deeper intuition for design tradeoffs and dynamic behavior than was obtained during earlier project activities. Based on this model-based design exploration activity, student groups were asked again to predict the relative importance of the design variables with respect to improving projectile range. At the end of the exercise, students used the model interface to create an automatically generated report that presented a summary of tested designs. A second experiment plan was constructed for use during field day #2. This plan was distinct from the first experiment plan in that designs were clustered around the predicted best design. Both the experiment plan and the model-based design exploration report were submitted to the instructor and were provided for students to use during the second field day tests.
During field day #2, students remained in their same respective groups as the first field day. Each group was allotted two rounds of eight launches. Most groups performed their 16 launches, but there were some that could not or chose not to finish all the launches. Unlike the first field day, the students were strongly encouraged to explore “on the fly” different values of the design variables to achieve the best range possible, learning from each physical experiment. The total number of launches for the second field day was 180, 42 more than the first field day.
4.2. Results and Discussion
4.2.1. Design Variable Rankings
Table 3 shows the student and instructor rankings of the design variables. The rankings for students (shown in DOE activity and MBD activity) is fractional since its averaged over all the student groups. The student rankings of design variables in the DOE activity case is completely based on intuition, where-in they assign highest importance to pivot position (score 1.8). After students complete the day 1 launches and model-based design (MBD) activity they on average identify that the finger angle is most important design variable (score 1.8). Lastly, the instructor’s ranking of design variables is based on results of comprehensive computer simulations, shown in Figure 9 and Figure 10. These results suggest that the combination of experiments during field day #1 and the model-based design activity improved the students’ intuition of the trebuchet design variables and is a direct quantitative measure of the learning outcomes [].

Table 3.
Student and instructor rankings of the design variables.
4.2.2. Statistical Analysis of Field Day Launch Distances
Descriptive statistics were used to build a profile for the two field day launch experiments. A summary of that profile is presented in Table 4. The statistics show that the mean launch distances for day 2 was 15.65 feet longer than that of day 1, and that the standard deviation of the launch distances for launch day 2 was 3.76 feet smaller than day 1. Figure 12 shows the difference between the launch distances between days providing a performance overview for both days. It also illustrates how day 2 launches were longer and less sporadic, however there were some outliers. It can be inferred that students were correctly adjusting the trebuchet variables to maximize launch distances. It is therefore hypothesized that the students’ improvements of launch distance on day 2 were due to student’s increased knowledge of the complete trebuchet system learned through the previous activities. A more appropriate experimental design to test the above hypothesis would be to randomize the sequence the students perform the first three activities (DOE, field day #1, and computer modeling lab) and to test the above hypothesis related to the effect of the activities.

Table 4.
Statistical analysis of the difference between field day #1 and #2 launch distances.
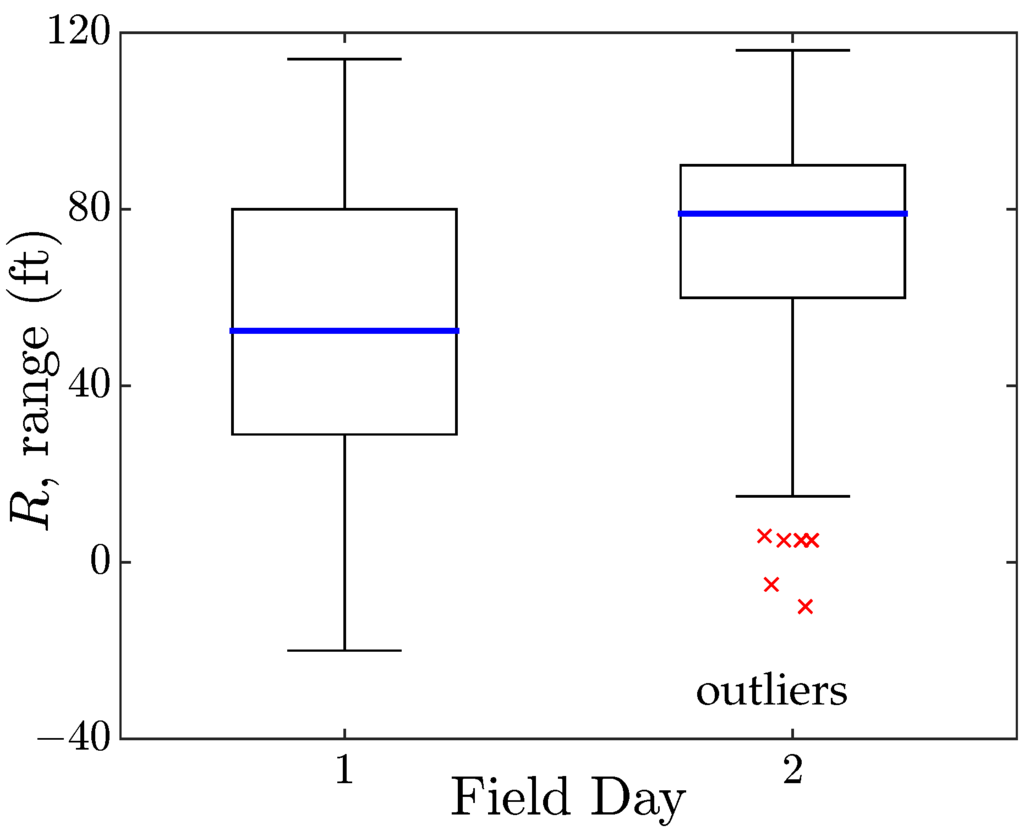
Figure 12.
Boxplots for launch distances for both field day #1 and field day #2.
The maximum launch distance for day 1 was 114 feet and it was performed by group 15 on launch #2. The maximum launch distance for day 2 was 116 feet and it was performed by group 15 on launch #6. Out of the total launches for both days, 77% of the maximum distances launched were launched on day 2. Fifty-two percent of day 1 launches traveled 90 feet or greater in comparison to 83% of day 2. The most repeated launch distance was 80 feet which had 12 occurrences on day 1 and 17 occurrences on day 2.
A before and after scenario was staged to determine if the project-based curriculum supported students’ engineering judgment. The experiment tests the influence a physics-based trebuchet model along with a computer simulated trebuchet launching activity has on launch distances.
- : field day #1 launch distance (before model-based design activity);
- : field day #2 launch distance (after model-based design activity and field day #1);
- ; There is no difference between mean launch distances of day 1 and day 2;
- ; There is a difference between mean launch distances of day 1 and day 2.
A paired sample t-test was used to test the hypothesis. The analyses indicated there was a statistically significant difference between the mean launch distances of day 1 and day 2; . Table 4 details the full results. With the knowledge that the mean of the two launch day distances were significantly different, the can be rejected and the is accepted. Since the earlier descriptive statistics data (in Table 4) showed day 2 having a greater mean launch distance, it can be concluded that there were statistically significantly greater distances launched on day 2.
The between day findings suggest that students were better equipped for the second field day launches. On the first field day, students relied heavily on nascent intuition to predict successful trebuchet design variable values using a space-filling strategy. The launches performed by students on second field day were heavily influenced by the preferred solutions they obtained through the simulation-based design exploration exercises. Although the individual student experiences were not reported, the data clearly showed some benefit of targeted experience with engineering analysis and simulation-based exploration on engineering judgment through improved launch distance performance. Analysis of student essays, combined with quantitative data, strengthens evidence that this pedagogical strategy does have an impact on the ability of students to integrate analytical engineering knowledge with practical design tasks to improve engineering decision making. Students were largely able to develop an understanding of how physical experiments differed from model results, especially after a larger number of test launches on the second field day.
It should be cautioned, however, that the study does not attribute these findings only to the model-based design because the analysis did not take into account other possible factors such as familiarity with the trebuchets due to field day #1 or ambient weather conditions.
The marginal means of the launch distance between the days for each group is shown in Figure 13. Group #6 and #19 representing low and high mean ranges respectively. Since the study was most concerned with improved range, the trebuchet design for group #19 perhaps could serve as an important reference point for maximum distance. We also see that 20 of the 23 groups (87%) having greater mean distances on day 2. However, to determine whether this meant there was a significant difference between groups, a univariate analysis was applied (see Table 5 for a summary of this analysis). The analysis found that there were statistically significant differences in launch distances between groups, between days, and between groups and days combined. Therefore, even though each group was unique, their progress between days favored longer launches. This is important because it signals that some groups outperformed other groups. What should be investigated is how well students in the different groups understood the various physics, mathematics, and engineering concepts involved in the activity, and whether these differences in understanding correlate with trebuchet design performance. The two-sample t-test that was performed in the study did not identify which groups had significantly lower launch distances than other groups. These groups can be identified by using an ad hoc test or by comparing trebuchet variable data with the optimization variable ranking model.
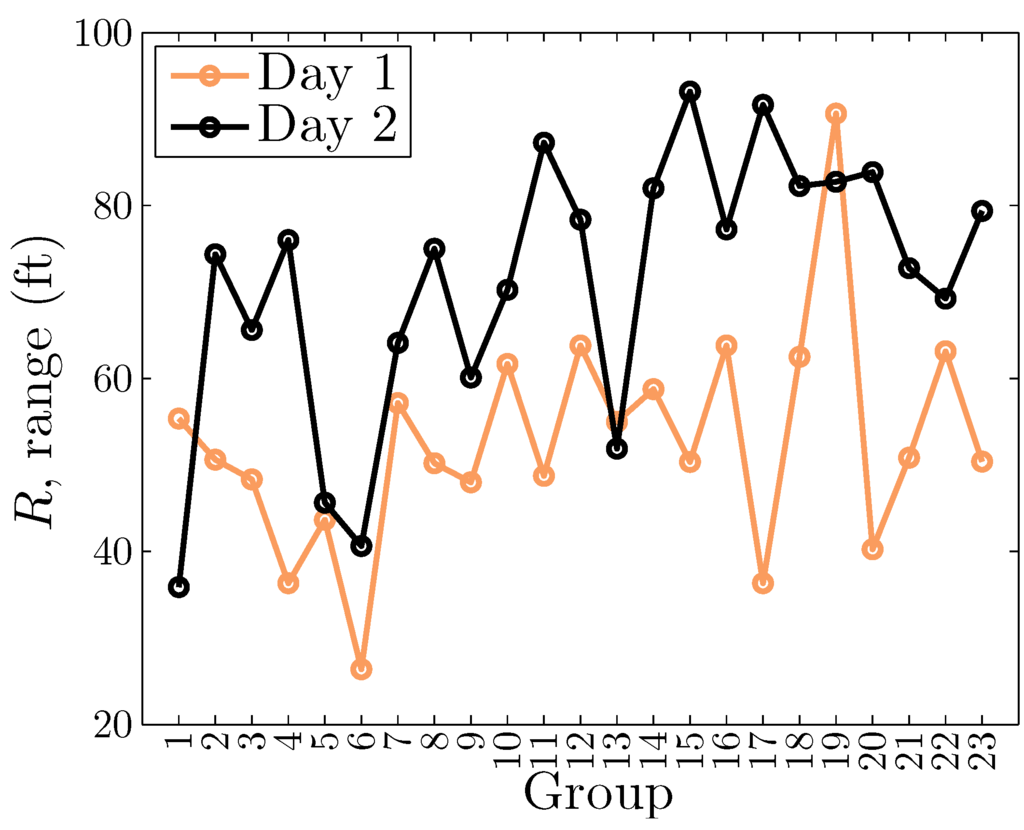
Figure 13.
Marginal means of distance between the field days for each group.

Table 5.
Univariate analysis on dependent variable launch distance.
4.2.3. Qualitative Assessment of Student Reflections on Mathematical and Scientific Tools in Engineering Practice
At the end of the course, the students were required to answer a few questions in short essay format. One of the required questions was:
How do mathematical and scientific tools, such as mathematical modeling and simulation, play an important role in engineering practice?
Understanding the role of mathematical and scientific tools in engineering practice is a requirement for good engineering judgment. Therefore the essay responses were qualitatively studied to see the student’s final thoughts on this concept.
After reviewing student responses, several themes surfaced. Intuition building, process improvements, prototyping, and optimization were all described as uses of the mathematical and scientific tools in the engineering design process. Many expressed that their current and future courses may primarily focus on building their technical knowledge but most practical engineering challenges require the application of this technical knowledge. Some students acknowledged that their fundamental engineering courses will form a basis for their engineering intuition and will teach them the quantitative tools required to solve complex engineering problems. All of these responses are aligned with good engineering judgment. This assessment was direct qualitative measure of the learning outcomes [].
4.2.4. Students vs. Optimization Algorithm
Students reported each test that they performed during the model-based design activity. Their test numbers were then compared to the tests performed by two common optimization algorithms to compare their search procedure and performance. The first optimization algorithm was gradient-based, namely fmincon in MATLAB® []. The other algorithm was gradient-free, namely patternsearch in MATLAB® []. Each data point in this comparison represents a distinct function call, i.e., a single execution of the trebuchet simulation (whether by student or optimization algorithm) for a unique trebuchet design. Optimization algorithm tolerances were loosened to allow faster termination, producing results that were better aligned with the number of tests performed by the students.
The first three designs tested by students were provided by the instructor so that students could gain some experience with the simulation process. The initial design was near the global minimum for range (see Figure 10); this corresponds to a very low-performance design. This low-performance design was used as the starting point for the optimization algorithms. In addition, the students were free to change the discrete wheels variable, while the optimization algorithm always had wheels on in the design (including wheels increases performance). Figure 14 compares the values at each test for the range and three continuous design variables. The two optimization algorithms are compared against three representative student project groups.
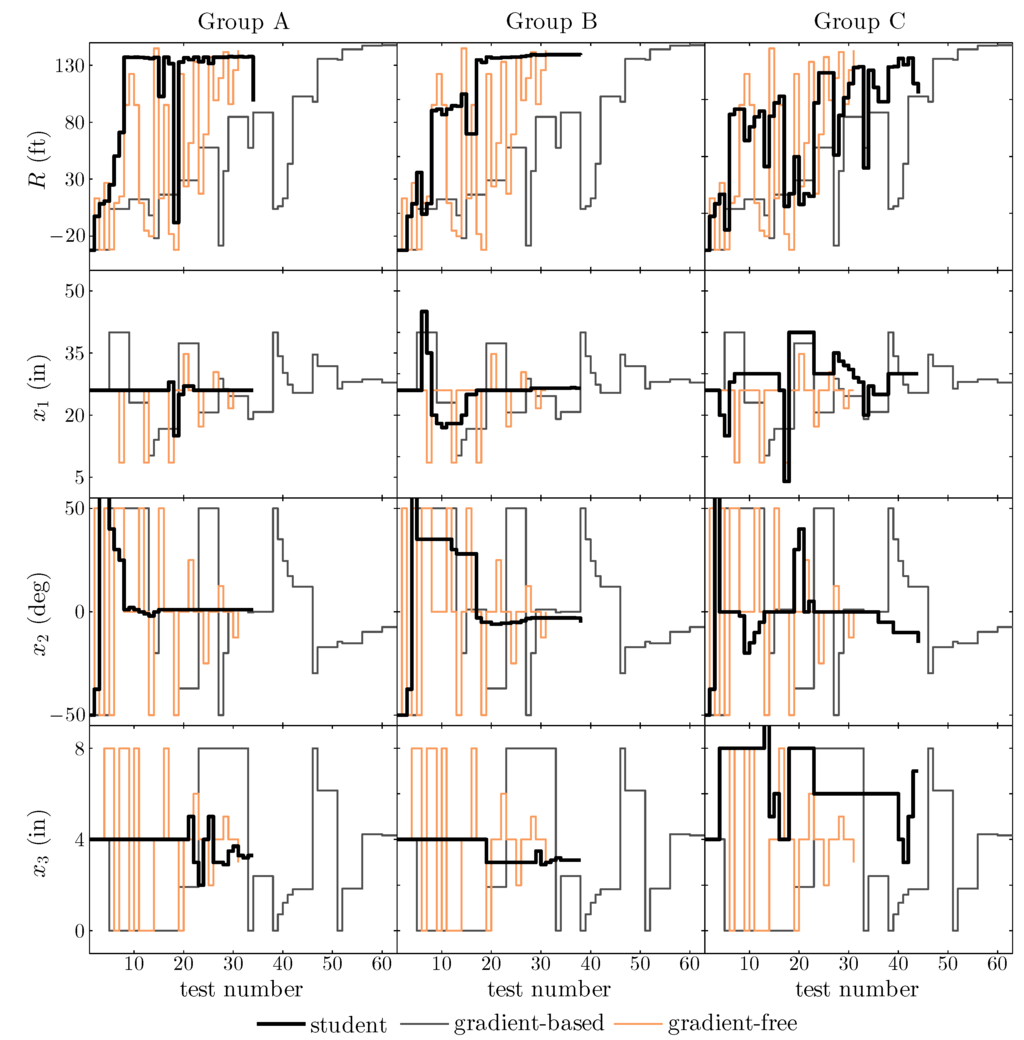
Figure 14.
Student tests with computational model compared with optimization algorithms (both gradient-based and gradient-free).
We first note that all groups eventually achieve a design near 130 ft (global optimum is 149 ft) even from a starting point that had a very poor range of −32 ft. Group A seems to understand the trebuchet design immediately with increasing range with every test until arriving near their best design very quickly. Group B had range progress similar to the gradient-based method, with consistently increasing range but with some lower values as well. The Group C test sequence was more chaotic, but still produced a general increase in range. The overall theme between the groups is their ability to greatly outperform the gradient-based methods with a lower number of tests and be on par with the gradient-free approach. This may be due to the students ability to use engineering intuition for physical systems in combination with quantitative analysis (i.e., engineering judgment), as opposed to being limited to quantitative understanding only (as is the case with the optimization algorithms). Optimization algorithms ultimately find better performing designs. It seems that, when student groups find a design that performs reasonably well, their design improvement stagnates.
These results may be explained by the approach the students use to explore the design space, namely, it is observed from the data that student groups tend to tune a single variable at a time []. This is in contrast to the process used by optimization algorithms, which can move in non-orthogonal search directions. Even though optimization algorithms may require more simulation executions than a human-in-the-loop approach, they eventually arrive near the global optimum. When variable coupling is present (as is evidenced in Figure 10), convergence is often slow when using the strategy of tuning a single variable at a time. Another factor here is that student groups were each given the same set of three sample designs to test initially. While the first design produced minimum range, the others were reasonable designs, and provided a good starting point for design exploration. Other starting points may have kept the students in the negative range for many of the tests (which explains why a reasonable guess was given). Further studies into this behavior may produce insights into how students think about design early in their engineering education and pave the way for education models that teach students how to combine human design intuition with quantitative tools (such as simulation and algorithmic optimization) to arrive at superior designs quickly. An important related topic is the influence that different types of hands-on and simulation-based design exploration activities has on enhancing design intuition.
5. Conclusions
The objective of the study presented here was to investigate how well a project-based curriculum: (1) helps first-year engineering students gain firsthand experience with the value of engineering analysis and mathematical models in practical engineering design; and (2) supports students in developing engineering judgment. A sequence of activities (both active and lecture forms) were created with these objectives in mind.
A mixed-methods (triangulation) approach was used to determine whether this project-based curriculum was effective at achieving the learning objectives [,]. A combination of direct/indirect and quantitative/qualitative measures were analyzed. Discussion of the improved design variable ranks (Section 4.2.1), improved launch distance measurements throughout the stages (Section 4.2.2), short essay responses aligned with learning objectives (Section 4.2.3), nonrandom input decisions made to the simulation model (Section 4.2.4), and successful completion of the written assignments (DOE activity and model-based design activity) complemented and converge towards the conclusion that the curriculum, to some degree, addressed the learning objectives.
The data also showed students making adjustments to the trebuchet variables that increased launch distances, even if these designs were notably different from the designs predicted as optimal using the model. This highlights the ability of students to combine knowledge gained through hands-on experience with quantitative investigations to strengthen engineering judgment and arrive as superior design solutions quickly. This insight paves the way for development of promising education models that teach students how to combine human design intuition with quantitative tools (such as simulation and algorithmic optimization) to design systems with superior performance. A more structured and comprehensive study in this area could lead to novel educational methods for improving engineering judgment of engineers at all experience levels. Additional assessment techniques not utilized in this study such as think-aloud protocols and pre/post evaluations could lead to novel insights that support successful development of these educational methods. Longitudinal studies could be conducted to understand how activities designed to improve engineering judgment early in the student’s academic journey affect their preparedness and final outlook on the engineering discipline. This research area is identified as future work.
Supplementary Materials
The following supplemental materials are made available online at http://systemdesign.illinois.edu/projects/trebuchets.php:
- SimMechanicsTM model described in Section 3.1;
- AnyLogic® model described in Section 3.2;
- Manufacturing instructions;
- Assembly instructions;
- Launch day instructions given to the students to help them understand the logistics and safety of the launch day;
- DOE activity assignment;
- Model-based design activity assignment;
- CAD files of the various trebuchet parts;
- Short video of the events.
Acknowledgments
The authors would like to acknowledge the efforts of many individuals who assisted with the development of the trebuchet kits, creation of curricular materials, and with managing the course project. Jason McDonald, Danny Lohan, Nick Farace, Allen Kaitharath, Tinghao Guo, Jeff Arena, Adam Cornell, and Lakshmi Gururaja Rao all made significant contributions. Several other graduate and undergraduate students at the University of Illinois at Urbana-Champaign (UIUC) beyond those listed above also made contributions. Several undergraduate research assistants were supported by the Department of Industrial and Enterprise Systems Engineering (ISE) at UIUC to make important improvements to trebuchet kits, create and test multi-agent models, and to make other direct contributions. Support for fabrication of the trebuchet kits was provided by both the ISE department and the College of Engineering at UIUC. MathWorks, Inc. provided support through a curriculum innovation award, including software licenses and specialized technical support.
Author Contributions
James Allison conceived the idea for this project, developed the curriculum, led the fabrication of reconfigurable kits and administered class as a lead instructor. Anand Deshmukh and Daniel Herber (and other graduate students) developed the interactive computers models. Anand Deshmukh and Daniel Herber (and other students) supported the fabrication of the trebuchet kits and helped conduct the field launches. Daniel Herber and Marlon Mitchell provided the data analysis in the paper. All authors equally contributed to literature review and writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- What is Project Based Learning (PBL)? Available online: http://bie.org/about/what_pbl (accessed on 20 February 2016).
- Solomon, G. Project Based Learning: The Primer. Tech Learn. Mag. 2003, 23, 20–26. [Google Scholar]
- Pilot, A.; Bulte, A.M.W. The use of “contexts” as a challenge for the chemistry curriculum: Its successes & the need for further development and understanding. Int. J. Sci. Educ. 2006, 28, 1084–1112. [Google Scholar]
- Mills, J.E.; Freagust, D. Engineering education—Is problem-based or project-based learning the answer? Australas. J. Eng. Educ. 2003, 3, 1–16. [Google Scholar]
- National Science Foundation. Systemic Engineering Education Reform: An Action Agenda; Technical Report; National Science Foundation: Arlington, VA, USA, 1997. [Google Scholar]
- Tempelman, E.; Pilot, A. Strengthening the link between theory and practice in teaching design engineering: An empirical study on a new approach. Int. J. Technol. Des. Educ. 2011, 21, 261–275. [Google Scholar] [CrossRef]
- Savage, R.N.; Chen, K.C.; Vanasupa, L. Integrating project-based learning throughout the undergraduate engineering curriculum. J. STEM Educ. 2007, 8, 15–27. [Google Scholar] [CrossRef]
- Dym, C.L.; Agogino, A.M.; Eris, O.; Frey, D.D.; Leifer, L.J. Engineering design thinking, teaching, and learning. J. Eng. Educ. 2005, 94, 103–120. [Google Scholar] [CrossRef]
- Hadim, H.A.; Esche, S.K. Enhancing the engineering curriculum through project-based learning. In Proceedings of the 32nd Annual Frontiers in Education, Boston, MA, USA, 6–9 November 2002; Volume 2.
- Silk, E.M.; Schunn, C.D.; Cary, M.S. The impact of an engineering design curriculum on science reasoning in an urban setting. J. Sci. Educ. Technol. 2009, 18, 209–223. [Google Scholar] [CrossRef]
- Wallace, K. (Ed.) Educating Engineers in Design; Royal Academy of Engineering: London, UK, 2005.
- Frost, R.B. A converging model of the design process: Analysis and creativity, the ingredients of synthesis. J. Eng. Des. 1992, 3, 117–126. [Google Scholar] [CrossRef]
- Daly, S.R.; Yilmaz, S.; Christian, J.L.; Seifert, C.M.; Gonzalez, R. Design heuristics in engineering concept generation. J. Eng. Educ. 2012, 101, 601–629. [Google Scholar] [CrossRef]
- Carberry, A.R.; McKenna, A.F. Exploring student conceptions of modeling and modeling uses in engineering design. J. Eng. Educ. 2014, 103, 77–91. [Google Scholar] [CrossRef]
- Basili, V.R.; Shull, F.; Lanubile, F. Building knowledge through families of experiments. IEEE Trans. Softw. Eng. 1999, 25, 456–473. [Google Scholar] [CrossRef]
- Evans, J.R. Engineering Design: Search and Evaluation; Coherence and Correspondence; Intuition and Analysis. M.S. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Papalambros, P.Y.; Wilde, D.J. Principles of Optimal Design: Modeling and Computation; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Brice, L.L.; Catania, S. A pedagogical trebuchet: A case study in experimental history and history pedagogy. Hist. Teach. 2012, 46, 67–84. [Google Scholar]
- Leifer, J. An Active Learning Design Project for a Junior-level Kinematics and Dynamics Class. In Proceedings of the 32nd Annual Frontiers in Education, Boston, MA, USA, 6–9 November 2002; Volume 1.
- Jahed, H. Trebuchet Design; ME380 Project Manual; University of Waterloo: Waterloo, ON, Canada, 2006. [Google Scholar]
- Brannan, K.P.; Murden, J.A.; Stout, R.H., Jr. The Great Trebuchet Project. In Proceedings of the 2002 ASEE Southeast Section Conference, Gainesville, FL, USA, 7–9 April 2002.
- Leonard, K.M.; Mastromonico, J.J., Jr. Integrating Engineering Design Heuristics into a First Year Engineering Course to Enhance Problem Solving and Team Building Skills. In Proceedings of the 2007 International Conference on Engineering Education, Coimbra, Portugal, 3–7 September 2007.
- Kenefic, R.; Lin, F.; Aschliman, D. Integrated design and analysis for a trebuchet using a high speed photographic measurement system and MATLAB. In Proceedings of the 2006 ASEE Illinois-Indiana and North Central Joint Section Conference, Fort Wayne, IN, USA, 31 March–1 April 2006.
- Slater, J. Making math and science exciting through engineering sport: The wright state university trebuchet competition. In Proceedings of the 2008 ASEE Annual Conference and Exposition, Pittsburgh, PA, USA, 22–25 June 2008. Number AC 2008-2221.
- Constans, E.; Constans, A. Treb-bot: Development and use of a trebuchet simulator. Phys. Teach. 2015, 53, 347–348. [Google Scholar] [CrossRef]
- English, L.D.; Hudson, P.; Dawes, L. Engineering-based problem solving in the middle school: Design and construction with simple machines. J. Pre-Coll. Eng. Educ. Res. 2013, 3. [Google Scholar] [CrossRef]
- Allison, J. Trebuchet Range Simulation and Optimization; MATLAB Central: Natick, MA, USA, 2012. [Google Scholar]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Fishman, G. Discrete-Event Simulation: Modeling, Programming, and Analysis, 1st ed.; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Thomas, E.W.; Marr, J.; Walker, N. Enhancement of Intuitive Reasoning through Precision Teaching and Simulations. In Proceedings of the Frontiers in Education Conference, Atlanta, GA, USA, 1–4 November 1995; Volume 2.
- Siano, D.B. Trebuchet Mechanics. Available online: http://www.algobeautytreb.com/trebmath356.pdf (accessed on 20 February 2016).
- Goebel, R.; Sanfelice, R.G.; Teel, A. Hybrid Dynamical Systems. IEEE Control Syst. 2009, 29, 28–93. [Google Scholar] [CrossRef]
- Breslow, L. Methods of Measuring Learning Outcomes and Value Added; Online Report; Teaching and Learning Laboratory: Cambridge, MA, USA, 2007. [Google Scholar]
- fmincon: version R2014a; The MathWorks, Inc.: Natick, MA, USA. Available online: http://www.mathworks.com/help/optim/ug/fmincon.html (accessed on 20 February 2016).
- patternsearch: version R2014a; The MathWorks, Inc.: Natick, MA, USA. Available online: http://www.mathworks.com/help/gads/patternsearch.html (accessed on 20 February 2016).
- Mathison, S. Why Triangulate? Educ. Res. 1988, 17, 13–17. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).