Learning Systems Biology: Conceptual Considerations toward a Web-Based Learning Platform

Abstract

Within recent years, there is an increasing need to train students, from biology and beyond, in quantitative methods that are relevant to cope with data-driven biology. Systems Biology is such a field that places a particular focus on the functional aspect of biology and molecular interacting processes. This paper deals with the conceptual design of a web-based course and its content for educating students in systems biology. We discuss several learning strategies and problems when dealing with structural hypertext patterns that might occur in the context of web-based learning platforms. Finally, we explain the content of the course modules and its features such as its usability and the impact on the learner.

1. Introduction

Within the last decade, systems biology formed a new and prospering discipline that is about to revolutionize the life sciences [1,2,3]. The novelty of this field is at least twofold. First, it integrates computational, statistical and mathematical methods and applies them to large-scale biological data. Second, it focuses on functional parts of biological organisms rather than on individual genes or proteins and properties thereof. Hence, it resembles a quantitative systems approach [4,5] that promises to reveal molecular and cellular causes of biological processes, but also the pathogenesis of diseases [6,7,8].

From an educational point of view, the appearance of systems biology requires a curriculum that equips students with knowledge and skills that enable them to conduct research in this area. Despite the fact that systems biology focuses on biological problems, traditional courses in biology or the biomedical sciences largely neglect a quantitative education of statistical, computational and mathematical methods that are vital to systems biology. This inevitably leads to quite large deviations of a curriculum for systems biology compared with these traditional fields. For example, [9] proposes a biology curriculum to be divided into two major parts, namely a compulsory part and an elective part. The compulsory part contains topics such as “Cells and Molecules of Life”, “Genetics and Evolution” and “Health and Diseases” [9]. In contrast, the elective part contains themes like “Applied Ecology”, “Microorganisms and Humans”, and “Biotechnology” [9]. Indeed, the just mentioned topics are clearly of non-mathematical and non-quantitative nature and, therefore, not sufficient to educate students in systems biology. Hence, we suggest an adequate curriculum for a web-based course for learning systems biology, see Section 5.2.

The recognition of the aforementioned problem is not new [10]. However, what is less clear is the way these students should be taught and educated in this direction. An issue complicating this endeavor is that biology students have frequently different expectations with respect to the way they expect to be taught quantitative methods. This can metaphorically be described as “spoon-fed”. The problem is that no mathematical, statistical or computational methods can be learned this way. Instead, these fields can and should be perceived as languages and the goal is to learn to “speak” in them by making creative use thereof. Another kind of evidence for the abovementioned arguments to set up a web-based course for learning systems biology stems from the recent results achieved in inquiry-based learning [11,12]. This method, somewhat related to active learning, includes approaches to promote the learning of scientific concepts from a scientist point of view, see [11]. For instance, important and recent development on inquiry-based learning can be found in [11,12]. If compared with classical learning approaches, the just mentioned inquiry approach is more focused on the learning content itself for developing concrete problem-solving skills on the subject. Consequently, inquiry-based learning could provide positive arguments to teach quantitative, statistical, computational and mathematical methods for learning systems biology in a web-based manner as those topics are very problem and skill-oriented.

The aim of this paper is to present the conceptual design of a web-based course that could be used as the core of a systems biology curriculum. This course, and accompanying tutorials, will provide the necessary mathematical, statistical and computational methods for students originally trained in the biological or biomedical sciences. This is a challenging problem since students with graduate or post-graduate qualifications in biological subjects may have little or no training in the abovementioned quantitative subjects.

To better highlight the structure of the paper, we briefly sketch the multifaceted topics we want to deal with:

• Learning strategies.
• Mathematical aspects of web-based learning systems.
• Graph-theoretical aspects of hypertextual learning patterns.
• Theoretical aspects of e-learning platforms.
• Educational details of the web-based e-learning platform.

The paper is organized as follows. Besides the introduction, we give some details about learning strategies necessary to tackle our problem in the Section 2 . Because we deal with web-based learning platforms, it is important to outline some facts about hypertext and graph-theoretical properties of hypertextual learning patterns. We provide a short review of such techniques in the section “Hypertext Learning and Graph-theoretical Aspects”. In the section “Aspects of E-Learning Platforms”, we also present some aspects of e-learning platforms that are helpful for a better understanding of web-based learning platforms. Detailed aspects of the learning platform will be discussed and assessed in the section “The Web-based Learning Platform”.

2. Learning Strategies

Teaching students knowledge and skills about a quantitative subject area, for instance statistics, mathematics or physics, is in general a very difficult task. For this, a learning strategy [13] needs to be chosen that represents a technique to achieve the learning objectives. From an abstract point of view, the overall problem relates back to the basic understanding of the cognitive abilities of the brain and its neuronal architecture in processing signals and performing actions. The principle understanding of the dynamical interplay between sensory processing, memory organization, prediction and action selection mechanism of an animal is a problem that has been studied since many decades [14,15,16,17]. The synthesis of these different components is usually just briefly called perception-action cycle. Despite the fact that this problem is ultimately connected to a neurobiological understanding of the cognitive learning behavior and organization of animals [18], it can also serve as a foundation for students’ education [19,20]. More precisely, the question is how to translate insights gained from studying the perception-action cycle best into the classroom in order to improve the learning outcome for the students in general. In this section we describe briefly the principle working mechanism of the perception-action cycle and outline a web-based learning platform that utilizes important elements thereof. These insight translations or learning strategies [13] are different schemes by which the usual multidimensional aspects of a topic are linearized into the one dimensionality of the time and the result is the sequence or, in web terms, navigation a learner takes through the learning materials.

2.1. Principle Outline

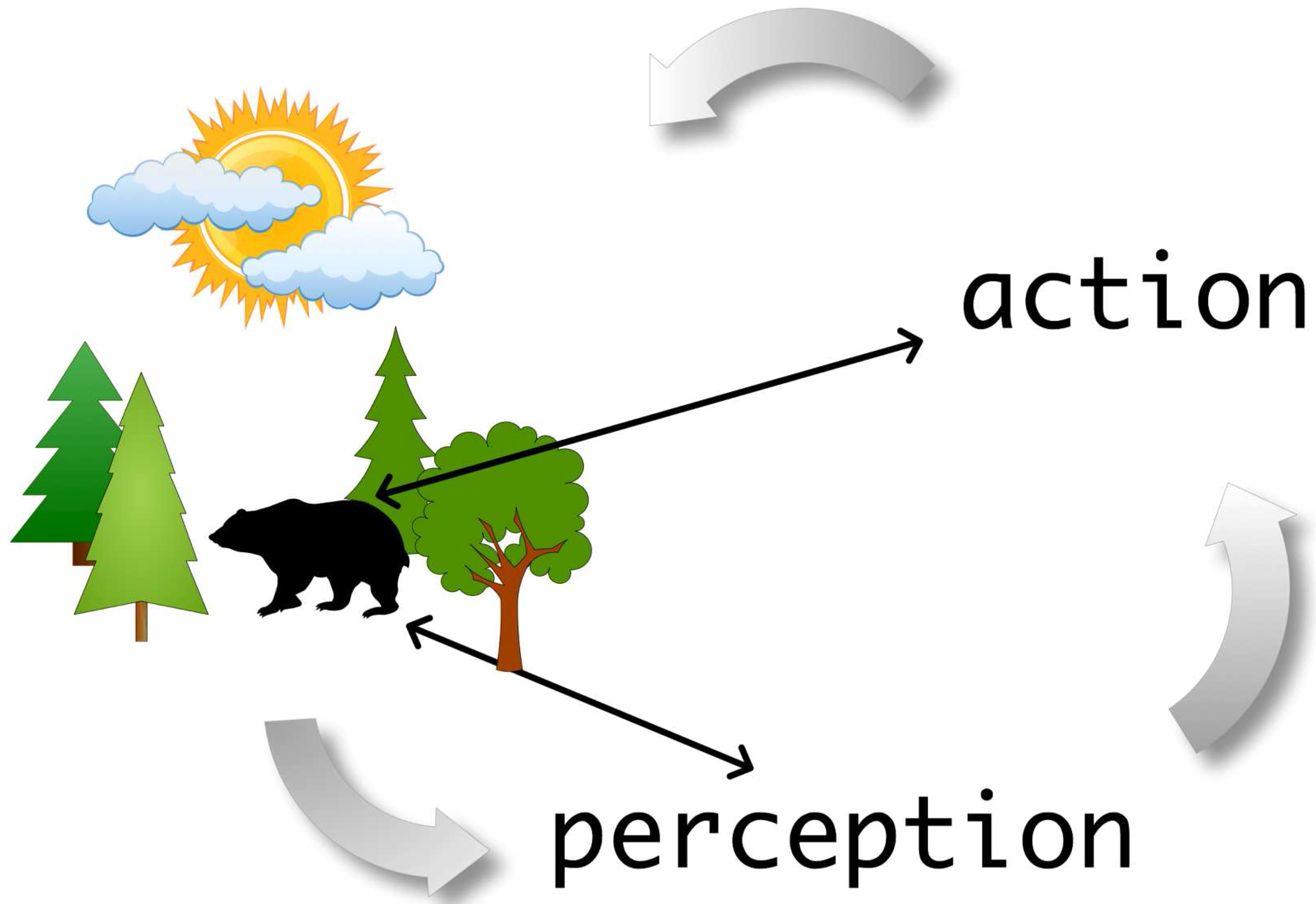
In Figure 1 we visualize the perception-action cycle schematically. The general idea is to describe the dynamical interplay between the perception of an individual in its environment, which results in the selection of an action (e.g., a certain movement) that in turn results in a new perception because the action of the animal has an influence on the environment of the individual. The difficulty of the perception-action cycle lies in the fact that neither are perceptions mapped to actions nor are actions mapped to perceptions, but every component is integrated in an endless circle without clearly distinguished beginning and end [14]. One aspect of the problem we encounter due to this cyclic behavior is that a tiny uncertainty at each step amplifies asymptotically to unbounded large values. Another aspect of this problem is visualized in Figure 1. Here we embedded an individual in an environment. However, this individual is also part of the abstract perception-action cycle, which could be perceived as the animal being an external observer of the scenario (black arrows). The above problems have been studied extensively and are well known in the literature.

Figure 1. Visualization of the perception-action cycle. Here the animal is not only part of the environment but also part of its perception-action cycle.

Figure 1. Visualization of the perception-action cycle. Here the animal is not only part of the environment but also part of its perception-action cycle.

Apparently, the active involvement is key in order to complete a cycle between two consecutive perceptions. In this paper we are not concerned with novel interpretations of the perception-action cycle in an educational context but with the question of how to utilize best a web-based system in order to integrate the learning cycle.

In general, we need to distinguish between two principally different aspects of educational components. One relates to the knowledge of a subject and the other to the skill set. Learning and teaching about knowledge is more straightforward than acquiring skills because the former relates to a mere reproduction of knowledge. In contrast, learning skills, which utilize and possibly transform knowledge, is generally considered more difficult. In a simplified form, knowledge learning has resemblance to an input-output mapping relating for instance a question to an answer. On the other hand, skill learning has a closer resemblance to the perception-action-cycle because it is a chain of abstract interactions with a problem. For this reason, we focus specifically on the skill learning aspect of systems biology.

3. Hypertext Learning and Graph-Theoretical Aspects

From a computer science oriented perspective, this paper has strong links to hypertext learning [21,22,23] because web-based learning patterns can often be considered as hypertext structures [24]. Major questions in this area deal with analyzing formal and technical aspects of hypertext systems [25,26,27]. We now start from the assumption that a learner acquires knowledge by using a web-based system whose patterns represent hypertexts (or more generally speaking hypermedia (Note that the term hypermedia is often used when multimedia objects such as graphics, audio and video are linked in a non-linear way [28]. However, for the sake of simplicity, we here subsume hypermedia under hypertext.)). In brief, classical hypertext is broadly understood as non-linear text [29,30] where textual units represent vertices that are connected by hyperlinks forming a directed network. We emphasize that such a graph can be understood as the underlying hypertext structure [24,31].

A crucial question when using a hypertextual environment is to investigate typical features of hypertext during the process of acquiring knowledge by a learner [22]. By taking into account that the most significant feature of a hypertext is its non-linearity [22,29,30], it is indeed important to examine how such a non-linear structure alters the mental representation or behavior of a learner when acquiring or using new knowledge, see [22]. In this context, it has often been assumed that the non-linearity leads to a larger flexibility when accessing information that might be beneficial for human learning [22,23]. We emphasize that the educational impact of hypertext learning has been investigated by performing studies using concrete hypertexts [23,32]. Among the questions examined in these studies, an important problem is to explore which structure is best for the learner [22].

A similar research question is the well-known lost in hyperspace problem. It deals with the question of how a learner navigates through a hypertext for acquiring knowledge optimally, see [23,33,34,35]. Note that there is a considerable body of literature for tackling this problem, see, e.g., [33,34,35,36,37]. For instance, graph measures [24,34,38,39] have been developed to determine the accessibility or influence of certain vertices in a given hypertext structure [33,34,35,36]. Further, other graph measures have been used to characterize hypertext structures globally [34] and to investigate typical structural features of hypertext structures such as linearity [34]. Another question in this area is to evaluate to what extent the underlying structure is hierarchical [34,40]. In this context, Shapiro [40] tackled a special problem, namely how relevant are hierarchies to information processing when learning biology. Other concrete studies for exploring related problems can be found in [23,41]. 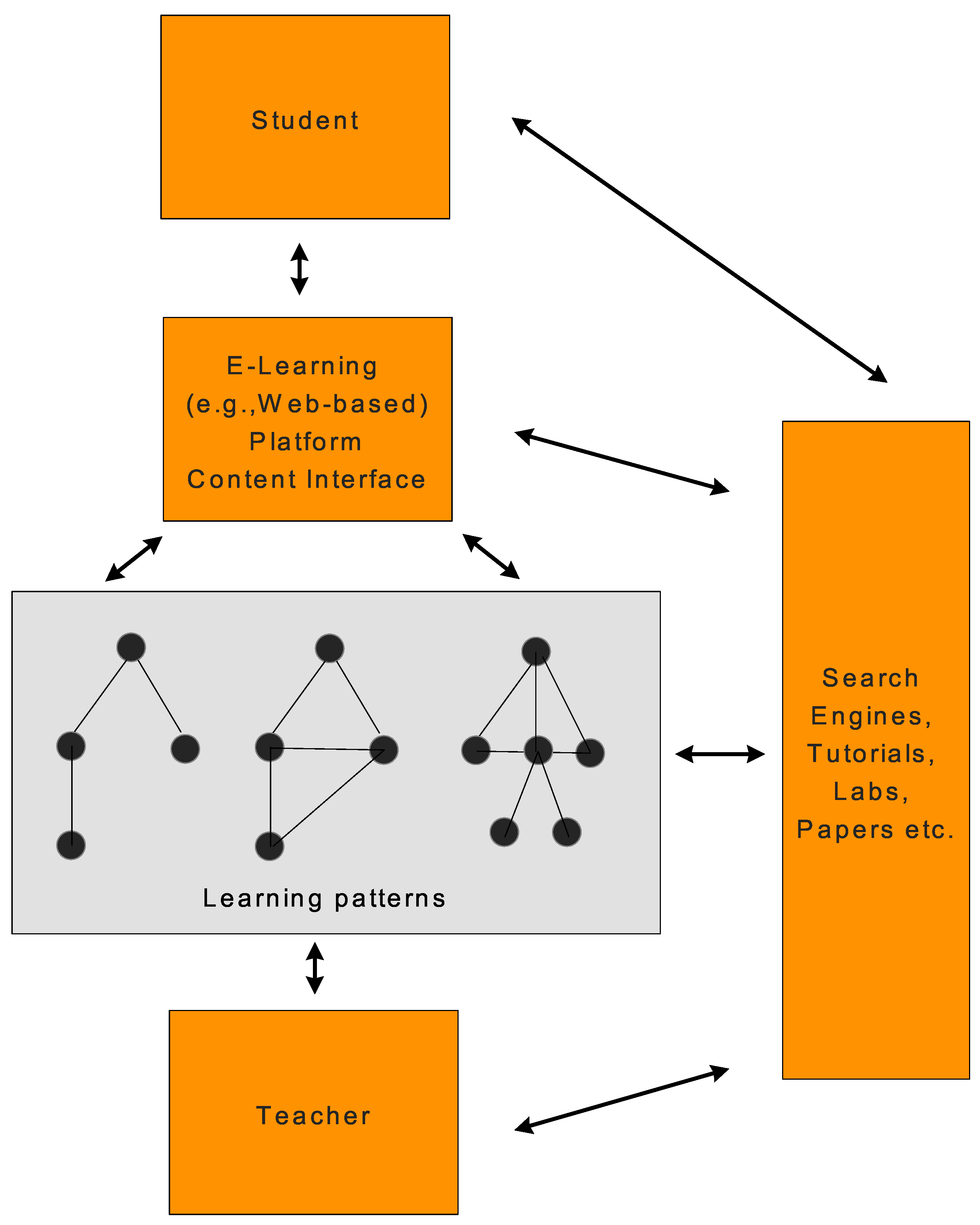Figure 2 shows a simplified environment of an e-learning system whose learning patterns represent graphs [42]. The Learning Strategies concept will play a key role by leveraging the already known set of navigation graphs that such strategies define, upon which further learning of actual learner behavior (navigation in our case) can help further tailoring the learning experience.

Figure 2. A typical e-learning environment dealing with graph-based patterns.

Figure 2. A typical e-learning environment dealing with graph-based patterns.

4. Aspects of E-Learning Platforms

As known, various definitions of e-learning have been developed [43,44], but in this paper we want to consider e-learning in the sense of Baumgartner et al. [43] who understand it as a general term for software-supported learning. When using this definition, it is evident that the outward appearance of learning devices does not matter because we could consider a wide range of such learning devices that are suitable for a problem, such as computers, mobile phones, etc. [43]. Further, e-learning could be considered as a kind of flexible learning [43] by using appropriate technologies expressing that the learner is independent of special qualifications, space and time [43]. In order to get an idea regarding the functionality of web-based e-learning platforms [43], we provide the following listing containing the most important functionalities [43,44]:

• Ways of communicating among learners and between students and tutors using email, news groups, chat, forum, etc.
• Tools for learners, e.g., full text search within course materials, possibility to add annotations, possibility to create an individual learning environment, etc.
• Authoring tools such as web editors, modular design of course materials and development of animations using programming languages, etc.
• Adopt a recognized standard such as SCORM to organize and distribute the learning materials.
• Individual tools: Data management, appointment schedule, working schedule, address book etc.
• Database connections to libraries or other institutions for storing and processing the data.

In view of the numerous learning platforms [43,44] that have been developed so far, the selection process of a concrete platform fulfilling the needs of a learner as well as tutor is an outstanding problem. Hence, it is crucial to find criteria that might be useful for selecting a concrete e-learning platform. We list some principal aspects divided into four categories as follows [43]:

• Composition of basic functionalities and desired operational area:
  • Necessary and optional functions of the platform.
  • Mission scenario: goals, requirements, individual wishes of tutors and learners, etc.
  • Service ability and usability.
• Review of special and individual requirements:
  • Hardware, software, administration, system integration.
  • User interfaces: layout, languages, functions, etc.
  • Cost factors.
• Decision making:
  • Acquirement of a commercial learning platform using an own server.
  • Acquirement of licenses from special service provider.
  • Using learning platforms that are free of charge.
  • In-house development of learning platforms.
• Non-technical factors of influence such as individual attitude and values of an institution, tutors, etc.

We emphasize that selecting a web-based learning platform for a particular problem may be challenging. First of all, this depends not only on the needs of a learner but also on the learning strategy [13] we want to apply, see Section 2. However, it is a fact that developments in e-learning have led to an enrichment of known learning methods and strategies [45].

5. The Web-Based Learning Platform

5.1. Course Design

The aim of the proposed paper is to provide an outline of a course that is focused enough to efficiently communicate skills and techniques necessary to embark on research in systems biology yet wide enough to offer students with diverse background and skill levels the opportunity to find the right entry point to the subject. In order to achieve these two counteracting goals, we designed the structure of the course hierarchically, consisting of three different levels. In the following, we briefly describe these three levels and their connections. The section “Course content” and “Usability” provide the details for the occurring modules and their interfaces.

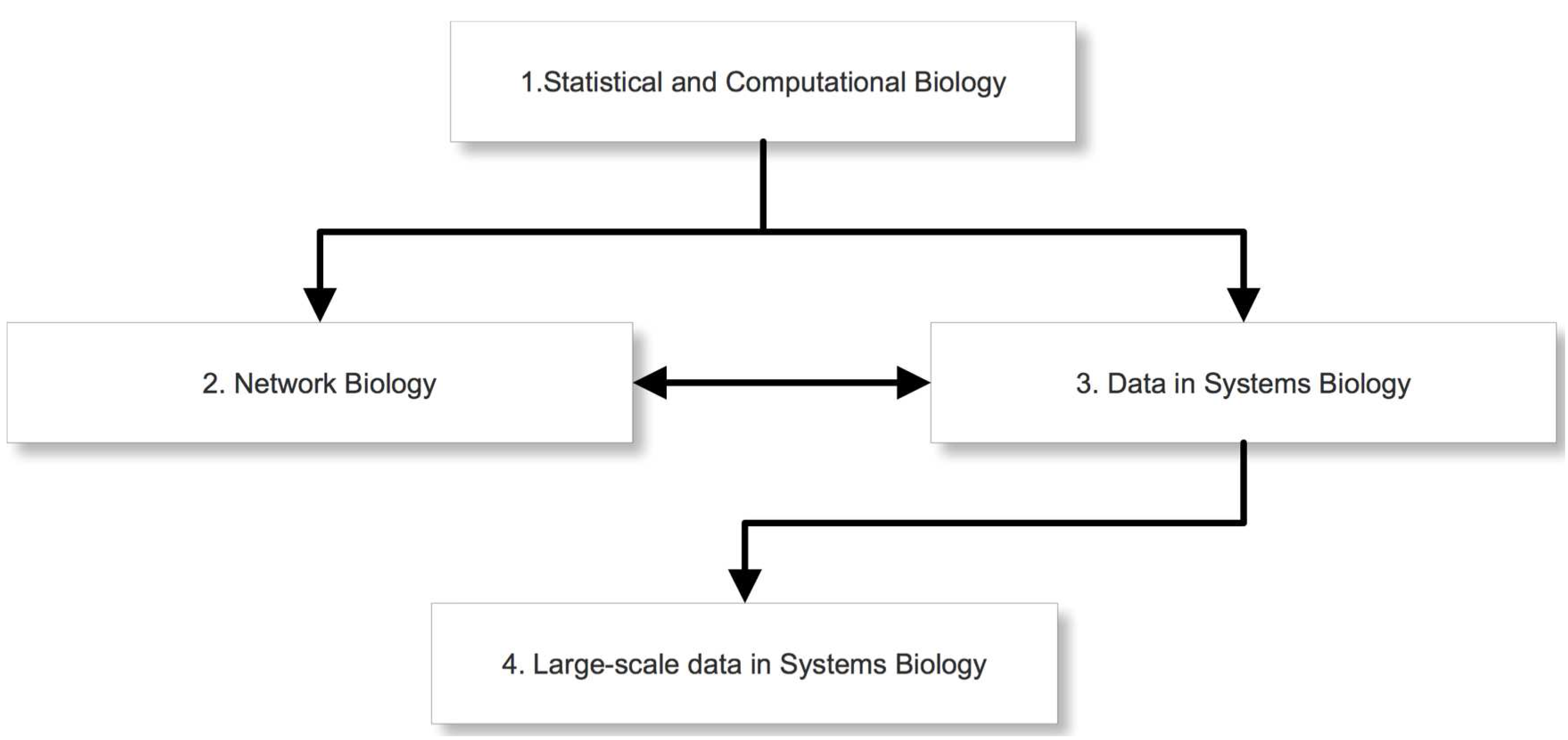
In Figure 3 we show a schematic outline of the overall design of our course. On the first level is module 1. This module will provide mathematical and statistical basics necessary to understand, in order to study problems in systems biology. The difficulty level of this module will be appropriate for students without prior training in the topics covered by this course. Especially for students without background in quantitative sciences of any kind, this should provide an opportunity to “catch up” regarding the essential mathematical and statistical skills. On level two we provide two modules. Module 2 covers the meaning and usage of various biological networks, as well as databases providing information about such networks. Module 3 discusses different high-throughput data and analysis methods. Both modules will be on an intermediate level understandable for students that either already have a background in mathematical and statistical methods or have attended successfully module 1 of our course. Module 2 and module 3 can be attended in arbitrary order because their topics are complementary to each other. Finally, on the third level we provide module 4. This module continues the topics covered in module 3 by providing advanced analysis methods for large scale high-throughput data. In order to profit fully from this module, students need to be familiar with basics of microarray data and applied statistics. For this reason, the difficulty level is higher than for the other modules.

Figure 3. Visualization of the content of the four modules.

Figure 3. Visualization of the content of the four modules.

Each of the above four modules will be accompanied by an on-line message board configured for tutorial style, student–tutor and student–student, interactions. These tutorials will allow the students to address specific or general problems they encountered while working through the modules, posting messages, code examples, data queries and images for the entire “class" to read.

The course will use entirely web-based media to deliver its content. Each module will have the following learning components.

• A text-based explanation of the course material in combination with multimedia illustrations, including pictures, video and animations to support the underlying text and enhance the learning experience.
• Each module will be accompanied by instructional video lectures in sync with presentation slides.
• Each of these components will be followed by self-assessment questions on the presented material.
• Development of programming skills by solving practical problems. Source code examples will be provided.
• A complete glossary of searchable keywords will allow a targeted selection of specific topics.

All web pages will have the ability to switch on keywords that exist in the glossary with mouse over definitions available.

5.2. Course Content

Module 1—Statistical and Computational Biology: In module 1 the students without a solid background in mathematics and statistics will receive an introduction to important topics necessary for Systems Biology. Basic analysis, linear algebra, statistics, network theory, differential equations and an introduction to the R programming language will be provided [46]. This should generate the general awareness by the students that regardless of the specific scientific questions one is working on, a computational component is always involved. Hence, mathematical and statistical basics are presented and examples involving programming are used to connect both skill sets seamlessly. Motivating examples are taken from modules 2 to 4 in order to demonstrate the utility and power of the discussed methods.

Module 2—Network Biology: Module 2 explains the students what Systems Biology is actually about. In order to communicate this in a clear way, various biological networks are introduced and explained [1,47]. For example, protein networks, transcriptional regulatory networks and metabolic networks are covered and their relation to molecular biology is established. In addition, the dynamic modeling of molecular processes (e.g., transcription regulation) is discussed. This will create an awareness of the fact that molecular processes are dynamic rather than static in time. From a methodological point of view, the students will extend and apply their knowledge in network theory and programming [48]. In addition, they will become familiar with databases and their usage, which can be used, e.g., to construct some of the discussed biological networks. Databases covered include BioGrid, BioCyc, DIP, IntAct, GO, Mips. Students will learn about basic database management and become familiar with several R packages that allow the access and manipulation of data in these databases.

Module 3—Data in Systems Biology: In module 3 important high-throughput data are discussed. These include data from microarray, proteomics and ChIP on chip experiments. It will be emphasized that these data allow a practical approach to Systems Biology studying molecular interactions on a genomic scale, and are hence vital for the successful translation of theoretical hypothesis into practical results. The basics of complex diseases such as cancer or cardiovascular disease are also discussed and contrasted to monogenetic diseases. The methodological skills that the students learn and extend include methods for an exploratory as well as confirmatory statistical analysis of data, e.g., hypothesis testing, multiple correction procedures, multivariate analysis, clustering, dimension reduction methods [7,49,50,51]. This will be complemented by various means to visualize these data. All methods will be discussed not only theoretically but also practically by providing source code in R demonstrating the various aspects of the discussed topics.

Module 4—Large-scale data in Systems Biology: Module 4 provides an extension of the topics from module 3. Its main purpose is to provide additional analysis methods that are appropriate to analyze large-scale high-throughput data from microarray experiments. Specifically, methods to detect pathological pathways from complex diseases are discussed. Also, approaches to infer regulatory networks from experimental as well as observations data are treated. Methodologically, advanced statistical analysis methods are discussed, including time series analysis and causal inference [7,52,53]. All methods are again discussed and used in the context of the R programming language, allowing to gain additional experience with this programming language.

5.3. Usability

In this section we describe various ways the course may be used in order to allow the largest gain for the students. These scenarios distinguish between different backgrounds of the students.

Scenario 1: The following outline of modules to attend is for students without prior knowledge in mathematics and statistics. For such students it is recommended to start with module 1, which will equip them with the necessary theoretical basics necessary to work on problems in Systems Biology. After module 1, either module 2 or module 3 can be attended. Both modules are on the same intermediate level covering complementing topics. Module 4 represents an advancement to module 3 and it is recommended to attend module 3 as preparation for this module. Overall, three courses are possible, $1\to 2\to 3\to 4$ or $1\to 3\to 2\to 4$ or $1\to 3\to 4$ (the number refers to the number of the module). The course $1\to 2\to 4$ is not recommended because students entering module 4 would not have the necessary basics with respect to the microarray technology, respectively the data resulting from such experiments.

Scenario 2: This course outline is for students familiar with basic mathematical and statistical methods, as covered in module 1. In this case, students may enter either module 2 or 3 directly without attending module 1 first. This results in the following three courses, $2\to 3\to 4$ or $3\to 2\to 4$ or $3\to 4$ (the number refers to the number of the module).

Scenario 3: Students that are already familiar with the mathematical and statistical methods needed to work on problems in Systems Biology and additionally have experience with data from microarray experiments may directly attend module 4. Not only is module 4 presented on an advanced methodological level, but also the biological topics covered are currently extended and improved almost annually. Hence, these topics are at the forefront of contemporary research within systems biology.

5.4. Assessment

The above outline of the modules and their usage corresponds to a sensible organization of a web-based course in systems biology. However, there are certainly alternative formulations possible that may be equally appropriate or even better adapted to the needs of the students. In order to find an optimal course design, it would be necessary to perform comprehensive tests involving students and the assessment of their performance. This would allow to obtain unambiguous information about differences in the course’s structure. In Section 3, we outlined graph-theoretical methods from hypertext learning. Here, we argue that those can be employed to analyze and optimize the design of a web-based course. Once we consider websites within the web-based learning system as hypertext structures, we may use methods from quantitative network analysis [54] to explore the underlying structures (graphs). However, note that the problem of mapping web pages or websites to graphs is not unique and several methods have been proposed to do so [31,55]. After deriving the hypertext graphs, concrete problems to use this apparatus would involve investigating navigational paths induced by different learners. Thus, strategies could be derived whose navigational paths are optimal for a particular learner. For instance, a linear path structure could be best for a learner possessing lower prior knowledge, whereas a hypertext graph structure with higher connectivity (hypertextual paths) could be a better fit for a learner possessing higher prior knowledge. Besides, corpora of graph-based learning patterns characterize the usage of certain course layouts, which may allow to detect the under- or overrepresentation of specific course topics and thus contribute to improve the quality of a web-based course.

For instance, it could be interesting to determine which navigational paths are recommended for which learner (e.g., linear, well-structured for low-achievers/lower prior knowledge, more hypertextual paths for high-achievers/higher prior knowledge).

6. Conclusions

In this paper, we investigated the conceptual design of a web-based course for educating students in systems biology. We started by discussing learning strategies to root our problem theoretically. Then, we briefly explained some interrelations between web-based learning systems and hypertextual (learning) patterns representing graphs. Because one can infer graphs from web pages, websites or usage pattern, see [31], several methods have been explored for investigating the relatedness between structural features of hypertext patterns and the behavior of a learner. In the future, it might be interesting to examine such graphs when using a concrete platform to implement our proposed modules. A typical problem would be then to evaluate certain features of hypertextual patterns such as linearity or hierarchy types and correlate them to other characteristics appearing while learning (e.g., learning performance). As mentioned, future attention should also be drawn to perform tests for assessing the performance of students when using the proposed modules. Moreover, tests will be needed to tackle the challenging problem of choosing a specific web-based platform that is best for the learner and our particular problem area.