Preservice Secondary School Teachers’ Knowledge and Competencies When Reflecting on the Incorporation of Gamification in the Teaching of Mathematics

Abstract

This study analyses how preservice mathematics teachers reflect on the incorporation of gamification in their teaching practices after participating in a training cycle focused on this active methodology. The cycle, applied to 31 students in the Secondary Mathematics Teacher Education Master’s programme in Catalonia, integrated game elements—such as narratives, quests, and badges—alongside the Didactical Suitability Criteria as a tool for developing competency in the analysis and evaluation of didactical suitability. The reasons preservice teachers provided for using gamification in mathematics teaching were analysed at two points: upon completing the training cycle and after implementing teaching proposals incorporating gamification with secondary education students in Catalonia. The results show that preservice teachers show an improvement in their reflective competency regarding gamification, as well as increased use of this active methodology. Additionally, the knowledge and competencies considered relevant by preservice teachers for working with gamification in mathematics teaching were identified. It is concluded that training in the use of gamification in mathematics teaching is necessary to apply this methodology appropriately, and that tools such as the Didactical Suitability Criteria are fundamental for reflection on, and improvement in, the use of active methodologies.

1. Introduction

Currently, education is characterised by constant social and technological changes, which demand a variety of competencies from individuals, including proactivity and reflection for decision-making. For educational systems to be able to adapt, it is necessary to adopt innovative methodologies that promote active learning (Franco-Segovia, 2023). For this reason, gamification emerges as an active learning methodology—in which students participate in the organisation and development of their own teaching and learning process (Jiménez Hernández et al., 2020, p. 77)—which uses the mechanics, aesthetics, and mindset of games to motivate students to solve problems (Kapp, 2012). Naseri et al. (2023) found that the integration of gamified elements in educational contexts fosters student engagement, enhances motivation, and therefore promotes learning, aligning with the perspectives proposed by Kapp. Similarly, Koch et al. (2025) reported that gamification not only strengthens students’ motivation and engagement but also supports more effective collaborative work. Moreover, recent evidence shows that gamification can promote educational inclusion; for instance, Ortiz-Panata et al. (2025) demonstrated that gamified strategies make learning more accessible and motivate students with special educational needs.

Font (1994) points out that motivation is one of the main challenges in the teaching and learning of mathematics. According to Bishop (1999), game, as a motivating element, has accompanied the practice of mathematics throughout history, and is therefore considered a key component in its teaching. Various psychopedagogical theories highlight the value of play in the teaching and learning process (Cornellà et al., 2020), as it promotes engagement and the development of skills (Hassan & Hamari, 2020). In that sense, a playful approach can improve academic performance by fostering motivation and meaningful learning (Pujolà, 2024). In particular, gamification, as a playful methodology, seeks to influence motivation through making the user the centre of any gamified activity (Ripoll, 2014).

In an analysis of the state of the art conducted by Swacha (2021), it is identified that scientific production in the field of gamification in education began to grow significantly starting in 2013; nevertheless, Mula-Falcón et al. (2022) explain that the literature does not present conclusive findings. As highlighted by Piñero (2020), this is a quite recent methodology, and there is still limited empirical evidence to support its effectiveness in learning.

Various authors (Delgado Palacios et al., 2022; García Collantes, 2020; Holguin García et al., 2020) have reported benefits in the development of mathematical skills thanks to gamification. However, Araya et al. (2019) evidenced an increase in anxiety and aversion to teamwork, and Reyssier et al. (2022) found that students began to see the exercises more as a game than as a serious learning activity and that gamified systems based on social comparison like rankings and scores are harmful to certain students’ motivation. Not only are there drawbacks about students’ behaviour in the literature, López et al. (2021) found that teachers did not use gamification due to a lack of resources. This can be explained by findings from some studies, such as those by Malvasi and Recio Moreno (2022) and Ortiz-Mendoza and Guevara-Vizcaíno (2021), which reveal that the effective implementation of gamification is limited by a lack of proper training in this methodology. Although the results obtained by Jiménez et al. (2020) encourage the application of gamification when learning algebra, they also found that the preparation and execution of these techniques require the teacher to invest more time and dedication. For these reasons, specific training for teachers is necessary to ensure that gamification tools are used appropriately.

In the Interuniversity Master’s in Secondary and Baccalaureate Teacher Education in Catalonia (Spain), within the module on Teaching Innovation and Introduction to Educational Research in Mathematics Education, mathematics preservice teachers acquire competencies in reflecting on the didactical suitability of mathematics teaching and learning processes through the unit “Tools to analyse the quality of didactic proposals”, and knowledge about gamification methodology in the units on “Manipulative and TAC resources”. The latter uses practical activities and resources such as GeoGebra, Genially, and Scratch (Font, 2024), with the aim that students will be able to design and implement didactic sequences that integrate this methodology into their pre-professional practice and, subsequently, reflect on its application in their Master’s Final Projects (MFP).

Previous studies (Cortés et al., 2024a, 2024b, 2026) analysed the MFP of 318 master’s students, revealing limited knowledge of gamification among preservice teacher (PT) participants, who mainly used it for motivational purposes. It was also observed that, along with statistics and geometry, algebra was one of the subjects in which PT participants most frequently applied gamification in the design and redesign of didactic sequences. Subsequently, the (Cortés et al., 2025) analysed the impact of gamification on the didactical suitability of the teaching and learning process in algebra and explored the reasons why PT participants used it, finding that this discipline is particularly well-suited to a gamified approach due to its syntactic–semantic duality.

This study presents the design and results of a training cycle (TC) aimed at gamifying the Manipulative and TAC resources units of a Master’s in Secondary Education with a specialisation in mathematics. Its objective is to train preservice teachers (PT) to implement the gamification methodology in the teaching–learning process of mathematics with students in secondary education.

The design of the TC was justified by the preservice teachers’ (PT) limited knowledge of gamification, the incorrect use of the term, the lack of reflection on mathematical quality when applying it, and the low proportion of teachers who implement it (Cortés et al., 2024a, 2024b, 2026).

The main objective of this study is to analyse how preservice teachers (PT) of mathematics in secondary education, who are participants in a master’s programme and a training cycle (TC) on gamification, incorporate this active methodology prior to the design, and during the design, implementation, and redesign, of didactic sequences, based on the justifications provided at two points in time: at the end of the TC and after the implementation of didactic sequences that include gamification elements with secondary education students in Catalonia, as documented in their Master’s Final Projects (MFP). Additionally, the study aims to infer the knowledge and competencies acquired by the participants, in particular the development of subcompetencies in analysing and evaluating didactical suitability, and how this development influences the aspects that PTs consider relevant when integrating gamification into mathematics teaching. Therefore, the following research questions are defined:

• To what extent does a gamified training cycle contribute to preservice mathematics teachers’ ability to incorporate gamification into their didactic proposals?
• Which arguments do preservice teachers give when justifying the use of gamification and what does this reveal about the development of their reflective competencies based on the Didactical Suitability Criteria?
• How do preservice teachers’ arguments about gamification evolve between the initial reflection after the training cycle and the subsequent redesign documented in their Master’s Final Projects?

1.1. Gamification

In this study, to define what gamification is and to differentiate it from other game-based methodologies, the definition of Deterding et al. (2011) is adopted, who conceive it as “the use of game design elements in non-game contexts” (p. 13). This definition implies that it is not necessary to use digital resources to gamify, and that gamification does not require the use of games, thus avoiding confusion with other methodologies, such as game-based learning. In this way, the authors emphasise that gamified contexts are independent of the objective and the means used to implement the activity, allowing the same activity to be gamified for different purposes (learning, motivational, social, etc.) and through various strategies.

Based on this definition, the present study distinguishes between gamified activities and those that do not use game design elements, even if they incorporate playful aesthetics or dynamics. This means that the use of manipulative materials or playful visual resources intended to capture students’ attention, but which do not integrate elements inherent to games, is not considered gamification (Torres-Toukoumidis & Romero-Rodríguez, 2019).

Gamification is distinguished from game-based learning as it involves the use of game design elements in non-game activities, whereas game-based learning employs complete games for educational purposes (Cornellà et al., 2020). Unlike platforms such as Kahoot!, which operate as closed game systems with predetermined rules and mechanics and limited adaptability to the context, gamification allows for the design of activities incorporating elements such as points, challenges, narrative, or levels, enabling greater customization by the teacher (Balaskas et al., 2023; Dellos, 2015). To categorise the game elements applicable to the design of gamified activities, Werbach and Hunter (2015) propose a model structured into three hierarchical levels (Figure 1).

Dynamics represent the overall vision of the game and constitute the most abstract level, integrating the most general aspects that guide participant motivation. Mechanics, in turn, describe the functioning of the gamified system through the processes that drive action and foster engagement. Finally, components are the visible manifestations for the player and the concrete expressions of the dynamics and mechanics, representing the way in which the user interacts with the gamified system.

In addition to the game elements, Kapp (2012) distinguishes two types of gamification: structural and content-based. Structural gamification involves incorporating game design elements, such as points, badges, or leaderboards, to motivate students to progress through the learning content, without the presence of a unifying narrative; the content remains in its traditional form, and the playful elements act as an external layer, often including progress-tracking tools, social components, and leaderboards. A typical example is awarding points for watching a video or completing a task, where the activity itself remains non-playful, but its completion is rewarded. On the other hand, content-based gamification involves modifying the educational content to make it more game-like, integrating narratives, challenges, simulations, characters, or settings that mediate learning. This does not mean turning the content into a complete game, but rather incorporating narrative resources or game mechanics to contextualise and energise the learning experience, such as presenting a course through a narrative or starting a lesson with a challenge instead of a list of objectives.

Considering these definitions, a third type can be inferred, hybrid gamification, which combines structural elements (points, badges, rewards) with content elements (narrative, setting, content transformation), so that both types of elements complement each other.

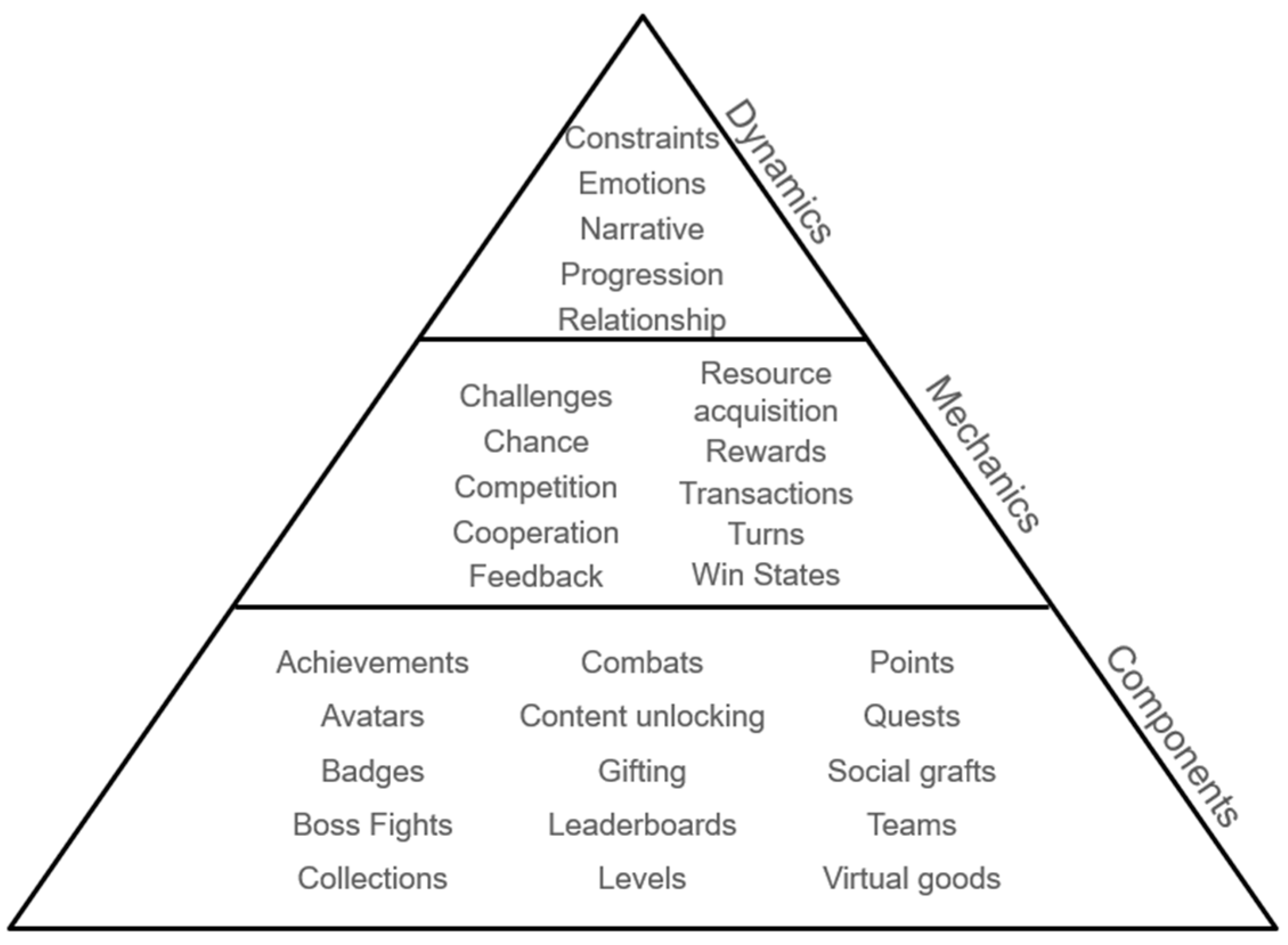
In this study, in addition to the definition of gamification, both the game elements and the different types of gamification were considered in the design of the training cycle (TC) implemented with preservice teachers (PT), considering these as central elements in their training process within the active methodology of gamification.

1.2. Model of Didactic–Mathematical Knowledge and Competencies

Within the theoretical framework of the Ontosemiotic Approach, Pino-Fan et al. (2015) propose a model to characterise teachers’ didactic–mathematical knowledge, integrating contributions from various models of mathematics teachers’ knowledge and using developments from the Ontosemiotic Approach. This didactic–mathematical knowledge model, part of the Didactic–Mathematical Knowledge and Competencies framework, structures teachers’ knowledge into three dimensions: mathematical (knowledge of content), didactic (teaching and learning processes), and meta-didactic–mathematical (reflection on instructional practices). Building on this, Pino-Fan et al. (2023) define two types of teacher competencies within Didactic–Mathematical Knowledge and Competencies: mathematical competency, with subcompetencies in task-solving, problem-posing, and practice analysis; and competency in didactic analysis and intervention, comprising subcompetencies in the analysis of mathematical activity, the management of interactions, the use of resources, and the evaluation of didactical suitability (Breda et al., 2017; Pino-Fan et al., 2023). This study focuses on the latter, specifically evaluating didactical suitability in the context of gamification-based teaching sequences.

Teacher reflective competency manifests at three points: a priori reflection, before the lesson, considering the objectives, methodology, resources, and strategies; in loco reflection, during the lesson, adjusting planning based on students’ responses, engagement, and lesson pace; and a posteriori reflection, after the lesson, identifying strengths and weaknesses to improve future practice. This reflective process addresses questions about the didactical suitability of the implemented processes and the adjustments required to improve instruction. To support this evaluation, the Didactic–Mathematical Knowledge and Competencies model offers the Didactical Suitability Criteria (DSC) as a systemic tool to optimise mathematics teaching.

Didactical suitability is defined as the degree to which a teaching and learning process aligns the personal meanings constructed by students with the intended institutional meanings, given the context and resources (Font et al., 2010). It is a multidimensional construct composed of six criteria, operationalised through components and indicators for each criterion, ensuring the coherent and systematic evaluation of the instructional process (Font et al., 2010).

Table 1. Didactical Suitability Criteria and their components. Adapted from (Ledezma et al., 2024).

Criteria	Conceptualization	Components
Epistemic	Assesses whether the mathematics lessons are of good quality.	− Errors − Ambiguities − Richness of processes − Representativeness of the complexity of the mathematical object
Cognitive	Assesses, before starting the teaching and learning process, whether the topic to be taught aligns with what the students already know, and, after this process, whether the learning achieved approximates the intended outcomes.	− Prior knowledge − Adaptation of the curriculum to the individuals’ different needs − Learning − High cognitive demand
Interactional	Assesses whether the interaction addresses the students’ doubts or difficulties.	− Teacher–student interaction − Interaction amongst learners − Autonomy − Formative evaluation
Mediational	Assesses the adequacy of the material and temporal resources used in the teaching and learning process.	− Material resources − Number of students, scheduling, classroom conditions − Time
Affective	Assesses the student’s involvement (interests and motivation) during the teaching and learning process.	− Interests and needs − Attitudes − Emotions
Ecological	Assesses the adaptation of instructional process to the school educational project, the curricular guidelines, and the conditions of the social and professional environment, etc.	− Adaptation to the curriculum − Intra/interdisciplinary connections − Social-professional practicality − Didactical innovation

, adapted from Godino et al. (2013) and presented by Breda et al. (2017), used in studies like that of Ledezma et al. (2024), outlines these six criteria, their conceptualisation, and their respective components, providing a practical tool for assessing and enhancing didactical suitability.

The components and indicators of the Didactical Suitability Criteria (DSC) were developed considering current trends in mathematics teaching, the principles of the NCTM (2000), and widely accepted research findings in mathematics education. For instance, regarding epistemic suitability, research shows that mathematical objects emerge from practices, reflecting their complexity, which informs the representation of the notion’s complexity to guide teachers in designing and refining didactical sequences. In this way, the DSC provide a consensual tool to structure teacher reflection across various training programmes (Breda et al., 2018), including secondary mathematics teacher training in Catalonia (Cortés et al., 2026; A. Sánchez et al., 2022).

In this study, the DSC fulfil a dual role. The first is that they serve as a tool for preservice teachers undertaking the University Master’s Degree in Teacher Training for Secondary Schools, Vocational Training and Language Centres, Specialisation in Mathematics in Catalonia (Spain), to develop their reflections on practice and, consequently, improve their competencies in the analysis and assessment of didactical suitability (Burgos et al., 2020; Burgos & Godino, 2022). The second role they serve is as an analytical tool—similar to what was achieved in the work of Seckel et al. (2021, 2022)—to study the reflections of preservice teachers at two points in the study: at the end of the TC and after the implementation of didactical sequences that incorporate gamification elements with secondary education students in Catalonia, as documented in their Master’s Final Projects (MFP).

2. Materials and Methods

This section describes the study’s approach; the training context of preservice teachers taking an Interuniversity Master’s in Secondary and Baccalaureate Teacher Education in Catalonia, particularly the TC regarding the incorporation of gamification in the teaching of secondary mathematics; the data used in the research; and the analytical treatment of these data.

2.1. Study’s Approach

This study adopts a qualitative and interpretative approach, focusing on the analysis of the reflective practices of secondary mathematics preservice teachers within the framework of a TC designed to promote the incorporation of gamification in mathematics teaching. The TC was implemented in the Interuniversity Master’s in Secondary and Baccalaureate Teacher Education in Catalonia (España) during the 2024–2025 academic year. Thirty-one preservice teachers participated in this TC, of whom thirty submitted their MFP.

2.2. Teachers’ Reflection in the Master’s Programme Focusing on the Gamified Training Cycle

The Interuniversity Master’s in Secondary and Baccalaureate Teacher Education is a professionalising master’s programme that, over the course of one year, trains preservice secondary mathematics teachers in the geographical area of Catalonia (Spain) for the teaching profession.

Among the compulsory subjects that make up the master’s, the module on Teaching Innovation and Introduction to Educational Research in Mathematics Education focuses, among other aspects, on (a) training PTs in reflecting on mathematics instruction processes and (b) training PTs in the use of manipulative and TAC resources and reflecting on their use in mathematics education. Finally, the knowledge acquired is documented in the MFP, the final subject of the programme.

The training of PTs in reflecting on their teaching practice is carried out in the block Tools to analyse the quality of didactic proposals. For this purpose, the DSC are treated as content to be taught, with the aim of using them as a guide to organise reflection on the teacher’s own practice. Rather than presenting the DSC as pre-established principles, spaces are created for their generation as a result of group consensus (Font et al., 2024), according to the following sequence:

(a)

Case analysis (without theory): Students are asked to read and analyse classroom episodes, making an assessment based on their prior knowledge without being provided with any guidelines.

(b)

Emergence of different types of didactical analysis (descriptive, explanatory, and evaluative): The sharing of analyses conducted by the different groups allows for observations of how the whole group considers these three types of didactical analysis, even though each group only addresses some of them.

(c)

Trends in mathematics teaching: The analysed episodes were selected so that participants implicitly apply some of the current trends in mathematics teaching (Breda et al., 2018). Then, participants are shown any of the trends that were used implicitly.

(d)

Theory (suitability criteria): The next step is to comment that, in mathematics didactics, different authors have made attempts to compile criteria to guide teachers’ practice so that it is of high quality (Charalambous & Praetorius, 2018; Hill et al., 2008; Prediger et al., 2022), and to note that one of these compilations is the DSC construct. It is explained that the DSC should be understood as principles emanating from the argumentative discourse of the educational community, oriented towards achieving consensus on what can be considered best practice. It is also explained that, for the development of the didactic suitability construct, current trends in mathematics teaching have been considered (NCTM, 2000), as well as principles and the contributions of different theoretical approaches in the area of mathematics didactics (Breda et al., 2018; Godino et al., 2013).

(e)

Read and comment on parts of some MFPs from previous courses in which the PTs used the DSC to assess the didactic sequence they implemented.

(f)

In the Internship and Master’s Final Project subjects, students use the DSC to assess their own practice, specifically the sequence they have designed and implemented. They are required to conduct a redesign and improve the aspects indicated in the assessment that can and should be enhanced.

The training of PTs in the use of manipulative and TAC resources is carried out in the Manipulative and TAC resources blocks of the Teaching Innovation and Introduction to Educational Research in Mathematics Education module. In this study, the implemented TC gamified these blocks with the aim of promoting the use of gamification among PTs through the methodology itself, with to the aim of enhancing didactical suitability of the teaching–learning process in mathematics. For this reason, in the design of the TC, the DSC were also considered, in addition to the game elements and the different types of gamification.

As an example, in the activity “Girl Scouts Cookie Sale” (original activity by Meyer, 2016a), PTs were shown a video of a car whose boot gradually filled with boxes of cookies. Based on this scene, they were presented with a challenge. Following the three-act structure, PTs were required to carry out the following actions:

Act 1: In the first act, a situation was presented that allowed the PTs to formulate questions, where no specific data were provided, and the PTs were encouraged to ask the questions themselves and begin to obtain a solution strategy. The PTs were asked to autonomously formulate the main question of the problem: “How many boxes fit in the trunk?” (Figure 2). In this act, it was anticipated that other questions might emerge, and it was the TC instructor’s role to guide the PTs towards formulating the main question to be solved. During this process, the available data were identified based on the video and estimates of the necessary data were made to answer the posed question.

Act 2: Once the main question in the problem was formulated, the solution was searched for. The participants were encouraged to request the necessary data and make the relevant estimations themselves.

Act 3: Finally, the answer obtained in the previous act was validated by revealing the real result, allowing the participants to verify their reasoning. During this act, discussion was encouraged regarding the outcome and the mathematical concepts involved in the solution.

This activity implicitly develops several DSC (since, at this stage, PTs had not yet learned the DSC tool), as it promotes components such as the richness of processes derived from the epistemic DSC—encouraging argumentation, problem-solving, and connections between mathematical ideas—as well as the high cognitive demand required by the cognitive DSC, activating processes such as generalisation, the formulation of conjecture, and intramathematical connections.

The TC was conducted in six sessions, one per week, comprising three two-hour sessions and three four-hour sessions. These combined moments of practice with various didactic materials—methodological, manipulative, or digital—and spaces for collaborative reflection. The guiding scenario placed the PTs in the role of “agents who save stories” within a gamified narrative based on the concept of a multiverse, structuring the sessions around different universes inspired by popular culture series, movies, or books, in which the PTs had to assist the main characters.

Throughout the TC, various game elements were incorporated, such as narrative, team missions, achievements, badges, points, and battles, with the aim that the PTs could experience and analyse different game components through implementation examples. The Socrative platform was used for quizzes to review key content and analyse didactic situations. Points were assigned to the PTs on a leaderboard, and the top three scorers in the final session received a symbolic prize in front of their peers.

Table A1. Gamified TC sessions. Source: authors’ own work.

Sessions	Activities	Description
Session 1: Introduction to the module and blocks (2 h).	Lisa Simpson: The Electoral Adventure toward the Student Council: First quest: voter’s profile. Second quest: Girl Scout cookie sale. Original activity from Meyer (2016a). Third quest: Edna’s inspection (chance to earn a badge). Agency review on Socrative. (Points for the leaderboard.)	Subject presentation, introduction to the subject methodology, and three acts presenting activities.
Session 2: Materials for Numerical Sense and Algebra Workshop (2 h)	Initial quest: “The Trail of Galactic Functions”. (Points for the leaderboard). Materials workshop by corners: Corner 1: The Secret of the Galactic Rhombus. Activity adapted from Aubanell i Pou (2015). Corner 2: Drax’s Tower Defense. Activity adapted from CESIRE—CREAMAT (2014). Corner 3: Gamora’s Tactical Training with Mysterious Polygons. Activity adapted from (Puig Adam, 1956; PuntMat, 2018). Corner 4: Groot’s Fraction Training. Corner 5: Star-Lord’s Rescue of the Out-of-balance Planets. Activity adapted from (Numberphile, 2018). Corner 6: Mantis’ Patience and Precision Training (chance to earn a badge). Activity adapted from (García Caballero, 2017).	Initial activity from a GeoGebra applet. 10 min materials workshop for experimentation and problem-solving. Activities were carried out in teams of 5–6 people. Materials: Corner 1: Rhombus made with Meccano pieces and angle protractor. Corner 2: Multilink cubes. Corner 3: Tangram and mosaic. Corner 4: Fraction dominoes. Corner 5: Graph plans and two-colour cards. Corner 6: Origami paper.
Session 3: Scratch Workshop (2 h)	Scratch Workshop with Jack Skellington Exercise 1: Setting the stage for decorations Exercise 2: − Option 1: Creating a new scenario for adventure. Activity adapted from A. Sánchez and Burgués (2020). − Option 2: Automating calculations with Scratch. − Option 3: Completing an unfinished code. − Option 4: Programming the “Twenty Wins” game (chance to earn a badge). Activity adapted from Deulofeu (2010). Agency review on Socrative. (Points for the leaderboard).	This is an initial use of Scratch for concrete math activities. The activities are performed in pairs and experimentation is encouraged in the programme to learn how to use the software.
Session 4: Geogebra Workshop (4 h)	GeoGebra Workshop: Avatar—The Return to Pandora: Quest 1: The points of the surveillance triangle. Quest 2: The Sacred Rectangles combat. Quest 3: Enemies’ troop data analysis. Quest 4: Viviani’s Sacred Triangle. Quest 5: The Fight against the Toruk: Heron’s Problem. Quest 6: The Battle of Shadows: Equivalent Rectangles. Quest 7: The Omen Cone and the Akula Fight. Quest 8: The Ancestral Vase of the Lumineras: A Revolution Solid. The Final Battle: Colonel Miles Quaritch showdown (chance to earn a badge): ○ Phase 1: Crack the Lock Button. ○ Phase 2: Dismantle the Three-Dimensional Equations. ○ Phase 3: The Final Combat—The Spear of Light. Agency review on Socrative. (Points for the leaderboard).	The programme is presented using examples of activities where the PT is the one who builds the applet. It is a set of activities where they work with the different views that the program offers.
Session 5: Geometry Materials Workshop (4 h)	Quest: The Wandering Knight’s potion: Geometry materials workshop by corners with Don Quixote: Corner 1: The wind giants. Corner 2: The enchanted castle’s adventure. Corner 3: The city roads. Corner 4: Dulcinea’s stars. Corner 5: The Wise Friston magic books. Corner 6: The Paper Dragon (chance to earn a badge).	The first activity is an experiment to demonstrate the volumes of different geometric figures. The workshop by corners shows six activities, adapted from (CESIRE—CREAMAT, n.d.), of 15 min each to experiment with manipulative materials while solving different problems. Material: Corner 1: Polydron Parts. Corner 2: Interlocking pieces to form pentominoes. Corner 3: Orthogonal geoplane and elastic bands. Corner 4: Polar and isometric geoplanes and elastic bands. Corner 5: Vegetable paper and compass. Corner 6: Origami paper.
Session 6: Statistic activities, BreakOut y blocks closure (4 h)	Probability and statistics activities adapted from (ADEMGI, n.d.; Grup Cúbic, 2017; Institut El Joncar, n.d.): The Horse Race. Monty Hall. The Ladder game. (Points for the leaderboard.) Stochastic Walk. (Points for the leaderboard.) BreakOut of Kafka’s Metamorphosis (A. Sánchez, 2021). Final debate of the subject’s methodology.	Session begins with various probability and statistical activities to encourage experimentation. BreakOut is a digital activity at Genially. This activity is made up of various problems; the resolution of some of them requires the use of different manipulative materials. Material: Six strings. Plasticine. Sheets of paper. Cutter. Abacus. As the closure of the block, a debate on the subject’s methodology is carried out.

provides a summary of the sessions that formed the TC.

The TC culminated in a final group debate, in which the PTs reflected on their experience, how they would adapt the active methodology in their future teaching practices, and possible improvements in the design of gamified activities for the teaching–learning process of mathematics. After this group debate, a plenary session was held to share the ideas that emerged during the debate. The questions used to guide the discussion were designed with the DSC in mind, with the aim of having the PTs assess the TC in a comprehensive manner.

For example, to address epistemic suitability, PTs were asked if they considered that the gamification of the subject helped them understand how to apply this strategy to teaching mathematics, how they would implement it in a secondary school class, and what content could be worked on using gamification. Regarding cognitive suitability, they were asked if they thought gamification was a good strategy to assess secondary school students’ prior knowledge and why. In relation to interactional suitability, TCs analysed whether the gamified dynamics of the subject encouraged collaboration or competition among peers, how they would assess such interactions, and how they would apply them in a secondary school setting. Concerning affective suitability, they were asked to reflect on how they could use gamification to engage students with different levels of interest or motivation to study mathematics. For mediational suitability, they were invited to consider how they would plan and manage time when applying gamification in their teaching practice, as well as what the most appropriate classroom conditions would be. Finally, regarding ecological suitability, they were asked if the strategies used in the subject—such as gamification, Scratch, GeoGebra, and manipulative resources—were aligned with the real needs of students today and how they would justify this assessment.

2.3. Data Source

To carry out the analysis of the competencies developed by the PTs in relation to the incorporation of gamification in the teaching of mathematics, three main sources of information were used.

Firstly, the group debate conducted at the end of the TC was recorded, with the intention of transcribing it later. The transcriptions were then analysed, in which the participants reflected on the TC and the possible implementation of the gamification methodology in their teaching practices. In the debate scenario transcriptions, the codes PT1, PT2, PT3, etc., refer to the preservice teacher that participated in the debates.

Secondly, a field diary was considered, created during the discussion following the debate, which recorded observations, spontaneous interventions, and shared assessments by the participants in a collective space. It is worth noting that, when the debate took place, the PTs were not yet familiar with the DSC; however, when designing the questions for the debate, these were taken into account by the researchers.

Finally, the 30 MFPs created by the PTs were examined, with particular attention paid to the justifications provided regarding the use of gamified activities, as well as explicit references to the DSC in the different phases of the mathematical instruction process: design (a priori), implementation (in loco), and redesign (a posteriori). It is worth noting that, at the time of creating the MFPs, the PTs were already familiar with the DSC.

The instructor’s role in the training cycle focused on designing and facilitating the gamified activities and moderating the spaces for collective reflection. It is important to note that participation in the debates and the quality of the arguments did not influence the grade for the module, nor did the incorporation of gamification in the didactic proposals improve the mark obtained for the MFP; indeed, the instructor was not part of any MFP evaluation tribunal. Therefore, there were no evaluative incentives for reflecting positively on gamification or for implementing the methodology in the MFP.

2.4. Data Analysis Process

The data obtained in the analysis process were organised into tables, following a similar approach to that used by Ledezma et al. (2024) and A. Sánchez et al. (2022). These tables included the title of the MFP, the name of the PT, the educational level at which the analysed learning situation was implemented, the branch of mathematics to which the didactic sequence belonged, the type of gamified activity used or mentioned in the MFP, whether the term gamification was used, the extracts justifying the use of gamification in the implementation, the DSC component referenced in the justification, the level of development of subcompetencies related to the analysis and evaluation of didactical suitability, and the points in the instructional process (a priori, in loco, and a posteriori) that were analysed (see example in

Table 2. Example of the data registered for an MFP. Source: authors’ own work, adapted from Ledezma et al. (2024) and A. Sánchez et al. (2022).

Title Preservice Teacher’s Name	Limits and Continuity in the First Year of Baccalaureate: Proposal for Improvement Alberca (2025)
Level	1st level of Baccalaureate (16–17 years old)
Branch of mathematics	Functions
Category of the game use approach	(2) Proposes gamified activities as a potential improvement in practical intervention.
Which games have been used or alluded to?	Roleplay
Does it use the term gamification?	No
Extract	(Alberca, 2025, p. 14) Finally, it was tried to make the content as attractive as possible for students through drama and the resolution of simple cooperative tasks. Setting organized goals makes it difficult for students to get lost and the dialogues where the theory is explained in a more fun way make the student see learning as a game and not as exercises that they cannot solve.
Which component of the DSC is being referenced?	Richness of processes (epistemic suitability)+
Level of development	L2

).

This example illustrates the type of information collected and how it was coded. The analysis process consisted of three phases.

2.4.1. Phase 1: Classification of MFPs According to Gamification Use

The MFPs developed by preservice teachers who participated in the training cycle were classified according to the categories established in

Table 3. Gamified classification for MFP. Source: authors’ own work.

Condition Number	Definition
1	It does not use gamification, nor does it propose the methodology as a potential improvement for practical intervention.
2	It proposes gamified activities as a potential improvement in practical intervention.
3	It occasionally uses gamification activities in practical intervention.
4	The entire intervention is based on gamification activities.

. This classification aimed to distinguish between projects that did not use gamification and those that did, as well as to identify how this methodology was presented and applied in each project.

During the review, one case was found in which an MFP with a gamification proposal for the whole intervention also included a specific gamified activity; therefore, conditions 3 and 4 were simultaneously met. It is important to highlight that the inclusion of one category does not exclude the inclusion of others in this classification, as a didactic sequence could be gamified as a whole while also including specific gamification activities.

Additionally, it could be that an MFP that used some gamification activities during the initial implementation, or a fully gamified processs, proposed other activities during the improvement phase, meaning that category 2 could appear simultaneously with categories 3 and/or 4. The only category that was essentially exclusive was the first one. Regardless of whether gamification was implemented or not, we also sought to identify in which MFPs the terms “gamification” or “ludification” were used and for what purpose.

2.4.2. Phase 2: Coding of Justifications Using DSC

Once an MFP that employed gamification were identified, the comments justifying the use of a gamified activity were obtained and classified using the DSC. In this classification with the DSC, the comments were also differentiated based on whether they were positive or negative in context. For example, in the “attitude” component of affective suitability, a justification that positively evaluated the implementation differed from a negative evaluation. Once the comments were differentiated as positive or negative, the difference between the total number of positive and negative comments for each component with any comment was calculated. In this way, the suitability of gamification for each DSC component was evaluated.

2.4.3. Phase 3: Assessment of Reflective Competency Levels

To analyse the competencies of didactical analysis and intervention in the justifications provided by the PTs for the use of gamification in their learning situations, the Didactic–Mathematical Knowledge and Competencies model of the Ontosemiotic Approach was used, focusing on the subcompetency of the analysis and evaluation of didactical suitability. However, a methodological limitation was detected when directly applying the development levels table proposed by (Pino-Fan et al., 2023), as this was designed to evaluate the development of this subcompetency in teachers (or PTs in this case) considering their reflections at different points in the instructional process (a priori, in loco, and a posteriori).

In this study, the data sources (debate transcripts and the MFP) did not allow for arguments to be linked to one another or for participants to be identified in the transcripts, which prevented a longitudinal analysis by individual. Moreover, many of the justifications were situated in specific reflective points (mainly a priori or a posteriori), which could bias the assessment if the column “phase of the instructional process” were maintained as a criterion for assigning the level.

Therefore, an adaptation of the original table was proposed, removing this column as a criterion for the level of development and retaining it solely as a contextual descriptor. This adaptation enabled each argument to be assessed independently, focusing on its analytical level and reflective depth, without penalising it based on the point at which it was expressed. The new table considered three dimensions: the type of analysis (descriptive, explanatory, or evaluative), the depth of analysis (superficial, medium, or deep), and the level of development of the argument (L₀–L₃), defined according to its articulation using the DSC and the Didactic–Mathematical Knowledge and Competencies model.

The data obtained in the first and second phases were organised into tables, following a similar approach to that used by Ledezma et al. (2024) and A. Sánchez et al. (2022). These tables included the title of the MFP, the name of the PT, the educational level at which the analysed learning situation was implemented, the branch of mathematics to which the didactic sequence belonged, the type of gamified activity used or mentioned in the MFP, whether the term gamification was used, the extracts justifying the use of gamification in the implementation, the DSC component referenced in the justification, the level of development of the sub-competency related to the analysis and evaluation of didactical suitability, and the parts of the instructional process (a priori, in loco, and a posteriori) that were analysed (see example in

Table 4. Levels of development of the subcompetency of the analysis and evaluation of didactical suitability. Adapted from Pino-Fan et al. (2023, p. 1425).

Ln	Description	Type of Analysis	Depth of Analysis
L0	There is no analysis or justification for the use of gamification.	The analysis is superficial and ambiguous, it does not describe, explain, or evaluate the instructional process or class period.	Superficial narrative (written or discursive). The narrative does not explain what happened during the class period.
L1	Superficial justification, focused on motivation or aesthetics.	Descriptive Describe what happened during the class period or study process.	Narrative that captures the essential elements of the class period analyzed. Anyone who reads or listens to the narration has an idea of what happened in the episode.
L2	Partial justification, with implicit or generic references to DSC.	Explanatory Try to answer: why what happened during the class period happened (related to a phenomenon, conflict, error, etc.).	A complete and understandable narrative, which involves a detailed analysis, attempting to follow a model (e.g., if a description of mathematical activity is made, components of the ontosemiotic configuration are used to identify some primary practices, objects, and processes; used explicitly or implicitly).
L3	Thorough justification, structured by the DSC components and/or the Didactic-Mathematical Knowledge and Competencies model.	Evaluative It includes elements from the previous two levels and answers the question: what can or should be improved during the class period and why?	Expert analysis of the narrative according to the systematic use of a model (e.g., a detailed description of the mathematical activity is made, the practices, primary objects, and processes, meanings of the notions used, are exhaustively identified; systems of norms that conditioned the interactions and learnings in the episode; or the eligibility criteria explicitly).

).

At the end of the third phase of the analysis, graphical tools from descriptive statistics were used to represent the results obtained in the previous phases. Additionally, through expert triangulation, the generated data were interpreted and the aspects that PT considered relevant when incorporating gamification into the teaching–learning process were inferred, based on the collected reflections and justifications.

3. Results and Discussion

To answer the research questions, the results of the study are organised into three topics, with each topic answering each question. The first relates to the use of gamification by the PT in their MFP. The second focuses on analysing the didactical suitability of incorporating gamification into instructional processes, based on the reflections made by the PT and the level of development of the sub-competency concerning the analysis and evaluation of didactical suitability achieved by them. Finally, the third addresses the evolution of the justifications provided by PT according to the point at which their teaching reflection occurred.

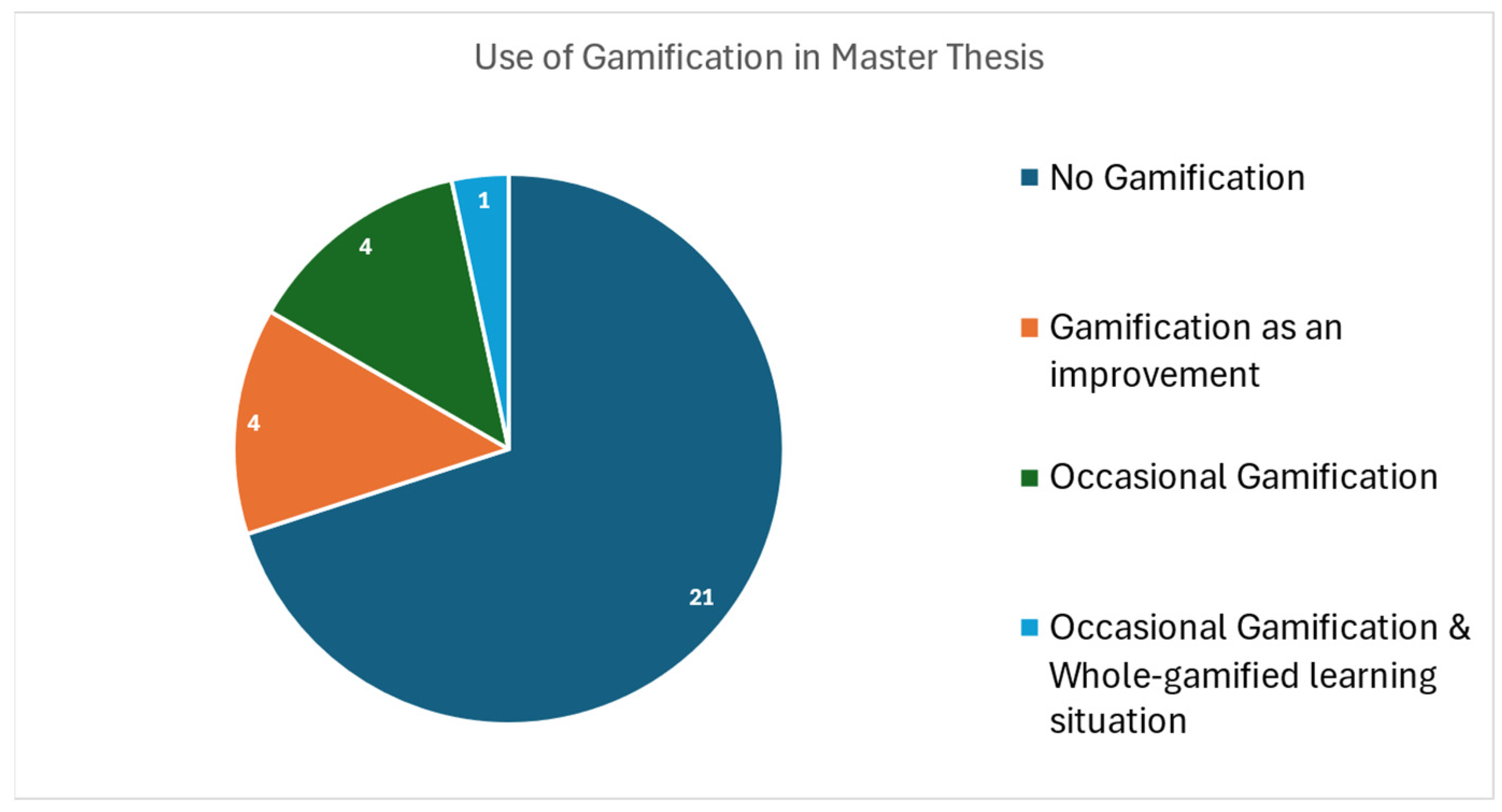
3.1. Use of Gamification in Master’s Final Projects

The initial results of this study concern the number of MFPs that employed gamification and how many explicitly used the term “gamification”. As it can be seen in Figure 3, of the 30 MFPs analysed, 9 include at least one gamified activity in the design, implementation, or redesign of the learning sequences. Of these nine, four propose gamification as a comprehensive improvement, while five include a single gamified activity in the design, one of which also proposes an entirely gamified didactic sequence. It is worth noting that, of the four MFPs that present gamification as an improvement, three aim to fully gamify the learning sequence, and in the remaining one, the idea is not fully developed; however, since it proposes the use of a reward system based on accumulative achievements (R. Sánchez, 2025, p. 16), it can be assumed that this MFP also refers to the complete gamification of the didactic sequence.

In percentage terms, this means that PTs who participated in the TC used gamification to a greater extent: 30% of them included it, compared to 14.4% (46 MFPs out of 318) identified in Cortés et al. (2026), which analysed previous cohorts of the same master’s programme. So, it could be presumed that the TC promoted the use of this methodology by PTs.

As it can be seen in

Table 5. Use of the term “gamification” in the analysed MFPs. Source: authors’ own work.

Type of Use of the Term Gamification	MFP (Authors)	Description
Imprecise/confused use (misuse)	(Bonavia, 2025, pp. 9, 15, 16, 18; Lapeña, 2025, p. 15; Llargués, 2025, pp. 40, 70; Picart, 2025, p. 32; R. Sánchez, 2025, p. 21)	Direct equivalence between gamification and complete games like Kahoot!
Proper/substantiated use	(Gimeno, 2025, pp. 16, 22; Jdayah, 2025, pp. 13, 21, 36; Rodríguez, 2025, pp. 29, 31, 37, 42, 44, 45, 49; R. Sánchez, 2025, p. 16)	Activities with game elements and pedagogical objectives
Generic use without development	(Lapeña, 2025, p. 16; Llargués, 2025, pp. 16, 25; Picart, 2025, p. 40)	Mentioned as a synonym for innovation or motivation, without specification
Theoretical definition use	(Rodríguez, 2025, p. 16)	The only case with an explicit bibliographic definition (Kapp, 2012)

, the analysis of the MFPs reveals a frequently imprecise use of the term “gamification”, identifying it solely with the use of playful digital tools such as Kahoot! or Desmos. From the 30 MFPs analysed, 8 explicitly use the term “gamification”. Although some projects show a more grounded use of the concept, incorporating strategies that include game elements, a high percentage of cases confuse it with game-based learning activities. This situation highlights the need to strengthen the conceptual training of preservice mathematics teachers regarding gamification and its distinction from other game-based methodologies.

The conceptual evolution of the term “gamification” is a relevant aspect that could be considered acquired knowledge by PTs. In studies such as those of Balaskas et al. (2023) and Dellos (2015), a clear distinction is made between game-based learning—using tools like Kahoot!—and gamification. However, in some of the MFP analysed, the term is used imprecisely, equating it with such tools, while other projects demonstrate a deeper understanding of the concept. This conceptual evolution is key to avoiding methodological confusion and ensuring that gamified proposals respond to well-defined pedagogical objectives. Therefore, it would be advisable for the TC to place greater emphasis on distinguishing between playful methodologies, as the results show signs of confusion between gamification and expressions such as “playing in the classroom” or “learning through play”, as already noted by Torres-Toukoumidis and Romero-Rodríguez (2019).

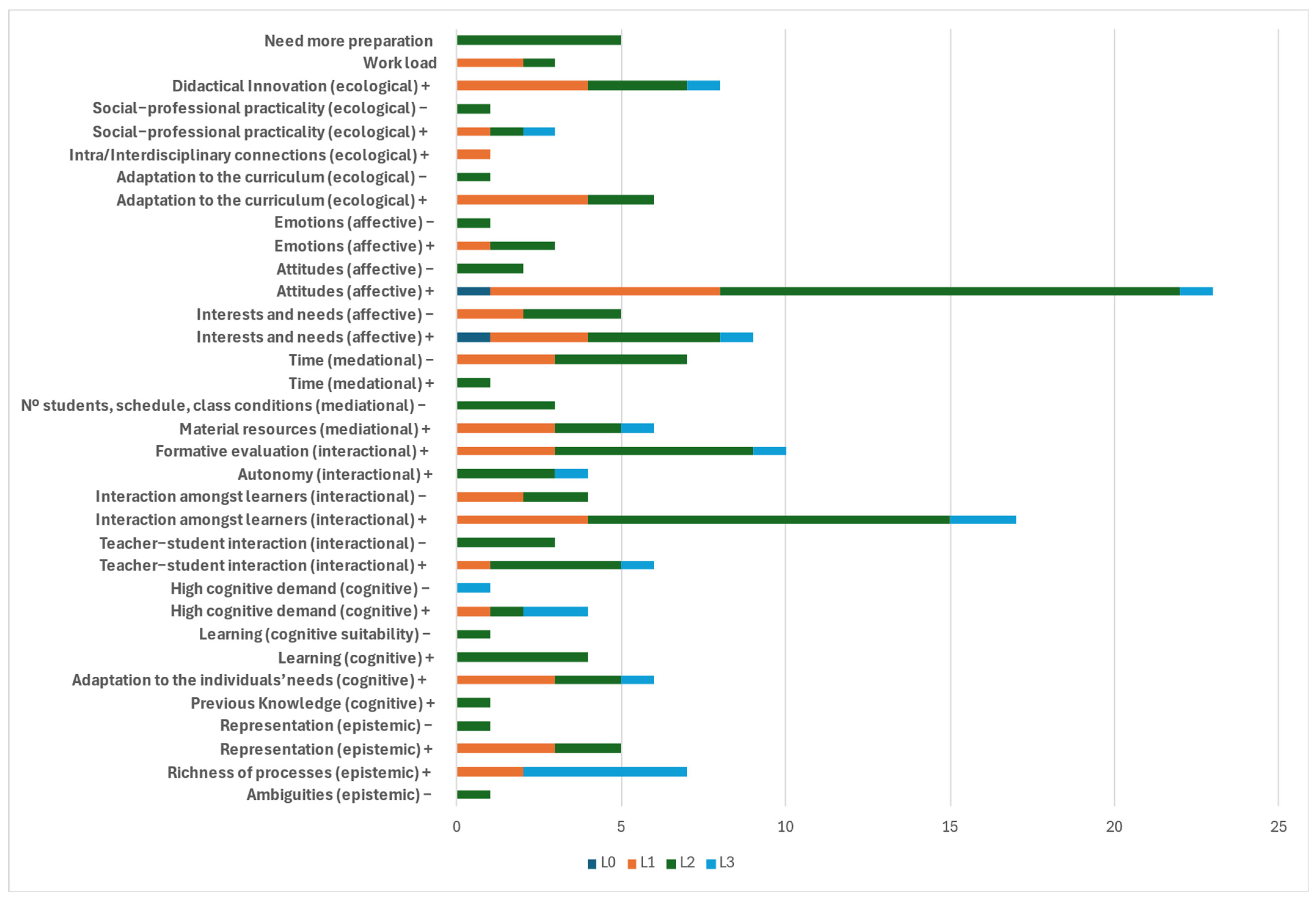
3.2. Analysis of Reflections Based on the DSC and the Level of the Subcompetency of Analysis and Evaluation of Didactical Suitability

The analysis of didactical suitability in PTs’ reflections on the incorporation of gamification into mathematics instruction, based on the transcripts after the TC debates and the MFP, reveals how PTs evaluate the use of this active methodology in mathematics teaching. A total of 163 extracts were coded, 74 from the MFPs and 89 from the transcripts. In this subsection, each extract was classified according to the components of the DSC and whether the evaluation was positive or negative.

It was observed that the affective component received the highest positive evaluation, followed by student interaction and formative evaluation. This result is understandable, as gamification, being a student-centred active methodology, aims to enhance motivation (affective suitability) by definition and simultaneously foster interaction (interactional suitability) in the teaching–learning process.

However, in the MFPs that demonstrated a higher level of didactical reflection, the richness of the processes, an element of epistemic suitability, was the most valued. This indicates how gamification influences the processes involved in mathematical activity. For instance, Alberca (2025) explains:

“[…] regarding epistemic suitability, it is improved the section of Richness of Processes. It is replaced the traditional method where it was prioritised mechanisation and memorisation by role-playing with challenges that encourage students to explore, discuss and translate into mathematical language, use different types of representation to better understand what is happening, and communicate with team members and other teams.”

(Alberca, 2025, p. 13)

Thus, he affirms that in the redesign of his learning sequence, the whole gamification of the sequence through role-play with challenges fosters the richness of processes in mathematics teaching and learning.

Although there are not many comments on this aspect, it is also worth highlighting the high cognitive demand (cognitive suitability), due to the presence of comments referencing a high level of development. Bergadà (2025) explains that in the redesign of a gamified activity, this high cognitive demand is improved on as follows:

“[…] the activity is designed to deepen the Derby Game project (…) So now we ask them to open the app and click on the ‘How is it made?’ or ‘See Inside’ button, and from there they can see how the game works. They need to read the code and write down on their notebook anything they understand from what is written and something they don’t. It’s normal not to understand everything, but they should find a line they do understand, what it means or what it’s for. This will allow them to make a first approach to programming using Scratch and start familiarising themselves with the code used to create the app. The final goal will be for them to make any improvement to the game.”

(Bergadà, 2025, p. 31)

Therefore, for this PT, gamification promotes high cognitive demand not only through computational thinking and programming, but also through understanding the functioning of the gamified activity itself and even improving it.

In the analysis of the DSC, comments emerged referring to a set of skills categorised as “game skills”; although most of them are already considered in the DSC—such as perseverance, self-regulation, or experimentation—in a playful context like gamification, they are articulated differently. For example, Bergadà (2025) states that perseverance and responsibility are encouraged thanks to the context, as in the gamified activity he proposes, there is a “reward” contextualised by reaching the end. There is also the case of Standeven (2025), who, in his redesign, proposes gamifying the whole didactic sequence to create a problem-solving experience through structuring activities around a story that serves as a narrative thread, making it the narrative itself that promotes problem-solving.

Similarly, Alberca (2025, p. 15), in his redesign, promotes not only problem-solving but also creativity in addressing problems, due to the playful context that provides greater freedom for creative expression. Some of these skills also fall under the interactional criterion, as detailed by Gimeno (2025, pp. 14–15), who, through the playful environment of gamification, fosters coordination and role assignment within groups. This is a skill that, although included in the component of student interaction, is specifically encouraged by the gamification context.

Overall, these examples illustrate how PTs perceive that gamification not only enhances individual and social skills but also redefines how these are developed in the classroom.

It is noteworthy that PTs identified the importance of “game skills” which, although they are already included in the DSC through affective, interactional, and epistemic criteria, show a particular dimension in gamified contexts. These skills were suggested by Grodal (2000), who found that when players had sufficient game skills, they experienced positive emotions and were able to overcome moments of crisis in the game. Additionally, as evidenced before, these skills enrich the teaching–learning process by enabling attention to be paid to student diversity, as evidenced in proposals that adapt roles and tasks according to individual strengths. These results also align with those of Cornellà et al. (2020), who explain that various psychopedagogical theories highlight the potential of games from perspectives such as intellectual and social development.

When observing the components with the most negative evaluations, time and classroom conditions, both components of mediational suitability, were identified as the only two with generally negative assessments. PTs, in the debate after the gamified TC, provided the following reasons:

“PT2: Which aspects of classroom management would you change if you were to implement gamified activities in secondary education?

PT1: More time. Time. Time. We were rushing through everything, to be honest.

PT3: And the time… maybe it’s what you’re saying, but I’d prefer that instead of doing six activities in half an hour, we did two and then had some time to digest, to explain. ‘Let’s explain, guys, let’s discuss: why didn’t it work for you? Why did it? Why didn’t we get feedback on why it did or didn’t?’

PT1: Well, I guess that it was this way…

PT3: Yes, because we’re adults. Yes, yes, yes…

PT1: We were interested in seeing as many as possible, because we have the capacity to check them later on our own.

PT3: But with students, it would be interesting to dedicate more time, wouldn’t it?”

This extract manifests the curricular pressure to cover content, which sometimes hinders the implementation of innovative methodologies. Therefore, to properly apply gamification, it is suggested that more time is needed than in traditional lecture-based teaching. On the other hand, in the debate held at the end of the TC, PTs also made the following argument:

“PT2: How would you plan and manage time if you wanted to apply gamification in your teaching practice? And what would be the most suitable classroom conditions?

PT3: Well, I really think the classroom needs to be a collaborative space, right? Because, I mean, a classroom like the one we have here is terrible for this kind of activity.

PT2: It must be a classroom…

PT4: In terms of furniture, it needs tables and chairs that…

PT2: …allow for group formation.

PT4: Exactly, that allow students to sit in circles, or if they’re desks, at least desks that can be actually rearranged. Because of course, if they’re fixed to the floor, there’s no way… then it’s not possible. Definitely, it’s not possible.

PT2: And the teacher needs to be able to move around easily, not just to help, but also to observe and assess. In the end, you can also evaluate based on what you’re seeing in classroom.”

This extract from the debate reveals the need for appropriate physical conditions to implement active methodologies like gamification. It is noted that a traditional classroom is not optimal for this type of methodology, and ideally, there should be enough space both to form groups and to allow the teacher to move freely around the classroom.

From the DSC analysis, two categories emerged that could not be classified within the DSC: workload and need for more preparation. Both came from the group debate, in which PTs pointed out that preparing gamified activities requires a considerable investment of time. Moreover, when answering the question of whether they feel prepared to implement gamification, they explained that although the TC provided them with resources, they still feel uncertain due to the short duration of the course and expressed that they would have liked it to be longer. For instance, during the group debate, PTs made the following comments:

“PT1: So, the idea was also to see whether the gamification of this subject helped us understand how this strategy can be applied to mathematics teaching. Yes, yes… but I find it quite complicated. All that stuff we did here with GeoGebra, that whole story…

PT2: It’s a lot more work.

PT1: Yes, I have to invent everything myself.

PT3: Sure, yes… no… but well, in the end you already have many resources made.

PT3: The only problem…

PT2: … is finding them.”

In turn, PTs expressed the following in the debate regarding the need for further preparation:

“PT1: How do you assess the connection between what you have learned in the course and what you could apply in schools with different educational projects, resources, and contexts? Do you feel prepared to adapt what you have learned to diverse contexts?

PT5: No.

PT4: I mean… thinking that with ten hours of lessons you become an expert in gamification… is a bit presumptuous…

PT5: Yes, I think now we have more options.

PT3: Sure, we have a basis, I think.

PT4: Exactly.”

It was noted that the TC served as an initial approach to gamification in mathematics education, but PTs still do not feel fully prepared due to the shortness of the cycle. Both comments express the need for more extensive training in gamification, as although the lack of resources can be partially mitigated through the TC, a longer cycle would provide more resources to support the implementation of this active methodology.

Nevertheless, one PT also commented:

“PT5: (…) if I think that in high schools or secondary schools where they already work with project-based learning and highly innovative pedagogies, I believe that it might be easier to apply this because students are already more used to different dynamics.”

This suggests that, for the effective implementation of gamification, collaboration with educational centres is also necessary. This argument is reinforced by another PT who stated the following:

“PT1: I also think it’s about strategies, in this case, thinking about all the resources, right? Whether it’s Scratch, GeoGebra, manipulative games… rather than responding to current needs, they respond to needs that have always existed. The difference is that now they’re being addressed. I mean, now there’s a bet on learning through experimentation, not just theory. And so, something is being done about it. Obviously not in all schools, but the focus is starting to shift towards the need for different tools to keep students engaged, connected, and motivated. How do we do that? With resources. Using things we already knew that worked, but which previously weren’t given the importance they deserved, because the traditional model placed a lot of emphasis on the teacher as the central figure, right? And students as sheep. ‘I recite and they repeat.’ And it has already been seen to be ineffective for the learning experience. So yes: we need strategies aligned with this new perspective.”

The PT explains that the use of innovative methodologies emerges as an opportunity to improve the teaching–learning process and that there are educational centres committed to this approach, which could facilitate a more concrete and effective implementation of the methodology.

Structural limitations that affect the implementation of gamification in the teaching–learning process, such as the need for more time to prepare and implement gamified activities, as well as the adaptation of the physical classroom space, are recurring themes in participants’ reflections and may also be linked to the use of active methodologies in general; for instance, Takele (2020) found that teachers’ main challenges when implementing active methodologies were large class sizes, the amount of content to cover, the lack of instructional materials, the lack of administrative support, and the fact that they required too much effort from teachers. Another case that reported challenges when implementing an active methodology is described in the work of Fang et al. (2023), as they explain that teachers lack training in implementing problem-based learning in mathematics and they also struggle to design appropriate problems, lack the time to guide students, struggle to maintain commitment, and have limited resources. Time constraints are also a limitation observed in university mathematics courses, for example, by Johnson et al. (2025), as teachers may perceive the methodologies to be beneficial, but their professional obligations—such as using abstract examples and requiring rigorous answers—increase the time and effort needed to implement even simple active learning strategies, which can limit their feasibility. This shows that professional responsibilities can lead some to reject these methodologies, even while recognising their advantages.

On the other hand, studies on real-world problem design, like that of Vale and Barbosa (2023), highlight that real-world tasks can support conceptual understanding, so incorporating this approach in gamified systems could reduce the risk of mathematics being overshadowed by the game context. It would be worthwhile to explore these barriers further so they can be considered in the design of the TC and in the planning of didactic sequences.

However, these limitations may be compensated by the benefits that active methodologies can provide; as suggested in the DSC (Font et al., 2010; Godino et al., 2013), a balance between the criteria must be found to enhance the suitability of the teaching and learning processes.

Once a clear picture emerges of which criteria PTs consider relevant when implementing gamification in the mathematics teaching–learning process, it will become possible to determine the participants’ level of reflective competency—that is, their level of competency in analysing and evaluating didactical suitability.

The analysis of the 163 coded extracts shows that most justifications fell within intermediate levels of reflective competency, with 92 cases at level L₂, 50 at L₁, 19 at L₃, and only 2 cases at L₀. It is worth noting that, at the time the group debate during the TC was conducted, PTs were not yet familiar with the DSC or the Didactic–Mathematical Knowledge and Competencies model, so references to these were frequently made because the questions proposed for the debate were designed with the DSC in mind. For this reason, lower levels are overrepresented, as level L₃ could not be reached during the collective reflection.

When filtering the comments by source (TC debate and MFP), it is observed that, in the debate, there were 29 cases at level L1 and 60 at level L2, while, in the MFP, 2 comments were at level L₀, 21 at L₁, 32 at L₂, and 19 at L₃.

These results indicate that PTs developed the sub-competency of analysing and evaluating didactical suitability when reflecting on how to implement gamification (see

Table 6. Levels of development of the subcompetency of analysis and evaluation of didactic suitability. Source: authors’ own work.

	L0	L1	L2	L3	Total
Debate	0	29	60	0	89
MFP	2	21	32	19	74
Total	2	50	92	19	163

).

This indicates that although explanatory analyses (L₂) predominate, once PTs become familiar with the DSC (as reflected in the MFP), they assess gamification more thoroughly, reaching level L₃ by articulating their arguments using the DSC and the Didactic–Mathematical Knowledge and Competencies model.

As noted by authors such as Malvasi and Recio Moreno (2022) and Ortiz-Mendoza and Guevara-Vizcaíno (2021), the effective implementation of gamification requires appropriate training. This study provides empirical evidence supporting that claim: some PTs who participated in the TC not only incorporated gamified activities into their MFP but also justified them using the DSC. This articulation using the components of didactical suitability demonstrates progress in the reflective competencies of PTs, especially when L₃ of development is reached.

One possible way to improve the development of this subcompetency would be to explicitly implement the DSC within the TC. This would enrich the debate and ensure that PTs could respond to questions using these components as a means of support. Additionally, activities focused on analysing the didactical suitability of real gamification examples could be incorporated, so that, through classroom discourse and collective debate, the ability to analyse gamified activities would be strengthened.

Another improvement, in line with the previous section, would be to extend the duration of the TC by dedicating more sessions to it. This aspect was mentioned by several groups during the debate, who pointed out the lack of time and the need to prioritise the presentation of a greater number of resources, which reduced the time available for an in-depth analysis of the activities.

“PT3: Because I think, for example, we were complaining that the GeoGebra part would have required more time—the introduction, and whatever—. But it’s also about whether you’re willing to lose or, rather, invest time, I mean, to dedicate more time, you know? Like… I always have that doubt. I was talking about it the other day with another teacher… With the teacher (name of another teacher)… this idea of: ‘Okay, I don’t know, I know that if I do this activity, it will probably take up three lessons, for example.’

PT5: Yes.

PT3: Am I willing to…?

PT5: Of course, because you still have to cover the syllabus.

PT3: Exactly. Spending more time on one thing means having less time for something else.”

In this way, the lack of time is projected onto their future teaching practice, meaning they were unable to develop, as they would have liked, the set of competencies they will need as PTs. At the same time, they perceive that gamification requires a significant investment of time, which may imply a potential sacrifice of syllabus coverage. Nevertheless, PTs recognise the role of gamification in promoting didactical suitability, both in the debates and in the MFPs, as noted by Fernández (2025), who, after discarding a gamified activity during the implementation of his learning sequence that was planned in the design, states that he wished to recover it, considering that, had it been implemented, the didactic sequence would have been more suitable:

“Regarding emotional suitability, it was observed that student motivation was higher in activities with a playful or creative component. Therefore, the initial idea of the contest ‘Put on the Function Glasses’ is recovered, and a return to a more formative evaluation is proposed, including co-evaluation and self-evaluation as tools for regulating one’s own learning.”

(Fernández, 2025, p. 41)

A similar case is exposed by Alberca (2025) in his redesign proposal:

“On the other hand, the usual approach to preparing for university entrance exams in Baccalaureate (formal explanation of theory, sample exam, mechanical exercise solving in isolation…) is replaced by collective learning in which everyone must participate and be responsible with their peers. Argumentation with group members is encouraged, as well as dialogue and the presentation of ideas to other groups in the classroom.”

(Alberca, 2025, p. 14)

In this case, the traditional teaching approach associated with university entrance exam preparation is criticised, and a whole gamified didactic sequence is proposed in the redesign to promote collective learning.

Moreover, given that the highest levels of development (L₃) of the sub-competency in analysis appear in the MFP, it can be inferred that the training had a positive impact on the PTs’ didactical analysis capacities, which is further supported by complementary training in the DSC. These results allow us to conclude that PTs developed the sub-competency of analysing and evaluating didactical suitability, especially after receiving training in the DSC, reaching advanced levels of reflection in their MFPs.

As a final result, considering the analysis of PTs’ reflections from the perspective of didactical suitability and the study of the level of development of the sub-competency in analysing and evaluating didactical suitability, it can be inferred that the highest level of reflection (L₃) is associated with the idea that gamification in mathematics teaching enhances the richness of mathematical processes (epistemic suitability component), followed by student interaction (interactional suitability). On the other hand, the lowest level (L₀) is associated with the idea that gamification in mathematics teaching promotes interest in and positive attitudes towards mathematics (affective suitability components), as shown in Figure 4.

The analysis based on the DSC reveals that gamification firstly enhances affective and interactional suitability. This is a logical result; as Ripoll (2014) explains, the goal of gamification is to influence the motivation to achieve a specific behaviour. He also specifies that gamification is measured by the player’s enjoyment during the process, so gamification is expected to improve the affective aspect. For this reason, it is even more noteworthy that gamification promotes epistemic suitability through the richness of processes, since gamification, by definition, does not necessarily do so. Cortés et al. (2025) found that gamification in algebra teaching increased the richness of processes due to the dual syntactic–semantic nature of algebra, but this study broadens that observation by showing that gamification, when properly articulated, can foster processes of exploration and argumentation, and the use of multiple representations in other branches of mathematics.

The results obtained in this study show that specific training in gamification, articulated through the DSC and the Didactic–Mathematical Knowledge and Competencies model, supports the development of professional competencies in mathematics PTs. On the one hand, an evolution is observed in the sub-competency of analysing and evaluating didactical suitability, which is reflected in the ability to justify the use of gamification from a didactical analysis perspective. On the other hand, increased knowledge is evident in both their reflections after completing the TC and in their MFPs.

3.3. Evolution of Justifications According to the Time at Which the Teaching Reflection Occurred

This section presents a qualitative analysis of PTs’ reflections according to the moment at which they occurred, with the aim of observing if the arguments made a priori remained consistent with those proposed a posteriori.

In the debate, the a priori idea emerged that gamification should not be applied in higher-level courses. This suggests that some curricular content is better-suited to active methodologies, while others may require a more traditional approach.

“PT4: The thing is, I don’t know to what extent, to work on all mathematics content, gamification is necessary. Yes, for some… I think for some concepts, yes, but not all. And also, not in every year group. I mean, in a baccalaureate course, maybe, I’m not sure to what extent gamification would just waste more time. In secondary education, you do need to give them a lot of prior knowledge, right? I mean, yes. With gamification, maybe you help consolidate knowledge in secondary education, but then in baccalaureate, I think it needs to be more nuanced, because maybe there you need to get more into the subject matter.”

Even so, as seen in the previous section, Alberca (2025) replaces this more traditional approach and prioritises more active learning; indeed, in his MFP, he articulates the learning sequence in accordance with the Catalan educational curriculum:

“The fact that all chapters are modelled problems in which students choose resolution strategies and apply logic means that Competency 1 of the curriculum (Department of Education, 2022) is fully addressed. Thanks to the fact that most chapters require justification of the procedure followed, students also work on Competency 2. As with Competency 1, Competency 3 is also present in all chapters, as each one creates a path where the team gradually builds mathematical knowledge through problem posing and solving them with reasoning and creativity. Competency 4 is mainly addressed in Annex C.6 (where students are asked to change functions and observe the new trend) and Annex C.9 (where they are explicitly asked to invent modifications to fix discontinuities). As for Competency 5, it is present in all chapters: the exercises constantly require changing representations and comparing different types. Competency 6 is clearly addressed in Annex C.10, where mathematics and technology are worked on simultaneously. All chapters are carried out collectively (in groups of three), aiming to develop Competencies 7 and 9.”

(Alberca, 2025, p. 15)

In this way, this PT reasons that gamification is indeed appropriate and can increase the suitability of the teaching–learning process in higher-level courses.

Regarding adaptation to individual differences, a priori, opposing ideas emerged in the debate among PTs. On the one hand, some expressed that did not possess knowledge and had not learned how to adapt their activities to address issues of diversity:

“PT3: I mean, if I understand the question, like whether you’ve learned things in the course that are relevant for addressing diversity. I haven’t learned anything in the course, nor in the master. I mean, no. I mean, let’s say, right? We have, I don’t know if you’ve done your internship, a class of 20 students and some have dyscalculia. Of course, how do you do a calculation or number activity with a student who has dyscalculia? You can’t give them the same exercise or the same activity.”

However, in another debate group, they expressed more generally that they had developed some knowledge of how to address diversity:

“PT1: What aspects of what you’ve learned in the course do you think are most relevant for addressing diversity in the classroom? Have you learned to design activities that consider different levels of knowledge?

PT3: The different levels of knowledge, yes, for example, the Halloween activity, in the end you had four tasks, some easier than others. You know, you propose different techniques.

PT2: And I suppose also, if you make groups, you’re also trying to…

PT1: Heterogenize.

PT2: Exactly. Collaborative work. Critical thinking…”

However, if we look at the a posteriori arguments, in Gimeno’s (2025) MFP, it is detailed how diversity was addressed in an entirely gamified didactic sequence:

“However, during the initial observation phase of the internship, I held conversations with the group tutors and also with the school’s counsellors to identify the most relevant educational needs. In the case of students with ASD, for example, I was informed that they showed strong skills in drawing. With this information, I tried to ensure they felt recognised and involved in the project, both in the roles distribution in cooperative work and in the application activities involving graphical representation with GeoGebra. One student surprised us by spontaneously creating a personalised map of their amusement park, while another proposed designing attractions using polygonal shapes with notable precision.”

(Gimeno, 2025, p. 10)

This indicates that, although not all PTs were fully aware of the process, their practice did support the development of inclusive strategies, suggesting a dissonance between perception and formative action that deserves further exploration, given the evidence that gamification is not only useful for engaging students but also for effectively addressing diversity, using tools and activities that enable active participation from students regardless of their abilities or difficulties.

A common concern expressed by PTs when using playful learning methodologies is the risk of “hiding” the mathematical object that students are meant to learn, which can lead to a loss of epistemic suitability in learning, as expressed in the following debate:

PT4: Sometimes, when I gamify a concept, I feel like I’m hiding the mathematics, you know? It’s like you’re so focused on the game, but you’re not really understanding the maths.

PT2: I was thinking the same, like maybe something more formal is missing, you know?

PT4: Because I was thinking the same thing, it’s true that you can use concepts to solve the games, but if you want those concepts to be learned effectively, they need to be formalised. I mean, you have to say, “this is this theorem.”

PT1: Yes, like we said, the complement, the institutionalisation.

However, in MFPs such as that of Jdayah (2025), it is observed that when gamification is properly structured, the mathematical process of institutionalisation is embedded in the gamified activity:

“The Design Project has a dual focus: oral communication to present the design to peers and teachers, and written communication in the final report.

The space for manipulation and experimentation was mainly reserved for the project work. Models studied in lectures were applied, and knowledge was later explored through the design and layout of the park. (…)

All the activities, including the competency-based tasks, involve argumentation, as does the Project. However, the level and depth of argumentation vary depending on the activity, with the Park Project offering greater depth due to the reflective level and the nature of the questions to be justified in the final report: purpose of the park, use of space, socio-cultural utility of the space, etc.”

(Jdayah, 2025, pp. 8–9)

In this way, through the preparation of the final report, the institutionalisation of learning is integrated into the gamified activity. The fact that the park project includes a reflective task requiring a final report with formal justifications demonstrates how gamification can be complemented with an approach that promotes critical thinking, argumentation, and deep conceptualisation, thus enhancing the richness of processes without compromising epistemic suitability.

Beyond the formal component, another aspect that generated debate was the narrative density used in gamified activities, as, during the TC debate, it was expressed that overly dense narratives can conceal the problem to be solved:

“PT2: There’s something that happens to me, because, for example, today’s activity (Kafka’s Metamorphosis) seemed perfect to me, as it was quite fun… But there wasn’t too much context. Because one thing I notice is that, for example, in the GeoGebra one, there was so much information, you know? To create the game, the game’s context… Then there was loads of information, and in the end, what you had to do was actually a small part. But you had to read a lot. That distracted me, maybe because I get… Yes, I get distracted easily. But I think of people who struggle…

PT5: Yes, yes, yes…

PT2: Because it kind of takes your focus away, a bit, because you have to create the characters. There was a story, and then what it asked you to do seemed much simpler than the story.

PT4: I agree. It’s like: ‘What’s the actual question? What are you asking me?’ And it was so hidden… and it’s like ‘I’m not getting it’.”

However, Alberca (2025) argues that setting clear, ordered goals helps prevent students from getting lost, and that dialogues explaining the theory in a more entertaining way help students to perceive learning as a game rather than as exercises they do not know how to solve (p. 14). In this sense, he even proposes a way to improve the TC by simplifying the narrative of some activities through ordered goals and using dialogues to explain the theoretical content.

In summary, the comparative analysis between the teaching reflections collected during the group debate after the TC and the evidence from the MFPs shows an evolution in the perception and application of gamification in the teaching–learning process and in the construction of pedagogical arguments. Although initial doubts were expressed about its suitability for higher-level courses or its capacity to address diversity, and considering the limitations of the debate due to the PTs’ lack of knowledge of the DSC, the analysed learning sequences demonstrate that, when well-designed, gamification can be appropriately integrated into teaching practice. Furthermore, the importance of complementing the playful approach with processes that institutionalise the mathematical knowledge becomes evident; these can be embedded in the active methodology. Moreover, the later incorporation of the DSC into the training enabled PTs to deepen their analyses and propose concrete improvements to their practices, reinforcing the idea that collective reflection, continuous training, and reflective support are essential for the development of teaching competencies.

4. Conclusions

The results of this study evidence the positive impact of training in gamification for secondary mathematics education on the development of the subcompetency of analysing and evaluating didactical suitability among PTs. The use of analytical tools such as the DSC and the Didactic Mathematical Knowledge and Competencies model made it possible to observe an evolution in their reasoning, moving from superficial justifications focused on motivation (L₁) to more in-depth arguments grounded in didactical suitability criteria (L₃).

Following the completion of the TC on gamification, PTs not only incorporated gamified activities into their didactic proposals but also recognised their potential to foster game-related skills that can be leveraged in the mathematics teaching–learning process, such as perseverance, creativity, problem-solving, and group coordination. These “game skills” are linked to various components of the DSC and are developed in particular ways within playful contexts. The results suggest that PTs acquired relevant knowledge during their initial training, especially through the TC focused on gamification.

However, certain challenges in implementing gamification were also identified, such as the need for more time to design and implement activities, the adaptation of the physical classroom space, institutional support from schools, and teacher training to apply innovative methodologies. These limitations, which were expressed by participants during the debates after the TC, reinforce the importance of expanding and deepening teacher training in gamification to overcome such barriers.

Future research should explore the impact of gamification not only on mathematics learning outcomes but also on other dimensions contemplated in the Didactical Suitability Criteria. These include collaborative work, autonomy, metacognition, self-regulated learning, and the effective use of manipulative and technological resources. Analysing these aspects would provide a more comprehensive understanding of how gamification influences both cognitive and affective components of the teaching–learning process, as well as its potential to foster the transversal competencies essential for didactical suitability on the teaching–learning process in mathematics. Another aspect that would be interesting to analyse is how the participants in the training cycle implement gamification in their classes once they become teachers, in order to assess a longitudinal effect.

Overall, the results show that gamification, when designed and implemented using structured and consensual didactical criteria, can significantly contribute to the suitability of the mathematics teaching–learning process. Nonetheless, it is considered necessary to continue strengthening PTs’ training in didactical analysis, to promote spaces for collaborative reflection, and to optimise the gamified TC to consolidate teaching competencies in innovative mathematics teaching and learning contexts.