How Teaching Practices Relate to Early Mathematics Competencies: A Non-Linear Modeling Perspective
Abstract
1. Introduction
2. Current Study
3. Methods
3.1. Participants
3.2. Intervention
3.3. Procedure
3.4. Measures
3.4.1. Research-Based Early Mathematics Assessment
3.4.2. Classroom Observation of Early Mathematics—Environment and Teaching
3.5. Overview of Analysis
4. Results
4.1. Preliminary Descriptive Analysis of COEMET Item Scores in the Spring of the Pre-K Year
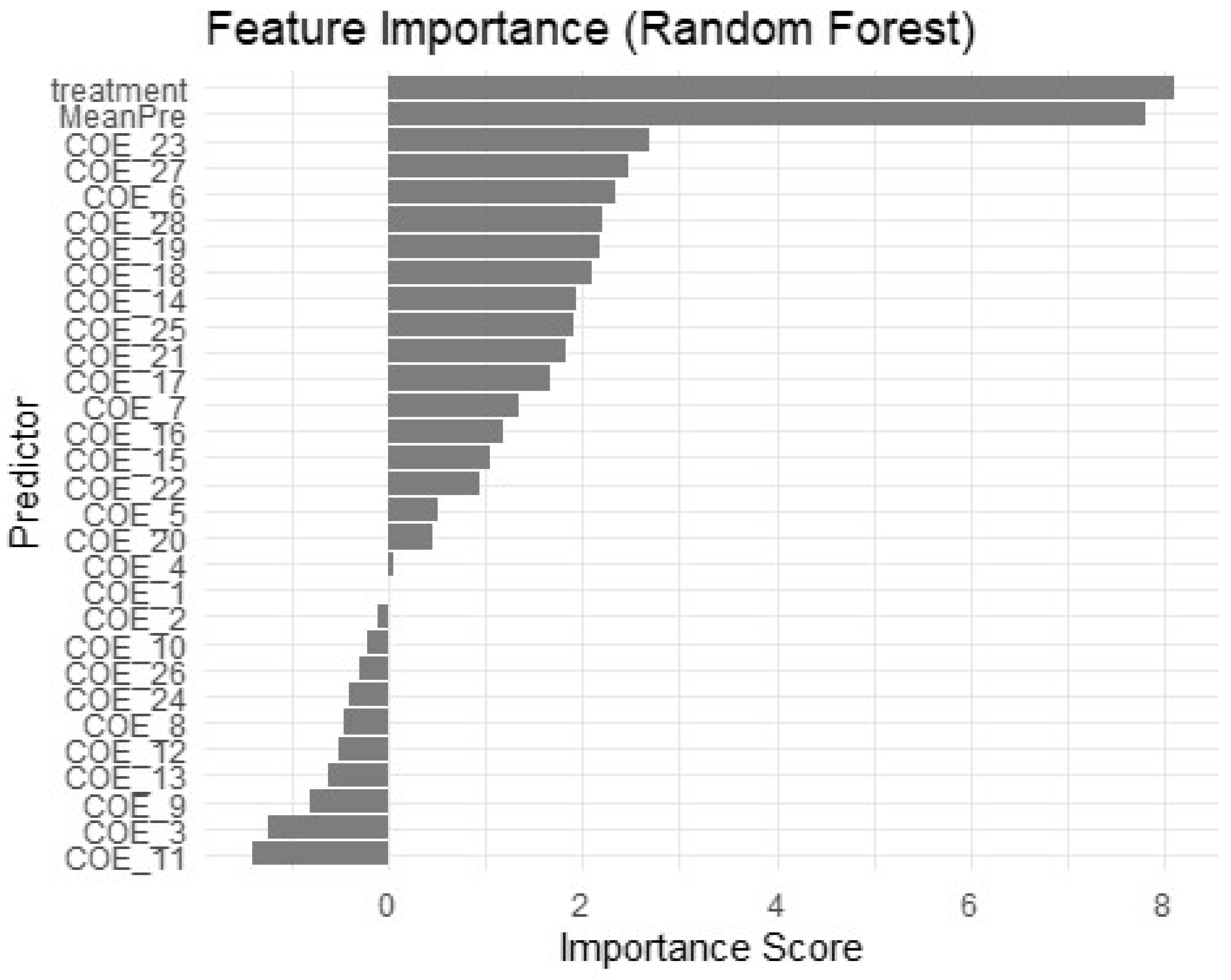
4.2. The Importance of COEMET Indicators in Predicting Early Math Competencies
4.3. Incremental Prediction of Early Math Competencies with Non-Linear Modeling and COEMET Items
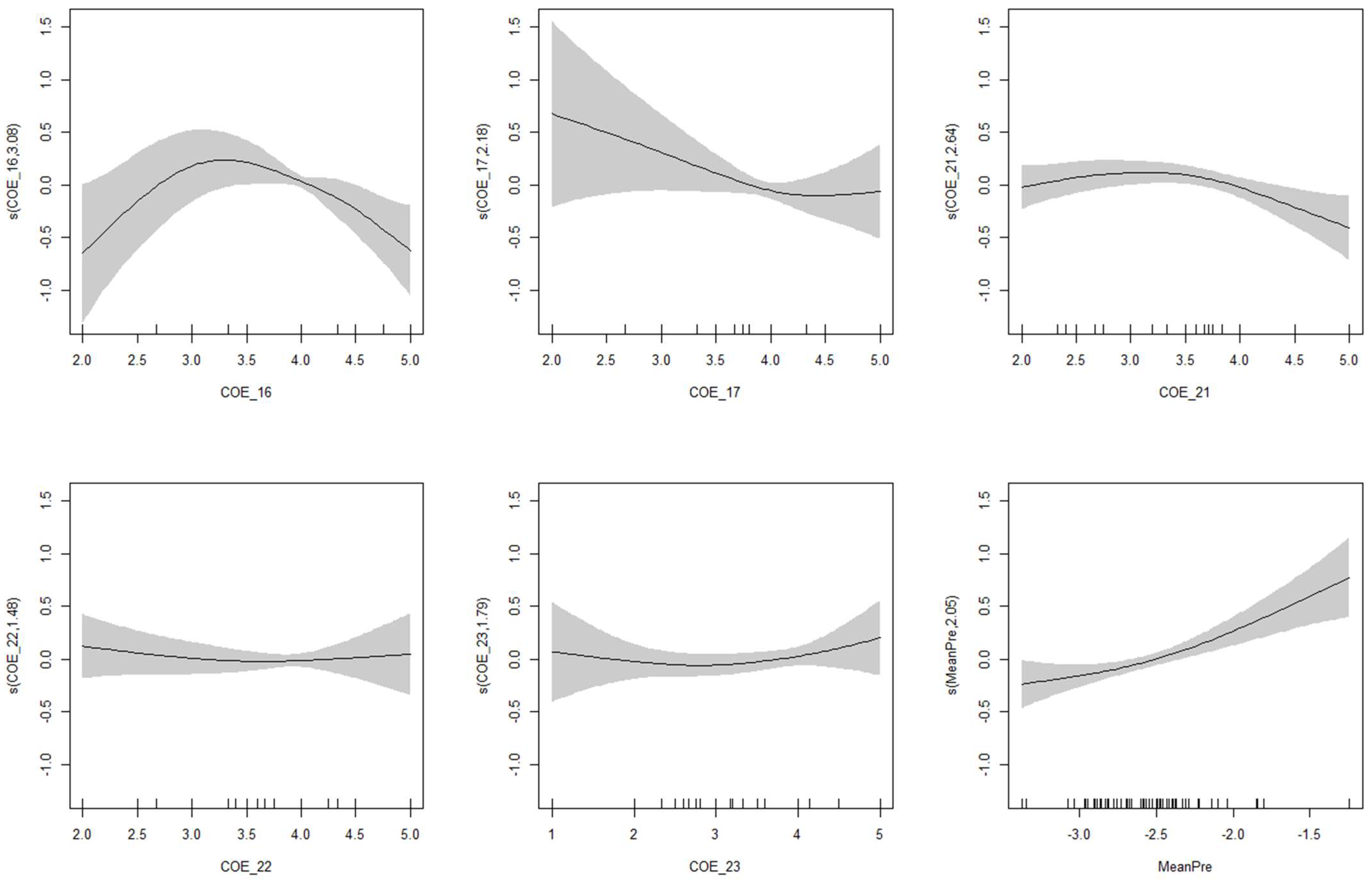
4.4. Non-Linear Associations Between Classroom Practices and Early Math Competency
5. Discussion and Implications
5.1. Non-Linear Relations Between Teaching Practices and Early Mathematics Learning
5.2. Potential Revisions to COEMET
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Archer, K. J., & Kimes, R. V. (2008). Empirical characterization of random forest variable importance measures. Computational Statistics & Data Analysis, 52(4), 2249–2260. [Google Scholar] [CrossRef]
- Attaway, D. S., Engel, M., Jacob, R., Erickson, A., & Claessens, A. (2025). Understanding mathematics instruction in Kindergarten. The Elementary School Journal, 125(3), 518–547. [Google Scholar] [CrossRef]
- Auret, L., & Aldrich, C. (2012). Interpretation of non-linear relationships between process variables by use of random forests. Minerals Engineering, 35, 27–42. [Google Scholar] [CrossRef]
- Bachman, H. J., Votruba-Drzal, E., El Nokali, N. E., & Castle Heatly, M. (2015). Opportunities for learning math in elementary school: Implications for SES disparities in procedural and conceptual math skills. American Educational Research Journal, 52(5), 894–923. [Google Scholar] [CrossRef]
- Bassok, D., Dee, T. S., & Latham, S. (2019). The effects of accountability incentives in early childhood education. Journal of Policy Analysis and Management, 38(4), 838–866. [Google Scholar] [CrossRef]
- Bassok, D., Magouirk, P., & Markowitz, A. J. (2021). Systemwide quality improvement in early childhood education: Evidence from Louisiana. AERA Open, 7, 23328584211011610. [Google Scholar] [CrossRef]
- Bognar, B., Mužar Horvat, S., & Jukić Matić, L. (2025). Characteristics of effective elementary mathematics instruction: A scoping review of experimental studies. Education Sciences, 15(1), 76. [Google Scholar] [CrossRef]
- Bos, S. E., Powell, S. R., Maddox, S. A., & Doabler, C. T. (2022). A synthesis of the conceptualization and measurement of implementation fidelity in mathematics intervention research. Journal of Learning Disabilities, 32(1), 1–21. [Google Scholar] [CrossRef]
- Botvin, C. M., Jenkins, J. M., Carr, R. C., Dodge, K. A., Clements, D. H., Sarama, J., & Watts, T. W. (2024). Can peers help sustain the positive effects of an early childhood mathematics intervention? Early Childhood Research Quarterly, 67, 159–169. [Google Scholar] [CrossRef]
- Breiman, L. (2001). Random forests. Machine Learning, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L., Cutler, A., Liaw, A., Wiener, M., & Liaw, M. A. (2018). Package ‘randomforest’ (Version 4.6-14) [R package]. University of California. [Google Scholar]
- Brunsek, A., Perlman, M., Falenchuk, O., McMullen, E., Fletcher, B., & Shah, P. S. (2017). The relationship between the Early Childhood Environment Rating Scale and its revised form and child outcomes: A systematic review and meta-analysis. PLoS ONE, 12(6), e0178512. [Google Scholar] [CrossRef]
- Burchinal, M. R., Zaslow, M., & Tarullo, L. (2016). Quality thresholds, features, and dosage in early care and education: Secondary data analyses of child outcomes. Monographs of the Society for Research in Child Development, 81(2), 1–126. [Google Scholar]
- Carr, R. C., Mokrova, I. L., Vernon-Feagans, L., & Burchinal, M. R. (2019). Cumulative classroom quality during pre-kindergarten and kindergarten and children’s language, literacy, and mathematics skills. Early Childhood Research Quarterly, 47, 218–228. [Google Scholar] [CrossRef]
- Chernyak, N., Harris, P. L., & Cordes, S. (2022). A counting intervention promotes fair sharing in preschoolers. Child Development, 93(5), 1365–1379. [Google Scholar] [CrossRef] [PubMed]
- Clements, D. H., Lizcano, R., & Sarama, J. (2023). Research and pedagogies for early math. Education Sciences, 13(839), 839. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2008). Experimental evaluation of the effects of a research-based preschool mathematics curriculum. American Educational Research Journal, 45(2), 443–494. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2011). Early childhood mathematics intervention. Science, 333(6045), 968–970. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2013). Building Blocks, Volumes 1 and 2. McGraw-Hill Education. [Google Scholar]
- Clements, D. H., & Sarama, J. (2024). Systematic review of learning trajectories in early mathematics. ZDM–Mathematics Education, 57(4), 637–650. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (in press). Learning and teaching early math: The learning trajectories approach (4th ed.). Routledge.
- Clements, D. H., Sarama, J., Layzer, C., Unlu, F., & Fesler, L. (2020). Effects on mathematics and executive function of a mathematics and play intervention versus mathematics alone. Journal for Research in Mathematics Education, 51(3), 301–333. [Google Scholar] [CrossRef]
- Clements, D. H., Sarama, J., & Liu, X. H. (2008). Development of a measure of early mathematics achievement using the Rasch model: The Research-Based Early Maths Assessment. Educational Psychology, 28(4), 457–482. [Google Scholar] [CrossRef]
- Clements, D. H., Sarama, J., Spitler, M. E., Lange, A. A., & Wolfe, C. B. (2011). Mathematics learned by young children in an intervention based on learning trajectories: A large-scale cluster randomized trial. Journal for Research in Mathematics Education, 42(2), 127–166. [Google Scholar] [CrossRef]
- Clements, D. H., Sarama, J., Wolfe, C. B., & Day-Hess, C. A. (2008/2025). REMA—Research-based early mathematics assessment. Kennedy Institute, University of Denver. [Google Scholar]
- Clements, D. H., Sarama, J., Wolfe, C. B., & Day-Hess, C. A. (2017). REMA-SF—Research-based early mathematics assessment short form. Kennedy Institute, University of Denver. [Google Scholar]
- Clements, D. H., Sarama, J., Wolfe, C. B., & Spitler, M. E. (2013). Longitudinal evaluation of a scale-up model for teaching mathematics with trajectories and technologies: Persistence of effects in the third year. American Educational Research Journal, 50(4), 812–850. [Google Scholar] [CrossRef]
- Cummings, T., Farran, D. C., Hofer, K. G., Bilbrey, C., & Lipsey, M. W. (2010, June 28–30). Starting a chain reaction: Encouraging teachers to support children’s talk about mathematics. IES Research Conference, Washington, DC, USA. [Google Scholar]
- Dong, Y., & Clements, D. H. (2025). Consequential validity of early childhood assessments. In O. Saracho (Ed.), Research methods for studying young children. Emerald Group Publishing. [Google Scholar]
- Dong, Y., Clements, D. H., Day-Hess, C. A., Sarama, J., & Dumas, D. (2021). Measuring early childhood mathematical cognition: Validating and equating two forms of the Research-Based Early Mathematics Assessment. Journal of Psychoeducational Assessment, 39(8), 983–998. [Google Scholar] [CrossRef]
- Dong, Y., Dumas, D., Clements, D. H., Day-Hess, C. A., & Sarama, J. (2023). Evaluating the consequential validity of the Research-Based Early Mathematics Assessment. Journal of Psychoeducational Assessment, 41(5), 575–582. [Google Scholar] [CrossRef]
- Duncan, G. J., & Magnuson, K. (2011). The nature and impact of early achievement skills, attention skills, and behavior problems. In G. J. Duncan, & R. Murnane (Eds.), Whither opportunity? Rising inequality and the uncertain life chances of low-income children (pp. 47–70). Sage. [Google Scholar]
- Elia, I., Baccaglini-Frank, A., Levenson, E., Matsuo, N., Feza, N., & Lisarelli, G. (2023). Early childhood mathematics education research: Overview of latest developments and looking ahead. Annales de Didactique et de Sciences Cognitives. Revue Internationale de Didactique des Mathématiques, 28, 75–129. [Google Scholar] [CrossRef]
- Engel, M., Jacob, R., Hart Erickson, A., Mattera, S., Shaw Attaway, D., & Claessens, A. (2024). The alignment of P–3 math instruction. AERA Open, 10, 23328584241281483. [Google Scholar] [CrossRef]
- English, L. D. (2023). Ways of thinking in STEM-based problem solving. ZDM—Mathematics Education, 55(7), 1219–1230. [Google Scholar] [CrossRef]
- Farran, D. C., Lipsey, M. W., & Wilson, S. J. (2011, November 7–8). Curriculum and pedagogy: Effective math instruction and curricula. Early Childhood Math Conference, Berkeley, CA, USA. [Google Scholar]
- Finders, J. K., Budrevich, A., Duncan, R. J., Purpura, D. J., Elicker, J., & Schmitt, S. A. (2021). Variability in preschool CLASS scores and children’s school readiness. AERA Open, 7, 23328584211038938. [Google Scholar] [CrossRef]
- Fullan, M. G. (1982). The meaning of educational change. Teachers College Press. [Google Scholar]
- Gerofsky, P. R. (2015). Why Asian preschool children mathematically outperform preschool children from other countries. Western Undergraduate Psychology Journal, 3(1), 1–8. Available online: http://ir.lib.uwo.ca/wupj/vol3/iss1/11 (accessed on 1 June 2025).
- Gripton, C., & Williams, H. J. (2023). The principles for appropriate pedagogy in early mathematics: Exploration, apprenticeship and sense-making: Part 2. Mathematics Teaching, 286, 5–7. Available online: https://www.atm.org.uk/write/MediaUploads/Journals/MT286/02.pdf (accessed on 1 June 2025).
- Hamre, B. K., Pianta, R. C., Burchinal, M. R., Field, S., LoCasale-Crouch, J., Downer, J. T., Howes, C., LaParo, K., & Scott-Little, C. (2012). A course on effective teacher-child interactions: Effects on teacher beliefs, knowledge, and observed practice. American Educational Research Journal, 49(1), 88–123. [Google Scholar] [CrossRef]
- Harpe, S. E. (2015). How to analyze Likert and other rating scale data. Currents in pharmacy teaching and learning, 7(6), 836–850. [Google Scholar] [CrossRef]
- Hill, H. C., Rowan, B., & Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42(2), 371–406. [Google Scholar] [CrossRef]
- Kilday, C. R., & Kinzie, M. B. (2009). An analysis of instruments that measure the quality of mathematics teaching in early childhood. Early Childhood Education Journal, 36(4), 365–372. [Google Scholar] [CrossRef]
- Konstantopoulos, S. (2011). Teacher effects in early grades: Evidence from a randomized study. Teachers College Record, 113(7), 1541–1565. [Google Scholar] [CrossRef]
- Liu, Y., Peng, P., & Yan, X. (2025). Early numeracy and mathematics development: A longitudinal meta-analysis on the predictive nature of early numeracy. Journal of Educational Psychology, 117(6), 863–883. [Google Scholar] [CrossRef]
- Maier, M. F., McCormick, M. P., Xia, S., Hsueh, J., Weiland, C., Morales, A., Boni, M., Tonachel, M., Sachs, J., & Snow, C. (2022). Content-rich instruction and cognitive demand in prek: Using systematic observations to predict child gains. Early Childhood Research Quarterly, 60(1), 96–109. [Google Scholar] [CrossRef]
- McCormick, M. P., Mattera, S. K., Maier, M. F., Xia, S., Jacob, R., & Morris, P. A. (2021). Different settings, different patterns of impacts: Effects of a Pre-K math intervention in a mixed-delivery system. Early Childhood Research Quarterly, 58, 136–154. [Google Scholar] [CrossRef]
- McCoy, D. C., Salhi, C., Yoshikawa, H., Black, M., Britto, P., & Fink, G. (2018). Home- and center-based learning opportunities for preschoolers in low- and middle-income countries. Children and Youth Services Review, 88, 44–56. [Google Scholar] [CrossRef]
- McCoy, D. C., Yoshikawa, H., Ziol-Guest, K. M., Duncan, G. J., Schindler, H. S., Magnuson, K., Yang, R., Koepp, A., & Shonkoff, J. P. (2017). Impacts of early childhood education on medium- and long-term educational outcomes. Educational Researcher, 46(8), 474–487. [Google Scholar] [CrossRef]
- Mesiti, C., Seah, W. T., Kaur, B., Pearn, C., Jones, A., Cameron, S., Every, E., & Copping, K. (Eds.). (2024). Research in mathematics education in Australasia 2020–2023. Springer Nature Singapore. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. (2024). A new vision for high-quality preschool curriculum. The National Academies Press. [Google Scholar] [CrossRef]
- National Research Council. (2009). Mathematics learning in early childhood: Paths toward excellence and equity. National Academy Press. [Google Scholar] [CrossRef]
- Nesbitt, K. T., & Farran, D. C. (2021). Effects of prekindergarten curricula: Tools of the Mind as a case study. Monographs of the Society for Research in Child Development, 86(1), 7–119. [Google Scholar] [CrossRef] [PubMed]
- Nicodemus, K. K. (2011). Letter to the Editor: On the stability and ranking of predictors from random forest variable importance measures. Briefings in Bioinformatics, 12(4), 369–373. [Google Scholar] [CrossRef] [PubMed]
- OECD. (2014). Strong performers and successful reformers in education—Lessons from PISA 2012 for the United States. OECD Publishing. [Google Scholar] [CrossRef]
- Orcan-Kacan, M., Dedeoglu-Aktug, N., & Alpaslan, M. M. (2023). Teachers’ mathematics pedagogical content knowledge and quality of early mathematics instruction in Turkey. South African Journal of Education, 43(4), 1–19. [Google Scholar] [CrossRef]
- Ottmar, E. R., Decker, L. E., Cameron, C. E., Curby, T. W., & Rimm-Kaufman, S. E. (2013). Classroom instructional quality, exposure to mathematics instruction and mathematics achievement in fifth grade. Learning Environments Research, 17(2), 243–262. [Google Scholar] [CrossRef]
- Perlman, M., Falenchuk, O., Fletcher, B., McMullen, E., Beyene, J., & Shah, P. S. (2016). A systematic review and meta-analysis of a measure of staff/child interaction quality (the classroom assessment scoring system) in early childhood education and care settings and child outcomes. PLoS ONE, 11(12), e0167660. [Google Scholar] [CrossRef]
- Phillips, D. A., Lipsey, M. W., Dodge, K. A., Haskins, R., Bassok, D., Burchinal, M. R., Duncan, G. J., Dynarski, M., Magnuson, K. A., & Weiland, C. (Eds.). (2017). The current state of scientific knowledge on pre-kindergarten effects. Brookings Institution and Duke University. [Google Scholar]
- Pianta, R., Hamre, B., Downer, J., Burchinal, M., Williford, A., Locasale-Crouch, J., Howes, C., La Paro, K., & Scott-Little, C. (2017). Early childhood professional development: Coaching and coursework effects on indicators of children’s school readiness. Early Education and Development, 28(8), 956–975. [Google Scholar] [CrossRef]
- Pohle, L., Hosoya, G., Pohle, J., & Jenßen, L. (2022). The relationship between early childhood teachers’ instructional quality and children’s mathematics development. Learning and Instruction, 82(1), 1–12. [Google Scholar] [CrossRef]
- Ran, H., Secada, W. G., Rhoads, C. H., Schoen, R., Tazaz, A., & Liu, X. (2022, April 22–26). The long-term effects of cognitively guided instruction on elementary students’ mathematics achievement. American Educational Research Association, San Deigo, CA, USA. [Google Scholar]
- R Core Team. (2024). R: A language and environment for statistical computing (Version 4.4.2) [Computer software]. R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 1 June 2025).
- Rosenfeld, D., Dominguez, X., Llorente, C., Pasnik, S., Moorthy, S., Hupert, N., Gerard, S., & Vidiksis, R. (2019). A curriculum supplement that integrates transmedia to promote early math learning: A randomized controlled trial of a PBS KIDS intervention. Early Childhood Research Quarterly, 49, 241–253. [Google Scholar] [CrossRef]
- Sanders, W. L., & Horn, S. P. (1998). Research findings from the Tennessee Value-Added Assessment System (TVAAS) database: Implications for educational evaluation and research. Journal of Personnel Evaluation in Education, 12(3), 247–256. [Google Scholar] [CrossRef]
- Sanders, W. L., & Rivers, J. C. (1996). Cumulative and residual effects of teachers on future student academic achievement (Research Progress Report) [not online]. University of Tennessee Value-Added Research and Assessment Center. [Google Scholar]
- Sarama, J., & Clements, D. H. (2019). COEMET: The classroom observation of early mathematics environment and teaching instrument. University of Denver. [Google Scholar]
- Sarama, J., & Clements, D. H. (2021). Long-range impact of a scale-up model on mathematics teaching and learning: Persistence, sustainability, and diffusion. Journal of Cognitive Education and Psychology, 20(2), 112–122. [Google Scholar] [CrossRef]
- Sarama, J., Clements, D. H., Starkey, P., Klein, A., & Wakeley, A. (2008). Scaling up the implementation of a pre-kindergarten mathematics curriculum: Teaching for understanding with trajectories and technologies. Journal of Research on Educational Effectiveness, 1(1), 89–119. [Google Scholar] [CrossRef]
- Sarama, J., Clements, D. H., Wolfe, C. B., & Spitler, M. E. (2016). Professional development in early mathematics: Effects of an intervention based on learning trajectories on teachers’ practices. NOMAD Nordic Studies in Mathematics Education, 21(4), 29–55. [Google Scholar] [CrossRef]
- Sarama, J., Lange, A., Clements, D. H., & Wolfe, C. B. (2012). The impacts of an early mathematics curriculum on emerging literacy and language. Early Childhood Research Quarterly, 27(3), 489–502. [Google Scholar] [CrossRef]
- Scalise, N. R., Gladstone, J. R., & Miller-Cotto, D. (2025). Maximizing math achievement: Strategies from the science of learning. Journal of Experimental Child Psychology, 257, 106281. [Google Scholar] [CrossRef] [PubMed]
- Schenke, K., Nguyen, T., Watts, T. W., Sarama, J., & Clements, D. H. (2017). Differential effects of the classroom on African American and non-African American’s mathematics achievement. Journal of Educational Psychology, 109(6), 794–811. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C., Boulesteix, A.-L., Zeileis, A., & Hothorn, T. (2007). Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinformatics, 8(1), 25. [Google Scholar] [CrossRef]
- Watts, T. W., Duncan, G. J., Siegler, R. S., & Davis-Kean, P. E. (2014). What’s past is prologue: Relations between early mathematics knowledge and high school achievement. Educational Researcher, 43(7), 352–360. [Google Scholar] [CrossRef]
- Watts, T. W., Gandhi, J., Ibrahim, D. A., Masucci, M. D., & Raver, C. C. (2018). The Chicago School Readiness Project: Examining the long-term impacts of an early childhood intervention. PLoS ONE, 13, e0200144. [Google Scholar] [CrossRef]
- Weiland, C., & Rosada, P. G. (2022). WIdely used measures of pre-k classroom quality: What we know, gaps in the field, and promising new directions. MDRC. Available online: https://www.mdrc.org/sites/default/files/Widely_Used_Measures.pdf (accessed on 1 June 2025).
- Whittaker, J. V., Kinzie, M. B., Vitiello, V., DeCoster, J., Mulcahy, C., & Barton, E. A. (2020). Impacts of an early childhood mathematics and science intervention on teaching practices and child outcomes. Journal of Research on Educational Effectiveness, 13(2), 177–212. [Google Scholar] [CrossRef]
- Wickham, H. (2023). ggplot2: Create elegant data visualisations using the grammar of graphics (Version 3.4.4) [R package]. Available online: https://CRAN.R-project.org/package=ggplot2 (accessed on 1 June 2025).
- Wood, S. N. (2017). Generalized additive models: An introduction with R. Chapman and Hall/CRC. [Google Scholar]
- Wood, S. N. (2023). mgcv: Mixed GAM computation vehicle with automatic smoothness estimation (Version 1.9-0) [R package]. Available online: https://CRAN.R-project.org/package=mgcv (accessed on 1 June 2025).
- Wright, B. D., & Masters, G. N. (1982). Rating scale analysis. MESA Press. [Google Scholar]
- Wright, S. P., Horn, S. P., & Sanders, W. L. (1997). Teacher and classroom context effects on student achievement: Implications for teacher evaluation. Journal of Personnel Evaluation in Education, 11(1), 57–67. [Google Scholar] [CrossRef]
- Yıldız, E., Koca, Ö., & Elaldı, Ş. (2025). Effectiveness of early intervention programs in developing early mathematical skills: A meta-Analysis. Journal of Theoretical Educational Science, 18(1), 54–80. [Google Scholar] [CrossRef]
| Control | Intervention | ||||
|---|---|---|---|---|---|
| Mean | SD | Mean | SD | ||
| Classroom Culture | |||||
| 1. | Teacher actively interacted | 4.79 | 0.48 | 4.99 | 0.12 |
| 2. | Other staff interacted | 4.13 | 1.07 | 4.67 | 0.67 |
| 3. | Used teachable moments | 3.29 | 1.14 | 3.79 | 0.84 |
| 4. | Students used math software | 1.88 | 1.56 | 4.36 | 1.19 |
| 5. | Environment showed signs of math | 3.39 | 1.03 | 3.94 | 0.71 |
| 6. | Student math work or thinking on display | 2.97 | 1.29 | 3.43 | 0.98 |
| 7. | Teacher knowledgeable about math | 3.79 | 0.74 | 3.99 | 0.59 |
| 8. | Teacher showed she believed math learning can be enjoyable | 3.71 | 0.87 | 3.99 | 0.64 |
| 9. | Teacher showed curiosity/enthusiasm for math | 3.53 | 0.99 | 3.85 | 0.87 |
| Specific Math Activity | |||||
| 10. | Teacher understanding | 3.91 | 0.61 | 4.00 | 0.43 |
| 11. | Content developmentally appropriate | 3.87 | 0.63 | 3.96 | 0.47 |
| 12. | Engage mathematical thinking | 3.57 | 0.72 | 3.90 | 0.46 |
| 13. | Pace appropriate for developmental level | 3.77 | 0.68 | 3.96 | 0.37 |
| 14. | Management strategies enhanced quality | 3.56 | 0.85 | 3.94 | 0.45 |
| 15. | Percent teacher involved in activity | 4.82 | 0.51 | 4.68 | 0.65 |
| 16. | Teaching strategies developmentally appropriate | 3.80 | 0.72 | 3.95 | 0.48 |
| 17. | High but realistic expectations of students | 3.65 | 0.82 | 3.94 | 0.51 |
| 18. | Acknowledged or reinforced effort of students | 3.86 | 0.66 | 4.01 | 0.34 |
| 19. | Asked students to share ideas | 3.43 | 0.94 | 3.75 | 0.62 |
| 20. | Facilitated students’ responding | 3.58 | 0.83 | 3.90 | 0.50 |
| 21. | Encouraged students to listen/evaluate thinking of others | 3.23 | 0.89 | 3.53 | 0.81 |
| 22. | Supported describers thinking | 3.56 | 0.80 | 3.80 | 0.58 |
| 23. | Supported listeners understanding | 2.93 | 1.08 | 3.43 | 0.84 |
| 24. | Just enough support provided | 3.61 | 0.88 | 3.93 | 0.42 |
| 25. | Elaborated math ideas of students | 3.19 | 1.00 | 3.62 | 0.70 |
| 26. | Encouraged mathematical reflection | 3.27 | 0.91 | 3.46 | 0.70 |
| 27. | Observed, listened and took notes | 2.34 | 0.82 | 3.49 | 0.74 |
| 28. | Adapted tasks to accommodate range of abilities | 3.43 | 0.88 | 3.64 | 0.69 |
| Models | Predictors | Smooth Terms | Adjusted R-Squared | Deviance Explained |
|---|---|---|---|---|
| Baseline Model | Pretest + Intervention | None | 0.51 | 52.00% |
| Model 1 | Pretest + Intervention + CC + SMA | None | 0.51 | 53.90% |
| Model 2 | Pretest + Intervention + 17 COEMET Items | None | 0.50 | 64.40% |
| Model 3 | Pretest + Intervention + 17 COEMET Items | Q14–17, Q19–Q23, Q25, Q27, and Pretest | 0.72 | 83.40% |
| Model 4 | Pretest + Intervention + 17 COEMET Items | Q16–17, Q21–Q23, and Pretest | 0.72 | 83.40% |
| Predictors | B | SE | t | p |
|---|---|---|---|---|
| COEMET Q4 | −0.04 | 0.03 | −1.42 | 0.163 |
| COEMET Q5 | −0.06 | 0.06 | −0.90 | 0.374 |
| COEMET Q6 | −0.01 | 0.04 | −0.24 | 0.811 |
| COEMET Q7 | 0.10 | 0.08 | 1.30 | 0.200 |
| COEMET Q14 | 0.34 | 0.11 | 3.19 | 0.003 |
| COEMET Q15 | −0.04 | 0.05 | −0.84 | 0.407 |
| COEMET Q18 | 0.07 | 0.13 | 0.55 | 0.585 |
| COEMET Q19 | −0.14 | 0.08 | −1.76 | 0.087 |
| COEMET Q20 | 0.29 | 0.12 | 2.47 | 0.018 |
| COEMET Q25 | 0.07 | 0.07 | 0.98 | 0.331 |
| COEMET Q27 | −0.05 | 0.05 | −0.96 | 0.346 |
| COEMET Q28 | −0.03 | 0.06 | −0.54 | 0.590 |
| Intervention | 0.56 | 0.11 | 5.00 | <0.001 |
| Approximate significance of smooth terms | ||||
| EDF | Ref. DF | F | p | |
| s(COEMET Q16) | 3.08 | 3.71 | 4.29 | 0.007 |
| s(COEMET Q17) | 2.18 | 2.67 | 1.46 | 0.284 |
| s(COEMET Q21) | 2.64 | 3.17 | 3.65 | 0.018 |
| s(COEMET Q22) | 1.48 | 1.78 | 0.63 | 0.608 |
| s(COEMET Q23) | 1.79 | 2.19 | 0.79 | 0.456 |
| s(Pretest) | 2.05 | 2.60 | 8.75 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Clements, D.H.; Mulcahy, C.; Sarama, J. How Teaching Practices Relate to Early Mathematics Competencies: A Non-Linear Modeling Perspective. Educ. Sci. 2025, 15, 1175. https://doi.org/10.3390/educsci15091175
Dong Y, Clements DH, Mulcahy C, Sarama J. How Teaching Practices Relate to Early Mathematics Competencies: A Non-Linear Modeling Perspective. Education Sciences. 2025; 15(9):1175. https://doi.org/10.3390/educsci15091175
Chicago/Turabian StyleDong, Yixiao, Douglas H. Clements, Christina Mulcahy, and Julie Sarama. 2025. "How Teaching Practices Relate to Early Mathematics Competencies: A Non-Linear Modeling Perspective" Education Sciences 15, no. 9: 1175. https://doi.org/10.3390/educsci15091175
APA StyleDong, Y., Clements, D. H., Mulcahy, C., & Sarama, J. (2025). How Teaching Practices Relate to Early Mathematics Competencies: A Non-Linear Modeling Perspective. Education Sciences, 15(9), 1175. https://doi.org/10.3390/educsci15091175






