Abstract
Situated within the Embodied Learning in Early Mathematics and Science project in Australia, this paper explores the relationships between ‘embodied activities’ used by a preschool teacher and the children’s development of number sense over six months. Using an instrumental case study approach, qualitative data from multiple sources including self-reported data from the teacher, activity descriptions, two task-based interviews with nine children, and number-knowledge data extracted from a mathematics achievement assessment (pretest and post-test) was analysed. Pattern searching techniques across text and video revealed connections between the embodied activities implemented by the teacher and the children’s development of subitizing and counting skills, mathematical drawing, and number magnitude knowledge. We propose that attending to specific aspects of children’s physical development, particularly finger dexterity and drawing skills, in experiences that focus on representing number concepts, can support their development of number sense.
1. Introduction
In Australia, as in other parts of the world, the principles that guide early childhood education advocate for practices that attend to the holistic development of the child. The Early Years Learning Framework (Australian Government Department of Education [AGDE], 2022) refers to children’s learning as “dynamic, complex and holistic” and explains, “This means that cognitive, linguistic, physical, social, emotional, personal, spiritual and creative aspects are all intricately interwoven and interrelated” (p. 8). However, we suggest that few early childhood teachers perceive the interrelatedness of physical development and cognitive development, particularly regarding the domain of mathematics. There is a tendency to view physical development in terms fundamental movement skills (such as walking, kicking, throwing), fitness and health. In contrast to visible, ‘external’ skills, a traditional view of mathematical development tends to support the notion that mathematics learning takes place abstractly within the brain. Although early childhood teachers may readily perceive connections between aspects of physical activity and the child’s development of spatial awareness and reasoning (McCluskey et al., 2023), we suggest that few are likely to envisage substantial connections between physical development and a child’s emerging sense of number. In recent years, there has been increasing recognition that comprehensive learning theory must include the role of embodied interactions with the external environment and embodied representations of both external experiences and internal thoughts (Macrine & Fugate, 2022; Mavilidi et al., 2022). Therefore, attending to embodied learning approaches presents opportunities to explore the interrelationship between physical actions, such as gesture, locomotion, motor control of the hands, and mathematical representations and learning. Such an exploration is the purpose of this paper, with a focus on the development of early number sense.
1.1. Early Number Sense
Early number sense begins development in very young children and continues to evolve during the 4-to-8-years age range. Early number sense can be described as consisting of three interrelated core competencies in relation to whole numbers: number, number relations, and number operations (Jordan et al., 2022). Children’s levels of competence in these three components of number sense (both individually and collectively) have been found to be predictive of subsequent mathematical achievement (Devlin et al., 2022; Nguyen et al., 2016). Jordan et al. (2022) caution that additional mediating factors include a child’s representational development (non-symbolic or symbolic) and the size of numbers (set size) with which the child is working. Also, the development of sub-skills within each of the three core competencies must be considered when seeking to monitor children’s number sense development. Consideration of the sub-skills reveals the interconnection between the three core competencies.
The number component focuses on awareness of quantity in the sense of ‘how many’. Even before learning the counting process, many children learn to ‘subitize’ quantities of one to four items; that is, immediately recognise, for example, the quantity ‘three’ when they see a group of three toys (Clements et al., 2019). Learning to count with conceptual understanding involves the combination of several processes: (1) the procedural skills of correctly reciting the list of number names (one, two three, four, etc.), (2) one-to-one correspondence of a number-name to an item in the group being counted, with (3) the conceptual understanding that the last number-name in the count indicates the total number or tells ‘how many’ (the cardinality principle), (4) being able to apply counting to any collection whether tangible or imagined (abstraction principle), and (5) the ability to vary the order in which objects are counted (order-irrelevance principle) (Dowker, 2008). Numeral recognition and the ability to match a numeral to a non-symbolic representation of that quantity (e.g., label a picture of 5 ducks with the numeral 5) is also a component skill.
Number relations refers to the ability to compare whole numbers, in the sense of judging whether a quantity is more, less or equal to another quantity (Jordan et al., 2022). This skill may begin with the ability to subitize, as in being able to visually distinguish between a group of four and a group of more-than-4. There is a strong connection to number sequencing though understanding that the next counting number is ‘one more’ (or the preceding number is ‘one less’) (Sella & Lucangeli, 2020). Number relations extends to recognising the relative magnitude of numerals (either written or spoken). For example, determining whether 6 is larger than 3.
Number operations involves the knowledge that whole numbers can be ‘taken apart’ and ‘put together’ (Jordan et al., 2022) and underpins understanding the operations of addition and subtraction. For example, recognising that a group of five apples can be separated into a group of three and a group of two, and that combining the two smaller groups reconstitutes the group of five. Subitizing and counting serve as tools to explore number operations, and a sense of number magnitude (more and less) supports understanding. Deepening understanding allows children to translate between various representations of numbers such as verbalised number stories, concrete quantities (including visualised objects) and numerals (Pape & Tchoshanov, 2001), to recognise and operate on numbers.
1.2. Embodied Representation in Early Mathematics Learning
Several modes of representation have already been mentioned in the previous section discussing early number sense; namely, concrete objects, pictorial, mental imagery, verbal, and symbolic. In this section we focus on representations of number sense components that engage children physically, through moving their hands and body. Over the last two decades, research into the educational applications of embodied cognition theory has accumulated substantial evidence that a range embodied approaches can enhance children’s learning of mathematics concepts and process (Mavilidi et al., 2022; for an early mathematics summary see Way & Ginns, 2024). Research from the field of neuroscience has begun to explain how and why multimodal learning approaches (Mathias & von Kriegstein, 2023) assist knowledge building and memory and highlights the role that embodied representations play in creating robust and retrievable memories (Kuhnke et al., 2023). Of particular relevance to the present study is the research focused on the four-to-six age range and the development of early number sense.
1.2.1. Finger-Based Number Representations
Fingers can be used to represent two aspects of numerosity. A cardinal representation involves displaying a specific quantity of fingers, such as in response to a request ‘show me four fingers’, or to a question ‘how old are you?’ Of interest is whether a child is able to immediately present a small number of fingers, reflecting subitizing skills, or whether fingers are displayed one at a time (indicating counting from 1) (Fischer et al., 2020; Holgersson et al., 2016). An ordinal representation involves displaying one finger at time to reflect the counting procedure of combining the number sequence and one-to-one correspondence (Fischer et al., 2020). Considerable variation occurs in children’s methods, such as the hand on which they start their count or the order in which they raise (or lower) their fingers, but this does not appear to greatly affect the benefits of connecting finger movement and numbers. Indeed, a child’s awareness of their finger positioning and their ability to effectively represent numbers with their fingers has been found to correlate with achievement in mathematics a few years later (Gracia-Bafalluy & Noël, 2008), and that training at age 5 can improve problem-solving performance (Ollivier et al., 2020). Some explanation is offered through neuroscience studies that show that finger representations and thinking about numbers activate overlapping neural pathways (Penner-Wilger & Anderson, 2013; Tschentscher et al., 2012).
An important consideration is the relationship between fine motor skill, in particular finger dexterity, and a child’s ability to effectively enact finger-based number representations, which has been linked to proficiency in counting and calculation. In a longitudinal study of 4-to-6-year-olds, Asakawa and Sugimura (2014) found a strong positive relationship between finger dexterity and addition calculation. Following investigation of the relationships between fine motor skills, cardinal and ordinal finger representations, and conceptual understanding of counting with children aged 3 to 6 years, Fischer et al. (2017, 2020) highlighted “the importance of supporting fine motor development in preschool children” (Fischer et al., 2017, p. 8) for the benefit of strengthening number sense. Collectively, these research findings present a convincing argument for promoting finger-based number representation in preschool.
1.2.2. Developing Representational Drawing
Overlapping with representational hand movement and fine-motor skill is the development of children’s mark-making and drawing skills. Early mark-marking and ‘scribble’ begins as sensorimotor play and evolves into meaning-making experiences and representational drawing (MacDonald, 2013; Wright, 2007). Representational drawing refers to the intentional use of marks, icons, pictures and diagrams to represent aspects of the external environment and/or internal thoughts and is therefore as much a cognitive skill as a graphomotor skill. In early years education, children’s drawing development is often viewed in terms of artistic development, or perhaps as an exercise in fine motor skills as a prelude to writing (Hall, 2009). Yet drawing also has a mathematical developmental pathway that is often not recognised by teachers (or parents). For example, drawing balloons as a representation of colour, or movement, or the joy of a prior experience is a very different representational act to drawing exactly three balloon to represent the mathematical concept of ‘three’.
The mathematising of drawing requires processes of organising, structuring, and symbolising ideas, and so reflects emerging mathematical reasoning (Poland & van Oers, 2007). Evolution of representational drawing skills leads to using drawing as a problem-solving tool (Csíkos et al., 2012; Edens & Potter, 2008), and the production and interpretation of mathematical diagrams. The association of drawing and mathematics has led researchers to examine the extent to which early drawing skill is a predictor of later mathematics achievement. In a large-scale longitudinal study Malanchini et al. (2016) investigated the relationship between drawing development at age 4 to 4.5 years and mathematics achievement at age 12 and found that the association was entangled with general cognitive development and fine-motor skills. Findings such as these highlight the interrelatedness of aspects of physical development and cognitive development.
1.2.3. Conceptual Body Movement
Larger body movements, such as locomotion, that engage the learner in the representation of mathematics concepts or processes have also been found to benefit learning. For example, a preschooler stepping forwards along a large-scale number track on the floor while counting aloud, links the spatial experience of forward locomotion (taking equal size steps) with the verbalised forward-number-word-sequence and written numerals. Several studies have found that the active mapping processes to construct spatial–numerical representations, enhances relational knowledge about numbers (Dackermann et al., 2017; Mavilidi et al., 2018). Such physical–spatial experience can reinforce the number magnitude aspect of number sense by relating distance travelled (one step more) and the ‘next number’ being one more in value. The use of whole-body movement to enact mathematical concepts such as lining up by ones or making pairs requires the co-ordination of two spatial alignments—linked to the structure and sequential ordering of numbers. At the same time, number thinking is activated through enacting one-to-one correspondence. Egocentric body movement in relation to objects in the environment, including lines, patterns, boundaries, and shapes, supports spatial awareness and the noticing of specific geometric and numerical features.
1.3. Pedagogy and Mathematics Education in Early Childhood
A debate that often arises in discussions of pedagogy in early childhood settings focuses on tensions between ‘play-based learning’ and ‘intentional teaching’. To some extent the debate hinges on interpretations and definitions. Often ‘play’ is seen as child-initiated and child-led and ‘intentional teaching’ can be interpreted as teacher-centred and directed. There are those in education who perceive play-based learning and intentional teaching as philosophically opposing practices and others that advocate the appropriateness of a continuum of approaches ranging between the two practices (Baroody et al., 2019; Edwards, 2017; Pyle & Danniels, 2017). In Australia, pedagogy and practice in early childhood education settings is shaped by The Early Years Learning Framework (EYLF) (Australian Government Department of Education [AGDE], 2022). Amongst the EYLF guidelines for pedagogical practice is the expectation for educators to utilise both practices in ways that relieve the perceived dichotomy, saying, “Play-based learning approaches allow for different types of play and recognise the intentional roles that both children and educators may take in children’s learning” (p. 21). This view acknowledges that children are often purposeful in their play and that educators can influence children’s learning through intentional (both planned and responsive) interactions and by shaping the learning environment (Australian Government Department of Education [AGDE], 2022).
Previous research has indicated that some early childhood teachers may be hampered by a negative disposition towards mathematics and have difficulty in reconciling their views of mathematics learning with pedagogy and practice in the early years (Knaus, 2017). However, more recent research in the Australian context has reported a more positive view of early childhood teachers’ capacity to recognise and respond to teaching/learning opportunities for nurturing young children’s mathematical development (MacDonald, 2025).
1.4. Research Question
Reviewing the research in embodied learning and early-years mathematics education leads to the expectation that engaging children in embodied representations of number concepts and processes is likely to support children’s mathematical development. However, absent from the research literature are rich examples of how preschool teachers might utilise a range of embodied modes with children and how this might influence both children’s physical development and cognitive development. The following research question guided our study: In the context of a preschool teacher’s utilisation of embodied modes of representation in mathematics, what relationships can be observed among aspects of children’s physical development, representational skills and their early number sense?
2. Materials and Methods
The broad context for this study is Phase 2 of the Embodied Learning in Early Mathematics and Science project. Phase 2 of the project implemented a quasi-experimental design to test the student-learning effect of teachers’ increased use of embodied learning approaches in mathematics with pre-school to Year 2 children (4–8 years). Teachers in the four intervention schools (with attached pre-schools) participated in 11 h of professional learning (PL) and received a Teaching Guide containing suggestions for embodied activities suitable for each age group. The PL, delivered in five sessions spread across six months, included information from research about different embodied modes and the ways in which they can be used with children to potentially support their learning, see Table 1 for PL structure. The sessions also included opportunities for teachers to discuss their experiences and exchange ideas.

Table 1.
Timing structure of the ELEMS PL.
Children from both the intervention and control schools were assessed across a range of mathematics learning indicators using individual interviews, at the start of the intervention and again six months later. The same interview protocols were used at Time 1 data collection and Time 2, six months later.
The study reported here takes an instrumental case study approach to focus on one preschool within one of the four intervention schools. The function of an instrumental case study is primarily to provide insight into a phenomenon or issue, rather than to understand the ‘case’ itself (Stake, 2003). The phenomenon we seek to understand better is the relationships between one preschool teacher’s increased use of embodied learning approaches and the children’s development of early number sense. The exploration of relationships requires rich data from a variety of sources and this particular preschool was selected because, compared to the other three preschools, it provided the largest quantity of data from both the teacher and the children. The case is bounded by the timeframe within which the intervention and related professional learning (PL) took place, being six months. The case is further bounded by the limitation of parental permission for their child to participate in the research, limiting the sample to nine children from the class.
2.1. Participants
The preschool in this study is one of the 100 preschools attached to public schools across the state of New South Wales. The preschool is located within a small school (75 students) in metropolitan Sydney, with 28% of students Aboriginal or Torres Strait Islander, and 58% of students from a language background other than English. There were 17 children in the preschool, nine of which participated in Phase 2 of the ELEMS study, and therefore this case study. At the start of the data collection the participants’ ages ranged from 3 years 11 months to 4 years 8 months. (see Table 2).

Table 2.
Preschool participant’s ages.
The preschool teacher, Melissa (pseudonym), has a master’s degree, has between 6 and 10 years’ experience as a preschool teacher and has been at the preschool for less than 12 months. Melissa participated in all 11 h of the ELEMS PL and regularly used the embodied learning activities.
2.2. Data Sources and Analysis
For this case study, a variety of qualitative data sources from both the teacher and the children were used to build a description of the apparent relationships between the embodied activities implemented by the teacher and the children’s development of number sense. Analysis was conducted within and across the data sources using a hybrid approach of deductive and inductive thematic analyses (Yukhymenko et al., 2014), depending on the nature of the data. Deductive analysis was used when an analysis framework existed from previous data analysis in other studies conducted by the authors, for example, for examining the finger-counting patterns of the children. An inductive approach was used when the data situation was open-ended, such as transcripts of the teacher’s verbal reporting, or when conducting pattern searching across data sources. The analysis for each data source was initially completed by one researcher, then cross-checked by the other researcher. Discrepancies were discussed and resolved. Details about data sources and analyses are provided in the next section.
2.2.1. Teacher Data
Several sources of self-reported data were used.
(a) A pre- and post-intervention (Time 1 and 2) questionnaire gathered information about the extent to which a range of embodied strategies were used deliberately in association with particular areas of mathematics; for example, “Deliberate (planned) use of teacher-gesture while teaching measurement”. The questionnaire had been previously piloted with teachers in Phase 1 of the ELEMS project. The questionnaire included 10 questions related to teacher use of embodied modes in mathematics specifically (The Phase 1 questionnaire included four additional questions in relation to science that were not a focus of Phase 2). A five-point Likert scale ranging from ‘never’ to ‘always’ was used. The purpose of the questionnaire was to gauge the extent to which the teacher’s use of embodied practices increased over the 6-month intervention period. Analysis was a comparison of the pre- and post- survey results to observe if the teachers reported an increase in their use of embodied strategies after the 6-month intervention.
(b) A weekly automated mini questionnaire recorded the teachers’ frequency of use of specific embodied activities contained in the Teaching Guide, as well as additional activities created by the teacher. The link to the questionnaire was shared weekly via the Twilio application (a phone messaging prompt). The data from this source provided valuable information about the experiences Melissa offered to the children. Analysis was a simple process of categorization of the reported activities and recording of frequency data.
(c) Verbal reports were obtained from Melissa on two occasions during some PL sessions that were conducted online via Zoom. The audio-recordings were transcribed, and the relatively small amount of text analysed using simple open-coding and categorization to identify information about the ways in which Melissa utilised embodied practices and how her children responded, along with any other insights she offered.
2.2.2. Child Data
Three sources provided data on the children’s development of number sense and embodied representation. All three utilised a one-to-one clinical interview conducted by the researchers who were trained and experienced in the interview protocols and interacting with young children. Clinical interview is considered to be one the most powerful methods for assessing a child’s mathematical thinking (Ginsburg, 2016), as it allows interaction between the interviewer and interviewee and close observation of the child’s multi-modal responses. Child interviews were approximately 30–40 min in total length and included a range of embodied tasks (video recorded) as well as a diagnostic mathematics assessment. Length of interviews varied based on concentration level of children due to age, and their ability to correctly answer the diagnostic interview questions (diagnostic interview stopped once child had three errors in a row).
(a) Finger Numbers Interview: The tasks invited the child to, (i) show me how you count to 10 using your fingers, (ii) hold up 3 fingers, (iii) hold your hands above your head (like bunny ears) and hold up 4 fingers, hold up 7 fingers. The interview was video recorded with the camera focused on the child with their hands in view. A pre-designed analysis framework (Way & Cartwright, 2024) was used to record details about how the fingers were used to represent the numbers, including the sequence of fingers, one-to-one correspondence, and accuracy. Any verbalizations and other observations were also recorded. A summary table was prepared to rate finger dexterity, one-to-one correspondence, subitizing with 3 fingers, and visual reliance for finger control. Changes from Time 1 to Time 2 were noted.
(b) Drawing Interview: The child was given a blank sheet of A4 paper and a marker pen and asked to listen to a story “Five birds sat on a fence. Two birds flew away. Draw what happened in the story”. When the child appeared to be finished, they were asked to ‘tell me about your drawing’. The interview was video recorded. An image of the child’s pen grip was recorded together with a rating of the fluidity of hand movement (simply ‘awkward’ or ‘adequate’). The drawing was analysed using a pre-prepared analysis framework of categories of drawing development (Way, 2018) focused on the representation of objects in the story, and the number in one, two or three groups relevant to the story. Changes from Time 1 to Time 2 were noted.
(c) The Research-based Early Mathematics Assessment (REMA) Short Form (Clements et al., 2008) is a diagnostic assessment that measures children’s mathematical knowledge and skills along research-based developmental progressions (Sarama & Clements, 2009). Data collection during the task-based interview was recorded via interviewer entries into an app, from which a spreadsheet was generated. For this paper, the interview tasks directly related to early number sense were selected and the relevant data extracted. The tasks selected were: highest count with no errors, matching numeral to a quantity (1 to 5 and subitizing), counting technique for 8 objects, subitizing/counting four objects, making a group of 5 objects, counting on from a group of 7 to make 12, which is biggest, 7, 9 or 5?, and which is smallest, 8, 6 or 10? Changes from Time 1 to Time 2 were noted.
2.2.3. Data Aggregation and Pattern Searching
A three-phase process was used to draw together the diverse data sources to create multiple layers of information and facilitate pattern searching across data sources. During this process relationships were revealed, and the main themes emerged.
Phase 1 involved both data reduction and data layering for the child data sets. Data from all three sources was summarised into a single table to facilitate comparisons and pattern searching. Looking across rows gave a profile for each child and supported connections to be made between points of overlap, for example, connecting the child’s ability to subitize three or four fingers (Finger Numbers) and subitize four objects (REMA task). Looking down columns allowed comparison between Time 1 and Time 2 results for each child, and detection of patterns amongst the nine children.
Phase 2 involved the compilation of summary tables for the teacher data from all sources. This allowed triangulation of the self-reported data sources. For example, noting alignment between the embodied activity frequency data and Melissa’s verbal reports about what she had been doing with the students.
Phase 3 engaged the researchers in data integration and further pattern searching. The summaries of child data and teacher data were brought together, examined and relationships between data categories were proposed and discussed by both researchers. The articulation of relationships and patterns in the data led to within-case generalisations.
3. Results
The results have been organised into three sections according to the main data sources—teacher data, finger number interview, and drawing interview. Each section begins with some detailed results from the main data source to give depth to the description, then draws on other data sources (e.g., teacher data or REMA results) to add another layer of interpretation and describe relationships. Each section concludes with a within-case generalisation statement to capture the researchers’ interpretation of patterns across the data.
3.1. The Pre-School Teacher’s Adoption of Embodied Learning Approaches
Melissa reported an increased deliberate use of embodied approaches in Time 2 embodied strategies questionnaire (compared to Time 1). For eight of the 10 statements (e.g., Explicit support for the development of drawing skills in mathematics), in Time 1 Melissa responded ‘sometimes’. For seven of these statements in Time 2, Melissa responded ‘often’. The large increases in usage were in the use of deliberate gestures for patterning (rarely to often), gesture for spatial concepts (never to often) and planned use of large body movements mathematics activities or guided play (rarely to sometimes).
The weekly teacher-reported data showed that Melissa reported using the embodied activities in 21 of 33 weeks, averaging five activities per week, with a maximum of eight in a single week. From the data, we noticed that the activities that Melissa used most often were related to finger-use aligned to all embodied modes, body movement, gesture and tracing, and drawing. Table 3 lists the activities from the Teacher Guide that Melissa used, and the frequency reported. Although the Teacher Guide included activities focused on spatial and geometric concepts such as position and 2D shapes, the activities Melissa used mainly focused on number concepts.

Table 3.
Embodied activity descriptions from the Teacher Guide and frequency of use.
While the questionnaire data indicated what activities Melissa was performing, the verbal data from the Zoom PL sessions added insights into how and when she adopted the embodied learning principles in her teaching. Melissa used a variety of phrases to describe how she was embedding the embodied modes into her classroom experiences with the children. Her comments related to intentional planning included phrases such: as I am “Starting to embed those practices”, it is “planned into the environment”, “building on what I had been doing”. Phrases related to flexible modification included: I am “Starting to experiment more” and I “Modify the activity” then “Encourage them to do it”, “… we keep trying and trying through play”, and “adding things that I think lend themselves to that”. These themes overlapped in one comment Melissa made regarding implementing the embodied activities: “Sometimes it’s planned, sometimes it’s modified and then sometimes it’s spontaneous”. The teacher verbal data provided insight into the modified and spontaneous embodied activities Melissa used, data that were not captured in the frequency data contained in Table 2.
In one session, Melissa explained how she had introduced two of the embodied activities involving whole-body movement, then how they had been adapted and integrated into the children’s play. Melissa shared photographs of her children using a large-scale outdoor number track (see ‘Number track counting’ in Table 2). In the image (Figure 1), the number track was empty, so children could add a quantity of items or draw representations for the numbers, then walk along the track counting. Melissa explained:

Figure 1.
Outdoor number track.
“Some of the things we sort of implemented early on and we planned into the environment, for example, the number track outside. We did that quite early on in the study and it’s kind of evolved in terms of we were making it at the start, now the children make it, they use it in different ways.”
The other activity Melissa referred to was ‘Throw a bean bag’ (See Table 2), and once again she reported making adaptions and the shift from a teacher-directed activity to child-initiated play:
“We have a beanbag throwing game that’s on the guide, but we also put some skittles some days where the children can knock the skittles down or where the children jump or do hopscotch. And now actually the children use that as their own play, whereas we would sort of introduce it before, now I just noticed the children go there by themselves and do their own thing with it which is great.”
Both the number track and the throwing task are designed to engage the child in representing concepts of number sequencing and magnitude by moving their bodies in ways that reflect distance and or direction. For example, moving forward in equal steps along the number track activates both spatial thinking and number magnitude thinking (one more each step). Having to throw the beanbag further to reach numbers further along the track connects physical effort and distance with larger numbers. Saying the number names additionally supports numeral recognition and counting skills. It is not clear from Melissa’s accounts whether any emphasis was placed on backwards or differences in distances during these activities.
Two of the REMA tasks targeted number magnitude but were presented abstractly, that is, as a spoken question. For ‘which is biggest 7, 9 or 5?’ three children answered correctly in Time 1, and six were correct in Time 2. For ‘which is smallest 8, 6 or 10?’, only two children answered correctly in Time 1, and four children in Time 2.
In a later Zoom PL session Melissa shared how she had continued to connect embodied modes such as touch tracing and ‘eyed closed’ tracing linked to ordering numbers (sequencing) and numeral recognition:
“When children were just playing, touching them [the numbers], ordering them and then we introduced the blindfolds and made it sort of into a game where they would pop the blindfold on and try and recognize that number and something else that’s slightly different but on the same track. We made these little plates that have got these sort of raised, the slightly raised numbers and then the amount of objects.”
One of the REMA tasks required the children to match numeral cards (1 to 5) to cards showing sets of individual grapes, giving an indication of both numeral recognition and associated quantity. In Time 1, four children were successful for all five numbers, and in Time 2, all but one (Adam) were successful.
In the REMA Highest Count task, children are asked: ‘How high can you count? Start at 1 and tell me’. Table 4 shows the children’s scores, which all improved in Time 2 (except Adam). The highest count presented is the highest count without error, before a prompt ‘what number comes next, can you go higher?’ was given, so some of the children went further.

Table 4.
Highest count without error.
Generalisation Statement
Melissa increased her use of planned and deliberate embodied representations and readily integrated them into daily activities and practices. She used pre-planned intentional teaching of the suggested activities in both indoor and outdoor environments and flexibility adapted the activities described in the Teacher Guide. The children improved performance in some of the number concepts involved in the embodied representations (counting sequence, number magnitude, numeral recognition).
3.2. Finger Numbers and Dexterity
The video recordings of the Finger Number interviews provided rich data on how children were able to use their fingers to represent numbers. Finger dexterity was observed when each child was asked to display three fingers and also count to 10 using their fingers. When first assessed (Time 1), four children could not move their fingers independently into the desired position, instead making a ‘claw’ as they struggled, or using their other hand to push fingers into place. In the second assessment (Time 2), six months later, all children could manage to raise their fingers individually to represent numbers, with four children progressing to fluid, confident finger movement. As well as the noticeable changes in finger dexterity, an increase in counting accuracy (one-to-one correspondence) was apparent, though two children still made a counting error. Most (7) children also changed the way they represented the count to ten by either varying the way they held their hands or the sequence in which they moved each finger. Three children have been selected to illustrate the variety of changes that were revealed through analysis of the videos from Time 1 and 2 data collection points.
Ben demonstrated particularly marked development in finger dexterity. At first (Time 1) Ben did not have sufficient finger control to display three fingers. His attempt to hold up three fingers produced a ‘claw’ of five fingers. Six months later (Time 2) he was able to hold up the three central fingers of his right hand while using his thumb to hold down his little finger (Figure 2). At Time 1, when asked to count to ten using his fingers, Ben tried to move one finger at a time but could not, instead raising two or three fingers at a time. He particularly struggled with controlling the fingers on his left hand. He did not say any number names. At Time 2, Ben was able to raise one finger at a time and match a number name (from one to ten) with each finger. With his palms facing away from him, he started with the little finger of his left hand and moved in order from left to right across both hands (Figure 2).
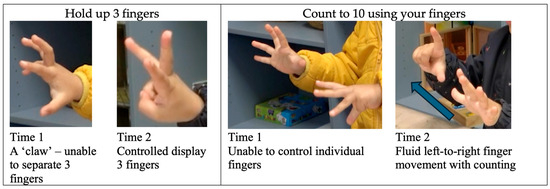
Figure 2.
Ben responding to finger-number tasks with increased dexterity.
Mia was one child who did not demonstrate a change in finger dexterity, being able to move individual fingers in both Time 1 and 2. However, she changed from starting her count on her right-hand to staring with her left-hand. In Time 1, she started her count with her right thumb, ending with 5 on her right little finger (Figure 3). She then raised the thumb of her left hand for 6, ending at her left little finger. By starting with her thumb each time, she was moving from the ‘outer side’ on both hands and counting ‘inwards’ in the direction of her other hand. At Time 2, Mia followed a similar pattern but started on the opposite hand.

Figure 3.
Mia’s change in representation of counting from 1 to 10.
Will successfully counted to ten as he raised one finger at a time, and at Time 2 his finger movements were more fluid (Figure 4). However, at Time 2 Will changed the orientation of his hands and completely reversed the direction of his representation of counting. At Time 1, Will held his hands vertically with his palms facing and began the count on his left thumb, then on 6 raised his right little finger and concluded the count with his right thumb. This method produced a continuous count across both hands, moving left to right.

Figure 4.
Will’s changes in representation of counting from 1 to 10.
The teacher, Melissa, reported the purposeful use of five activities likely to have supported the development of finger dexterity in relation to representing numbers, on at least 30 occasions. Each of the activities (Finger numbers, Finger counting to 5, Finger counting to 10, Hold up and Finger stories—see Table 2 for descriptions) engage children with raising and lowering fingers and making connections with number-names and quantities. For example, the teacher guides the children to model the rhyme/song/story of the ‘five little ducks’ by starting with five raised fingers and lowering a finger each time a little duck goes missing. Evidence that the improvements observed by the researchers in the Time 2 assessments can be attributed to the children’s participation in the embodied activities comes from Melissa’s own observations.
In an online sharing session with teachers from another preschool and school, Melissa talked about how the children had become engaged with iPad app Fingu (see fingertips activity in Table 2). In the game, some images of fruit appear (e.g., two strawberries and three pears) and the child has a short time in which to place the corresponding number of fingertips on the screen (Figure 5). Melissa explained that the children found it difficult at first but wanted to persist, so she used activities like Hold Up (Bunny Ears) as training:

Figure 5.
Children using Fingu.
“…we play the bunny finger numbers and things like that and so I can see how all of that helps them with this because they’ll see three and where at the start, they would sort of be going one two three and then put it down. Now they see the fruit come up and immediately they get their fingers ready”.
Melissa further commented on the difference she saw in the children who had missed out on the opportunities to develop finger dexterity and subitizing skills:
“I had two children who were absent for a while and here she was really struggling to work out how many fingers to get. And one boy had been away, and you can see he was really having to sort of use his other hand, sort of force his fingers down and out of the way. And I just thought it was really interesting because neither of those have been there for many of the finger activities.”
Unfortunately, we do not know who the two absent children were so cannot look for connection to their finger dexterity of subitizing skills in the assessments. The data collected for the REMA task ‘Matching numeral to a quantity (1 to 5)’ included whether the child subitized the number of grapes on the card or counted by ones. Table 5 gathers together the data for finger dexterity, holding up three fingers (subitize or count), counting to 10 on fingers with 1 to 1 correspondence, and the REMA task (subitize or count). The green highlights aspects which improved from Time 1 to Time 2 and shows particular improvement by Ben, Theo, Lily, and Theo.

Table 5.
Children’s finger dexterity and subitizing performance.
Generalisation
A lack of finger dexterity inhibited some children’s ability to achieve one-to-one correspondence of number-names to fingers. Children who began with poor finger dexterity benefited from the embodied activities implemented by Melissa, not only regarding improved finger control, but also in counting accuracy and subitizing skills. The changes in several children’s patterns of finger counting also reflect the influence of the embodied tasks and the children’s more focused and controlled use of their fingers.
3.3. Drawing Development and Representing Number
The main purpose of the ‘5 birds’ drawing task was to gain an indication of how each child was progressing in their natural drawing development and whether they were disposed towards attending to, and representing, the number of birds in any of the groups mentioned (or implied) in the story, ‘5 birds sat of a fence. Two birds flew away’. The task also afforded the opportunity to observe how each child held the pen and the ease with which they moved their wrist during drawing. While the main focus was on what the children drew, their verbalizations assisted with the interpretation of the intention behind the marks they made.
In the first assessment, most children had what could be described as an adequate pen grip that allowed reasonable control over their mark-making movements. All children showed a more relaxed grip and more fluid wrist movement at Time 2. However, three children had a hesitant and awkward pen grip at Time 1, suggesting a lack of experience. The teacher questionnaire data supports this suggestion in that Melissa at Time 1 reported only ‘sometimes’ including drawing tasks in her classroom experiences. This supposition was supported by the limited natural drawing development they demonstrated. As can be seen in Table 6, these three children were emerging from the ‘scribble phase’, exploring shape and form in drawing, and had not yet begun to represent the characteristics of real objects at Time 1. By Time 2 representational drawing was emerging. Even at this early stage of representational drawing, the beginnings of mathematical drawing are evident in the children’s attention to representation of ‘group’ and number. These developments suggest the children had received increased encouragement and opportunity to engage with drawing. In the teacher questionnaire data at Time 2 Melissa’s inclusion of drawing tasks and explicit support for the development of drawing skills in mathematics has both shifted to ‘often’. Indeed, the teacher’s records show that she purposefully used finger tracing/drawing and pencil tracing/drawing activities 31 times. The most frequently used activities were Finger Tracing (9) and Finger Drawing (10) which involved helping children focus on lines, shapes and hand movement, often including the sense of touch, and sometimes in response to other non-visual stimuli such as story or music. During a teacher-sharing session, Melissa confirmed her purposeful use of these activities and made connections between children attending to shape structure through finger-tracing in the air and the children’s increasing skill in drawing and writing:

Table 6.
Development of pen grip and drawing for three children.
“I found after doing all the air shapes together and then we drew them on the board, they could then really create some good shapes with their Play -Doh. And something else that we kind of do a lot as the pencil tracing. I think that lends itself quite well to both shape work and number writing. We’ve just got some little cards they sort of write over with a whiteboard pen and then they do it in pencil in their little special book. So yeah those are some of the things I’ve been sort of really focusing on.”
The other children also demonstrated drawing development, both in terms of their change in drawing schema, and in mathematical representation. The examples in Table 6 illustrate the variety of the children’s responses and changes in representational drawing. Adam moved from being confused by the request to draw in response to a story to being able to represent three features from the story—a fence, a group of birds on the fence, and two birds flying away. Mia progressed from representing the group of five birds to also showing the two that flew away. Yousef began with drawing a tree and one bird, to representing five birds on a fence and the idea of birds flying away. Ann was able to produce a mathematical drawing that represented the entire subtraction process of a group of five being partitioned into a group of two and a group of three, using the device of crossing out two birds. At Time 2, Mia again represented the subtraction process but used arrows to signify the separation of two birds from the five. Interestingly, the teacher had reported introducing the children to arrow drawing in an activity. Ben did not use representational drawing at all, but instead revealed experiences beyond the pre-school by attempting to use symbolic representation to record the subtraction process. At Time 2, he was able to correctly construct the subtraction equation and used mathematical language to state the calculation which he had carried out mentally. Table 7 lists the descriptions of the drawing categories for each child in Time 1 and Time 2.

Table 7.
Changes in children’s representations of ‘5 birds sat on a fence. 2 birds flew away’.
Of relevance to interpreting the children’s drawing is whether they understand the quantity of five and can visualise or ‘think in groups’. Two of the REMA tasks offer some indication of these capabilities. In the ‘Make a group of 5′ tasks the child was asked to take objects from a larger pile. In the ‘Start with 7 make 12′ task the child was shown a group of 7 objects and asked to turn it into a group of 12. Children who are able to ‘think in groups’ can count on from seven rather than starting the count from one. Table 8 shows the children’s drawing development categories in Time 1 and Time 2, together with the results for the two REMA tasks. The green shading highlights more sophisticated responses in Time 2. Almost all children were capable of counting five objects accurately.

Table 8.
Drawing groups, counting and grouping.
Generalisation
Increased attention to hand movements, shape tracing, and actual drawing benefits children’s drawing development. Children with awkward pen grip and/or pre-representational drawing (Category A) particularly benefited from the increased motor control and practice of drawing.
4. Discussion
The purpose of the study reported here was to build a rich description of any relationships that could be detected through the analysis of multiple data sources gathered from a context in which a preschool teacher had deliberately increased her use of embodied learning activities. The embodied activities engaged the teacher and children in the creation of mathematical representations through various body movements. The physicality of the representations and the involvement of children ranging in age from 3 years 11 months to 5 years 3 months, raised questions about the role that the development of motor skills might play in the creation of the representations themselves, and in the development of the mathematics concepts being represented. The selected case was situated within a larger project, and the data had already been collected. An initial scan of the activities that the preschool teacher had reported using, revealed an increase in the use of embodied activities and focus on number sense. These circumstantial factors led to the research question: In the context of a preschool teacher’s utilisation of embodied modes of representation in mathematics, what relationships can be observed among aspects of children’s physical development, representational skills and their early number sense?
Detailed descriptions of the relationships revealed through data analysis have been provided in the extensive Section 3 of this paper. Each subsection of the results produced a with-in case generalisation as a type of summary of the meanings inferred from the findings. Synthesis of these generalisations provides a broad response to the research question, framed within the boundary of the case, as follows. The preschool teacher included the deliberate and planned use of embodied representations into daily practice, and the children repeatedly and voluntarily integrated some activities into their play, allowing the teacher to observe the children’s physical and mathematical development. To begin with, some children’s production of number representations was inhibited by insufficient development of fine motor skills, in particular finger dexterity in number representation, and pen grip in drawing. These children seemed to benefit the most from the embodied activities that supported fine motor development in conjunction with mathematics concepts. Most children improved both their mathematical representation skills and the related aspects of number sense over the six-months period.
To structure the discussion of key findings in relation to existing literature we put forward two propositions arising from reflection on the outcomes of the multi-layered data analysis. The first proposition is that purposeful embodied representation can be readily incorporated in play-based learning approaches that account for the intentionality of both teachers and children. The second proposition is that relational triads describe the interconnectedness of motor development, mathematical representation and number sense development.
4.1. Purposeful Embodied Representation Can Be Readily Incorporated in Play-Based Learning Approaches That Account for the Intentionality of Both Teachers and Children
This proposition is deliberately stated using the language of Early Years Learning Framework (Australian Government Department of Education [AGDE], 2022) as it expresses well the approach taken by the pre-school teacher in this case study. The descriptions that Melissa, the preschool teacher, shared during the online sessions proved to be an invaluable source of insights into her pedagogical decision-making and practice. She did not give any indication that she was troubled by the common debate about the perceived dichotomy of intentional teaching and children’s play (Pyle & Danniels, 2017).
Melissa’s adoption of embodied learning approaches can be characterised through several strategies she employed which reflect her stance of “Sometimes it’s planned, sometimes it’s modified and then sometimes it’s spontaneous”. The strategies she reported using can be summarised as:
(a) Intentional planning and teaching to engage children in guided activities with clear learning purposes. For example, she describes leading the children in the ‘bunny ears’ activity to train them in finger control and develop subitizing, or introducing the children to the number track to practice the forward number sequence and numeral recognition.
(b) Adapting activities and managing the play environment environments to encourage exploration and the transfer of intentionality to the children. For example, by leaving an ‘empty’ number track setup and encouraging children to create their own number representations and ‘games’.
(c) Flexible modification and variation in the activities to promote further play and repetition of the learning experiences. For example, varying the number track and beanbag throwing activity to make use of skittles or hopscotch frames to achieve similar learning in numeral recognition and number magnitude.
(d) Observing children’s responses and progress and responding to their interests. For example, supporting their enthusiasm to master the physical/cognitive challenges of the Fingu digital game (finger dexterity and subitizing).
(e) Making conceptual connections between physical representations and number concepts to select and sequence complimentary activities. For example, connecting air tracing, touch-tracing and pencil tracing activities to developing drawing and numeral writing skills.
The approach taken by Melissa resonates with the model developed by Edwards (2017) that advocates the equal valuing of three types of play that can be used in multiple combinations. Purposefully framed play involves co-developed understandings of concepts between teachers and children, modelled play demonstrates a “concept in action by teachers with children”, and open-ended play “promotes children’s exploration of a new concept” (p. 9).
4.2. Relational Triads Describe the Interconnectedness of Motor Development, Mathematical Representation and Number Sense Development
Three relational triads arose from exploring the relationships between the information provided by the analysis within and across the data sources. Each triad identifies an aspect of motor development; an embodied mode of representation and one or more aspects of number sense that were related to the case being studied.
4.2.1. The Finger-Number Triad
The ‘finger-number triad’ (Figure 6) connects finger dexterity, the use of the fingers to display both ordinal and cardinal number representations, and the associated elements of number sense, subitizing and one-to-one correspondence in the counting process. The layering of data within the case study revealed relationships between the children’s fine-motor skills (finger dexterity) and their ability to represent numbers with their fingers, the teacher’s efforts to support the children’s finger counting skills, and changes in the performance of some children.
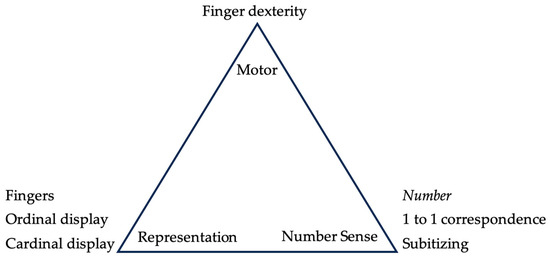
Figure 6.
The finger-number triad.
For example, when first assessed Ben was not able to control his fingers in a way that allowed him to raise his fingers one at a time—a process required to create an ordinal display by linking the sequence of counting numbers in one-to-one correspondence with each finger (See Figure 2). Nor was Ben able to use his fingers to immediately display a group of three fingers without counting by ones (cardinal number and subitizing). We assume that Ben participated in many of the activities and games orchestrated by the teacher because when assessed six months later, Ben demonstrated fluid finger movement and effective number representation. Although our data does not allow causal inference, our assumption that improved finger dexterity is related to number sense development is well supported by other research designed to detect causal relationships. For example, the Suggate et al. (2017) study of 81 children with an average age of 4 years 9 months, concluded that fine motor skills “are closely related to early numerical skill development through finger-based numerical counting that aids the acquisition of mathematical mental representations” (p. 1085)
4.2.2. The Drawing-Number Triad
The ‘drawing-number triad’ connects the representational mode of drawing with the ability to effectively hold and control the movement of a pen/pencil to create representations of number by drawing groups of objects (Figure 7). The teacher provided the children with opportunities to develop fluid hand movement and notice shape and form, through finger tracing and pencil tracing and drawing experiences. Seven of the children demonstrated substantial changes in development of representational drawing skills, which included being may alert to noticing number, and the changes in number, in the ‘Five Birds’ drawing tasks. Three children (Theo, Will, Lily, see Table 5) showed a remarkable change in both pen-grip and representational drawing ability in just six months.
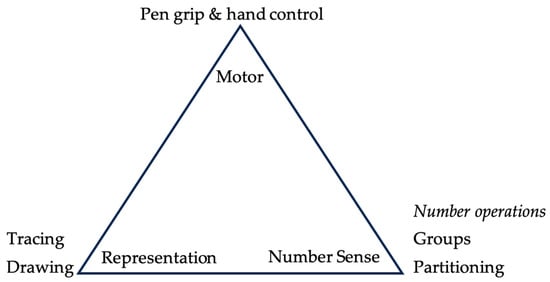
Figure 7.
The drawing-number triad.
Research is yet to clearly define the nature of the relationships between early representational drawing, fine motor skills and children’s mathematical development (Malanchini et al., 2016), but research consistently confirms representational drawing as a useful tool in mathematics learning and problem solving (Csíkos et al., 2012; Poland & van Oers, 2007). Our observations in this study suggest that playful activities such as finger drawing in sand trays and ‘air-drawing’ shapes may be helpful in supporting the development of children’s drawing skills.
4.2.3. The Movement-Number Triad
The ‘movement-number triad’ connects spatial representations, gross-motor movement and concepts of number sequence and magnitude (Figure 8). Melissa reported using activities that engaged the children in physically interacting with outdoor setups of number tracks, hopscotch frames and number targets, with the intention of supporting numeral recognition, the counting sequence and a sense of number magnitude. We do not have any information on the children’s gross-motor development so cannot comment on potential connections with the children’s ability to balance and co-ordinate equal steps with each number as they walk or jump along the number track or hop/jump on numbers in hopscotch. Nor can we comment on the children’s ability to effectively throw a bean bag at a target number in the track, hop-scotch or skittles games. However, reflecting on the movement-number triad highlights the role of spatial awareness and spatial thinking in embodied representations of number concepts, which offers a different perspective on number understanding to the other two triads.
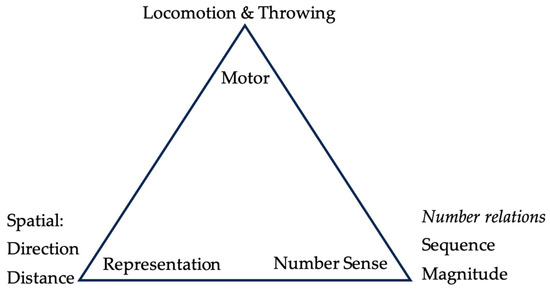
Figure 8.
The movement-number triad.
A common feature of the activities related to this triad is their scale. Each of the setups provided a spatial structure (containing an arrangement of numbers) in which the children could physically locate themselves and enact movements related to direction and distance. Previous research has established that making connections between spatial properties and number properties (e.g., moving forwards/back and counting forwards/back) can enhance early number sense (Dackermann et al., 2017; Mavilidi et al., 2018). Each whole-body movement activity also enacted mathematically ‘conceptually appropriate’ movements, for example, learning to throw a bean bag with greater force to reach a number further away on the number track (number magnitude).
5. Conclusions
An instrumental case study, with its multiple data sources, affords a rich description of the phenomenon under investigation, but the findings are bounded within the case. It is not the purpose of a case study to enable generalisation across a broader population, yet the insights gained from this study offer interesting possibilities to be explored across other contexts. While the data analysis in this study provided evidence of relationships between motor functions and number sense learning, the methods do not enable causal claims to be made. Further research involving multiple case studies across diverse contexts, or larger scale investigations, is needed to accumulate a greater weight of evidence for the benefits of a stronger focus on embodied learning practices in early years mathematics. The completion of analysis of the data sets from the larger ELEMS Project is likely to contribute substantially to the evidence base. A question that remains unanswered in the literature relates to the amount of engagement with embodied representation that is needed to make positive learning gains. Indeed, this question was expressed by the case-study teacher, “I’m going to be very interested to see how many lessons a week has the impact”.
Our contribution to the field of early years mathematics education is an illustration of the interrelatedness of physical development and cognitive development and, more specifically, the value of supporting fine motor development that is explicitly connected to number sense development. The ‘naturalness’ of using body movement as part of mathematical thinking allows for the easy integration of embodied learning practices into the pedagogy of early childhood education.
Author Contributions
Conceptualization, J.W. and K.C.; methodology, J.W., interviews, J.W. and K.C.; formal analysis, J.W. and K.C.; investigation, all writing J.W. and K.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSW Department of Education, Strategic Research Fund (2021–2024). ID: G212850.
Institutional Review Board Statement
The study was reviewed and approved by the Human Research Ethics Committee of the University of Sydney (Protocol 2023/040 9 March 2023).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study. Ethics approval 2023/040 Human Research Ethics Committee, The University of Sydney.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Asakawa, A., & Sugimura, S. (2014). Developmental trajectory in the relationship between calculation skill and finger dexterity: A longitudinal study. Japanese Psychological Research, 57(2), 189–200. [Google Scholar] [CrossRef]
- Australian Government Department of Education [AGDE]. (2022). Belonging, being and becoming: The early years learning framework for Australia (V2.0). Australian Government Department of Education for the Ministerial Council. Available online: https://www.acecqa.gov.au/sites/default/files/2023-01/EYLF-2022-V2.0.pdf (accessed on 15 July 2025).
- Baroody, A. J., Clements, D. H., & Sarama, J. (2019). Teaching and learning mathematics in early childhood programs. In C. Brown, M. B. McMullen, & N. File (Eds.), Handbook of early childhood care and education (pp. 329–353). Wiley Blackwell Publishing. [Google Scholar]
- Clements, D. H., Sarama, J., & MacDonald, B. L. (2019). Subitizing: The neglected quantifier. In A. Norton, & M. W. Alibali (Eds.), Constructing number. Research in mathematics education. Springer. [Google Scholar] [CrossRef]
- Clements, D. H., Sarama, J. H., & Liu, X. H. (2008). Development of a measure of early mathematics achievement using the Rasch model: The research-based early math assessment. Educational Psychology, 28(4), 457–482. [Google Scholar] [CrossRef]
- Csíkos, C., Szitányi, J., & Kelemen, R. (2012). The effects of using drawings in developing young children’s mathematical word problem solving: A design experiment with third-grade Hungarian students. Educational Studies in Mathematics, 81, 47–65. [Google Scholar] [CrossRef]
- Dackermann, T., Fischer, U., Nuerk, H. C., Cress, U., & Moeller, K. (2017). Applying embodied cognition: From useful interventions and their theoretical underpinnings to practical applications. ZDM Mathematics Education, 49, 545–557. [Google Scholar] [CrossRef]
- Devlin, B. L., Jordan, N. C., & Klein, A. (2022). Predicting mathematics achievement from subdomains of early number competence: Differences by grade and achievement level. Journal of Experimental Child Psychology, 217, 105354. [Google Scholar] [CrossRef] [PubMed]
- Dowker, A. (2008). Individual differences in numerical abilities in preschoolers. Developmental Science, 11, 650–654. [Google Scholar] [CrossRef] [PubMed]
- Edens, K., & Potter, E. (2008). How students “unpack” the structure of a word problem: Graphic representations and problem solving. School Science and Mathematics, 108(5), 184–196. [Google Scholar] [CrossRef]
- Edwards, S. (2017). Play-based learning and intentional teaching: Forever different? Australasian Journal of Early Childhood, 42(2), 4–11. [Google Scholar] [CrossRef]
- Fischer, U., Suggate, S. P., Schmirl, J., & Stoeger, H. (2017). Counting on fine motor skills: Links between preschool finger dexterity and numerical skills. Developmental Science, 21, e12623. [Google Scholar] [CrossRef]
- Fischer, U., Suggate, S. P., & Stoeger, H. (2020). The implicit contribution of fine motor skills to mathematical insight in early childhood. Frontiers in Psychology, 11, 1143. [Google Scholar] [CrossRef]
- Ginsburg, H. P. (2016). Helping early childhood educators to understand and assess young children’s mathematical minds. ZDM Mathematics Education, 48(1), 941–946. [Google Scholar] [CrossRef]
- Gracia-Bafalluy, M., & Noël, M. P. (2008). Does finger training increase young children’s numerical performance? Cortex, 44(4), 368–375. [Google Scholar] [CrossRef] [PubMed]
- Hall, E. (2009). Mixed messages: The role and value of drawing in early education. International Journal of Early Years Education, 17(3), 179–190. [Google Scholar] [CrossRef]
- Holgersson, I., Barendregt, W., Emanuelsson, J., Ottosson, T., Rietz, E., & Lindström, B. (2016). Fingu—A game to support children’s development of arithmetic competence: Theory, design and empirical research. In P. Moyer-Packenham (Ed.), International perspectives on teaching and learning mathematics with virtual manipulatives. Mathematics education in the digital era (Vol. 7). Springer. [Google Scholar] [CrossRef]
- Jordan, N., Devlin, B., & Botello, M. (2022). Core foundations of early mathematics: Refining the number sense framework. Current Opinion in Behavioral Science, 46, 101181. [Google Scholar] [CrossRef]
- Knaus, M. (2017). Supporting early mathematics learning in early childhood settings. Australasian Journal of Early Childhood, 42(3), 4–13. [Google Scholar] [CrossRef]
- Kuhnke, P., Beaupain, M. C., Arola, J., Kiefer, M., & Hartwigsen, G. (2023). Meta-analytic evidence for a novel hierarchical model of conceptual processing. Neuroscience and Biobehavioral Reviews, 144, 104994. [Google Scholar] [CrossRef]
- MacDonald, A. (2013). Using children’s representations to investigate meaning-making in mathematics. Australasian Journal of Early Childhood, 38(2), 65–73. [Google Scholar] [CrossRef]
- MacDonald, A. (2025). When and how do educators facilitate mathematical learning opportunities for babies and toddlers? International Journal of Early Childhood, 1–17. [Google Scholar] [CrossRef]
- Macrine, S. L., & Fugate, J. M. (2022). Embodied cognition and its educational significance. In S. Macrine, & J. Fugate (Eds.), Movement matters: How embodied cognition informs teaching and learning (pp. 13–24). MIT Press. [Google Scholar]
- Malanchini, M., Tosto, M. G., Garfield, V., Dirik, A., Czerwik, A., Arden, R., Malykh, S., & Kovas, Y. (2016). Preschool drawing and school mathematics: The nature of the association. Child Development, 87(3), 929–943. [Google Scholar] [CrossRef] [PubMed]
- Mathias, B., & von Kriegstein, K. (2023). Enriched learning: Behavior, brain and computation. Trends in Cognitive Sciences, 27(1), 81–97. [Google Scholar] [CrossRef]
- Mavilidi, M. F., Okely, A., Chandler, P., Domazet, S. L., & Paas, F. (2018). Immediate and delayed effects of integrating physical activity into preschool children’s learning of numeracy skills. Journal of Experimental Child Psychology, 166, 502–519. [Google Scholar] [CrossRef]
- Mavilidi, M. F., Ouwehand, K., Schmidt, M., Pesce, C., Tomporowski, P. D., Okely, A., & Paas, F. (2022). Embodiment as a pedagogical tool to enhance learning. In S. A. Stolz (Ed.), The body, embodiment, and education (pp. 183–203). Routledge. [Google Scholar]
- McCluskey, C., Kilderry, A., Mulligan, J., & Kinnear, V. (2023). The role of movement in young children’s spatial experiences: A review of early childhood mathematics education research. Mathematics Education Research Journal, 35(2), 287–315. [Google Scholar] [CrossRef]
- Nguyen, T., Watts, T. W., Duncan, G. J., Clements, D. H., Sarama, J. S., Wolfe, C., & Spitler, M. E. (2016). Which preschool mathematics competencies are most predictive of fifth grade achievement? Early Childhood Research Quarterly, 36, 550–560. [Google Scholar] [CrossRef]
- Ollivier, F., Noël, Y., Legrand, A., & Bonneton-Botté, N. (2020). A teacher-implemented intervention program to promote finger use in numerical tasks. European Journal of Psychology of Education, 35(3), 589–606. [Google Scholar] [CrossRef]
- Pape, S., & Tchoshanov, M. (2001). The role of representation(s) in developing mathematical understanding. Theory Into Practice, 40(2), 118–127. [Google Scholar] [CrossRef]
- Penner-Wilger, M., & Anderson, M. L. (2013). The relation between finger gnosis and mathematical ability: Why redeployment of neural circuits best explains the finding. Frontiers in Psychology, 4, 877. [Google Scholar] [CrossRef] [PubMed]
- Poland, M., & van Oers, B. (2007). Effects of schematising on mathematical development. European Early Childhood Education Research Journal, 15(2), 269–293. [Google Scholar] [CrossRef][Green Version]
- Pyle, A., & Danniels, E. (2017). A continuum of play-based learning: The role of the teacher in play-based pedagogy and the fear of hijacking play. Early Education and Development, 28(3), 274–289. [Google Scholar] [CrossRef]
- Sarama, J., & Clements, D. H. (2009). Early childhood mathematics education research: Learning trajectories for young children. Routledge. [Google Scholar]
- Sella, F., & Lucangeli, D. (2020). The knowledge of the preceding number reveals a mature understanding of the number sequence. Cognition, 194, 104104. [Google Scholar] [CrossRef]
- Stake, R. E. (2003). Case studies. In N. Denzin, & Y. Lincon (Eds.), Strategies of qualitative inquiry (pp. 134–164). Sage. [Google Scholar]
- Suggate, S., Stoeger, H., & Fischer, U. (2017). Finger-based numerical skills link fine motor skills to numerical development in preschoolers. Perceptual and Motor Skills, 124(6), 1085–1106. [Google Scholar] [CrossRef]
- Tschentscher, N., Hauk, O., Fischer, M. H., & Pulvermüller, F. (2012). You can count on the motor cortex: Finger counting habits modulate motor cortex activation evoked by numbers. NeuroImage, 59, 3139–3148. [Google Scholar] [CrossRef] [PubMed]
- Way, J. (2018). Two birds flew away: The ‘jumble’ of drawing skills for representing subtraction pre-school to year 1. In J. Hunter, P. Perger, & L. Darragh (Eds.), Making waves, opening spaces (Proceedings of the 41st annual conference of the mathematics education research group of Australasia) (pp. 98–101). MERGA. [Google Scholar]
- Way, J., & Cartwright, K. (2024, July 7–14). Finger counting patterns in year 1 children [Paper presentation]. 15th International Congress on Mathematics Education (ICME-15), Sydney, Australia. [Google Scholar]
- Way, J., & Ginns, P. (2024). Embodied learning in early mathematics education: Translating research into principles to inform teaching. Education Sciences, 14, 696. [Google Scholar] [CrossRef]
- Wright, S. (2007). Graphic-narrative play: Young children’s authoring through drawing and telling. International Journal of Education and the Arts, 56(8), 1–28. [Google Scholar]
- Yukhymenko, M. A., Brown, S. W., Lawless, K. A., Brodowinska, K., & Mullin, G. (2014). Thematic analysis of teacher instructional practices and student responses in middle school classrooms with problem-based learning environment. Global Education Review, 1(3), 93–109. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).