From Abstract to Tangible: Leveraging Virtual Reality for Playful Math Education

Abstract

This study investigates the use of GeoGebra, a Dynamic Geometry Software (DGS) for math learning in Virtual Reality (VR) using head-mounted displays. We conducted a study with n = 20 middle school students receiving a mathematics tutoring intervention over time in a VR environment. Using theories of embodied cognition and playful mathematics, this paper focuses on distinguishing between mathematical play and general play in VR environments. We also look at interactions that led to instances of play. Key findings highlight how mathematical play in an immersive VR environment using DGS allows mathematical misconceptions to surface, students to explore mathematical ideas, and opportunities for mathematical reasoning about target concepts to build off play experiences. General play allows for the embodied engagement of learners in the mathematical learning environment and includes engagement and rapport-building. The integration of play fits well into VR environments that uniquely allow for immersion and embodiment, and play should be purposefully integrated into such VR environments in the future.

Motivation to learn mathematics has been shown to decline throughout adolescence, with the middle grade years being particularly problematic (Scherrer et al., 2020). While face-to-face tutoring has been found to often be effective in mathematics education (Nickow et al., 2020), recent results from human online mathematics tutoring (Sass & Ali, 2023; Schueler & Rodriguez-Segura, 2023; Zhang et al., 2023; Zydney & Hord, 2023) and generative AI online mathematics tutoring (Bastani et al., 2024) are not promising. There is clearly some key element to the success of face-to-face tutoring that is not always happening with AI agents or in traditional online environments. Studying novel approaches to mathematics tutoring is thus strongly needed.

Virtual Reality (VR) technologies can be an innovative method for enhancing mathematics tutoring. VR allows users to experience a 3D artificially constructed environment in a seemingly real way through electronic equipment like a head-mounted display (HMD) that occludes information from the real environment to present virtual worlds (Rauschnabel et al., 2022). VR transcends geography, enabling synchronous interactions that closely mimic in-person experiences where tutors and learners can engage in a shared virtual space, enabling a sense of presence and interaction that traditional delivery platforms lack (Merchant et al., 2014). Meta-analyses of VR in education show significantly positive effects of VR interventions on student learning and also suggest that immersive forms of VR are more effective than non-immersive forms (Villena-Taranilla et al., 2022; ES = 1.11). VR can allow learners to embody mathematical concepts (Johnson-Glenberg & Megowan-Romanowicz, 2017) in a collaborative space, discovering new ways to interact within a dynamic, virtual world designed to immerse learners with interactive mathematical objects. While using VR HMDs with hand controllers can provide an immersive experience, using your hands to interact directly with objects in VR allows for new kinds of embodied learning experiences and dynamic participation (Hmelo-Silver & Barrows, 2006).

VR also offers unique opportunities for teachers to facilitate play-based instructional strategies. We define mathematical play as a process where individuals or groups willingly create and test mathematical ideas (Williams-Pierce, 2019; Williams-Pierce & Thevenow-Harrison, 2021). We contrast this with general play, which is often intrinsically driven, free-form, and not necessarily attached to explicit learning goals or related to mathematical structure or objectives (Kolb & Kolb, 2010). Both general play and mathematical play exist along a continuum from more teacher-directed to more student-directed (Pyle & Danniels, 2017). While traditional math tutoring may not be an obvious place to integrate elements of play, there is potential for the unique affordances of VR to promote different kinds of play. Playful experiences may be vital in building rapport between students and tutors, establishing common language and allowing for discussion of mathematical ideas, promoting engagement, and allowing students to embody and apply their emerging mathematical understandings physically. Having “play breaks” may also increase students’ focus during the more traditional tutoring times (Fiorilli et al., 2021).

In the present study, 20 middle school students engaged in a 7-week tutoring intervention in an immersive VR environment. Our research questions examine (1) the kinds of mathematical play and (2) general play learners engaged in, as well as (3) interactions that led to and resulted from instances of play. Through our analyses, we show how using VR can support the goals of mathematics tutoring, and how mathematical play can surface students’ mathematical conceptions and misconceptions. We seek to inform the integration of play into future virtual tutoring interventions as an effective practice for student engagement and learning and argue that that play is particularly well-suited for VR environments.

1. Conceptual Background

We start with our conceptual background, which spans the affordances of VR, embodied learning in mathematics, mathematical play, and learning geometry in dynamic environments. The affordances of VR drove the design of the tutoring environment, as well as the kind of behaviors we looked for when analyzing the data (i.e., we were interested in behaviors unique to VR). Theories of embodied learning drove the design of the problem tasks students would be completing and the pedagogical instructions we gave to the tutors, as well as how we conceptualized mathematical understanding and the kinds of multi-modal interactions and ideas we paid attention to when examining videos. Theories of mathematical play were not used up front in the design or conceptualization of the research but instead were brought in post hoc to interpret and delineate particular emergent behaviors we saw in the data analytic phase that included playful embodied interactions. Finally, theories of learning geometry (such as the geometric habits of mind) determined how we initially designed both the learning tasks and the dynamic environment, how we trained the tutors in pedagogy and content, as well as what interactions we counted as signifying important geometric reasoning or geometric understanding in the analysis.

1.1. Mathematics Learning in Virtual Reality

Johnson-Glenberg and Megowan-Romanowicz (2017) identify three dimensions as key to the effectiveness of VR for learning: engagement of the motor system during learning, gestural congruency between physical movements and STEM concepts, and perception of immersion through VR. Recent advances in VR technology allow for these criteria to be met in mathematics education in ways that were not previously possible. Motoric engagement is high, as learners can gesture to modify mathematical objects and walk around and within objects. Gestural congruency is high, as advanced hand tracking allows for stretching gestures to enlarge shapes, rotation gestures to turn shapes, etc. Immersion refers to an experience that sensorially engages students as being inside of a virtual world, with fidelity to real experiences (Berkman & Akan, 2024). Learners can become immersed using wireless headsets that layer mathematical representations onto rich virtual environments, all while seeing their peers’ avatars and actions. Indeed, three-dimensional immersive environments like VR can allow students to have a better spatial understanding of 3D mathematics concepts through seeing shapes from multiple perspectives, to have more peripheral awareness, and to stimulate multiple sensory levels (Simonetti et al., 2020).

1.2. Embodied Learning in Mathematics

This investigation is built on theories of embodied learning, which posit that mathematical knowledge is perceptual and action-based in nature (e.g., Wilson, 2002). This is at odds with a view of mathematics as a discipline disconnected from the body and from action, based on abstract formalisms that have few real-world referents (Lakoff & Núñez, 2000; Nathan, 2012). From an embodied cognition perspective, mental simulations of actions, gestures, and physical movements (including actions on real objects) are all central kinds of cognitive processes (Abrahamson & Sánchez-García, 2016; Barsalou, 2008; Hostetter & Alibali, 2019; Shapiro, 2019). Little research has examined embodiment in a distance education context; one exception is Shvarts and van Helden (2023), who found some students could successfully leverage embodied principles obtained during independent practice, while others needed the guidance of a tutor.

The need for embodied theories of learning in mathematics education is made clear by Abrahamson and Sánchez-García (2016): “Extant theory of learning is by and large a theory of learning with paper, informed neither by the interaction possibilities of emerging technologies nor by what these possibilities could imply for mathematical epistemology and pedagogy” (p. 204). VR provides a unique embodied learning experience. In VR, learners can make pointing gestures indicating mathematical objects and representational gestures depicting mathematical objects (Alibali & Nathan, 2012; McNeill, 1992). Gestures are the spontaneous or purposeful arm and hand movements that people produce when reasoning or communicating (McNeill, 1992). During collaborative exchanges, multimodal resources like gestures and actions can become shared mathematical resources that are accessible to collaborators (Arzarello et al., 2009), with repeated gestures signifying cohesion of mathematical ideas (Yoon et al., 2014). In VR, students can also engage in functional actions (Walkington et al., 2023) with mathematical objects—like students using their hand to rotate, reflect, or dilate a shape—to have gestural congruency (Lindgren & Johnson-Glenberg, 2013) with the mathematical transformation they were enacting. Further, students can view objects from different perspectives by engaging in whole-body movements, using their bodies as part of the perceiving process (Bock & Dimmel, 2021; Dimmel et al., 2021).

1.3. Playful Mathematics

Play is defined as being free-form (but often rule-based within its paradigm), as involving stepping out of “real life” and balancing the irrational and rational as well as the imaginary and the real, and as involving both goal-specific behavior as well as behavior focused “in the moment” (Kolb & Kolb, 2010). Play exists on a continuum (Pyle & Danniels, 2017)—on one end is adult-guided play (which can be either child- or adult-initiated), facilitated by adults. This kind of play, however, can still place the locus of control with the child, with teachers acting as commentators, co-players, and demonstrators. On the other end of the continuum, free play is exclusively child-directed, voluntary, and flexible. In one type of play along this continuum, collaborative play involves teachers directing the outcomes, teachers and students collaboratively determining the context of the play, and children leading the play itself.

Recent research has indicated that playful mathematics has the potential to enhance engagement, mathematical understanding, and problem-solving skills (Pound & Lee, 2022; Williams, 2022). This learning method encourages students to explore and manipulate mathematical concepts in a more relaxed and interactive environment (Pound & Lee, 2022). Indeed, numerically focused playful activities can significantly reduce disparities in numerical knowledge among preschoolers from varied backgrounds (Ramani & Siegler, 2011). Using a pre-kindergarten curriculum that intertwines understanding mathematical trajectories with playful mathematics and technology, Sarama et al. (2008) show that the integration of playful learning with modern technology potentiates mathematical understanding.

Some research has also been conducted on mathematical play with older students. Williams-Pierce and Thevenow-Harrison (2021) studied middle schoolers learning about fractions, defining play as “voluntary engagement in cycles of mathematical hypotheses with occurrences of failure” (p. 510). Williams-Pierce and Thevenow-Harrison (2021) suggest that “provocative objects” are key to supporting play, and that these objects often give consistent and useful feedback, include difficulty/ambiguity, and offer alternative paths and non-standard mathematical representations. Objects in VR certainly can serve the role of being “provocative,” given their surprising and immersive nature, the open-ended ways in which they can be interacted with, and the ability to toggle mathematical notation and structure. Williams-Pierce and Thevenow-Harrison (2021) show how mathematical play can progress through different “zones” that range from initial free exploration to observation of outcomes, to attributing causality, to anticipating future actions.

1.4. Playful Learning in Geometry

We explore mathematical play in the context of geometry, which we define according to Clements (2003) as “the study of spatial objects, relationships, and transformations” (p. 151). The epistemology of geometry learning often draws on Piaget, who made the case that geometric and spatial reasoning develops in children through progressive formalization of students’ actions and simulated actions with objects and materials. This is compatible with conceptualizations of mathematical play that are child-centered and exploratory, and gives an account of how play can provide the foundation for formalized geometric understanding. This epistemology also draws on the work of Van Hiele, who described how geometric reasoning progresses from visually identifying shapes as whole objects, to recognizing shapes by their characteristics and properties, to forming abstract definitions of shapes and providing logical arguments. This framework suggests that layering abstraction and formal geometric terminology onto intuitive play actions might allow learners to eventually come to better understand geometric principles.

This framework highlights the importance of precise language and definitions in geometry and links between language, real-world experiences, and conceptual understanding (Clements, 2003). Other work in mathematics education supports the idea that students need significant time to explore and develop their own understanding of definitions of geometric ideas—like what an angle is or what properties different types of quadrilaterals have—before being given a formal definition to apply (Herbst et al., 2005; Keiser, 2000). Mathematical play may be an ideal way for children to develop the deep meaning of geometric ideas that must underlie formal definitions, and the important distinctions they imply, to be fully understood.

Driscoll et al. (2007) proposed four important geometric habits of mind, of which we focus on the three most relevant to mathematical play. The first is reasoning with relationships, where learners explore to find relationships between geometric figures and within geometric figures. Mathematical play can allow for such relationships to become visible, as shapes are manipulated and discussed. The second is investigating invariants, where geometric figures are transformed (including through rotations, reflections, dilations, and translations), and students reason about what changes or stays the same and why. Mathematical play in a DGS specifically is ideal for enacting this mathematical practice, as students can test out many different cases and engage in different kinds of manipulations in an agentic manner. The third is balancing exploration and reflection, where students try out different approaches to solve a geometric task, while regularly stepping back and taking stock of their attempts. This fits particularly well with mathematical play where many different strategies are improvised and opportunities are provided (and scaffolding is given when necessary) for reflection.

Dynamic Geometry Software (DGS) is one way students can engage dynamically (and playfully) with geometric objects (Hollebrands, 2007). In DGS, through intuitive dragging motions, students can modify the positions of specific points within a figure, observing in real time the relationship the changes have to the shape’s measurements (Leung & Lee, 2013). This embodiment fosters a collaborative atmosphere, enabling learners to co-engage with dynamic mathematical objects (Hegedus & Otálora, 2023). DGS can move students’ mathematical explanations from informal, everyday reasoning, to more precise reasoning in the context of the DGS, to general explanations in a purely mathematical context (Jones, 2000).

1.5. Research Purpose and Questions

This study aims to understand the use of HMDs for promoting play in middle school math tutoring as a way to address problems of practice with mathematics tutoring, described earlier. Integrating VR with DGS marks a significant advancement in mathematics education. When combined with DGS tools, VR and AR can allow students to actively explore math concepts (Ahmad & Junaini, 2020; Bujak et al., 2013) while immersed and collaborating with peers. This imaginary, creative, gesture-based VR environment can naturally and powerfully promote playful learning. We argue that play is a useful way of facilitating student learning of mathematics—both through mathematical play, which gives students direct novel experiences with mathematical concepts, and through general play, which can create an engaging, collaborative, safe environment for students to learn mathematics together. VR can both promote mathematical play, which in turn can promote mathematical learning, and create a unique environment that allows for general play to emerge to increase students’ focus on and investment in subsequent tutoring activities. Both instances of mathematical and general play can be built upon to provide new learning opportunities, if educators are able to notice the play and then make critical connections between the play and the concepts or mechanics being learned or leverage the play as an opportunity for rapport-building. The research questions are:

• What kinds of mathematical play do middle school students and tutors generate in a VR math tutoring environment?
• What kinds of general play do middle school students and tutors generate in a VR math tutoring environment?
• What are the kinds of interactions and situations that lead to mathematical play taking place?

2. Methodology

2.1. Participants and Tutors

This study involved n = 20 students (13 males and 7 females). Twelve students were in grade 7 (Year 7), and 8 students were in grade 8 (Year 8). Seven of the 20 students were classified as English learners. All 7th- and 8th-grade students at two middle schools were given the opportunity to volunteer to participate in the research, but given scheduling and other afterschool responsibilities, ultimately only 38 students assented to participate and had parent consent. Twenty students were included in this study, while the remaining 18 students were included in a different study. The students exhibited diverse self-reported math grades: 5 students with “A,” 5 students with “B,” 7 students with “C,” and 3 with “D” grades. This demographic information came from a pre-survey distributed to students 2 weeks before the study began. Participants were recruited from existing after-school programs in two urban middle schools in the Southern United States. These schools had a predominant enrollment of students qualifying for free or reduced lunch. Both schools had existing relationships with research team members and had participated in prior research. Working collaboratively, leaders from the school sites and researchers delineated an intervention to help 7th-grade students prepare for the 3-dimensional figures portion of their standardized tests and 8th-grade students prepare for the motion geometry portion of their standardized test. These topics were selected by the students’ mathematics teachers as the most important concepts being covered during the general period when the tutoring intervention would be taking place.

The tutors were students at a local university. Among them, three undergraduate education majors with previous middle school math teaching experience were included. The fourth was working in the university’s technology design lab and brought his in-depth knowledge of the virtual tutoring platform. They opted for the pseudonyms Jandy, Norbert, Yuxi, and Kevin. Before the study commenced, all tutors were briefed on the VR tutoring platform and the geometry concepts. They also engaged in weekly meetings throughout the tutoring to deliberate on teaching strategies and challenges.

This study received ethical approval from a university institutional review board, and all participants had parental informed consent for participation.

2.2. Description of Environment and Activities

GeoGebra (Hohenwarter & Fuchs, 2004) designed the VR tutoring environment for the Oculus Quest 1/2 HMD in collaboration with the researchers. The design of this VR tutoring environment took place over the course of 6 months before the study began and involved back-and-forth testing and revising. The version of the tutoring environment we used in this study is still a prototype and is undergoing further refinement. Most DGS is built, by necessity, for one learner or teacher to be in control of the simulation. Our DGS implementation, however, was collaborative in that multiple learners would appear around the mathematical objects, and all of them could interact with the shapes and see the results of others’ transformations. DGS is typically implemented in two-dimensional screens like tablets or laptops; our approach is novel in that VR allows for immersive experiences with 3D shapes. We will next describe the environment in more detail.

Visual and Spatial Layout: The VR tutoring environment was designed to replicate a large, open floor plan room inside a building with windows and doors (Figure 1 and Figure 2). The room had a blue tile floor and a vaulted ceiling above, displaying a pastoral landscape with trees and a sun that moved overheard.

Choosing a Role and Avatar: After opening the VR tutoring application, users would choose their role as either a teacher or a student. The selected role determined the functionality of the avatar within the environment, which we will explore more in the following section. After selecting a role, users could choose one of 12 avatars to represent themselves. The avatar appears as a torso and head, which would turn or lean as the student turned and leaned their real body. The avatar also had fully rendered virtual hands, updating as users move their real hands. Students could use physical walking to move around the environment or could instantly teleport to different locations they targeted using specific gestures. Students could hear each other’s voices and see each other’s names displayed above their heads. As participants moved closer together in the VR environment, the audio of their voices could be heard more loudly and clearly. As participants moved farther from each other, the audio reduced in volume and clarity.

Interacting in the VR Environment: The core activities in the VR tutoring environment revolved around 3D geometric objects that participants could see and interact with. Tutors, because of their role as “teachers,” could select various geometric objects from a menu that would appear in the center of the VR tutoring environment. For example, a tutor could select a rectangular prism from a list of geometric shapes, and that prism would populate in the center of the room. After a geometric object was selected, participants could then manipulate the object by selecting points or lines on the object and moving them. For example, both students and tutors could select an edge of the rectangular prism and drag the edge farther away from the center of the shape, thus elongating the figure. Furthermore, participants could select the entire geometric object and move it across the room. While interacting with geometric objects was possible for both tutors and students, there were many actions that only tutors could accomplish. For example, tutors could use a menu to turn on a coordinate plane that displayed an X, Y, and Z axis within the tutoring environment. Also, tutors could use a menu to turn on dimensional measures, which displayed length, area, and volume measurements of some geometric figures. For example, if students were stretching a rectangular prism, the tutor could turn on the coordinate plane and dimensional measures so that students could see the shape transforming along a grid and witness the changing height, surface area, and volume.

The Tutoring Activities: The VR tutoring activities involved 15 dynamic mathematics simulations (see Figure 1 and Figure 2 and Appendix A). Seven simulations were developed for seventh-grade content and focused on 2D geometric shapes (e.g., triangles and parallelograms) and 3D geometric shapes (e.g., prisms and pyramids). Eight simulations covered eighth-grade content focused on translations, reflections, rotations, and dilations. Appendix A details which of the theoretical key elements of learning geometry each simulation involves (e.g., Clements, 2003; Driscoll et al., 2007; Herbst et al., 2005; Keiser, 2000). A typical VR tutoring session involved three parts. First, tutors and students would gather in the VR tutoring environment for a warm-up. For example, some tutors would play “Simon Says,” while others would conduct virtual “races” around the room. For context, “Simon Says” is a children’s game that explores listening skills and body movements. The game has two roles: a single leader and multiple followers. The leader begins by saying “Simon says” and then adds a body movement command. For example, “Simon says pat your head with your left hand.” Followers must complete the command correctly, or otherwise, lose the game. If the leader provides a command without saying “Simon says,” the followers are not supposed to follow the command. If they do accidentally follow the command, they lose the game. The game proceeds until there is one follower left, who is the winner. This was done to familiarize tutors and students with one another while also providing an opportunity to practice acting and interacting within the VR tutoring environment. The process of learning how to use the VR environment took time. The first three tutoring sessions spent more time focused on learning to use the mechanics of the VR; therefore, these sessions had longer streams of mathematical and general play. Following this brief warmup, tutors would select one of the 7–8 simulations for the grade level to use for the day. Tutors would ask students questions about the chosen simulation and provide time for students to work together to answer the questions or solve mathematical problems (see Appendix A for the exact questions and problems). To close out the tutoring session, the tutors would either provide students the opportunity to ask questions, would select a new simulation, or would allow students to engage in open-ended exploration of the VR tutoring environment.

2.3. Research Design

In a typical tutoring session, 1 tutor and 2–3 students worked with one or more dynamic simulations for 30–45 min (average = 34 min). A second adult was present to video record the session. Tutoring sessions occurred once a week for seven weeks. There were 46 total tutoring session videos collected as part of this study, given that several sessions were canceled due to student absences (7 sessions × 4 tutors × 2 schools = 56 possible instances). The students’ assigned tutor and classmates were the same throughout the seven sessions. The average student attended 54% of the sessions (Weeks 1–2: 12 students present; Weeks 3–4: 14 students present; Week 5: 7 students present; Week 6: 6 students present, Week 7: 8 students present). Issues related to attendance occurred because the study took place after school hours, and therefore, students sometimes had other familial obligations. Although this may have shaped the mathematical learning that occurred, it did not change the forms of mathematical play that took place during tutoring sessions. The students took a demographic survey 2 weeks prior to participating in the study. They also took pre- and post-mathematics assessments, which occurred immediately before and/or after the intervention was administered.

A full accounting of learning gains as a result of the intervention is given in Walkington et al. (2025), but we summarize some of the highlights here. The full study included 38 participants, of which 20 were randomly assigned to use the GeoGebra VR environment for math tutoring, and 18 were assigned to a control group doing other VR activities. Students in the intervention group significantly outperformed students in the control group on two math learning measures. The first was an assessment aligned with the Illustrative Mathematics curriculum from which the VR activities were developed; students in the experimental group performed 1.07 standard deviations higher on this post-test when controlling for pre-test scores (p = 0.0054, 95% CI [0.39, 1.75]). The second was a validated standardized assessment, the Dynamic Geometry Assessment (DGA; Masters, 2010), which was only distributed during the post-test. Students in the intervention group scored 0.77 standard deviations higher on this assessment (p = 0.0227, 95% CI [0.15, 1.39]), controlling for their pre-test performance on the curriculum assessment.

2.4. Data Analysis

This research drew on techniques of interaction analysis (Jordan & Henderson, 1995) and qualitative data analysis (Ragin & Becker, 1992). These methods emphasize deep, team-based viewing and analyzing of video data, taking into account the complex social systems and interactions that underlie and define behaviors in educational settings. These analysis methods often involve selecting instances from the corpus that show key learning moments or trouble spots, with a rich analysis of different multimodal forms of communication that are uniquely accessible through video. Our analysis proceeded through six steps.

First, five members of the research team (2 education faculty, 2 education post-docs, and 1 education PhD student) divided the 46 video recordings among each other. Each member of the research team watched their assigned set of videos and took notes on potential recurring themes that emerged across their set of videos. Second, the research team gathered to discuss these preliminary themes. Some examples of themes that emerged throughout the discussion were (a) student’s use of gesture, (b) confusions about dimensionality, and (c) mathematical and general play. During these discussions, the research team shared excerpts from the video data that displayed each of the preliminary themes and refined our understanding of each theme. In this manuscript, we dive deeper into this final category: mathematical and general play.

Because of our familiarity with the literature on play, we had some preliminary notions of what to look for within the video data. However, throughout the data collection process, a member of the research team met with tutors on a weekly basis to review the tutoring session topics and discuss any practical or pedagogical issues in the VR tutoring environment. During these discussions, the tutors shared that play became central during the tutoring sessions. For example, the tutors explained that they played games—like racing, tag, or Simon Says—before beginning the tutoring sessions in order to engage students in the lesson. The research team understood these types of play as “general,” because both the tutors and the students thought of them as ancillary to the mathematical activities. Furthermore, in between the planned tutoring activities, the tutors found ways to engage students in play related to the mathematical activities at hand. For example, one tutor challenged students to make geometric shapes with their avatars’ bodies, while another tutor used the building-block simulation to allow students to construct geometric shapes with small, moveable cubes. The research team understood these types of play to be “mathematical” because they were directly related to the mathematical concepts the tutors were trying to teach students but were open-ended, free-form, and expressive in nature. Finally, many instances of play emerged from the students themselves, without being directed by the tutors. For example, students would act out scenarios using the mathematical objects, hide from the tutor, or attempt to “walk through” other avatars. In summary, the stories that tutors shared with researchers during weekly meetings helped to sensitize the researchers to instances of play within the video data and, therefore, deductively reason about mathematical and general play.

Having been informed by the literature on play and with notes from weekly meetings with tutors, the research team carried out the third step of our analysis, which involved the research team devising a criterion for rewatching and coding the entire corpus of video recordings to identify instances of mathematical and general play. To ensure reliability, they created a codebook to help guide the process of viewing and coding the 46 videos (

Table 1. Codebook.

Word	Definition
Mathematical play	Students act out a scenario or engage in an activity that includes movement or theatrics related to a math concept. This could include a game where the teacher used vocabulary words as part of the activity. Alternatively, this could include instances when the teacher and/or students built shapes with the blocks, discussed new concepts, or used them to introduce basic math tool manipulation. Students can also lead mathematical play by challenging a classmate to help them or compete against them in an activity based on learning math concepts.
General play	This involves playful interactions that were not explicitly mathematical. An example of this was thumb wars. While this does have movement and some theatrics, it is not focused on learning math concepts. Another example was when the students moved to different places in the room to explore their space.

). Fourth, two additional members from the research team (2 education master’s students) reviewed each of the 46 video recordings, coded any instances of mathematical and general play, and created a data table to summarize each of these instances. Fifth, the research team met to review the entire list of events classified as mathematical or general play. Each of these instances was viewed, transcribed, and analyzed using multi-modal analytical techniques (Walkington et al., 2023). Multimodal analysis involves an in-depth examination of the interaction of different modalities of communication, including speech (including pauses and intonation), hand gestures (including representational, dynamic, pointing, and beat gestures), whole-body movements like walking or turning, head and eye movements that demonstrate attention, and actions to manipulate real or virtual objects (e.g., using your fingers to change the size of a virtual cube). These different modalities are first identified separately in the corpus through detailed coding and then become woven together as each modality is used to understand how students reason and learn from and with real or virtual materials. Attention is paid to the extended nature of cognition—including how mathematical reasoning becomes distributed across different collaborators, as well as across different tools and representations. Our final step was to re-review the duration of video tutoring sessions to ensure other instances of play did not get overlooked.

3. Results

3.1. Instances of Mathematical Play

We discuss our data at two levels—a “session” is an entire intact tutoring interaction with 1 tutor and 2–3 students typically lasting 30–45 min. An “instance” is a conversational exchange between tutors and students, usually lasting 1–5 min, that occurred during a tutoring session and that involved some element of play. Out of 46 video-recorded tutoring sessions (

Table 2. Instances of mathematical play per session.

Session	Session 1	Session 2	Session 3	Session 4	Session 5	Session 6	Session 7	Grand Total
Total	13	10	7	5	2	4	9	50
Percent of instances of mathematical play per session (out of the total)	26%	20%	14%	10%	4%	8%	18%	100%

), there were 23 sessions, or 50%, that did not have any instances of mathematical play (i.e., were not coded with the “mathematical play” code at all; these could still contain general play) and 23 sessions that did have instances of mathematical play (i.e., were coded with the “mathematical play” code at least once). In those 23 sessions with play, there were 50 instances of mathematical play documented (Table 2). This resulted in an average of just over one instance of mathematical play per session. Almost two thirds of the instances of mathematical play happened within the first three sessions. There could be a variety of reasons for this that include a higher rate of attendance, the newness of the VR environment, or excitement by the students. In addition, play could occur as students were in the process of learning new embodied mechanics—which we would expect would take place more at the beginning of a learning sequence in a VR environment.

We found that 70% of the instances of mathematical play occurred in the seventh-grade sessions, while 30% occurred in eighth-grade sessions. Most of the instances of mathematical play (78%) occurred in Norbert’s and Jandy’s tutoring sessions. This is likely because of all the tutors, Norbert and Jandy had the most significant and sustained pedagogical training in teaching K–12 mathematics. Both were seniors and were part of a mathematics teacher preparation program at a university. Yuxi was also an education major but had less coursework and teaching experience in K–12 education, while Kevin was a technology specialist without the same pedagogical training. Indeed, our results suggest that pedagogical style may be an important factor in facilitating the presence of play.

3.2. Instances of General Play

Overall, there were more than three times the number of instances of general play versus mathematical play (

Table 3. Instances of general play per session.

Session	Session 1	Session 2	Session 3	Session 4	Session 5	Session 6	Session 7	Grand Total
Total	38	28	34	26	9	15	27	177
Percent of instances of general play per session (out of the total)	21.5%	16%	19%	15%	5%	8%	15.5%	100%

), meaning that general play was quite common. Of the 46 sessions, 25 sessions had at least one instance of general play, while 21 did not have any instances of general play. In the 25 sessions with general play (i.e., 25 sessions that had at least one general play code), there were 177 instances of general play. Like mathematical play, the first three sessions made up almost two thirds of the instances of general play. Norbert’s and Jandy’s sessions again made up the majority (83%) of sessions with general play, likely due to their more substantial pedagogical skills.

We next present multimodal analyses of instances of play, identifying where they fall along the continuum of more teacher-directed to more student-directed. In the images, the tutor is often labeled generically as “Teacher” rather than by their pseudonym.

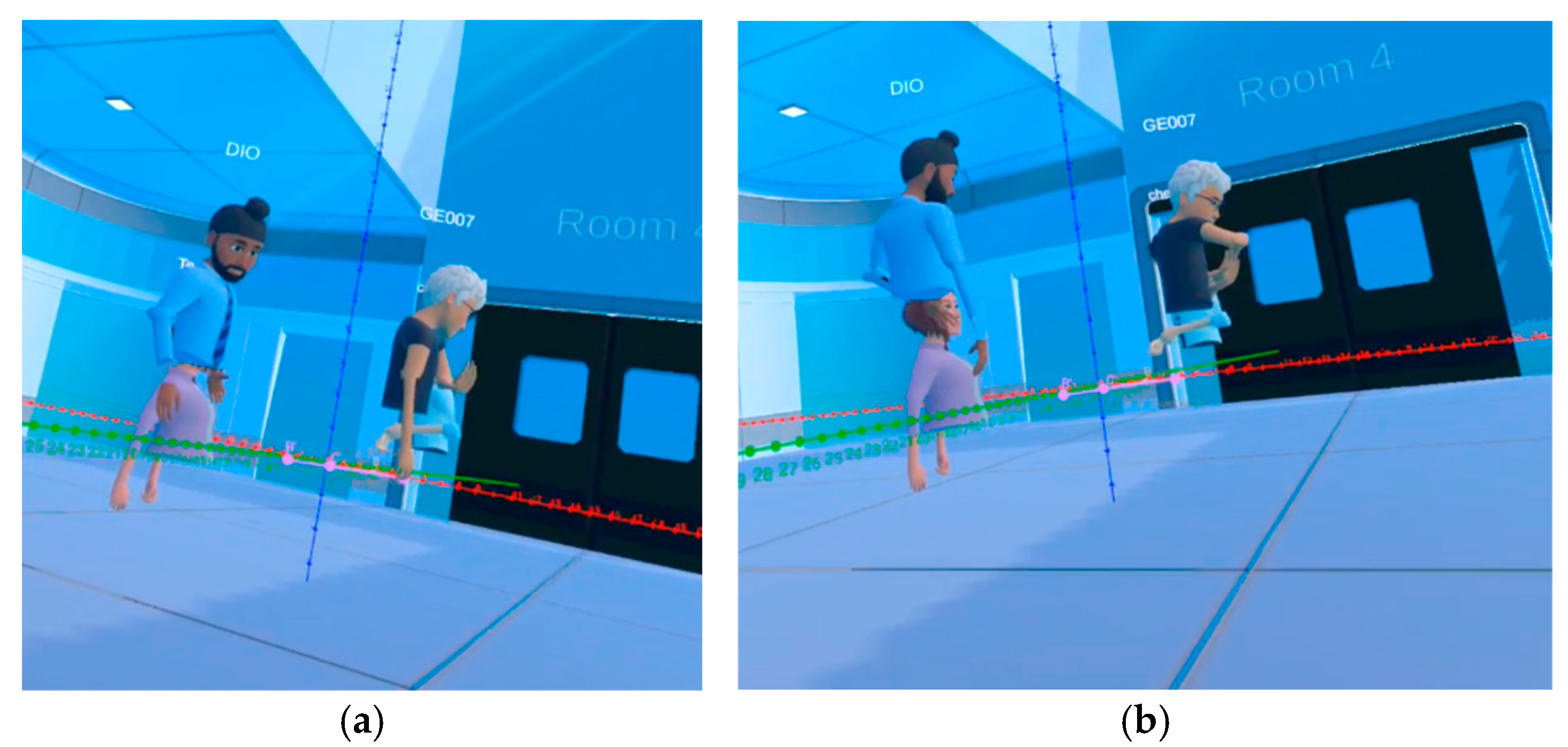
3.3. Multimodal Analysis of Mathematical Play: Rotation and Reflection (Teacher-Directed)

We first discuss some instances of mathematical play that are more teacher-directed or -initiated. In Figure 3, Jandy (the tutor) works with students DIO, Cherry, and GE007 on the topic of geometric rotation. We see the students being instructed to play the game “Simon Says” with their virtual bodies to practice rotation. “Simon Says” is a game where the leader (called “Simon”) tells other people to take particular physical actions with their bodies. If the leader says, “Simon says to raise your hand,” the participating players must raise their hands. However, if the leader simply says, “Raise your hands,” the participating players must not raise their hands, because the leader did not preface the instruction with “Simon says.”

Jandy begins in line 1 telling the students that Simon says to rotate their bodies 90 degrees clockwise. Interestingly, this idea was actually student-initiated by an immediately prior conversation where Jandy had asked the students to show her 180 degrees (intending for them to raise two arms out to make a straight line), and GE007 asked if he could rotate his body 180 degrees instead. As a result, here she asks the students to use whole-body movements (rather than just arms) to “become” or fully embody the mathematical concept of rotation. In line 3, Jandy asks the students to rotate 90 degrees counterclockwise, in the opposite direction. Cherry is obscured by GE007 in Figure 3, but has followed the rotation directions correctly, and in line 3 Jandy congratulates her. Jandy sees by watching the other two students’ avatars’ body movements that the other two students have become confused about the meaning of a “counterclockwise” rotation, which she then moves to address (lines 6–8). This shows how play was able to surface mathematical misconceptions, allowing students to test hypotheses and receive feedback after failure, an important element of mathematical play. Students were able to engage in the geometric habit of mind of balancing exploration and reflection, where reflecting on their play in the context of their partners’ actions and their teachers’ feedback allowed them to gain new mathematical insights. Here the VR tutoring environment allowed students and the tutor with bodies located in physically distant locations to enact full-body mathematical transformations together. In addition, this shows how incorporating mathematical play can ground students’ understanding of geometric ideas like “rotation” and “counterclockwise” in embodied experiences, allowing for definitions of mathematical terminology to be connected to prior mathematical investigations (Herbst et al., 2005; Keiser, 2000).

• Jandy: Simon says rotate your body 90 degrees clockwise.
  [Dio and GE007 spin in opposite directions, GE007 spins fully around.]
• DIO: Oh, clockwise? I think it’s; I think it’s… [GE007 spins fully around in clockwise direction.]
• Jandy: Yeah, you did it, okay good job Cherry. Simon says move your body 90 degrees counterclockwise. [Dio spins counterclockwise, GE007 clockwise.] I think you moved… I think you moved… Seven, I think you moved clockwise. I think you moved clockwise. [Jandy points and make spinning gesture with hand.]
• GE007: Seven, where are you going to go? Where are you going to go?
• DIO: Oh, wait.
• Jandy: Yeah, because you should’ve come back to the position where you originally started.
• DIO: Oh, because I turned this, and then I, oh dang it. How do I keep doing this? [motions in different directions with both hands, pointing fingers]
• Jandy: That’s why I wanted to explain a little bit the context of clockwise and counterclockwise as well perspective, because we’re all, you know, looking at different places. So, we should always be in the same spot.

In Figure 4, the tutor (Norbert) directs play using an imaginary “mirror” to discuss the concept of geometric reflection. In line 2, Cat initiates the play by playfully observing that the dynamic parallelogram shape hovering in the air could be imagined to be a mirror between Tiger and Norbert. Tiger realizes he is Norbert’s mirror image according to this parallelogram mirror. In line 7, Norbert initiates a reflection activity and asks the students to do what he does with his arms but reflected through the mirror. We see both Tiger and Jo getting involved in the motions, as well as some playful gestures where Tiger raises both hands over his head, Jo pretends the mirror is tangible, and Jo pretends to go through the mirror. In this way, the students are using whole-body motions and directed body motions to embody mathematical concepts in a playful collaborative manner. As an additional challenge, in line 9 Norbert asks the students to predict the reflection of him raising his other hand.

This activity represented a scenario that could have also been hypothetically conducted in the real world, although the element of a floating see-through frame would have had to be constructed. However, the experience may not have been as playful since the floating parallelogram that represented the mirror would not have been possible. This element of whimsy excited the kids, as seen in their responses in lines 1–4. We also see students testing hypotheses and receiving feedback from the tutor when they fail (line 11). Here, rather than the bodies moving in tandem (as in Simon Says), the bodies are moving in a related but opposite manner (of the reflection). In this way, the mathematical play served to reason about geometric relationships, one of the geometric habits of mind (Driscoll et al., 2007). Students were able to model and reason about how the reflection of an image related to the original image. They also had to recognize invariants—like the distance of the person from the mirror.

• Tiger: Ok oh wait. Wait, right there. [manipulates top vertex of quadrilateral]
• Cat: Looks like a mirror, looks like a mirror. [manipulates side vertex]
  [Jo approaches quadrilateral and looks up and down at it.]
  [Tiger raises both hands above head, mimicking looking in a mirror.]
• Norbert: Looks like a mirror. Alright, ready?
• Tiger: I’m your mirror, oh my God!
  [Jo pats flat hands on mirror, pretending it is tangible.]
  [Norbert playfully mirrors patting gesture from other side.]
  [Jo goes through the mirror and laughs.]
• Norbert: Here let’s…
• Tiger: Get over there.
• Norbert: Alright, so Tiger let’s pretend this is a mirror.
  If I raise up this hand, [raises right hand] which hand are you gonna raise up?
• Tiger: This one? [raises both hands, and then only right hand]
• Norbert: If I raise this hand [raises left hand], which hand are you gonna raise up?
• Tiger: This one? [raises left briefly, then right hand]
• Norbert: So, not that hand. You’re gonna raise up your left hand, right?
  [Tiger raises left hand]
  [camera pans to show Jo raising left hand, beside Tiger]
  That’s your left hand, perfect, because it is a reflection.
  It’s a reflection, right? Mirrors reflect.

3.4. Multimodal Analysis of Mathematical Play: Building 3D Shapes (Collaborative)

We next discuss two instances of mathematical play that are more central along the continuum of teacher-directed to student-directed collaborative play. Figure 5 shows two students (Cat and Tiger) discussing what to build with 3D cubic blocks, with tutor Norbert as the facilitator. The blocks can be picked up with the students’ virtual hands (detected via the HMD’s hand-tracking capabilities) and piled in different ways in the environment, much like real blocks, but without the constraints of gravity (i.e., the blocks can hover in midair). Cat begins moving the virtual cubic blocks around and asks Tiger what he wants to build in Spanish. In line 2, Tiger tells Cat that he wants to build a pyramid. In lines 3 and 5, Cat expresses confusion and asks Tiger to clarify given that there are only cubic blocks for building, and a pyramid needs to have a triangle to be built. In line 7, Norbert asks Tiger if a pyramid is possible and asks Cat to clarify the term “pyramid.” In line 8, Cat repeats “pyramid” in Spanish. All three interlocutors have their bodies positioned in reference to the geometric shape, and Cat engages in dynamic functional actions on the object while simultaneously participating in the discussion.

This building activity with the cubes elicited playful interactions that allowed students to explore mathematical ideas like how a pyramid might be constructed (or might be impossible to construct) from given geometric building materials. Students test hypotheses about being able to build the shape, receiving feedback while engaging in embodied, functional actions to manipulate the cubes. This instance of play leverages the presence of dynamic mathematical objects in a virtual environment, an important affordance of VR. It also shows how the VR experience facilitated the geometric habit of mind of balancing exploration and reflection (Driscoll et al., 2007), where students both attempt to build the pyramid and continually reflect on what is possible with the given shapes. Indeed, the students do not reflect on whether a pyramid is possible first and then build; instead, they engage in this geometric habit of mind by interweaving their exploration and their reflection, learning about the affordances of the shapes as they interact with them in an exploratory manner.

• Cat: Que quieres hacer Tiger? [hands positioned to indicate blocks]
• Tiger: Una pirámide.
• Cat: How are you gonna do that if there’s only squares? [places block on level two of shape]
• Norbert: Yeah?
• Cat: You need a triangle. [places block on level two of shape]
• Tiger: No, you don’t.
• Norbert: What do you think? Can we build a… can you build a pyramid? That’s what it means, right? What did you say? [beat gesture] What? Como se dice pyramid en español?
• Cat: Una pirámide. [places block on level two of shape]
• Norbert: Ah, pirámide.

In another instance of collaborative play relating to rotation, in Figure 6, Dio is working on building a dinosaur using cubes when exploring a mathematical task about the surface area of rectangular prisms. Building the dinosaur (which is not a rectangular prism) with the cubes was a spontaneous decision by Dio, rather than an instructed objective of the mathematical task. Dio spins the dinosaur built out of blocks in a circle repeatedly using the rotating functionality of the mathematical objects in the environment, expressing excitement that it moves (“Wow, wow”). Jandy (the tutor) realizes GE007 may also want to try this fun rotation activity, and GE007 begins rotating the dinosaur too. GE007 responds by playfully punching at the dinosaur, pretending he is fighting it. In lines 7–14, the group discusses what might be the axis of rotation that the dinosaur is spinning with respect to, using pointing gestures. In lines 15–18, the students laugh about making the dinosaur “dance” through rotation, and they decide together to name the dinosaur “Rexy.”

This activity was a more collaborative instance of play because the students were not prompted to build or rotate the dinosaur, but spontaneously did it on their own using functional embodied actions on virtual mathematical objects. Throughout the transcript we see them manipulating, gesturing at, and interacting with the virtual object. This became connected to the concept of rotation and center of rotation, making the play mathematical in nature as students could test out their ideas for where the center of rotation is and what the rotation would look like. This instance also related to the geometric habit of mind of investigating invariants (Driscoll et al., 2007), where learners tried to discover the point around which the object could be rotating. In order to do this, the students had to consider the point at which the distance from the dinosaur to the point would be invariant by dynamically testing different possibilities to uncover this invariant relationship. We next discuss instances where the play was not explicitly mathematical in nature.

• Dio: Wow wow. [Dio spins the dinosaur.]
• Jandy: Wait wait hold on [flat hand stopping gesture] Dio. Dio lets have [GE007] explore it. [Dio lets go of dinosaur] Okay [GE007] now you can rotate it… There you go.
  [GE007 spins dinosaur]
• Dio: Rawr… oh no! [playfully punches in the air, pretending to fight dinosaur]
• Jandy: Is that what you expecting when rotating?
• Dio: Yep. [totally expected] [continues to spin dinosaur]
• GE007: [Mhm]
• Jandy: What would be our axis of rotate? I mean our center of rotation here?
• Dio: The two squares. [spins dinosaur fast and then slow]
• GE007: Wow.
• Jandy: The two squares?
• Dio: Rawr.
• Dio: Would it be the nose? [Dio points to position on dinosaur, and then manipulates blocks in that position.]
• Jandy: ‘Cause everything is moving around the tail [makes circular gesture in air], the tail.
  Like the tail just stays in the same location. [points to tail]
• GE007: Yeah. Yeah. And everything is going to move around the center of rotation.
• Dio: Oh my God. [continues to manipulate blocks]
• Jandy: We have a dancing dinosaur. [GE007 spins dinosaur]
• Jandy: Lets name it.
• GE007: Rexy.

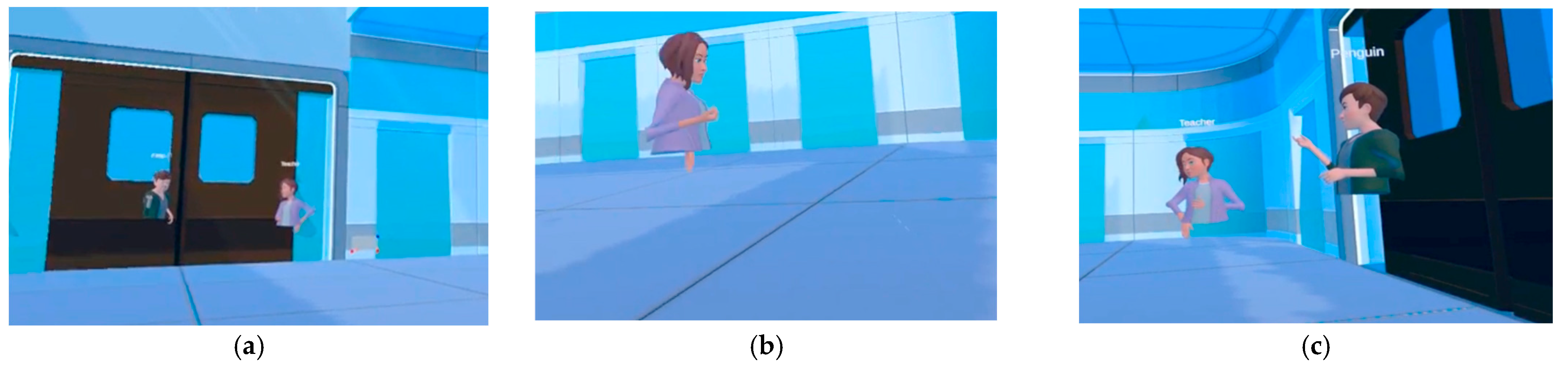
3.5. Multimodal Analysis of General Play: Climbing a Tree (Student-Initiated)

General play can also serve important pedagogical functions in mathematics tutoring environments. During reflection sessions, the tutors explained how such play could get students back on track if they had become disengaged, bored, or tired of answering questions about mathematical content. In Figure 7, GE007 spontaneously decides to exploit a bug in the software that allows an avatar to leave the tutoring building and climb a tree outside. The trees were intended to be scenery and improve the immersion of the environment, but the avatars were able to stand on top of them if they used the teleportation feature. However, the environment was designed so that the students should not have been able to leave the building. In line 4, Jandy, the tutor, realizes that a previous bug in the program still exists as the group watches GE007 leave the building and launch up into the tree. GE077 waves from the top of the tree, continuing to enjoy the antics, and then returns to the tutoring building.

This affordance of the VR environment allowed students to do something that might be difficult in the real world (climbing a large tree effortlessly) and have a fun break from the activities. Although this was classified as general play, the students’ view from the top of the tree of the dynamic shapes could have been made mathematically relevant by talking about different visual perspectives on the shapes. For example, the tutor could have asked the students to pretend to be a bird or an ant, and view the object from above or below—enacting different perspectives on an object. Thus, instances of general play can be capitalized upon to become mathematical play.

• GE007: I’m going to try to climb a tree.
• Jandy: I’m glad. You can still climb trees?
• GE007: Uh-huh.
• Jandy: Huh. Really? The bug was fixed!
• GE007: Dunno. See, look, and then this other thing you can step on right here. See.
• Jandy: Huh. I’m seeing, I’m seeing. Oh, they can. Okay. Okay, he’s able to come back.

3.6. Multimodal Analysis of General Play: Competitive Racing (Teacher-Initiated)

General play was often initiated by the tutor at the beginning of session or in the middle of the session. At the beginning of the session, it was explained by tutors during reflection sessions that teacher-initiated general play could serve to get students excited to participate in the tutoring session while also allowing them to practice certain technical features of the VR environment. Early on, tutors figured out that “racing” from one side of the tutoring building in the VR environment to the other was an engaging way to begin the lesson. In the VR environment, you can instantly teleport to another location in the virtual building by aiming your cursor at it and selecting the location. In Figure 8, the tutor, Jandy, has students prepare to engage in a race across the virtual room to see who can get across the room first using teleporting features. In line 2, Jandy reminds Penguin of the rules, then in line 3, Jandy ensures Penguin remembers how to “run” by teleporting in the virtual environment. In Figure 8b, Jandy can be seen teleporting across the room. In Figure 8c, Penguin and Jandy are on the opposite side of the room, having competed in the race. Jandy, the tutor, leveraged a feature in the VR environment that was impossible in the real world (teleporting) to make for a novel playful experience. Races involve geometric distance and elapsed time, and thus could also be leveraged as mathematical play if desired.

• Jandy: All ready? Yeah, you remember we do our daily race? So, I’m going to start with it and I’m going to finish with it.
• Jandy: Okay. Oh no, one time. You must’ve started glitching. Okay, there you go. Yeah.
• Jandy: Ready? Remember, don’t run in real life. Ready?
• Penguin: Yeah.
  [Student and tutor teleport across the room.]
• Jandy: Oh, you won. By a little bit. By your head. It’s fine. I’m a fair loser.

3.7. What Led to the Initiation of Mathematical Play?

To understand how and why mathematical play happened, the 50 transcripts and videos that showed instances of mathematical play were reviewed. For each instance, an explanation was documented to describe what initiated or led to the play. These analyses showed six themes for how mathematical play was initiated, shown in

Table 4. Themes with example of each theme for how mathematical play was initiated.

Theme	Example of theme
1. Tutor encourages exploration after explanation	The teacher explains reflection and encourages students to explore the concept using a mirror.
2. Tutor prompts student to repeat actions	A student translates an object and the teacher encourages the use of gestures to show what is happening with the object.
3. Tutor poses a question	How can you use the Pythagorean theorem in real life? Students play with the shapes to explore possible answers.
4. One student begins spontaneously playing and the tutor encourages the others to try it	A student rotated a shape after discovering that rotation was possible. The tutor encouraged others to try it.
5. Tutor interrupts play and redirects using math terminology and concepts	A student is making a cube out of many small cubes. The teacher and student discussed how it is a 3D shape called a rectangular prism.
6. Play happens out of necessity to understand a math concept	A student dramatically jumps around the room to view and manipulate the shape from different angles and perspectives.

, with an example of each.

It is clear from Table 4 that a variety of possibilities exist for encouraging mathematical play. We first discuss instances from our data where the tutors initiated mathematical play (Table 4, first 3 rows). Some of these instances were pre-planned prior to the tutoring session. Before each tutoring session, the tutors met with a member of the research team to review the lessons and discuss any issues that were emerging. One of the primary issues that the tutors discussed in these meetings was management of student engagement—strategies to ensure that students were following the rules, paying attention, and staying engaged. Because of the absence of physical presence, the tutors were not able to manage classrooms in typical manners, like pulling students aside for a private conversation or moving closer to the students. Therefore, the tutors had to devise new methods for managing student behavior and engagement, including play. As an example, there were regularly planned instances during the tutoring activities where the tutors would ask the students to playfully create and share their own embodied hand gestures—for concepts like rotation, reflection, or translation. This was intended to ground the students’ understanding of geometric terms and definitions in physical actions and concrete experiences (Clements, 2003; Herbst et al., 2005; Keiser, 2000). There were also instances where the tutors would playfully ask the students to test interesting hypotheses about shapes and space, perhaps with the intention of them experiencing failure—for example, the tutor would ask the students to try to fill up the whole room with a parallelogram or with a rectangular prism as part of the activity sequence. This connected to several of the geometric habits of mind—including investigating invariants, exploring geometric relationships, and balancing exploration and reflection (Driscoll et al., 2007). While these tutor/teacher-directed practices were pre-planned, they were not tested in any systematic way. Therefore, we believe these strategies should be more rigorously tested in the future to better understand the conditions under which they become useful for engaging students in playful mathematics.

We next discuss instances where students initiated mathematical play (Table 4, bottom 4 rows). Sometimes the play would be “purely” spontaneous—where a student was exploring a mathematical concept, and their exploration became a playful way to better understand what they were working on. For example, students would use body motions, like movement around the environment, as well as actions on objects, like playful arranging of cubes, to both engage with mathematics and be dramatic or creative. Alternately, students might initially be choosing to engage in some form of play, then something would happen where the tutor would notice that mathematical play, and either elevate it or elevate and restructure it. When the tutors would see play emerging, they would make its importance explicit to the group, often highlighting what is mathematical and compelling about the play. They would encourage other students to engage in the play or encourage the play to continue, while also sometimes adding additional layers or structures onto the play—like explicit mathematical goals or terminology. A comparative summary of these play types, with examples and their pedagogical implications, is provided in Table 5 in Section 4.

4. Discussion and Significance

To address our three research questions, Table 5 summarizes the types of mathematical and general play observed in the VR tutoring environment, along with representative examples and their pedagogical implications. This visual overview is intended to help readers quickly see how each category of play connects to the themes developed in the results and to the theoretical constructs in our conceptual framework.

Table 5. Summary of play types, examples, and pedagogical implications.

Type of Play	Definition	Example from Study	Pedagogical Implications
Mathematical play: teacher-directed	The tutor initiates play linked to specific math concepts or goals.	“Simon Says” rotations to embody clockwise and counterclockwise turns	Grounds abstract concepts in embodied actions; surfaces misconceptions for immediate correction; promotes geometric reasoning habits such as investigating invariants
Mathematical play: collaborative	The students and tutors jointly create mathematically relevant play scenarios.	Building 3D shapes from cubes to explore the feasibility of constructing a pyramid	Encourages hypothesis testing, collaborative problem-solving, and reflection; reinforces mathematical vocabulary in context
Mathematical play: student-initiated	The students initiate play that becomes connected to math concepts through tutor scaffolding.	Spinning “Rexy” the dinosaur while discussing center of rotation	Leverages student curiosity; provides authentic entry points for introducing or reinforcing mathematical terminology and ideas
General play: teacher-initiated	The tutor introduces non-mathematical play to build rapport or practice VR skills.	Teleportation races at session start	Increases engagement and familiarity with environment; can be adapted into math-related tasks
General play: student-initiated	The students engage in free-form, non-mathematical play.	Exploiting VR “bug” to climb a tree	Offers opportunities to transition into math discussions (e.g., perspectives, spatial reasoning); supports social connection and motivation

Table 5. Summary of play types, examples, and pedagogical implications.

Type of Play	Definition	Example from Study	Pedagogical Implications
Mathematical play: teacher-directed	The tutor initiates play linked to specific math concepts or goals.	“Simon Says” rotations to embody clockwise and counterclockwise turns	Grounds abstract concepts in embodied actions; surfaces misconceptions for immediate correction; promotes geometric reasoning habits such as investigating invariants
Mathematical play: collaborative	The students and tutors jointly create mathematically relevant play scenarios.	Building 3D shapes from cubes to explore the feasibility of constructing a pyramid	Encourages hypothesis testing, collaborative problem-solving, and reflection; reinforces mathematical vocabulary in context
Mathematical play: student-initiated	The students initiate play that becomes connected to math concepts through tutor scaffolding.	Spinning “Rexy” the dinosaur while discussing center of rotation	Leverages student curiosity; provides authentic entry points for introducing or reinforcing mathematical terminology and ideas
General play: teacher-initiated	The tutor introduces non-mathematical play to build rapport or practice VR skills.	Teleportation races at session start	Increases engagement and familiarity with environment; can be adapted into math-related tasks
General play: student-initiated	The students engage in free-form, non-mathematical play.	Exploiting VR “bug” to climb a tree	Offers opportunities to transition into math discussions (e.g., perspectives, spatial reasoning); supports social connection and motivation

4.1. RQ1: What Kinds of Mathematical Play Do Middle School Students and Tutors Generate in a VR Math Tutoring Environment?

In the present study, we showed how instances of mathematical play exist along a continuum of being initiated fully by the students or initiated by the tutors to reach a variety of pedagogical goals. What was striking about the play was the degree to which both the students and the tutors appreciated that the VR environment could allow them to do things that are impossible or unlikely in the real world—such as resizing gigantic mathematical figures to fill the room, teleporting to obtain a different view of a mathematical object, or moving around together on a world-sized coordinate plane. The facilitation of mathematical play was not in our original plans for the tutoring intervention; however, these “fantasy” elements of VR gave rise to play quite naturally, and both the tutors and the students led the implementation of mathematical play into the VR environment. Although some mathematical play we saw could have worked equally well in the real world (e.g., Simon Says), the majority of instances would be difficult or impossible to implement in traditional face-to-face settings (e.g., filling a room with a geometric shape or having blocks that can float midair). Even for those instances that would be possible in the real world, like Simon Says, delivering face-to-face mathematics tutoring is often not logistically possible, making their implementation in a virtual setting with effective levels of embodiment an important contribution.

Further, although research on DGS (Hollebrands, 2007) does not often forefront opportunities for play, the dynamic nature of these systems with the real-time measurement and feedback may, when implemented appropriately, allow important opportunities for mathematical play. This combination also allows for unique opportunities to allow students to grasp geometry concepts, as we demonstrated by showing instances of how mathematical play led to students demonstrating geometric habits of mind like investigating invariants, exploring geometric relationships, and balancing exploration and reflection (Driscoll et al., 2007). We also showed how mathematical play allowed for geometric definitions to become grounded in students’ experience exploring their environment and interacting with others using their virtual bodies (Herbst et al., 2005; Keiser, 2000).

We further highlight ways in which our findings on types of mathematical play differed from Williams-Pierce and Thevenow-Harrison (2021), likely due to our different technology context. Our observations were consistent with Williams-Pierce and Thevenow-Harrison (2021) in that hypothesis-testing (which is closely related to the geometric habits of mind; Driscoll et al., 2007) was a key element of mathematical play—students wanted to know what would happen because of their actions and found enjoyment in seeing what things would look like in the virtual environment if they acted in certain ways. However, unlike Williams-Pierce and Thevenow-Harrison (2021), we did not find failure to always be an important element of mathematical play. If a student is playfully slicing a shape in half with their imaginary lightsaber, or playfully reflecting another avatar’s movements as if there were a mirror between them, there is not necessarily an element of failure and revision involved. We certainly saw some instances of mathematical play that involved failure and revision—for example, a group of students tried to build a circle with cubic blocks. But there were many examples of play that were broader than what has been identified in previous literature. These other instances of play were usually short in duration, were easy rapport-builders, involved some level of silliness/humor, and were still often mathematical. It may be that there are various levels of sophistication of mathematical play.

4.2. RQ2: What Kinds of General Play Do Middle School Students and Tutors Generate in a VR Math Tutoring Environment?

As shown in Table 4, general play appeared in both teacher-initiated and student-initiated forms, each serving distinct purposes in the tutoring context. These instances often provided rapport-building, engagement, or opportunities for technical skill practice, and in some cases could be adapted to support mathematical learning.

In our analysis of instances of general play, we saw play that balanced the imaginary and the real, the rational and the irrational (Kolb & Kolb, 2010). This balance was facilitated by the fact that VR allows you to perform imaginary, irrational actions. In VR, blocks can hover in midair, and you can teleport or instantly climb a tall tree. These kinds of capabilities seemed to have an inherent playfulness to them, which our instructors sometimes made pedagogical decisions to allow or even capitalize on. Some of the most powerful instances we saw were of collaborative play (Pyle & Danniels, 2017), where the instructor and students collaboratively designed the play context, with the instructor determining key outcomes to highlight and the children directing the play as it unfolded.

General play has been found to increase self-regulation and engagement, release tension, and enhance creativity (Guirguis, 2018; Resnick, 2017), all of which may be particularly important in mathematics tutoring environments, to which students may arrive with negative views of mathematics and with the idea that they are being remediated. We saw this easing of tension and playful, fun interactions emerge in our data as students engaged in general play, as shown in Figure 7 and Figure 8. Future work could examine how general play could in some cases be leveraged to lead to mathematical play. For example, instances of general play, like students pretending to chop virtual objects with their cursors (which looked like lightsabers), could be used as a jumping-off point to discuss mathematical ideas like symmetries in 3D shapes. Exploring these ideas could in turn build key geometric habits of mind (Driscoll et al., 2007).

4.3. RQ3: What Are the Kinds of Interactions and Situations That Lead to Mathematical Play Taking Place?

Table 4 also highlights the initiating conditions linked to different play types, ranging from pre-planned tutor strategies to spontaneous student actions that tutors leveraged for mathematics. This framing helps situate our observations along the continuum from student-directed to teacher-directed play, as discussed in the analysis that follows. Results show examples of play that lay along the continuum from being child-directed and voluntary to being adult-guided and adult-initiated (Pyle & Danniels, 2017). Where individual interventions should locate themselves along this continuum likely depends upon their pedagogical and mathematical goals, the size of each group of students working together, and the relationships between tutors and instructors that are in place. With this continuum in mind, results suggest that facilitators sometimes explicitly enact play-based activities to go over pre-planned mathematics concepts (like rotation). In addition, sometimes play emerges as a result of an explicit goal that a student would want to accomplish (e.g., to climb the tree or obtain another perspective), while other times it emerged from the students as free-form and organic (e.g., play fighting a friend with lightsabers; Kolb & Kolb, 2010).

Still other times, play was student-initiated, but then structure was layered onto the play by the tutors. In this case, we show how facilitators play an important role in encouraging meaningful play, especially when breaking down more complex and abstract concepts like those often found in a math classroom. For example, the play described in Figure 4 demonstrates how the tutor, Norbert, encouraged students to mimic each other’s movements to demonstrate the mathematical concept of mirroring geometric figures. Prior to this episode, Norbert and other tutors expressed how conceptually difficult mirroring is in comparison to other geometric transformations (like translations, rotations, and dilations). To help students make sense of mirroring, Norbert improvised this technique and shared it with other tutors during weekly meetings. Facilitators who know how to interject play in the moment can help learners turn abstract mathematical concepts into tangible knowledge, giving meaning to geometric terminology like “reflection” and allowing learners to see how reflections work by investigating invariants (Driscoll et al., 2007).

4.4. Implications

Our findings support other research suggesting that playing in a mathematics learning environment can support engagement (Williams, 2022; Pound & Lee, 2022) and interaction with geometry concepts (e.g., the geometric habits of mind in Driscoll et al., 2007), but we extend these findings to the unique affordances of an embodied VR system. The embodied nature of the VR tutoring environment, and the ability of students to use whole-body movements, gestures, and hand-based manipulations of virtual objects, allowed opportunities for mathematical ideas to become embodied and tied to intuitive physical actions. In this way, theories of mathematical play can be combined with theories of mathematical embodiment (Wilson, 2002). Students’ engagement in mathematical play almost always involved either gestures, where hand motions with virtual hands were used for mathematical communication or reasoning (Alibali & Nathan, 2012); functional actions (Walkington et al., 2023), where students playfully manipulated mathematical objects; or whole-body movements (Bock & Dimmel, 2021; Dimmel et al., 2021; Gerofsky, 2011), where students move their whole bodies to perceive or even model mathematical ideas. Thus, mathematical play and embodiment emerged as inexorably intertwined, which has important implications.

Virtual environments that are intended to promote mathematical play need to be designed with embodied interactions in mind—learners should be able to move their hands and their bodies, and interact with dynamic objects, all while acting in a collaborative manner. Some motions can be directed by facilitators or tutors (e.g., Nathan et al., 2014), but caution should be used when considering making learners feel like they are in control of their bodies and have autonomy. Environments should also be built for gestural congruency, such that playful movements can be explicitly related to mathematical concepts like rotation, reflection, etc. (Lindgren & Johnson-Glenberg, 2013). When educators implement activities in VR, they should pay attention to both the gestures that they are using and the gestures that students in the environment are using, even if attending to gestures in VR might seem unfamiliar. They should think about ways to get students moving around the space, spatially positioning their bodies with respect to mathematical representations, and gesturing and manipulating objects in mathematically relevant ways, like the examples shown in this article.

4.5. Limitations and Future Directions

Some limitations of our study include that it only involved 20 middle school students and 4 tutors, and that it involved a specially designed sequence of activities in VR that may not be generalizable to other contexts. Furthermore, this study only follows a single group of students, rather than comparing these students against a control group. In the future, we plan to more explicitly design and implement playful activities into VR environments and test the effectiveness of play-based interventions on student attitudes and understanding of mathematics by including a control group. We think that both mathematical play and general play will be key to continuing to engage 21st-century adolescents in learning mathematical concepts, and that thinking about both how play can be explicitly facilitated and how the environment and task can give rise to spontaneous play are important future directions for the field of mathematics education. In addition, looking both at more and less sophisticated kinds of mathematical play will be important to capitalizing on the opportunities play offers for mathematics learning. We point to VR-based DGS as an important future avenue for research on mathematical play. We highlight that future tutoring interventions in VR could be designed to more explicitly capitalize on opportunities for play, and to leverage fantasy elements relating to VR that students might find compelling. Regarding the technology, while VR devices have decreased in price, the cost is still sometimes prohibitively expensive for wider adoption in schools. Even when purchased, this technology may need high-speed internet connections, regular maintenance, and a technical support team. In addition, resources must be invested in teacher training to use VR systems effectively. This study explores a possible intervention using VR technologies in an afterschool tutoring program but makes no recommendations for whether and how schools should adopt these technologies in a broader sense. More research is needed that investigates mathematical learning, educational policy, and educational finance before recommendations can be made about implementing VR tutoring at scale. Finally, we note that the VR software we used, GeoGebra VR, was still at the early stage of development and was being tested through a grant that was a partnership between GeoGebra and university researchers. There is a variety of other tools available to model geometric ideas in VR, such as Curio XR, Prisms VR, and NeoTrie VR.

4.6. Conclusions

Both mathematical and general play can be a useful way of teaching mathematics, particularly in environments that do not have the same types of management structures as traditional classrooms, such as tutoring contexts. General play has the potential to build rapport and establish a history of positive attitudes and interactions, as well as provide breaks for students grappling with difficult mathematical concepts. In some cases, general play could become a launching-off point for mathematical discussion and embodiment—such as discussing the spatial implications of different viewpoints on mathematical figures as students explore virtual spaces, or discussing the mathematical dimensions of body movements as students make their virtual avatar do different actions like racing. In addition, we think that even play that does not lead to mathematics is still valuable, given the difficulty and negative affect many students experience with respect to mathematics, and the ways in which students might view the need to participate in mathematics tutoring outside of school. Mathematical play can also foster engagement among students, specifically aimed at mathematical principles that can be made increasingly explicit from the play. This kind of play has the advantage of being more easily targeted to particular mathematical outcomes that are the goal of instruction. Play in VR environments can capitalize off of elements of movement and embodiment, which are often intrinsic to play, and allow students to have new, positive experiences with doing and learning mathematics. Additionally, our findings suggest that tutor experience and pedagogical style may influence the frequency and nature of mathematical play, warranting further exploration in future work. This paper thus makes an argument for the integration of play into virtual reality environments, particularly in mathematics education.