Abstract
Mental calculation is key to the development of number sense and flexibility in thinking, but in practice, it is often neglected in favour of written algorithms. The aim of this study was to examine the relationship between the success in mental calculation and the number of strategies used, as well as to explore differences between age groups and genders. The study included 233 participants from various age groups, and data were collected through a mental calculation test and individual interviews regarding the strategies employed. The study follows quantitative, cross-sectional, correlational-comparative design, and the data was analyzed using key statistical techniques including the Kolmogorov–Smirnov test, Pearson’s correlation analysis, linear regression, one-way ANOVA with Bonferroni post hoc correction, and two-way ANOVA to examine main effects and interactions. The results showed a statistically significant positive correlation between the number of strategies and success in mental calculation. Differences between age groups were marginally significant; it was found that upper primary and secondary school students used a greater number of strategies. Additionally, boys, on average, applied more strategies than girls. In conclusion, the variety of mental calculation strategies positively correlates with accuracy in mental calculation, and teaching a greater number of strategies may contribute to the development of flexibility and confidence in mathematical thinking. It is recommended that greater emphasis is placed on the development of mental strategies within formal education.
1. Introduction
Numerical calculations can be performed using three primary methods: mental calculation, written calculation (using paper and pencil), or calculators. Despite rapid technological advancements, Mead (2014) found that mental calculation remains the most common approach to solving real-world mathematical problems. Mental arithmetic is not only a cornerstone of children’s primary education but also an essential skill in daily adult life. Proficiency in basic arithmetic operations: addition, subtraction, multiplication, and division, is integral to modern life, enabling individuals to navigate diverse problem-solving situations. Furthermore, basic arithmetic underpins more advanced mathematical skills, which are vital across scientific disciplines. Pourdavood et al. (2020) emphasize that “mental computation is the most common form of computation used in everyday life. It is used for quick calculations and estimations” (p. 241). Northcote and McIntosh (1999) found that approximately 85% of daily calculations are performed mentally, with 58% being estimates 25% in contexts involving time and 23% related to purchases and money. Real-life scenarios often demand quick mental calculations, requiring individuals to understand relationships between numbers and identify appropriate operations efficiently (Bruinsma, 1969). In many cases, approximate answers suffice for solving complex everyday arithmetic problems (Ganor-Stern, 2018).
Mental computation and mathematical reasoning are critical for cultivating higher-order thinking. These skills enhance an individual’s ability to discern relationships among numbers and foster number sense, which is the key to developing flexibility and relational thinking.
The aim of this paper is to examine the correlation between mental calculation performance and the number of strategies employed. We provide a theoretical overview of mental calculation, focusing on its connection with mathematical reasoning, flexibility and relational thinking, and we discuss the results of our research to find out how the number of strategies employed correlates with mental calculation performance.
2. Theoretical Background
In this section, the relationship between mental calculation and flexibility, mental calculation and relational thinking will be addressed. Furthermore, we will provide an overview of mental calculation strategies. Some of the key concepts that we will mention will be defined immediately in order to enable an easier understanding of the theoretical framework and the previous research that follows in the subsections.
According to Haylock (2007), in the context of primary education, mental calculation is a child’s manipulation of the numbers involved in the calculation in the child’s mind, using their own knowledge and the relationships between numbers in order to operate with them. In some cases, when it is difficult for them to remember all the information involved in the calculation, the child may help themselves with a brief note on paper, but the main focus remains on the mental process. The highest level and use of mental calculation is possessed by students who are confident in their thinking, recognize the importance of alternative thinking, and see the creation of strategies as a strong outcome of their understanding of mathematical relationships (McIntosh et al., 1997).
Let us now turn to the aforementioned mental calculation strategies. According to Threlfall (2002), the way in which we calculate mentally can be viewed as an individual reaction of knowledge in accordance with one’s own number sense in a specific problem, and as the result of an interaction between observation and knowledge accompanied by experience, from which the choice of the path we will take to reach the solution arises. Thompson (1999) defines mental calculation strategies as the application of knowledge or quickly calculable facts about numbers combined with the properties of numbers with the aim of finding the solution to a task. The path to the solution that an individual follows depends on which elements of the task covered by their computational skills they have noticed, and which is the easiest for them given the knowledge they are most comfortable applying (Threlfall, 2002).
In this paper, mental calculation is studied. However, it is also necessary to define written calculation because it appears in the research results, given that it is highly prevalent in school mathematics. As for the methods of calculation, numerical calculations can be performed by three methods: mental calculation, written calculation, or with the help of a calculator (McIntosh et al., 1995). Teachers usually use the term algorithm to describe the methods of written calculation for addition, subtraction, multiplication, and division of whole numbers as they are traditionally taught in schools (Stacey, 2004). The phrase “written calculation procedures” is also used, as it fosters the development of procedural knowledge. It should be noted that when defining mental calculation, when we say “in the head” or “in the mind”, we do not mean calculating a task using the written calculation method but without using paper and pencil. Furthermore, algorithms can be easily applied without understanding and even without that being noticed, which results in students perceiving mathematics as a field that is not built on understanding—at least not for them (Gravemeijer et al., 2004). Kamii and Lewis (1993) believe that algorithms are harmful because they encourage students to give up their own thinking and ideas, thereby preventing the development of number sense. Children enter school with enormous potential for thinking, and the role of the teacher is to develop that potential rather than “moulding” and “putting all the cards on the table.” Mental calculation strategies differ from written algorithms because they require more than the application of an automated procedure. The key difference is the need for deeper knowledge of how numbers work (Hartnett, 2007). Most of us as adults do not use the written calculation algorithms we learned in school when we have to solve everyday practical problems (Stacey, 2004). Furthermore, one of the benefits of applying a wide range of mental calculation strategies in school is that analyzing the chosen strategies provides the teacher with information about the student’s stage of cognitive development, individual learning style, and readiness to adopt a new concept (Sharma, 2001). Through classroom discussions, different applications of mental calculation strategies to the same task can be compared. Many times, students’ invented approaches are based on a good understanding of numbers and operations, and they can often be used effectively and accurately (NCTM, 2000).
2.1. Mental Calculation and Flexibility
Mental calculation strategies continue to be taught in schools worldwide, often as calculation-oriented approaches with limited focus on their conceptual foundations (Kuzu & Nührenbörger, 2021). However, research highlights that the effective use of mental strategies requires “cognitive flexibility”, an adaptive and agile mind-set critical for fostering mathematical reasoning and problem-solving (Baroody, 2003; Hatano, 2003; Rathgeb-Schnierer & Green, 2013; Selter, 2009; Threlfall, 2009; Verschaffel et al., 2009). Over the past decade, significant progress has been made in understanding the mental processes that contribute to flexibility and adaptive expertise, with numerous empirical studies exploring flexibility in mental arithmetic (e.g., Rathgeb-Schnierer & Green, 2013, 2015; Torbeyns et al., 2009; Torbeyns & Verschaffel, 2013).
Researchers have developed nuanced definitions of mental calculation and flexibility (e.g., J. T. Sowder, 1988; Rathgeb-Schnierer & Green, 2013, 2019). As we have previously mentioned, we define mental calculation as solving arithmetic problems mentally without relying on standard written procedures and without the use of calculator. It is a powerful tool for deepening students’ understanding of numbers and their properties (Reys, 1984). Mental calculation enables learners to explore numerical relationships, make decisions about procedures, and create personalized strategies (Tsao & Lin, 2011; Everett et al., 2014).
Flexibility in mental calculations refers to the ability to switch between strategies and adapt them based on task characteristics and individual performance (Verschaffel et al., 2009; Star & Newton, 2009). Torbeyns et al. (2009) describe strategy flexibility as selecting the most efficient and accurate method for a given problem. Verschaffel et al. (2007) distinguished between mental mathematics performed in one’s head and mental mathematics performed with one’s head. Mental mathematics “with one’s head” involves the flexible use of strategies, as opposed to mental mathematics “in one’s head,” which relies on memorization and routine algorithms. Written calculation algorithms privilege knowledge of basic facts and implementation of taught procedures whereas mental calculations focus on the structure of number operations and their relationships (Rathgeb-Schnierer & Green, 2019).
After learning written calculation algorithms, students often abandon previously taught number-based strategies which are founded on developed number sense and conceptual understanding, even when those are more efficient or appropriate for specific problems (Hickendorff et al., 2018; Selter, 2001; Torbeyns & Verschaffel, 2013). Sequentially teaching strategies by example appears to hinder the development of flexibility. Instead of understanding general principles, students acquire specific procedures and tend to persist with the first-taught strategy, even in unsuitable contexts (Heirdsfield & Cooper, 2004; Klein & Beishuizen, 1994; Schütte, 2014). Suitable strategy use depends on various factors, including the target operation, numerical characteristics of a problem, and students’ ability to recognize patterns and relationships (Torbeyns et al., 2009; Blöte et al., 2000; Macintyre & Forrester, 2003; Peltenburg et al., 2012; Rathgeb-Schnierer & Green, 2015, 2017a, 2017b; Threlfall, 2009). Flexibility involves dynamically adaptation of strategies to specific problem situations from a repertoire of known methods, emphasizing both appropriateness and efficiency (Star & Newton, 2009; Verschaffel et al., 2009). Verschaffel et al. (2009) distinguish between “flexibility” as the ability to switch smoothly between strategies and “adaptivity” as selecting the most appropriate strategy. In practice, flexibility and adaptivity overlap, as both contribute to efficient problem-solving. For example, students with high flexibility can select strategies based on task demands and individual preferences, demonstrating more sophisticated mathematical reasoning (Anghileri, 1999; Buys, 2001; Thompson, 2010).
Despite the potential benefits of mental calculation, school practices often prioritize written algorithms, leaving limited space for developing flexibility (Jurić, 2022; Jurić & Pjanić, 2023). Students typically revert to written methods even when tasks require mental skills. This rigid adherence to written procedures may undermine students’ ability to effectively use mental strategies. Although certain researches (e.g., Anghileri, 1999; Caney & Watson, 2003; Carpenter et al., 1998; Heirdsfield et al., 1999; Zhou et al., 2021) show that older students apply a wider range of mental calculation strategies for all four arithmetic operations, independently modifying them or combining several known strategies to suit them in order to be as efficient as possible in a given task, other studies (e.g., Schütte, 2014; Selter, 2009; Jurić & Pjanić, 2023) indicate that students’ use of mental strategies decreases with age, potentially due to curriculum demands emphasizing written calculations. Studies also show that encouraging students to develop their own strategies fosters better numerical understanding and flexibility. For example, Carpenter et al. (1998) found that students who independently created addition and subtraction strategies demonstrated superior knowledge of numbers and adapted their methods effectively to more complex tasks. Similarly, systematic work on mental calculation promotes the development of personalized and efficient strategies, which results in fewer common errors associated with rote algorithm use (Carvalho & da Ponte, 2013a).
2.2. Mental Calculation and Relational Thinking
Relational thinking involves understanding equivalence and numerical relationships. It emphasizes the coordination of quantities within mathematical expressions, often without performing explicit computations. This type of thinking relies on flexible reasoning to transform mathematical expressions into equivalent forms, guided by an implicit or explicit understanding of mathematical properties and a relational interpretation of the equal sign (Empson et al., 2011; Stephens & Ribeiro, 2012).
A shared observation in mathematics education literature is that both relational thinking and mental calculation exhibit overlapping characteristics (Jacobs et al., 2007; Stephens & Ribeiro, 2012; Thompson, 2010; Threlfall, 2002). Jacobs et al. (2007) provide a foundational definition of relational thinking as reasoning that involves observing numbers and expressions holistically and recognizing relationships among them. For instance, when solving 98 ∙ 3, students can use the distributive property to compute via the equivalent expression: 98 ∙ 3 = (100 − 2) ∙ 3 = 300 − 6 = 294. This process exemplifies relational thinking, leveraging mathematical properties to simplify calculations. Fostering relational thinking is critical because it provides a conceptual foundation for arithmetic, promotes understanding of numbers and their properties, and enhances students’ ability to generalize mathematically (Jacobs et al., 2007; Molina et al., 2008; Stephens, 2007).
Mental calculation involves performing calculations without external tools, relying on a series of transformations beyond rote counting or standard algorithms (Maclellan, 2001; Proulx, 2013; Threlfall, 2002). Cognitive models of mental calculation generally highlight two major processes: (a) selecting a manageable strategy, and (b) executing the calculation based on that strategy (Maclellan, 2001; J. Sowder, 1992; Thompson, 2010). Choosing a mental calculation strategy inherently engages relational thinking. It involves identifying transformations that reduce cognitive load, often by applying implicit knowledge of numerical properties (Ambrose et al., 2003; Thompson, 2010). For instance, selecting a strategy for mental calculation aligns with relational principles such as substitution and equivalence (Jones et al., 2013). Furthermore, performing the necessary calculations after selecting a strategy relies on foundational number knowledge, including basic facts and place value (Maclellan, 2001; J. Sowder, 1992).
Mental calculation is valued for its emphasis on understanding mathematical properties and relationships. It encourages learners to calculate “with their head” rather than solely “in their head,” highlighting the relational and conceptual dimensions of mathematics (Linsen et al., 2015; Torbeyns & Verschaffel, 2013; Verschaffel et al., 2007). Numerous studies emphasize the importance of mental calculation in fostering strategic reasoning, critical thinking, and a deep understanding of numbers and operations (Almeida et al., 2015; Carvalho & da Ponte, 2013b; Reys et al., 1995; Varol & Farran, 2007). Reys et al. (1995) further underscore its role in promoting higher-level mathematical thinking and its practical benefits in daily life.
2.3. Mental Calculation Strategies
Building on the connections between mental calculation, flexibility and relational thinking, this section focuses on the specific strategies’ individuals employ during mental calculation. The ability to adapt and transition between strategies, as highlighted in previous research, is not only a marker of flexibility, but also a reflection of relational thinking, where mathematical operations and relationships are utilized for efficient problem-solving. This section provides an overview of mental calculation strategies and examines studies that explore their role in determining performance, further illustrating the intricate link between strategy use and success in mental calculation. The tables (Table 1, Table 2 and Table 3) were made in accordance with the framework set by Jurić and Pjanić (2023) who categorized mental calculation strategies including prime numbers and four basic arithmetic operations.

Table 1.
Strategies for mental addition and subtraction.

Table 2.
Strategies for mental multiplication.

Table 3.
Strategies for mental division.
The connection between mental calculation, flexibility and relational thinking is evident in the ability to select appropriate strategies and easily transition between them during calculations. Investigating the relationship between mental calculation strategies and success in solving mathematical tasks is, therefore, of particular importance.
Hope and Sherrill’s (1987) study on mental multiplication highlighted a strong relationship between strategy use and performance. Their research divided upper secondary students into high-performing and low-performing groups, revealing significant differences in their strategic approaches. Lower-performing students predominantly relied on inefficient “paper-and-pencil-like” mental strategies, often with limited success. In contrast, higher-performing students utilized more sophisticated distributive strategies, transforming one or both factors into sums or differences. While this research focused on mental multiplication, its findings about the connection between strategic choices and performance can offer valuable insights and hypotheses for other mental arithmetic operations. Further studies reinforce the relationship between strategy choice and performance in various arithmetic tasks. Torbeyns et al. (2006) examined second-grade pupils’ mental strategies for two-digit addition and subtraction. Their findings revealed that only high-achieving students adapted their strategy choices to the characteristics of specific tasks. Similarly, Torbeyns et al. (2009) demonstrated that young adults’ selection of direct subtraction or indirect addition strategies was closely linked to their success in solving three-digit subtraction problems. Foxman and Beishuizen (2002) provided additional evidence by reanalyzing the results from a nationwide survey of 11-year-old students. One task involved mentally adding two three-digit numbers (238 + 143 = ?). While 81% of students achieved the correct answer, the analysis of strategy use revealed notable differences among achievement groups. High and middle achievers frequently employed a “paper-and-pencil mental analogue” strategy (termed an “algorithm” by the authors), achieving greater success. In contrast, lower-achieving students tended to favour the split strategy, which proved less effective for this task.
This study builds upon previous research exploring the relationship between mental calculation success and the strategies employed. Specifically, the aim of this paper is to investigate the correlation between performance in mental calculation and the variety of strategies utilized by individuals.
2.4. Purpose of the Study
Although numerous studies highlight the importance of strategies, few have statistically examined the relationship between the number of strategies employed and the actual accuracy of task performance. The aim of this study is to investigate the diversity of mental calculation strategies and to explore whether there is a correlation between the number of strategies employed and success in solving mental calculation tasks. An additional aim is to determine whether there are statistically significant differences in the number of strategies with respect to the participants’ age, as well as differences between genders within age groups.
In line with the study’s objectives, we formulated three hypotheses to be tested:
- There is a statistically significant positive correlation between success in mental calculation and the number of mental calculation strategies used.
- There is a statistically significant difference in the number of mental calculation strategies between participant groups based on age.
- There is a statistically significant difference between genders, observed within participant age groups, in the number of mental calculation strategies used.
3. Materials and Methods
3.1. Participants
The research was implemented in the Republic of Croatia, and it included 233 respondents, the youngest attending 4th grade of primary school and the oldest last year of university education. The research participants were selected randomly in classes where we obtained permission from both the parents and the institution to conduct the research. It should be noted that obtaining permission was not a straightforward process, since, in addition to the test itself, which did not take too long, the interviews required considerable time, and everything took place during regular classes. This meant that cooperation was needed from a large number of teachers and professors, not only in mathematics but also in other subjects. The respondents were selected in several schools and faculties in order to obtain as diverse sample as possible considering prior mathematical knowledge, and in order to exclude the impact of teaching methods used with the respondents. As for a more precise specification of the secondary schools and faculties, the participants were students from the following institutions: mathematical high school, language high school, general high school, vocational technical schools, Faculty of Electrical Engineering, Mechanical Engineering and Naval Architecture, Faculty of Humanities and Social Sciences—Pedagogy, Faculty of Teacher Education, and Faculty of Chemistry and Technology. Table 4 shows the number of students in each age group in total and in relation to gender, as well as the number of educational institutions attended by the examined students.

Table 4.
Number of respondents per age and gender.
3.2. Measuring Instruments
In order to collect the data for the research implementation, mental calculation test was designed in accordance with the one by McIntosh et al. (1995), and an interview was implemented after the test. The study was conducted within a quantitative, cross-sectional, correlational–comparative design.
The mental calculation test consisted of 20 mental calculation tasks: 5 addition tasks, 5 subtraction tasks, 5 multiplication tasks, and 5 division tasks. These tasks (Table 5) were divided into three groups according to age categories and task difficulty: the first group for grades 4–6 of primary school, the second for grades 7–8, and the third group for high school students and university students. The tasks were selected in such a way that each was best suited for the application of a specific and efficient mental calculation strategy. The respondent would obtain 1 point for a correct answer. Incorrect or unsolved task would result with 0 points.

Table 5.
The mental calculation test—tasks.
The interview included only one question: Which strategy did you use to solve this task? In cases where the participant had not previously completed a given task using mental calculation, the question was phrased: Which strategy would you use to solve this task? This part of the study necessarily required an interview, rather than offering multiple-choice responses or allowing participants to write their answers independently. A skilled interviewer can use follow-up questions to clarify what is being asked and better understand the participant’s explanation, especially since students are generally not taught a wide variety of strategies in school, nor are they familiar with their names. Providing predefined options could lead participants to select a strategy that was suggested to them, while asking them to write answers independently could result in many unanswered questions, as participants may not know how to express, describe, or name the strategy they used. The result of this part of the study was the number of different mental calculation strategies used, both overall and for each specific arithmetic operation, as well as the frequency of written calculation, i.e., the number of mental calculation tasks in which written calculation was applied. The authors categorized or coded the participants’ responses based on the framework by Jurić and Pjanić (2023), which was discussed in more detail in the theoretical introduction. Although participants were explicitly instructed to solve the tasks using mental calculation, some applied written methods by mentally visualizing them.
Before designing the final test and questionnaire, a pilot study was implemented in one primary school class with 17 students, and with 14 students studying at the 1st year of graduate study. After the test and the questionnaire, the respondents took part in the interview concerning the strategies, but also concerning the task difficulty, the length and the volume of the loudspeakers producing mental calculation tasks, clarity of the claims in the questionnaire and similar. Originally, there were 28 mental calculation tasks which were eventually decreased to 20. These changes were made as it was noticed that 28 tasks are a lot and that the students, especially those attending primary school, but also students, lost focus by the end of the questionnaire. Apart from the mentioned, the interview took at least 30% longer, and the respondents were not motivated to explain strategies used for such a long time (approximately 20 min). Therefore, considering detailed interviews conducted after the pilot research, the instrument was adjusted to the answers obtained from the respondents.
3.3. Data Collection and Processing Methods
All the respondents accepted to take part in the research. Written approval was signed by the parents of minor respondents. The overall procedure was implemented by the paper authors independently as such procedure makes the research results the most valid, especially in terms of interview. After entering certain class, the respondents were presented with the plan: they first do the mental calculation test, and then they take part in a one-to-one interview. Mental calculation tasks were played via mobile phone with the help of a wireless loudspeaker, in order for all respondents to have the same conditions in terms of volume, task duration, number of repetitions, and time available to do the calculation, and in order to give task instructions orally, not visually, as the goal was to avoid written calculation. The test was completely anonymous so each respondent had to come up with a code that would connect their test to the strategies obtained via interview. The test took 10 min in total (different time was provided for each individual task, depending on its complexity, ranging from minimally 30 s to maximally 80). Each task was repeated twice using a loudspeaker.
To assess the normality of the data, part of the obtained research results was tested using the Kolmogorov–Smirnov test and further analyzed using parametric methods. Data were considered significant if p < 0.05. In presenting the data for each hypothesis, descriptive statistical parameters were first reported (arithmetic mean ± standard deviation (M ± SD), median (MED), minimum (MIN), maximum (MAX), range (R)), followed by the test results. All analyses were conducted using the software Statistica 13.5. In the context of the first hypothesis, Pearson’s correlation coefficient (r), the coefficient of determination (r2), and a linear regression model (y = b0 + b1x) representing the relationship between variables, along with the associated statistical significance, were calculated. For the second hypothesis, a one-way analysis of variance (ANOVA) was used. The statistical significance of the main effect was calculated, and Bonferroni post hoc correction was applied to examine significant differences among individual subgroups of participants. Partial eta squared (η2) was used as a measure of effect size, and the F value with associated degrees of freedom was reported. In the context of the third hypothesis, a two-way analysis of variance 2 × 7 (Gender × Age Category) was conducted, calculating the F value and the statistical significance of the main effects (Gender and Age Category), as well as their interaction. In the case of a significant main effect or interaction, Bonferroni post hoc correction was applied.
4. Results
4.1. Correlation Between Mental Calculation Success and Number of Mental Calculation Strategies
In this section, the correlation between the variable referring to the Mental Calculation Success (MCS) and variable referring to the Number of Mental Calculation Strategies (NSTR) will be analyzed in the context of the first posed hypothesis: There is a statistically significant positive correlation between success in mental calculation and the number of mental calculation strategies used. The variable NSTR referred to the number of different strategies applied throughout the entire test, from which we can deduce that the maximum is 20, meaning one different calculation strategy for each task. We will also present some examples of students’ responses during the interviews so that the coding (according to the table in the theoretical review) is clearer to the reader: 70 + 80: “That’s like 7 and 8, and then I add another 0.” 54 + 99: “I see 99 as 100, so that’s 154, and then I subtract 1.” 26 + 25: “I know that 25 and 25 is 50, and then plus 1 more.” 200 – 54: “From 54 to 100 is 46, and then another 100.” 85 – 78: “I count from 78 to 85.” 14 × 4: “That’s double 28, and then double again is 56.” 19 × 5: “20 times 5 is 100, and then minus 5.” 40 × 20: “4 times 2 is 8, and then two zeros.” 60 ÷ 5: “I know by heart that it’s 12.” 143 ÷ 13: “130 is 13 times 10, and then one more, the result is 11.”
In the table below, there are descriptive statistics indicators for the above stated variables.
Table 6 clearly indicates that the poorest mental calculation tasks result refers to one correct answer out of 20 that were performed by the respondents. The best result refers to 100% correct answers, which indicates great differences in the success in mental calculation tasks among respondents. As for the mental calculation strategies, some respondents applied only three different strategies in solving 20 mental calculation tasks, which is surprising considering that even the youngest respondents were formally educated in the field of given tasks. Generally, the average number of used strategies is low, and it refers to only 10 different strategies used in solving 20 tasks. Furthermore, after having implemented correlation analysis which was used to inspect the connection between the variable referring to the Mental Calculation Success and variable referring to the Number of Mental Calculation Strategies, Pearson’s correlation coefficient r = 0.543 was established, and it indicates moderately to good statistically positive and significant correlation (p < 0.001) between the observed variables (Table 7).

Table 6.
Descriptive statistic data on the mental calculation success.

Table 7.
Success correlation in mental calculations.
Furthermore, we observe that 29.5% of the variability in the criterion variable is explained by the predictor (r2 = 0.295). The results indicate that mental calculation success is closely correlated with the number of strategies used. Figure 1 presents a graphical display of the regression line. Thus, we have confirmed the hypothesis, and we can state that participants who are familiar with a greater number of strategies are more successful in mental calculation. Consequently, it is recommended that students are taught as many strategies as possible during formal mathematics education in order to improve their performance in mental calculation. On the other hand, since these two concepts are closely linked, we can also say that students who are confident in their mental calculation skills will be more likely to explore and develop their own strategies, thereby continuing to progress in mental calculation.
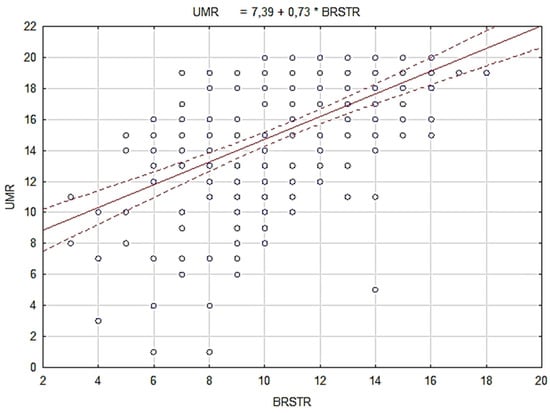
Figure 1.
Scatter plot and regression line with 95% confidence interval (UMR is MCS, BRSTR is NSTR).
4.2. Analysis of the Difference Between Age Categories in the Number of Mental Calculation Strategies
This section will focus on analyzing the differences between the groups of respondents starting from the 4th grade of primary school onwards, in relation to the variable of the Number of Mental Calculation Strategies (NSTR) and in the context of the second hypothesis stating: There is a statistically significant difference in the Number of mental calculation strategies between the following groups: respondents attending 4th, 5th, 6th, 7th and 8th grade of primary school, respondents attending 1st and 2nd grade of secondary school and respondents older than 17. The Table 8 indicates descriptive statistics indicators for the above stated variables.

Table 8.
Descriptive statistic data on the number of mental calculation strategies per age.
From the table above, we can see low minimal number of strategies used by the respondents over the age of 17. They used only five mental calculation strategies in 20 tasks, which is similar result to the result obtained by the primary school students who used minimal number of 4, 5, 4 and 3 strategies, in such order, starting from the students attending 4th grade of primary school. As for the average number of strategies, it was shown that the students attending 8th grade of primary school and students attending 1st and 2nd grade of secondary school were the most successful as they averagely used 12 strategies. Furthermore, in order to examine the statistical significance of differences in the mean values of the variable Number of mental calculation strategies among the observed groups, a one-way analysis of variance for independent samples (ANOVA) was used. The results are presented in Table 9.

Table 9.
Variance analysis results.
Although an inspection of the results in Table 9 shows that the main effect is not statistically significant (0.056 > 0.05), the detailed results of the post hoc analysis in Table 10 revealed some differences between groups (seventh-grade students compared to eighth-graders and students in the first and second years of secondary school, as well as fifth-grade students compared to first-grade secondary school students). Accordingly, we can state that the hypothesis is not confirmed considering borderline p value (0.056). These results suggest that, for most respondents, the number of mental calculation strategies does not increase with years of schooling. This leads us to the conclusion that students are not encouraged to use a variety of mental calculation strategies during formal education. We will also briefly address the “school-based” mental calculation strategies. Based on a review of the Croatian national curriculum (Ministarstvo Znanosti i Obrazovanja, 2019) for the subject of Mathematics, we list below the mental calculation strategies represented in the document, and thus reflected in direct classroom teaching:

Table 10.
Bonferroni post hoc test results.
- Addition of a one-digit or multi-digit number with a one-digit number is performed by rounding up to the nearest ten, and the same principle applies to subtraction,
- When adding and subtracting two two-digit numbers, sequencing is applied,
- Multiplication of a two-digit and a one-digit number is carried out by separating from left to right, while factorization appears only when multiplying a number by multiples of 10 or 100. In such cases, the factor is broken down into the product of a one-digit number and a decimal unit (e.g., 34·200 = 34·2·100 = 68·100 = 6800),
- In division of a two-digit or three-digit number by a one-digit number, partitive division is encountered.
By analyzing several strategies which are a result of the implemented interview, we have obtained the following average number of used ‘school’ strategies in mental calculation for 20 tasks:
Fourth- to sixth-graders → 8 strategies,
Seventh- to eighth-graders → 7 strategies,
First- and second-graders of secondary school and older → 6 strategies.
Therefore, we can see that students slowly deviate from the methods learned in school during mathematics instruction with the increase in the number of years spent in formal education. We assume that the reason can be found in the development of number sense and increased level of self-confidence, resulting in the courage to experiment and use self-taught strategies. It has to be noted that students used strategy taught at school the least when performing mental addition, because addition is a mathematical operation which students perceive as the easiest, thus feeling confident in their own knowledge and free to apply their own creations and modifications when calculating. Generally, the above results also indicate that ‘school’ strategies are not largely applied. Therefore, it can be concluded that the students learned mental calculation methods independently.
4.3. Analysis of Gender Differences per Age Categories in the Number of Mental Calculation Strategies per Age Categories
This section focuses on the gender differences per age groups, starting from the students attending 4th grade onwards, in relation to the variable Mental Calculation Success and in the context of the following hypothesis: There is a statistically significant difference in genders per following groups of respondents: respondents attending 4th, 5th, 6th, 7th and 8th grade of primary school, respondents attending 1st and 2nd grade of secondary school and respondents older than 17, in the Number of mental calculation strategies. The table below contains descriptive statistics indicators for the above variables.
From Table 11, we observe that male participants across all age groups used more strategies in mental calculation than female participants (except in the second year of secondary school, where the number of strategies used is virtually the same). It is interesting to note that the 20 mental calculation tasks given to participants were designed so that each individual task was best solved using a different strategy. Yet, the table shows that some participants used only 3 strategies across all 20 tasks. This suggests that certain tasks may not have been solved using a mental calculation strategy at all, but rather with a written calculation strategy (given that there were 5 tasks for each of the four basic arithmetic operations, implying at least 4 different strategies, one for each operation). Figure 2 further illustrates the number of mental calculation strategies by gender.

Table 11.
Descriptive statistic data on the number of mental calculation strategies per gender.
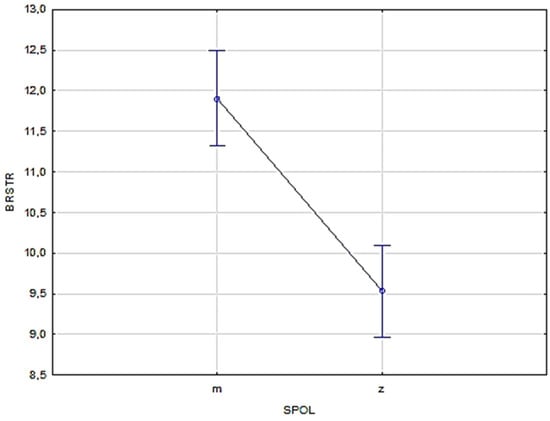
Figure 2.
Graphical representation of the number of mental calculation strategies per gender (m are boys, z are girls, BRSTR is NSTR).
To examine the statistical significance of differences in the mean values of the variable Number of mental calculation strategies among the observed groups by age and gender, a two-way analysis of variance for independent samples (ANOVA) was used. The results are presented in Table 12.

Table 12.
Variance analysis results.
After inspecting Table 12, it is clear that the difference in the Number of Mental Calculation Strategies is significant in terms of gender and in favour of male gender (Figure 2). Furthermore, the difference in the Number of Mental Calculation Strategies observed per age is at the significance borderline. Therefore, Bonferroni post hoc test results are shown in Table 13, in order to additionally analyse the difference in the pairs belonging to certain age groups. We can see that the difference is not statistically relevant in most pairs. Apart from the mentioned, the difference in the Number of Mental Calculation Strategies observed through an interaction effect of gender x age was not proved to be statistically relevant. Detailed presentations of some differences can be seen in Table 14. When observing respondents attending 4th, 5th, 6th, and 8th grade, there is a statistically relevant difference in the number of mental calculation strategies used, in favour of boys. Hence, what we can observe is that male respondents use somewhat more strategies when performing mental calculation tasks than female respondents.

Table 13.
Bonferroni post hoc test results.

Table 14.
Bonferroni post hoc test results (m are boys, z is girls).
5. Discussion and Research Limitations
The results of this study showed a moderately strong positive correlation between the number of mental calculation strategies used and task performance (r = 0.543; p < 0.001), thereby confirming the first hypothesis. This finding is consistent with the theoretical framework, which highlights the importance of flexibility and adaptability in mental calculation (Baroody, 2003; Star & Newton, 2009; Verschaffel et al., 2009). Participants who applied a greater number of strategies achieved better results, supporting the claims of Heirdsfield and Cooper (2004) that flexibility is key to success, not only in terms of knowing a particular strategy, but also in terms of the ability to select the one most appropriate to the characteristics of the task.
Similar findings have been reported in previous studies that recommend a shift from teaching exclusively “school” algorithms, procedures, and strategies toward encouraging students to discover, innovate, and create their own strategies, thus contributing to greater success in conceptual understanding and mental calculation (Macintyre & Forrester, 2003). The authors also emphasize that less time should be devoted to teaching written algorithms and more to systematically exploring mental strategies. It is also recommended to identify students who have difficulties with mental calculation and provide them with direct instruction in various strategies in order to improve their performance (Cooper et al., 1996). As part of the results for this hypothesis, we also listed mental calculation strategies included in the Croatian curriculum. Let us also consider the European recommendations for mathematics education. The European Mathematics Curriculum Intermath—Mathematics Syllabus (Primary P1–P5), implemented in the European Schools and covering the first five grades of primary school, stresses the importance of teaching mental calculation strategies and recommends that teachers systematically encourage their use (Europaea, 2012). The learning outcomes and recommendations emphasize the need for students to acquire and apply appropriate strategies to support mental calculation (e.g., 25 + 7 = 25 + 5 + 2; 29 + 13 = 30 + 12; 82 − 6 = 82 − 2 − 4; 67 − 19 = 67 − 20 + 1; 15 + 17 = 15 + 15 + 2; 42 + 35 = 40 + 30 + 2 + 5). Strategies such as bridging through tens and hundreds, halving and doubling, and partitioning numbers are recommended, along with practice and use of mental calculation. Furthermore, students should develop mental calculation strategies for multiplication and division, for example, by transferring knowledge of simple multiplication and division facts to multiples of 10 and 100, using partitioning, and applying mental strategies for multiplying and dividing whole and decimal numbers by 10, 100, and 1000. All of the above is also reflected in the learning outcomes and recommendations of the Croatian curriculum.
An analysis by age group showed that the number of strategies used does not increase linearly with years of schooling. The highest average number of strategies was recorded among eighth-grade students and first-year secondary school students, while university students used only slightly more strategies than the youngest participants. This pattern is consistent with the findings of Hickendorff et al. (2018) and Selter (2009), according to which older students often abandon diverse mental approaches and revert to written algorithms, even for tasks more suitable for mental calculation. An analysis of the curriculum further showed that Croatian schools teach a relatively narrow set of “school” strategies, which may limit the long-term development of flexibility and number sense (Haylock, 2007; Hartnett, 2007).
Gender differences were in favour of boys in most age groups, which is consistent with earlier studies (Carr et al., 2008; Fennema et al., 1998) indicating that boys exhibit higher levels of self-confidence and more frequently use a wider range of cognitive strategies, whereas girls tend to prefer more concrete approaches, such as modelling and counting. Tasks requiring flexibility and adaptation of algorithms showed better performance among boys. The authors recommend targeted instruction to encourage girls to use more abstract strategies, including verbalizing procedures, exploring multiple solutions, and building confidence in mathematical thinking. Teachers should create an environment where mistakes are accepted as part of the learning process and experimentation with strategies is encouraged among all students, especially girls.
Overall, the results confirm that mental calculation is not merely a technical skill, but a key tool for developing fluency, flexibility, and number sense, both in the educational context and in everyday life. As previous studies have pointed out (Reys, 1984; Torbeyns & Verschaffel, 2013), systematic teaching of a greater number of strategies and encouraging students to apply and adapt them to the situation can significantly enhance mathematical thinking and long-term mathematical literacy.
A limitation of this study relates to the size and geographic area of the sample, which may restrict the generalisability of the findings. For broader applicability, it would be advisable to conduct research in different countries and cultural contexts, although it should be noted that mental calculation is equally represented in the Croatian curriculum as in the European educational recommendations mentioned earlier.
Furthermore, conducting the research required considerable time due to the inclusion of interviews, transcription, and data coding, with an additional challenge being the fact that not all invited mathematics teachers and school principals were willing to cooperate, meaning that substantial effort was invested in recruiting voluntary participants. For future research, it is recommended to formally validate the mental calculation test, possibly developing a version that also includes tasks with natural numbers, which would provide even more detailed diagnostics and insight into students’ knowledge.
6. Conclusions and Implication
The results of this research indicate the importance of developing a variety of mental calculation strategies among students. Observed positive correlation between the number of used strategies and mental calculation success confirms that the greater flexibility in applying strategies contributes to success in task solution and to a higher level mathematical success, which might bring numerous benefits through life, not just in the context of formal education, but in everyday situations as well.
The pedagogical implications of these results indicate the need for systematic teaching of different mental calculation strategies and careful selection of tasks that encourage students to explore multiple solutions to a same problem, or to observe it from different perspectives. It is also important to encourage procedure verbalization and comparison of different strategies among students, considering that this develops metacognition and deeper understanding of numerical relations. Such approach contributes not just to the development of flexibility, but it also strengthens students’ self-confidence in their own mathematical thinking. It has to be emphasized that the variety of strategies enables the inclusion of all students in the process of learning—there is no one unique method of calculating. Some students are better with visual approaches, and some rely on verbal or operative strategies. By enabling more approaches and tools, deeper understanding of mathematical concepts is enabled, whereas students develop a sense of control and self-confidence in their own calculations.
Although gender differences are not consistently expressed across all age groups, the results suggest that certain strategies may be more suited to girls, while others may be more suited to boys. These further highlight the need to offer a broad repertoire of strategies so that every student, regardless of gender, learning style, or prior knowledge, can find an approach that suits them best. The observed gender differences in the number of strategies used should not be interpreted as biologically determined but rather considered in the context of cultural and social factors, such as different teacher expectations and variations in self-confidence. Girls tend to rely more on concrete strategies, while boys more easily transition to abstract approaches, possibly as a result of early encouragement in different directions. Therefore, it is essential to cultivate a classroom environment that equally encourages all students, particularly girls, to explore, discuss, and solve problems using different approaches.
In conclusion, the findings of this study highlight the importance of encouraging students to develop a diverse repertoire of mental calculation strategies. By fostering the exploration of strategies, promoting metacognitive reflection, and guiding students toward selecting the approach that best suits the task, teachers can enhance problem-solving efficiency and conceptual understanding. Such practice not only strengthens mathematical competence in the classroom but also equips students to apply the acquired skills in a variety of real-life situations.
Author Contributions
Conceptualization, K.P.; methodology, J.J.; investigation, J.J.; writing—review & editing, I.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the principles of the Declaration of Helsinki. Ethical review and approval were waived for this study since it involved voluntary and anonymous participation, did not collect sensitive personal data, and was carried out in line with the institutional guidelines.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Almeida, R., Bruno, A., & Perdomo-Díaz, J. (2015). Strategies of number sense in pre-service secondary mathematics teachers. International Journal of Science and Mathematics Education, 14(5), 959–978. [Google Scholar] [CrossRef]
- Ambrose, R., Baek, J., & Carpenter, T. P. (2003). Children’s invention of multidigit multiplication and division algorithms. In A. J. Baroody, & A. Dowker (Eds.), The development of arithmetic concepts and skills: Constructive adaptive expertise (pp. 305–336). Erlbaum. [Google Scholar]
- Anghileri, J. (1999). Issues in teaching multiplication and division. In I. Thompson (Ed.), Issues in teaching numeracy in primary schools (pp. 184–194). Open University. [Google Scholar]
- Baroody, A. J. (2003). The development of adaptive expertise and flexibility: The integration of conceptual and procedural knowledge. In A. J. Baroody, & A. Dowker (Eds.), The development of arithmetic concepts and skills (pp. 1–34). Lawrence Erlbaum Associates. [Google Scholar]
- Blöte, A. W., Klein, A. S., & Beishuizen, M. (2000). Mental computation and conceptual understanding. Learning and Instruction, 10, 221–247. [Google Scholar] [CrossRef]
- Bruinsma, B. (1969). Nieuw rekenen. Algemene inleiding. Bosch en Keuning. [Google Scholar]
- Buys, K. (2001). Mental arithmetic. In M. Van den Heuvel (Ed.), Children learn mathematics (pp. 121–146). Freudenthal Institute, University of Utrecht. [Google Scholar]
- Caney, A., & Watson, J. M. (2003). Mental computation strategies for part-whole numbers. In AARE 2003 conference papers: International education research conference. Australian Association for Research in Education. Available online: https://aare.edu.au/data/publications/2003/can03399.pdf (accessed on 15 April 2025).
- Carpenter, T. P., Franke, M. L., Jacobs, V. R., Fennema, E., & Empson, S. B. (1998). A longitudinal study of invention and understanding in children’s multidigit addition and subtraction. Journal for Research in Mathematics Education, 29(1), 3–20. [Google Scholar] [CrossRef]
- Carr, M., Steiner, H. H., Kyser, B., & Biddlecomb, B. (2008). A comparison of predictors of early emerging gender differences in mathematics competency. Learning and Individual Differences, 18(1), 61–75. [Google Scholar] [CrossRef]
- Carvalho, R., & da Ponte, J. P. (2013a). Students’ mental computation strategies with fractions. In B. Ubuz, C. Haser, & M. A. Mariotti (Eds.), Proceedings of the eighth congress of the European Society for research in mathematics education (CERME 8) (pp. 283–292). Middle East Technical University and ERME. [Google Scholar]
- Carvalho, R., & da Ponte, J. P. (2013b, February 6–10). Student’s mental computation strategies with rational numbers represented as fractions. Eighth Congress of European Research in Mathematics Education (CERME 8), Ankara, Turkey. [Google Scholar]
- Cooper, T., Heirdsfield, A., & Irons, C. (1996). Children’s mental strategies for addition and subtraction word problems. In J. Mulligan, & M. Mitchelmore (Eds.), Children’s number learning (pp. 147–162). Australian Association of Mathematics Teachers Inc. [Google Scholar]
- Empson, S. B., Levi, L., & Carpenter, T. P. (2011). The algebraic nature of fractions: Developing relational thinking in elementary school. In J. Cai, & E. Knuth (Eds.), Early algebraization: A global dialogue from multiple perspectives (pp. 409–426). Springer. [Google Scholar]
- Europaea, S. (2012). Mathematics syllabus—Primary cycle (P1–P5). Office of the Secretary-General of the European Schools, Pedagogical Development Unit. [Google Scholar]
- Everett, G. E., Harsy, J. D., Hupp, S. D. A., & Jewell, J. D. (2014). An investigation of the look-ask-pick mnemonic to improve fraction skills. Education & Treatment of Children, 37(3), 371–391. [Google Scholar] [CrossRef]
- Fennema, E., Carpenter, T. P., Jacobs, R., Franke, M. L., & Levi, L. W. (1998). A longitudinal study of gender differences in young children’s mathematical thinking. Educational Researcher, 27(5), 6–11. [Google Scholar] [CrossRef]
- Foxman, D., & Beishuizen, D. (2002). Mental calculation methods used by 11-year-olds in different attainment bands: A reanalysis of data from the 197 APU survey in the UK. Educational Studies in Mathematics, 51, 41–69. [Google Scholar] [CrossRef]
- Ganor-Stern, D. (2018). Do exact calculation and computation estimation reflect the same skills? Developmental and individual differences perspectives. Frontiers in Psychology, 9, 1316. [Google Scholar] [CrossRef]
- Gravemeijer, K. P. E., van Galen, F. H. J., Boswinkel, J. G. H., & van den Heuvel-Panhuizen, M. H. A. M. (2004). Semi-informal routines as alternatives for standard algorithms in primary school. In A. McIntosh, & L. Sparrow (Eds.), Beyond written computation (pp. 126–136). MASTEC—Edith Cowan University. [Google Scholar]
- Hartnett, J. (2007). Categorisation of mental computation strategies to support teaching and to encourage classroom dialogue. In J. Watson, & K. Beswick (Eds.), Mathematics: Essential research, essential practice (Volume 1, pp. 345–352). Mathematics Education Research Group of Australasia. [Google Scholar]
- Hatano, G. (2003). Foreword. In A. J. Baroody, & A. Dowker (Eds.), The development of arithmetic concepts and skills (pp. xi–xiii). Erlbaum. [Google Scholar]
- Haylock, D. (2007). Key concepts in teaching primary mathematics. Sage. [Google Scholar]
- Heirdsfield, A., Cooper, T., Mulligan, J., & Irons, C. (1999). Children’s mental multiplication and division strategies. In Proceedings of 23rd conference of the international group for the psychology of maths education (pp. 3–89). Psychology of Mathematics Education. [Google Scholar]
- Heirdsfield, A. M., & Cooper, T. J. (2004). Factors affecting the process of proficient mental addition and subtraction: Case studies of flexible and inflexible computers. Journal of Mathematical Behavior, 23(4), 443–463. [Google Scholar] [CrossRef]
- Hickendorff, M., Torbeyns, J., & Verschaffel, L. (2018). Grade-related differences in strategy use in multidigit division in two instructional settings. British Journal of Developmental Psychology, 36(2), 169–187. [Google Scholar] [CrossRef]
- Hope, J. A., & Sherrill, J. M. (1987). Characteristics of unskilled and skilled mental calculators. Journal for Research in Mathematics Education, 18, 99–111. [Google Scholar] [CrossRef]
- Jacobs, V. R., Franke, M. L., Carpenter, T. P., Levi, L., & Battey, D. (2007). Professional development focused on children’s algebraic reasoning in elementary school. Journal for research in mathematics education, 38(3), 258–288. [Google Scholar] [CrossRef]
- Jones, I., Inglis, M., Gilmore, C., & Evans, R. (2013). Teaching the substitutive conception of the equals sign. Research in Mathematics Education, 15(1), 34–49. [Google Scholar] [CrossRef]
- Jurić, J. (2022). Analysis of the Correlation between the Use of Written Algorithms and Success in Mental Calculation. In A. Ben Attou, M. L. Ciddi, & M. Unal (Eds.), Proceedings of ICSES 2022—International conference on studies in education and social sciences (pp. 44–60). ISTES Organization. [Google Scholar]
- Jurić, J., & Pjanić, K. (2023). An overview of mental calculation strategies and the frequency of their application. Revija za Elementarno Izobraževanje = Journal of Elementary Education, 16(3), 277–294. [Google Scholar] [CrossRef]
- Kamii, C., & Lewis, B. A. (1993). The harmful effects of algorithms in primary arithmetic. Teaching PreK-8, 23(4), 36–38. [Google Scholar]
- Klein, T., & Beishuizen, M. (1994). Assessment of flexibility in mental arithmetic. In J. E. H. LuitVan (Ed.), Research on learning and instruction in kindergarten and primary school (pp. 125–152). Graviatt Publishing Company. [Google Scholar]
- Kuzu, T., & Nührenbörger, M. (2021). The conceptual understanding of mental calculation strategies: Meaning-making in the case of the ‘Auxiliary task’. In J. Novotná, & H. Moraová (Eds.), Proceedings of the international symposium on elementary maths teaching (pp. 270–280). Charles University, Faculty of Education. [Google Scholar]
- Linsen, S., Verschaffel, L., Reynvoet, B., & De Smedt, B. (2015). The association between numerical magnitude processing and mental versus algorithmic multi-digit subtraction in children. Learning and Instruction, 35, 42–50. [Google Scholar] [CrossRef]
- Macintyre, T., & Forrester, R. (2003). Strategies for mental calculation. Proceedings of the British Society For Research Into Learning Mathematics, 23(2), 49–54. [Google Scholar]
- Maclellan, E. (2001). Mental calculation: Its place in the development of numeracy. Westminster studies in education, 24(2), 145–154. [Google Scholar] [CrossRef]
- McIntosh, A., Bana, J., & Farrell, B. (1995). Mental computation in school mathematics: Preference, attitude and performance of students in Years 3, 5, 7, and 9. Research report. Edith Cowan University, Mathematics, Science and Technology Education Centre. [Google Scholar]
- McIntosh, A., Reys, R., & Reys, B. J. (1997). Mental computation in the middle grades: The importance of thinking strategies. Mathematics Teaching in the Middle School, 2(5), 322–327. [Google Scholar] [CrossRef]
- Mead, K. C. (2014). Exploring everyday math without using technology [Master’s thesis, State University of New York]. SUNY Open Access Repository. Available online: https://soar.suny.edu/bitstream/handle/20.500.12648/227/Mead,%20Karla%20-%20thesis.pdf?sequence=1 (accessed on 20 April 2025).
- Ministarstvo Znanosti i Obrazovanja. (2019). Kurikulum nastavnog predmeta Matematika za osnovne škole i gimnazije. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2019_01_7_132.html (accessed on 20 April 2025).
- Molina, M., Castro, E., & Mason, J. (2008). Elementary students’ approaches to solving true/false number sentences. Revista de Investigacion en Didactica de la Matematica PNA, 2(2), 75–86. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. National Council of Teachers of Mathematics (NCTM). [Google Scholar]
- Northcote, M., & McIntosh, A. (1999). What mathematics do adults really do in everyday life? Australian Primary Mathematics Classroom, 4(1), 19–21. [Google Scholar]
- Peltenburg, M., van den Heuvel-Panhuizen, M., & Robitzsch, A. (2012). Special education students’ use of indirect addition in solving subtraction problems up to 100—A proof of the didactical potential of an ignored procedure. Educational Studies in Mathematics, 79(3), 351–369. [Google Scholar] [CrossRef]
- Pourdavood, R., McCarthy, K., & McCafferty, T. (2020). The impact of mental computation on children’s mathematical communication, problem-solving, reasoning and algebraic thinking. Athens Journal of Education, 7(3), 241–254. [Google Scholar] [CrossRef]
- Proulx, J. (2013). Mental mathematics, emergence of strategies, and the enactivist theory of cognition. Educational Studies in Mathematics, 84(3), 309–328. [Google Scholar] [CrossRef]
- Rathgeb-Schnierer, E., & Green, M. (2013). Flexibility in mental calculation in elementary students from different math classes. In B. Ubuz, Ç. Haser, & M. A. Mariotti (Eds.), Proceedings of the eighth congress of the European society for research in mathematics education (pp. 353–362). Middle East Technical University. [Google Scholar]
- Rathgeb-Schnierer, E., & Green, M. (2015). Cognitive flexibility and reasoning patterns in American and German elementary students when sorting addition and subtraction problems. In K. Krainer, & N. Vondrová (Eds.), Proceedings of CERME 9—ninth congress of the european society for research in mathematics education (pp. 339–345). [Google Scholar]
- Rathgeb-Schnierer, E., & Green, M. (2017a). Mental arithmetic and cognitive flexibility in elementary students. In Proceedings of the international technology, education, and development conference (pp. 492–499). INTED. [Google Scholar] [CrossRef]
- Rathgeb-Schnierer, E., & Green, M. (2017b). Profiles of cognitive flexibility in arithmetic reasoning: A cross country comparison of German and American elementary students. Journal of Mathematics Education, 10(2), 1–16. [Google Scholar] [CrossRef]
- Rathgeb-Schnierer, E., & Green, M. G. (2019). Developing flexibility in mental calculation. Educação & Realidade, 44(2), e87078. [Google Scholar] [CrossRef]
- Reys, R. E. (1984). Mental computation and estimation: Past, present, and future. The Elementary School Journal, 84, 546–557. [Google Scholar] [CrossRef]
- Reys, R. E., Reys, B. J., Nohda, N., & Emori, H. (1995). Mental computation performance and strategy use of Japanese students in grades 2, 4, 6, and 8. Journal for Research in Mathematics Education, 26, 304–326. [Google Scholar] [CrossRef]
- Schütte, M. (2014). Language-related learning of mathematics: A comparison of kindergarten and primary school as places of learning. ZDM, 46(6), 923–938. [Google Scholar] [CrossRef]
- Selter, C. (2001). Addition and subtraction of three-digit numbers: German elementary children’s success, methods and strategies. Educational Studies in Mathematics, 47, 145–173. [Google Scholar] [CrossRef]
- Selter, C. (2009). Creativity, flexibility, adaptivity, and strategy use in mathematics. ZDM—The International Journal on Mathematics Education, 41(5), 619–625. [Google Scholar] [CrossRef]
- Sharma, M. C. (2001). Matematika bez suza. Ostvarenje. [Google Scholar]
- Sowder, J. (1992). Estimation and number sense. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 371–389). Macmillan. [Google Scholar]
- Sowder, J. T. (1988). Mental computation and number comparison: Their roles in the development of number sense and computational estimation. Number Concepts and Operations in the Middle Grades, 2, 182–197. [Google Scholar]
- Stacey, K. (2004). Rethinking the algorithms of school mathematics. In A. McIntosh, & L. Sparrow (Eds.), Beyond written computation (pp. 91–100). Mathematics, Science & Technology Education Centre, Edith Cowan University. Available online: https://ro.ecu.edu.au/ecuworks/6741 (accessed on 2 January 2025).
- Star, J. R., & Newton, K. J. (2009). The nature and development of experts’ strategy flexibility for solving equations. ZDM—The International Journal on Mathematics Education, 41(5), 557–567. [Google Scholar] [CrossRef]
- Stephens, M. (2007). Students’ emerging algebraic thinking in the middle school years. Mathematics: Essential Research, Essential Practice, 2, 678–687. [Google Scholar]
- Stephens, M., & Ribeiro, A. (2012). Working towards algebra: The importance of relational thinking. Revista Latinoamericana de Investigación en Matemática Educativa, 15(3), 373–402. [Google Scholar]
- Thompson, I. (1999). Mental calculation strategies for addition and subtraction: Part 1. Mathematics in School, 28(5), 2–4. Available online: http://www.jstor.org/stable/30215422 (accessed on 1 October 2024).
- Thompson, I. (2010). Getting your head around mental calculation. In I. Thompson (Ed.), Issues in teaching numeracy in primary schools (pp. 145–156). Open University Press. [Google Scholar]
- Threlfall, J. (2002). Flexible mental calculation. Educational Studies in Mathematics, 50(1), 29–47. [Google Scholar] [CrossRef]
- Threlfall, J. (2009). Strategies and flexibility in mental calculation. ZDM—The International Journal on Mathematics Education, 41(5), 541–555. [Google Scholar] [CrossRef]
- Torbeyns, J., Ghesquière, P., & Verschaffel, L. (2009). Efficiency and flexibility of indirect addition in the domain of multi-digit subtraction. Learning and Instruction, 19, 1–12. [Google Scholar] [CrossRef]
- Torbeyns, J., & Verschaffel, L. (2013). Efficient and flexible strategy use on multi-digit sums: A choice/no-choice study. Research in Mathematics Education, 15, 129–140. [Google Scholar] [CrossRef]
- Torbeyns, J., Verschaffel, L., & Ghesquière, P. (2006). The development of children’s adaptive expertise in the number domain 20 to 100. Cognition and Instruction, 24, 439–465. [Google Scholar] [CrossRef]
- Tsao, Y. L., & Lin, Y. C. (2011). The Study of Number Sense and Teaching Practice. Journal of Case Studies in Education, 2(1), 1–14. [Google Scholar]
- Varol, F., & Farran, D. (2007). Elementary school students’ mental computation proficiencies. Early Childhood Education Journal, 35(1), 89–94. [Google Scholar] [CrossRef]
- Verschaffel, L., Greer, B., & De Corte, E. (2007). Whole number concepts and operations. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 557–628). Information Age. [Google Scholar]
- Verschaffel, L., Luwel, K., Torbeyns, J., & Van Dooren, W. (2009). Conceptualizing, investigating, and enhancing adaptive expertise in elementary mathematics education. European Journal of Psychology of Education, 24, 335–359. [Google Scholar] [CrossRef]
- Zhou, D., Liu, J., & Liu, J. (2021). On the different effects of teacher–student rapport on urban and rural students’ math learning in China: An empirical study. Psychology in the Schools, 58(2), 268–285. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).