Positioning K-8 Classroom Teachers as Mathematics Instructional Leaders
Abstract
1. Introduction
2. Theoretical Framework
3. Methods
3.1. Participants
3.2. Data Sources
- selected modules in elementary and middle-level mathematics from the Learning Mathematics for Teaching (LMT) assessments (Hill et al., 2008) administered at three timepoints. The elementary was completed with the application process, prior to project activities (pre; April 2021), following one semester of content-focused coursework (post; December 2021), and at the conclusion of the Fellows’ coursework (post-post/maintenance; June 2024). The middle-level modules were completed prior to project activities (pre; August 2021), following the second semester of content-focused coursework (post; December 2022), and at the conclusion of the Fellows’ coursework (post-post-maintenance; June 2024).
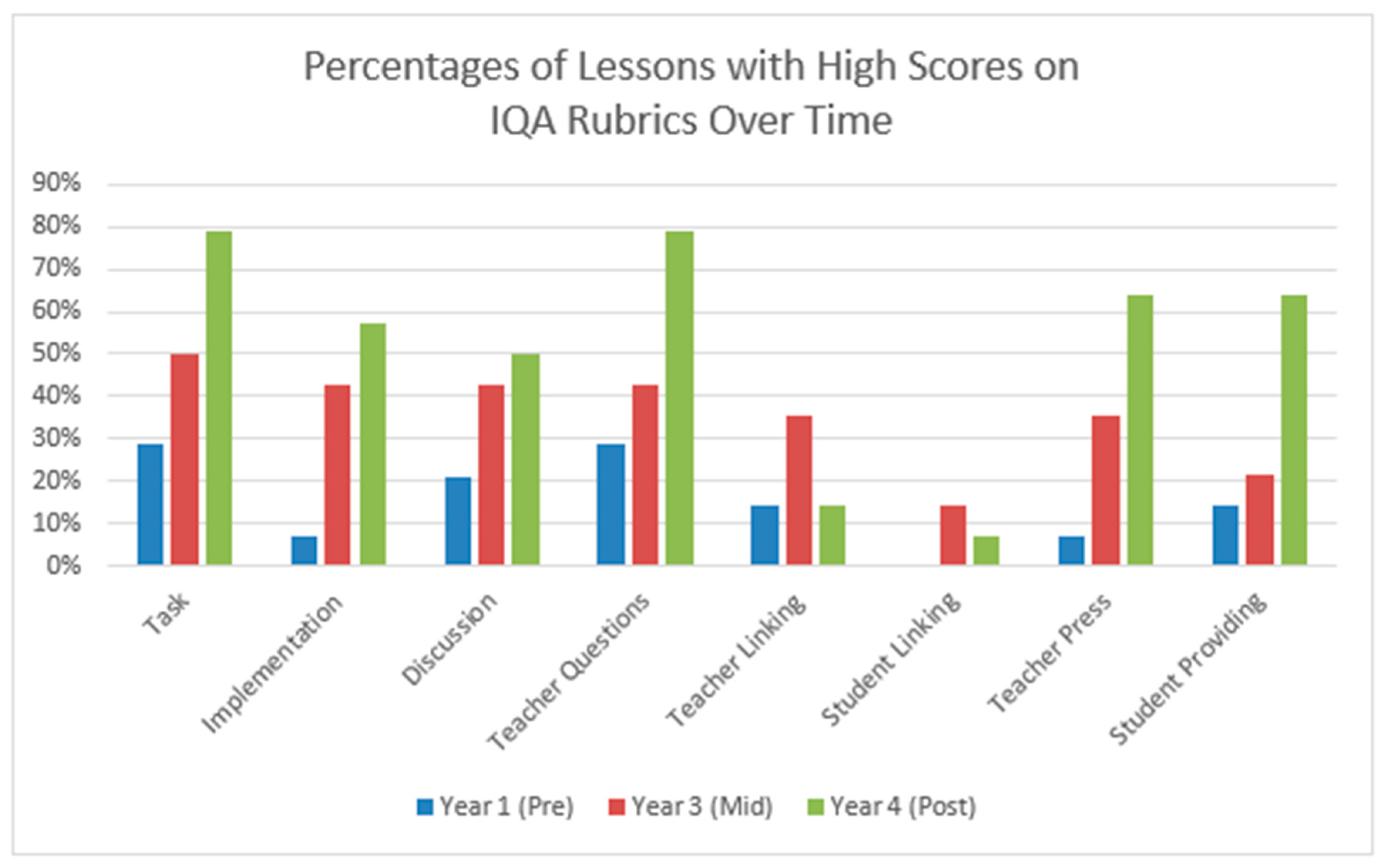
- videos of Fellows teaching mathematics lessons in their own classrooms, analyzed with the Instructional Quality Assessment (IQA) Toolkit in Mathematics (Boston, 2012). Fellows self-record a lesson of their choosing using a video-tracking platform (e.g., SWIVL). Videos were collected during Fellows’ Year 1 (pre; Fall 2021), Year 3 (mid; January 2023), and Year 4 (post; January 2024). The IQA is a set of classroom observation rubrics that specifically target ambitious mathematics teaching practices. The rubrics assess the rigor of the following components of ambitious mathematics instruction (rubric titles in parentheses): instructional tasks (Task), task implementation (Implementation), students’ mathematical contributions to the discussion (Discussion), teacher’s questioning (Questioning), teacher’s discourse actions (Teacher Linking and Teacher Press), and students’ responses (Student Linking and Student Providing) during mathematical discussions. In the IQA coding scheme, a score of 0 indicates the construct was absent, scores of 1–2 indicate low cognitive demand or low rigor in a construct, and scores of 3–4 indicate high cognitive demand or high rigor in a construct. In each data collection, a subset of 10 of 14 (71%) randomly selected lessons were rated by discussion and consensus between the external evaluator and a trained rater; the other 4 lessons were rated by the external evaluator.
- Focus groups for Fellows were held in groups of 4–5 Fellows for approximately one hour, in each year of the project. Prompts for the Fellows’ focus groups are provided in Appendix A, with prompts that align with the main goals of the project (mathematics, teaching mathematics, and leadership) in bold font. Qualitative data from focus groups and project artifacts were used to assess Fellows’ roles as instructional leaders in their schools and how those roles changed over time. Focus group responses were also used to assess Fellows’ self-perception of (and confidence in) their roles as instructional leaders over time, as another indication of their development as instructional leaders. For the Discussion, we examine data from RQ1 and RQ2 to identify factors that seem to support Fellows’ engagement as mathematics instructional leaders.
- A focus group was conducted for the four project leaders, for approximately an hour in each year of the project. Each project leader was invited to share events and insights from their specific role on the project and to reflect on Fellows’ overall growth and change over that year. In this report, data from project leaders’ focus groups are used to support and triangulate other data sources.
- Focus groups for school administrators were conducted each year of the project. School administrators (e.g., principals, assistant principals, and/or instructional coaches) signed up for 1-hour time slots, with focus groups consisting of 4–6 participants. In this report, data from project leaders’ focus groups are used to support and triangulate other data sources.
3.3. Data Analysis
4. Results
4.1. Research Question 1: Changes in Mathematical Knowledge and Instructional Practices: Mathematical Knowledge for Teaching
4.1.1. Mathematical Knowledge
- “I’m reflecting back on how I was teaching before the …program, and how we never truly went over the “why” because again, I didn’t understand why things worked one hundred percent… We are conceptually understanding every aspect within the mathematics, which I did not have full background of, except for …whatever my teacher taught me when I was in first grade.” (Year 2)
- “…for me, one of the biggest (changes) I do now is, I now understand when kids solve it with a different strategy. I can make connections and make sense of their math. Because I can see what they’re doing, because a lot of it has been previewed with [the course instructor], and because I now can make the connections, I see my own students making connections” (Year 2)
- “So this semester specifically we’re going over middle school math, and I teach middle school math. I have literally taken segments of what she’s done with us in class and brought it into my classes. There was one lesson where we modeled equations using algebra tiles, and I immediately did that with my class that same week.” (Year 2)
- “I really feel like I’m becoming more of an expert in mathematics.” (Year 3)
- “I feel like now I could understand the student’s perspective a little bit more. And it helps me to make the math more accessible to my students.” (Year 4)
4.1.2. Instructional Practices
- “I’ve started actually evaluating the tasks that I present to my students. So I look at the potential of the task …and then my implementation of the task. I look at the students’ evidence and teachers’ questions to make sure that the quality of the tasks that I’m doing is more level four tasks where there’s that justification.” (Year 2)
- “now that we’ve been talking about the [observation tool] I’ve been noticing as I’m giving problems, ‘Boy, there’s a lot of procedural problems here.’ I need to change up what I’m asking the students. That’s fairly new, because we’ve recently started doing that, but it’s almost automatic. Now, when I’m looking at a lesson, I start rethinking what I need to start asking kids because I’m not asking the right questions.” (Year 2)
- “I did a lot of the talking prior to this, and now I’ve become more comfortable, like letting the student voice dominate the conversation, even if what they say isn’t correct. I give them some time to explain their thought process.” (Year 4)
- “before, I was so focused on, ‘Hey, what’s the answer?’ But now going through that process …something that used to scare them, is something that they look forward to… They enjoy engaging in math, because I have learned how to make math accessible and not scary.” (Year 4)
- “So I think just being able to take a little bit more time exploring the math at a deeper level is something that I wasn’t doing before this program.” (Year 4)
- “the students’ voice guides the conversation, and that’s something that’s really stuck with me…. Now, it’s like mistakes are springboards in my classroom. So when we go through a math problem, we look for evidence of where students made mistakes to understand why, and then we use that as a point of learning. So that’s something that I’ve definitely learned from [project leader] that I can utilize mistakes to help progress students’ learning.” (Year 4)
4.2. Research Question 2: Change in Fellows’ Leadership Activities
4.2.1. Project Components That Position Fellows as Teacher Leaders
TLA and Coursework
- “we have to have a one on one with our principal about things that we’ve noticed in data we’ve collected, and for me that was really outside of my comfort zone.”
- “to step really out of my comfort zone and have those types of conversations with my principal and the curriculum resource teacher about changes that we may need to start making in math in our school, has really pushed me to be more outspoken.”
- “This is really pushing me and building me to have better leadership skills… I think the Catalyzing Change assignment really built my confidence, my ability for leadership.”
Recognition as Teacher Leaders
Mentoring School-Based Interns
Milestones and Dissertation Research
- “So I feel like I’ve gotten a lot more brave, and … I think that the brave part comes from knowing that what I’m advocating for is grounded in research, right? It is not just based on my feelings… But I think now that I am more confident in what I know in the literature, I am a lot more vocal about it.” (Year 3)
- “I think, throughout the program, especially in the last year or so, it’s more of like, no, this isn’t what’s good for kids. And I’m going to tell you what’s good for kids, and I can support why it’s good for kids. And then, do you want me to go have the conversation with other grade levels? … taking on that stance, I think, has changed my outlook in the program. And then, just feeling like, I do have something to say that matters, has been a big change.” (Year 4)
- “at the beginning, …I asked a lot of permission, and now, I know what’s best for our kids, at least, when it comes to this. This is what we went to school for. This is what I’m voicing more. And people are actually listening.” (Year 4)
Professional Community
4.2.2. Fellows’ Self-Reported Leadership Activities
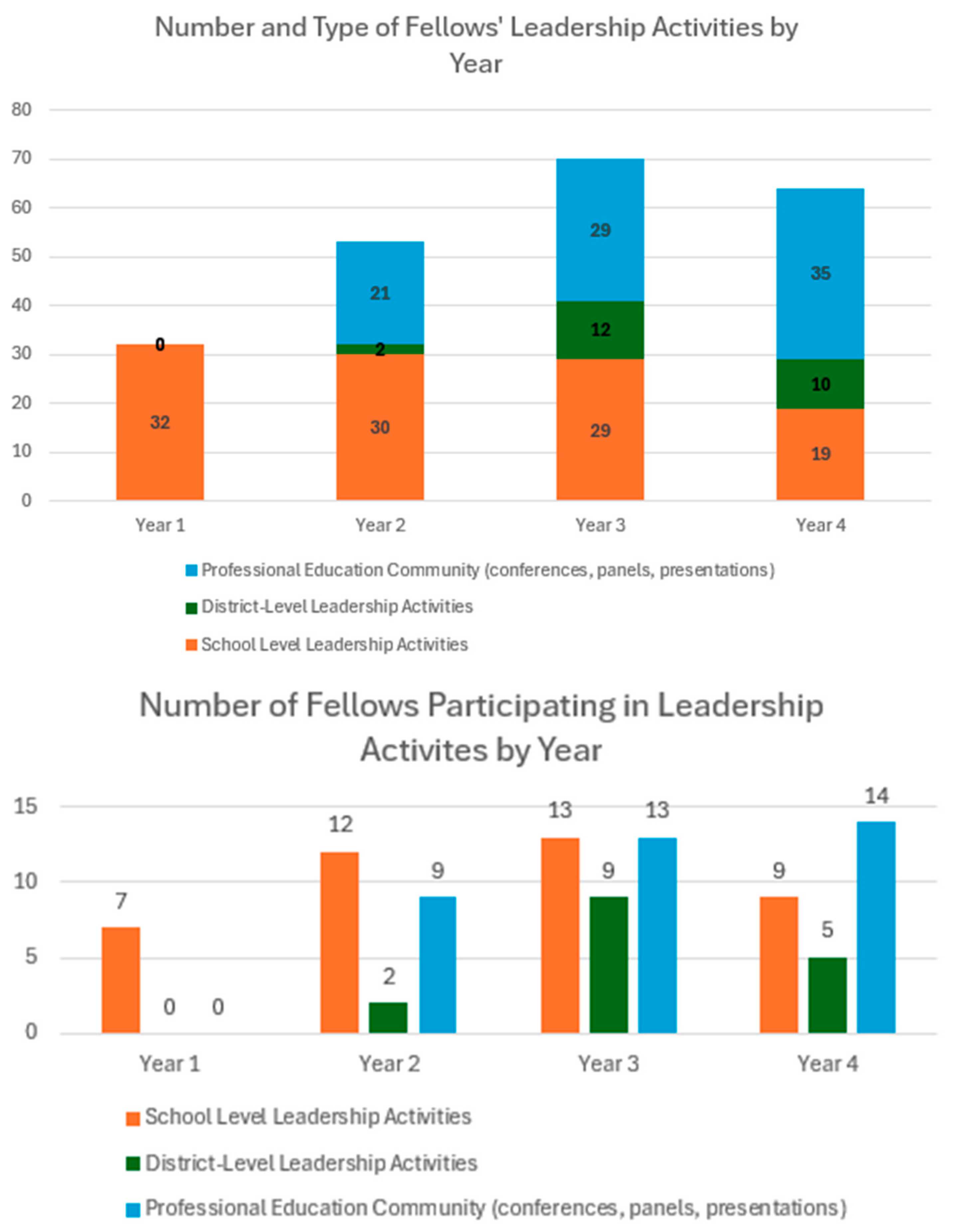
4.2.3. Analysis of Types of Leadership Activities from Focus Group Data
- Classroom-based, informal leadership activities (Rutledge, 2023): Fellows describe being the “math go-to person” at their school or grade-level; colleagues seeking them out and generating organic opportunities to provide support; providing colleagues with resources and instructional materials; sharing their knowledge of mathematics, mathematical strategies, and the development of students’ mathematical knowledge; and offering teaching suggestions to grade-level teams. In Year 4, more Fellows described modeling instructional practices for colleagues or inviting colleagues to observe their classrooms.
- School-wide or district-wide formal leadership activities: Fellows describe mentoring new teachers and pre-service teachers; presenting professional learning sessions; leading PLCs or grade-level teams; conducting Affirming Learning Walks; hosting district-wide observers in their classroom; observing classrooms and providing feedback; and initiating and leading school-wide or district-wide programs or presenting to other administrators. In Year 3, Fellows and administrators described how Fellows were now initiating and leading leadership activities with teachers and developing activities and programs for students (e.g., math or STEM teams or after-school programs).
- Participation in the professional mathematics education community: Fellows describe writing articles; participating in professional organizations; attending professional conferences and/or making presentations, including National Council of Teachers of Mathematics (NCTM) Virtual Conference, Noyce Leadership Summit, their [State] Council of Teachers of Mathematics, NCTM Annual Meeting and Research Conference, and NCSM Leadership in Mathematics Education Annual Conference. In Year 4, two Fellows gave international invited presentations, and four Fellows were selected as members of professional boards, committees, working groups, and/or journal department editors. Fellows also began encouraging their colleagues to attend and/or present at conferences, even assisting in securing funding for colleagues to attend these events.
5. Discussion: Factors That Appear to Support the Development of Instructional Leadership
“What makes me a leader in my school is the fact that my content knowledge can just fly… this week a first grade teacher came up to me and said, I hate balance equations … and so I immediately am able to pull out, ‘Well, you know, we want them to understand about the equal sign and what that means. That it doesn’t mean that the answer is coming next. And have you tried using a balance scale and helping them to understand what’s happening there?’ And she’s like, I never thought of that. Let me go try it.’ And so that content knowledge is, I think, what makes us leaders”.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Focus Group Prompts for Fellows
- What has been the best part of the project so far?
- What leadership activities have you done to this point? How have you grown as a leader? What is the best part of the leadership role?
- What do you feel you have gained or benefited from the courses and project activities related to mathematics?
- What do you feel you have gained or benefited from the courses and project activities related to mathematics pedagogy?
- Describe any change to your teaching practices. What do you feel are the important messages/ideas about teaching from the project?
- What do you hope is the outcome of our participation in this project? What are you excited about? What are you apprehensive or nervous about?
- What suggestions for changes, additions, or revisions do you have for project leaders? Is there something additional or different you need to be successful?
- Anything else to share?
References
- Barth, S. G., Lotter, C., Yow, J. A., Irdam, G., & Ratliff, B. (2023). Understanding the process of teacher leadership identity development. International Journal of Leadership in Education, 1–28. [Google Scholar] [CrossRef]
- Berg, J. H., & Zoellick, B. (2019). Teacher leadership: Toward a new conceptual framework. Journal of Professional Capital and Community, 4(1), 2–14. [Google Scholar] [CrossRef]
- Boston, M., Maldonado, A., Rutledge, T., Brooks, L., & Dixon, J. (2024, September 25–28). Evolution of classroom teachers’ self-perceptions as teacher leaders in mathematics. Research Conference for the National Council of Teachers of Mathematics Annual Conference, Chicago, IL, USA. [Google Scholar]
- Boston, M. D. (2012). Assessing the quality of mathematics instruction. Elementary School Journal, 113(1), 76–104. [Google Scholar] [CrossRef]
- Boston, M. D., Henrick, E. C., Gibbons, L. K., Berebitsky, D., & Colby, G. T. (2017). Investigating how to support principals as instructional leaders in mathematics. Journal of Research on Leadership Education, 12(3), 183–214. [Google Scholar] [CrossRef]
- Bush, S. B., Dixon, J., Brooks, L., Moore, B., Boston, M., Rutledge, T., Butler, M., & Maldonado, A. (2025). Catalyzing the courage to lead: A two-pronged approach to empower mathematics teachers as leaders. eJournal for Research in Science and Mathematics Education. in press. [Google Scholar]
- Carver, C. L. (2012). Developing leadership content knowledge during school leader preparation. International Journal of Educational Leadership Preparation, 7(3), n3. [Google Scholar]
- Cobb, P., & Jackson, K. (2011). Analyzing educational policies: A learning design perspective. Journal of the Learning Sciences, 21(4), 487–521. [Google Scholar] [CrossRef]
- Collins, A., Brown, J. S., & Newman, S. E. (1987). Cognitive apprenticeship: Teaching the craft of reading, writing, and mathematics. Technical Report No. 403. Center for the Study of Reading. [Google Scholar]
- Creswell, J., & Plano Clark, V. (2007). Designing and conducting mixed methods research. Sage. [Google Scholar]
- Creswell, J. W. (2003). Research design: Qualitative, quantitative, and mixed methods approaches. Sage. [Google Scholar]
- Darling-Hammond, L., Hyler, M., & Gardner, M. (2017). Effective teacher professional development. Learning Policy Institute. [Google Scholar] [CrossRef]
- Desimone, L. M. (2011). A primer on effective professional development. Phi Delta Kappan, 92(6), 68–71. [Google Scholar] [CrossRef]
- Dey, E. L., & Astin, A. W. (1993). Statistical alternatives for studying college student retention: A comparative analysis of logit, probit, and linear regression. Research in Higher Education, 34(5), 569–581. [Google Scholar] [CrossRef]
- Grossman, P. (Ed.). (2021). Teaching core practices in teacher education. Harvard Education Press. [Google Scholar]
- Grossman, P., Hammerness, K., & McDonald, M. (2009). Redefining teaching, re-imagining teacher education. Teachers and Teaching, 15(2), 273–289. [Google Scholar] [CrossRef]
- Hill, H. C., Ball, D. L., & Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. Journal for Research in Mathematics Education, 39(4), 372–400. [Google Scholar] [CrossRef]
- Johnson, J. F., Jr., Uline, C. L., & Perez, L. G. (2019). Teaching practices from America’s best urban schools: A guide for school and classroom leaders. Routledge. [Google Scholar]
- LeCompte, M., Preissle, J., & Tesch, R. (1993). Ethnography and qualitative design in educational research. Academic Press. [Google Scholar]
- Margolis, J. (2016). Hybrid teacher leaders and the new professional development ecology. In Teacher leadership and professional development (pp. 129–153). Routledge. [Google Scholar]
- Margolis, J. (2020). The semiformality of teacher leadership on the edge of chaos. Harvard Educational Review, 90(3), 397–418. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics (NCTM). (2014). Principles to actions: Ensuring mathematical success for all. NCTM. [Google Scholar]
- National Council of Teachers of Mathematics (NCTM). (2020a). Catalyzing change in early childhood and elementary mathematics: Initiating critical conversations. NCTM. [Google Scholar]
- National Council of Teachers of Mathematics (NCTM). (2020b). Catalyzing change in middle school mathematics: Initiating critical conversations. NCTM. [Google Scholar]
- National Governors Association Center for Best Practices & Council of Chief State School Officers (NGA-CSSO). (2010). Common core state standards for mathematics. NGA-CSSO. [Google Scholar]
- Pynes, D., Kloser, M., Wagner, C., Szopiak, M., Wilsey, M., Svarovsky, G. N., & Trinter, C. (2024). Bridging theory and practice: A framework for STEM teacher leadership. School Science and Mathematics, 1–15. [Google Scholar] [CrossRef]
- Quebec Fuentes, S. Q., & Jimerson, J. B. (2020). Role enactment and types of feedback: The influence of leadership content knowledge on instructional leadership efforts. Journal of Educational Supervision, 3(2), 6. [Google Scholar] [CrossRef]
- Ross, D., Lamb, L., & Johnson, J. (2023). Using affirming learning walks to build capacity. Journal of School Administration Research and Development, 8(1), 47–54. [Google Scholar] [CrossRef]
- Rutledge, T. (2023). An exploration of K-8 classroom-based mathematics teacher leader development [Unpublished doctoral dissertation]. University of Central Florida.
- Steele, M. D., Johnson, K. R., Otten, S., Herbel-Eisenmann, B. A., & Carver, C. L. (2015). Improving instructional leadership through the development of leadership content knowledge. Journal of Research on Leadership Education, 10(2), 127–150. [Google Scholar] [CrossRef]
- Stein, M. K., & Nelson, B. S. (2003). Leadership content knowledge. Educational Evaluation and Policy Analysis, 25(4), 423–448. [Google Scholar] [CrossRef]

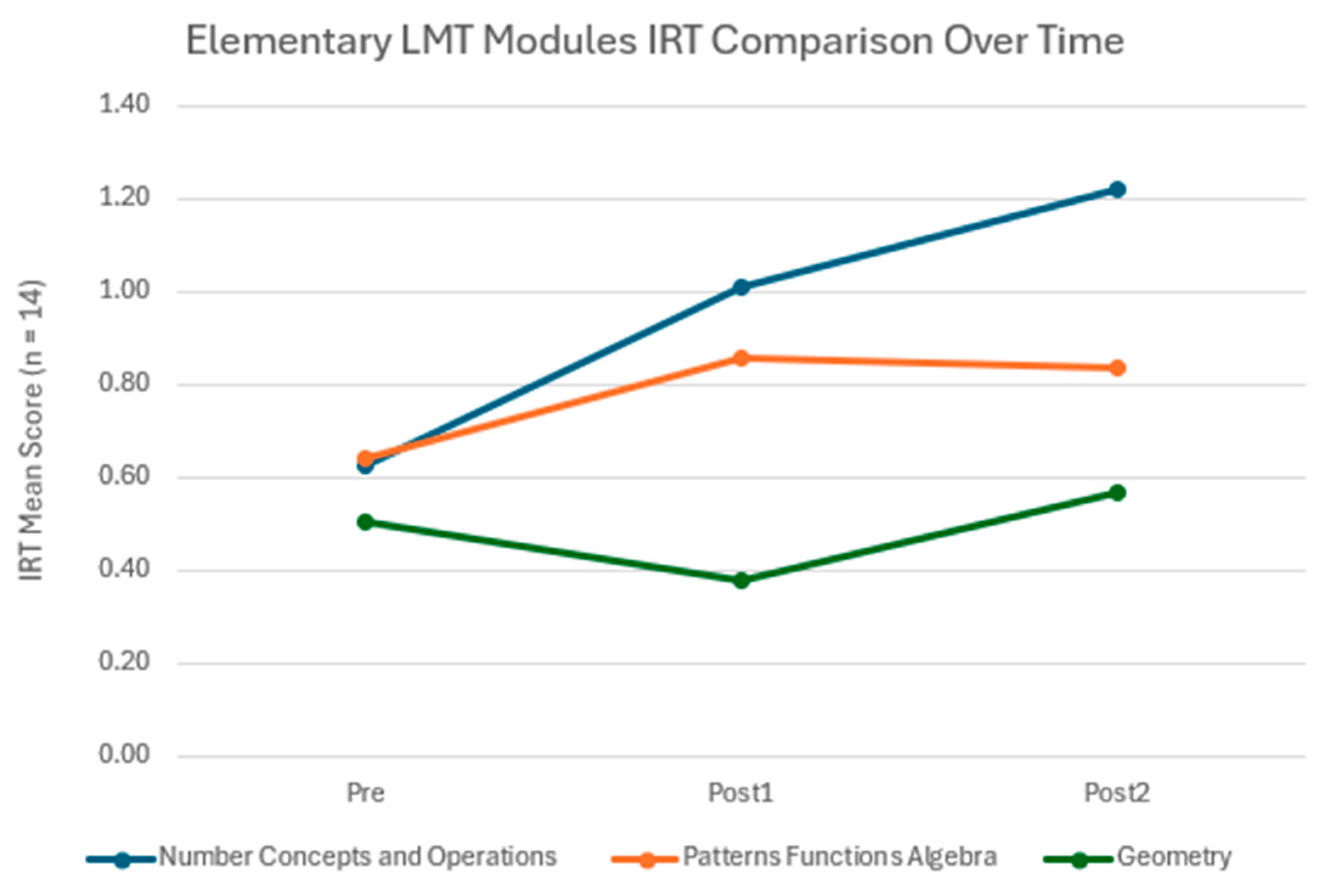

| Mean IRT Scores | Pre-Post1 (n = 14) | Pre-Post2 (n = 13) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Elementary | Pre | Post1 | Post2 | Change | t | p | Effect Size | Change | t | p | Effect Size |
| NCOP | 0.62 | 1.01 | 1.22 | 0.38 | 0.8 | 0.44 | 0.17 | 0.60 | 3.01 | 0.01 * | 0.44 |
| PFA | 0.64 | 0.86 | 0.84 | 0.22 | 1.55 | 0.15 | 0.29 | 0.20 | 0.73 | 0.48 | 0.16 |
| GEOM | 0.51 | 0.38 | 0.57 | −0.13 | −0.56 | 0.58 | −0.1 | 0.06 | −0.05 | 0.96 | 0.01 |
| Middle Level | |||||||||||
| NCOP | −0.54 | 0.24 | 0.22 | 0.78 | 2.95 | 0.01 * | 0.66 | 0.76 | 3.49 | 0.005 * | 0.7 |
| PFA | −0.74 | −0.32 | −0.26 | 0.42 | 2.37 | 0.04 * | 0.39 | 0.48 | 3.12 | 0.01 * | 0.44 |
| GEOM 4–8 | −0.56 | 0.06 | 0.04 | 0.62 | 4.45 | <0.001 * | 1.07 | 0.59 | 3.92 | 0.002 * | 0.77 |
| PDS 4–8 | −0.50 | −0.30 | −0.07 | 0.20 | 2.09 | 0.06 ** | 0.6 | 0.43 | 2.29 | 0.04 * | 0.73 |
| Mean (Median) Year 1 | Mean (Median) Year 4 | Mean Difference | W(ns/r) ** | z | p (One-Tailed) | |
|---|---|---|---|---|---|---|
| Task | 2.29 (2) | 3.00 (3) | 0.71 | W(8) = 31 | none given | <0.025 * |
| Implementation | 2.07 (2) | 2.71 (3) | 0.64 | W(7) = 28 | none given | <0.01 * |
| Discussion | 2.07 (2) | 2.36 (2.5) | 0.29 | W(11) = 16 | 0.69 | 0.25 |
| Questioning | 2.00 (2) | 3.14 (3.5) | 1.14 | W(12) = 70 | 2.73 | 0.003 * |
| Teacher Linking | 1.64 (2) | 1.86 (2) | 0.22 | W(8) = 12 | none given | none given |
| Student Linking | 1.29 (1) | 1.21 (1) | −0.08 | W(7) = 3 | none given | none given |
| Teacher Press | 1.93 (2) | 2.79 (3) | 0.86 | W(13) = 57 | 1.97 | 0.02 * |
| Student Providing | 1.79 (2) | 2.50 (3) | 0.71 | W(11) = 40 | 1.76 | 0.04 * |
| Overall Score (paired t-test) | 15.07 | 19.57 | 4.50 | t = 2.43 | 0.015 * |
| Year 1 | Year 2 | Year 3 | Year 4 | |
|---|---|---|---|---|
| Teacher Leader Academy | x | x | x | x |
| Mentoring of school-based interns from a non-profit | x | x | x | x |
| Catalyzing Change Needs Assessment | x | |||
| Milestone 1 Gap Assessment | x | |||
| Affirming Learning Walks | x | x | x | |
| Dissertation Research | x | |||
| Intentional Recognition within the District | x | x | x | x |
| Opportunities to Participate in the Mathematics Education Professional Community | x | x | x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boston, M.D.; Dixon, J.K.; Bush, S.B.; Brooks, L.A.; Moore, B.E.; Rutledge, T.; Maldonado, A.M. Positioning K-8 Classroom Teachers as Mathematics Instructional Leaders. Educ. Sci. 2025, 15, 982. https://doi.org/10.3390/educsci15080982
Boston MD, Dixon JK, Bush SB, Brooks LA, Moore BE, Rutledge T, Maldonado AM. Positioning K-8 Classroom Teachers as Mathematics Instructional Leaders. Education Sciences. 2025; 15(8):982. https://doi.org/10.3390/educsci15080982
Chicago/Turabian StyleBoston, Melissa D., Juli K. Dixon, Sarah B. Bush, Lisa A. Brooks, Brian E. Moore, Treshonda Rutledge, and Angel M. Maldonado. 2025. "Positioning K-8 Classroom Teachers as Mathematics Instructional Leaders" Education Sciences 15, no. 8: 982. https://doi.org/10.3390/educsci15080982
APA StyleBoston, M. D., Dixon, J. K., Bush, S. B., Brooks, L. A., Moore, B. E., Rutledge, T., & Maldonado, A. M. (2025). Positioning K-8 Classroom Teachers as Mathematics Instructional Leaders. Education Sciences, 15(8), 982. https://doi.org/10.3390/educsci15080982






