Next Article in Journal
Medical Education: Are Reels a Good Deal in Video-Based Learning?
Previous Article in Journal
Probabilistic Language in Spanish Secondary Textbooks
Previous Article in Special Issue
A Culturally Responsive Math Program: A Case Study in a Rural Tribal College in the United States
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 15
Issue 8
10.3390/educsci15080980
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Culturally Inclusive Mathematics Learning Environment Framework: Supporting Students’ Representational Fluency and Covariational Reasoning

by
Nigar Altindis
1,* and
Nicole L. Fonger
2
1
College of Education, The University of Alabama, Tuscaloosa, AL 35487, USA
2
Department of Mathematics, School of Education, Syracuse University, Syracuse, NY 13244, USA
*
Author to whom correspondence should be addressed.
Educ. Sci. 2025, 15(8), 980; https://doi.org/10.3390/educsci15080980 (registering DOI)
Submission received: 12 June 2025 / Revised: 10 July 2025 / Accepted: 24 July 2025 / Published: 31 July 2025
(This article belongs to the Special Issue Supporting Mathematics Teaching and Learning in Indigenous, Migrational, and Multilingual Contexts)
Browse Figures
Versions Notes

Abstract

This study explores how to support Turkish–American secondary school students to co-develop covariational reasoning (CR) and representational fluency (RF) in solving contextually based quadratic function tasks in an after-school community center learning setting. We conducted a teaching experiment (n = 8) at a community center. Ongoing and retrospective analyses of classroom interaction and video transcripts revealed a culturally inclusive mathematics learning environment framework with several intertwined components: co-developing CR and RF and community-based practices. This study provides evidence that students coordinate symbolic, tabular, and graphical representations, which not only deepen their understanding of how quantities change in relation to one another but also enable them to interpret and construct representations in increasingly flexible ways. This reciprocal process of co-developing CR and RF allowed students to recognize and express quantitative relationships as meaningful functional relationships, demonstrating a dynamic interplay between reasoning about change and fluency across representations. This study situates learning within culturally inclusive learning environments and acknowledges the reflexive positionality of the teacher–researcher in relation to students. We highlight how shared community-based practices can enhance mathematics teaching and learning.

1. Introduction

A focus of mathematics education means to support students in developing a deep understanding of how varying quantities relate to one another and how these relationships can be represented mathematically (National Council of Teachers of Mathematics, 1989, 2000). This goal is especially critical in contexts where students must make sense of co-varying change, such as interpreting motion, modeling growth, or analyzing other dynamic phenomena. Two interrelated cognitive processes underpin this work: covariational reasoning and representational fluency. Covariational reasoning (CR) involves students’ ability to coordinate two quantities by recognizing how changes in one correspond to changes in the other (Carlson et al., 2002), while representational fluency (RF) entails constructing, interpreting, and connecting multiple representations—such as graphs, equations, and tables—in ways that maintain the accuracy and meaning of the underlying mathematical relationships (Fonger, 2019). These processes of CR and RF mutually reinforce each other and are central to students’ ability to mathematize real-world phenomena (Altindis, 2021; Fonger & Altindis, 2019).
Despite their importance, students often struggle to understand functions as relationships between covarying quantities (Carlson et al., 2002; A. B. Ellis & Grinstead, 2008) and to meaningfully generate and connect multiple representations to make sense of these relationships (Adu-Gyamfi et al., 2012; Altindis, 2021, 2025; Dreyfus, 2002; Even, 1998; Zaslavsky, 1997). Too often, students approach functions as isolated symbolic procedures, detached from the dynamic phenomena they are intended to represent (Stephens et al., 2017). While research on early algebraic reasoning (M. Blanton et al., 2015) and quantitative reasoning frameworks (Thompson & Carlson, 2017) has identified key difficulties in students’ learning, questions remain about how students develop and coordinate CR and RF in authentic problem contexts (Altindis & Fonger, 2019; Fonger & Altindis, 2019; Moore & Carlson, 2012).
Importantly, students’ development of CR and RF does not occur in a vacuum but is mediated by the cultural, social, and linguistic contexts of the learning environment. Research has shown that instructional supports aimed at developing teaching and learning of mathematics often remain “neutral” or “underspecified” in terms of race, culture, and teacher–student relational dynamics (Battey, 2013). This lack of contextual sensitivity can be problematic, as students from different racial and ethnic backgrounds bring diverse ways of knowing and engage with mathematics through community-based practices that shape their participation and meaning-making (Averill et al., 2009). While “culture-free” studies have illuminated important cognitive mechanisms (Bartell, 2011), there remains a need to more explicitly attend to the sociocultural dimensions of learning.
This study contributes to existing research by situating the co-development of CR and RF within a culturally inclusive mathematics learning environment that draws upon students’ community-based practices. Specifically, we examine how instructional supports—designed to reflect the cultural, linguistic, and social experiences of Turkish–American secondary school students—can foster meaningful engagement with contextually grounded quadratic function tasks (e.g., modeling the height of a cannonball over time) in an after-school community center setting. Our research question is as follows: How does a culturally inclusive mathematics learning environment support Turkish–American secondary school students in co-developing covariational reasoning and representational fluency in solving contextually-based quadratic function tasks in an after-school community center learning setting?

2. Literature Review

2.1. Representational Fluency

Representational fluency is foundational for understanding functions and reasoning about covarying quantities (Altindis, 2021; Fonger et al., 2020). When students develop RF, they create and model relationships by understanding how two variables change in relation to one another. For instance, filling in a table requires students to examine patterns across values, often revealing invariant structures in functional relationships (Altindis, 2021, 2025; Confrey & Smith, 1995). At the same time, constructing graphs or writing equations provides opportunities to visualize or formalize those relationships, fostering a deeper understanding of how change is represented across contexts (Carlson et al., 2002; Moore & Thompson, 2015). As students navigate among these representations, they engage in a process of coordinating meaning—seeing how a pattern of numerical values aligns with a curve on a graph, or how parameters in an equation shape that curve (Dreyfus & Halevi, 1991; Even, 1998). These connections help students move beyond surface-level manipulation of symbols or interpretation of visual features, enabling them to develop more robust and flexible understandings of functional relationships (Lobato, 2012; Wilkie, 2019).
Research highlights that students often struggle to establish connections with and among multiple representations. Many students tend to rely on a single representation—most commonly symbolic equations—without fully understanding how it relates to tabular data or graphical trends (A. B. Ellis & Grinstead, 2008; Hitt, 1998). This can result in a disconnected understanding, such as overgeneralizing the slope concept to quadratic parameters (A. B. Ellis & Grinstead, 2008) or failing to recognize the equivalence between factored and standard forms of a function (Even, 1998; Hitt, 1998). Similarly, students may interpret graphs as bounded or pictorial rather than continuous representations of covarying quantities (Moore & Thompson, 2015), which can lead to misconceptions, such as overlooking key features like y-intercepts or inflection points (Bieda & Nathan, 2009; Zaslavsky, 1997). Even students with a strong conceptual foundation may struggle to construct graphs that accurately reflect dynamic relationships, particularly in capturing smoothness or concavity (Carlson et al., 2002; Oehrtman et al., 2008).

2.2. Covariational Reasoning

Covariational reasoning has been studied across various mathematical domains due to its critical role in understanding functions and rates of change. It is relevant in exponential relationships (Castillo-Garsow, 2012; Confrey & Smith, 1995), quadratic relationships (Altindis, 2021, 2025; Fonger et al., 2020), trigonometry (Moore, 2010), rates of change (Johnson, 2012), functions (Carlson et al., 2002; Johnson, 2012), logarithmic–exponential functions (Ferrari-Escolá et al., 2016), the fundamental theorem of calculus (Thompson, 1994), graphs of functions (Carlson et al., 2002; Moore et al., 2013), logistic functions (Altindis et al., 2024), and differential equations (Castillo-Garsow, 2012). These studies emphasize that CR is essential for understanding functions and underscore the cognitive challenges involved. Students must coordinate multiple quantities that change simultaneously, which complicates their ability to conceptualize functional relationships (Thompson, 1993).

2.3. Co-Development of CR and RF

An increasing number of studies have explored how students’ use of representations is intertwined with their reasoning concerning quantities and their interrelationships (Altindis, 2021, 2025; Even, 1998; Fonger & Altindis, 2019; Moore et al., 2013). For instance, Even (1998) notes that “…linking representations are interrelated with another kind of knowledge and understanding, seeing the connection between the given equation and the related quadratic functions [such as the graph of the quadratic function]” (p. 108). Moore and colleagues (2013) likewise highlight that students’ use of representations is closely grounded in their covariational reasoning. Collectively, these studies suggest that students’ reasoning about functions often emerges through their coordination of multiple representations and their attention to underlying functional relationships.
This intertwined development is especially evident in students’ modeling of functional relationships, where making sense of dynamic changes between quantities requires the coordination of tables, graphs, equations, and verbal descriptions. Such tasks are cognitively demanding, as they compel students to attend simultaneously to how quantities covary and how these relationships are encoded and expressed across multiple representational forms (Carlson et al., 2002; Potgieter et al., 2008; Thompson, 1994). This study aims to bridge two distinct areas of literature—quantitative and covariational reasoning, and representational fluency—to explore how to support students’ reasoning about quantities and quantitative relationships when creating and connecting multiple representations.
The co-development of CR and RF can be illustrated through a falling object task (Table 1). In this activity, students engage with a simulation involving a projectile, such as a cannonball, and reason about how its height changes over time. The task provides a partially filled table and prompts students to identify changing quantities (e.g., time and height) versus constants (e.g., gravity). Then, students complete the table, graph the relationship, and generate a symbolic equation to model the covariation. For instance, consider modeling the height of a cannonball over time using the quadratic function f x = − x − 4 2 + 16 , where x represents time in seconds and f x represents the height in meters. This function illustrates how the cannonball’s height changes over time, with the vertex x = 4 indicating the moment when the maximum height of 16 m is reached, requiring students to coordinate how height changes with time, initially increasing, then decreasing symmetrically. This coordination exemplifies CR. At the same time, students draw on RF as they move among the table, graph, and equation to make sense of the relationship. For example, from the table, a student might observe that the differences in height follow a second-order pattern, then interpret or construct a parabolic graph that reflects this rate. By aligning features such as vertex, symmetry, and curvature across representations, students demonstrate how CR and RF co-emerge to support a deeper understanding of quadratic relationships.

3. Conceptual Framework

3.1. Characteristics of Culturally Inclusive Mathematics Learning Environments

A well-designed mathematics learning environment provides resources for students and teachers to construct bridges between mathematical facts, beliefs, and cultural, mathematical, and linguistic practices (Esmonde, 2009; Wager, 2012). In these environments, students develop pride in learning mathematics, using their culture, identity, and language as resources, while establishing caring relationships with their teachers (Averill et al., 2009; Bartell, 2011). Such environments allow students to maintain cultural integrity, foster academically successful identities, and take on the role of active constructors of knowledge in learning mathematics (Brown & Campione, 1996; Ladson-Billings, 1995). Therefore, students benefit from instruction that integrates community and cultural practices (Wager, 2012; Civil, 2002). From this perspective, students’ interactions and the learning environment are linked to their culture, language, and community-based practices.
At a broad level, we conceptualize a culturally inclusive mathematics learning environment to establish clear links to students’ culture, language, and community-based practices. We focus on four characteristics: (a) student autonomy, (b) collaborative social interactions in classroom culture, (c) norms, and (d) teacher–student caring relationships. We define community-based practices as the everyday ways of knowing, communicating, and interacting that students bring from their cultural, linguistic, and familial contexts.

3.2. Position Students as Autonomous

Culturally inclusive mathematics environments position students as autonomous. Students benefit from having cultural tools that give them a role as active constructors of knowledge in a learning environment (Averill et al., 2009; Brown, 1992; Nasir et al., 2006). A learning environment nurtures students to move away from viewing the teacher as the ultimate authority to rely on their accurate and relevant scientific inferences (Cornelius & Herrenkohl, 2004). Such learning environments provide opportunities for students by interacting with the students where their culture, language, and community-based practices are the resources in developing mathematical understandings and reasoning.
Research on practices of supporting students to develop mathematical understanding and reasoning are far away from positioning students’ learner autonomy in their culture, identity, race, historical practices, and community-based practices (Gutiérrez, 2002). As a field of mathematics education, we are struggling to position students with substantial autonomy (Ruef, 2021) as situated in their cultural, linguistic, and community-based mathematical practices.

3.3. Collaborative Social Interactions Within Classroom Culture

We view mathematics learning as socially constructed in purposefully designed learning environments (Boaler, 2000; Nasir et al., 2006). Students develop skills in different settings because they communicate and interact depending on the space with teachers or students (Cornelius & Herrenkohl, 2004). Social classroom interactions and students’ mathematical understanding and reasoning are connected.
Researchers have explored classroom culture and created opportunities for students learning through a process of developing classroom culture (Bowers et al., 1999). Scholars have documented a link between classroom social interactions and students’ mathematical thinking and reasoning (Esmonde, 2009; Walker, 2006; Wood et al., 2006). Wood and co-authors argued that complexity in students’ mathematical thinking is closely related to a pattern of interactions formed in classroom culture. Furthermore, students’ intellectual peer interactions and family interactions at a community level create opportunities to succeed in mathematics (Walker, 2006). Like Walker, Esmonde (2009) argued about the link between students’ classroom social ecology and the interactions. They claimed that the link between social interactions and social ecology creates learning opportunities for students to make sense of mathematics. These interactions take place in the form of small and whole group settings—collaborative interactions. Collaborative interactions are student-to-student interactions and teacher-to-student interactions that create learning opportunities for students’ mathematical understanding and reasoning (DeJarnette & González, 2015).

3.4. Norms

Social and sociomathematical norms (discipline-specific mathematical norms) are foundational to shaping how students explain their thinking, reason mathematically, and make sense of their peers’ ideas (Cobb & Yackel, 1996; Yackel & Cobb, 1996). Social norms refer to the expectations for participation and discourse jointly negotiated by the classroom community, not imposed by the teacher alone (Cobb, 2000). These norms are collaboratively developed through teacher–student and student–student interactions and can significantly influence students’ confidence and engagement in learning mathematics (Hackenberg, 2010). Scholars emphasize the importance of negotiating both social and sociomathematical norms so that students develop a sense of agency and shared responsibility in classroom discourse (Cobb et al., 2009; Ruef, 2021; Staples, 2007).
Sociomathematical norms, in particular, govern what counts as mathematically valid reasoning, sophisticated solutions, and acceptable explanations. Yackel and Cobb (1996) define these norms as “a way of analyzing and talking about mathematical aspects of teachers’ and students’ activity in a mathematics classroom” (p. 474). These norms support the development of mathematical argumentation and intellectual autonomy, creating measurable differences in students’ mathematical sophistication. Crucially, the development of individual reasoning cannot be separated from participation in the collective construction of shared mathematical meaning (Yackel & Cobb, 1996). Building on this, Stephan (2003) highlighted that cognitive development is deeply intertwined with social and cultural processes, noting that “students’ development cannot be adequately explained in cognitive terms alone” (p. 28). Thus, students’ reasoning and representing evolve through interactions that involve justifying, validating, and building on one another’s ideas within a classroom culture shaped by negotiated norms (Cobb et al., 2009; Ruef, 2021).

3.5. Teacher–Student Caring Relationships

The caring theory characterizes caring relationships as evolving interactions between teachers and students (Noddings, 2002). Caring is not simply a feeling; it is a form of signal for participation in social interactions between teachers and students which includes responsiveness of both parties (Bartell, 2011; Hackenberg, 2010; Noddings, 2002). Caring relationships involve teachers not simply trying to think like a student or project their energy onto the students. They include being non-judgmental and trying to understand and connect to the way students think, act, and be themselves (Bartell, 2011; Noddings, 2002).
Research on teacher–student caring relationships suggests a positive association between high-quality teacher–student relationships and students’ success in mathematics (O’Connor & McCartney, 2007) and a source of motivation for students to pursue social and academic goals (Wentzel, 1997). Building on these, this study will report how shared community-based practices between teachers and students served as a foundation for caring relationships that, in turn, created a supportive environment for the co-development of CR and RF.

4. Method

4.1. Research Design

We carried out a teaching experiment in which we designed “a small-scale version of a learning ecology” (Cobb et al., 2003, p. 9; Steffe & Thompson, 2000). In doing so, we integrated theoretical perspectives on quantitative reasoning and representations to guide our theorizing about instructional supports for interactions among learners and teachers (cf. Fonger & Altindis, 2019). Quantitative reasoning involves the ability to conceptualize a situation and imagine the measurable attributes of objects (quantities) within it, covariational reasoning builds upon this foundation by focusing on the dynamic relationship between covarying quantities (Carlson et al., 2002; Smith & Thompson, 2008; Thompson, 2011).
The theory of representation sets a foundation for RF (Dreyfus, 2002; Kaput, 1987a, 1987b). RF develops as students create, interpret, and connect representations grounded in a deep understanding of mathematical phenomena (Fonger, 2019). We combined and coordinated theories of representations (Kaput, 1987a; Dreyfus, 2002) and quantitative reasoning (Thompson, 1993) by operationalizing these constructs as design principles and direct teaching actions to support students’ CR and RF. Table 2 shows the definitions of each of CR and RF and the corresponding design principles that we sought to engender in student activity vis-à-vis hypothesized instructional supports.

Design of Instructional Supports

We curated a sequence of three instructional tasks that required students to use CR and RF. This study drew on three tasks to investigate students’ reasoning: the paint roller task, the growing rectangle task, and the falling object task (Altindis, 2021, 2025). The paint roller and growing rectangle tasks are examples of “Gamma tasks,” originally developed by A. Ellis et al. (2020) to support covariational reasoning. The falling object task was adapted from an interactive simulation available on the Projectile Motion website (2002), which features physics-based modeling scenarios. Details of the task design characteristics, instructional sequence, and student and teacher handouts can be found in the Altindis (2021).

4.2. Experimenting

4.2.1. Episodes, Location, and Participants

The teaching experiment comprised eight one-hour instructional sessions that took place over approximately two weeks within the 2019–2020 school year. The research team included four graduate students. The teaching experiment was conducted at the Turkish Community Center in New York (hereafter referred to as “the center”)
We employed purposeful sampling (Patton, 2014). The main sampling criteria included recruiting students who share community-based practices, as Author 1 (see the next section for researcher positionality). Therefore, we invited all secondary and high school students who are members of the center. The participants were Turkish–American middle and high school students in grades 8 through 10, attending schools in both urban and suburban districts. We categorized students’ language fluency into two categories: Turkish and English, based on their elementary and middle school education. We classified students as fluent in Turkish if they had completed their elementary and middle school education in Turkish-speaking schools prior to arriving in the United States. Conversely, students who attended elementary and middle school in English-speaking schools in the U.S. were categorized as fluent in English. For example, Salim, a 10th-grade participant, had spent eight years in school in Turkey before relocating to the U.S., where he has attended school for the past two years. As such, he was categorized as fluent in Turkish. In contrast, Tarik, who was born in the U.S. and is able to read and write in Turkish, has been educated entirely within English-speaking schools; therefore, he was categorized as fluent in English. All student names mentioned in this paper are pseudonyms. A summary of participant demographics is presented in Table 3. Given the community-based nature of the center, the participants are arranged in a mixed-age group setting.

4.2.2. First Author Positionalities and Reflexivity

I intentionally engaged in reflexivity, which is understood as the practice of maintaining conscious awareness of participants’ culture throughout the research process (Hesse-Biber & Piatelli, 2007). As a bilingual researcher, I positioned myself as an “insider” researcher who had already established rapport and trust with the participants (Narayan, 1993). In designing and conducting the study at the center, I remained mindful of my positionality and the cultural identities of the participants, from developing research questions to data collection, analysis, and writing. To mitigate potential biases associated with this insider role, I also included “outsiders” such as the second author in the process (Narayan, 1993).
Having known the participants for three to seven years, I had established relationships that likely fostered trust and influenced how they engaged with me and the broader research team. I have witnessed the participants grow up within the same neighborhood and community, which shaped the ways they perceive my role. To them, I may be seen as an “auntie,” a mother figure, a neighbor, or a fellow community member, who shares their language, humor, and cultural background. These multiple, overlapping roles reflect our shared experiences and likely influenced the nature of our interactions throughout the study.
On several occasions, the participants and I spent time together in the local coffee shop or ice cream shop near the community center. This demonstrated a connection, shared activities, and time spent with the students and the teacher–researcher—the first author. For example, during the teaching experiment, Mert (8th grade) called me: “Elif 1teyze” [Elif aunty], and the whole group laughed, including myself. Then Mert turned to the other participants and asked, while pointing at me, “How am I supposed to call her?” The other research team members were quiet and just observed, not understanding the shared background. This represents a way of enjoying the same joke and recognizing shared, multidimensional community relationships while learning mathematics. I interpret these interactions as indicating that students are in a space where they feel safe while engaging in quantitatively rich quadratic function tasks.

4.2.3. Ongoing Analysis

Ongoing analysis was conducted concurrently with the teaching experiment (Cobb et al., 2017), with the primary goal of supporting students’ meaningful learning of quadratic functions. This analysis unfolded through two main processes: brief debriefing sessions (20–30 min) and co-planning meetings. During the debriefings, the research team formulated conjectures grounded in emerging evidence about what might enhance students’ understanding of quadratic functions. These conjectures were then refined and tested in subsequent co-planning sessions, where the team collaboratively prepared the next teaching episodes and developed new instructional strategies based on prior insights.

4.3. Retrospective Analyses

Retrospective analyses were conducted on various data sources: lesson plans, video recordings of small-group and whole-class instruction, and students’ journals and handouts. We utilized Cobb and Whitenack’s (1996) techniques, which were informed by Glaser and Strauss’s (1967/1999) constant comparison method. Retrospective analyses were conducted to explore the relationship between students’ learning and ways to support it. Table 4 presents the rounds of analyses along with their corresponding outcomes. We performed three rounds of analyses on the enhanced transcripts of classroom video recordings: (a) an initial analysis focusing on phase one; (b) an episode-by-episode analysis encompassing phases two, three, and four; and (c) analysis of analyses, addressing phases five and six.
In the initial analysis (Phase 1), we identified patterns in students’ interactions during small- and whole-group settings by generating enhanced transcripts of video recordings and analytical memos. The episode-by-episode analysis began with the development of an initial coding schema, based on coding the transcripts (Phase 2). We then re-coded the data to challenge, refine, or confirm existing codes and to construct top-level categories, resulting in an emergent coding schema (Phase 3). This schema was further refined and formalized in Phase 4. In the analysis of analyses (Phase 5), we applied predetermined analytical frameworks—representational fluency (Fonger, 2019) and covariational reasoning (Thompson & Carlson, 2017)—to interpret patterns across episodes. Finally, in Phase 6, we examined students’ evolving understanding of functions in relation to the instructional supports provided throughout the teaching experiment.
Finally, we established intercoder agreement and verified the codebook by coding 25% of the data during Phase 6 (Campbell et al., 2013). The guest coder, a graduate student in mathematics education, who has training in qualitative research methodology, independently coded 25% of the enhanced transcription of small-whole data sets. We then collaboratively reconciled our coding decisions by posing clarifying questions, identifying commonalities and discrepancies across codes, and providing supporting evidence for each coding choice. These conversations ensued until we established intercoder agreement among all codes.

5. Results

In this study, we introduce a culturally inclusive mathematical learning environment framework and present evidence of how community-based practices supported students’ co-development of CR and RF. We introduce four vignettes from small-group interactions to exemplify how instructional supports (1) foster the co-development of CR and RF, and (2) are embedded within students’ cultural and communal ways of knowing. Each vignette begins with a brief introduction and contextual background on the task and the students involved. Students’ speech, written work, and—when relevant—gestures are documented. 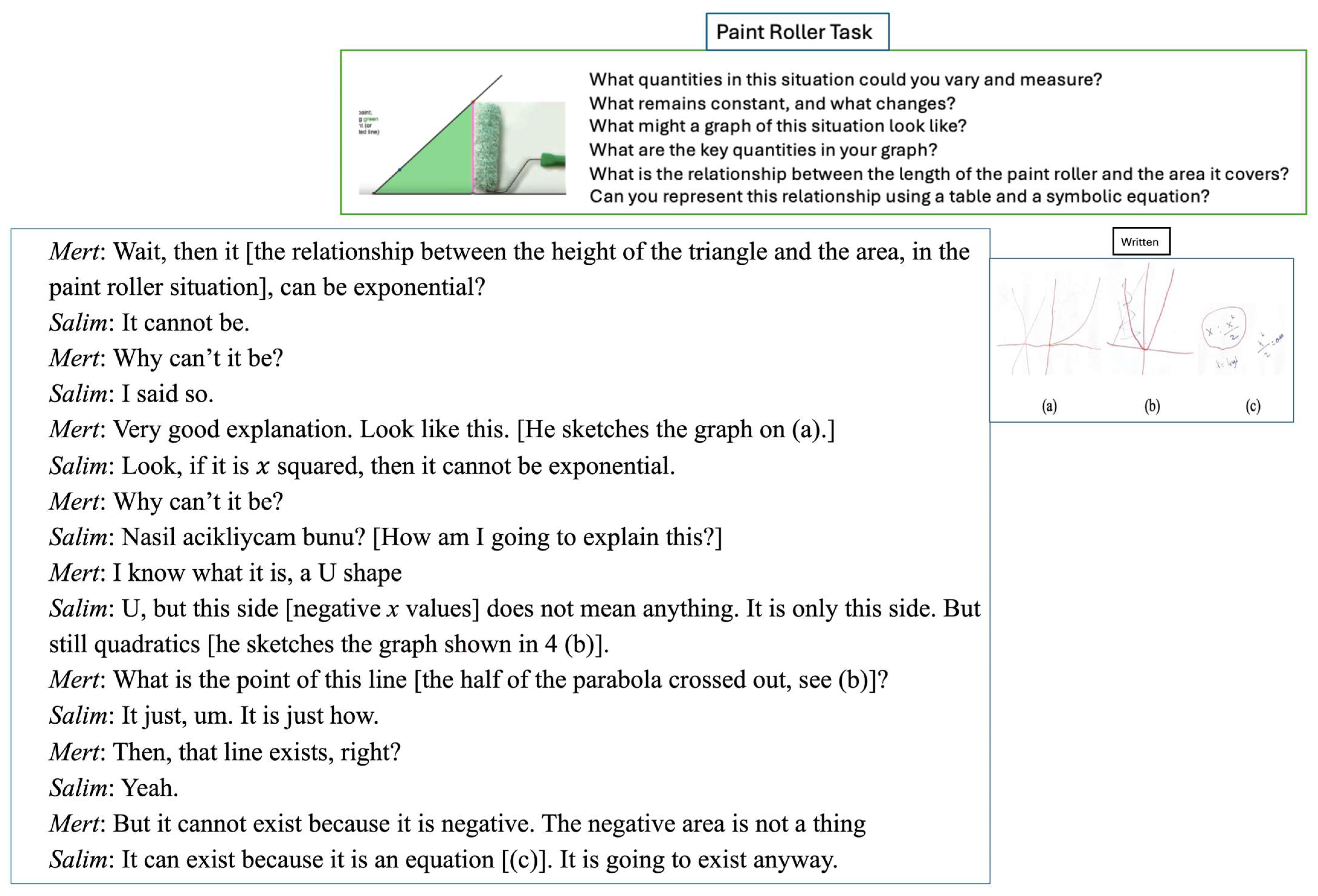Our interpretation will first describe students’ reasoning and representational activity, then explore interactions among students and with the teacher (if present) to identify how community-based practices surface within the learning process.

5.1. Prompting Students to Choose Units for Measuring Quantities

Vignette 1 is based on Salim and Eren’s small-group interactions as they investigated the relationship between height and area in the growing rectangle task (Figure 1).
As seen in Vignette 1, students may initially focus on the numerical values of quantities without fully grasping that these values represent different magnitudes. To support this shift in thinking, Elif the teacher–researcher, encouraged Eren and Salim to articulate their understanding of units for these quantities. For instance, when Elif asked, “How are they [cm and cm squared] similar or different from each other? How is that centimeter different than cm squared?” she prompted the students to reflect on the differences between line and area measurements.
Eren hesitated at first, responding, “Cm squared means the area, and cm means... Uhm, I do not know,” while gesturing with his fingers to represent height. Elif then personalized the context, asking, “Let’s say you will teach someone younger, like Bahar (his sister), how are you going to teach someone what are the area and height?” This approach drew on their shared social context, making the mathematical concepts more relatable.
Salim then contributed, saying, “Area is the amount of place covered,” encouraging Eren to continue. Eren built on this idea, explaining, “Yeah, amount of it covered,” while gesturing to indicate area, and added, “the height, how long is one of the sides,” tracing his hand along the side of a piece of paper. Salim reaffirmed this understanding, emphasizing, “How long is the side.” This exchange indicates that encouraging students to articulate the unit for measuring quantities is a way a teacher can support them in reasoning about those quantities, ultimately laying the groundwork for their ability to understand the relationship between them.
Additionally, the teacher leveraged established social connections to support students’ quantitative reasoning. For instance, Elif referenced someone familiar to both Eren and Salim—a sister—when probing them about appropriate units for measuring an object’s attributes. This approach draws on background knowledge of students’ personal contexts, making the mathematical concepts more relatable and meaningful. By framing questions around familiar relationships, Elif not only elicited precise responses but also reinforced the importance of selecting appropriate units for magnitude comparison. The established teacher–student caring relationships helped Elif organically connect with Eren and Salim when comparing and contrasting the units of these quantities.
In summary, Vignette 1 exemplifies two results. First, an instructional support for co-developing CR and RF is to ask or probe students to articulate and select units for measuring magnitudes of quantities. Second, situating these interactions within prior shared knowledge about the community is also supportive of students’ learning.

5.2. Shrinking and Enlarging Portions of Quantitative Magnitudes

Vignette 2 exemplifies teacher–student interactions as they explore the relationship between height, time, and range in the falling object task (Figure 2).
As illustrated in Vignette 2, Yener initially focused on the points themselves, asserting that “the point is not the change” and emphasizing that the points remained fixed. He identified specific intervals such as 0–1, 1–2, and 2–3 s for time, and 0–21, 21–36, and 36–45 m for height, but his attention was directed toward the discrete points, not the continuous changes occurring between them.
To challenge this point-centered view, Elif adjusted the scale, encouraging Yener to think about the smaller intervals within these broader ranges. She prompted, “If you take this table and break down the seconds as 0.0001, 0.0002, what will happen?” This question encouraged Yener to reconsider his interpretation. Initially, he resisted, responding, “It’s still the points. One to the other is the change. It changes from one point to the other.” Mert supported this idea, adding, “Yeah, there are numbers between the things it doesn’t tell, like the 0 s 21 m instantly. There are some points in between them, in this. It only shows by ones.”
Elif then drew smaller portions in Figure 2, illustrating 0 to 0.0001 and 0.0001 to 0.0002 s, and asked, “Where are the changes happening here?” This shift in scale prompted Yener to refine his understanding, visualizing the continuous nature of change. He responded by drawing arrows and stating, “It will go from 0 to 0.0001 s, and then 0.0001 to 0.0002 s,” capturing the idea that change is not isolated to fixed points but occurs continuously over smaller intervals.
As a final prompt, Elif asked, “We’re trying to differentiate between the points and the change.” Yener responded, “There is also change between these two [0 to 1] seconds… The point is like at that where the ball is,” signaling a shift toward a more continuous perspective. His use of both small and large time intervals suggests an evolving understanding of change not just at discrete points but across intervals. This exchange supported the students in developing an understanding of CR.
Although teacher–student interactions focused on shrinking and enlarging intervals to push students to engage in continuous covariational reasoning, we argue that the teacher–student caring relationship further opens up this engagement. The conversation between Elif, Mert, and Yener focused on the changes and points, an essential discussion for determining whether or not there was change happening on the points. The component of this conversation includes the delicate, entwined nature of a well-established teacher–student caring relationship. Yener and Mert stated that the point is not the change; Elif created smaller and larger increments, which furthered the conversation. As we see, Elif easily slips into the conversation by asking what the change is. Yener and Mert were united in explaining Elif’s questions during the conversation. The discussion extended by creating smaller and larger increments. These interactions between Elif and the students are cultivated in their shared community-based practices.
In summary, Vignette 2 exemplifies two results. First, an instructional support for students’ co-development of CR and RF is shrinking and enlarging portions of quantitative magnitudes. Second, a community-based practice is teacher–student caring relationships.

5.3. Comparison Between Graphs of Quadratic and Exponential Functions

In Vignette 3, Salim and Mert explored the relationship between the length of the paint roller and the area being covered (Figure 3). In small group time, students were arguing whether a quadratic or an exponential form of a graph represents the relationship between the height and area of growing rectangle.
Although Salim was in 10th grade and Mert was in 8th grade, their conversation reflected a sophisticated level of peer-to-peer mathematical engagement. Mert challenged Salim’s claim that the relationship between the height of a triangle and its area must be quadratic by proposing a counterexample: “Wait, then it [the relationship in the paint roller situation] can be exponential?” When Salim replied, “It cannot be,” Mert pressed further, asking, “Why can’t it be?” Salim initially offered a vague justification—“I said so”—which Mert immediately critiqued sarcastically: “Very good explanation.” To substantiate his argument, Mert sketched an exponential graph close to the origin, visually eliminating the negative domain (Figure 3a). This visual move served as a contradiction to Salim’s claim and pushed the discussion forward. In response, Salim attempted to clarify the distinct nature of quadratic functions, stating, “Look, if it is x squared, then it cannot be exponential.” However, Mert persisted: “Why can’t it be?”—a moment that visibly challenged Salim, who hesitated, asking aloud, “Nasil acikliycam bunu?” [How am I going to explain this?]. As the dialogue unfolded, Mert pointed to Salim’s sketch of a parabola, asking, “What is the point of this line?”—referring to the left half of the parabola (Figure 3b) that had been crossed out. Salim replied vaguely, “It just, um. It is just how.” Mert responded, “Then, that line exists, right?” Salim agreed: “Yeah.” Mert countered, “But it cannot exist because it is negative. The negative area is not a thing.” Salim concluded, “It can exist because it is an equation. It is going to exist anyway” (Figure 3c).
Vignette 3 exemplifies how translanguaging and cross-age group settings serve as powerful community-based practices that support students’ co-development of CR and RF. In this vignette, Salim and Mert have already established social interactions in community-based practices and flexibly used languages between English and Turkish (e.g., Salim saying, “Nasil acikliycam bunu?” [How am I going to explain this?]). Mert critically engages with Salim’s statement by providing a contradictory example and asking why. In Vignette 3, we see that the students felt safe and cared for by their peers. Mert freely expresses opposing ideas or examples. As a result, Salim does not feel judged because these students believe they are safe and that others value their thoughts. Based on these results, we argue that students benefited from mathematics instruction that aligns with their community-based practices, embraces cross-age learning, welcomes translanguaging, and encourages peer challenges in a supportive way.
The mathematics learning environment site is the students’ community center, where they have gathered for several cultural and social weekly gatherings. In this setting, the community-based practices at the center are not new to the students. For example, Salim and Mert are used to being grouped into mixed-age groups, where an eighth grader—Mert—interacts with a tenth grader—Salim—in learning about their culture and language. When learning about quadratic functions, they developed a form of communication that allowed them to take an active role in constructing knowledge about representing the quantitative relationship by explaining their own thinking, asking questions to peers, and pushing boundaries for further investigation.
In summary, Vignette 3 exemplifies two main results. First, an instructional support for students’ co-development of CR and RF is to invite students to compare graphs of quadratic functions and exponential functions. Second, two community-based practices evident in the social interactions of the classroom culture are translanguaging and cross-age group settings.

5.4. Creating and Connecting Representations to Present Quantitative Relationships

Vignette 4, below, is taken from Eren and Salim’s small-group interactions while they explored the relationship between the length of the paint roller and the area covered by the paint roller task (Figure 4).
In Vignette 4, Salim asserted, “As the height of the triangle increases, area increases,” but was unclear about which representations to use. When prompted by the task instructions—“Respond to this question using two different representations (e.g., diagram, graph, table, or symbolic equations)”—Eren pointed directly to the prompt and emphasized the need for more formal representations: “Diagram, table, or symbolic equation.” Salim initially conflated the triangle with these representations, stating, “It is the same thing,” referring to the triangle as equivalent to a table. Eren disagreed: “This is not,” signaling a distinction between triangle and table.
Salim then offered a symbolic equation—“Al sana [Here you go]: height times length divided by two”—and suggested, “Should we make a graph?” to which Eren responded, “We should draw the graph. And then we should write a table.” Still, Salim persisted, “Triangle is mantıklı [Triangle makes sense],” but Eren clarified again: “Triangle is not a, not a diagram or a table or a graph. We just draw the graph and the table.” This exchange reflects how Eren’s insistence on selecting appropriate representations pushed Salim to reconsider his choices and align them more closely with the task’s demands.
Through this negotiation, they ultimately coordinated the length of the paint roller with the area it covered by constructing both a table and a graph (Figure 4). Their reasoning—“as the length of the paint roller increased, the area covered increases”—illustrates a developing understanding of covarying quantities. Although they did not initially articulate the magnitude of change, the process of selecting and justifying multiple representations helped them begin to identify and coordinate these changes.
Furthermore, in Vignette 4, we note that community-based practices, translanguaging, and cross-age group settings played a role for students in developing QR and RF. Eren and Salim created multiple representations to illustrate the relationship and to identify the magnitudes of change in covarying quantities—coordination of growth. In Salim and Eren’s vignette, a graph was chosen to discuss quantitative relationships. When they agree or disagree on which type of representation to use for presenting the quantitative relationship, they employ translanguaging—“Graph mi yapalim?” or “triangle is mantikli”—as we see, these sentences are not meaningful for a person who knows only English or Turkish; they are meaningful for those who speak both languages. They used words from both languages; Salim stated that “Triangle is mantikli.” This sentence is a mixture of two languages: the words “triangle” and is” are English, while “mantikli” is a Turkish word. For instance, for participants and the first author, translanguaging is a community-based communication that is rooted in the community. Such webs of interactions are meaningful resources for students. We consider these cases as evidence supporting QR and RF, which stem from community-based practices—cross-aged groups—and community resources—translanguaging.
In summary, Vignette 4 exemplifies two main results. First, instructional activities that demand students create and connect representations to present quantitative relationships support students’ co-development of CR and RF. Second, these instructional supports were in situations of community-based practices of translanguaging and cross-age group structure.

5.5. Summary

Across Vignettes 1–4, we have introduced the characteristics of a culturally inclusive mathematics learning environment framework. We introduce four key instructional supports for students’ co-development of CR and RF as (1) probing for a unit to measure an object’s attributes, (2) shrinking and enlarging portions of quantitative magnitudes, (3) comparing graphs of quadratic and exponential functions, (4) creating and connecting representations to present quantitative relationships. We also introduce three community-based practices: (5) teacher–student caring relations, (6) cross-age group setting, and (7) translanguaging. These findings are summarized in Table 5.

6. Discussion

This study provides insights into how culturally inclusive mathematics learning environments can support the co-development of CR and RF. By situating function learning within meaningful, context-rich experiences rooted in students’ community-based practices, and facilitating this learning through interactions with peers and an instructor who served as an insider, Turkish–American students developed sophisticated ways of reasoning about and representing quantitative relationships of quadratic functions.

6.1. Co-Development of CR and RF

Consistent with prior work on representational fluency (Fonger et al., 2020), students in this study demonstrated that representational fluency emerges not only from exposure to multiple representations but through active engagement in constructing, interpreting, and coordinating those representations of quantitative relationships. As Salim and Eren (Vignette 1) discussed the meaning of area and length, their articulation of measurable quantities served as evidence of grounding abstract representations in contextualized experiences, which facilitates meaning-making (Dreyfus & Halevi, 1991). In Vignettes 2 and 4, we observed a bidirectional co-development of CR and RF as students progressed beyond surface-level manipulation of symbols and isolated interpretation of visual features of representations. They coordinated symbolic, tabular, and graphical representations, which not only deepened their understanding of how quantities change in relation to one another (Vignette 2) but also enabled them to interpret and construct representations in increasingly flexible ways (Vignette 4). This reciprocal process allowed students to recognize and express quantitative relationships as meaningful functional relationships, demonstrating a dynamic interplay between reasoning about change and fluency across representations.
CR, as observed in Yener’s shift (Vignette 2) from reasoning at discrete points to recognizing continuous change across infinitesimal intervals, corroborates the work by Carlson et al. (2002) and Moore et al. (2013), who emphasize that CR involves attending to how two quantities change in tandem across a graphical domain. Importantly, Yener’s learning was not simply a function of content exposure but was shaped by targeted prompting and adjusting of the scale of the task. We found that probing for a unit to measure an object’s attributes (Vignette 1) and prompting students to shrink and enlarge portions of a quantities magnitude (Vignette 2) were supportive of students’ co-development of CR and RF across table, symbolic, and graphic representations. This both aligns with Thompson’s (1994) notion that CR development can be fostered through carefully sequenced prompts that shift students’ attention from static snapshots to dynamic processes, and extends his work to include a focus on RF across representations.
While earlier studies have primarily focused on teacher-facilitated transitions across representations of quantities (Wilkie, 2019), this study emphasizes the student-led nature of representing and reasoning when a culturally inclusive learning environment is established within community practices for collaborative meaning-making. The peer negotiation between Mert and Salim (Vignette 3) provides further evidence supporting existing claims (Altindis, 2021, 2025; Even, 1998; Fonger & Altindis, 2019) that CR and RF are intertwined in modeling quantitative relationships. Additionally, this study extends that work by demonstrating that peer-generated inquiries, through questioning, counterexamples, and challenges, can serve as informal yet powerful mechanisms for learning. Additionally, Salim and Eren’s attempts to justify why a quadratic model best fits the paint roller scenario (Vignette 4) illustrates how representational fluency is strengthened by the demand for explanation and justification. Through the construction of tables and graphs, students were not merely using representations as computational tools but as reasoning tools to model dynamic relationships—evidence of productive coordination of multiple representational forms.
While the previous literature has documented the separate development of CR and RF, and a few studies have explored their intersection (e.g., Altindis, 2021; Fonger & Altindis, 2019; Moore et al., 2013), this study makes a distinct contribution by situating the co-development of CR and RF within a culturally inclusive learning environment. Specifically, this study demonstrates how CR and RF co-develop through peer dialogue, particularly when students are encouraged to justify, critique, and compare mathematical models in a culturally inclusive learning environment that centers teacher–student caring relationships, cross-age group, and translanguaging. These peer dynamics have received less emphasis in prior research, which has traditionally centered on teacher-directed scaffolding. The community-based setting fostered a sense of belonging and shared responsibility, allowing students to draw on their linguistic and social resources to build understanding collaboratively—an extension of sociocultural learning perspectives (e.g., Nasir & Hand, 2006) rarely connected directly to function learning.

6.2. Community-Based Practices

Historically, productive mathematics learning environments emphasize students’ roles in explaining their thinking, asking questions, justifying ideas, and engaging in critique (Yackel & Cobb, 1996; Ruef, 2021). This study provides empirical evidence that instructional supports aligned with community-based practices connected to teacher and students’ culture and language, play a vital role in supporting students’ understanding of quadratic functions. Our findings underscore the importance of culturally grounded interactions in shaping how secondary students reason about and represent functions extending prior work on instructional supports (Fonger et al., 2020).
We complement Wood et al.’s (2006) work, which argues that each classroom has its own interactional patterns shaped by the community of teachers and students. Our study expands this framing by showing how these patterns, when deeply embedded in cultural and communal practices, form a dense web of social interactions that yield learning opportunities. While Wood et al. focused primarily on student–teacher interactions, our findings also highlight peer collaboration. In our context, students engaged in productive negotiations with one another, while the teacher acted as a participant-observer rather than the central authority. For instance, in Salim and Mert’s Vignette 3, their collaborative effort to determine whether a quadratic or exponential graph best represents the growth of a shape illustrates how social norms around revising thinking were normalized, not as correcting errors, but as an accepted part of mathematical discourse. This process reflects how well-established community-based practices, such as teacher–student caring relationships, cross-age group settings, and translanguaging, can support the development of CR and RF, including discerning whether two quantities change linearly or nonlinearly in graphs, tables, and diagrams.

6.2.1. Teacher–Student Caring Relationship

We relate the identified student reasoning and representational activities to the well-established teacher–student caring relationships that pre-existed between the teacher–researcher and the students. These relationships were grounded in shared cultural and social norms—Elif, the teacher–researcher, had long served as a community educator, teaching Turkish culture and heritage at the community center. This shared sociocultural background and history of interaction formed the foundation for a classroom climate of mutual respect and understanding. As Noddings (2002) and Bartell (2011) argue, caring is not merely an emotional stance but a relational practice rooted in responsiveness and attentiveness to students’ ways of thinking, acting, and being.
In Vignette 3, when Elif transitioned into her role as a teacher–researcher probing for a unit to measure an object’s attributes, her questions were interpreted as part of an ongoing dialogue embedded in mutual trust. For instance, in Vignette 1, Elif engages Salim and Eren in a discussion about the appropriate units for measuring the area of a growing rectangle—centimeters versus square centimeters. The conversation organically extends to how they might explain the concept to their younger siblings, a connection made possible because Elif and the students share relationships with these siblings through their community ties.
This interaction exemplifies what Hackenberg (2010) describes as a complex web of perturbations and responses that give rise to teacher–student caring relationships. The present study builds on this model by demonstrating that these caring relationships are not only constructed in the moment but are also embedded in long-standing community-based practices. These shared cultural values and communal affiliations support a learning environment where students feel safe to articulate and refine their mathematical ideas in the context of this study (Vignette 1), regarding the magnitudes of quantities and units to measure them. Such an environment, as O’Connor and McCartney (2007) and Wentzel (1997) suggest, is critical for both academic success and motivation. In our case, these relational dynamics facilitated the co-development of CR and RF, as students were positioned as capable thinkers whose ideas mattered within a culturally familiar and supportive environment.

6.2.2. Community Structures and Cross-Age Collaboration

Students’ learning also unfolded in cross-age groupings where cultural practices, language, and heritage were shared and reinforced. Within this structure, students brought pre-existing social relationships into mathematics learning spaces. These interactions became central to their co-development of CR and RF, as students continuously revisited and re-evaluated their ideas. As Elif’s observations at the community center show, these group settings offered rich, culturally coherent environments for mathematical exploration. Rather than focusing on teacher-centered explanations, the structure of group work supported peer-to-peer negotiations, where ideas were built collectively.
This environment also shifted traditional group dynamics. Whereas prior studies (e.g., DeJarnette & González, 2015) reported instances of students positioning themselves as experts or authorities within group work, our findings revealed students acting as collaborators. Even with age differences, students such as Salim and Mert co-constructed arguments and compared function types without hierarchical dynamics (Vignette 3). Their discussion about whether exponential or quadratic functions better represented a quantitative relationship illustrates how collaborative reasoning and shared representational work supported conceptual development, within a culturally inclusive learning environment.

6.2.3. Translanguaging as a Cultural Resource

A key finding of this study is the role of translanguaging in supporting the co-development of CR and RF. In Vignette 4 with Eren and Salim, students fluidly alternated between English and Turkish, often within the same utterance. Rather than being a barrier, this practice became a communicative resource for expressing mathematical ideas. Translanguaging—an established practice in multilingual communities—was not just a linguistic feature but a cultural one, allowing students to make meaning in ways most natural to them (Moschkovich, 2007; Setati, 2005).
Understanding these interactions required linguistic and cultural awareness. Elif, as an instructional insider, was able to facilitate and participate in these exchanges meaningfully, reinforcing the idea that language and culture are intertwined with cognition. Through translanguaging, students articulated how quantities and relationships changed across multiple representations, thus enhancing their CR and RF. These findings align with sociocultural perspectives that frame language not merely as a medium of instruction but as a resource for reasoning (Bartell, 2011; Chitera, 2009; Moschkovich, 2007; Narayan, 1993).

6.3. Concluding Remarks

This study provides insight into how students’ CR and RF co-develop when instructional supports are meaningfully connected to their community-based practices. By situating learning within culturally inclusive learning environments and acknowledging the reflexive positionality of the teacher–researcher in relation to Turkish–American students, we highlight how shared community-based practices can enhance mathematics teaching and learning. This work contributes to mathematics education scholarship by detailing how such environments can be intentionally crafted to honor and leverage the diverse cultural and linguistic resources that students bring to the classroom.
We argue there is a need for additional research on students’ mathematics learning as situated in culturally inclusive learning environments. Studies that explore cognition (and development of conceptual understanding) should be situated within the spaces of students’ own practices. We recommend teachers center teacher–student caring relations, and aim to see students’ ways of socially interacting with their peers as assets to mathematics learning environments. Moreover, we encourage teachers to invite multilingual learners to use their own ways of expressing mathematical ideas with multiple languages as a resource for students’ mathematics learning.

Author Contributions

Conceptualization, N.A. and N.L.F.; methodology, N.A. and N.L.F.; formal analysis, N.A.; data curation, N.A.; writing—original draft preparation, N.A.: writing—review and editing, N.A. and N.L.F.; visualization, N.A.; supervision, N.L.F.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board of Syracuse University (protocol code 18-224, date of approval: 26 August 2019).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data from the classroom transcripts supporting the article’s conclusions are included in part within the article and are available in whole from the author upon reasonable request.

Conflicts of Interest

The authors declare that there are no competing interests.

References

  1. Adu-Gyamfi, K., Stiff, L. V., & Bossé, M. J. (2012). Lost in translation: Examining translation errors associated with mathematical representations. School Science and Mathematics, 112(3), 159–170. [Google Scholar] [CrossRef]
  2. Altindis, N. (2021). Exploring The nature of The co-emergence of students’ representational fluency and functional thinking [Doctoral dissertation, Syracuse University]. [Google Scholar]
  3. Altindis, N. (2025). Networking theories of quantitative reasoning and mathematical reasoning to explore students’ understanding of functions. The Journal of Mathematical Behavior, 80, 101276. [Google Scholar] [CrossRef]
  4. Altindis, N., Bowe, K. A., Couch, B., Bauer, C. F., & Aikens, M. (2024). Exploring the role of disciplinary knowledge in students’ covariational reasoning during graphical interpretation. International Journal of STEM Education, 11(1), 32. [Google Scholar] [CrossRef]
  5. Altindis, N., & Fonger, L. N. (2019, November 14–17). Seeing exponential function despite representational fluency in a quantitatively rich quadratic function task [Research report]. The Forty-First Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, St Louis, MO, USA. [Google Scholar]
  6. Averill, R., Anderson, D., Easton, H., Te Maro, P., Smith, D., & Hynds, A. (2009). Culturally responsive teaching of mathematics: Three models from linked studies. Journal for Research in Mathematics Education, 40(2), 157–186. [Google Scholar]
  7. Bartell, T. (2011). Caring, race, culture, and power: A research synthesis toward supporting mathematics teachers in caring with awareness. Journal of Urban Mathematics Education, 4(1), 50–74. [Google Scholar] [CrossRef]
  8. Battey, D. (2013). “Good” mathematics teaching for students of color and those in poverty: The importance of relational interactions within instruction. Educational Studies in Mathematics, 82(1), 125–144. [Google Scholar] [CrossRef]
  9. Bieda, K. N., & Nathan, M. J. (2009). Representational disfluency in algebra: Evidence from student gestures and speech. ZDM, 41, 637–650. [Google Scholar] [CrossRef]
  10. Blanton, M., Stephens, A., Knuth, E., Gardiner, A. M., Isler, I., & Kim, J. S. (2015). The development of children’s algebraic thinking: The impact of a comprehensive early algebra intervention in third grade. Journal for Research in Mathematics Education, 46(1), 39–87. [Google Scholar] [CrossRef]
  11. Boaler, J. (2000). Exploring situated insights into research and learning. Journal for Research in Mathematics Education, 31(1), 113–119. [Google Scholar] [CrossRef]
  12. Bowers, J., Cobb, P., & McClain, K. (1999). The evolution of mathematical practices: A case study. Cognition and Instruction, 17(1), 25–66. [Google Scholar] [CrossRef]
  13. Brown, A. L. (1992). Design experiments: Theoretical and methodological challenges in creating complex interventions in classroom settings. Journal of the Learning Sciences, 2(2), 141–178. [Google Scholar] [CrossRef]
  14. Brown, A. L., & Campione, J. C. (1996). Psychological theory and the design of innovative learning environments: On procedures, principles, and systems. Lawrence Erlbaum Associates, Inc. [Google Scholar]
  15. Campbell, J. L., Quincy, C., Osserman, J., & Pedersen, O. K. (2013). Coding in-depth semistructured interviews: Problems of unitization and intercoder reliability and agreement. Sociological Methods & Research, 42(3), 294–320. [Google Scholar] [CrossRef]
  16. Carlson, M., Jacobs, S., Coe, E., Larsen, S., & Hsu, E. (2002). Applying covariational reasoning while modeling dynamic events: A framework and a study. Journal for Research in Mathematics Education, 33(5), 352–378. [Google Scholar] [CrossRef]
  17. Castillo-Garsow, C. (2012). Continuous quantitative reasoning. In L. L. Hatfield, & R. Mayes (Eds.), WISDOMe monograph: Vol. 2. Quantitative reasoning and mathematical modeling: A driver for STEM integrated education and teaching in context (pp. 55–73). University of Wyoming. [Google Scholar]
  18. Chitera, N. (2009). Code-switching in a college mathematics classroom. International Journal of Multilingualism, 6(4), 426–442. [Google Scholar] [CrossRef]
  19. Civil, M. (2002). Chapter 4: Everyday mathematics, mathematicians’ mathematics, and school mathematics: Can we bring them together? Journal for Research in Mathematics Education. Monograph, 11, 40–62. [Google Scholar] [CrossRef]
  20. Cobb, P. (2000). Conducting teaching experiments in collaboration with teachers. In A. E. Kelly, & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 307–333). Lawrence Erlbaum Associates. [Google Scholar]
  21. Cobb, P., Confrey, J., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9–13. [Google Scholar] [CrossRef]
  22. Cobb, P., Gresalfi, M., & Hodge, L. L. (2009). An interpretive scheme for analyzing the identities that students develop in mathematics classrooms. Journal for Research in Mathematics Education, 40(1), 40–68. [Google Scholar] [CrossRef]
  23. Cobb, P., Jackson, K., & Dunlap, C. (2017). Conducting design studies to investigate and support mathematics students’ and teachers’ learning. In J. Cai (Ed.), First compendium for research in mathematics education (pp. 208–233). National Council of Teachers of Mathematics. [Google Scholar]
  24. Cobb, P., & Whitenack, J. W. (1996). A method for conducting longitudinal analyses of classroom video recordings and transcripts. Educational Studies in Mathematics, 30(3), 213–228. [Google Scholar] [CrossRef]
  25. Cobb, P., & Yackel, E. (1996). Constructivist, emergent, and sociocultural perspectives in the context of developmental research. Educational Psychologist, 31(3/4), 175–190. [Google Scholar]
  26. Confrey, J., & Smith, E. (1995). Splitting, covariation, and their role in the development of exponential functions. Journal for Research in Mathematics Education, 26(1), 66–86. [Google Scholar] [CrossRef]
  27. Cornelius, L. L., & Herrenkohl, L. R. (2004). Power in the classroom: How the classroom environment shapes students’ relationships with each other and with concepts. In Investigating participant structures in the context of science instruction (pp. 467–498). Routledge. [Google Scholar] [CrossRef]
  28. DeJarnette, A. F., & González, G. (2015). Positioning during group work on a novel task in Algebra II. Journal for Research in Mathematics Education, 46(4), 378–422. [Google Scholar] [CrossRef]
  29. Dreyfus, T. (2002). Advanced mathematical thinking processes. In D. Tall (Ed.), Advanced mathematical thinking (pp. 25–41). Springer. [Google Scholar]
  30. Dreyfus, T., & Halevi, T. (1991). QuadFun—A case study of pupil computer interaction. Journal of Computers in Mathematics and Science Teaching, 10(2), 43–48. [Google Scholar]
  31. Ellis, A., Ely, R., Singleton, B., & Tasova, H. (2020). Scaling-continuous variation: Supporting students’ algebraic reasoning. Educational Studies in Mathematics, 104(1), 87–103. [Google Scholar] [CrossRef]
  32. Ellis, A. B., & Grinstead, P. (2008). Hidden lessons: How a focus on slope-like properties of quadratic functions encouraged unexpected generalizations. The Journal of Mathematical Behavior, 27(4), 277–296. [Google Scholar] [CrossRef]
  33. Esmonde, I. (2009). Ideas and identities: Supporting equity in cooperative mathematics learning. Review of Educational Research, 79(2), 1008–1043. [Google Scholar] [CrossRef]
  34. Even, R. (1998). Factors involved in linking representations of functions. The Journal of Mathematical Behavior, 17(1), 105–121. [Google Scholar] [CrossRef]
  35. Ferrari-Escolá, M., Martínez-Sierra, G., & Méndez-Guevara, M. E. M. (2016). “Multiply by adding”: Development of logarithmic-exponential covariational reasoning in high school students. The Journal of Mathematical Behavior, 42, 92–108. [Google Scholar] [CrossRef]
  36. Fonger, L. N. (2019). Meaningfulness in representational fluency: An analytic lens for students’ creations, interpretations, and connections. The Journal of Mathematical Behavior, 54, 100678. [Google Scholar] [CrossRef]
  37. Fonger, L. N., & Altindis, N. (2019, November 14–17). Meaningful learning; networking theories of multiple representations and quantitative reasoning [Research report]. The Forty-First Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, St Louis, MO, USA. [Google Scholar]
  38. Fonger, N. L., Ellis, A. B., & Dogan, M. F. (2020). A quadratic growth learning trajectory. The Journal of Mathematical Behavior, 59, 100795. [Google Scholar] [CrossRef]
  39. Glaser, B., & Straus, A. (1999). Discovery of grounded theory. Aldine Transaction. (Original work published 1967). [Google Scholar]
  40. Gutiérrez, R. (2002). Enabling the practice of mathematics teachers in context: Toward a new equity research agenda. Mathematical Thinking and Learning, 4(2–3), 145–187. [Google Scholar] [CrossRef]
  41. Hackenberg, A. J. (2010). Mathematical caring relations in action. Journal for Research in Mathematics Education, 41(3), 236–273. [Google Scholar] [CrossRef]
  42. Hesse-Biber, S. N., & Piatelli, D. (2007). Holistic reflexivity: The feminist practice of reflexivity. In S. N. Hesse-Biber, & D. Piatelli (Eds.), Handbook of feminist research: Theory and praxis. Sage. [Google Scholar]
  43. Hitt, F. (1998). Difficulties in the articulation of different representations linked to the concept of function. The Journal of Mathematical Behavior, 17(1), 123–134. [Google Scholar] [CrossRef]
  44. Johnson, H. L. (2012). Reasoning about variation in the intensity of change in covarying quantities involved in rate of change. Journal of Mathematical Behavior, 31, 313–330. [Google Scholar] [CrossRef]
  45. Kaput, J. J. (1987a). Representation systems and mathematics. In C. Janvier (Ed.), Problems of representations in the teaching and learning of mathematics (pp. 19–27). Lawrence Erlbaum Associates. [Google Scholar]
  46. Kaput, J. J. (1987b). Towards a theory of symbol use in mathematics. In C. Janvier (Ed.), Problems of representations in the teaching and learning of mathematics (pp. 159–197). Lawrence Erlbaum Associates. [Google Scholar]
  47. Ladson-Billings, G. (1995). Toward a theory of culturally relevant pedagogy. American Educational Research Journal, 32(3), 465–491. [Google Scholar] [CrossRef]
  48. Lobato, J. (2012). The actor-oriented transfer perspective and its contributions to educational research and practice. Educational Psychologist, 47(3), 232–247. [Google Scholar] [CrossRef]
  49. Moore, K. C. (2010). The role of quantitative reasoning in precalculus students learning central concepts of trigonometry [Unpublished doctoral dissertation, Arizona State University]. [Google Scholar]
  50. Moore, K. C., & Carlson, M. P. (2012). Students’ images of problem contexts when solving applied problems. The Journal of Mathematical Behavior, 31(1), 48–59. [Google Scholar] [CrossRef]
  51. Moore, K. C., Paoletti, T., & Musgrave, S. (2013). Covariational reasoning and invariance among coordinate systems. The Journal of Mathematical Behavior, 32(3), 461–473. [Google Scholar] [CrossRef]
  52. Moore, K. C., & Thompson, P. W. (2015). Shape thinking and students’ graphing activity. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano, & A. Sépulveda (Eds.), Proceedings of the 18th meeting of the maa special interest group on research in undergraduate mathematics education (pp. 782–789). P, RUME. [Google Scholar]
  53. Moschkovich, J. (2007). Using two languages when learning mathematics. Educational studies in Mathematics, 64(2), 121–144. [Google Scholar] [CrossRef]
  54. Narayan, K. (1993). How native is a ‘native’ anthropologist. American Anthropologist, 95(3), 671–686. [Google Scholar] [CrossRef]
  55. Nasir, N. I. S., & Hand, V. M. (2006). Exploring sociocultural perspectives on race, culture, and learning. Review of Educational Research, 76(4), 449–475. [Google Scholar] [CrossRef]
  56. Nasir, N. S., Rosebery, A. S., Warren, B., & Lee, C. D. (2006). Learning as a cultural process: Achieving Equity through diversity. In R. K. Sawyer (Ed.), The Cambridge handbook of: The learning sciences (pp. 489–504). Cambridge University Press. [Google Scholar]
  57. National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics: Executive summary. National Council of Teachers of Mathematics. [Google Scholar]
  58. National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. National Council of Teachers of Mathematics. [Google Scholar]
  59. Noddings, N. (2002). Educating moral people: A caring alternative to character education. Teachers College Press. [Google Scholar]
  60. O’Connor, E., & McCartney, K. (2007). Examining teacher–Child relationships and achievement as part of an ecological model of development. American Educational Research Journal, 44(2), 340–369. [Google Scholar] [CrossRef]
  61. Oehrtman, M. C., Carlson, M. P., & Thompson, P. W. (2008). Foundational reasoning abilities that promote coherence in students’ 485 understandings of function. In M. P. Carlson, & C. Rasmussen (Eds.), Making the connection: Research and practice in undergraduate 486 mathematics (pp. 27–42). Mathematical Association of America. [Google Scholar]
  62. Patton, M. Q. (2014). Qualitative research & evaluation methods: Integrating theory and practice. Sage Publications. [Google Scholar]
  63. Potgieter, M., Harding, A., & Engelbrecht, J. (2008). Transfer of algebraic and graphical thinking between mathematics and chemistry. Journal of Research in Science Teaching: The Official Journal of the National Association for Research in Science Teaching, 45(2), 197–218. [Google Scholar] [CrossRef]
  64. Ruef, J. (2021). How Ms. Mayen and her students co-constructed good-at-math. Journal for Research in Mathematics Education, 52(2), 152–188. [Google Scholar] [CrossRef]
  65. Setati, M. (2005). Teaching mathematics in a primary multilingual classroom. Journal for Research in Mathematics Education, 36(5), 447–466. [Google Scholar]
  66. Smith, J., & Thompson, P. W. (2008). Quantitative reasoning and the development of algebraic reasoning. In J. J. Kaput, D. W. Carraher, & M. L. Blanton (Eds.), Algebra in the early grades (pp. 95–132). Lawrence Erlbaum Associates. [Google Scholar]
  67. Staples, M. (2007). Supporting whole-class collaborative inquiry in a secondary mathematics classroom. Cognition and Instruction, 25(2–3), 161–217. [Google Scholar] [CrossRef]
  68. Steffe, L. P., & Thompson, P. W. (2000). Teaching experiment methodology: Underlying principles and essential elements. In R. Lesh, & A. E. Kelly (Eds.), Research design in mathematics and science education (pp. 267–307). Lawrence Erlbaum Associates. [Google Scholar]
  69. Stephan, M. (2003). Reconceptualizing linear measurement studies: The development of three monograph themes. In M. Stephan, J. Bowers, & P. Cobb (Eds.), Journal for research in mathematics education monograph, Vol 12. Supporting students’ development of measuring conceptions: Analyzing students’ learning in social contexts (pp. 17–35). National Council of Teachers of Mathematics. [Google Scholar]
  70. Stephens, A., Fonger, N. L., Strachota, S., Isler, I., Blanton, M., Knuth, E., & Gardiner, A. M. (2017). A learning progression for elementary students’ functional thinking. Mathematical Thinking and Learning, 19(3), 143–166. [Google Scholar] [CrossRef]
  71. Thompson, P. W. (1993). Quantitative reasoning, complexity, and additive structures. Educational Studies in Mathematics, 25(3), 165–208. [Google Scholar] [CrossRef]
  72. Thompson, P. W. (1994). Images of rate and operational understanding of the fundamental theorem of calculus. Educational Studies in Mathematics, 26(2–3), 229–274. [Google Scholar] [CrossRef]
  73. Thompson, P. W. (2011). Quantitative reasoning and mathematical modeling. In S. A. Chamberlain, & L. L. Hatfield (Eds.), New perspectives and directions for collaborative research in mathematics education: Papers from a planning conference for WISDOMe (Vol. 1, pp. 33–56). University of Wyoming College of Education. [Google Scholar]
  74. Thompson, P. W., & Carlson, M. P. (2017). Variation, covariation and functions: Foundational ways of mathematical thinking. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 421–456). National Council of Teachers of Mathematics. [Google Scholar]
  75. Wager, A. A. (2012). Incorporating out-of-school mathematics: From cultural context to embedded practice. Journal of Mathematics Teacher Education, 15(1), 9–23. [Google Scholar] [CrossRef]
  76. Walker, E. N. (2006). Urban high school students’ academic communities and their effects on mathematics success. American Educational Research Journal, 43(1), 43–73. [Google Scholar] [CrossRef]
  77. Wentzel, K. R. (1997). Student motivation in middle school: The role of perceived pedagogical caring. Journal of Educational Psychology, 89(3), 411. [Google Scholar] [CrossRef]
  78. Wilkie, K. J. (2019). Investigating secondary students’ generalization, graphing, and construction of figural patterns for making sense of quadratic functions. The Journal of Mathematical Behavior, 54, 100689. [Google Scholar] [CrossRef]
  79. Wood, T., Williams, G., & McNeal, B. (2006). Children’s mathematical thinking in different classroom cultures. Journal for Research in Mathematics Education, 37(3), 222–255. [Google Scholar] [CrossRef]
  80. Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458–477. [Google Scholar] [CrossRef]
  81. Zaslavsky, O. (1997). Conceptual obstacles in the learning of quadratic functions. Focus on Learning Problems in Mathematics, 19(1), 20–44. [Google Scholar]
Education 15 00980 g001
Figure 1. Vignette 1: Salim and Eren’s small-group interactions; (a) table; (b) Eren’s gesture showing height in centimeters; (c) Eren’s gesture showing area as “Amount of It Covered;” and (d) Eren’s gesture representing height, in centimeters, as the side of the paper on his desk.
Figure 1. Vignette 1: Salim and Eren’s small-group interactions; (a) table; (b) Eren’s gesture showing height in centimeters; (c) Eren’s gesture showing area as “Amount of It Covered;” and (d) Eren’s gesture representing height, in centimeters, as the side of the paper on his desk.
Education 15 00980 g001
Education 15 00980 g002
Figure 2. Vignette 2: Mert and Eren small-group interactions.
Figure 2. Vignette 2: Mert and Eren small-group interactions.
Education 15 00980 g002
Education 15 00980 g003
Figure 3. Vignette 3: Mert and Salim small-group interactions; (a) Mert’s sketch of exponential function, (b) Salim’s sketch of quadratic function, and (c) Salim’s symbolic equation of the relationship of the length and area of the triangle.
Figure 3. Vignette 3: Mert and Salim small-group interactions; (a) Mert’s sketch of exponential function, (b) Salim’s sketch of quadratic function, and (c) Salim’s symbolic equation of the relationship of the length and area of the triangle.
Education 15 00980 g003
Education 15 00980 g004
Figure 4. Vignette 4: Salim and Eren’s vignette when working on the paint roller task.
Figure 4. Vignette 4: Salim and Eren’s vignette when working on the paint roller task.
Education 15 00980 g004
Table 1. Illustrating a quadratic function through concrete representations.
Table 1. Illustrating a quadratic function through concrete representations.
SimulationTableGraphSymbolic Equation
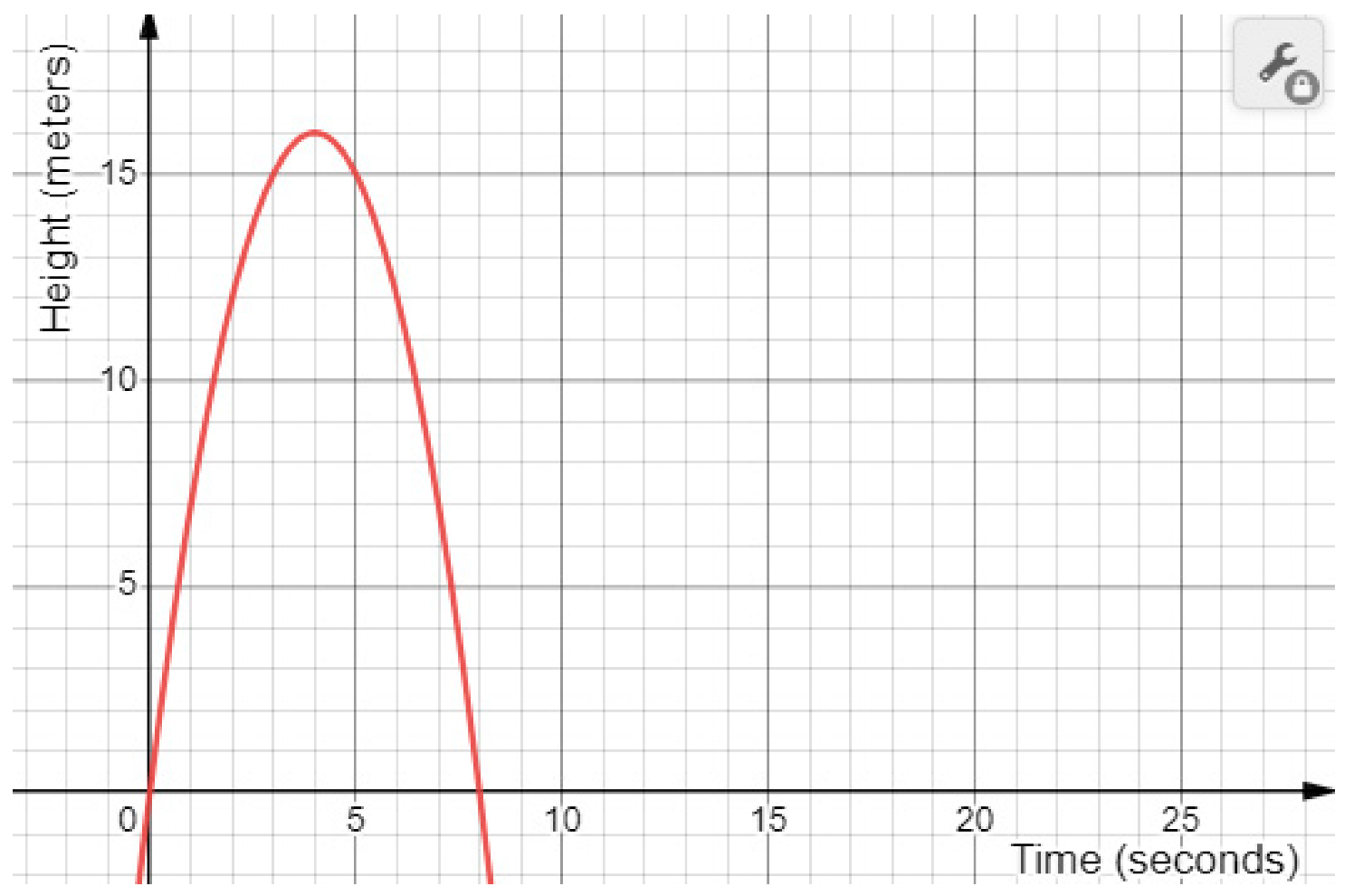Education 15 00980 i001x (time) f ( x ) (height)Education 15 00980 i002 f x = − ( x − 4 ) 2   + 16
00
17
212
315
416
515
612
77
80
x − x − 4 2 + 16
Table 2. Characteristics of student activity and hypothesized instructional supports for the co-development of representational fluency and covariational reasoning.
Table 2. Characteristics of student activity and hypothesized instructional supports for the co-development of representational fluency and covariational reasoning.
Characteristics of Student Activity (Learning Goals)Hypothesized Instructional Supports (Socio-Mathematical Norms and Practices)
Representational fluency (RF). “The ability to create, interpret, translate between and connect representations” in doing and communicating about mathematics (Fonger, 2019, p. 1).RF1. Create and interpret representations.
RF2. Exercise choice in creating representations.
RF3. Create multiple representations of the same phenomena.
RF4. Connect multiple representations by identifying invariant features of the idea being represented.		H1. Invite students to identify contextual features as measurable attributes, generate new quantities (e.g., height, speed), and create initial representations based on these quantities.
H2. Utilize dynamic contexts (e.g., motion simulations or animated graphs) to help students observe and describe how quantities increase or decrease in tandem, and represent this coordination with tables, graphs, and symbolic equations.
H3. Emphasize the role of concrete representations in the coordination process.
H4. Provide opportunities to compute and interpret average rates of change from tables and graphs, and to explain how the rate is represented and consistent across multiple representations.
H5. Ask students to translate their mental models of quantities to concrete representations.
Covariational reasoning (CR). The “cognitive activity involved in coordinating two quantities while attending to the ways in which they change in relation to each other” (Carlson et al., 2002, p. 354).CR1. Notice, name, or otherwise, identify quantities that are measurable.
CR2. Coordinate the direction of change between two covarying quantities (e.g., as one increases, the other decreases).
CR3. Coordinate the amount of change in one variable with the corresponding change in another, including recognizing additive or multiplicative relationships.
CR4. Interpret rate of change dynamically:
(a) Coordinate average rate of change across uniform intervals of the independent variable.
(b) Coordinate instantaneous rate of change as it varies continuously over the function’s domain.
Table 3. Participant demographics and attendance.
Table 3. Participant demographics and attendance.
NameDays AttendedGenderGrade LevelLanguage Fluency
Mert 8MaleGrade 8English
Asli 8Female Grade 10 English
Yener 7Male Grade 8English
Tarik 7MaleGrade 9English
Eren 7Male Grade 9English
Salim 7Male Grade 10Turkish
Bahar 5Female Grade 10Turkish
Zerrin4Female Grade 10Turkish
Note. All students were invited to participate in all 8 sessions. Some students were unable to attend all sessions (Altindis, 2021).
Table 4. An overview of the methods of analysis.
Table 4. An overview of the methods of analysis.
Initial AnalysisEpisode-by-Episode AnalysisAnalysis of Analyses
PhasesPhase 1: Identifying regularities and patterns in participants’ and teachers’ interactions in small-group and whole-class interactions. Phase 2. Developing an initial coding schema.
Phase 3. Refining an emergent coding schema.
Phase 4. Constructing a developed coding schema—a learning environment framework.		Phase 5. Coding within analytical frameworks—representational fluency and covariational reasoning.
Phase 6. Identifying shifts in students’ understanding of quadratic functions and establishing intercoder agreement.
Outcomes Enhanced transcripts of video recordings
Memos 		Initial coding schema.
Emergent coding schema.
Developed learning environment framework.		Coding within predetermined frameworks.
Coding within the developed codebook.
Establishing intercoder agreement.
Table 5. Culturally inclusive mathematics learning environment framework.
Table 5. Culturally inclusive mathematics learning environment framework.
Co-Developing CR and RFCommunity-Based Practices
Probing for a unit to measure an object’s attributes
Shrinking and enlarging portions of quantitative magnitudes
Comparison between graphs of quadratic and exponential functions
Creating and connecting representations to present quantitative relationships		Teacher–Student Caring
Cross-Age Group Setting
Translanguaging
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Altindis, N.; Fonger, N.L. A Culturally Inclusive Mathematics Learning Environment Framework: Supporting Students’ Representational Fluency and Covariational Reasoning. Educ. Sci. 2025, 15, 980. https://doi.org/10.3390/educsci15080980

AMA Style

Altindis N, Fonger NL. A Culturally Inclusive Mathematics Learning Environment Framework: Supporting Students’ Representational Fluency and Covariational Reasoning. Education Sciences. 2025; 15(8):980. https://doi.org/10.3390/educsci15080980

Chicago/Turabian Style

Altindis, Nigar, and Nicole L. Fonger. 2025. "A Culturally Inclusive Mathematics Learning Environment Framework: Supporting Students’ Representational Fluency and Covariational Reasoning" Education Sciences 15, no. 8: 980. https://doi.org/10.3390/educsci15080980

APA Style

Altindis, N., & Fonger, N. L. (2025). A Culturally Inclusive Mathematics Learning Environment Framework: Supporting Students’ Representational Fluency and Covariational Reasoning. Education Sciences, 15(8), 980. https://doi.org/10.3390/educsci15080980

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop