The Role of Non-Digital and Digital UNO-Type Card Games as Learning Media in Different Levels of Mathematics Education: A Systematic Review

Abstract

This systematic review explores the number and role of the UNO^® card game and UNO-type learning media across different levels of mathematics education. UNO^®-inspired games have gained recognition as innovative pedagogical tools that promote engagement, motivation, and active learning among students in various mathematics topics in the last few years. This review synthesises existing research on the application of these games in preschool, primary, secondary, and higher education settings. We employed a hybrid approach, combining database searches and the snowball method, to ensure a comprehensive and thorough selection of the relevant literature for our systematic review. Published research studies between January 1980 and June 2025 that employed UNO^® or UNO-type card games in education were collected. Forty-one research studies met the inclusion criteria for this review. We sought answers to three research questions. At first, we made a time analysis to organise the collected records. Based on the collection, we identified the mathematical topics for which teachers and researchers used the original UNO^® game or developed UNO-type games at various educational levels, as well as the role of UNO^® and UNO-type games in mathematics education. In approximately 68.29% of the cases, the authors introduce their own educational games modelled after UNO^®. In contrast, just less than one-third of the records (31.71%) utilise the original UNO^® playing cards in the teaching–learning process. The findings indicate that UNO-type educational maths games can enhance conceptual understanding, foster collaborative skills, and improve learning outcomes when appropriately integrated into curricula. This review also offers educators recommendations for effectively introducing these games at various educational levels. We aim to provide an evidence-based, well-structured insight into the potential of UNO^® and UNO-type learning tools.

1. Introduction

During the last decade, many teachers at various levels of education have recognised the benefits of incorporating game-based methods into their mathematics teaching practises (Russo et al., 2024). They realised that these approaches not only increase student participation, but also promote active learning, critical thinking, and collaboration (Katual et al., 2023; Noroozi et al., 2020). Teachers understood that when students are motivated and interested, they tend to absorb material more effectively and develop a deeper understanding of the subject matter. As a result, didactic card games and other educational tools have become increasingly popular and valuable resources, helping educators create more interactive, dynamic, and enjoyable learning environments that cater to diverse learning styles and needs from the primary level of education to university practise (Debrenti, 2024a; Körei et al., 2021).

One of the most enjoyable and successful examples of game-based learning is the UNO^® card game, which has been used in mathematics education for decades (Leonard & Tracy, 1993; McBride & Lamb, 1991). Originally known as an entertaining card game, it has been increasingly used in education in recent years, especially in teaching mathematics and other STEM disciplines (Ananta & Shofiyah, 2024; Jumaroh et al., 2022; Mahartika et al., 2020; Redzuan & Tien, 2023). Different versions of UNO^® are now suitable not only for developing basic skills, but also for teaching more complex topics such as mathematical operations, logic tasks, ratios, and algebraic concepts.

Following the terminology used Tursyngozhayev et al. (2024), we define an UNO-type educational game as a card game inspired by the gameplay of the popular card game UNO^® with a clear educational purpose. These learning media typically involve matching cards based on colour or number, to be the first player to empty their hand. The deck often includes action cards, like skipping a player’s turn or reversing the order of play, that can affect gameplay. What makes UNO-type games stand out is their fast pace, simple rules, and how easily they can be adapted creatively to support teaching and learning. In recent years, educators have been integrating UNO^® and UNO-type games into an increasing number of subjects and at various educational levels (Aprilia & Nugraheni, 2025).

For game-based learning to be effective, didactic games are essential tools that serve specific educational purposes. These games are carefully designed to target specific skills or knowledge areas, making the learning process more focused and goal-oriented. The article of Körei et al. (2021) on the classification of educational games is based on the categories previously defined by Kárová (1996) and Krejcová and Volfová (2001), which are grouped according to the purpose of the game, the number of players, the reactions, and the type of use. However, the authors supplement this existing system with a new criterion based on equipment requirements. This additional category takes into account whether the game requires special equipment and, if so, what type. Accordingly, games that require special educational tools can be distinguished, and within this category, a further distinction can be made between those that require information and communication technology (ICT) tools and those that require traditional tools (such as cards or board games). In addition, there are games that do not require any special tools and can therefore be played almost anywhere and at any time, such as algorithmic puzzles. The authors consider this addition important because the usage of educational games in the classroom environment must take into account the available resources and students’ access to different tools.

In 2020, a new educational game, LimStorm, was developed at the University of Miskolc, which is an adaptation of a world-famous card game (Szilágyi & Körei, 2021). LimStorm is a non-digital card game that can be classified as an UNO-type learning media and belongs to the category of educational games that require equipment. In recent years, LimStorm has undergone extensive testing, as we organise workshops for university students every year to provide opportunities for game-based learning (Deák & Kumar, 2024; Szilágyi et al., 2023a, 2023b). Not only have we collected students’ experiences and feedback over the past four years in connection with LimStorm, but we have also monitored the development of UNO-type games related to mathematical topics worldwide. Given that the number of articles collected reached 20 in 2024, we decided to conduct a comprehensive literature review to gain a complete overview of the existing literature on the subject. The aim of our systematic literature review was to summarise and systematise existing knowledge about the topic of UNO-type games. Our current collection was created through well-planned research using a search methodology that combined the snowball method with keyword searches in databases to identify relevant articles. We are currently aware of 41 publications that discuss the use of the UNO^® card game as a mathematical teaching aid or the development and testing of UNO-type card games. Due to the relatively large number of publications collected, we decided to prepare a systematic review of the role of UNO-type card games in mathematics education. We analysed each article in detail to provide a comprehensive overview. We organised our findings into tables for easy reference and management.

Our paper is structured as follows: the Literature Review presents the history of the UNO^® card game; the Methodology section describes the research questions and the procedure used to search for records, as well as the methods used to process the data. The Results section presents the systematised data and information from the 41 papers processed, as well as summary tables. This is followed by the Discussion session, where we answer the research questions. This study concludes with conclusions, recommendations, and limitations.

2. Literature Review

The UNO^® card game originated in the USA more than 50 years ago. Interestingly, the circumstances surrounding its creation are well documented, and every important stage of its success story is well-known.

2.1. The History of UNO^®

The story of UNO^® begins in 1971 when Merle Robbins, an American barber and passionate gamer, created the game. Crazy Eights was a family favourite for Merle and his loved ones, but it came with a common problem: its often-complex rules frequently sparked friendly squabbles, especially concerning cards that involved drawing more or reversing play. To smooth things over, Merle had a brilliant idea: he wrote straightforward instructions right on each card, instantly making the game easier for everyone to understand and enjoy (Lloyd, 2021). The first decks were quite basic, featuring a khaki green colour (see Figure 1), without a registered trademark on the cards. Initially, the game was sold exclusively at Merle’s barbershop (McGlynn, 2016). The Strong National Museum of Play in New York explores the history and significance of play, games, and toys. Visitors to the museum’s exhibition dedicated to the history of games can see numerous editions of UNO^®, including the first khaki green boxed deck from the 1971 series (see Figure 1, left).

The popularity of the game spread quickly. Robert Tezak bought and redesigned the game in 1973, introducing the red cards and packaging (see Figure 1, middle and right). International Games Inc. (IGI) was founded by Robert Tezak in 1972. Under IGI’s leadership, UNO^® truly took off, achieving national prominence by the late 1970s. By then, you could find it in big stores like Kmart and Walmart, and annual sales had skyrocketed to eleven million decks by 1980. UNO’s simplicity, colourful design, and energetic gameplay have made it a household staple, appealing to a broad audience across generations (McGlynn, 2016). In the 1980s, the game experienced remarkable sales growth, and despite receiving offers from numerous toy and game manufacturers, Tezak retained the rights until 1992, when Mattel officially acquired the rights to UNO^®. A major turning point in the game’s popularity happened in 1997 when Mattel started licensing popular franchises and adding them to UNO^®. Figure 2 shows a retro and a modern version of the deck.

Over the years, UNO^® has exploded in popularity, now featuring well over 700 different versions, each with its own themes, rules, and gameplay twists. This wide variety and focus on innovation help keep UNO^® fresh and highly popular. Themed decks often feature favourite movies, TV shows, or characters and started out looking like regular decks. Over time, they have added new rules and special wild cards with extra effects to make the game more exciting and strategic. Most of these themed decks have around 112 cards (more than the classic 108), giving players new ways to enjoy the game while still keeping the familiar mechanics intact.

The continuous evolution has transformed UNO^® into more than just a family game; it has become a creative universe offering fans a diverse array of themed decks and gameplay variations. In 2016, UNO^® was the second most popular game after Monopoly, which was released forty years earlier (McGlynn, 2016). In 2017, UNO^® was recognised as the world’s top-selling card game (The Strong National Museum of Play, 2018). These days, the UNO^® scene is extremely varied, with approximately 729 different versions and spinoffs, each offering unique themes and gameplay rules. More than a billion people around the globe have played UNO^® at some point, demonstrating just how enduring and widespread the game’s popularity continues to be. According to its publisher, Mattel, nearly one UNO^® deck was sold every second in the United States in 2023. That’s nearly 60 UNO^® decks per minute, a significant increase from 17 decks per minute in 2021. In recent years, UNO^® has continued to grow in popularity, particularly on online gaming platforms, mobile apps, and in educational settings.

2.2. UNO^® Cards and Game Settings

An original UNO^® deck contains 108 cards: 19 blue cards from 0 to 9 (just one 0, and two of everything else), 19 green cards from 0 to 9, 19 red cards from 0 to 9, 19 yellow cards from 0 to 9, 8 Draw Two cards (2 each in all four colours), 8 Reverse cards (2 each in all four colours), 8 Skip cards (2 each in all four colours), 4 Wild cards, and 4 Wild Draw Four cards (Demaine et al., 2014).

UNO^® is a fun and fast-paced card game where the main goal is to be the first to discard all of your cards and score points. The game is suitable for 2 to 10 players. At the start of the game, each player receives seven cards, and the remaining cards form the draw pile (Hikmah & Mustikawati, 2017). The top card of the draw pile is turned over to begin the discard pile; if this card is a Wild or Wild Draw Four, it is replaced with another card until a number or action card appears. During their turn, players may play a card that matches the top card on the discard pile by colour or number or play a Wild card to change the current colour. If a player cannot make a valid move, they must draw a card from the draw pile. If the drawn card is playable, they can play it immediately; otherwise, their turn ends. When a player has only one card remaining, they must shout “UNO!” If they forget to do so and are caught, they must draw two penalty cards. The game continues until one player plays all of their cards. The round then ends, and players score points based on the cards remaining in opponents’ hands. Number cards score their face value, action cards (Skip, Reverse, and Draw Two) score 20 points each, and Wild and Wild Draw Four cards score 50 points each. The functions of the action cards are described by Demaine et al. (2014). The goal is to be the first to reach 500 points, although players can choose to play for a set number of rounds or until a certain time limit. The player with the highest score at the end of the game wins (Benson, 2022).

2.3. The Computational Complexity of UNO^®

UNO^® is a seemingly simple yet surprisingly complex game. As a non-cooperative game, UNO^® effectively demonstrates a scenario where participants pursue strategies to optimise their individual rewards in light of anticipated competitive actions. UNO^® requires players to strike a balance between strategically managing their own hand and restricting the plays available to their opponents. Players aim to make choices that give them an edge, such as retaining cards with high strategic value, such as Wild cards, while trying to discard less useful ones. Although UNO^® is fundamentally a competitive game, players may occasionally form temporary, unspoken alliances or engage in cooperative behaviours, despite these not being formally defined by the rules.

Demaine et al. (2014) explored the computational complexity of the game UNO^® and presented mathematical models for cooperative and uncooperative versions of UNO^®. A single-player version of UNO^® is NP-complete, but becomes solvable in polynomial time with certain restrictions. A non-cooperative two-player version is PSPACE-complete.

Ramadhan et al. (2015) investigated the application of game refinement theory in relation to the game UNO^®. The aim was to characterise the complexity of UNO^® in the context of multiplayer, incomplete information games. The authors sought to determine an optimal player count and quantify relative player enjoyment through an analysis of the game’s refinement value zone. To this end, they used a computational approach, conducting extensive simulations utilising defined computer player archetypes (amateur, offensive, defensive, and observer) to model strategic decision-making. Key performance indicators, including turn counts, card plays, and instances of “UNO” declaration, were recorded. The simulation results were then benchmarked against empirical data obtained from human-player games. The authors’ findings suggest that UNO^® exhibits a non-trivial degree of game refinement, with an apparent optimal player count in the range of 4–6 individuals. Analysis of player enjoyment metrics showed that a disproportionately higher level of engagement was observed among players who occupy the penultimate and terminal positions in the game sequence.

3. Methodology

3.1. Research Questions

Our article aims to address three research questions (

Table 1. Research questions.

No.	Question
RQ1	In which mathematical topics can the original UNO® deck be used at the different educational levels?
RQ2	What mathematical topics have UNO-type games been developed for at different levels of education?
RQ3	Which learning variables are developed through the original UNO® and non-digital and digital UNO-type card games?

). Our research questions focus on exploring the educational use of UNO^® and UNO-type games in mathematics learning. The first question investigates which specific mathematical topics can be taught or reinforced using the original UNO^® deck at various educational levels (preschool, primary school, secondary school, and higher education). For this question, we only focus on records related to the original UNO^® game, i.e., the base cards have integers from 0 to 9. The second research question examines UNO-type games that relate to various mathematical topics. The question examines the mathematical topics at different educational levels for which researchers have developed UNO-type games to implement GBL. This means that the content of the basic cards can be converted into numerical values or attributes using mathematical knowledge. The third question analyses which learning variables, such as skills, understanding, or attitudes, are influenced or developed through both the original UNO^® game and UNO-type games, both in digital and non-digital formats. The aim is to explore and demonstrate the effectiveness and significance of introducing such games at different levels of mathematics education. We used a systematic literature review to answer the research questions.

3.2. Strategy for Systematic Search

A well-designed search strategy is fundamental to creating a successful systematic literature review (Wohlin et al., 2022). Our research approach is based on the general problem-solving process outlined by Agnew and Pyke (2007) and Wohlin et al. (2022). We planned our work in this spirit. The steps of the research approach are detailed in

Table 2. Steps of the research approach.

No.	Phase	Activities
1	Preparation	We developed a comprehensive search plan that included selecting relevant keywords, defining inclusion and exclusion criteria, and determining the appropriate databases and filters to be used. It required establishing a systematic process for documenting search strategies and results to ensure transparency and reproducibility. Sample searches were performed in Google Scholar.
2	Implementation	We made searches in the selected databases using predefined search strategies and retrieved relevant records using filters. Two-step screening. In the first step, screening is based on the title and abstract; in the second step, the full text is screened. We get the initial set of records for snowballing (forward and backward). The search results were organised for analysis.
3	Evaluation	The records were evaluated based on predefined acceptance and exclusion criteria, and their relevance and quality were determined.

.

In our study, we adopted a systematic search approach to identify all of the relevant literature related to UNO-type games in mathematics education. We began by developing a detailed search protocol, identifying keywords, synonyms, and phrases related to our research topic. These were combined using Boolean operators (AND, OR, NOT) to fine-tune the search results. We used multiple reputable academic databases and search engines such as Google Scholar, ERIC, JSTOR, ScienceDirect, SpringerLink, Taylor & Francis Online, SAGE Journals, ProQuest, Scopus, and Web of Science to ensure broad coverage and avoid missing relevant studies. Filters were used, such as publication date ranges, language, and peer-reviewed status, to narrow down the results selectively, without excluding valuable records.

The initial search results were screened in two stages. We applied clear inclusion and exclusion criteria to make sure the records were relevant. This process gave us the first set of results. After that, we used snowballing methods, checking the reference lists of important articles (backward snowballing) and following citations of key studies (forward snowballing). Throughout the process, we kept detailed notes on everything, like the search terms, databases we used, and how many records we found, to keep everything transparent and easy to reproduce. By combining database searches with the snowball method, we aimed to compile an extensive collection of the relevant literature on UNO^® and UNO-type games in mathematics education. This hybrid approach proved effective in uncovering key studies that might otherwise have been overlooked. The search covered articles published between 1980 and 2025.

We started our exploratory work with Google Scholar. Google Scholar is one of the most comprehensive academic search engines, offering a better chance of finding relevant articles than specialised databases (Yasin et al., 2020). Another advantage is that it provides better coverage of the grey literature (e.g., conference papers; dissertations) than traditional databases, and Google Scholar finds articles cited by other relevant articles produced in the search (Atkinson & Cipriani, 2018). At the same time, Google Scholar has several limitations. These include incomplete support for Boolean operators, a short search string length limit, automatic query expansion, which can lead to inaccurate results, a lack of reproducibility, and limitations on the number of accessible hits. These issues make it difficult to conduct precise and thorough searches needed for systematic reviews (Gusenbauer & Haddaway, 2020). Duplicate results often occur, and metadata (e.g., authors, titles, and publication details) is often inaccurate. However, its wide coverage makes it an excellent starting point. Google Scholar results are not necessarily reproducible and therefore do not meet the reproducible search methods required by systematic reviews. Google Scholar was used in combination with other sources, as advised by experts (Atkinson & Cipriani, 2018; Gusenbauer & Haddaway, 2020). During the preparatory step, we conducted sample searches using the Google Scholar search engine. For example, the search for “UNO game” yielded 219,000 results, “UNO card game” yielded 28,800 results, “UNO game AND mathematics AND learning media” yielded 17,400, and “UNO mathematics card game” yielded 5650 results. In accordance with the recommendation described by Haddaway et al. (2015), in the last two cases, we retained the first 200 hits from Google Scholar in order to select the relevant studies. We supplemented these 400 records with 30 records obtained from database searches, resulting in a total of 430 records. This was followed by an initial screening to identify potentially relevant articles based on their titles and abstracts.

To visualise the record searching process, we have created a flowchart that shows how records are identified, as shown in Figure 3.

3.3. Sample

A total of 430 records were identified as suitable for screening. A preliminary screening, which was based on the title and abstract, led to the exclusion of 297 records for various reasons, including obvious irrelevance to the topic and duplication. For the remaining 133, the full text was examined, as shown in Figure 3. During full-text screening, 105 records were excluded because they did not address the research topic, even though the title and/or abstract appeared relevant or the full text of the record was not available. So, 28 records provided the starting set of snowballing, 22 in English and 6 in Indonesian. Applying the two-way snowballing method, which involved both examining the reference lists of these studies and conducting citation analysis to identify publications that cited them, we discovered an additional 4 English and 9 Indonesian records. In total, the hybrid method search yielded 41 relevant records that matched the research topic, 26 in English and 15 in Indonesian. Approximately 9.53% of the total records were included in the sample.

After identification, the documents were initially sorted by year. The frequency by year is shown in Figure 4. The first record dates back to 1989. We found only three records before 2000, and all the others were published after 2000. Before 2016, there were very few articles on the subject; however, since 2019, at least three new articles have been published annually, enriching the literature on the topic. Our review identified 2022 as the most productive year, with six relevant papers published. Journal articles constituted the majority of the included records, accounting for 31 of the sources, along with 7 conference papers and 3 theses.

Due to the relatively large number of records, we made a time analysis and organised the records into a table arranged by year of publication.

Table 3. Records sorted by year with author(s), title, type, and platform information.

No.	Author(s)	Title	Year	Type	Platform
1	Campbell, M. D.	Basic facts drill-card games	1989	paper	JSTOR
2	McBride, J. W., & Lamb, C. E.	Using commercial games to design teacher-made games for the mathematics classroom	1991	paper	JSTOR
3	Leonard, L. M., & Tracy, D. M.	Using games to meet the standards for middle school students	1993	paper	JSTOR
4	Baturo, A., Norton, S., & Cooper, T.	The mathematics of indigenous card games: Implications for mathematics teaching and learning	2004	conference paper	Google Scholar
5	Woodruff, S. E.	Cognitive strategy intervention for second grades experiencing mathematics difficulties	2009	thesis	Google Scholar
6	Rahmatin, R. & Khabibah, S.	Development of Umath (UNO Mathematics) card game media in mathematics learning on the subject matter of integer operations	2016	paper	Google Scholar
7	Ulfah, T. A., Wahyuni, E. A., & Nurtamam, M. E.	Development of UNO card game learning media in mathematics learning on length units	2016	conference paper	Google Scholar
8	Sulisawati, D. N., & Murtinasari, F.	Modification of UNO cards as a learning medium for flat shapes to improve students’ understanding	2018	paper	Google Scholar
9	Anggraini, R.	Development of UMATH card game media (UNO Mathematics) for mathematics learning in junior high school students	2018	thesis	Google Scholar
10	Mayangsari, S. N., & Mahardhika, L. T.	Characteristics of learning media that motivate learners	2019	paper	Google Scholar
11	Srintin, A. S., Setyadi, D., & Mampouw, H. L.	Development of Umino card game media in integer operation mathematics learning	2019	paper	Google Scholar
12	Perales, F. J., Negre, F., & Riera, L.	GENIUS UP! an educational experience through serious video games for the learning of science in a ludic way	2019	conference paper	Google Scholar
13	Fitri, A., Nur, Y., & Fauzi, M.	Application of Numbered Heads Together (NHT) type cooperative learning models with UNO card media to improve mathematics learning results	2020	paper	Google Scholar
14	Robiana, A., & Handoko, H.	The effect of implementing UnoMath media to improve mathematical communication skills and learning independence in students	2020	paper	Google Scholar
15	Suciati, I.	The application of UNO Mathematics game method on fraction numbers	2020	paper	Google Scholar
16	Kholida, A., Sutama, I. W., & Suryadi, S.	Development of U-Kids (UNO Kids) card game to stimulate logical–mathematical intelligence in children aged 5-6 years	2020	paper	Google Scholar
17	Ramani, G. B., & Scalise, N. R.	It’s more than just fun and games: Play-based mathematics activities for Head Start families	2020	paper	ScienceDirect
18	Najiah, N. A. & Panggabean, E. M.	Development of UNO Spin card game media for mathematics learning on algebraic form material for junior high school students	2021	paper	Google Scholar
19	Ficky, M. R.	Development of media game UMATH (Uno Mathematics) in the material of constructing flat side spaces as a learning exercise for class VIII students at Madrasah Tsanawiyah Jauharul Islam	2021	thesis	Google Scholar
20	Wulandari, G. A., & Ambara, D. P.	Interactive multimedia-based UNO card media on cognitive abilities of early childhood in recognising and counting numbers	2021	paper	Google Scholar
21	Szilágyi, S., & Körei, A.	LimStorm—A didactic card game for collaborative math learning for Gen Z students	2021	conference paper	SpringerLink
22	Anita, F. D., Balkist, P. S., & Nurcahyono, N. A.	UNO cards to improve middle school students’ mathematical conceptual understanding	2022	paper	Google Scholar
23	Harahap, M., Mujib, A., & Nasution, A. S.	Development of UNO math media to measure understanding of flat shape concepts	2022	paper	Google Scholar
24	Szilágyi, S., & Körei, A.	Using a math card game in several ways for teaching the concept of limit	2022	conference paper	SpringerLink
25	Jumaroh, J., Surachman, S. P. & Yaroh	Development of UNO game media in mathematics learning integer operations	2022	paper	Google Scholar
26	Chong, W. W. N., Shahrill, M., Asamoah, D., & Latif, S. N. A.	Non-digital card game and year 8 students’ performance in integers	2022	paper	Google Scholar
27	Scalise, N. R., DePascale, M., Tavassolie, N., McCown, C., & Ramani, G. B.	Deal me in: Playing cards in the home to learn math	2022	paper	ERIC
28	Harlin, M. D., & Arini, N. W.	Development of UNO card media for weight measurement in Grade IV elementary school	2023	paper	Google Scholar
29	Syafitri, Z.	The effect of UNO card-based mathematics games on the ability to recognise numbers 1–10 in children with mild intellectual disabilities in grade III at Bangun Putra Kasihan Special School	2023	paper	Google Scholar
30	Utami, S. F., & Leonard	Development of U-Math (UNO Mathematics) card-based mathematics learning media	2023	paper	Google Scholar
31	Szilágyi, S., Körei, A., & Török, Z.	A game-based learning project—Calculating limit of sequences with the didactic game LimStorm	2023	conference paper	SpringerLink
32	Szilagyi, S., Korei, A., Torok, Z., & Vaičiulytė, I.	Introducing the card editing application of the LimStrom didactic game	2023	paper	Google Scholar
33	Meyrath, T., Mincu, C. I., & Perucca, A.	Training mathematical thinking with the inclusive card game UNO	2024	conference paper	Google Scholar
34	Ahsan, J. F., & Avita, D.	Utilization of smart cards in integer operations material to improve junior high school students’ understanding	2024	paper	Google Scholar
35	Fuentes A. B., Jr.	Using the TrigOno card game for mastery learning of trigonometric identities	2024	paper	ERIC
36	Lutfi, A., Rusyid, H. K., Mukhibin, A., & Basir, M. A.	Students’ motivation in learning mathematics using Uno Math media	2024	paper	Google Scholar
37	Ziliwu, F., Febri, F., Hidayatullah, M. A. N. & Subekti, R.	Learning design on basic probability theory using UNO game: Efforts to enhance understanding of probability concepts	2024	paper	Google Scholar
38	Grünke, M., Braunwarth, I., Connelly, V., & Barwasser, A.	The effects of the pegword method on the multiplication skills of students with math difficulties	2025	paper	ProQuest
39	Murtiana, A. D., & Yulianto, S.	Development of NumeriUNO media in improving mathematics learning outcomes of grade III students	2025	paper	Google Scholar
40	Aprilia, D., & Nugraheni, N.	Development and effectiveness of UN-MATH cards in enhancing problem-solving skills for elementary school students	2025	paper	Google Scholar
41	Kurniati, R., Sugiarto, S., Mattoliang, L. A., & Sairlona, S.	The development of UNO cards as a medium for learning mathematics is linked to traditional games	2025	paper	Google Scholar

includes the records, indicating the author(s), title, year, type and platform where the record was first identified. Rows from 1 to 5 show records from 1989 to 2009. We consider this to be the early period, when UNO^® began to appear in primary and secondary education. As can be seen, only five records were found during the early period: three papers, one conference paper, and one thesis. American authors wrote all articles and the thesis; Australian authors wrote the conference article. We did not find any sources related to the topic under review between 2010 and 2015. The main period began in 2016. The authors come from all over the world, mainly from Asia and Europe.

4. Results

Non-digital and digital game-based learning have been growing in popularity since the 1990s, so it is not surprising that the first record of using UNO^® as an educational tool dates back to 1989. The wider and more widespread use of game-based learning has been observed since the 2000s, especially since 2016. Parallel to the spread of digital games, non-digital games have also gained a permanent place in educational methodology toolkits, and this is also true for UNO-type games, as shown in Figure 4.

To answer the first two research questions, we identified the educational level for which the UNO^® or UNO-type game was designed and the specific area of mathematics for which it was developed, based on all records.

Table 4. Records supplemented with information on educational level, game used, and educational topic.

No.	Record	Level	Used Game	Maths Topic
1	Campbell (1989)	primary	original UNO® with modified rules	basic arithmetic facts (addition, subtraction, multiplication, and division)
2	McBride and Lamb (1991)	primary	original UNO® without action cards, with modified rules	combination of integer operations, double-digit numbers
3	Leonard and Tracy (1993)	secondary	original UNO®, not detailed	patterns and functions
4	Baturo et al. (2004)	primary	original UNO® with modified rules	number recognition, counting
5	Woodruff (2009)	primary	original UNO® with modified rules and extra cards	counting, counting up or down from a selected number on a number line, addition and subtraction
6	Rahmatin and Khabibah (2016)	primary	UNO-type game, U-Math	integer operations
7	Ulfah et al. (2016)	primary	UNO-type game	measuring length, units of length
8	Sulisawati and Murtinasari (2018)	secondary	UNO-type game, GEO	different types of quadrilateral flat shapes
9	Anggraini (2018)	secondary	UNO-type game, U-Math	quadratic functions
10	Mayangsari and Mahardhika (2019)	secondary	UNO-type game, not detailed	general description without a specific topic
11	Srintin et al. (2019)	primary	UNO-type game, Umino	integer operations
12	Perales et al. (2019)	primary and secondary	UNO-type game, Maze Cards	general description without a specific topic
13	Fitri et al. (2020)	primary	Original UNO® without action cards	addition, subtraction
14	Robiana and Handoko (2020)	secondary	UNO-type game, UnoMath	linear equations in two variables
15	Suciati (2020)	primary	UNO-type game, UNO Mathematics	comparison of fractions
16	Kholida et al. (2020)	preschool	UNO-type game, U-Kids	number recognition
17	Ramani and Scalise (2020)	preschool	UNO-type game, Match It	colour and shape
18	Najiah and Panggabean (2021)	secondary	UNO-type game, UNO Spin Maths	algebraic equations
19	Ficky (2021)	secondary	UNO-type game, U-Math	volume and surface area of 3D shapes
20	Wulandari and Ambara (2021)	preschool	digital version of original UNO®	recognising and counting numbers
21	Szilágyi and Körei (2021)	university	UNO-type game, LimStorm	calculating limits of sequences
22	Anita et al. (2022)	secondary	UNO-type game, UNO Matematika	financial mathematics
23	Harahap et al. (2022)	primary	UNO-type game, UNO math	area of flat shapes
24	Szilágyi and Körei (2022)	university	UNO-type game, LimStorm in online education	calculating limits of sequences
25	Jumaroh et al. (2022)	primary	Original UNO®	integer operations
26	Chong et al. (2022)	primary	UNO-type game, Intego	integer operations
27	Scalise et al. (2022)	preschool	UNO-type game, Match It	colour and shape
28	Harlin and Arini (2023)	primary	UNO-type game	weight measurement, units of weight
29	Syafitri (2023)	primary	original UNO®	recognise number symbols 1-10
30	Utami and Leonard (2023)	primary	UNO-type game collection, U-MATH	integer operations, fractions, units of measurement, flat shapes, and simple 3D shapes
31	Szilágyi et al. (2023a)	university	UNO-type game, LimStorm	limits of sequences
32	Szilágyi et al. (2023b)	university	UNO-type game, LimStorm	card generator application, limits of sequences
33	Meyrath et al. (2024)	secondary and university level	original UNO® with some modifications	probability, game theory, binary relations, algebra
34	Ahsan et al. (2024)	primary	UNO-type game, Smart Card	integer operations
35	Fuentes (2024)	secondary	UNO-type game, TrigOno	trigonometric identities
36	Lutfi et al. (2024)	secondary	UNO-type game, Uno Math	geometry of 3D shapes
37	Ziliwu et al. (2024)	secondary	original UNO®	basic probability theory
38	Grünke et al. (2025)	primary	original UNO®	number recognition
39	Murtiana and Yulianto (2025)	primary	UNO-type game, NumeriUNO	multiplication
40	Aprilia and Nugraheni (2025)	primary	UNO-type game, UN-MATH	story problems involving addition and subtraction tasks
41	Kurniati et al. (2025)	primary	a modified version of UNO® integrated with a traditional Indonesian game	integer operations

also shows whether the original UNO^® game or a UNO-type game was used as an educational tool for each record.

The first publication on a modified UNO-type game was written in 2016. In earlier papers, the original UNO^® cards were used with modification. In more than two-thirds of the records, authors present UNO-type educational games (68.29%), while in the entire sample, only slightly less than one-third use the original UNO^® cards (31.71%) for educational purposes.

The number of records per educational level is illustrated by a bar chart in Figure 5. Most records relate to the primary school level (48.78%), followed by secondary school (26.82%). There is only one conference paper where the game discussed can be used in primary and secondary education (2.44%). The same number of records deal with games for pre-school (9.76%) and university level (9.76%). Furthermore, in one case (2.44%), both upper secondary and university levels are relevant. In our classification, primary school covers ages 6 to 12, while secondary school covers ages 12 to 18.

We have created tables that organise the mathematical topics covered by UNO^® and UNO-type card games into thematic units per educational level. At the preschool level, records can be categorised into three main subject areas, as shown in

Table 5. Mathematical topics in UNO^® or UNO-type card games for preschool level.

Topic	Description	References
Basic Colours and Shapes	Activities are designed to help identify different colours and shapes, and develop skills in matching and classifying them.	Kholida et al. (2020); Ramani and Scalise (2020); Scalise et al. (2022)
Number Recognition and Counting from 1 to 10	Activities focus on helping recognise and identify number symbols from 1 to 10 and practise counting with these numbers.	Baturo et al. (2004); Grünke et al. (2025); Kholida et al. (2020); Syafitri (2023); Wulandari and Ambara (2021)
Associating Numbers with Quantities	The aim is for children to understand the relationship between numbers and the quantities they represent (e.g., recognising how many objects are in a pile or group through counting).	Kholida et al. (2020)

.

We have also included records in Table 5 where the level of education is a primary school, but the game was used on a remedial basis in connection with numbers 1 to 10. In the records related to the basic colours and shapes topic, exclusively UNO-type games were used (Match It, U-Kids). In the other topic (number recognition and counting from 1 to 10), the original UNO^® card game was used in most cases, except one (U-Kids). The U-Kids game, developed by Kholida et al. (2020), is suitable to help children understand and practise the relationship between numbers and the quantities that they represent during game-based learning activities.

Most of the records in the sample are related to teaching various chapters of primary school mathematics (see

Table 6. Mathematical topics in UNO^® or UNO-type card games for primary school level.

Topic	Description	References
Number Recognition and Counting from 1 to 10	Recognising numbers, counting step-by-step from 1 to 10, maintaining the correct order, understanding number symbols, single-digit numbers.	Baturo et al. (2004); Grünke et al. (2025); Sulisawati and Murtinasari (2018); Syafitri (2023); Utami and Leonard (2023)
Counting on the Number Line	Counting from a given number in ascending or descending order.	Kurniati et al. (2025); Woodruff (2009)
Integer Operations	Addition, subtraction, multiplication, division, two-digit, or multi-digit numbers. Combining basic operations. Solving text-based tasks using basic operations.	Ahsan et al. (2024); Aprilia and Nugraheni (2025); Baturo et al. (2004); Campbell (1989); Chong et al. (2022); Fitri et al. (2020); Jumaroh et al. (2022); Kurniati et al. (2025); McBride and Lamb (1991); Murtiana and Yulianto (2025); Rahmatin and Khabibah (2016); Srintin et al. (2019); Syafitri (2023); Utami and Leonard (2023); Woodruff (2009)
Fractions	Understanding of the concept of fractions; basic concepts: numerator, denominator, equivalent fractions, and same denominator. Comparing the magnitude of different fractions.	Suciati (2020); Utami and Leonard (2023)
Measuring and Units	Measurement of length, weight, and area; units of length, weight, and area.	Harahap et al. (2022); Harlin and Arini (2023); Ulfah et al. (2016); Utami and Leonard (2023)
2D and 3D Shapes	Quadrilaterals, their properties and types. Recognising geometric shapes, measuring area, and basic knowledge about simple 3D shapes.	Harahap et al. (2022); Sulisawati and Murtinasari (2018); Utami and Leonard (2023)

).

We identified six main topics for which UNO^® or UNO-type games can be used as teaching tools in classroom practise at the primary school level. At the preschool and primary school levels, there is an overlap in mathematical topics because knowledge of numbers and counting, progressing step by step up to 10, is also a relevant part of the first-year curriculum in primary school. For this reason, the topic number recognition and counting from 1 to 10 has also been included in the first row of Table 6, but we have added additional content to it. There are numerous overlaps, as some UNO-type educational games belong to more than one topic. The number of records per identified topic is illustrated by a bar chart in Figure 6.

There are 15 records in the integer operations topic. This is the most significant subset. Topics related to number recognition, counting, and integer operations together cover 70.97% of records belonging to the primary school level. The use of the original UNO^® card game primarily relates to these topics, as shown in

Table 7. Number of UNO^® and UNO-type card games per identified topic at primary school level.

Topic	Original UNO® Game	UNO-Type Game
Number Recognition and Counting from 1 to 10	3	2
Counting on the Number Line	2	0
Integer Operations	8	7
Fractions	0	2
Measuring and Units	0	4
2D and 3D Shapes	0	3

. With one exception, papers published in the early period also belong to these topics (see Table 3 and Table 4).

We found a total of thirteen records related to the secondary school curriculum, but two of them are not specified. We have classified eleven records into six different topics; see

Table 8. Mathematical topics in UNO-type card games for secondary school level.

Topic	Description	References
Functions	The most important characteristics of quadratic functions: representation, the effect of coefficients, domain and range sets, symmetry axis, extreme values, and roots.	Anggraini (2018); Leonard and Tracy (1993)
Equations and Equation Systems	Algebraic equations, systems of linear equations.	Najiah and Panggabean (2021); Robiana and Handoko (2020)
2D and 3D Shapes	Main types of 3D shapes (cube, sphere, cone, pyramid, rectangular prism, and cylinder). Geometry, volume and surface area of 3D shapes.	Ficky (2021); Lutfi et al. (2024); Sulisawati and Murtinasari (2018)
Trigonometry	The trigonometric identities and expressions are related to the fundamental, reciprocal, quotient, and Pythagorean identities, and simplify to $sin\theta$, $cos\theta$, or 1.	Fuentes (2024)
Probability Theory	Basic probability theory, simple tasks with UNO® cards. For example, the probability of drawing a given coloured card or a given numbered card. Calculating the number of cards that can be played after a given card.	Meyrath et al. (2024); Ziliwu et al. (2024)
Financial Mathematics	The aim is to understand basic financial concepts, such as profit and loss, taxes, simple interest, discount, gross, and net.	Anita et al. (2022)

. We found an overlap between primary school topics and secondary school topics only in geometry in the context of UNO-type games, related to the topic of 2D and 3D shapes. In secondary education, the authors mainly use their developed UNO-type games (76.92%). The exception is probability theory. For the probability topic, the original UNO^® was used in both records. Probability exercises leverage the known quantities of cards in the UNO^® deck to pose questions about the likelihood of certain events occurring during gameplay. For example, Meyrath et al. (2024) use a 100-card UNO^® deck with modifications, which makes it easy to calculate probabilities as percentages.

Game-based education has gained ground relatively late at the university level (Szilágyi et al., 2025), as reflected in the number of UNO-type games used at this level compared to other educational levels, as shown in Figure 5 and

Table 9. Mathematical topics in UNO^® and UNO-type card games for university level.

Topic	Description	References
Algebra	Using UNO® to teach binary relations to illustrate the properties of reflexive, symmetric, and transitive relations. Applying UNO® to teach and explore algebraic relations between game statistics, such as the number of rounds, the number of cards played, drawn, and remaining in the hand of the losing player, and the number of cards in the discard pile.	Meyrath et al. (2024)
Calculus	Limits of sequences, convergence, null sequence. Commonly occurring sequences and limits. Calculating limits, basic operations by convergent sequences. Practising to get sufficient routines to determine the limit of a given sequence by performing the necessary calculations in mind.	Szilágyi and Körei (2021, 2022); Szilágyi et al. (2023a, 2023b)
Game Theory	Employing UNO® to teach strategic decision-making, risk assessment, and adapting to hidden information.	Meyrath et al. (2024)

. At the same time, it should be noted that research into the mathematics, complexity, and various modelling tasks of UNO^® represents the application of the original UNO^® game in a university environment. However, in these studies, the UNO^® game is not a didactic tool to support learning. However, Meyrath et al. (2024) suggested using UNO^® as a didactic tool for learning game theory. The authors discuss the use of UNO^® in other mathematical topics, such as binary and algebraic relations.

In the field of calculus, which is of the most interest to us, we created a UNO-type game five years ago to practise the determination of sequence limits, named LimStorm. The concept, the rules, and the structure of the LimStorm game were introduced in (Szilágyi & Körei, 2021). During the pandemic, we were only able to use the game in a limited form because it had to be adapted to the requirements of online education (Szilágyi & Körei, 2022). Classroom testing of the non-digital LimStorm game with students took place in a classroom environment after the pandemic (Szilágyi et al., 2023a). For the LimStorm game, we edited the cards using a card generator application (Szilágyi et al., 2023b).

5. Discussion and Answer for Research Questions

Some documented examples of the use of UNO^® cards in mathematics education date back more than 30 years, as shown in the articles of Campbell (1989), McBride and Lamb (1991), and Leonard and Tracy (1993), but their widespread use mainly took place later, in the 2000s, followed by explosive and global growth from 2020 onwards.

5.1. Answer to Research Question RQ1

The original UNO^® deck can be used in various mathematical topics at different educational levels, as summarised in

Table 10. Mathematical topics suitable for using the original UNO^® deck at different educational levels.

Educational Level	Mathematical Topics
Preschool	Number recognition and counting from 1 to 10
Primary School	Number recognition, counting, basic integer operations, and foundational numeracy concepts
Secondary School	Basic set relations, elementary algebraic concepts, and probability exercises
University	Relations, algebra, probability theory, and game theory

. Based on records on the use of UNO^® cards at the kindergarten level, we concluded that the UNO^® deck is an effective educational tool to recognise numbers and develop basic counting skills. The UNO^® game can be used not only in non-digital form but also in a digital version for this purpose. On the next level, at primary school education, the deck is a didactic tool for teaching number recognition, counting, and basic arithmetic operations, helping students understand concepts such as sequencing and simple calculations. In secondary education, the original UNO^® card deck is mainly used in probability, where the probability of drawing certain cards is analysed, and a basic understanding of the concept of probability is developed. The UNO^® deck is well suited to introduce some basic algebraic concepts (such as binary relations) in a classroom environment. Still, modified card sets are needed for more advanced topics. In university education, the original UNO^® card deck supports the introductory teaching of set theory, relations, and probability by illustrating basic concepts through practical activities and tasks. The original UNO^® card game is a versatile tool for all levels of education (Table 10). The deck is most commonly used for basic topics involving integers, counting, and probability. Sometimes, using the UNO^® deck(s) is combined with other teaching activities.

5.2. Answer to Research Question RQ2

UNO-type games have been developed to support various mathematical topics across various educational levels (

Table 11. Mathematical topics supported by UNO-type games at different educational levels.

Educational Level	Mathematical Topics
Preschool	Colours, shapes, number recognition, counting from 1 to 10
Primary School	Number recognition, counting, basic arithmetic operations, fractions, measurements, 2D and 3D shapes
Secondary School	Functions, equations and systems of equations, trigonometry, probability theory, financial mathematics
University	Set theory, algebra, calculus (limits of sequences), game theory

).

At the preschool level, these games focus on basic concepts such as colours, shapes, number recognition, and counting from 1 to 10. For primary school students, UNO-type games are used to teach number recognition, counting, integer operations (addition, subtraction, multiplication, and division), fractions, measurements, and basic geometry involving 2D and 3D shapes. In secondary education, these games cover more advanced topics such as functions, equations, systems of equations, trigonometry, probability theory, and financial mathematics. At the university level, UNO-type games are applied in teaching set relations, algebra, calculus (e.g., sequence limits), and game theory. These games are versatile tools that facilitate understanding of both foundational and advanced mathematical concepts across educational stages.

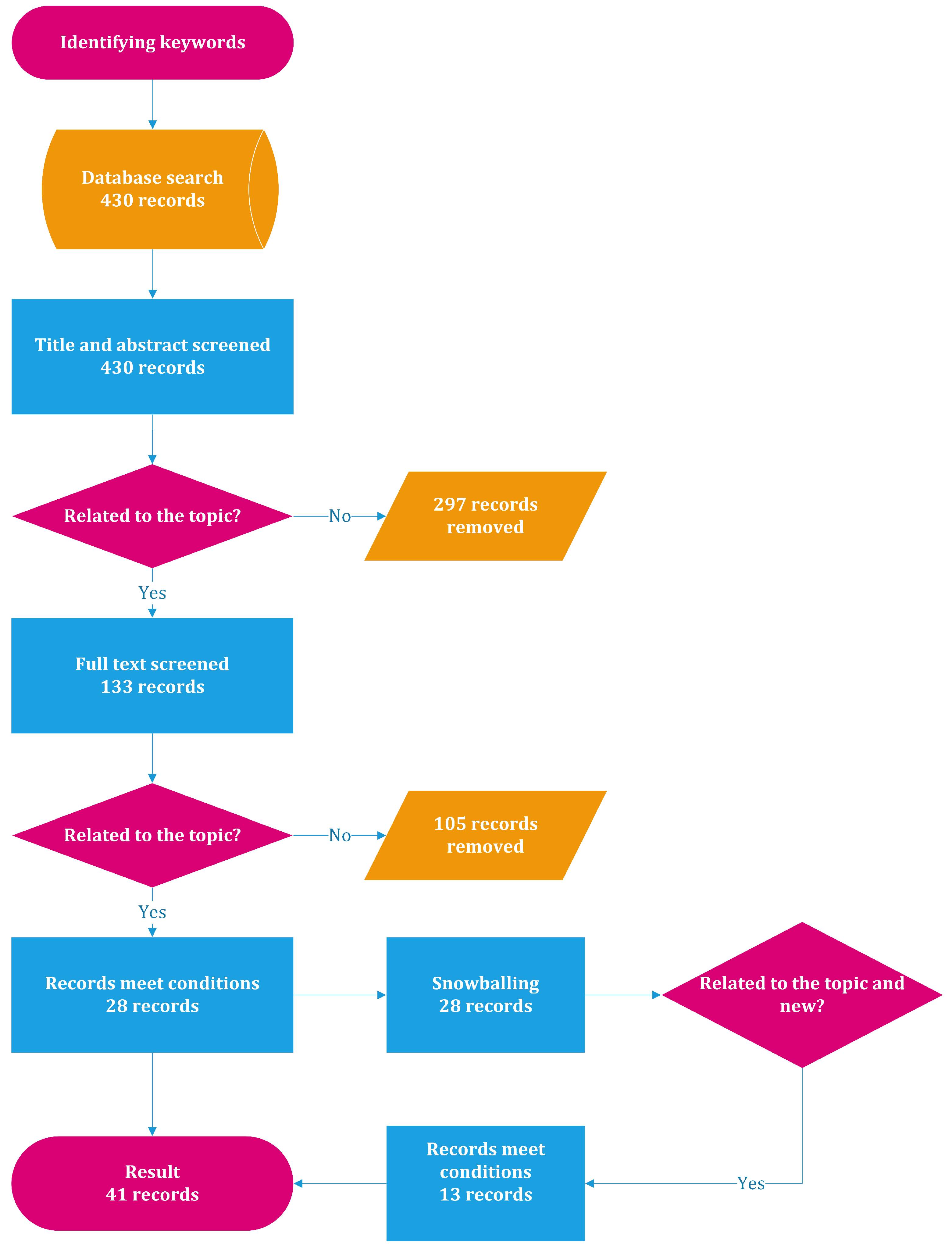
5.3. Answer to Research Question RQ3

As we have seen, UNO^® and UNO-type games are becoming increasingly integrated into mathematics education. We also sought to answer the question of what role these games play in mathematics education. First, we review the information found in the records regarding the educational role of the game used.

The article of Campbell (1989) describes a collection of card games designed to help primary students practise basic maths facts. This early paper suggests that card games used in maths education can help students practise and reinforce basic maths facts in a fun and interactive way. The article emphasises that the games can involve elementary students of varying ability levels. The rules can be modified to align with the curriculum, and teachers can change the size and composition of the groups. The article concludes that card games with regular mathematics instruction can help teach and reinforce basic skills. Two years later, McBride and Lamb (1991) discusses the adaptation of existing popular games, such as UNO^®, for mathematical practise at the primary level. The authors suggested modifying the rules of UNO^® so that players throw out cards by forming equations or combinations instead of matching numbers or colours. It was mentioned that, in order to practise combinations involving two-digit numbers, adaptations of UNO^® allow two or more numbers to be used in sequence to create a larger number or operation. The article highlights that teacher-made maths games can be an effective way to practise specific maths skills. Fourteen articles cited the work of McBride and Lamb (1991) according to Google Scholar, but only one is relevant to the research topic: Leonard and Tracy (1993) collected and organised games to support mathematics learning for middle school students. Their paper includes a detailed table of maths-related games that meet the National Council of Teachers of Mathematics (NCTM) standards. According to the table, UNO^® meets the standards for problem-solving, mathematics as communication, mathematics as reasoning, and the topics of patterns and functions. The table suggests that UNO^® was a potential tool for teachers to reinforce maths skills in accordance with learning standards in the 1990s.

Baturo et al. (2004) wrote about mathematics education for indigenous children in Australia and examined how games familiar to them could be incorporated into teaching. The authors observed that many indigenous children perform poorly on maths tests and recommend linking maths to children’s home and community experiences. The article presents several card games played by indigenous children. One of these is UNO^®. The original UNO^® cards were used during the game, but they were not played according to the original rules; instead, the deck was used as a teaching tool with new rules. According to the authors, UNO^® enables players to develop number recognition, counting, and strategic thinking; however, no test data are included in the article. The article highlights that incorporating such games can help children understand mathematical concepts and provide teachers with opportunities to assess children’s knowledge and improve teaching effectiveness. Woodruff (2009) conducted six UNO^®-based intervention sessions with second-grade students experiencing difficulties in mathematics, using both control and treatment groups. However, the results showed no statistically significant differences between the groups regarding addition and subtraction accuracy, cognitive strategy use, spatial ability, or place value knowledge. According to Jumaroh et al. (2022), the UNO^® game media plays a multifaceted role in education, primarily focused on enhancing the learning experience for students. Its introduction aims to improve students’ understanding of integer operations by making the learning process more enjoyable and engaging. By reducing boredom and promoting active participation, the UNO^® game medium positively impacts student learning outcomes and encourages them to become more independent learners. This practical and accessible tool also helps sharpen students’ counting skills, making it a valuable asset in mathematics education.

Numbered Heads Together (NHT) is an alternative questioning strategy which can be used to improve student performance in general education classrooms. During the NHT teaching method, students work in groups to solve a problem within a given time frame (Revilla-Cuesta et al., 2020). The study of Fitri et al. (2020) examines the use of UNO^® cards in conjunction with the NHT cooperative learning model to improve students’ maths performance. UNO^® cards, with their numerical values, help students practise arithmetic operations. The authors used standard UNO^® decks for the maths problems, with the numbers on the cards serving as a basis for practising arithmetic operations. Only numbered cards were used during the experiment; action cards were not used. Research indicates that using UNO^® cards in the classroom increases student motivation and improves maths learning outcomes. In this context, the use of UNO^® cards within the NHT cooperative learning model contributes to active student participation and collaboration.

Special education programmes are common in primary schools to support students with learning disabilities or other needs. Using a quantitative approach, the study of Syafitri (2023) found that the UNO^® card game positively affected the ability of children with mild intellectual disabilities to recognise number symbols 1-10, effectively increasing this ability through engaging gameplay. UNO^® is not just a game but a tool that can serve as a practical, versatile alternative or complementary learning method to improve students’ learning abilities. The research study of Grünke et al. (2025) assesses the effectiveness of the pegword method in enhancing multiplication skills among students with maths difficulties. The pegword method is a mnemonic strategy that pairs numbers with rhyming words, creating both visual and verbal associations to aid memory. This method is designed for sixth-grade students who experience persistent learning challenges in mathematics. Before the intervention, the students played the UNO^® card game for 30 min during the baseline phase. Our interpretation is that this activity was included to allow students to start with a familiar task, potentially easing them into the session before tackling multiplication problems. Moreover, because UNO^® involves working with numbers, it may have provided a helpful warm-up for students struggling with maths, activating their number recognition and numerical skills before the multiplication test.

The original UNO^® game also offers a promising avenue in secondary and university mathematics education, in areas such as basic probability theory, algebra, and game theory, where students often face comprehension challenges. Its appeal lies in the ability to capture student interest and foster active participation, transforming learning from a passive reception of facts into an engaging exploration of mathematical concepts. Research indicates that integrating UNO^® cards as a learning medium can significantly increase mathematical thinking skills, paving the way for a more intuitive grasp of probability (Meyrath et al., 2024; Ziliwu et al., 2024).

Wulandari and Ambara (2021) used the digital version of the UNO^® card game to develop number recognition and counting skills in preschoolers during the pandemic. According to the study, UNO^® cards can provide a solution to the challenges of online teaching because they are interactive and engaging, which helps to maintain children’s attention. The authors’ measurements suggest that interactive UNO^® cards can support the development of children’s cognitive abilities beyond number recognition and counting.

The U-Kids card game is a graphic-based educational tool designed to stimulate logical–mathematical intelligence in children aged 5–6 years, created by Kholida et al. (2020). The game incorporates colours, shapes, and numbers. It functions as a type of active learning game that encourages children to use strategic thinking. The game is designed to stimulate a child’s awareness of numbers, with an understanding of the concepts of less and more, arranging things in serial, categorical, and hierarchical ways, analysing objects quickly, understanding numeric symbols, and counting. Instead of numbers, geometric shapes (circle, triangle, square, and rectangle) are depicted on the base cards to represent different quantities, as shown in Figure 7.

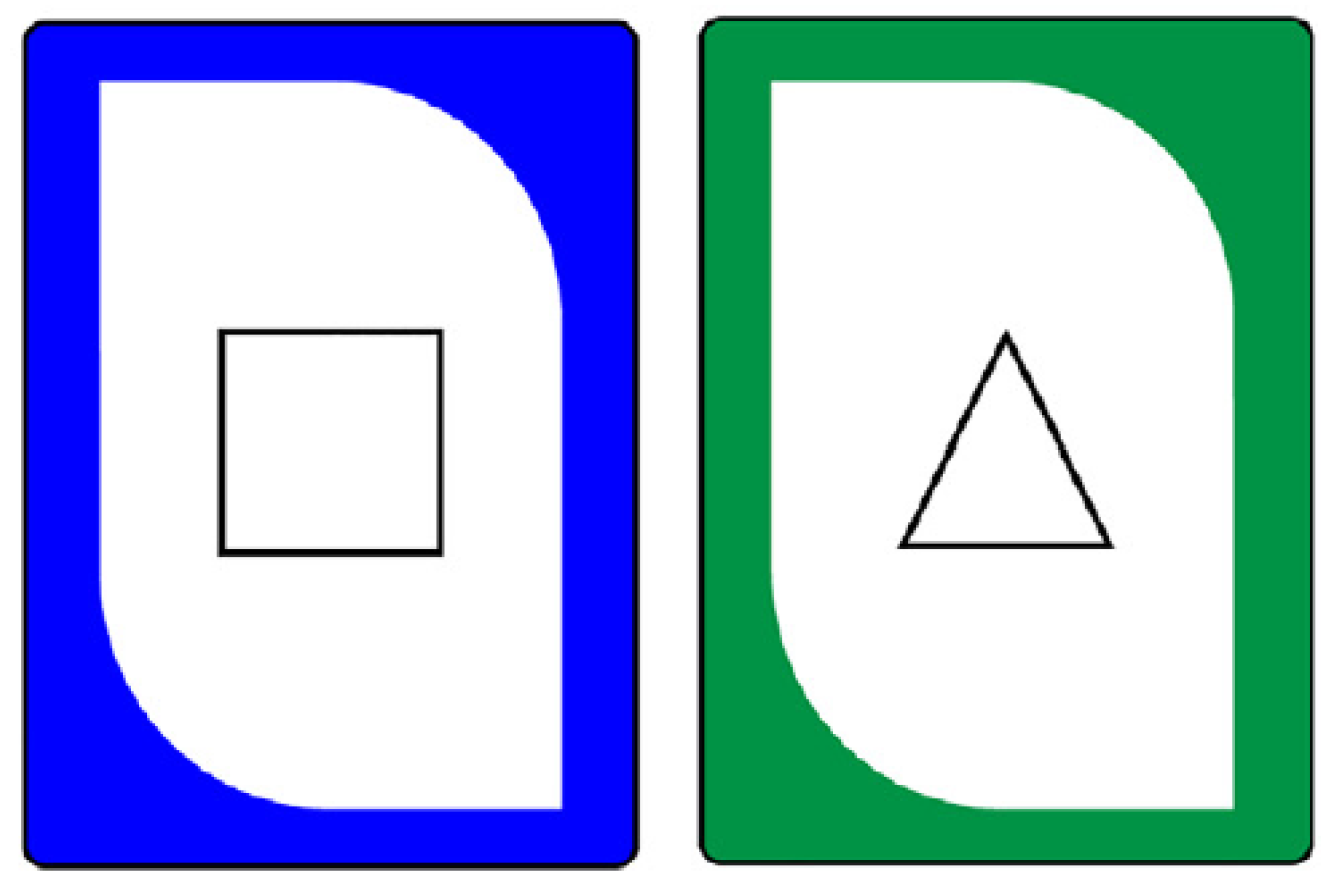
The Match It game is a shape and colour matching game at the preschool level (Ramani & Scalise, 2020). It allowed researchers to tease apart the improvements in children’s numerical skills that could be attributed to practice with the numerical game, as opposed to other maths-related experiences. Additionally, because the game involved labelling shapes, it was hypothesised that playing it would improve children’s shape knowledge. According to Scalise et al. (2022), children who played the Match It matching game had significantly higher post-test scores on both shape naming and shape matching measures. In Figure 8, two cards can be seen from the Match It deck.

The article by Rahmatin and Khabibah (2016) discusses the development of the UNO-type card game, called U-Math (UNO Mathematics), as a learning medium for integer operations at the primary school level. The card game was designed to provide students with a more engaging and enjoyable way to practise integer operations, addressing the students’ lack of ability in this area. The study involves testing the card game on 31 students and evaluating its effectiveness through observation, tests, and questionnaires. Research results indicated that the U-Math card game is a good learning medium that meets the goals. The game developed by Chong et al. (2022) (Intego, a combination of UNO^® and integers) is a tool to teach and learn integer operations. Their study suggests that using this non-digital card game can effectively improve students’ performance in integer operations and promote concrete mathematics instruction, critical thinking, and problem-solving skills, aligning with student-centred learning approaches. The Intego game allows students to think critically and discover how to treat the sign roles in integer operations. According to Murtiana and Yulianto (2025), the NumeriUNO game is a valuable tool to improve mathematics learning among primary school students. By integrating game-based elements, such as the familiar concept of UNO^® cards, NumeriUNO transforms traditional learning into an engaging and interactive experience. This approach not only captures students’ interest but also fosters a deeper understanding of the mathematical concept of multiplication. Through hands-on participation, teamwork, and healthy competition, NumeriUNO promotes a constructivist learning environment where students actively build their knowledge. Its effectiveness has been demonstrated through improved learning outcomes, increased student motivation, and positive feedback from both educators and learners, highlighting its potential to make mathematics more accessible and enjoyable for young students. The UN-MATH card game, developed by Aprilia and Nugraheni (2025), was designed to improve problem-solving skills, specifically in addition and subtraction, for elementary school students. This game-based learning approach promotes active participation and engagement, making the learning process more enjoyable and motivating. By focusing on mathematical story problems, the UN-MATH card game aids in the development of conceptual understanding.

The findings of Suciati and Wahyuni (2018) highlighted the challenges students face with fractions. They found that students had a concept error of 80.70%, a principle error of 13.16%, and a calculation error of 6.15% when adding fractions. These errors suggested that students struggle with understanding and applying fraction concepts and operations. To address the problem, one of the authors developed a UNO-type game. The article by Suciati (2020) details the UNO Matematika game which is an engaging method to teach fractions. The game aims to strengthen students’ understanding of fraction concepts.

Ulfah et al. (2016) described the development of another UNO-type educational game. The primary goal of this new game was to help fourth-grade students understand and practise concepts related to units of length. The authors provided data supporting the effectiveness and feasibility of the developed UNO-type learning game. Expert evaluations and student evaluations indicated strong effectiveness, through ratings of student engagement and a high level of interest. Similarly, Harlin and Arini (2023) concluded that their UNO-type card game is an appropriate and effective tool for teaching weight units to fourth-grade students because it offers an engaging and interactive approach that improves learning outcomes.

The U-Math game has a multifaceted role in elementary mathematics (Utami & Leonard, 2023). It fosters motivation, transforming mathematics into an enjoyable subject rather than an intimidating one. Through gameplay, students better understand mathematical principles, with the game serving as an engaging evaluation tool. U-Math also develops critical cognitive skills such as memory and problem-solving, all while contributing to a positive and stress-free learning environment. Its versatility extends to various mathematical topics, including integer arithmetic, measurement, geometry, fractions, and spatial reasoning, making it a comprehensive educational tool.

The thesis of Anggraini (2018) dealt with the development process and methodology of the U-Math (quadratic functions) game as an engaging and effective teaching tool for learning quadratic functions. The study highlighted the game’s effect on fostering participation, enhancing understanding, and positively influencing education. Students’ responses showed that the most important factors were learning motivation, positive character, language use, and design. The study by Mayangsari and Mahardhika (2019) explores using an UNO-type card game with mathematical questions to motivate secondary school students in learning maths. The game is an interactive tool, with the teacher supervising and facilitating the activity to encourage active problem-solving and engagement. Qualitative feedback indicates that students found this approach motivating and enjoyable, offering a fresh learning experience.

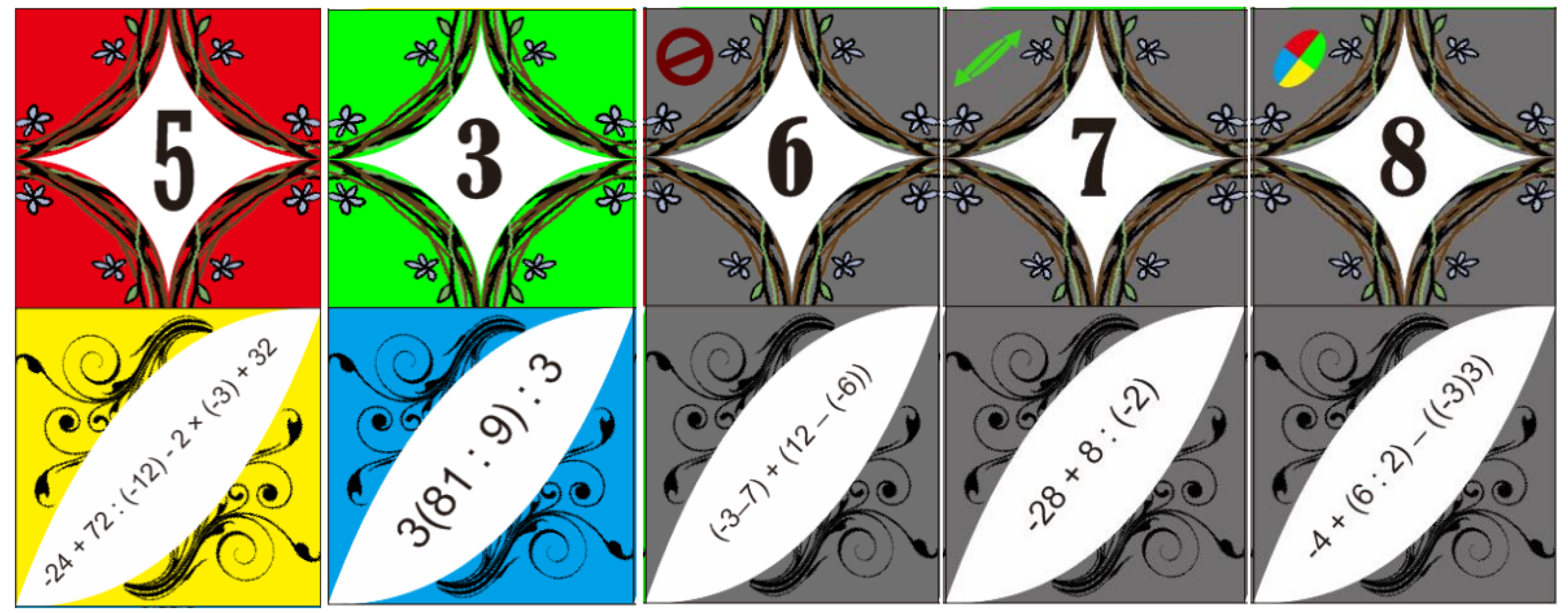
The great advantage of UNO-type games is that almost everyone knows the rules, so minimal time is needed to explain how to play. The research paper of Srintin et al. (2019) details the development and evaluation of the Umino game, a card game designed to teach integer operations (Figure 9). Umino aims to provide an engaging and effective learning experience by leveraging the familiar mechanics of popular card games. A key aspect of Umino’s design is its deliberate connection to UNO^®. The gameplay structure of Umino mirrors that of UNO^®, with players taking turns matching cards based on specific characteristics. This familiar structure allows students to quickly grasp the rules and focus on the mathematical content.

Robiana and Handoko (2020) developed the UnoMath card media designed to enhance mathematical communication skills and self-regulated learning. The authors employed a quantitative experimental approach, using a pre- and post-test design with a control group. Data collection involved tests to measure mathematical communication skills and questionnaires to assess self-regulated learning. The study found that applying UnoMath led to a statistically significant improvement in mathematical communication skills. Furthermore, the use of UnoMath also significantly enhanced self-regulated learning.

UNO^® Spin is a variation of the classic UNO^® card game that includes a spinning wheel. The wheel introduces a random element to the game, altering the rules or affecting players in various ways. The purpose of UNO^® Spin is to make the game more exciting and unpredictable, but the core gameplay remains similar to that of the original UNO^® (Peña Pérez Negrón et al., 2023). The game typically includes action cards that force players to spin the wheel. The wheel might make players discard cards, draw more cards, skip their turn, or even swap hands with another player. The UNO^® Spin game also provides a directed learning experience, offering students the opportunity to discuss with each other (Ridwan et al., 2024). Najiah and Panggabean (2021) created the UNO Spin Maths game because they identified a need for more engaging and varied mathematics learning tools in the topic of algebra. While maintaining core UNO^® Spin gameplay elements, such as matching cards and using a spinning wheel to introduce dynamic changes, the authors differentiated their version by integrating algebraic equations on the cards. This key difference transforms the game from purely recreational to an educational tool specifically designed for junior high school students. By blending entertainment with learning, the UNO Spin Maths game offers several advantages, including increased student engagement, active participation, improved understanding of algebraic concepts, collaborative learning opportunities, and a multi-sensory learning experience.

The UNO-type game by Sulisawati and Murtinasari (2018), the GEO cards, is a learning medium for the topic of quadrilateral flat shapes. It is intended to make learning more engaging, practical, and effective. The validation process was detailed in the article, which showed the establishment of the credibility and reliability of the GEO cards as a valuable educational resource. The educational game U-Math, developed by Ficky (2021), aims to reinforce mathematical concepts related to the volume and surface area of three-dimensional shapes. U-Math helps to consolidate understanding of geometric formulas and concepts while developing problem-solving skills and strategic thinking. Teachers have found the game to be extremely effective, and students have found it very practical. Another UNO-type game with a geometry topic is the Uno Math game. It is a practical and effective tool for mathematics education, particularly for understanding the concept of the area of flat shapes (Harahap et al., 2022). It aims to improve student engagement, offering a more interactive and enjoyable way to learn mathematics. By implementing the Uno Maths game, educators can overcome negative perceptions of mathematics, fostering a more active and interesting learning environment. Ultimately, the game functions as a medium to facilitate deeper understanding and improve student performance in mathematics. Similarly, the role of the UNO Matematika game in education is to improve the understanding of mathematical concepts among junior high school students on the topic of financial mathematics. This learning medium was designed to make learning more engaging and effective (Anita et al., 2022). The study of Lutfi et al. (2024) identified several key benefits of Uno Math. It increases student motivation, makes learning more enjoyable, aids in understanding mathematical formulas, and generally has a positive impact on the learning process. The use of Uno Math helps to sharpen students’ learning while reducing boredom and attracting their attention. The research indicates that Uno Math can be a valuable tool for teachers to facilitate student learning and generate motivation in mathematics. The results also suggest that female students tend to exhibit higher levels of math learning motivation when using Uno Math compared to male students.

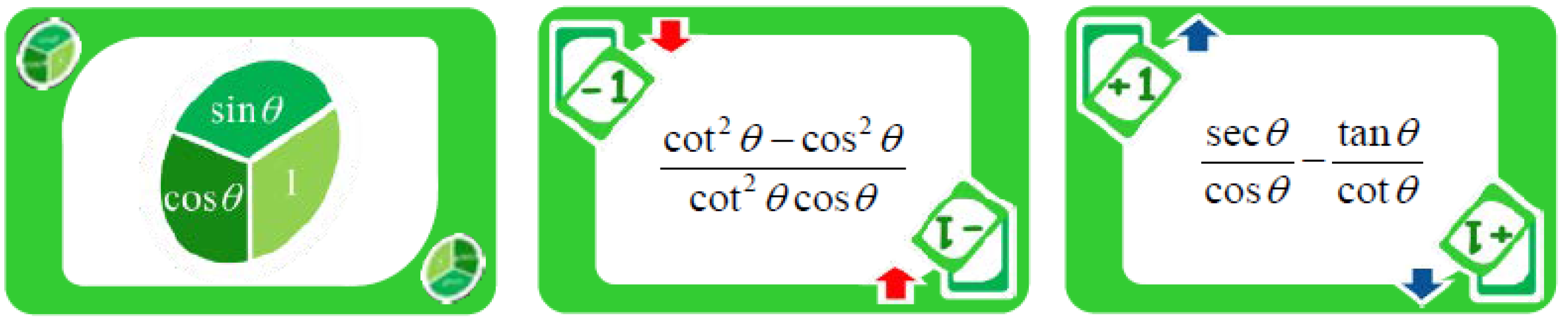
The TrigOno card game is a valuable tool in education by fostering mastery learning, particularly in trigonometry (Fuentes, 2024). It addresses the common issue of limited practice opportunities that hinder students’ progress in mathematics. In Figure 10, three cards can be seen from the TrigOno deck.

The game’s design promotes engagement, motivation, and repeated practise of essential skills, leading to better retention and conceptual understanding. As a non-digital, game-based learning intervention, TrigOno offers a remedial approach that enhances social interaction and encourages students to develop problem-solving strategies. By improving computational reasoning, mathematical thinking, and self-efficacy, TrigOno aims to minimise negative perceptions of mathematics and create a more enjoyable and effective learning experience.

Kurniati et al. (2025) focused on enhancing mathematics education through contextual learning. Their study aimed to make maths more relatable and engaging for local students by developing UNO-type cards linked to a traditional Indonesian game. Instead of abstract concepts, the card game provides a practical, real-world connection to mathematical operations. The integration of a familiar cultural element into the learning process was expected to boost student motivation and facilitate better understanding, thus bridging the gap between theoretical maths and its practical application within the students’ environment. The developed UNO-type game was designed to help children practise maths operations in a familiar and enjoyable setting, showcasing the benefits of contextual learning. The study of Ahsan et al. (2024) indicates that incorporating the Smart Cards game, which is a UNO-type learning medium, into the learning process leads to increased student engagement and enthusiasm, making the maths subject more approachable. The Smart Card game helps visualise abstract mathematical concepts, making them easier to understand and remember, as students can observe the cards, hold them in their hands, and analyse their content. By offering interactive activities and immediate feedback, they allow students to actively participate in their learning and develop a deeper conceptual grasp. So, using the Smart Card game contributes to a more effective and enjoyable learning environment, improving student mathematics performance.

Genius Up! is an educational project designed to promote scientific and technological literacy among students, particularly those who are potentially entering university. It uses gamification, specifically serious video games and adapted card games, to make science learning more engaging and accessible. The project aims to expand knowledge transfer in areas such as mathematics, physics, chemistry, and biology through these engaging and interactive methods (Perales et al., 2019). The Maze Cards non-digital game was developed at the Universitat de les Illes Balears (UIB) in Spain, as part of the Genius Up! project. The Maze Cards game combines UNO^® with questions related to mathematics, physics, chemistry, and biology, reinforcing knowledge entertainingly. Maze Cards retains the basic game mechanics of UNO^®, but the theme, educational purpose, questions, and special codes differ significantly from traditional UNO^®.

LimStorm integrates learning into the gameplay by requiring players to calculate the limit of a sequence on the card before discarding it, reinforcing understanding of limits and providing immediate feedback (Szilágyi & Körei, 2021). LimStorm aims to address the challenge of keeping students engaged in mathematics by introducing a fun, interactive approach to learning, which complements traditional teaching methods in university and can be used in practical classes, consultation sessions, workshops, or even at home (Szilágyi & Körei, 2022). Through gameplay, students not only practise calculating limits but also develop logical thinking, memory, problem-solving, and teamwork skills. LimStorm seeks to improve motivation and create a more successful learning experience for higher education students. Figure 11 shows the red cards from the LimStorm deck.

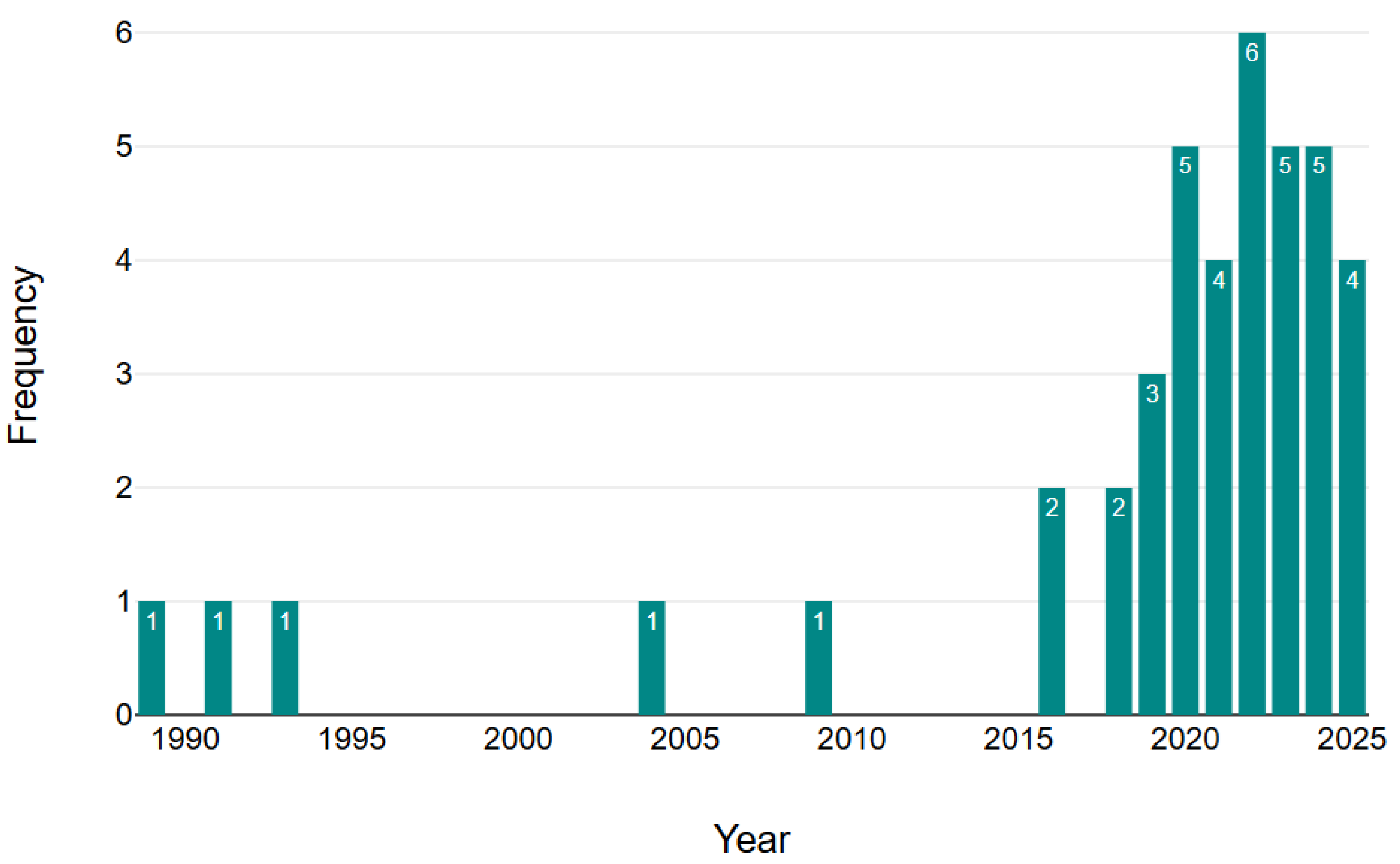
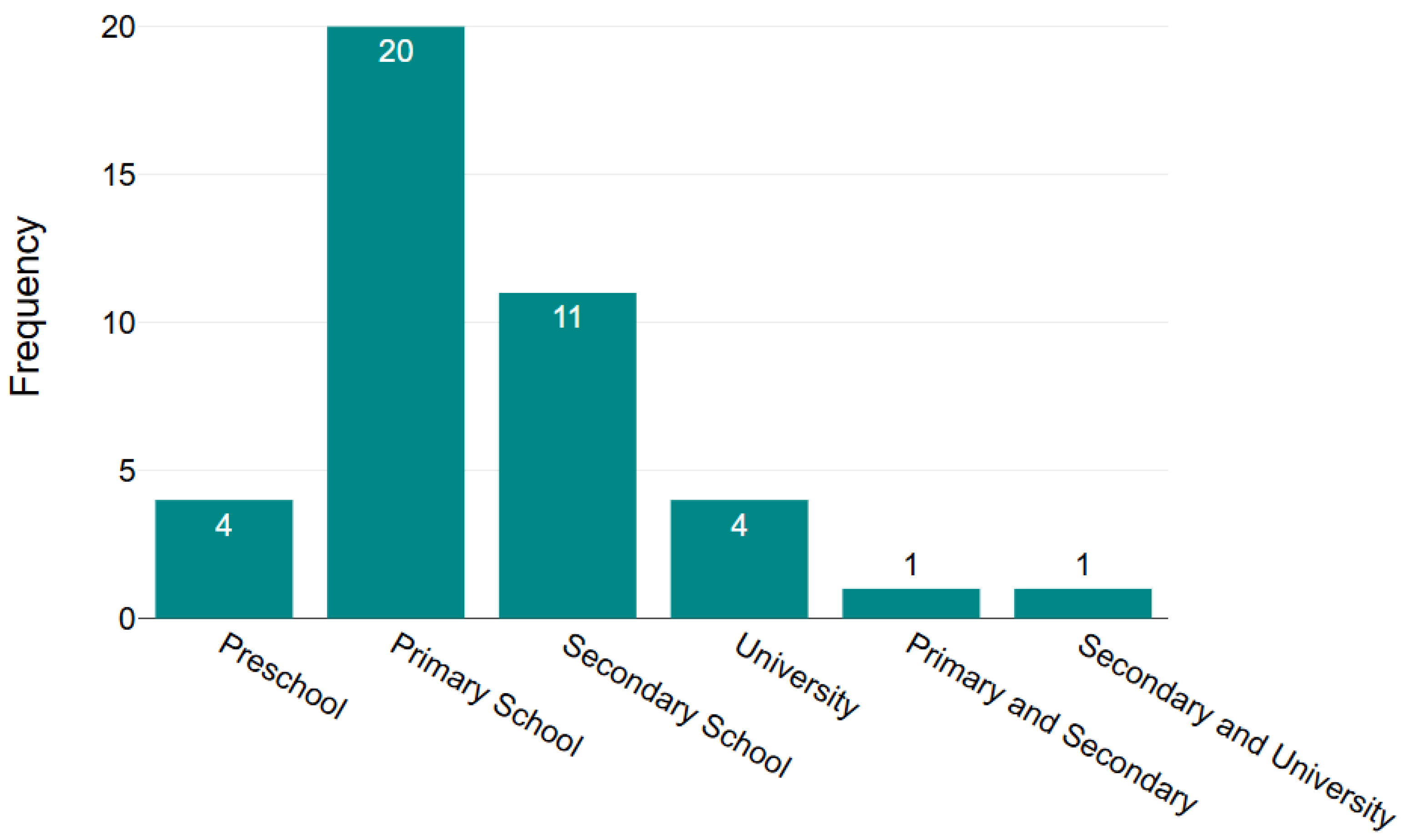
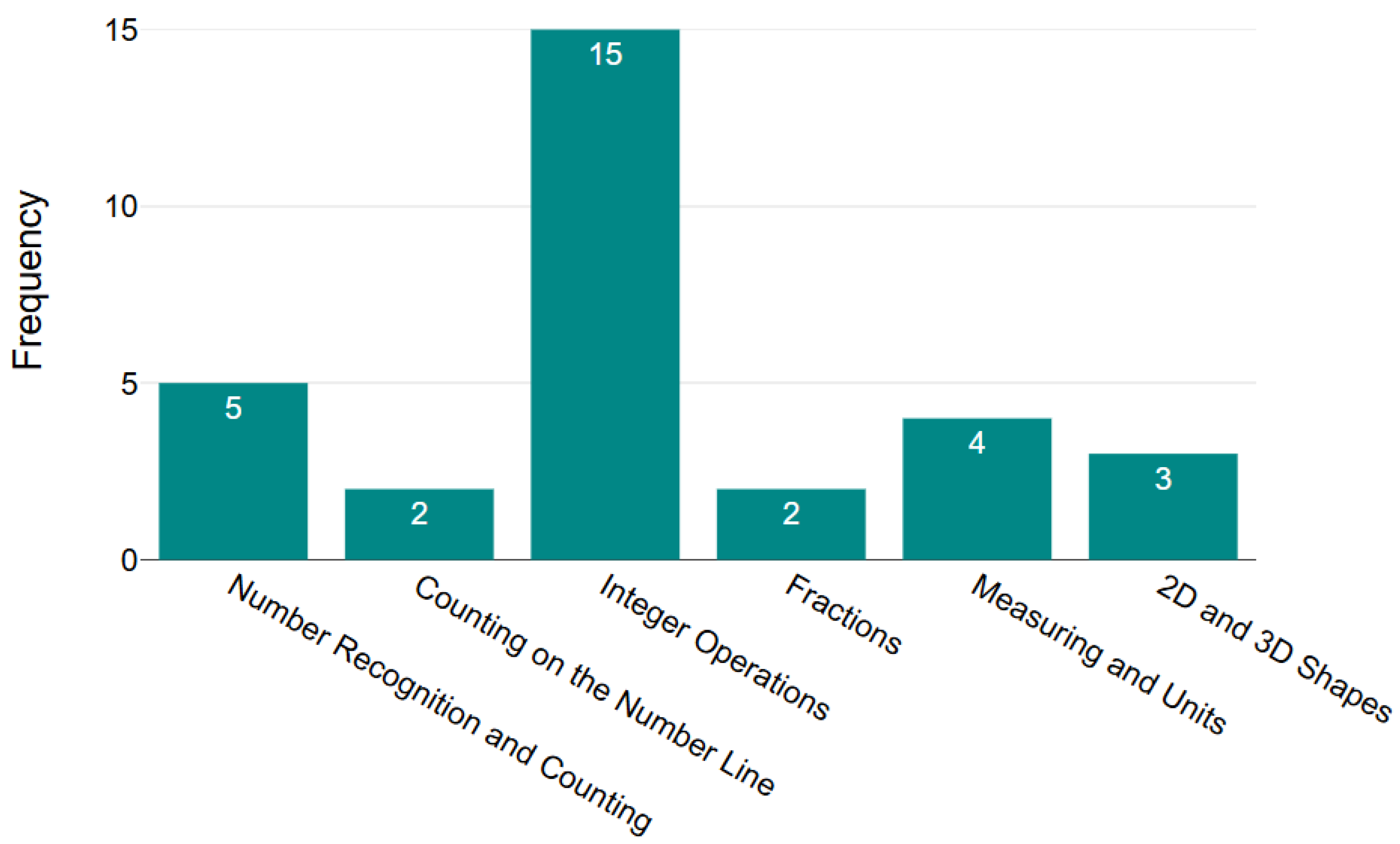
Based on the analysed 41 records, we answer research question RQ3. The primary role of UNO^® and UNO-type games in mathematics education is to make learning more attractive and effective for students. These games transform learning into engaging, fun, and interactive experiences that help students understand and reinforce mathematical concepts at various levels. They use the familiar mechanics of UNO^® cards, but with mathematical content on the cards, providing both entertainment and educational value. During gameplay, students can strengthen their understanding of concepts such as number recognition, arithmetic, algebra, geometry, fractions, and probability, while simultaneously developing critical skills such as problem solving, independent learning, collaboration, and reasoning. These games promote inquiry-based learning environments that focus on students and bridge the gap between abstract theoretical ideas and tangible applications in the real world. Their versatility allows for adaptation to diverse topics and educational contexts, including special education, community-based learning, and digital platforms. In general, UNO^® and UNO-type games serve as effective tools to foster deeper mathematical understanding, increase motivation, and improve active participation, making mathematics education more engaging and meaningful for learners.

6. Conclusions and Recommendations

The 41 records in the collection were organised into four groups according to the educational level at which the original UNO^® or the developed UNO-type card game is used. The results show that these games have been successfully integrated into mathematics education in many topics. Based on the sample and results, it can be concluded that the original UNO^® and UNO-type games can be used as a valuable educational tool at all levels of maths education. The numbers on the cards and the rules clearly define the mathematical topics for which the original card deck can be used for educational purposes. However, researchers were not satisfied with these limited possibilities. Numerous developments demonstrate that UNO-type games are well-used tools for teaching mathematics. In each case, the game mechanics were slightly modified, such as adding new cards with specific educational tasks or questions, to reinforce learning objectives. At the same time, well-defined rules and cards make the game easily adaptable to different educational areas and almost any learning level and subject matter. The cards provide the basis for variability, as information can be placed on the cards in the deck. This allows for educational activities tailored to specific learning objectives, enabling the game to be adapted to various topics, skill levels, and educational contexts. By customising the content of the cards, educators created engaging, targeted experiences that reinforce desired concepts while preserving the core mechanics of the game. The researchers suggest exploring similar game-based learning methods for other subjects and grade levels (Harlin & Arini, 2023).

Building on this foundation, the principles of variation theory can be employed to further refine and customise UNO-type games, making them even more effective as educational tools by systematically highlighting and exploring key concepts through controlled variations. In variation theory, the teacher focuses on variations in content management. From the perspective of variation theory, critical aspects of the subject matter must be varied in teaching, as these must become visible to the learner (Kullberg et al., 2024). The Variation Theory of Learning suggests that learning occurs when individuals discern differences in how they experience something. By strategically varying certain aspects of a concept while keeping others constant, educators can help learners notice and understand what is essential. This theory emphasises that students learn by experiencing different dimensions of variation, enabling them to distinguish critical features of a concept and construct a more profound understanding. The variation theory of learning can be directly applied to designing and improving UNO-type games to enhance their educational value. The foundational components are always constant. The objective of matching, the central ruleset, and basic card types need to be constant. By thoughtfully leveraging variation, games can move to tools strategically supporting educational content.

Opinions are divided on which type of game is most effective at the different school levels. For example, Russo and Roche (2024) examined primary school teachers’ preferences for digital and non-digital game modes to enhance mathematics instruction and learning. Eighty-four teachers played both digital and non-digital addition and subtraction games that were functionally identical. The majority of teachers expressed a preference for using the non-digital mode. In the same year, Debrenti (2024b) tested three digital games alongside their non-digital equivalents. The results suggest that students enjoyed completing tasks in both types of game-based learning. During the pandemic, some education continued online, leading to increased demand for digital games for educational purposes, as they are effective tools for supporting the learning process. In the sample Wulandari and Ambara (2021) used the digital version of the original UNO^® game during the pandemic, and Szilágyi and Körei (2022) integrated the LimStorm game into online education. As a future plan, Harlin and Arini (2023) considered the possibility of applying the technology in their UNO-type game. In the conclusion of the article, Murtiana and Yulianto (2025) suggests directions for future research and development of NumeriUNO media. One of the specific recommendations is to develop a digital version of the game. The authors see potential benefits in creating a digital adaptation of NumeriUNO, possibly to reach more students, provide greater accessibility and flexibility, or offer more interactive features in various learning settings. The growing trend towards creating digital versions of non-digital games can mainly be explained by technological developments, market demands, and changing user habits. The online and digital format makes educational games easily accessible from different locations and at various times. Moreover, these games offer opportunities for group learning and collaboration, even when students are physically distant from each other. There are numerous advantages to online game versions. The online system can record players’ results, progress, and even overall statistics, making it easier to track learners’ development. Online versions can be easily updated, improved, or expanded with additional content, ensuring that the game remains up-to-date and relevant. Decks with different difficulty levels can be created, allowing the game to be better tailored to individual learning abilities. Online games reduce paper and material consumption, providing an environmentally friendly solution, as the online version does not require printing or the replacement of worn or damaged physical equipment. Didactic mathematical UNO-type games, while successful and usable in their traditional non-digital format, face challenges in adapting to the rapid technological advancements and changing expectations of today’s generation. However, alongside the advantages of online games, the effectiveness of GBL should not be overlooked. Greater accessibility to online games does not necessarily mean greater effectiveness. Depending on the level of education, it is worth considering the appropriate ratio of digital and non-digital formats.

Two years ago, we started a comprehensive evaluation and redesign of the LimStorm non-digital card game to align it with contemporary pedagogical practises and technological advancements. Thanks to these efforts, the digital version of LimStorm was completed and named LIM (Szilágyi & Körei, 2025). We are currently working on developing a methodological model that creates an optimal combination using non-digital LimStorm and digital LIM game versions for learning limits of sequences to first-year engineering and IT students in the university practise.

Another interesting question is how various UNO-type games engage with mathematical representations. Some of the reviewed games appear to heavily rely on symbolic forms, such as numbers and operations, while others incorporate visual or spatial representations, such as shapes and measurement contexts. Future research could explore how different versions of UNO-type games facilitate the development or application of mathematical representations—whether concrete, pictorial, symbolic, or abstract. This type of examination may shed light on how these games function as learning tools within mathematics education. Furthermore, it could help differentiate between UNO-type games that primarily promote mathematical fluency and those that support deeper conceptual understanding.

Our review shows that UNO^® and UNO-type games are valuable didactic tools for mathematics education, capable of increasing student motivation and improving learning outcomes in line with 21st-century expectations. Digital adaptations offer further opportunities for personalised learning and immediate feedback. Future research should focus on exploring optimal ways to integrate games for different learning styles and mathematical topics. We believe that game-based learning with UNO-type games is a promising avenue for modernising mathematics education and improving students’ mathematical knowledge.

7. Limitation

We have made every effort to provide the most comprehensive overview of the relevant literature. However, certain limitations have affected the completeness of this systematic review, as not all relevant research or publications are publicly available. The keywords used for the search were provided in English, so initially only those records with an English title and/or abstract were included in our search results. However, for some records that appeared in the snowball search neither the title nor the abstract were in English. It is therefore possible that relevant works have been published in languages other than those included in our search criteria. Despite these limitations, we believe that our review provides a thorough summary of the available knowledge on the subject.