Abstract
Preschool mathematics support remains insufficient, which can limit children’s skill development and impact their long-term academic success. This study explores how collaboration between researchers and teachers can enhance these practices. It is based on the Classroom Assessment Scoring System (CLASS) model, which examines three key dimensions: concept development, language modeling, and the quality of feedback. This theoretical framework highlights the importance of pedagogical interactions in supporting early mathematical learning. A mixed-methods, longitudinal approach was adopted. Over three years, six teachers participated in five collaborative sessions per year. Systematic CLASS observations, questionnaires, interviews, and reflective journals were used to assess the evolution of teaching practices. The results reveal a significant improvement in the quality of mathematics support, particularly in concept development. However, feedback and language modeling progressed more slowly. Integrating mathematics into spontaneous situations, such as free play, remains a challenge. The discussion emphasizes the importance of continuous pedagogical support to further strengthen these practices and promote more interactive and contextualized learning experiences.
1. Introduction
The Impact of Educational Success and Mathematics
Preschool education plays an important role in the holistic development of young children, fostering their cognitive, linguistic, and social skills (Clements & Sarama, 2008, 2021; Ginsburg & Ertle, 2008). Among the fundamental learning domains, mathematics holds a pivotal place in the development of logical thinking, spatial reasoning, and knowledge structuring (Sarama & Clements, 2012).
In this regard, the longitudinal study by Watts et al. (2014) demonstrates that attending high-quality preschool environments, where children are exposed to rich and varied early mathematical experiences, promotes a positive academic trajectory with lasting effects through secondary education. Engaging and interactive learning experiences also strengthen problem-solving skills, facilitating the transition to primary school and contributing to long-term mathematical proficiency (Piasta et al., 2012). Moreover, early exposure to a diverse mathematical vocabulary is associated with more structured reasoning and an enhanced ability to manipulate abstract concepts (Wasik & Hindman, 2014).
Conversely, a lack of support in early mathematical development can have significant negative consequences. Children who experience difficulties in mathematics from an early age are at risk of developing mathematical anxiety and adopting negative attitudes toward the subject, ultimately hindering their motivation and long-term engagement (Sarama & Clements, 2012). Furthermore, the quality of mathematical support provided in preschool—particularly through adult-child interactions—has a substantial impact on later academic achievement (Ginsburg & Ertle, 2008; St-Jean et al., 2022; Vlassis & Demonty, 2019). Yet, this support often remains underdeveloped compared to other domains, such as language acquisition (Houben et al., 2022).
Several studies (Ginsburg & Ertle, 2008; Sarama & Clements, 2012; St-Jean et al., 2022; Vlassis & Demonty, 2019) indicate that the quality of mathematical learning support in early childhood is generally low. Significant gaps are observed in key areas such as concept development, language modeling, and the quality of feedback. These findings highlight the urgent need to improve educational practices in early mathematics in order to provide a strong foundation for future learning.
Research by Sarama and Clements (2012) emphasizes the importance of a rich and stimulating learning environment, where children develop mathematical thinking through play, exploration, and interactions with peers and adults. This approach aligns with the principles of the Preschool Education Program (Ministère de l’Éducation du Québec, 2023), which highlights the joy of learning, hands-on manipulation of objects, and problem-solving in concrete situations, fostering the comprehensive and harmonious development of children.
2. Theoretical Framework
The quality of learning support in early childhood education is a key determinant of children’s cognitive and language development (Pianta et al., 2008). In this regard, several empirical studies rely on tools such as the Classroom Assessment Scoring System (CLASS) to describe and measure various aspects of this support. The dimensions assessed by CLASS—concept development, language modeling, and quality of feedback—provide valuable insights into teaching practices that foster children’s engagement, deepen their understanding of mathematical concepts, and encourage their autonomy in problem-solving (Cloney et al., 2017).
Concept development refers to the teacher’s ability to stimulate thinking, reasoning, and exploration of mathematical concepts in children, helping them understand the underlying principles rather than simply memorize information (Pianta et al., 2008). Language modeling includes the teacher’s verbal interventions aimed at enriching the child’s vocabulary and encouraging them to articulate their mathematical reasoning (Justice et al., 2018). Finally, the quality of feedback refers to the teacher’s constructive responses that help the child refine their thinking and adjust their reasoning (Schachter, 2017).
2.1. The Limited Quality of Mathematical Learning Support
Research consistently highlights that mathematical learning support in preschool remains underdeveloped compared to other domains, such as language acquisition (Houben et al., 2022; St-Jean et al., 2022). Specifically, essential pedagogical dimensions—including concept development, language modeling, and feedback quality—are often underutilized in mathematics-related interactions (Vlassis & Demonty, 2019). While some progress has been made in encouraging mathematical exploration, opportunities for verbalization and feedback remain scarce. This limitation can hinder children’s early mathematical development and reduce their engagement with the subject (Ginsburg & Ertle, 2008; Sarama & Clements, 2012).
A restricted focus on concept development can shape teaching practices in ways that prioritize routine memorization exercises over in-depth exploration (Vlassis & Demonty, 2019). In such contexts, the ability to generalize mathematical concepts across different situations may be limited (Sarama & Clements, 2012), and open-ended questioning—critical for eliciting children’s explanations of their reasoning—tends to be infrequent (Wasik & Hindman, 2014). As a result, children may develop a surface-level understanding of mathematical concepts, making it harder for them to transfer their learning to new contexts (Watts et al., 2014).
A lack of language modeling in mathematics can further reduce the use of mathematical vocabulary in the classroom. Teachers sometimes introduce limited domain-specific terminology (e.g., greater than, groups together, subtract) (Ginsburg & Ertle, 2008), which can restrict mathematical discussions and minimize children’s opportunities to verbalize their reasoning (Justice et al., 2018). Additionally, oral interactions are generally more frequent during literacy activities than during mathematics instruction (Schachter, 2017). A weaker exposure to mathematical language may thus make it more challenging for some children to articulate their ideas, ultimately affecting both their comprehension and engagement with the subject (Hamre, 2014).
Finally, limited feedback often results in binary validation (correct/incorrect), without necessarily prompting deeper reflection (Ginsburg et al., 2008). This type of feedback, which lacks nuance, may undermine children’s persistence when faced with mathematical challenges (St-Jean et al., 2022). Furthermore, teachers may not always encourage children to explain the strategies they used, relying instead on generic comments (e.g., “Good job!”) rather than prompts that foster deeper reasoning (e.g., “Explain how you arrived at that answer.”). This approach can restrict the development of children’s problem-solving skills (Watts et al., 2014).
2.2. High-Quality Teaching Practices in Mathematical Support
Certain pedagogical practices foster optimal mathematical learning support in preschool by stimulating children’s thinking, engagement, and comprehension.
First, concept development relies on encouraging reflection and generalizations. Asking open-ended questions such as “Why do you think this works this way?” (Sarama & Clements, 2012) helps children structure their reasoning. Relating mathematical concepts to real-life situations also enhances understanding. For example, “You have four apple slices, you give me two, how many do you have left?” (Vlassis & Demonty, 2019). Additionally, hands-on exploration and manipulating concrete objects strengthen concept construction and problem-solving skills by allowing children to engage in active experimentation (Watts et al., 2014).
Second, high-quality feedback plays a critical role in developing mathematical skills. Providing detailed and constructive responses, such as “Look closely at this part of the problem—do you see another way to solve it?” (Ginsburg et al., 2008), helps children to refine their reasoning. Rather than limiting feedback to binary validation (correct/incorrect), it is more beneficial to emphasize problem-solving strategies: “You’re close to the answer, try again.” (St-Jean et al., 2022). Encouraging children to analyze their mistakes rather than immediately providing the correct answer fosters autonomy in problem-solving (Watts et al., 2014).
Finally, integrating mathematical language into daily interactions is an essential practice. Teachers can enrich children’s mathematical vocabulary by using and encouraging precise terms such as add, compare, and subtract (Justice et al., 2018). Reformulating children’s responses helps them to clarify their thinking, for example, “Yes, you grouped the shapes together. What do we call this group?” (Ginsburg & Ertle, 2008). Extending these discussions through conversations, symbolic play, and real-world activities promotes a deeper conceptual understanding (Schachter, 2017).
Despite the effectiveness of these practices, mathematical support in preschool remains insufficient, particularly in concept development, language modeling, and feedback (Ginsburg & Ertle, 2008; St-Jean et al., 2022). Integrating mathematical concepts into play-based contexts, such as the free play, allows children to explore mathematics spontaneously and without pressure (Ramani & Eason, 2015). Subtle scaffolding by teachers through strategic questioning can enhance comprehension while preserving children’s autonomy (Clements & Sarama, 2014). This approach helps establish a positive relationship with mathematics, which is essential for long-term success (Weisberg et al., 2016).
This study explores how collaboration between researchers and teachers can enhance the quality of mathematical support and facilitate a smoother transition to formal schooling. It is based on research examining the implementation of a preschool coaching model and its impact on classroom pedagogical practices.
2.3. Research Objectives
This article is part of a broader research project on the implementation of a support model aimed at enhancing the quality of mathematical learning support in preschool education. It examines how a collaborative approach between researchers and teachers can foster the emergence of more effective and child-centred pedagogical practices while facilitating the transition to formal schooling. More specifically, this study pursues two objectives:
- To analyze how close collaboration between researchers and teachers can improve the quality of mathematical learning support in the classroom.
- To examine the impact of this shared approach on the implementation of pedagogical practices that promote children’s engagement and understanding of mathematical concepts.
By emphasizing joint efforts between researchers and teachers, this study seeks to understand how collective reflection and the gradual adaptation of teaching practices can enrich classroom interactions and support the development of mathematical skills from an early age.
3. Methodology
Given the nature of the research objectives, a qualitative mixed-methods approach with a descriptive framework was adopted (Fortin & Gagnon, 2016). This methodological choice allows for an in-depth examination of the evolution of teachers’ learning support quality over the three-year research project while providing a detailed account of the gradual implementation of mathematical support practices.
3.1. Participants
Six teachers participated in the study. The only inclusion criteria were a minimum of five years of experience in preschool education, an expressed interest in and need for reflection on learning support practices, and the ability to implement interventions in the classroom. The Table 1 presents key sociodemographic data on the participants.

Table 1.
Sociodemographic data of participants.
3.2. Research Project Implementation
The collaborative research project on which this study is based (Bourassa & Boudjaou, 2013) was conducted over three years and included five collaborative sessions per year. The project followed an iterative process of data collection and analysis, integrating the concerns and needs of all stakeholders throughout the study. The ultimate goal was to develop a model for supporting early mathematical learning.
A variety of data collection tools and methods were used to document these concerns and needs. The analysis of the gathered data guided the themes discussed during the collaborative sessions. This article focuses specifically on data related to learning support quality and high-quality teaching practices in mathematics.
3.3. Data Collection and Analysis Tools
3.3.1. Assessing the Quality of Learning Support
Observations on teachers’ learning support quality were conducted before the first year and after each subsequent year (Years 1, 2, and 3) using the Classroom Assessment Scoring System (CLASS) (Pianta et al., 2008). The CLASS observers, who were certified, were present solely for data collection purposes and conducted four consecutive 20-minute observation cycles, each followed by 10 minutes of rating in each classroom. To ensure inter-rater reliability, 20% of the observation sessions were jointly evaluated by two certified observers, following the recommendations in the literature (Downer et al., 2010; Pianta et al., 2008). The assessment was based on a 7-point Likert scale, distinguishing three levels of support quality:
- Low (1–2);
- Moderate (3–5);
- High (6–7).
The scores obtained provided an overall measure of learning support quality. Descriptive analyses were conducted using IBM SPSS Statistics (version 29), examining both the global average score and the scores for each quality dimension across the three years.
3.3.2. Assessing High-Quality Teaching Practices in Preschool Education
Before and after each year (Years 1, 2, and 3), a semi-structured questionnaire and an interview were administered to all participating teachers. The questionnaire focused on four themes:
- Understanding early mathematical learning in preschool (three questions);
- Implementing a support model for mathematics in preschool (three questions);
- High-quality teaching practices in mathematics (three questions);
- Challenges and facilitators in implementing mathematical support practices during different moments of the day (routines and transitions, structured activities, and free play) (four questions).
The interview followed the same structure and provided deeper insights into the questionnaire responses.
Between collaborative sessions, participants were asked to record an audio journal to document the following:
- Challenges and facilitators in implementing high-quality teaching practices
- Examples of interventions carried out in the classroom.
A thematic content analysis (Braun & Clarke, 2006) was conducted throughout the project, using NVivo (version 14) software and drawing on the theoretical framework of high-quality teaching practices in learning support. The analysis of data from all three tools (questionnaires, interviews, and audio journals) informed the themes discussed during the collaborative sessions. Table 2 provides a summary of these themes, and the tools used.

Table 2.
Summary of key themes identified in questionnaire, interview, and journal analysis.
Data collection tools included a questionnaire, interviews, and weekly audio journals documenting challenges and facilitators in implementing a mathematics support model.
In the first year, the analysis of questionnaire responses and interview data revealed a single overarching theme: collaborative work leading to a shared understanding of the developmental progression of early mathematical learning in children. Between sessions, teachers were required to schedule collaborative meetings, plan classroom interventions, and document their implementation. They also maintained weekly audio journals to record both the challenges encountered and the facilitating factors in implementing support practices.
In the second year, the analysis of questionnaires and interviews identified a first theme related to the integration of mathematics into different classroom contexts, including routines, transitions, structured activities, and free play. The analysis of audio journals later revealed a second theme, focusing on the role of the observer in the classroom. This reflection aimed to enhance teachers’ understanding of mathematical development and adjust the support provided to children. Between sessions, teachers continued their collaborative discussions, planned classroom interventions, and documented their implementation. They also recorded weekly audio journal entries, detailing the challenges faced and the factors that facilitated their practices.
In the third year, the collaborative sessions explored two key themes. The first theme, emerging from the analysis of questionnaires and interviews conducted between the second and third years, focused on the quality of learning support in preschool education and the functions of scaffolding (Cloutier, 2012). The second theme, identified through the analysis of audio journals, addressed the integration of mathematical learning support across all classroom contexts, with particular attention to free play periods. Figure 1 illustrates the progression of the research project.

Figure 1.
Progression of the research project.
As in previous years, teachers were required to ensure regular follow-ups, plan their interventions, and document their experiences, notably through weekly audio journal entries.
4. Results
The results section is structured according to the two objectives of this study. First, we present findings related to the influence of a co-construction process on the quality of teachers’ learning support. Second, we examine the impact of this process on the implementation of high-quality pedagogical practices in mathematics.
4.1. The Quality of Teachers’ Learning Support
Four observation periods were conducted: one before the implementation of the Year 1 collaborative sessions and one after each subsequent year (Years 1, 2, and 3), allowing for an assessment of how participation in a collaborative project for mathematical support influenced the evolution of teachers’ learning support quality over time, as illustrated in Figure 2. In this study, the internal consistency for the learning support measure was found to be acceptable (α = 0.92).
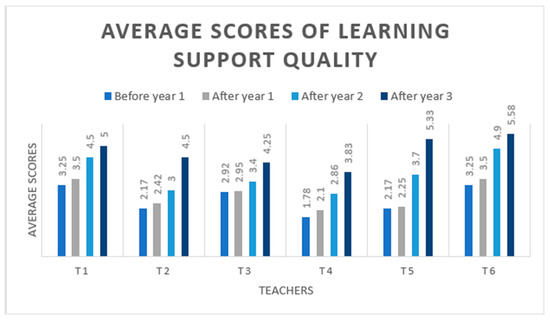
Figure 2.
The four observations of teachers’ learning support quality during the collaborative project.
The average score for learning support, measured at different stages of the project, revealed a general progression over time. Before Year 1, scores ranged from 1.78 to 3.25, indicating a relatively low level of support. However, after Year 1, a moderate increase was observed, with scores rising to between 2.10 and 3.50. This initial improvement suggests an early enhancement in learning support practices, likely linked to teachers’ adaptation to new pedagogical approaches and the development of their instructional skills.
From Year 2 onward, the increase became more pronounced, with scores ranging from 2.86 to 4.90. This progression indicates a significant strengthening of support, characterized by a more attentive response to children’s needs and a deeper integration of strategies that facilitate learning.
By Year 3, scores continued to rise, reaching values between 3.83 and 5.58. This steady and more uniform progression suggests that teachers had consolidated their pedagogical practices and improved their effectiveness across various dimensions of learning support, particularly concept development, language modeling, and the quality of feedback.
Moreover, these results indicate that after three years of collaboration, all teachers had reached the minimum threshold of 3.25 out of 7 for learning support quality, as defined by Burchinal et al. (2010). This suggests that their instructional practices had a measurable impact on children’s learning and development, thereby contributing to their academic success (Burchinal et al., 2010, 2016; Hatfield et al., 2016; Perlman et al., 2016; Zaslow et al., 2016).
Finally, descriptive analyses were conducted to examine each dimension of learning support quality in greater detail. Table 3 presents these results across the four data collection periods.

Table 3.
Average scores of the dimensions of teachers’ learning support quality across the four data collection points.
Regarding concept development, the results showed a steady progression over the years, with a mean (M) of 2.69 before Year 1 and a mean (M) of 4.83 after Year 3. The standard deviation (SD) increased slightly over time, indicating greater variability in scores. However, the significant rise in the mean suggests an overall improvement in support for concept development.
Regarding feedback quality, after a slight decrease in the mean (from M = 3.00 before Year 1 to M = 2.79 after Year 1), scores gradually increased, reaching a mean (M) of 3.71 after Year 3. This gradual increase suggests an improvement in teachers’ ability to provide relevant feedback, although the progression was more moderate compared to concept development.
As for language modeling, a trend similar to the other dimensions was observed: there was a slight decline after Year 1 (from M = 2.88 to M = 2.71), followed by a steady increase, reaching M = 3.75 after Year 3. This progression suggests an improvement in teachers’ ability to enrich students’ language. However, the increasing standard deviation (SD) indicates greater variability in the implementation of these practices.
Overall, the three dimensions of learning support showed improvement over the years, with the most significant progress in concept development. Feedback quality and language modeling followed a more moderate trend, with a slight decline after Year 1, followed by a progression. This pattern may be linked to an adjustment period before achieving a real improvement in pedagogical practices.
The increase in standard deviations (SD) in all dimensions after Year 2 and Year 3 suggests greater variability in the application of teaching strategies, which could be an area of focus to ensure consistency in practices.
These results indicate a gradual improvement in learning support over the years, with a particularly notable impact on concept development. Teachers appear to be implementing increasingly effective strategies to support students’ thinking and language, although the variability in practices remains a factor to monitor.
4.2. Implementation of High-Quality Pedagogical Practices in Mathematics
Through qualitative analyses, the evolution of teachers’ mathematical support practices was documented over three years, based on the dimensions of learning support quality. Each dimension was compared before and after the research project. The analysis, drawing from questionnaire excerpts, interviews, and audio journals, highlights the progression of these practices.
4.2.1. Teaching Practices Related to Concept Development
The analysis of teaching practices related to concept development reveals a notable evolution between the beginning and the end of the collaborative project.
Before the Collaborative Project
Initially, very few teachers implemented strategies that promoted the development of mathematical concepts in the classroom. Two key aspects emerged from the analysis. First, only one teacher (T6) reported using open-ended questions to stimulate children’s reasoning and analytical thinking: “I use open-ended questions to encourage children to reflect and explain why.” Second, only T5 incorporated a hands-on approach, particularly during the morning routine, by introducing mathematical riddles involving concrete materials (exploring concepts through object manipulation/creating activities). Overall, the use of open-ended questions, problem-solving, and hands-on object manipulation to explore concepts was limited, reducing opportunities for children to deepen their mathematical understanding.
After the Collaborative Project
By the end of the project, a significant transformation in teaching practices was observed. All teachers now reported using open-ended questions to encourage children to analyze and explain their reasoning (promoting analysis and reasoning). T4 described this shift: “Whenever possible, I ask children questions to make them think. I do this especially during the morning routine and snack time.” T3 further explained that she now plans these questions in advance to help children to generalize concepts and apply them to different situations. Unlike at the beginning of the project, when only T5 used this approach, all teachers now reported encouraging the exploration of mathematical concepts through concrete manipulations (exploring concepts through object manipulation/creating activities). ENS2 described this shift: “Whenever there’s a math problem, children use materials or environmental displays—for example, the calendar for counting.” This increased accessibility of materials allowed children to explore and structure their learning more independently. The integration of mathematical concepts into diverse, real-life situations appeared more challenging to implement. By the end of the second year, only T1 explicitly reported incorporating this approach into her teaching: “I try to show them why it’s useful. For example, counting backward helps with subtraction. If you have $10 and want to buy two flowers for $1 each, you count: 10-9-8, and you have $8 left. Before, I didn’t do this.”
By the end of the project, half of the teachers had adopted this practice. T6 highlighted the challenge of real-life integration: “Making connections to real-life situations requires advance planning. Now, I try to connect all the concepts, give them meaning, and whenever possible, show how they are useful.” T3 mentioned her effort to integrate mathematics into other subjects. For instance, to teach rhyming and phonology, she organized rhyme hunts and then created bar graphs with the children to analyze the results. This interdisciplinary approach helps contextualize mathematical concepts. Table 4 presents teachers’ reported support practices related to concept development.

Table 4.
Reported teaching practices for concept development.
The results indicate that the collaborative project significantly improved teaching practices related to mathematical concept development. Instruction shifted from a transmissive approach to a more interactive and exploratory approach, where open-ended questions stimulate reasoning, object manipulation becomes an integrated strategy, and the application of concepts to diverse situations shows progress. However, anchoring mathematical concepts in real-life contexts remains a challenge. By the end of the project, only half of the teachers had adopted this approach, emphasizing that it requires prior planning, which limits its spontaneous integration.
4.2.2. Teaching Practices Related to the Quality of Feedback
The analysis of teaching practices regarding the quality of feedback highlights significant changes between the beginning and the end of the collaborative project.
Before the Collaborative Project
At the outset, the only widely present scaffolding function in the classroom was modeling (Cloutier, 2012), as indicated by teachers’ self-reported practices. T4 described this approach: “When a child struggles, I sit next to them and show [model] how to do it.” Regarding encouragement and providing information, only T1 and T6 reported using strategies that support these aspects. As T1 explained: “I always ask children what is not working. For example, at the block corner, I encourage them to reflect on why their tower falls by giving them information about the importance of the base [providing explanations].”
T6 emphasized the importance of recognizing children’s successes: “In my class, I pause whenever a child accomplishes something meaningful. I encourage them and highlight their achievement. For example, yesterday, a child created a pattern using grapes and raspberries during snack time. I took the opportunity to praise them [encouragement] and share it with the other children.” Finally, before the project, no teacher reported using looped feedback or encouraging a deeper reflective process in children.
After the Collaborative Project
By the end of the project, all teachers reported using a wider range of scaffolding functions (Cloutier, 2012), no longer relying solely on modeling. They now mentioned incorporating the following:
- Simplification: “I break it down into small steps when a child faces a challenge.” (T3)
- Complexification: “For more advanced children, I plan additional challenges that push them to think further.” (T2)
- Peer support: “I use peer assistance a lot to help those who are struggling. I find that they understand better this way.” (T6)
Regarding encouragement and affirmation, a notable improvement was observed: all teachers now reported using these strategies to recognize children’s efforts and achievements. However, only T1, T3, T4, and T6 stated that they provide explicit information to support the development of children’s mathematical thinking development.
The most significant change concerned looped feedback and reflective processes. While no teachers had previously mentioned using these strategies, all teachers—except T4—now reported incorporating them into their practice. As T3 explained, “Now, I always ask children, ‘why.’ Why are you doing it this way? Why do you think it works?” T6 added that he encourages children to consider alternative solutions, frequently reformulates their statements, and integrates their reflections into the morning discussion to stimulate collective thinking. Table 5 present teachers’ reported support practices related to the quality of feedback.

Table 5.
Reported teaching practices for the quality of feedback.
These results indicate that the collaborative project fostered diversification and enrichment of teaching practices related to feedback. Instruction shifted from an approach primarily based on modeling to a broader use of scaffolding strategies, open-ended questioning, and feedback that promotes reflection and self-regulation in children.
While all teachers now incorporate open-ended questions, some do not fully encourage reasoning justification or error analysis. Feedback remains descriptive rather than constructive and guiding in some cases, which limits opportunities for children to rethink their strategies and refine their understanding.
Before the Collaborative Project
Before the project, language modeling in mathematics was limited and lacked diversity. Three key findings emerged. Mathematical discussions were confined to the morning circle time. Only T1, T2, and T3 reported organizing mathematical conversations, but exclusively during morning discussions. T3 explained that “On the school district’s website, we have a bank of images that I use for mathematical discussions. It allows me to engage children in conversations about math.”
Open-ended questions therefore encouraged reasoning justification. Some teachers used open-ended questions, but these did not encourage children to explain their thinking. It was not until the end of the second year that T4 and T5 began incorporating questions that promoted justification.
Repetitive drills and limited vocabulary were common. Teachers reported repeating certain elements, but in a superficial manner, without structuring children’s thinking. T2 illustrated this trend: “I often repeat the number rhyme.” Only T1 and T2 reported introducing advanced mathematical vocabulary, primarily through word labels.
After the Collaborative Project
By the end of the project, a marked improvement in language modeling practices was observed. Mathematical discussions became more frequent and integrated into daily activities. All teachers now used mathematical discussions as spontaneous opportunities to engage children in mathematics. Instead of relying on an institutional image bank, they now took their own photos of children’s real-life experiences. T4 illustrated this shift: “I take pictures of mathematical moments that can spark discussions. For example, a structure where children arranged cars from largest to smallest. I find that it makes more sense to them.” T1 also highlighted this new approach: “Now, everything is an opportunity to talk about math. The other day, we were outside in nature class, and the children decided to sort tree leaves. So we talked about classification.”
Open-ended questions now encourage reasoning justification. Previously, teachers asked open-ended questions without a clear purpose. Now, they understood their role in supporting reasoning justification. T4 reflected on this change: “Before, I asked questions just for the sake of asking. Now, I have an intention—I want to understand whether their way of thinking makes sense.”
Repetition and language extension improved, but only among some teachers. Only T1 and T6 reported adapting their repetition techniques to help children structure their thinking. T6 described this evolution: “My little student, Théo, I know it’s difficult for him. Now, I ask him questions to encourage full responses and have him explain how he does things.” Few teachers systematically rephrased children’s statements to help them refine their reasoning. Before the project, no teachers used this strategy. After the project, only three teachers reported implementing it. T6 explained this shift: “Now, I always ask children to explain how they do things, and I verbalize it with them.” T1 and T3 also reported using this strategy, helping children better structure their mathematical thinking.
Use of advanced mathematical vocabulary expanded to all teachers. Before the project, only T1 and T2 reported using advanced vocabulary in class. T2 explained: “I use word labels with mathematical terms. This allows me to name them at the right moment.” By the end of the project, all teachers stated that they used more precise mathematical vocabulary to support concept learning. T5 emphasized the impact of mathematical word labels, which had been shared during a collaborative session: “Now, I use word labels. It makes talking about math so much easier!” Table 6 presents teachers’ reported support practices related to the quality of language modeling.

Table 6.
Reported teaching practices for the quality of language modeling.
The collaborative project led to a significant evolution in mathematical language modeling. Teaching practices shifted from a limited approach, characterized by occasional mathematical discussions and a restricted vocabulary, to a more intentional and integrated strategy, where mathematical discussions are embedded in daily activities based on real-life situations. Open-ended questions are now used to support reasoning justification, repetition and language extension are more effectively leveraged to structure children’s thinking, self-verbalization and parallel verbalization are incorporated to foster reflection, and mathematical vocabulary has been enriched and shared among teachers.
While teachers have increased their use of mathematical word labels and mathematical discussions, only some have implemented strategies that encourage children to verbalize their thought processes. The lack of systematic use of these practices may hinder children’s ability to structure and articulate their mathematical reasoning.
5. Discussion
Three key findings emerge from the analysis of the results: (1) the quality of learning support significantly influences children’s learning and development, (2) the collaborative process facilitates the implementation of high-quality pedagogical practices in mathematics, and (3) challenges remain in contextualizing learning and integrating mathematical concepts into spontaneous situations, particularly in free play.
5.1. The Impact of Learning Support on Children’s Development
The results indicate a notable improvement in the quality of learning support after three years of participation in the collaborative project. All teachers reached the minimum threshold of 3.25 out of 7, as established by Burchinal et al. (2010), allowing them to exert a significant influence on children’s learning and development (Burchinal et al., 2010, 2016; Hatfield et al., 2016; Perlman et al., 2016; Zaslow et al., 2016). This progression aligns with the findings of Pianta et al. (2008) and Sylva et al. (2011), which suggest that coaching and ongoing professional development improve teaching practices and enhance children’s development.
Among the dimensions assessed, concept development showed the greatest improvement, increasing from M = 2.69 before Year 1 to M = 4.83 after Year 3. This progression reflects a stronger adoption of teaching strategies that foster reflection and structured learning. However, the quality of feedback and language modeling improved at a slower pace, despite showing positive trends. After an initial decline, feedback quality reached M = 3.71, while language modeling reached M = 3.75. These findings confirm the observations of Sarama and Clements (2012) and St-Jean et al. (2022), who suggest that concept development is the first to benefit from pedagogical interventions, whereas feedback and language modeling requires more specific support and a longer adjustment period.
5.2. The Effect of the Co-Construction Process on Mathematical Teaching Practices
The analysis of teachers’ practices, based on questionnaires, interviews, and reflective journals, reveals a shift from a primarily transmissive approach to a more interactive and exploratory approach.
Three key factors appear to have particularly contributed to this improvement:
- Encouraging analysis and reasoning showed significant progress. While at the beginning of the project only one teacher used open-ended questions, by the end of Year 3, all teachers reported employing this strategy. This evolution aligns with the findings of Sarama and Clements (2012) and St-Jean et al. (2022), which emphasize that open-ended questions support the structuring of thought and mathematical reasoning.
- The integration of concrete object manipulation became widespread. Initially observed in only one teacher’s practice, it had become a common strategy among all participants by the end of the project. This approach is strongly supported by Ginsburg and Ertle (2008) and Pianta et al. (2008) and anchors learning in a more meaningful and engaging way, promoting long-term understanding.
- The integration of mathematical concepts into diverse contexts and daily life showed moderate progress. By the end of the project, half of the teachers reported adopting this approach, reinforcing the practical significance of the concepts taught (Burchinal et al., 2016; Justice et al., 2018).
5.3. Persistent Challenges: Contextualization and Integration in Spontaneous Situations
Despite these advancements, integrating mathematics into real-life contexts remains a challenge, as it requires advance planning, limiting opportunities for spontaneous exploration. Marinova and Drainville (2020) and Vlassis and Demonty (2019) and highlight that curriculum constraints often push teachers toward structured approaches, at the expense of more open-ended and contextualized practices. However, several studies (Ramani & Eason, 2015; St-Jean et al., 2022; Wolfgang et al., 2003) demonstrate that embedding mathematics in real-world situations, such as classroom material management or symbolic play, enhances children’s conceptual understanding and fosters autonomy.
Free play, in particular, remains an underutilized tool, primarily due to the difficulty of structuring interventions without compromising children’s autonomy. The findings of this study align with those of Nolin and Marinova (2023), who note that formal teaching methods still dominate preschool mathematics instruction, limiting opportunities for natural learning experiences. Ginsburg et al. (2008) as well as Clements and Sarama (2014) stress the importance of pedagogical support, enabling teachers to balance guidance and exploration by adopting the role of facilitator rather than knowledge transmitter.
Another challenge concerns the quality of feedback. While teachers ask more open-ended questions and encourage children, looped feedback and error reformulation remain inconsistently applied. Yet, studies (Schachter, 2017; Wasik & Hindman, 2014) indicate that these elements are critical in helping children adjust their reasoning and deepen their understanding.
Finally, despite progress in language modeling, with the adoption of mathematical discussions and increased use of specialized word labels, self-verbalization and parallel verbalization remain scarce. Cloutier (2012) and Ginsburg et al. (2008) show that without active verbalization of thought processes, children struggle to structure and articulate their mathematical reasoning.
5.4. Toward a More Contextualized and Interactive Approach to Preschool Mathematics
This study highlights a shift in mathematical teaching practices while also revealing persistent challenges related to contextualizing learning and integrating concepts into spontaneous situations. Although teachers have adopted strategies that support concept development, the integration of mathematics into diverse and meaningful contexts remains limited. Nolin and Marinova (2023) and St-Jean et al. (2022) confirm that a lack of training and curriculum pressures hinder the adoption of more contextualized and exploratory practices.
The analysis of teaching practices shows that mathematics instruction primarily occurs during structured activities, such as morning routines or planned learning periods, rather than through free play. This trend, also noted by Nolin and Marinova (2023), reflects an ongoing reliance on formal instruction, where mathematical concepts are taught in isolation rather than embedded in authentic experiences. However, Ramani and Eason (2015) and Wolfgang et al. (2003) demonstrate that symbolic play and autonomous activities provide ideal opportunities for children to experiment with and strengthen mathematical skills.
Despite this evidence, teachers struggle to integrate these practices, primarily due to the challenge of balancing autonomy and guidance. Marinova and Drainville (2020) emphasize the importance of ongoing professional development to equip teachers with strategies for seamlessly incorporating mathematics into children’s daily activities, thereby reducing the gap between structured learning and spontaneous experiences.
Thus, while progress has been observed, this study underscores the need for a pedagogical shift, ensuring that mathematics learning is more embedded in everyday life and better aligned with children’s natural ways of learning.
6. Limitations
While this study provides valuable insights into the evolution of mathematical teaching practices in preschool, certain limitations must be considered.
First, the small sample size, consisting of teachers actively engaged in a collaborative process, limits the generalizability of the findings (Desimone & Hill, 2017). Additionally, self-reported teaching practices may introduce social desirability bias, making classroom observations necessary to objectively validate the data (Tourangeau & Yan, 2007).
The three-year follow-up is also insufficient to assess the long-term impact of these practices on children’s learning, warranting a longitudinal study (Brooker, 2010). Furthermore, institutional and curricular constraints may affect teachers’ ability to maintain exploratory approaches once external support is removed (Ginsburg et al., 2008).
Moreover, this study does not take into account children’s perceptions, which are essential for understanding their engagement in mathematics (Pramling Samuelsson & Asplund Carlsson, 2008). Finally, although the integration of mathematics into free play was identified as an underutilized approach, the study does not propose a specific intervention model to support teachers in this transition (Weisberg et al., 2016). Thus, future research should focus on the following:
- Prudently generalizing the findings;
- Conducting long-term follow-up;
- Incorporating classroom observations;
- Developing concrete models for integrating mathematics into free play.
7. Conclusions
This study highlights significant progress in preschool mathematics teaching, particularly through the collaborative process, which has helped to shift pedagogical practices toward more interactive and exploratory approaches. The results show that concept development experienced the greatest improvement, while feedback quality and language modeling progressed more slowly, suggesting the need for more targeted pedagogical support.
However, despite these advancements, integrating mathematics into real-life contexts and spontaneous situations—particularly through free play—remains a challenge.
Several factors contribute to these difficulties:
- Institutional constraints and curriculum pressures lead teachers to adopt more structured approaches, limiting opportunities for emergent learning (St-Jean et al., 2022). Vlassis and Demonty (2019) note that the emphasis on formally assessed skills restricts the contextualization of mathematics and the implementation of exploratory activities.
- The lack of specific training is a major barrier. Nolin and Marinova (2023) report that many teachers express a need for support to integrate mathematical concepts more naturally into daily interactions. Bouchard et al. (2017) emphasize that preschool teacher training focuses primarily on global development and language acquisition, leaving mathematics in the background.
- This lack of training is reflected in teaching practices: Deshaies and Boily (2023) show that teachers would benefit from structured guidance to better integrate mathematics into everyday activities, such as problem-solving situations, collaborative reasoning, and free play, which remain underutilized.
- Despite the recognition of play as an effective learning tool, it remains underused due to limited teacher support and a lack of adapted pedagogical tools (Nolin & Marinova, 2023). Striking a balance between child-led exploration and structured pedagogical interventions is difficult without proper guidance (Weisberg et al., 2016).
Given these challenges, it is essential to continue exploring approaches that promote a more fluid and contextualized integration of mathematics, equipping teachers to balance structured instruction with emergent learning opportunities.
Recommendations
- 1.
- Strengthen Teacher Training and Pedagogical Support
Ongoing professional development focused on integrating mathematics into real-life and spontaneous contexts is necessary. Training programs should include concrete examples, classroom observations, and hands-on workshops, helping teachers to better leverage emergent learning opportunities, particularly through free play.
- 2.
- Develop Pedagogical Tools to Support Mathematical Exploration
The creation of instructional guides, learning scenarios based on everyday situations, and strategic questioning tools would help teachers to naturally integrate mathematics into their teaching. These resources should be designed to support flexible instruction, where mathematical concepts emerge through spontaneous interactions and meaningful experiences for children.
Funding
This research was funded by CRHS engagement partenariat, grant number 892-2021-1058.
Institutional Review Board Statement
This study was conducted in accordance with the Decla-ration of Helsinki and approved by the Institutional Review Board (Ethics Committee) of Université du Québec à Trois-Rivières (protocol code CER-22-290-07.03 and date of approval 13 September 2022) for studies involving humans.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Bouchard, C., Duval, S., & Bigras, N. (2017). La qualité des interactions éducatives à l’éducation préscolaire: État des lieux et perspectives. Presses de l’Université du Québec. [Google Scholar]
- Bourassa, B., & Boudjaou, M. (2013). Des recherches collaboratives en sciences humaines et…. Presses de l’Université Laval. [Google Scholar]
- Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3(2), 77–101. [Google Scholar] [CrossRef]
- Brooker, L. (2010). Learning to play, or playing to learn? Children’s participation in the cultures of homes and settings. Early Years, 30(3), 227–241. [Google Scholar]
- Burchinal, M., Vandergrift, N., Pianta, R., & Mashburn, A. (2010). Threshold analysis of association between childcare quality and child outcomes for low-income children in pre-kindergarten programs. Early Childhood Research Quarterly, 25(2), 166–176. [Google Scholar] [CrossRef]
- Burchinal, M., Xue, Y., Anger, A., Tien, H.-C., Mashburn, A., Cavadel, E. W., & Peisner-Feinberg, E. (2016). II. Quality thresholds, features, and dosage in early care and education: Methods. Monographs of the Society for Research in Child Development, 81(2), 27–45. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2008). Experimental evaluation of the effects of a research-based preschool mathematics curriculum. American Educational Research Journal, 45(2), 443–494. [Google Scholar] [CrossRef]
- Clements, D. H., & Sarama, J. (2014). Learning and teaching early math: The learning trajectories approach (2nd ed.). Routledge. [Google Scholar]
- Clements, D. H., & Sarama, J. (2021). Engaging young children in mathematics: Standards for early childhood mathematics education. Lawrence Erlbaum Associates. [Google Scholar]
- Cloney, D., Page, J., Tayler, C., & Church, A. (2017). Assessing the quality of teacher-child interactions in early childhood education and care. Early Childhood Research Quarterly, 41(1), 21–34. [Google Scholar] [CrossRef]
- Cloutier, S. (2012). L’étayage: Agir comme guide pour soutenir l’autonomie: Pour un enfant à son plein potentiel. PUQ. [Google Scholar]
- Deshaies, I., & Boily, M. (2023). Le modèle de transposition didactique en mathématique à l’éducation préscolaire: Niveaux de jeu des enfants et utilisation des savoirs mathématiques dans le jeu symbolique. Revue Internationale de Communication et Socialisation, 10(1), 22–43. [Google Scholar]
- Desimone, L. M., & Hill, H. C. (2017). Inside the black box of teacher professional development: Teachers’ decisions about mathematics instruction. Teachers College Record, 119(5), 1–30. [Google Scholar]
- Downer, J. T., Booren, L. M., Lima, O. K., Luckner, A. E., & Pianta, R. C. (2010). The individualized classroom assessment scoring system (inCLASS): Preliminary reliability and validity of a system for observing preschoolers’ competence in classroom interactions. Early Childhood Research Quarterly, 25(1), 1–16. [Google Scholar] [CrossRef]
- Fortin, M.-F., & Gagnon, J. (2016). Fondements et étapes du processus de recherche. Méthodes quantitatives et qualitatives. Chenelière Éducation. [Google Scholar]
- Ginsburg, H. P., & Ertle, B. (2008). Knowing the mathematics in early childhood mathematics. In O. Saracho, & B. Spodek (Eds.), Contemporary perspectives on mathematics in early childhood education (pp. 45–66). Information Age Publishing. [Google Scholar]
- Ginsburg, H. P., Lee, J. S., & Boyd, J. S. (2008). Mathematics education for young children: What it is and how to promote it. Social Policy Report, 22(1), 1–23. [Google Scholar] [CrossRef]
- Hamre, B. K. (2014). Teachers’ daily interactions with children: An essential ingredient in effective early childhood programs. Child Development Perspectives, 8(4), 223–230. [Google Scholar] [CrossRef]
- Hatfield, B. E., Burchinal, M. R., Pianta, R. C., & Sideris, J. (2016). Thresholds in the association between quality of teacher–child interactions and preschool children’s school readiness skills. Early Childhood Research Quarterly, 36(3), 561–571. [Google Scholar] [CrossRef]
- Houben, L., Bouchard, C., Mroué, R., & Maillart, C. (2022). Portrait de la qualité des interactions pour soutenir l’oral des enfants dans des classes de maternelle en Belgique. Éducation et Francophonie, 50(1), 1–20. [Google Scholar] [CrossRef]
- Justice, L. M., Jiang, H., & Strasser, K. (2018). Linguistic environment of preschool classrooms: What dimensions support children’s language growth? Early Childhood Research Quarterly, 42, 79–92. [Google Scholar] [CrossRef]
- Marinova, K., & Drainville, S. (2020). L’importance de la formation continue pour soutenir l’intégration des mathématiques au quotidien au préscolaire. Journal of Early Childhood Mathematics Education, 9(2), 157–178. [Google Scholar]
- Ministère de l’Éducation du Québec [MEQ]. (2023). Programme-cycle de l’éducation préscolaire. Éducation préscolaire. Gouvernement du Québec. [Google Scholar]
- Nolin, R., & Marinova, K. (2023). Soutenir le développement de la pensée mathématique des enfants: Portrait des besoins ressentis par des enseignants à l’éducation préscolaire québécois. Revue Internationale de Communication et de Socialisation (RICS), 10(2), 324–350. [Google Scholar]
- Perlman, M., Falenchuk, O., Fletcher, B., McMullen, E., Beyene, J., & Shah, P. S. (2016). A systematic review and meta-analysis of a measure of staff/child interaction quality (the Classroom Assessment Scoring System) in early childhood education and care settings and child outcomes. PLoS ONE, 11(12), e0167660. [Google Scholar] [CrossRef] [PubMed]
- Pianta, R. C., La Paro, K. M., & Hamre, B. K. (2008). Classroom Assessment Scoring System [CLASS] Manual: Pre-K. Brookes Publishing. [Google Scholar]
- Piasta, S. B., Justice, L. M., Cabell, S. Q., Wiggins, A. K., Turnbull, K. P., & Curenton, S. M. (2012). Impact of professional development on preschool teachers’ conversational responsivity and children’s linguistic productivity and complexity. Early Childhood Research Quarterly, 27, 387–400. [Google Scholar] [CrossRef]
- Pramling Samuelsson, I., & Asplund Carlsson, M. (2008). The playing learning child: Towards a pedagogy of early childhood. Scandinavian Journal of Educational Research, 52(6), 623–641. [Google Scholar] [CrossRef]
- Ramani, G. B., & Eason, S. H. (2015). Role of play and games in building children’s foundational numerical knowledge. Early Childhood Research Quarterly, 36, 232–243. [Google Scholar]
- Sarama, J., & Clements, D. H. (2012). Mathematics for the Whole Child. In S. Suggate, & E. Reese (Eds.), Contemporary debates in childhood education and development (pp. 71–80). University of Buffalo Library. [Google Scholar]
- Schachter, R. E. (2017). Early childhood teachers’ pedagogical reasoning about how children learn during language and literacy instruction. International Journal of Early Childhood, 49(1), 95–111. [Google Scholar] [CrossRef]
- St-Jean, C., April, J., Bigras, N., Maïano, C., & Dupuis-Brouillette, M. (2022). Relations entre la qualité des interactions enseignante-enfants et le développement du raisonnement spatial des enfants de maternelle quatre ans à temps plein en milieu défavorisé. Canadian Journal of Education, 45(2), 400–427. [Google Scholar] [CrossRef]
- Sylva, K., Melhuish, E., Sammons, P., Siraj-Blatchford, I., & Taggart, B. (2011). Pre-school quality and educational outcomes at age 11: Low quality has little benefit. Journal of Early Childhood Research, 9(2), 109–124. [Google Scholar] [CrossRef]
- Tourangeau, R., & Yan, T. (2007). Sensitive questions in surveys. Psychological Bulletin, 133(5), 859–883. [Google Scholar] [CrossRef] [PubMed]
- Vlassis, J., & Demonty, I. (2019). Conceptualisation, symbolisation et interactions enseignante/enseignant-élèves dans les apprentissages mathématiques: L’exemple de la généralisation. Éducation et Francophonie, 47(3), 98–120. [Google Scholar] [CrossRef]
- Wasik, B. A., & Hindman, A. H. (2014). Improving preschool teachers’ interactive book reading: A randomized controlled trial. Journal of Educational Psychology, 106(1), 120–132. [Google Scholar] [CrossRef]
- Watts, T. W., Duncan, G. J., Siegler, R. S., & Davis-Kean, P. E. (2014). What’s past is prologue: Relations between early mathematics knowledge and high school achievement. Educational Researcher, 43(7), 352–360. [Google Scholar] [CrossRef]
- Weisberg, D. S., Hirsh-Pasek, K., Golinkoff, R. M., Kittredge, A. K., & Klahr, D. (2016). Guided play: Principles and practices. Current Directions in Psychological Science, 25(3), 177–182. [Google Scholar] [CrossRef]
- Wolfgang, C. H., Stannard, L. L., & Jones, I. (2003). Advanced mathematical thinking: The influence of primary caregivers. Journal of Educational Psychology, 95(1), 157–167. [Google Scholar]
- Zaslow, M., Burchinal, M., Tarullo, L., & Martinez-Beck, I. (2016). V. Quality thresholds, features, and dosage in early care and education: Discussion and conclusions. Monographs of the Society for Research in Child Development, 81(2), 75–87. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).