The Design & Pitch Challenges in STEM: A Theoretical Framework for Centering Mathematics Learning in Entrepreneurial Pitch Competitions
Abstract
1. Introduction
2. The Design & Pitch Challenges in STEM
2.1. A Brief Overview of PBL, DBL, and EBL
2.2. Introducing the Competition
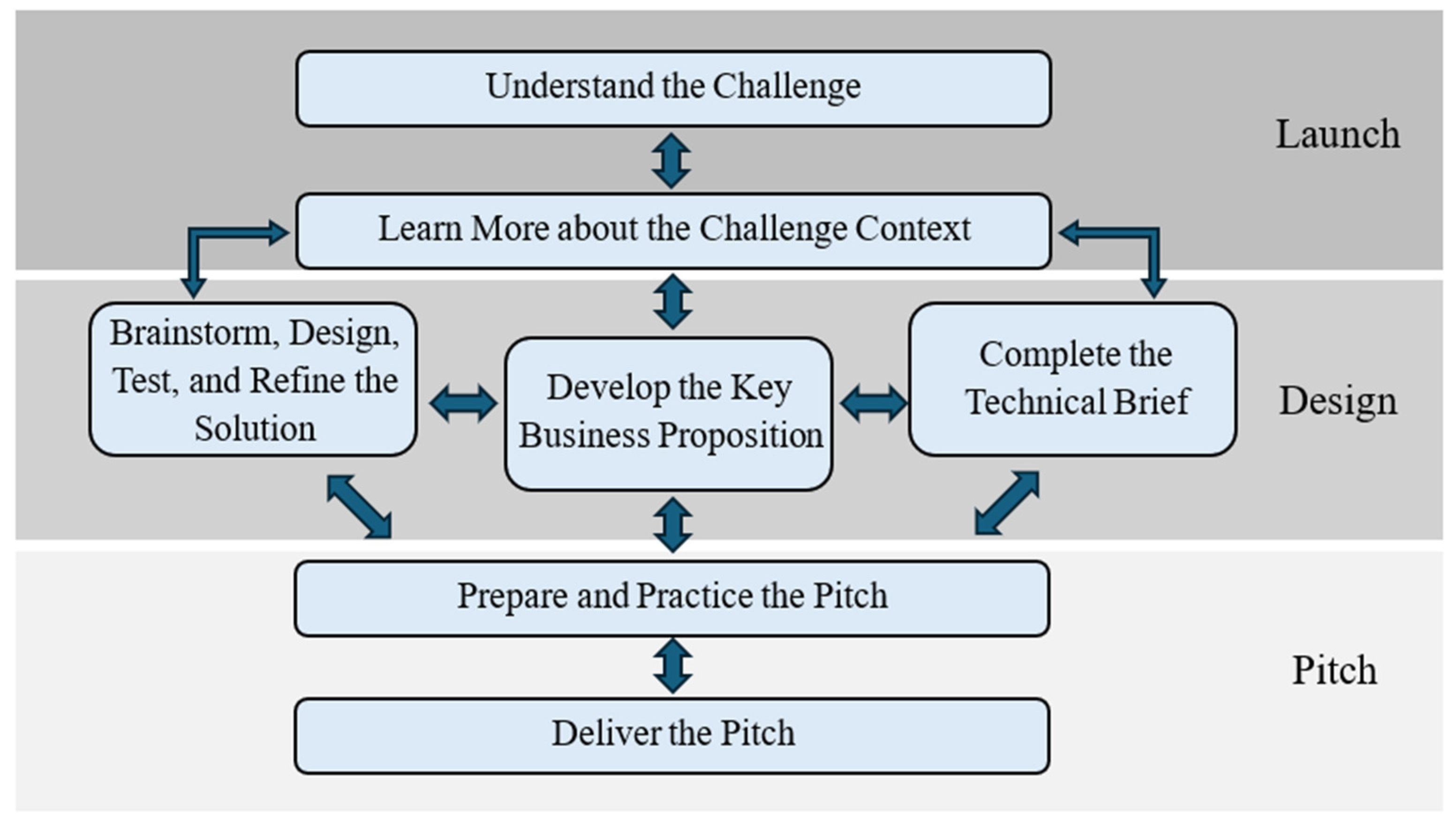
2.3. The D&P Learning Framework
2.3.1. Launch
- Understand the Challenge
- Learn More about the Challenge Context
2.3.2. Design
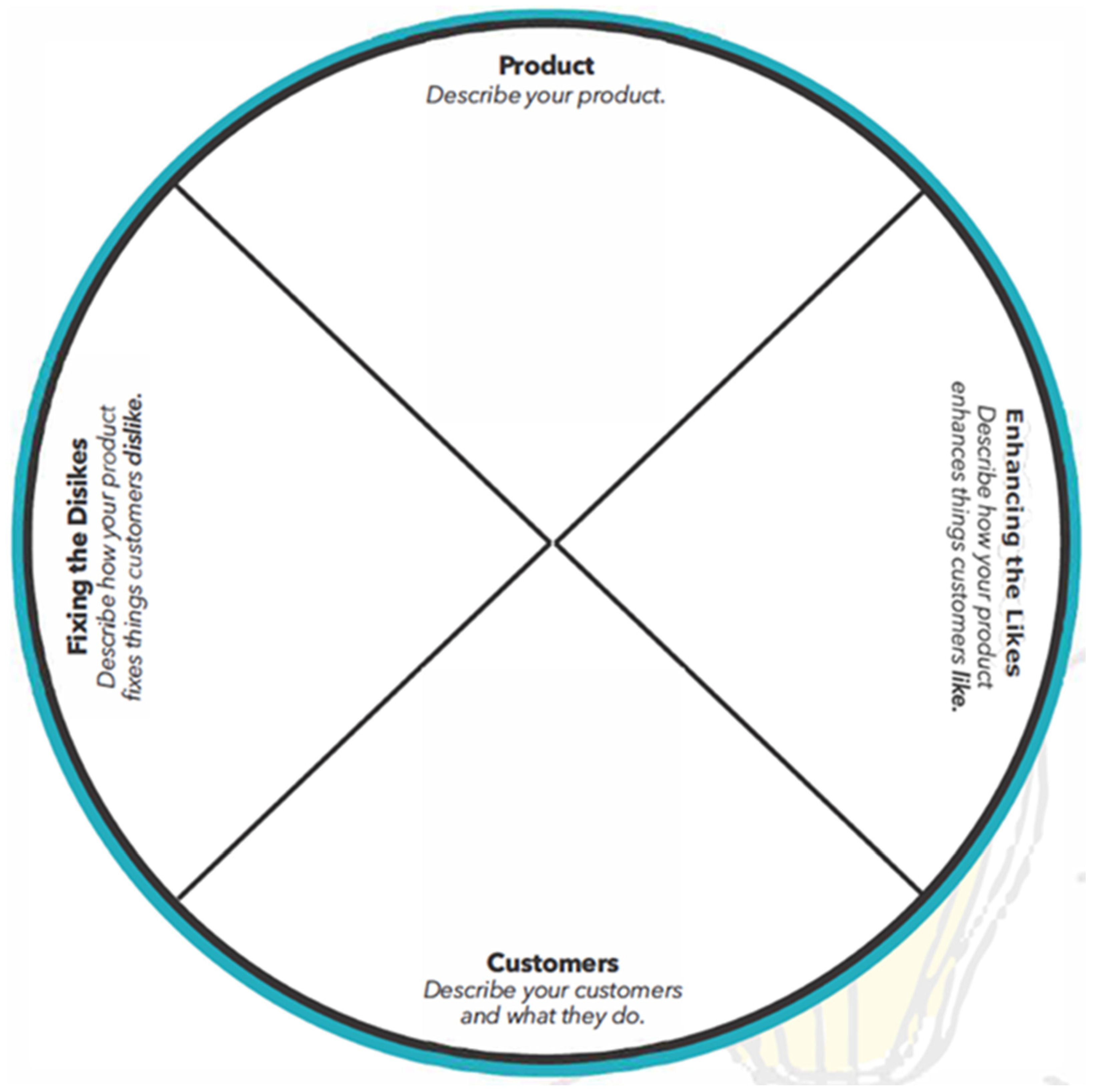
- Brainstorm, Design, Test, and Refine Solutions
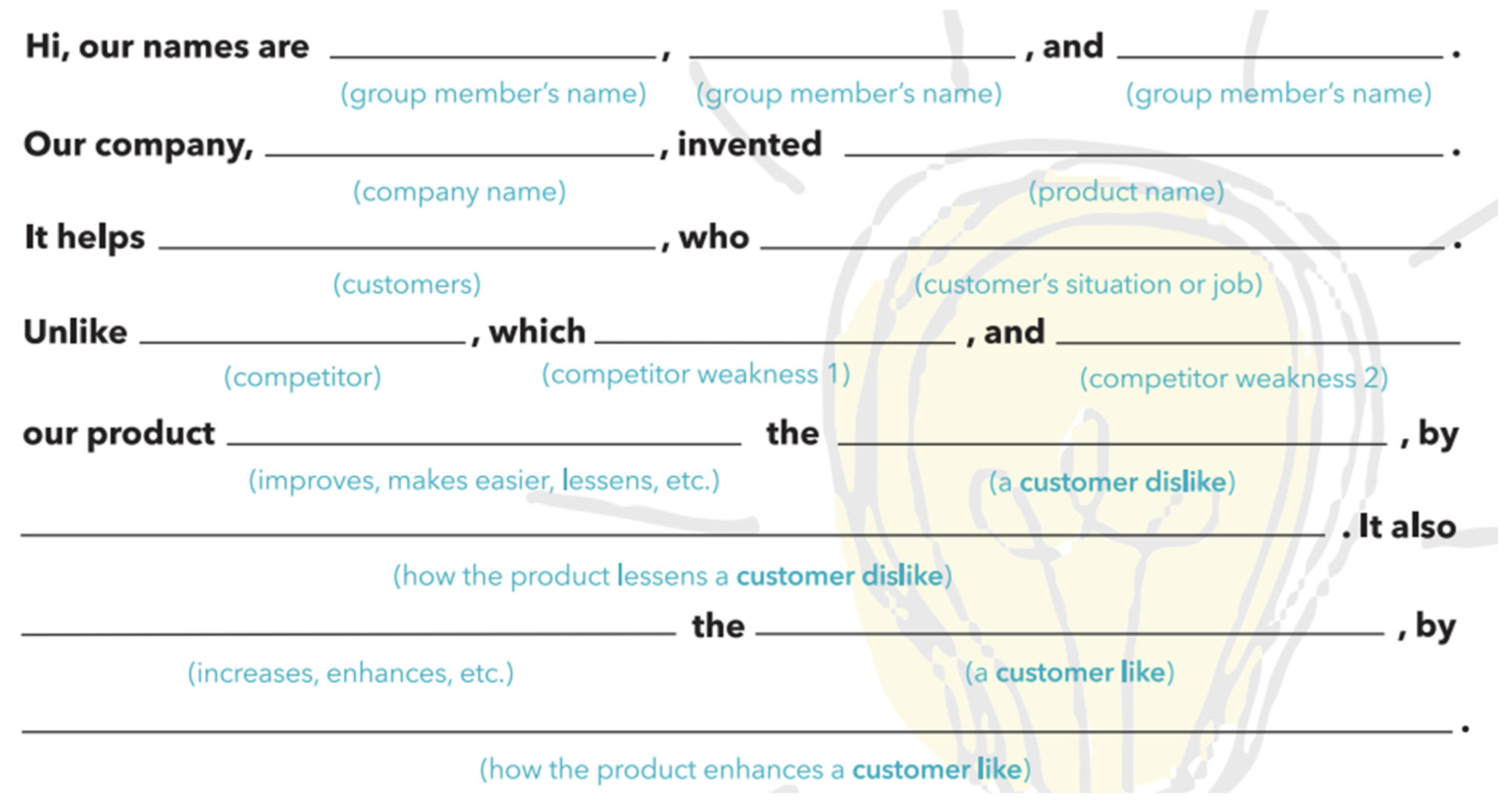
- Develop the Key Business Proposition
- Build the Technical Brief
- Exposing Ideas to Critique
2.3.3. Pitch
- Prepare and Practice the Pitch
- Deliver the Pitch
2.3.4. Summary
2.4. The D&P Learning Framework Challenges
2.4.1. Contexts
2.4.2. Champions
2.4.3. Mathematics Content
2.4.4. Technology Tools
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| STEM | Science, Technology, Engineering, and Mathematics |
| PBL | Project-Based Learning |
| DBL | Design-Based Learning |
| EBL | Entrepreneurial-Based Learning |
References
- Ainley, J., Bills, L., & Wilson, K. (2005). Designing spreadsheet-based tasks for purposeful algebra. International Journal of Computers for Mathematical Learning, 10(3), 191–215. [Google Scholar] [CrossRef]
- Apedoe, X. S., & Schunn, C. D. (2013). Strategies for success: Uncovering what makes students successful in design and learning. Instructional Science, 41(4), 773–791. [Google Scholar] [CrossRef]
- Autodesk. (2025). TinkerCAD [Computer software]. Available online: https://tinkercad.com (accessed on 18 February 2025).
- Barron, B. J., Schwartz, D. L., Vye, N. J., Moore, A., Petrosino, A., Zech, L., & Bransford, J. D. (1998). Doing with understanding: Lessons from research on problem-and project-based learning. Journal of the Learning Sciences, 7(3–4), 271–311. [Google Scholar]
- Belcher, M., Confrey, J., & Krupa, E. (2024). Algorithms, spreadsheets and functions: Exploring middle graders’ functional reasoning during a STEM entrepreneurial pitch competition. International Journal of Mathematical Education in Science and Technology. [Google Scholar] [CrossRef]
- Belcher, M., Mannix, J. P., & Krupa, E. E. (2021, October 14–17). Exploring students’ statistical thinking during an entrepreneurial design challenge. The 43rd Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA), Philadelphia, PA, USA. [Google Scholar]
- Bilen, S., Kisenwether, E., Rzasa, S., & Wise, J. (2005). Developing and assessing students’ entrepreneurial skills and mind-set. Journal of Engineering Education, 94(2), 233–243. [Google Scholar] [CrossRef]
- Blumenfeld, P. C., Kempler, T. M., & Krajcik, J. S. (2006). Motivation and cognitive engagement in learning environments. In K. R. Sawyer (Ed.), The Cambridge handbook of the learning sciences (pp. 475–488). Cambridge University Press. [Google Scholar]
- Borasi, R., & Finnigan, K. (2010). Entrepreneurial attitudes and behaviors that can help prepare successful change-agents in education. The New Educator, 6(1), 1–29. [Google Scholar] [CrossRef]
- Brantlinger, A. (2022). Critical and vocational mathematics: Authentic problems for students from historically marginalized groups. Journal for Research in Mathematics Education, 53(2), 154–172. [Google Scholar] [CrossRef]
- Bruner, J. S. (1960). The process of education. Harvard University Press. [Google Scholar]
- Capraro, R. M., & Slough, S. W. (2013). Why PBL? Why STEM? Why now? An introduction to STEM project-based learning: An integrated science, technology, engineering, and mathematics (STEM) approach. In STEM project-based learning (pp. 1–5). Brill. [Google Scholar]
- Condliffe, B., Visher, M. G., Bangser, M. R., Drohojowska, S., & Saco, L. (2016). Project-based learning: A literature review. MDRC. [Google Scholar]
- Confrey, J. (1991). Learning to listen: A student’s understanding of powers of ten. In E. von Glasersfeld (Ed.), Radical constructivism in mathematics education (pp. 111–138). Springer Netherlands. [Google Scholar]
- Confrey, J., Krupa, E., & Belcher, M. (2019). Design & pitch challenges in STEM. Available online: https://sites.ced.ncsu.edu/design-and-pitch/ (accessed on 18 February 2025).
- Confrey, J., & Krupa, E. E. (2012). The arrival of the Common Core State Mathematics Standards: How did we get here and what needs to happen next? In C. R. Hirsch, G. Lappan, & B. J. Reys (Eds.), Curriculum issues in an era of common core state standards for mathematics. National Council of Teachers of Mathematics. [Google Scholar]
- Confrey, J., & Maloney, A. (2007). A theory of mathematical modelling in technological settings. In W. Blum, P. L. Galbraith, H. W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education: The 14th ICMI study (pp. 57–68). Springer Science + Business Media. [Google Scholar]
- Cristal Glanchai, L. (2019). The case for youth entrepreneurship education. Venture Lab. Available online: https://venturelab.org/wp-content/uploads/2019/12/State-of-Youth-Entrepreneurship_2019.pdf (accessed on 18 February 2025).
- Cruz, S., Viseu, F., & Lencastre, J. A. (2022). Project-based learning methodology as a promoter of learning math concepts: A scoping review. Frontiers in Education, 7, 1–11. [Google Scholar] [CrossRef]
- Datawrapper GmbH. (2025). Datawrapper [Computer software]. Available online: https://www.datawrapper.de/ (accessed on 18 February 2025).
- Deveci, İ., & Seikkula-Leino, J. (2023). The link between entrepreneurship and STEM education. In Enhancing entrepreneurial mindsets through STEM education (pp. 3–23). Springer International Publishing. [Google Scholar]
- Dewey, J. (1981). Logic: The theory of inquiry. In J. J. McDermott (Ed.), The philosophy of John Dewey (Vol. 1–2, pp. 442–453). The University of Chicago Press. (Original work published 1938). [Google Scholar]
- Doppelt, Y., Mehalik, M. M., Schunn, C. D., Silk, E., & Krysinski, D. (2008). Engagement and achievements: A case study of design-based learning in a science context. Journal of Technology Education, 19(2), 22–39. [Google Scholar]
- Dym, C. L., Agogino, A. M., Eris, O., Frey, D. D., & Leifer, L. J. (2005). Engineering design thinking, teaching, and learning. Journal of Engineering Education, 94(1), 103–120. [Google Scholar] [CrossRef]
- English, L. D., Adams, R., & King, D. (2020). Design learning in STEM education. In Handbook of research on STEM education (pp. 76–86). Routledge. [Google Scholar]
- English, L. D., & King, D. T. (2015). STEM learning through engineering design: Fourth-grade students’ investigations in aerospace. International Journal of STEM Education, 2(1), 14. [Google Scholar] [CrossRef]
- Filion, L. J. (1994). Ten steps to entrepreneurial teaching. Journal of Small Business & Entrepreneurship, 11(3), 68–78. [Google Scholar]
- Filloy, E., Rojano, T., & Puig, L. (2007). Educational algebra: A theoretical and empirical approach (Vol. 43). Springer Science & Business Media. [Google Scholar]
- Fisher, D., Kusumah, Y. S., & Dahlan, J. A. (2020). Project-based learning in mathematics: A literatur review. Journal of Physics: Conference Series, 1657, 012032. [Google Scholar] [CrossRef]
- Forde, E. N., Robinson, L., Ellis, J. A., & Dare, E. A. (2023). Investigating the presence of mathematics and the levels of cognitively demanding mathematical tasks in integrated STEM units. Disciplinary and Interdisciplinary Science Education Research, 5(1), 3. [Google Scholar] [CrossRef]
- Fortus, D., Dershimer, R. C., Krajcik, J., Marx, R. W., & Mamlok-Naaman, R. (2004). Design-based science and student learning. Journal of Research in Science Teaching, 41(10), 1081–1110. [Google Scholar] [CrossRef]
- GeoGebra. (2025). GeoGebra [Computer software]. Available online: https://geogebra.org (accessed on 18 February 2025).
- Grossman, P., Dean, C. G. P., Kavanagh, S. S., & Herrmann, Z. (2019). Preparing teachers for project-based teaching. Phi Delta Kappan, 100(7), 43–48. [Google Scholar] [CrossRef]
- Gutiérrez, R. (1999). Advancing urban Latina/o youth in mathematics: Lessons from an effective high school mathematics department. The Urban Review, 31(3), 263–281. [Google Scholar] [CrossRef]
- Herbel-Eisenmann, B. A., Steele, M. D., & Cirillo, M. (2013). (Developing) teacher discourse moves: A framework for professional development. Mathematics Teacher Educator, 1(2), 181–196. [Google Scholar] [CrossRef]
- Jones, C., Penaluna, K., & Penaluna, A. (2020). Value creation in entrepreneurial education: Towards a unified approach. Education + Training, 63, 101–103. [Google Scholar] [CrossRef]
- Jukic Matić, L. (2019). The pedagogical design capacity of a lower secondary mathematics teacher and her interaction with curriculum resources. REDIMAT—Journal of Research in Mathematics Education, 8(1), 53–75. [Google Scholar] [CrossRef]
- Kolodner, J. L. (2002). Facilitating the learning of design practices: Lessons learned from an inquiry into science education. Journal of Industrial Teacher Education, 39(3), 9–40. [Google Scholar]
- Krajcik, J., McNeill, K. L., & Reiser, B. J. (2007). Learning-goals-driven design model: Developing curriculum materials that align with national standards and incorporate project-based pedagogy. Science Education, 92(1), 1–32. [Google Scholar] [CrossRef]
- Krajcik, J. S., & Blumenfeld, P. C. (2006). Project-based learning. In K. R. Sawyer (Ed.), The Cambridge handbook of the learning sciences (pp. 317–333). Cambridge University Press. [Google Scholar]
- Lackéus, M. (2015). Entrepreneurship in education—What, why, when, how. Entrepreneurship 360. Background paper. OECD. [Google Scholar]
- Laptev, G., & Shaytan, D. (2022). Co-design-based learning for entrepreneurs in the digital age. Measuring Business Excellence, 26(1), 93–105. [Google Scholar] [CrossRef]
- Mann, A., Denis, V., Schleicher, A., Ekhtiari, H., Forsyth, T., Liu, E., & Chambers, N. (2020). Dream jobs: Teenagers’ career aspirations and the future of work. Available online: https://www.mmllen.com.au/wp-content/uploads/2021/10/dream-jobs-teenagers-report.pdf (accessed on 18 February 2025).
- Mehalik, M. M., Doppelt, Y., & Schuun, C. D. (2008). Middle-school science through design-based learning versus scripted inquiry: Better overall science concept learning and equity gap reduction. Journal of Engineering Education, 97(1), 71–85. [Google Scholar] [CrossRef]
- Moberg, K. (2014). Two approaches to entrepreneurship education: The different effects of education for and through entrepreneurship at the lower secondary level. The International Journal of Management Education, 12(3), 512–528. [Google Scholar] [CrossRef]
- Moore, R. A., Newton, S. H., & Baskett, A. D. (2017). The InVenture challenge: Inspiring STEM learning through Invention and Entrepreneurship. International Journal of Engineering Education, 33(1), 361–370. [Google Scholar]
- Moore, T. J., Johnston, A. C., & Glancy, A. W. (2020). STEM integration: A synthesis of conceptual frameworks and definitions. In Handbook of research on STEM education (pp. 3–16). Routledge. [Google Scholar]
- Moschkovich, J. (2002). A situated and sociocultural perspective on bilingual mathematics learners. Mathematical Thinking and Learning, 4(2–3), 189–212. [Google Scholar] [CrossRef]
- National Governors Association Center for Best Practices, Council of Chief and State School Officers [CCSSO]. (2010). Common core state standards for math. National Governors Association Center for Best Practices, Council of Chief State School Officers. [Google Scholar]
- Newton, S. H., Alemdar, M., Moore, R. A., & Cappelli, C. J. (2018, June 24–27). An investigation of students’ experiences in a K-12 invention program (evaluation). The 2018 ASEE Annual Conference & Exposition, Salt Lake City, UT, USA. [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD). (2018). The future of education and skills: Education 2030. OECD. [Google Scholar]
- Passaro, R., Quinto, I., & Thomas, A. (2017). Start-up competitions as learning environment to foster the entrepreneurial process. International Journal of Entrepreneurial Behavior & Research, 23(3), 426–445. [Google Scholar]
- Pearson, G. (2017). National academies piece on integrated STEM. The Journal of Educational Research, 110(3), 224–226. [Google Scholar] [CrossRef]
- Penner, D. E., Lehrer, R., & Schauble, L. (1998). From physical models to biomechanics: A design-based modeling approach. Journal of the Learning Sciences, 7(3–4), 429–449. [Google Scholar] [CrossRef]
- Pérez Yuste, A., Herradón Díez, R., Blanco Cotano, J., Sánchez Fernández, J. A., & de Diego Martínez, R. (2014, July 9–10). An entrepreneurship-based learning (EBL) experience in information and communication technologies (ICTs). The 2nd International Conference of E-Learning and E-Educational Technology (ICELEET 2014), Zurich, Switzerland. [Google Scholar]
- Razzouk, R., & Shute, V. (2012). What is design thinking and why is it important? Review of Educational Research, 82(3), 330–348. [Google Scholar] [CrossRef]
- Rojano, T. (1996). Developing algebraic aspects of problem solving within a spreadsheet environment. In Approaches to algebra (pp. 137–145). Springer. [Google Scholar] [CrossRef]
- Schneider, R. M., Krajcik, J., Marx, R. W., & Soloway, E. (2002). Performance of students in project-based science classrooms on a national measure of science achievement. Journal of Research in Science Teaching, 39(5), 410–422. [Google Scholar] [CrossRef]
- Skinner, R. K., & Harlow, D. B. (2022). Recognition of design failure by fourth-grade students during an engineering design challenge. Journal of Pre-College Engineering Education Research (J-PEER), 12(2), 10. [Google Scholar] [CrossRef]
- Stevens, R. (2000). Who counts what as math? Emergent and assigned mathematics problems in a project-based classroom. In J. Boaler (Ed.), Multiple perspectives on mathematics teaching and learning (pp. 105–144). Ablex Publishing. [Google Scholar]
- Tabach, M., Hershkowitz, R., & Arcavi, A. (2008). Learning beginning algebra with spreadsheets in a computer intensive environment. The Journal of Mathematical Behavior, 27(1), 48–63. [Google Scholar] [CrossRef]
- Thomas, J. W. (2000). A review of research on project-based learning. Available online: https://tecfa.unige.ch/proj/eteach-net/Thomas_researchreview_PBL.pdf (accessed on 18 February 2025).
- von Glasersfeld, E. (1982). An interpretation of Piaget’s constructivism. Revue Internationale de Philosophie, 36(4), 612–635. [Google Scholar]
- Warshauer, H. K. (2015). Strategies to support productive struggle. Mathematics Teaching in the Middle School, 20(7), 390–393. [Google Scholar] [CrossRef]
- Wendell, K., & Rogers, C. (2013). Engineering design-based science, science content performance, and science attitudes in elementary school. Journal of Engineering Education, 102(4), 513–540. [Google Scholar] [CrossRef]
- Yu, W., Zheng, Z., & He, J. (2025). Integrating entrepreneurial education into STEM education: A systematic review. Research in Science Education, 55(1), 159–185. [Google Scholar] [CrossRef]


| D&P Components | PBL | DBL | EBL |
|---|---|---|---|
| Launch | |||
| Understand the Challenge | Identify content and skills needed to address the driving question. | Focus the problem and understand the design challenge. | |
| Learn More about the Challenge Context | Consider authentic constraints. | Define the authentic constraints and user-focused criteria. | Consider entrepreneurial opportunities and available resources. |
| Design | |||
| Brainstorm, Design, Test, and Refine Solutions | Collaboratively build an artifact that addresses the driving question. | Iteratively design a prototype that meets user criteria. | Design a viable product or service. |
| Develop the Key Business Proposition | Evaluate design against user-focused criteria. | Define how the product/service creates values for users (clients). | |
| Complete the Technical Brief | Connect project work to intended disciplinary content. | Reflect on the process using a design journal. | Define product specifications for the users (clients). |
| Pitch | |||
| Prepare and Practice the Pitch | Give, receive, and incorporate feedback. | Test and expose prototypes to critique. | Practice pitch with external experts. |
| Deliver the Pitch | Deliver culminating presentation. | Deliver a persuasive pitch to external judges. | |
| Challenge Title | Description | Champion | |
|---|---|---|---|
 Building Algorithms | Students build algorithms that use people’s opinions to rate or rank something they care about. Math Focus: Expressions and Equations |  | Cathy Yee CEO, Founder, Incluvie |
 Erase Food Waste | Students design food-related businesses that use sliding price scales to reduce food waste. Math Focus: Percents, Data Analysis |  | Oscar Ekponimo Founder, CEO Chowberry |
 Fix It: Design for Community Impact | Students design physical products that will help solve a problem facing their communities. Math Focus: 3-D Figures, Surface Area, Volume |  | Gitanjali Rao Inventor, STEM Promoter |
 Flashy Fashion | Students design wearable technology products that use LED lighting systems. Math Focus: Transformations, Coordinate Plane |  | Kelsy Dominick Designer, CEO DiDomenico Design |
 Keep It Real | Students design apps that use data representations to help people put down their phones and connect, face-to-face. Math Focus: Data Analysis and Representation |  | Dr. Cardell PatilloExecutive Director, Head StartProgram |
 Operation Lifeline | Students design medical packs that can be used to deliver refrigerated medications in times of natural disasters. Math Focus: 3-D Figures; Surface Area, Volume |  | Kris Ludwig Scientist, US Geological Survey |
 Pollution Solution | Students design containers, made from dissolvable or edible materials, to package and sell liquid products. Math Focus: 3-D Figures, Surface Area, Volume |  | Clifford Okoth Owino Founder, CEO Chemolex |
 Power Me Up | Students design companies that make it easier for people to charge their electric vehicles. Math Focus: Ratios, Data Analysis, Equations |  | Kristin Vicari Senior Chemical Engineer, Tesla |
 Prototype to Profit | Students build business plans and pitches to make existing product ideas economically viable. Math Focus: Building Linear Functions, Solving Linear Equations |  | Tyler Maloney Materials Science Engineer, Entrepreneur |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belcher, M.; Confrey, J.; Krupa, E.E.; Borden, M.L. The Design & Pitch Challenges in STEM: A Theoretical Framework for Centering Mathematics Learning in Entrepreneurial Pitch Competitions. Educ. Sci. 2025, 15, 651. https://doi.org/10.3390/educsci15060651
Belcher M, Confrey J, Krupa EE, Borden ML. The Design & Pitch Challenges in STEM: A Theoretical Framework for Centering Mathematics Learning in Entrepreneurial Pitch Competitions. Education Sciences. 2025; 15(6):651. https://doi.org/10.3390/educsci15060651
Chicago/Turabian StyleBelcher, Michael, Jere Confrey, Erin E. Krupa, and Margaret L. Borden. 2025. "The Design & Pitch Challenges in STEM: A Theoretical Framework for Centering Mathematics Learning in Entrepreneurial Pitch Competitions" Education Sciences 15, no. 6: 651. https://doi.org/10.3390/educsci15060651
APA StyleBelcher, M., Confrey, J., Krupa, E. E., & Borden, M. L. (2025). The Design & Pitch Challenges in STEM: A Theoretical Framework for Centering Mathematics Learning in Entrepreneurial Pitch Competitions. Education Sciences, 15(6), 651. https://doi.org/10.3390/educsci15060651






