Abstract
We investigated written self-reflections in an undergraduate proof-writing course designed to mitigate the difficulty of a subsequent introductory analysis course. Students wrote weekly self-reflections guided by mechanical, structural, creative, and critical thinking modalities. Our research was guided by three research questions focused on the impact of student self-reflections on student metacognition and performance in the interventional and follow-up class. To address these questions, we categorized the quality of the students’ reflections and calculated their average course grades within each category in the proof-writing, the prerequisite, and the introductory analysis courses. The results demonstrated that writing high-quality self-reflections was a statistically significant predictor of earning higher average course grades in the proof-writing course and the analysis course, but not in the prerequisite course. Convergence over the semester of the students’ self-evaluations toward an experts’ scorings on a modality rubric indicates that students improve in their understanding of the modalities. The repeated writing of guided self-reflections using the framework of the modalities seems to support growth in the students’ awareness of their proof-writing abilities.
1. Introduction
In the US, the transition from early university mathematics courses that are calculational in nature to proof-based courses—where students are expected to read, write, and assess proofs—has been a significant modern pedagogical challenge [1]. Even students who were successful in prior calculational courses, such as calculus and differential equations, may struggle when confronted with a proof-based course [2]. Historically and inter-institutionally, an alarmingly high number of students earn non-passing grades in their first proof-based course. At many institutions of higher education, a first course in proof writing aligns with one of two categories: (1) a course with a primary focus and learning objectives that address specific mathematical content, which we describe as a Content-Based Introduction to Proof (CBIP); or (2) a course for which the primary focus is on proof structure and techniques, which we call a Fundamental Introduction to Proof (FIP) [3]. In CBIPs, proofs (and the associated linguistic and logical content) are taught through the lens of other mathematical content, for example, linear algebra, abstract algebra, or real analysis. Alternatively, FIPs teach the fundamentals of proof writing through symbolic logic, sets, relations, and elementary number theory.
In the early 1980s, there was a concerted national movement to address students’ difficulty in transitioning to proof-based courses by creating FIP courses [4]. These courses aimed to teach students how to effectively communicate in the language of mathematics and, in particular, how to write formal proofs such as those required in upper-level courses. Today, most collegiate mathematics departments in the U.S. have incorporated some form of an FIP course as a requirement for baccalaureate math programs, although the syllabus and learning objectives of FIPs vary widely [3,4,5]. Marty [4] addressed the effectiveness of CBIP and FIP courses through a 10-year study at their institution. Longitudinal data, based on grade outcomes in future courses, were compared between student populations who took CBIP-type courses and student populations who took FIP-type courses. The findings, based on a population of approximately 300 students, led the author to suggest that it is more effective to focus on developing students’ approaches to mathematical content (as emphasized in FIPs) than to focus on the mathematical content itself. The study concluded that FIPs also increase students’ confidence and ability to take ownership in their mathematical maturation.
Developing best practices for teaching proof writing in the mathematical sciences has been the focus of much scrutiny and has proven to be a formidable task [6,7,8,9,10,11,12,13,14]. Alcock’s study [15], based on interviews with mathematicians teaching introductory proof material, addressed the complexity of the thought processes involved in proof writing. The article concludes with the suggestion that the transition to proof courses should address four independent thinking modes: instantiation, structural, creative, and critical modes. The study of Moore [2] looked specifically at the cognitive difficulties for students transitioning to proofs at a large university, concluding that the three main difficulties are (a) foundational concept understanding, (b) mathematical language and notation, and (c) starting a proof. The FIP in our study focuses on skills in (b) and (c) through novel self-reflective writing. Consequently, we identified a previously unaddressed opportunity to directly analyze the effectiveness of transition-to-proof reflective writing strategies.
The present study focused on an FIP course we recently developed to bolster the success rate of students in the subsequent Introduction to Real Analysis class. The latter course is considered difficult by many students and instructors. The modified course sequence begins with (1) a prerequisite introductory linear algebra course, followed by (2) the optional FIP course, predicted to prime student success in (3) the subsequent introductory analysis course. This sequencing allows for a direct comparison of students who choose the path of linear algebra to real analysis and those who choose to take the FIP between these core courses. The newly developed FIP course includes active learning techniques that have been shown to increase the efficacy of teaching mathematical proofs [4]. While building from the thinking modality work of Alcock [15], our approach of using reflective writing as a framework for students to develop self-awareness of their understanding of their proof-writing skills represents a novel interventionist [13] pedagogical approach compared to the traditional pedagogical approaches to transition-to-proof courses.
The goal of the present work was to assess the innovative use of student self-reflective writing-to-learn (WTL) exercises, scaffolded by a modality-based prompt and assessment rubric. Specifically, we developed a modality rubric that consists of a Likert-scale evaluation and field(s) for open-ended response self-evaluations for each of four modalities: mechanical (the mechanical modality corresponds to remembering, which is different from [15] the instantiative modality, which corresponds to a deeper understanding of the definitions), structural, creative, and critical thinking modalities of proof writing. Students were also asked to evaluate their use of the type-setting program LaTeX. However, here, we focus on the conceptual elements of proof writing, that is, the mechanical, structural, creative, and critical modes of thinking (see Appendix B for example modality rubrics and Section 2 for detailed descriptions of the modalities). The framework of these modalities and the modality-based rubric are inspired by prior, related work [8,16,17]. In weekly homework assignments, students were asked to reflect on their performance specifically in the context of their comfort with the modalities. With this structure, we posed three research questions:
- Does having students write reflections in the interventional (FIP) course support their ability to be metacognitive about their own proof-writing processes?
- Does having students write reflections in the interventional course impact their performance and success in that course?
- Does having students write reflections in the interventional course impact their performance in the subsequent Introduction to Real Analysis course?
We addressed these questions over three semesters of the FIP course through analyzing students’ weekly self-reflections (both with Likert ratings and open-ended responses) and correlating with students’ grades in the prerequisite, interventional, and subsequent introductory analysis courses. As such, we addressed a gap in the research in mathematics education regarding the cognitive processes involved in proof writing [1]. Specifically, we investigated the effectiveness of a novel approach that has students engage in reflective writing in a transition-to-proof course. While there is extensive research on reflective writing and student success, our novel contribution is combining the modality rubric, one of the best practices for teaching proof writing, with reflective writing.
While the focus of this work is on the impact of reflective writing on student achievement in an introductory proof-writing course, there is a related question of the impact of the new course as an intervention relative to a student’s overall success. We analyze the impact of the new course in a subsequent paper [18] using data from a pre–post-assessment and analyzing students’ grades in the prerequisite course, the interventional course, and the subsequent course for students who took and did not take the interventional course. Preliminary results show a positive effect of the interventional course on student learning and success [18].
The next section lays out the theoretical framework for our study design and methodologies. The Materials and Methods section describes the interventional course, the learning modalities, the instruments used, and the qualitative and quantitative methods used to analyze the student reflections. The Results section includes a discussion of student performance in the progression of courses as a function of the quality of their reflections, an analysis of their growth in metacognition, and an analysis of student reflections relative to the grader’s evaluation of student performance. Finally, the Discussion section contains a summary of our results, conclusions, and other considerations.
2. Theoretical Framework and Related Literature
In this section, we synthesize theory and the relevant literature to provide framing for the pedagogical practice of having students engage in reflective writing in mathematics and how and why to provide students with instructional scaffolding to support their reflection on their proof-writing processes. We also trace the origins of our framing of the four thinking modalities involved in proof writing.
2.1. Reflective Writing-to-Learn in Mathematics
Writing stimulates thinking and promotes learning [19,20,21,22,23]. In the process of composing, writers put into words their perceptions of reality. As Fulwiler and Young describe it, “…language provides us with a unique way of knowing and becomes a tool for discovering, for shaping meaning, and for reaching understanding” [22] (p. x). Writing enables us to construct new knowledge by symbolically transforming experience [24] because it involves organizing ideas to formulate a verbal representation of the writer’s understanding.
For more than 50 years, research in the movements known as writing-to-learn (WTL) and writing in the disciplines (WID) has shown the connections between writing, thinking, and learning and has demonstrated that writing may contribute to gains in subject area knowledge [25], and specifically in mathematics [26,27,28,29,30]. One strand of theorization around the mechanisms by which writing may lead to gains or changes in understanding in a particular subject area holds that the act of writing spontaneously generates knowledge, without attention to or decisions about any particular thinking tools or operations [31,32]. The writing process commonly referred to as free writing is associated with this strand of theory. Another conceptualization of the role of writing in thinking and learning is the idea that when thinking is explicated in the written word, the writer (and readers) can then examine and evaluate those thoughts, which may allow for the development of deeper understanding [33], as cited in [32]. Pedagogical approaches that follow from this view include reflective and/or guided writing processes. Other theories of the relationship between writing and learning focus on the role of attention to genre conventions [34] and rhetorical goals [35] and how attending to these concerns allows writers to transform their understanding. Together, these theories of the connection between writing and learning, along with empirical studies of the effects of writing-to-learn, argue for the value of having students articulate their thinking about a subject matter through the written word.
Indeed, a recent meta-analysis of more than 50 studies of WTL activities in math, science, and social studies at the K-12 level found that writing in these subject areas “reliably enhanced learning (effect size )” [36] (p. 179). Furthermore, Bangert-Drowns et al.’s earlier (2004) [25] meta-analysis of writing-to-learn studies had found that scaffolding students’ writing through prompts that guided them to reflect on their “current level of comprehension” (p. 38) of the topic was significantly more effective than other kinds of prompts or than unguided writing.
Such metacognitively focused reflective writing is a mode of WTL that supports learning by engaging the writer in the intentional exploration and reconstruction of knowledge and personal experience in a way that adds meaning [37,38]. In the process of reflection, the learner’s own experience and understanding become the focus of their attention. Done well, reflection in writing enables the writer to abstract from, generalize about, and synthesize across experiences [39]. When reflective WTL is supported pedagogically through well-constructed writing prompts and instructor and peer feedback, the writing process may enable student writers to become aware and in control of their own thinking and learning processes, in other words, to become metacognitive and self-regulating [38]. Such an ability to self-regulate their learning processes also contributes to learners’ perceptions of greater self-efficacy [40,41]. Thus, guided, reflective WTL activities hold particular promise for helping learners to organize their knowledge, thereby deepening their understanding, gaining more awareness and control over their learning processes, and experiencing a sense of greater self-efficacy.
In mathematics, guided, reflective WTL aims to support learners’ making connections to prior knowledge, developing awareness of and improving problem-solving processes (i.e., metacognition), bringing to consciousness areas of confusion or doubt as well as the development of understanding, and/or expressing the learner’s feelings and attitudes toward math [42]. A small body of the literature on reflective WTL in college-level mathematics exists, but even fewer studies have aimed to connect reflective WTL with improved student outcomes in mathematics courses. Much of the existing literature on reflective WTL in mathematics focuses on students’ feelings and attitudes, specifically helping students to express and alleviate math anxiety [42,43]. In a notable departure, Thropp’s controlled study aimed to show benefits from reflective writing for student learning outcomes in a graduate statistics course. Students who participated in reflective journal writing in the interventional statistics course performed significantly better on an assignment and a test than students in the control section who did not engage in reflective journaling [44].
2.2. Scaffolding Reflection on Proof Writing
For reflection in writing to be productive, many students need some support and guidance [25,30,38,45,46,47,48,49]. Guiding questions and other forms of “scaffolding” [50] can help students focus on the elements of their thinking and problem solving that are important for their success in the course. Bangert-Drowns et al.’s meta-analysis [25] found that the metacognitive scaffolding of writing-to-learn activities, such as interventions that had students “reflect on their current understandings, confusions, and learning processes”, were associated with gains in student learning. Applying it to proof writing, we posit, therefore, that focusing students’ attention on modes of thought associated with constructing and justifying proofs might help them to understand proofs better and become more adept at writing them [6,51]. Another more streamlined approach toward the thinking modes involved in proof writing is Alcock’s four modes [15]: instantiation, structural thinking, creative thinking, and critical thinking. Engaging students on these fronts likely requires classroom approaches and techniques beyond standard lecture. Therefore, our study adapted the above approaches to guide students’ reflection on their proof writing using four thinking modalities, as outlined below.
2.3. The Modalities for Thinking about Proof Writing
The mechanical modality refers to the precise use of definitions and formal manipulation of symbols. Accurate and precise use of language in definitions is a new skill for students as they begin to write proofs [52,53], and they often find it difficult to understand and apply many of the definitions of advanced mathematics [2,54]. Instantiation, as described by Alcock [15], goes beyond the simple memorization of a definition and includes understanding the definitions to the extent of successfully applying them to an example. Instead of Alcock’s instantiation [15], we chose to focus the mechanical modality on the more basic skill of memorization, since this was an introduction to proof writing class. Alcock’s instantiation [15] might be better for the real analysis course, so students can build on the mechanical modality as their proof-writing acumen increases. The mechanical modality as used here does not require the level of understanding of Alcock’s instantiation [15], and instead refers to memorizing, a very basic learning skill.
The structural modality focuses on viewing the whole proof as a sum of its constituent parts. For instance, standard proof writing begins with stating the hypothesis and ends with stating the conclusion. To prove an if-then statement , one must justify how the hypothesis leads to the correct conclusion. The proof of an if-and-only-if statement , however, must include proving both the forward implication and backward implication . Thus, the proof comprises two pieces. This is similar to “zooming out” as described by Weber and Mejia-Ramos [55] and reminiscent of the idea of the “structured proof” studied by Fuller et al. [56]. The structural modality corresponds to more complex cognitive skills than the mechanical modality since it requires students to see both the whole proof and the parts that contribute to the whole.
The creative modality involves making appropriate connections between concepts to correctly ascertain the crux of the statement/proof. For a simple if-then style proof, the creative modality is the crucial idea that connects the hypothesis to the conclusion. Still, there is no algorithmic method to teaching students how to connect the hypothesis to the conclusion because it will be different for each proof. The creative modality is similar to the “zooming in” strategy proposed by Weber and Mejia-Ramos [55] as “filling in the gaps” or a line-by-line strategy or “key idea” or “technical handle” as suggested by Raman et al. [57]. This modality is more challenging than either the structural or mechanical modalities because it requires creating a logical sequence of statements.
The critical modality involves ascertaining the overall truth or falsity of a statement/proof, thus verifying a sequence of logical steps or producing a viable counterexample [58]. Critically assessing whether a proof is correct, well written, valid, and has the right amount of detail for readers to follow is an advanced skill that results in differences in interpretation even among mathematical experts [7,8,9,12,57,59,60,61,62]. Students find this modality challenging for several reasons. For one thing, they typically read less skeptically than experts. They also tend to trust every line of proof by default if it is written by a mathematician [63]. To verify the validity of a proof, students must think abstractly to decide if the hypotheses and line-by-line details warrant the conclusion [64]. Students struggle with the critical modality because it involves both “zooming in” and “zooming out”, as referenced by Weber and Mejia-Ramos [55] (p. 340).
3. Materials and Methods
3.1. Context of Research
3.1.1. FIP Interventional Course Description
We piloted a 4-credit class, Introduction to Mathematical Reasoning, with a maximum capacity of 30 students. The course was offered to students who had not yet taken, or attempted, a CBIP and had previously completed a second-year introductory course in linear algebra with a grade of “C” or better. The textbook we used was Edward R. Scheinerman’s (2013) Mathematics: A Discrete Introduction, 3rd Edition, Brooks/Cole [65]. Twice a week, students met with the faculty instructor for 75 min for a content-focused lecture and guided examples. A subsequent weekly, 50 min discussion section, led by a teaching assistant (TA), engaged students actively in small groups working on low-risk assessments. Students were expected to complete homework assignments independently each week. Throughout the semester, students took three unit exams and a cumulative final exam with questions aligned to student learning objectives (see Appendix A). Overall, the FIP course format facilitated deliberate practice of proof-writing skills through both traditional (i.e., lecture) and active learning (i.e., group work) methods.
The focal interventional course was developed by one of the authors of this manuscript, some colleagues in the Department of Mathematics and Statistics, as well as pedagogical experts in the Faculty Development Center, with the aim of decoupling the structural foundational difficulties of proof writing from specific mathematical concepts, such as mathematical analysis and abstract algebra. To this end, the students developed proof-writing skills based on topics including basic number theory ideas (e.g., odd, even, prime, and divisibility), sets, logic and truth tables, and relations. The course focused on basic proof techniques such as if-then and if-and-only-if but also introduced more advanced proof techniques, including induction, contradiction, contraposition, and smallest counterexample. The final weeks of the course focused on applying these techniques to set-based function theory using ideas such as injective, surjective, and bijective. We addressed these competencies among others through the eight specific learning objectives listed in Appendix A. The scope of the interventional course was consistent with 81% of FIPs offered at R1 and R2 universities [3]. During this study, this newly designed FIP course was taught by the same instructor (who is an author and the course developer) and two different TAs for three semesters from Fall 2019 through Fall 2020. Data collection for this study was impacted by the COVID-19 pandemic. This course abruptly switched to an online course during the second semester and was taught completely online for the third semester of data collection. We further comment on the impact of the pandemic in the Discussion.
3.1.2. The Role of the Teaching Assistant
Each semester the course was offered, there was one teaching assistant (TA) assigned to the course. Over the three semesters that data were collected for this study, two different individuals served as the teaching assistant for this course: one individual for Fall 2019 and Spring 2020, and a different individual for Fall 2020. The role of the teaching assistant for this course is multifaceted. The TA, as mentioned previously, led a 50 min discussion section each week. In addition, the TA graded the weekly homework assignment, which consisted of the worksheets given during the discussion, questions from the book, and the modality rubric. For the purposes of this study and after grading the discussion worksheet and questions from the book, the TA evaluated each student on a Likert scale for their proficiency in each modality each week. As a TA for the course, the individual had extensive experience in writing proofs and was fluent in the meaning of each of the modalities. The TA was not required to write self-reflections such as the ones that the students wrote, nor did they participate in the part of the research that involved reading and rating the students’ reflections.
3.1.3. Participants
Prospective participants for this study included students who completed the interventional FIP course, the subsequent introductory analysis course, Introduction to Real Analysis, and the prerequisite core course, Introduction to Linear Algebra, with a grade of C or better. Prospective participants reviewed an informed consent letter, approved by the Institutional Review Board, before actively joining or declining to join the study. Only students consenting to the study () had their course data included in research analyses. All participants were enrolled in the interventional FIP course during one of the first three semesters that it was offered at the focal institution, a mid-sized, public, minority-serving research university in the mid-Atlantic region of the United States. According to institutional data, 39% of student participants in this study identified as female and 61% as male. In total, 38% of the participants identified their race/ethnicity as White, while 62% identified as people of color.
3.1.4. Reflection Guided by Thinking Modalities
The development of a new course allows opportunities for innovations in pedagogy to better achieve course goals. The innovation described here involved students in writing self-reflections on their proof-writing processes and abilities, scaffolded by a rubric that defined four thinking modalities of proof writing: mechanical, structural, creative, and critical. The goals of having students write self-reflections included: (1) supporting students’ metacognitive awareness of their proof-writing processes and abilities by giving them a framework for identifying specific areas of struggle; (2) assessing students’ development in these skills over the semester; and (3) allowing the instructor to evaluate the role of interventional self-reflection in students’ learning of proof writing. The four thinking modalities were described to students routinely throughout the entire interventional course, both in lectures and in the discussion sections. Each weekly homework prompted students to evaluate their proof-writing performance through the lens of each modality. Students began this reflective process by evaluating their performance on a Likert scale, followed by writing justifications of their Likert ratings in an open-ended response field (see Appendix B). The Likert ratings served a multifaceted purpose. They (1) corresponded to a modality rubric containing descriptors developed by the instructor to approximate novice-to-mastery level achievement with each modality; (2) encouraged students to carefully consider their achievement-level(s) using each modality, thereby preparing them to write a more meaningful self-evaluation in the open-ended response portion of the reflection; and (3) provided a means for the instructor to quickly compare students’ perceptions of their modality skills to that of the grader, a TA considered to have expert-level fluency with the modalities and proof writing.
The cognitive difficulty associated with each of the modalities increased over the semester. Early in the course, the mechanical modality consisted of learning basic definitions such as “even”, “odd”, “prime”, and “composite” (among others). As the semester progressed, students learned new definitions, such as “relation” and “equivalence relation”, which were more abstract and challenging for the students to remember and apply. Similarly, the structural modality was concrete for the proof of an “if-then” statement, introduced near the beginning of the semester. However, toward the end of the course, students were asked to construct more complex proofs, such as an “if-and-only-if” statement in conjunction with a hypothesis and conclusion that involved “set equality”. The structure of such a proof is more advanced because it comprises four separate parts. Given this increase in complexity, we would not expect linear progress in students’ development of these modalities over the course of the semester. The open-ended response justifications and explanations in the written reflections provide insight into the students’ thinking and learning processes throughout the course.
3.2. Research Methodology
3.2.1. Instruments
While students worked toward mastery of the learning objectives (Appendix A) through a variety of formative and summative assessments, the focal instrument for this study was a novel reflection tool assigned to students along with each weekly homework assignment. Students’ evaluations were guided by a modality rubric with an accompanying Likert scale and field(s) for open-ended response self-evaluations for each modality (see Appendix B). Students were assigned to complete one reflection for each of 12 weekly homework assignments. The TA graded students’ weekly homework and evaluated students’ performance of each modality using the same Likert scale that students used to self-evaluate. While the TA provided written feedback on weekly homework problems, the TA did not comment on the students’ written reflections, and the students were not aware of the TA’s Likert scale ratings on the modalities. Students were given credit for completing the weekly modality rubric and reflection.
Over the three-semester study, the self-reflection prompts changed in response to direct feedback from the students and the recognition of a misalignment between the instructor’s expectations for open-ended response content versus the observed content submitted by students. The rubric for each semester can be found in Appendix B. In the first semester of the study, some students provided vague or off-point comments in relation to modalities, which provoked re-examination of the instrument’s phrasing. For example, the original mechanical modality required “insightful” use of definitions. Recognizing that this was vague, we changed the requirement to a more basic skill of memorizing definitions “precisely”. Likewise, student feedback drove a change to the Likert scale range used to self-rate performance. Below, we describe these changes in detail.
During the first semester, the students self-rated their mastery of each thinking modality using a four-point Likert scale, attached to the descriptors superior, proficient, acceptable, and poor (see Appendix B). In addition to these four categories, students could choose “not applicable for this homework”. Subsequently, students were prompted to write a short self-reflection on “substantial gaps or significant improvement” with respect to their mastery of the modalities. Students typically focused on only one of the modalities, and their reflective responses lacked specificity. During the first semester of the study, students used a Learning Management System tool to enter both the Likert scale responses and open-ended response reflections/justifications. For the subsequent two semesters of the project, these responses were entered into a Google form.
The student feedback and instructor’s evaluation of student responses drove a change in the Likert scale students used to rate their performance during the second and third semesters that the course was offered (see Appendix B). The Likert scale for each modality was expanded to include seven increments, where a rating of “7” indicated confident mastery, and a “1” indicated a significant need for more instructional support. Consistent with the first semester, students were also given the choice of “not applicable for this homework”. The explanation for each increment on the Likert scale changed as well. For example, the highest self-rating or TA rating of superior on the mechanical modality was described during the first semester as “Student shows flawless and insightful use of definitions and logical structures, and formal manipulation of symbols”. During the second semester of the study, the revised rating of “7” on the Likert scale read “I consistently and correctly use definitions, logical structures, and formal manipulation of symbols”. While the first description tacitly asked the students to rate their performance and the language implied an almost unattainable perfection, the revised prompt is more student-centric (such as the use of “I”) and explicitly asks students to evaluate their own skills. In an effort to elicit more details from the students, the prompt for the open-ended self-reflection was also revised in the second semester to read “Please comment on why you chose each of the ratings above” in an effort to guide students to comment on each of the four modalities, every week. During the second offering of the course, the instructor explicitly discussed the reflection prompt with students and reinforced expectations with an example of an ideal reflection.
During the third semester of the interventional FIP course, the seven-point Likert scale on which students evaluated their performance with respect to each modality was retained. However, in a further effort to elicit high-quality self-reflections for each of the modalities, the prompt for the written self-reflection instructed students to respond to each modality separately by writing four different self-reflections. In addition, more explicit instructions were given to the students (see Appendix B for details). The prompt for the mechanical modality, for example, became “Using the format claim → evidence → reasoning, justify your chosen ranking for the Mechanical Modality. Be sure to include specific examples for evidence to support your claim, and carefully describe your reasoning for how your evidence supports your claim”.
3.2.2. Qualitative Methods
Three raters (the authors) independently read and rated all the reflections provided by participants, for a total of responses, out of a possible 432 responses. (The difference between the total and possible numbers of responses reflects the fact that some participants did not write all 12 reflections during the semester.) The overall quality of each participant’s set of reflections was initially rated as one of four levels: exceptional, acceptable, developing, or incomplete. The definitions of each quality level were refined ad hoc as the raters made iterative passes through the data and patterns of completion and specificity emerged from the data, a method adapted from analytic coding techniques as described by Coffey and Atkinson [66]. While the prompts were refined in the second and third offerings of the course, the criteria by which we rated students’ responses were consistent over all three semesters of data. Table 1 provides descriptions with which each participant’s open-ended response reflections were rated for quality. In order for a student’s response profile to be categorized as exceptional, acceptable, developing, or incomplete, criteria had to be satisfied for both the aligned “Completion of Assigned Reflections” and “Adherence to the Prompt” columns of Table 1. For example, if a student’s reflections were 75% complete over the semester, yet only 50% of the reflections adhered to the prompt, then the student’s response profile would be categorized as Acceptable, not Exceptional. Assessing reflection quality is crucial to addressing our research questions.

Table 1.
Parameters for rating the quality level of students’ written reflections.
In developing the rating categories for students’ reflections, we considered the percent of reflection assignments completed over the semester. However, the percent of reflections completed could not be the sole definition of quality since several students completed most assignments with little effort or adherence to the prompt. In order to specifically address the prompt, reflections went beyond stating, for example, that the homework was “easy” or “hard”; ideal reflections provided explanations and reasoning for any of the four modalities the student struggled with or felt confident about. Rephrasing the prompt without additional context did not constitute a highly specific reflection, nor did commenting on one’s rating of the respective homework assignment. Likewise, several students provided thoughtful, targeted reflections in some instances but neglected to write them or wrote vague ones in other instances. It is important to note that the rating process did not address the correctness of any mathematical claims students made since the prompt did not require them to make mathematical claims. Rather, the focus of the reflection was on their own thinking, with reference to the thinking modalities. Therefore, our ratings of the quality of student reflections is based on the extent to which they showed such metacognition, not on mathematical accuracy.
After independently coding written reflections, the three raters deliberated and reached consensus, following [67], on appropriate quality ratings for all 36 participants’ reflections. The methodological flow diagram in Figure 1 shows how these 310 individual written reflections were categorized throughout the research process.
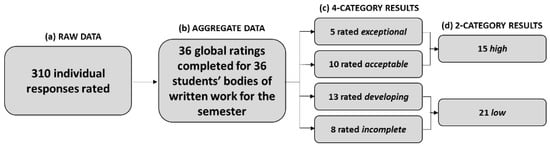
Figure 1.
Data analysis flow diagram: This figure shows the data analysis process we conducted and the relationships among (a) the raw data, or individual student responses; (b) the aggregate data, or the global rating assigned to each student’s collection of responses; and the analytical categories these collections of responses first assigned to (c) four categories, which were later collapsed into (d) two categories.
3.2.3. Quantitative Methods
Quantitative analyses treated written reflection data on a broader level of two groups: low or high quality. Developing and incomplete reflections were grouped together in a “low quality” category. Likewise, acceptable and exceptional data were treated as a group of “high-quality” reflections. We decided to explore the broader categories for two reasons. First, while deliberating and reaching consensus for rating the reflections qualitatively, we often struggled with distinguishing incomplete reflections from developing reflections, and acceptable reflections from exceptional ones. Second, given the small sample size and variance, we expected that creating two larger categories would allow relationships to emerge.
To determine whether a relationship existed between content-specific reflection quality and students’ performance in relevant mathematics coursework, quality identifiers for each participant’s written reflections were aligned with their respective final grades in the prerequisite course, the interventional course, and the subsequent required core course (on a five-point scale: and ). The real analysis course was chosen because it is a required course for all math majors at the focal institution, and students from the FIP course would then enroll in that course. The majority of the grade in each of these courses was determined by in-class exams and a cumulative final exam. Quantitative analyses accompanied qualitative analyses to provide support for emerging patterns. The weekly modality rubric prompted students to rate their use or understanding of the four modalities on a Likert scale (see Appendix B). We calculated the difference between grader and student modality rubric ratings for each modality, per student, per week of the semester. These difference data were used in a Pearson’s Correlation test to determine if they shared a significant linear relationship with time in the interventional course (assignment week over the duration of a semester). With this test, we asked, as the weeks passed, do grader–student differences in rubric ratings decrease? A smaller difference in grader–student ratings was intended as a proxy for students’ modality use reaching expert level.
3.2.4. Statistical Analyses
Descriptive quantitative statistics were applied to determine whether course grade data sets followed a normal distribution, for which statistical tests were warranted. Both Shapiro–Wilk and Kolmogorov–Smirnov tests for normality revealed that none of these data sets of interest met the criteria for parametric tests, except for tthe modality rubric data. Therefore, non-parametric tests were applied to compare multiple groups of unpaired, non-normal data, while parametric tests were used to analyze the modality rubric data, as described below.
After categorizing students’ reflections as one of two quality groups, the corresponding grade data were analyzed with independent samples Mann–Whitney U tests. This test was selected because we wished to compare the same variable (grade earned) across two completely different groups of subjects (those producing “low-” vs. “high-quality” reflections). Similarly, we applied the independent samples Kruskal–Wallis test to compare the course grades of four completely different groups of subjects, those whose set of reflections were rated as (1) exceptional, (2) acceptable, (3) developing, or (4) incomplete quality.
Pearson’s Correlation test was applied to the normative modality rubric numeric data to elucidate possible direct or inverse relationships between subjects’ course grades and the quality of their written reflections. Likewise, parametric beta linear regression analysis with independent variables of linear algebra grades and “high-quality” written reflections and the dependent variable of the Real Analysis couce grade allowed us to investigate the significance on “beta” for the binary variable; the binary variable was whether students earned a passing grade in the interventional course. In other words, the selected statistical test considered whether some combination of prerequisite course performance, interventional course performance, and/or written reflection quality could reliably predict or explain course performance in the next, rigorous course in sequence.
Data were organized in Microsoft Office Excel, and all statistical tests were performed in IBM SPSS Statistics 26. The study was classified by UMBC’s Office of Research Protections and Compliance as exempt (IRB protocol Y20KH13003), 25 July 2019.
4. Results
4.1. Analyses of Reflections for Quality, Metacognition, and Variability across Cohorts
The three raters independently rated the body of each student’s written reflections over the 12 homework assignments to provide a single, holistic rating for each student’s work. In determining these ratings, we agreed that typical “exceptional” reflections explicitly addressed the prompt by explicating multiple modalities and consistently provided examples and/or reasoning. Reflections rated “acceptable” often explicitly responded to the prompt, sometimes provided specific examples of areas of struggle or success from the student’s proofs, and/or provided some reasoning for the self-rating. A holistic rating of “developing” was assigned if the student neglected to submit some responses and/or the reflections responded to the prompt in nonspecific ways. A rating of “incomplete” was assigned where a student did not complete the reflections or the writing was extremely vague with respect to the prompt. See Table 1. Example responses characteristic of each quality level are shown in Table 2. One participant completed over 50% of reflection opportunities, yet their reflections were rated as “incomplete” (instead of “developing”, as suggested by the completion parameter) because the majority of their reflections were a single word, which was insufficient for addressing the prompt. Nearly all participants whose reflections were rated as exceptional completed at least 11 of 12 assignments. However, the reflections of one participant who completed only nine assignments were rated as exceptional due to their overall quality.

Table 2.
Example participant reflections characteristic of four quality levels (one example provided per semester per level).
As shown in Table 2, students whose writing was rated as “developing” or “incomplete” skipped writing the reflections or wrote them using very vague language. They generally did not describe their struggles or successes and did not refer to the modalities or any specific elements of the proofs they wrote that week. Thus, their reflections did not provide good evidence that they understood the four modalities and could appreciate how to operationalize them in order to write their proofs.
4.2. Analysis of Student Growth in Metacognition
In this section, we analyze student growth in metacognition based on a longitudinal analysis of student reflective writing over the semester, as well as a longitudinal comparison of student ratings with the ratings of the grader, whom we consider an expert in this context.
4.2.1. Longitudinal Analysis of Student Reflective Writing
To frame our analysis of metacognition in the students’ reflective writing over the semester, we looked for evidence of their awareness of and ability to control their own thinking and learning processes, specifically their use of the four thinking modalities to self-regulate their learning of the proof-writing process, as well as evidence of metacognitive growth in their reflective writing over the semester. Students who were able to articulate their thinking processes through accurate use of the modalities to explain their approaches to the homework in their reflections and/or were able to clearly express the extent of their understanding of how the modalities supported their ability to write the homework proofs were judged as showing evidence of metacognition. All 15 students whose sets of reflections were rated exceptional or acceptable showed evidence of metacognition in one or more of the reflections they wrote.
As an example of metacognition in reflection, we highlight a few of Student 13’s reflections, which were selected for their typicality as well as their richness in detail. This student’s set of reflections was rated exceptional overall and showed early and consistent evidence of metacognition. In Homework 2, Student 13 wrote:
Mechanical: I think I did a better job at using symbols than homework 1, but I’m still not sure whether it’s greater than, as good, and hopefully not worse than homework 1…(Student 13, Homework 2)
In the first clause of this statement (“I think I did a better job at using symbols than homework 1”), Student 13 shows awareness of improvement in their use of symbols compared to in the previous week’s homework. In the second clause (“but I’m still not sure whether it’s greater than, as good, and hopefully not worse than homework 1”), they also demonstrate awareness of the limits of their current understanding, mentioning what they struggled with or were still unsure about. Like all students whose reflections were rated exceptional , Student 13 cited specific elements of that week’s proof exercise that showed they understood how the modalities relate to the thinking involved in writing those proofs. See, for example, the rest of Student 13’s Homework 2 reflection:
…[Structural]: I think I was able to show off parts of the statement in the truth table in order to fully determine if two statements were equivalent, but there could be something that I could be missing from the tables. Creative: I was able to show some connection between statements in order to determine if statements were logically equivalent, but I feel like I wasn’t able to fully explain some of the statements as to why they were either true or false. Critical: I think I was able [to] show how statements were either true or false, and was able to show my thought process with the truth tables.(Student 13, Homework 2)
In response to the creative modality, Student 13 was able to articulate an awareness of strengths (“I was able to show some connection between statements”) but also identify areas of improvement (“I feel like I wasn’t able to fully explain some of the statements”). Thus, Student 13 is demonstrating signs of metacognition in their reflections by being able to identify their own strengths and weaknesses in writing the proofs in Homework 2.
While Student 13’s set of reflections are representative of writing that was rated exceptional overall, it is noteworthy that only five students out of 36 across the entire data pool wrote reflections that were rated this highly. In total, 9 of the 10 students whose sets of reflections we rated as acceptable wrote some entries that were highly metacognitive and self-critical (39 out of 108 instances of reflection across 12 homeworks for 9 students), but they did not consistently, throughout the entire semester, ground their references to the modalities in actual performance or the particulars of that week’s proofs. In total, 8 of 10 students whose set of reflections were rated acceptable showed inconsistent evidence of progress in metacognition over the semester. However, two students whose reflections were rated acceptable showed consistent development in their ability to reflect metacognitively about proof writing over the semester. Student 9’s reflections, for example, are representative of such growth, and were selected to highlight here because the contrast between their early and later writings is vivid. Compare Student 9’s reflection on Homework 3 with what they wrote for their final reflection on Homework 12:
I believe that the proofs I provided used adequate detail and included logical connections between statements in this homework.(Student 9, Homework 3)
I believe that I have made a lot of improvement on how to approach a proof problem. I think I really built the mechanical and [structural] modality being that I can see a proof and immediately be able to break it down into the multiple subsections in order to solve it in [its] entirety. However, going from one point to the next is where I think I struggle. I have a tendency to set up each part of the proof or create a form of a shell of what needs to be filled in and then I have a hard time filling in some of the gaps. I think the repetition of proofs in class and on the homework have allowed me to improve on doing so, however I think I need a bit more practice on my own over the winter break…(Student 9, Homework 12)
In the earlier reflection on Homework 3, Student 9 wrote in generalities with no explicit reference to the modalities or to their process, whereas by Homework 12, Student 9 articulated strengths and weaknesses in their proof-writing process with explicit reference to the modalities. Thus, while Student 13, classified as writing exceptional reflections, showed signs of metacognition in their responses as early as Homework 2, Student 9, classified as writing acceptable reflections, showed development of metacognition over the semester.
4.2.2. Longitudinal Analysis of Student–Grader Differences
We examined the question of whether grader–student differences in rating decrease over time using Pearson’s Correlation test and found that as the semester progressed, student and grader ratings became more similar in the structural and creative modalities (, Table 3). A similar trend is evident for both the mechanical and critical modalities, but not significantly so. The negative Pearson Correlation values show that the linear relationship for all four modalities is negative: As time passed, the difference in ratings between graders and students decreased.

Table 3.
Correlations between time and the difference between grader and student reflective rubric ratings.
The symbol indicates that the p-value of significance is less than . Through analyzing student reflections as well as comparing student–grader differences over time, there is evidence of student growth in metacognition over the semester. Below, we will show that students who wrote high-quality reflections demonstrated strong performances in both the interventional course and the advanced course.
4.3. Comparison across Semesters
The proportion of the students classified as writing either high- or low-quality reflections was fairly consistent over the three semesters (see Table 4). Notably, the relative proportions of reflection quality observed in the second iteration of the course, which coincided with an abrupt transition to emergency remote instruction in spring 2020 due to the COVID-19 pandemic, stand out in comparison to the semesters prior and following.

Table 4.
Descriptive statistics of participant reflections by quality.
In summary, students were grouped by the quality of their reflection responses over the course of the semester. Student reflections showed both evidence of metacognition as well as growth in reflective writing and development of metacognition. Despite changes to the prompt in an effort to elicit better self-reflections and an abrupt transition to online instruction, the proportions of reflection quality remained fairly consistent over the three semesters.
4.4. Analyses of Quantitative Trends
We compared the achievement of participants in the prerequisite course (linear algebra), the interventional course (FIP), and the subsequent course (Introduction to Real Analysis) based on participants’ quality of self-reflections in the interventional course. Specifically, we analyzed math course grade data on the basis of reflection quality. We proceeded with two statistical perspectives: (1) comparisons of students’ course grades between multiple groups of written reflection quality and (2) beta linear regression analyses to evaluate the possible role(s) of linear algebra grades, FIP grades, and written reflection quality as predictors of course grades in Introduction to Real Analysis.
Course performance diverged between those students who had high-quality (exceptional or acceptable quality) reflections in the interventional course compared to those who had low-quality (developing or incomplete quality) reflections as shown in Figure 2. This difference in performance between the reflection quality groups is more prominent in both the interventional and introductory analysis course grades, as compared to prerequisite core course grades. Figure 2 illustrates that the performance differential between the students who wrote high-quality reflections and the students who wrote low-quality reflections increases with course progression. A non-parametric, individual samples test (Mann–Whitney U) was applied to the data, with reflection quality (high vs. low) as the group qualifier. Statistical results suggest that differences between course grades among those students () who wrote high- vs. low-quality reflections were significant in the interventional () and introductory analysis courses (), and not significant in the prerequisite core course ().

Figure 2.
Relationship between average course grades and two categories of reflection quality: We classified each participant’s responses as either high quality (“exceptional/acceptable”, black bars) or low quality (“developing/incomplete”, gray bars); the participants’ grades in the prerequisite core course (linear algebra), the interventional (FIP) course, and the introductory analysis course (real analysis) were determined. The course grade results are shown in the bar graph, where a grade of ‘A’ corresponds to 4, ‘B’ corresponds to 3, ‘C’ corresponds to 2, ‘D’ corresponds to ‘1’, and 0 to ‘F’ or ‘W’ (withdraw). While each course shows a higher average grade for the “exceptional/acceptable” participants (black bars), only the grades in the interventional FIP course () and introductory analysis course () are statistically significant.
4.5. Reflection Quality and Prior Student Course Achievement as Predictors of Future Success
A beta linear regression test shows that reflection quality, treated as two category levels, is a significant predictor of the Real Analysis grade (, ). A separate beta linear regression test shows that the Linear Algebra grade (scale of 0–4) is not a significant predictor of the Real Analysis grade (). A third beta linear regression test shows that the FIP grade is a significant predictor of the Real Analysis grade (, p = 0.022), where the beta variable represents whether students passed the interventional course with a C grade or higher. In summary, whether we apply regression analysis or a group comparison approach to the quantitative data, we see similar results. Specifically, reflection quality during the FIP is a significant predictor of future success in the Real Analysis course, while grades in the prerequisite Linear Algebra course are not. Likewise, group comparison results suggest that differences between course grades among those students who wrote high- vs. low-quality reflections were significant in the interventional (FIP) and introductory analysis courses, and not significant in Linear Algebra. Together, these aligned findings reinforce our confidence that having students write reflections throughout the interventional FIP had a positive impact on students’ success in both that course and the subsequent introductory analysis course.
5. Discussion
5.1. Summary
Based on best practices in the literature [3,4,5], we created an interventional FIP course, Introduction to Mathematical Reasoning, to mitigate the difficulty of the CBIP course, Introduction to Real Analysis. The interventional FIP course utilized active learning and the novel approach of self-reflections focused on four learning modalities within mathematical reasoning—mechanical, structural, creative, and critical—inspired by [15]. In this study, we analyzed the quality of self-reflections pertaining to students’ proof-writing self-efficacy for evidence of meaningful learning. We first rated each student’s reflections in the categories of exceptional, acceptable, developing, or incomplete. We then combined these four categories of student reflections into two groups: high quality, i.e., those meeting exceptional/acceptable criteria, and low quality, i.e., those aligned with developing/incomplete criteria. Both classification systems demonstrated similar quantitative results. Figure 2 illustrates the average letter grade for each of the three sequenced courses based on the two-category classifications, respectively. Specifically, the increased performance gap was statistically significant for the interventional and introductory analysis courses, but not for the prerequisite course. In other words, success in the prerequisite course alone does not predict success in the upper-level CBIP course.
5.2. Addressing the Research Aims
5.2.1. Does Having Students Write Reflections in the Interventional (FIP) Course Support Their Ability to be Metacognitive about Their Own Proof-Writing Processes?
In answering our first research question, we see evidence that some students are marshaling the concepts behind the four thinking modalities post hoc to write their reflections. Student 13, whose reflections were rated exceptional, showed consistent evidence of metacognition throughout the semester. Student 9’s reflections, on the other hand, were rated acceptable, but they also showed growth in their metacognitive abilities over the semester. While we are able to draw conclusions about the metacognitive abilities of students who write high- quality reflections, we are not able to draw any conclusions about students who either did not write reflections every week or whose reflections were vague or nonspecific. However, our study design did not allow us to determine whether or not any students are consciously applying the modalities while they are in the process of writing proofs. A future study that has students think aloud as they engage in proof writing might shed more light on their use of various thinking strategies, including the four modalities, during the process.
5.2.2. Does Having Students Write Reflections in the Interventional Course Impact Their Performance and Success in That Course?
Figure 2 shows that there is a statistically significant relationship between the high-quality (exceptional/acceptable) reflections and students earning higher average grades in the interventional course. Thus, the intervention may have impacted the performance of the students who thoughtfully completed the self-reflections. Specifically, based solely on the average course grade, students who wrote better self-reflections performed better in the interventional course than students who wrote low-quality (developing/incomplete) reflections. Thus, corroborating [25], it appears that merely assigning students to write self-reflections does not necessarily affect their performance and success in the interventional course. However, on average, writing high-quality reflections correlated with higher grades in both the interventional course and subsequent introductory analysis course, thus suggesting a positive impact of the intervention. Students whose reflections qualified as high quality did not necessarily have greater success in the prerequisite course, as evidenced by the lack of significant correlation between writing a high-quality reflection and respective performance in the prerequisite course. However, on average, these students did perform better in both the interventional and subsequent introductory analysis courses.
5.2.3. Does Having Students Write Reflections in the Interventional Course Impact Their Performance in the Subsequent Introduction to Real Analysis Course?
Analysis of modality reflections showed that students who wrote high-quality reflections performed better in the interventional course. Perhaps more surprising and more important is the correlation between high-quality (exceptional/acceptable) reflections and the respective students’ performance in Introduction to Real Analysis, where students were not asked to use the modalities. Not only did students writing high-quality reflections reliably achieve higher grades in the introductory analysis course, but also the performance gap between students who wrote high- and low-quality reflections increased relative to the performance gap in the interventional course. Combined with the lack of correlation between writing high-quality reflections and students’ grades in the prerequisite course, success in the CBIP course was not predicted solely by performance in the prerequisite course, and performance in the real analysis course seems to have been impacted by thoughtful self-reflections.
5.3. Other Considerations
In an effort to elicit high-quality reflections from students, the prompt was revised twice during the course of the study to clarify expectations and provide more structure for the students’ ability to reflect metacognitively [25,45,68,69]. Despite these efforts, the data (Table 4) do not support an obvious correlation between the quality of reflections and our efforts to clarify our expectations with regard to modality self-reflections. Dyment and O’Connell [70] describe several limiting factors to reflective writing that might explain this. For instance, over the course of the three semesters of our study, neither the instructor nor the TA provided personalized feedback on students’ individual reflections. The instructor, however, did attempt to provide extra structure to the prompts and also frequently provided examples of each of the modalities during class. However, these efforts did not appear to impact students’ reflections. In another attempt to improve student reflections, the instructor also clarified expectations by providing examples of high-quality reflections and conveyed the positive impact of self-reflective writing exercises on course outcomes. Subsequent to this study, to provide additional support to students for reflective writing, we added a short, small-group discussion on the modalities at the beginning of the discussion section. We predicted that students will benefit from this additional, deliberate learning opportunity.
As the semester progressed, students showed increased understanding of the modalities, as evidenced by the decrease in the difference in ratings between graders and students for all four modalities. While the correlation results for the structural and creative modalities were statistically significant, the trends for mechanical and critical modalities did not meet the criteria for statistical significance (Table 3). The correlational findings for the structural and creative modalities show that grader–student differences in rating decrease as the semester progresses, which suggests student conceptual growth in these modalities over the semester. We speculate that the evaluative demands of the critical modality may have been the most challenging for the students to master, even by the end of the term. On the other hand, the mechanical modality is less cognitively demanding than the other modalities. Thus, many students may have found the mechanical modality manageable from very early in the term, leaving little room for growth over time. We posit that the structural and creative modalities are more cognitively challenging than the mechanical modality, but not as challenging as the critical modality. Thus, it is in the structural and creative modalities where we would expect students to make the greatest gains in awareness of their own abilities over the semester.
While our results indicate that students who submit high-quality reflections are more successful proof writers, our research methodology was not designed to prove causation. One may speculate that the convergence between grader ratings and student self-ratings may partly be attributable to the students adjusting to the TA’s expectations. Given that the TA is an expert, the natural conclusion is that the student is becoming better at proof writing. It may be the case that students who are naturally good at writing reflections are also good at writing proofs. Since the prerequisite class is more calculational, students with strong proof-writing abilities would not necessarily stand out. While this may contribute to some of the results, subsequent detailed analysis found in [18] shows that the greatest impact the interventional course had was on the students who received a B or a C in the prerequisite course. Thus, while these alternative explanations are plausible, one may reasonably conclude that the reflective writing and the interventional class positively impact student performance.
We further speculate that our findings were impacted both by the global COVID-19 pandemic, which emerged during the second of the three semesters of this study, and by data-driven changes in instruction. Data analysis from the first semester resulted in changing the self-reflection prompt, as well as the Likert scale for the student rating of the modalities. During the second semester that the course was offered, instruction abruptly switched from in-person to online due to the onset of the COVID-19 pandemic. Students were impacted by external factors such as the lack of reliable internet connections, flagging motivation, and challenges of time management [71], which may have influenced their performance in the course in a variety of ways. We also noted challenges surrounding active learning during discussions that continued into the following semester, despite a variety of adaptations that the instructor tried to improve the situation. The class was redesigned for the third semester to improve outcomes in the online environment. Lectures were recorded, and students were required to submit lecture notes to ensure they had viewed the recording. Student attendance was required at both a synchronous question session and a synchronous discussion section. We do not believe that these challenges and modifications to the course influenced our findings in any significant way. On the contrary, despite the challenges of teaching and learning during a pandemic, our findings suggest the significant impact of high-quality self-reflections on student performance in both the FIB and CBIP courses across both in-person and online instructional environments.
6. Conclusions
Our analysis of students’ written reflections structured around thinking modalities of proof writing showed that students who wrote high-quality reflections performed better in both the interventional course and the subsequent introduction to analysis course. Furthermore, student performance in the prerequisite course did not predict student performance in the interventional and introduction to analysis courses. It was not just that diligent students performed well both with reflective writing and in the math content of their courses. If that were the case, we would expect their performance in the prerequisite course to correlate with their categorization as writing high-quality reflections, which it did not. Thus, we conclude that repeated exposure to guided self-reflection using the lens of the modalities supports growth in the students’ awareness of their own abilities pertaining to proof writing. In particular, the modalities provided students with a framework for discerning what they understood and what they needed help with to understand. Our results support the potential power of repeated, modality-based self-reflection as a strategy to improve students’ ability to write better proofs, and thus impact outcomes in future proof-based courses.
While the current work highlights the impact of reflective writing to support students’ metacognition around proof writing, future work could focus on the best way to guide students toward more effective reflective writing, thus improving both their self-awareness and outcomes in future courses. For example, future work could investigate the role of the frequency and intensity of reflective writing activities on developing proof-writing abilities. Additionally, our work did not directly measure how the students used the modalities while writing their proofs. Further research into students’ metacognitive processes—specifically think-aloud-type methods that reveal students’ thought processes as they write proofs—could yield additional insights into common misconceptions and misconstruals that would help instructors tailor their lectures, activities, and assignments accordingly. Lastly, supporting instructors and TAs in understanding theory and practice around reflective writing could enable them to better help students develop reflective writing skills.
Author Contributions
Conceptualization , K.K. and K.H.; methodology, K.K. and K.H.; software, T.H.W.; validation, T.H.W. formal analysis, K.H., T.H.W. and K.K.; investigation, K.K. and K.H.; resources, K.H.; data curation, T.H.W.; writing—original draft preparation, T.H.W., K.K. and K.H.; writing—review and editing, T.H.W., K.K. and K.H.; visualization, T.H.W.; supervision, K.H.; project administration, K.H.; funding acquisition, K.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded internally by a Hrabowski Innovation Fund grant at UMBC.
Institutional Review Board Statement
This study was classified by the University of Maryland Baltimore County’s Office of Research Protections and Compliance as exempt (IRB protocol Y20KH13003), 25 July 2019.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Deidentified, aggregate data may be shared upon individual request to comply with the study’s IRB protocol.
Acknowledgments
The authors thank Kalman Nanes and JustinWebster for their input in the design and implementation of the interventional course, as well as many subsequent discussions. Additionally, special thanks go to Linda Hodges and Jennifer Harrison in the Faculty Development Center who provided crucial insight into the design of the interventional course and corresponding assessment methods. We are indebted to Linda Hodges and Keith Weber who provided very helpful feedback on the draft manuscript. We are also grateful to Jeremy Rubin and Teddy Weinberg, teaching assistants for the course, who were essential to the data collection for this study.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| FIP | Fundamental Introduction to Proof; |
| CBIP | Content-Based Introduction to Proof; |
| WTL | Writing-to-learn; |
| WID | Writing in the disciplines; |
| SLO | Student learning objective. |
Appendix A. Student Learning Objectives

Table A1.
Student learning objectives (SLOs) for the FIP Course.
Table A1.
Student learning objectives (SLOs) for the FIP Course.
| SLO 1 | Construct basic proofs of if-then statements about integers and sets. |
| SLO 2 | Evaluate the truth or falsity of given statements; defend this decision by providing justifications or counterexamples as appropriate. |
| SLO 3 | Manipulate and negate simple and compound mathematical statements using propositional logic and truth tables. |
| SLO 4 | Quantify (and negate) precise mathematical statements with proficiency in mathematical statements and propositions. |
| SLO 5 | Utilize common proof techniques such as induction, proof by contraposition, and proof by contradiction; recognize the need for these strategies in given problems. |
| SLO 6 | Apply skills of mathematical reasoning, as listed above, to topics including functions, probability, number theory, and group theory. |
| SLO 7 | Evaluate the validity of a given mathematical argument. |
| SLO 8 | Demonstrate correct and precise use of mathematical language. |
Appendix B. Modality Rubrics
Appendix B.1. Fall 2019

Table A2.
Modality rubric for Semester 1.
Table A2.
Modality rubric for Semester 1.
| Superior | Proficient | Acceptable | Poor | No Applicable | |
|---|---|---|---|---|---|
| Mechanical | Student shows flawless and insightful use of definitions and logical structures, and formal manipulation of symbols | Student shows appropriate use of definitions and logical structures, and formal manipulation of symbols, with only small mistakes. | Student has gaps in their use of definitions and logical structures, and in formal manipulation of symbols, but still largely achieves associated goals. | Student’s poor use of definitions, logical structures, and formal manipulation of symbols prevents them from achieving goals. | This assignment does not make significant use of mechanical factors. |
| Structural 1 | Student demonstrates flawless and insightful ability to view the whole statement/proof in terms of the comprising parts. | Student demonstrates the ability to view the whole statement/proof in terms of the comprising parts, with only minor errors. | Student demonstrates gaps in their ability to view the whole statement/proof in terms of the comprising parts, but still largely achieves associated goals. | Student demonstrates inability to view the whole statement/proof in terms of the comprising parts, preventing them from achieving goals. | This assignment does not make significant use of instantiative factors. |
| Creative | Student makes insightful connections between concepts to correctly ascertain the crux of the statement/proof. | With only minor errors, student makes appropriate connections between concepts to correctly ascertain the crux of the statement/proof. | Student shows gaps in their connections between concepts. They ascertain the crux of the statement/proof with difficulty or sometimes miss the point. | Student largely does not make connections between concepts. They cannot ascertain the crux of the statement/proof or cannot complete proofs because of this inability. | This assignment does not make significant use of creative factors. |
| Critical | Student demonstrates superior insight in ascertaining the truth or falsity of the statement/proof, and in verifying a sequence of logical steps or producing a viable counterexample, as appropriate. | With only minor errors, student demonstrates proficiency in ascertaining the truth or falsity of the statement/proof, and in verifying a sequence of logical steps or producing a viable counterexample, as appropriate. | Student demonstrates gaps in their ability to ascertain the truth or falsity of the statement/proof. Student struggles to verify a sequence of logical steps or to produce a viable counterexample, as appropriate, but does largely achieve associated goals. | Student largely cannot ascertain the truth or falsity of the statement/proof. Student’s inability to verify a sequence of logical steps or to produce a viable counterexample, as appropriate, is a significant impediment to their achievement. | This assignment does not make significant use of critical factors. |
| Latex | Student’s LaTeX typesetting adds significantly to the quality of the written work. | Student’s work is typeset in LaTeX proficiently and with only minor errors. Typesetting does not detract from the flow of the reading. | Student’s LaTeX typesetting contains significant errors, and detracts significantly from the reader’s experience. | Student’s LaTeX typesetting is poor enough to make reading the work difficult or impossible. Or, student did not typeset the submission using LaTeX despite a requirement to do so. | This assignment was not to be typeset using LaTeX. |
1 Although students were presented with a category labeled instantiative, what was actually described to the students in the scope of this study is commonly referred to as structural by literature.
Please reflect on your performance on homework 1. Please comment on substantial gaps or significant improvements on your performance with respect to the modalities.
Appendix B.2. Spring 2020

Table A3.
Mechanical modality rubric for Semester 2.
Table A3.
Mechanical modality rubric for Semester 2.
| Self-Rating | Description of Performance |
|---|---|
| 7 | I consistently and correctly use definitions, logical structures, and formal manipulation of symbols. |
| 6 | Between a 5 and 7. |
| 5 | I appropriately use definitions, logical structures, and formal manipulation of symbols, with small or occasional mistakes. |
| 4 | Between a 3 and 5. |
| 3 | I have some ability to use definitions, logical structures, and formal manipulation of symbols. I could use more support/feedback to meet associated goals. |
| 2 | Between a 1 and 3. |
| 1 | I need more exposure to the definitions, logical structures, and in formal manipulation of symbols. I need more practice developing my skills in this area. |
| 0 | This assignment does not make significant use of mechanical factors |

Table A4.
Structural modality rubric for Semester 2.
Table A4.
Structural modality rubric for Semester 2.
| Self-Rating | Description of Performance |
|---|---|
| 7 | I consistently and correctly view the whole statement/proof in terms of the comprising parts and/or ideas. |
| 6 | Between a 5 and 7. |
| 5 | I appropriately view the whole statement/proof in terms of the comprising parts and/or ideas, with only minor or occasional errors. |
| 4 | Between a 3 and 5. |
| 3 | I have some ability to view the whole statement/proof in terms of the comprising parts and/or ideas. I could use more support/feedback to meet associated goals. |
| 2 | Between a 1 and 3. |
| 1 | I need more exposure to the whole statement/proof in terms of the comprising parts and/or ideas. I need more practice developing my skills in this area. |
| 0 | This assignment does not make significant use of structural factors |

Table A5.
Creative modality rubric for Semester 2.
Table A5.
Creative modality rubric for Semester 2.
| Self-Rating | Description of Performance |
|---|---|
| 7 | I consistently and correctly make connections between concepts. Or, I correctly approach the crux of the statement/proof in a unique or novel way. |
| 6 | Between a 5 and 7. |
| 5 | I appropriately ascertain the truth or falsity of the statement/proof and can recognize a correct and complete proof or counterexample, with only minor or occasional errors. |
| 4 | Between a 3 and 5. |
| 3 | I have some ability to ascertain the truth or falsity of the statement/proof. It is still difficult to recognize a correct and complete proof or counterexample, and I could use more support/feedback. |
| 2 | Between a 1 and 3. |
| 1 | I need more exposure to verifying the truth or falsity of the statement/proof and need more practice recognizing correct and complete proofs or counterexamples. |
| 0 | This assignment does not make significant use of mechanical factors |

Table A6.
Critical modality rubric for Semester 2.
Table A6.
Critical modality rubric for Semester 2.
| Self-Rating | Description of Performance |
|---|---|
| 7 | I consistently and correctly ascertain the truth or falsity of the statement/proof, and can recognize a correct and complete proof or counterexample. |
| 6 | Between a 5 and 7. |
| 5 | I appropriately ascertain the truth or falsity of the statement/proof and can recognize a correct and complete proof or counterexample, with only minor or occasional errors. |
| 4 | Between a 3 and 5. |
| 3 | I have some ability to ascertain the truth or falsity of the statement/proof. It is still difficult to recognize a correct and complete proof or counterexample, and I could use more support/feedback. |
| 2 | Between a 1 and 3. |
| 1 | I need more exposure to verifying the truth or falsity of the statement/proof and need more practice recognizing correct and complete proofs or counterexamples. |
| 0 | This assignment does not make significant use of mechanical factors |

Table A7.
Latex for Semester 2.
Table A7.
Latex for Semester 2.
| Self-Rating | Description of Performance |
|---|---|
| 7 | I consistently and correctly use LaTeX to clearly and aesthetically format typeset. |
| 6 | Between a 5 and 7. |
| 5 | I typeset in LaTeX appropriately, with only minor or occasional errors. |
| 4 | Between a 3 and 5. |
| 3 | I have some ability to use LaTeX typesetting and I could use more support/feedback. My LaTeX contains errors that might detract significantly from the reader’s experience. |
| 2 | Between a 1 and 3. |
| 1 | I need more exposure to and practice with LaTeX typesetting. It is difficult to read my work, or, I did not typeset the submission using LaTeX. |
| 0 | This assignment does not make significant use of mechanical factors |
Please comment on why you chose each of the ratings above.
Appendix B.3. Fall 2020
These rubrics used the same Likert scale as Spring 2020, except for a change to the prompt for commenting on why the student chose their self-ratings. After the ratings for each modality, students were prompted as follows:
Using the format “claim → evidence → reasoning”, justify your chosen ranking for [this modality]. Be sure to include specific examples for evidence to support your claim, and carefully describe your reasoning for how your evidence supports your claim.
References
- Stylianides, G.J.; Stylianides, A.J. Research based interventions in the area of proof: The past, the present, and the future. Educ. Stud. Math. 2017, 96, 119–127. [Google Scholar] [CrossRef]
- Moore, R.C. Making the transition to formal proof. Educ. Stud. Math. 1994, 27, 249–266. [Google Scholar] [CrossRef]
- David, E.J.; Zazkis, D. Characterizing introduction to proof courses: A survey of US R1 and R2 course syllabi. Int. J. Math. Educ. Sci. Technol. 2020, 51, 388–404. [Google Scholar] [CrossRef]
- Marty, R.H. Getting to Eureka!: Higher Order Reasoning in Math. Coll. Teach. 1991, 39, 3–6. [Google Scholar] [CrossRef]
- Savic, M. Does Content Matter in an Introduction-to-Proof Course? J. Humanist. Math. 2017, 7, 149–160. [Google Scholar] [CrossRef][Green Version]
- Alcock, L.; Hodds, M.; Roy, S.; Inglis, M. Investigating and improving undergraduate proof comprehension. Not. AMS 2015, 62, 742–752. [Google Scholar] [CrossRef]
- Davies, B.; Alcock, L.; Jones, I. What do mathematicians mean by proof? A comparative-judgement study of students’ and mathematicians’ views. J. Math. Behav. 2021, 61, 100824. [Google Scholar] [CrossRef]
- Inglis, M.; Alcock, L. Expert and novice approaches to reading mathematical proofs. J. Res. Math. Educ. 2012, 43, 358–390. [Google Scholar] [CrossRef]
- Inglis, M.; Mejia-Ramos, J.P.; Weber, K.; Alcock, L. On mathematicians’ different standards when evaluating elementary proofs. Top. Cogn. Sci. 2013, 5, 270–282. [Google Scholar] [CrossRef]
- Ko, Y.Y.; Knuth, E.J. Validating proofs and counterexamples across content domains: Practices of importance for mathematics majors. J. Math. Behav. 2013, 32, 20–35. [Google Scholar] [CrossRef]
- Lee, K. Students’ proof schemes for mathematical proving and disproving of propositions. J. Math. Behav. 2016, 41, 26–44. [Google Scholar] [CrossRef]
- Lew, K.; Mejía Ramos, J.P. Linguistic conventions of mathematical proof writing across pedagogical contexts. Educ. Stud. Math. 2020, 103, 43–62. [Google Scholar] [CrossRef]
- Melhuish, K.; Fukawa-Connelly, T.; Dawkins, P.C.; Woods, C.; Weber, K. Collegiate mathematics teaching in proof-based courses: What we now know and what we have yet to learn. J. Math. Behav. 2022, 67, 100986. [Google Scholar] [CrossRef]
- Weber, K. How mathematicians determine if an argument is a valid proof. J. Res. Math. Educ. 2008, 39, 431–459. [Google Scholar] [CrossRef]
- Alcock, L. Mathematicians’ perspectives on the teaching and learning of proof. Res. Coll. Math. Educ. 2010, VII, 63–92. [Google Scholar]
- Bleiler-Baxter, S.K.; Pair, J.D. Engaging students in roles of proof. J. Math. Behav. 2017, 47, 16–34. [Google Scholar] [CrossRef]
- Hodds, M.; Alcock, L.; Inglis, M. Self-explanation training improves proof comprehension. J. Res. Math. Educ. 2014, 45, 62–101. [Google Scholar] [CrossRef]
- Hoffman, K.; Williams, T.; Webster, J.T.; Harrison, J.M.; Nanes, K. Assessing the Impacts of An Interventional Proof-Writing Course. submitted.
- Britton, J.; Burgess, T.; Martin, N.; McLeod, A.; Rosen, H. The Development of Writing Abilities (11–18). Rev. Brittonism 1975, 9, 7–16. [Google Scholar]
- Bruner, J.S. The ontogenesis of speech acts. J. Child Lang. 1975, 2, 1–19. [Google Scholar] [CrossRef]
- Emig, J. Writing as a Mode of Learning. Coll. Compos. Commun. 1977, 28, 122–128. [Google Scholar] [CrossRef]
- Fulwiler, T.; Young, A. Language Connections: Writing and Reading Across the Curriculum; National Council of Teachers of English: Urbana, IL, USA, 1982. [Google Scholar]
- Langer, J.A.; Applebee, A.N. Learning to Write: Learning to Think. Educ. Horizons 1985, 64, 36–38. [Google Scholar]
- Boland, S. How I started using writing across the curriculum and ended up taking algebra again: A review of useful works on writing across the curriculum. WAC Ourna 1989, 8, 111–122. [Google Scholar] [CrossRef]
- Bangert-Drowns, R.L.; Hurley, M.M.; Wilkinson, B. The effects of school-based writing-to-learn interventions on academic achievement: A meta-analysis. Rev. Educ. Res. 2004, 74, 29–58. [Google Scholar] [CrossRef]
- Cross, D.I. Creating optimal mathematics learning environments: Combining argumentation and writing to enhance achievement. Int. J. Sci. Math. Educ. 2009, 7, 905–930. [Google Scholar] [CrossRef]
- Greer, A.R. Mathematical Communication: A Study of the Impact Expository Writing in the Mathematics Curriculum Has on Student Achievement. Ph.D. Thesis, Capella University, Minneapolis, MN, USA, 2010. [Google Scholar]
- Idris, N. Enhancing students’ understanding in calculus trough writing. Int. Electron. J. Math. Educ. 2009, 4, 36–55. [Google Scholar] [CrossRef]
- Kenney, R.; Shoffner, M.; Norris, D. Reflecting to learn mathematics: Supporting pre-service teachers’ pedagogical content knowledge with reflection on writing prompts in mathematics education. Reflective Pract. 2013, 14, 787–800. [Google Scholar] [CrossRef]
- Menz, P.; Xin, C. Making Students’ metacognitive knowledge visible through reflective writing in a mathematics-for-teachers course. Collect. Essays Learn. Teach. 2016, 9, 155–166. [Google Scholar] [CrossRef]
- Britton, J. Writing-to-learn and learning to write. In Selected essays of James Britton; Boynton/Cook Publishers: Portsmouth, NH, USA, 1982; pp. 94–111. [Google Scholar]
- Klein, P.D. Reopening inquiry into cognitive processes in writing-to-learn. Educ. Psychol. Rev. 1999, 11, 203–270. [Google Scholar] [CrossRef]
- Young, R.; Sullivan, P. Why write? A reconsideration. In Essays on Classical Rhetoric and Modern Discourse; Southern Illinois Press: Carbondale, IL, USA, 1984; pp. 215–225. [Google Scholar]
- Bereiter, C.; Scardamalia, M. The Psychology of Written Composition; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1987. [Google Scholar]
- Flower, L.; Hayes, J.R. The dynamics of composing: Making plans and juggling constraints. In Cognitive Processes in Writing; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1980; pp. 31–50. [Google Scholar] [CrossRef]
- Graham, S.; Kiuhara, S.A.; MacKay, M. The effects of writing on learning in science, social studies, and mathematics: A meta-analysis. Rev. Educ. Res. 2020, 90, 179–226. [Google Scholar] [CrossRef]
- Dewey, J. How We Think; D. C. Heath and Co.: Boston, MA, USA, 1910. [Google Scholar]
- Silver, N. Reflective pedagogies and the metacognitive turn in college teaching. In Using Reflection and Metacognition to Improve Student Learning; Stylus Publishing: Sterling, VA, USA, 2013; pp. 1–17. [Google Scholar]
- Di Stefano, G.; Gino, F.; Pisano, G.P.; Staats, B. Learning by Thinking: Overcoming the Bias for Action Through Reflection; Harvard Business School: Cambridge, MA, USA, 2015. [Google Scholar]
- Moon, J.A. Learning Journals: A Handbook for Reflective Practice and Professional Development; Routledge: New York, NY, USA, 2006. [Google Scholar]
- Yancey, K. A Rhetoric of Reflection; University Press of Colorado: Denver, CO, USA, 2016. [Google Scholar]
- Borasi, R.; Rose, B.J. Journal writing and mathematics instruction. Educ. Stud. Math. 1989, 20, 347–365. [Google Scholar] [CrossRef]
- Guce, I.K. Investigating College Students’ Views on Mathematics Learning through Reflective Journal Writing. Int. J. Eval. Res. Educ. 2017, 6, 38–44. [Google Scholar] [CrossRef]
- Thropp, J. Using reflective journaling to promote achievement in graduate statistics coursework. Int. J. Learn. Teach. Educ. Res. 2017, 16, 120–134. [Google Scholar]
- Dunlap, J.C. Using guided reflective journaling activities to capture students’ changing perceptions. TechTrends 2006, 50, 20–26. [Google Scholar] [CrossRef]
- Grossman, R. Structures for facilitating student reflection. Coll. Teach. 2009, 57, 15–22. [Google Scholar] [CrossRef]
- McDonald, C.R. Toward Defining a Social Reflective Pedagogy for ePortfolios. In A Rhetoric of Reflection; University Press of Colorado: Denver, CO, USA, 2016; pp. 203–226. [Google Scholar]
- Sommers, J. Problematizing Reflection. In A Rhetoric of Reflection; University Press of Colorado: Denver, CO, USA, 2016; pp. 271–287. [Google Scholar]
- Steven, D.; Cooper, J. Journal Keeping: How to Use Reflective Writing for Learning, Teaching, Professional Insight and Positive Change; Routledge: London, UK, 2009. [Google Scholar]
- Vygotsky, L.S.; Cole, M. Mind in Society: Development of Higher Psychological Processes; Harvard University Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Samkoff, A.; Weber, K. Lessons learned from an instructional intervention on proof comprehension. J. Math. Behav. 2015, 39, 28–50. [Google Scholar] [CrossRef]
- Edwards, B.S.; Ward, M.B. Surprises from mathematics education research: Student (mis) use of mathematical definitions. Am. Math. Mon. 2004, 111, 411–424. [Google Scholar] [CrossRef]
- Vinner, S. The role of definitions in the teaching and learning of mathematics. In Advanced Mathematical Thinking; Springer: Berlin/Heidelberg, Germany, 1991; pp. 65–81. [Google Scholar]
- Dubinsky, E.; Elterman, F.; Gong, C. The student’s construction of quantification. Learn. Math. 1988, 8, 44–51. [Google Scholar]
- Weber, K.; Mejia-Ramos, J.P. Why and how mathematicians read proofs: An exploratory study. Educ. Stud. Math. 2011, 76, 329–344. [Google Scholar] [CrossRef]
- Fuller, E.; Weber, K.; Mejia-Ramos, J.P.; Rhoads, K.; Samkoff, A. Comprehending structured proofs. J. Int. De Estud. Em Educ. MatemÁTica 2014, 7, 84–102. [Google Scholar]
- Raman, M.; Sandefur, J.; Birky, G.; Campbell, C.; Somers, K. Is that a proof? Using video to teach and learn how to prove at the university level. In Proof and Proving in Mathematics Education: The 19th ICMI Study; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 154–159. [Google Scholar]
- Selden, A.; Selden, J. Validations of proofs considered as texts: Can undergraduates tell whether an argument proves a theorem? J. Res. Math. Educ. 2003, 34, 4–36. [Google Scholar] [CrossRef]
- Evans, T.; Mejía-Ramos, J.P.; Inglis, M. Do mathematicians and undergraduates agree about explanation quality? Educ. Stud. Math. 2022, 111, 445–467. [Google Scholar] [CrossRef]
- Mejia-Ramos, J.P.; Weber, K. Why and how mathematicians read proofs: Further evidence from a survey study. Educ. Stud. Math. 2014, 85, 161–173. [Google Scholar] [CrossRef]
- Stylianides, A.J.; Komatsu, K.; Weber, K.; Stylianides, G.J. Teaching and learning authentic mathematics: The case of proving. In Handbook of Cognitive Mathematics; Springer: Berlin/Heidelberg, Germany, 2022; pp. 727–761. [Google Scholar]
- Weber, K. Mathematics majors’ perceptions of conviction, validity, and proof. Math. Think. Learn. 2010, 12, 306–336. [Google Scholar] [CrossRef]
- Weber, K.; Mejia-Ramos, J.P. Mathematics majors’ beliefs about proof reading. Int. J. Math. Educ. Sci. Technol. 2014, 45, 89–103. [Google Scholar] [CrossRef]
- Alcock, L.; Weber, K. Proof validation in real analysis: Inferring and checking warrants. J. Math. Behav. 2005, 24, 125–134. [Google Scholar] [CrossRef]
- Scheinerman, E.A. Mathematics: A Discrete Introduction; Brooks/Cole: Pacific Grove, CA, USA, 2012. [Google Scholar]
- Coffey, A.; Atkinson, P. Making Sense of Qualitative Data: Complementary Research Strategies; Sage Publications, Inc.: Thousand Oaks, CA, USA, 1996. [Google Scholar]
- Saldaña, J. The coding manual for qualitative researchers. Am. J. Qual. Res. 2021, 6, 232–237. [Google Scholar]
- Harris, M. Scaffolding reflective journal writing–Negotiating power, play and position. Nurse Educ. Today 2008, 28, 314–326. [Google Scholar] [CrossRef]
- Power, J.B. Has this begun to change the way they think? Moving undergraduate learners’ level of reflection from where it is to where it needs to be. Teach. High. Educ. 2016, 21, 235–248. [Google Scholar] [CrossRef]
- Dyment, J.E.; O’connell, T.S. The quality of reflection in student journals: A review of limiting and enabling factors. Innov. High. Educ. 2010, 35, 233–244. [Google Scholar] [CrossRef]
- Almendingen, K.; Morseth, M.S.; Gjølstad, E.; Brevik, A.; Tørris, C. Student’s experiences with online teaching following COVID-19 lockdown: A mixed methods explorative study. PLoS ONE 2021, 16, e0250378. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).