Abstract
This study investigates the role of teacher talk moves in cultivating a mathematical modeling classroom community. From the models and modeling perspective, it explores how specific teacher talk moves promote student participation in modeling phases and the exchange of ideas with other students. Through a four-week after-school program involving eight secondary students, data were collected from small-group and whole-class discussions. The findings reveal that teacher talk moves can be categorized into three core types: eliciting students’ ideas, introducing key terms and ideas used in mathematical modeling, and encouraging students to take a position during discussions. These moves are shown to influence classroom discussion norms and facilitate the ways that students interact and reason with the mathematical modeling tasks. While the findings suggest that teacher talk moves can contribute to fostering a reflective learning environment where students collaboratively construct, analyze, and refine mathematical models, further research is needed to better understand the extent of their impact and how similar learning opportunities might arise through alternative instructional strategies. Future research should explore how these teacher moves can be implemented across different classroom contexts and extended periods to enhance modeling-based learning.
1. Introduction
Mathematical modeling in education is increasingly acknowledged for its ability to integrate academic learning with real-world problem solving (Siller et al., 2024). Research has shown that fostering a classroom community centered on mathematical modeling is critical for supporting all students in their participation in authentic mathematical modeling experiences (Jung & Brady, 2023; R. Lesh & Lehrer, 2003). In group presentations during whole-class discussions, the students’ emerging mathematical reasoning is revealed at different modeling phases (Brady & Jung, 2022; Wickstrom & Jung, 2024). Teachers have the opportunity to listen to students as they reflect on and engage with each other’s solutions, while simultaneously deciding on how to intervene and facilitate these discussions (Borromeo Ferri, 2018). Such classroom environments allow teachers to become more responsive to their students’ reasoning and needs while developing follow-up modeling tasks for implementation (Blum, 2015; English & Doerr, 2004; R. Lesh et al., 2000). Thus, teachers play an essential role in establishing a learning community for mathematical modeling (Greefrath et al., 2022; R. A. Lesh & Doerr, 2003). In this study, we focus on how teacher talk moves can build a mathematical modeling classroom community that fosters student participation in modeling phases and encourages the exchange of ideas.
2. Literature Review
2.1. Classroom Norms as a Foundation for Student Participation in Mathematical Modeling
Establishing a coherent definition of mathematical modeling and its epistemological foundations presents a significant challenge (Kaiser & Sriraman, 2006). Internationally, six distinct perspectives on mathematical modeling have been identified: realistic, theoretical, educational, sociocritical, cognitive, and models and modeling. Each perspective highlights different aspects of the system being modeled and the objectives of the modeling process, utilizing diverse frameworks that range from mathematical representations of real-world phenomena to considerations of broader societal implications and theoretical constructs (Abassian et al., 2020).
Aligning with the models and modeling perspective (R. A. Lesh & Doerr, 2003), this study defines mathematical modeling as a multi-phase process in which students work through open-ended real-world problems, make assumptions, construct mathematical models using representations such as graphs and equations, interpret the representations, and check their solutions within real-life contexts. This perspective emphasizes the co-development of students’ mathematical reasoning and their understanding of real-world situations. Model-eliciting activities (MEAs) play a crucial role within this perspective, as they engage students in small-group collaboration and whole-class discussions where they iteratively communicate, test, and refine their mathematical constructs (R. Lesh et al., 2000). Through this process, students not only reflect on their own reasoning but also articulate their ideas in ways that facilitate peer evaluation. Student participation in modeling phases and class interactions foster collaborative sense making through description and explanation, helping students uncover and understand the mathematical structures embedded in their solutions (English, 2003; R. Lesh & Lehrer, 2003).
Since mathematical modeling relies heavily on student communication, collaboration, and iterative reasoning, establishing a supportive classroom culture is essential (Brady et al., 2024; R. Lesh & Sriraman, 2005; Ozturk, 2024). Classroom norms, which are shared expectations between teachers and students, guide communication and behavior (Stephan, 2020). In mathematics education, these norms are classified as social and sociomathematical norms (Yackel & Cobb, 1996; Yackel et al., 2000). Social norms are general rules that define roles and behaviors within a group (Elia et al., 2009), while sociomathematical norms pertain to student participation in mathematical activities and the development of mathematical practices (Hofmann & Ruthven, 2018). Key aspects of sociomathematical norms include mathematical communication (Yackel & Cobb, 1996), mathematical efficacy (Partanen & Kaasila, 2015), explanation and evaluation (T. Campbell, 2023), and the use of critical and creative reasoning in problem solving (Savuran & Akkoç, 2021). Social and sociomathematical norms are interdependent, as effective learning relies on the sharing and listening of ideas (T. G. Campbell & Yeo, 2021; Cobb et al., 1997).
Recent studies on norms in mathematical modeling classrooms have highlighted the importance of students working in groups to solve modeling problems, present solutions, and participate in discussions to foster a reflective learning environment (Brady et al., 2024). This collaborative process nurtures a classroom culture centered on mathematical modeling, where peer feedback (Brady & Jung, 2022) and community-based learning (Anhalt & Cortez, 2015) are essential. Furthermore, group work helps teachers establish new sociomathematical norms during whole-class discussions (Yenmez & Erbaş, 2023), especially when questions are designed to synthesize students’ ideas and introduce follow-up modeling tasks that promote reflective classroom discussions (Borromeo Ferri, 2018; Jung & Brady, 2023). Collectively, these studies emphasize the growing body of research on the crucial role of teacher moves in facilitating classroom discussions and building mathematical modeling classroom communities.
2.2. Teacher Moves in Facilitating Mathematical Modeling Classroom Discussions
Teacher moves associated with the development of norms in mathematics classrooms are categorized as preparatory or in-the-moment teaching moves (T. G. Campbell & Yeo, 2021). Preparatory teaching moves occur before classroom discussions and include the designing of tasks, anticipating student responses, and creating rules for group work and reflective whole-class discussions (Langer-Osuna, 2016; Stein et al., 2008; Wilhelm, 2014). In-the-moment teaching moves include instantaneous decision making to support students’ mathematical experiences, communication, and efficacy (T. Campbell, 2023; Chapin et al., 2009; Kang & Kim, 2016). In this study, we refer to in-the-moment teacher moves as “teacher talk moves”.
In mathematical modeling classrooms, researchers associate preparatory teaching moves with following a theoretical perspective on modeling in accordance with the goals of the selected modeling tasks (Abassian et al., 2020). For instance, the models and modeling perspective (R. Lesh & Lehrer, 2003) emphasize that modeling tasks should aim to reveal the students’ emergent mathematical reasoning, whereas the educational modeling perspective (Kaiser et al., 2010) focuses on using modeling tasks to teach specific concepts. From the cognitive modeling perspective, Galbraith and Stillman (2006) introduced a framework that outlined the elements of a modeling task that corresponded to the phases of the modeling process. This framework aimed to predict where students were apt to encounter blockages. More recently, Jung and Brady (2023) argued that different types of modeling tasks engage students in whole-class discussions in distinct ways. These examples can be seen as preparatory teaching moves, as they facilitate the anticipation of teacher talk moves when implementing modeling tasks.
Different researchers have used various interchangeable terms to describe teacher talk moves in mathematical modeling classrooms. Stender (2019) referred to teacher talk moves as teachers’ “strategic interventions” that foster student independence by minimally assisting individual students, allowing them to work autonomously, if possible. Siller et al. (2023) highlighted “scaffolding practices”, in which teachers introduce a four-step solution plan to guide students or provide worked-out examples to enhance their participation in problem solving (Tropper et al., 2015). Schukajlow et al. (2015) used “instructional prompts” to help students overcome cognitive barriers while solving problems.
Several researchers have identified categories of teacher talk moves during whole-class discussions (Aroeira et al., 2024; de Oliveira & Barbosa, 2013; Doerr & English, 2006; Jung & Brady, 2024; Manouchehri et al., 2020). They include listening to students’ approaches to problem solving, requesting descriptions, using waiting time, asking follow-up questions to highlight mathematical connections between solutions, and expanding on examples to synthesize students’ responses. Other studies have focused on teacher talk moves in small-group discussions, investigating their impact on students’ success in solving modeling problems and comparing the differences between intervention and control groups’ approaches to modeling tasks (Schukajlow et al., 2023; Zahner & Moschkovich, 2010).
Despite a growing body of the literature on classroom norms and teacher moves in mathematical modeling classrooms, much of the research has focused on two key areas: the theoretical aspects of designing or selecting modeling tasks for classroom implementation (e.g., preparatory teaching moves) and the general impact of teacher interventions (e.g., scaffolding and strategic prompts) on students’ performance in mathematical modeling (Siller et al., 2023). While prior studies emphasize the importance of student group work and whole-class reflective discussions (e.g., Borromeo Ferri, 2018; Brady et al., 2024), they have yet to fully investigate how these interactions dynamically shape the evolving classroom norms in mathematical modeling environments. Furthermore, there is a notable research gap in understanding how specific teacher talk moves during in-the-moment classroom discussions influence the development of norms that support student participation in mathematical modeling. Addressing this gap is essential, as the interplay between teacher talk moves and the establishment of classroom norms during discussions can profoundly influence student participation in the various phases of mathematical modeling, their reasoning processes, and their communication. These components are critical for fostering a communal approach to mathematical modeling (Jung & Brady, 2023).
Building on prior research, this study seeks to bridge this gap by identifying specific teacher talk moves that foster the establishment of a mathematical modeling classroom and examining their relationship with student participation in modeling phases, both individually and as part of a learning community. This research is guided by the following question: How do teacher talk moves shape a classroom environment that promotes student participation in the phases of mathematical modeling and facilitates the exchange of ideas among peers in both whole-class and small-group discussions?
2.3. The Framework
Drawing from the models and modeling perspective (R. A. Lesh & Doerr, 2003) we employed model-eliciting activities (MEAs) to facilitate student participation in modeling phases and classroom discussions. As English (2003) describes, model-eliciting activities can be used to study collaborative learning environments where students develop models, reflect on their solutions, and refine their interpretations. Following her description, we examined classroom discussions, focusing not on students’ individual learning and reasoning systems but rather on the classroom interactions that occur during the processes of model creation and utilization.
Within the model-eliciting activities, student participation in modeling phases entails active involvement in key modeling activities—making assumptions and constructing a model, working mathematically, interpreting findings, and checking and refining solutions. In each phase, student–student and student–teacher interactions play a critical role in fostering a collaborative learning community (Brady et al., 2024; Jung & Brady, 2023). The implementation of MEAs in the classroom encourages students to collaborate through communication, experimentation, and iterative refinement as they develop solutions (R. Lesh & Sriraman, 2005). These activities promote metacognitive awareness by prompting students to articulate their ideas, engage in peer evaluation, and participate in a cycle of description, explanation, and prediction throughout the modeling process (English, 2003).
We adapted Lesh and Doerr’s mathematical modeling cycle (Figure 1) as a guiding framework to analyze students’ approaches to solving MEA tasks. This adaptation provided empirical data for capturing and examining student participation in the phases of mathematical modeling, allowing us to describe how students communicate and reason in each stage—making assumptions and constructing a model, working mathematically, interpreting findings, and checking and refining solutions. These data further informed our identification of teacher talk moves that support the development of a mathematical modeling community, with particular emphasis on student–teacher interactions during model creation and utilization at each phase of the modeling process (see Figure 1).
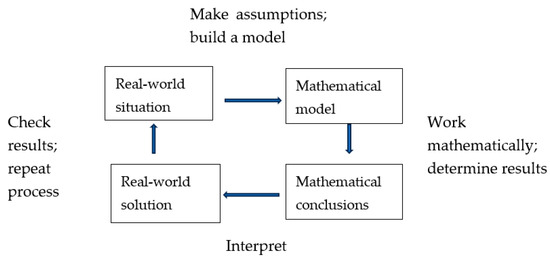
Figure 1.
Mathematical modeling phases. Note: Adapted from R. A. Lesh and Doerr’s (2003) modeling cycle.
Figure 1 illustrates the modeling cycle, which delineates the phases of the mathematical modeling process. When students work through this process, they are presented with a real-world complex problem that prompts them to construct representations in a modeled world. These representations enable students to apply mathematical tools to derive a solution, which is then validated through the model. If the solution proves unsatisfactory or requires refinement, students iteratively revise their models until the problem is adequately addressed.
Although the mathematical modeling process is often depicted as cyclical, progressing through consecutive and linear steps (R. A. Lesh & Doerr, 2003), students working on tasks frequently follow non-linear pathways based on their available resources and individual decision making (Ozturk, 2024; de Oliveira & Barbosa, 2013). The final model is assessed within a real-world context and communicated to others for further refinement and validation. Therefore, fostering a communicative and collaborative classroom environment is essential for tracking student participation at each stage of modeling and for supporting interactions among students and between students and the teacher (Jung & Brady, 2023).
3. Methods and Materials
The research team conducted a four-week after-school program to explore student–teacher interactions in both small-group and whole-class discussions, with a focus on identifying teacher talk moves for building a mathematical modeling community. Using the foundational principles of teaching experiment (Steffe & Ulrich, 2020) as a study guiding approach, the team designed classroom activities that were responsive to students’ ideas and positioned the research team as co-constructors of the learning experience. Throughout each instructional session, the team engaged in an iterative process, performing in-the-moment teaching moves, developing conjectures about classroom events, and revising tasks accordingly.
While the teaching experiment methodology informed the data collection, the focus of this study was not on developing or testing hypotheses about students’ learning or mental models. Instead, the data analysis centered on identifying themes in how teacher talk moves supported mathematical modeling activities within the classroom community. To achieve this, we employed content analysis method (Mayring, 2015), which requires categorizing and coding qualitative data and systematic interpretation of classroom interactions.
3.1. Research Setting, Participants, and Classroom Activities
This study was conducted with secondary school students who met twice a week at a public university in a midwestern state in the U.S. Following approval from the Institutional Review Board and the school district, we distributed consent forms to students in five 10th-grade classrooms across four urban public high schools. In total, we recruited eight students (aged 14–15) who returned signed consent forms and enrolled in an after-school program. These students, who came from three different schools, had no prior experience with mathematical modeling. The research team comprised a teacher-researcher and two observer-researchers who recorded videos of the students’ work. The class met for 16 h over eight sessions. All names mentioned in this paper are pseudonyms.
The classroom environment was structured based on the models and modeling perspective (R. A. Lesh & Doerr, 2003) and followed MEA principles (R. Lesh et al., 2000). The approach included constructing models to solve open-ended real-life problems, self-assessing models to enhance solutions, documenting models to showcase students’ reasoning, and testing the effectiveness and general applicability of the solutions. These activities took place during classroom discussions, with the teacher-researcher acting as a facilitator and the students discussing and challenging ideas.
The research team devised a preliminary sequence of activities to identify and relate the quantities required to develop the models. However, the teaching experiment methodology requires flexibility, with the initial task sequence serving only as a general instructional guide. Thus, the research team brainstormed sessions after each class to plan subsequent sessions. Table 1 presents the mathematical goals for the weekly sessions and sample tasks.

Table 1.
Mathematical goals and sample tasks from four weeks of sessions.
Each task aimed to derive solutions using relevant quantities and evaluate their applicability in real-world contexts through collective interpretation. The task selection followed the MEA principles and focused on three key dimensions. First, the mathematical goal was set to use and generate quantities that naturally engaged students in the modeling process (Ozturk, 2021, 2023). Second, the tasks were designed to align with the modeling cycle framework (Figure 1) by encouraging students to construct representations for sense making within specific real-life scenarios. Third, the tasks were structured with working in the small groups and reporting to whole class, which guided the formation of the mathematical modeling community. Adapting and sequencing weekly modeling tasks and organizing the class sessions were the preparatory teaching moves.
3.2. Data Collection, Coding, and Analysis
Video and audio recording from each session were obtained from four positions. Three cameras focused on the student groups, and one captured the presentations using an overhead projector. The video recordings included 16 h of classroom activities. Data sources included transcripts from video-recorded whole-class and group discussions, along with the students’ written work. Direct observations of all sessions, coupled with notes in the research logbook, served as supplementary data.
After transcribing each session’s video using content analysis (Mayring, 2015), we conducted open coding, initially concentrating on three aspects of the classroom environment: classroom dynamics (particularly whole-class and small-group interactions), teacher talk moves, and student participation in modeling phases. Three researchers independently coded each session and then compared and discussed their codes. This iterative process led to an initial code list organized around emerging themes in teacher talk moves, which supported subsequent focused coding.
In the focused-coding phase, the research team independently recoded the dataset using the framework shown in Figure 1 to identify students’ participation in modeling phases alongside the occurrence of teacher talk moves. Patterns in student–teacher interactions were noted at each modeling phase. The research team gathered four times to resolve any coding discrepancies, improve coding consistency, and refine the code descriptions and examples.
The resulting scheme identified three core categories of teacher talk moves in student–teacher interactions while building a mathematical modeling community: eliciting students’ ideas, introducing terms and ideas used in mathematical modeling, and encouraging students to take a position during the discussions. Eliciting moves involved prompting students to share their ideas or solutions for a particular task with the entire class and listening to others. Introducing terms and ideas used in mathematical modeling involved having a common set of terms to ensure that all students were on the same page and could follow each other’s explanations; this fostered a shared understanding. Encouraging students to take a position involved prompting them to defend their viewpoints using evidence. Table 2 lists the core teacher talk moves and provides descriptions and examples from the transcripts.

Table 2.
Teacher talk moves, descriptions, and examples.
After identifying the core categories of teacher talk moves, the research team performed cross-code checking for validation. Teacher talk moves were noted, and software was used to tally their occurrences.
3.3. Findings and Discussion
Table 3 details the observations of teacher talk moves during the modeling sessions, and Table 4 summarizes how these moves correspond with each modeling phase. Sample vignettes illustrate the student–teacher interactions that facilitated student participation in modeling phases.

Table 3.
Frequencies of teacher talk moves across the four weeks.

Table 4.
Frequencies of teacher talk moves during modeling phases.
Table 3 presents the relative frequency of each category of teacher moves observed each week. During Weeks 1 and 2, most moves focused on eliciting students’ ideas by listening to ideas and encouraging them to think aloud. During these weeks, classroom norms were established to promote brainstorming and the sharing of ideas in groups and as a class for two reasons: understanding how students called on their mathematical experiences in real-life contexts and increasing students’ confidence in their reasoning.
In Weeks 3 and 4, the percentages for introducing terms and ideas and encouraging students to take a position in the discussions were higher than those for eliciting ideas. As students became more familiar with reflecting on their own and each other’s ideas, classroom norms focused more on establishing mathematical connections and alternative representations. The teacher moves were geared toward encouraging students to take a position that helped create an environment for students to share their opinions regarding the model solutions, convince each other of their reasonableness, and defend and modify their arguments. The percentages in Table 3 do not reflect the value of each category of teacher moves but display the range of moves occurring across the sessions.
Table 4 shows that the highest proportions of teacher moves were observed when students were in the interpreting and checking/repeating phases. These phases occurred in whole-class discussions when the small groups were ready to present their solutions. In small groups, students did not naturally seek ways to check the accuracy of their solutions or justify them, which might have been due to their lack of experience in mathematical modeling. Thus, the teacher urged the students to collaboratively reflect on each group’s solutions in the whole-group discussions to build a communal learning environment.
In the phase of making assumptions and building a model, the teacher focused more on eliciting students’ ideas. While the students were working on the problems in small groups, the teacher’s questions and comments aimed to activate their prior knowledge and explore how they devised and carried out solution plans, made assumptions, and prioritized the selected variables. In this phase, more teacher moves were directed toward eliciting ideas; this may have been because the students were unfamiliar with an open-ended question structure. The teacher questions supported small-group discussions that called on the students’ mathematical experiences in real-life contexts.
In the phases of working mathematically, determining results, and interpreting, the teacher moves focused more on introducing terms and ideas used in mathematical modeling. This was intended to create a problem space for defining common variables and mathematical tools among the groups and make the students more attentive to others’ mathematizing practices. The teacher interacted with the students to discover the rules and tools that they used to construct the mathematical models, guided them to notice their mathematical mistakes, and suggested alternate resources.
In the checking and repeating phase, the teacher moves focused more on encouraging students to take a position in whole-class discussions. This phase occurred when students were ready to present and discuss their solutions and was significant for collective sense making and self-reflection on the students’ approaches to the modeling tasks. Sharing agreements or disagreements regarding the models that each group created led the students to reason inductively about the mathematical results and make arguments, taking account of the context in which they arose. Encouraging students to take a position helps them understand how their mathematical tools engage with solutions, and inviting them to justify different strategies helps them co-construct an understanding of the mathematical relationships between quantities.
The following vignettes illustrate the student–teacher interactions during students’ work on the “giving raises” problem (see Table 1) in Week 2 of this study. They show how the teacher elicited students’ ideas, introduced terms and ideas, and encouraged them to take a position during the small-group and whole-class discussions, through the teacher moves in each modeling phase.
3.4. Phase of Making Assumptions and Building a Model
The “giving raises” problem (see Table 1) asked students to identify variables that may be needed in a mathematical method for distributing pay raises among five employees. Working in pairs, they read the problem aloud and began brainstorming and contextualizing the problem by thinking about companies, job positions, and employee qualities. The teacher’s questions focused on eliciting students’ ideas to support the retrieval and application of their existing knowledge when making assumptions and building a model, as shown in the following example:
- Alyse:
- So far, our key components are how long employees have worked there, their job positions, and salaries.
- Ann:
- And job experience.
- T:
- May I ask how you thought about job experience?
- Alyse:
- I think that higher-level jobs already mean more experience. You cannot be a manager without having experience. It is part of the job position.
The teacher’s questioning caused the students to consider the difference between the job experience and job position variables, leading Alyse to explain how she thought about the differences, which helped her group clarify their list of variables. Students used extra-mathematical knowledge, such as their general perceptions of the context of the problems and their life experiences, to finalize and organize the variables.
Another group chose to consider a fast-food restaurant. When introducing terms and ideas in this modeling phase, the teacher reiterated the students’ ideas by summarizing what she heard or saw, to enhance familiarity with the terms used in mathematical modeling, as illustrated below:
- Cora
- We made a list. The five employees work in a fast-food place; they all do the same job, work for the same amount of money, and the same hours. We would like to keep things simple.
- T:
- So, you are saying you made some assumptions.
- Cole:
- Yeah, we are thinking of building a rating system, so that whoever gets more rating points could receive the highest raise.
The teacher rephrased Cora’s statement using the term “assumptions” to highlight that all five employees had the same position, salary, and hours. This rephrasing helped the students focus on the terms that they later used in group presentations. “Assumptions” became one of the keywords in the whole-class discussions, particularly when interpreting solutions.
In the phase of making assumptions and building a model, significant time was required to organize the variables that were influenced by students’ perspectives. Encouraging students to take a position involved guiding them to evaluate their strategies as described below.
- T:
- What I see is that you listed your key components and thought about what is essential for you. I am curious how you will convince anyone that your method works?
- Cora:
- I will show examples from the graph once we create it.
- Cole:
- Yes, it is different from the first method, which simply divides USD 10,000 by 5, thereby giving an equal share of USD 2000 to each employee.
- Cora:
- Agree. It would be easier to explain why our method makes sense using our graph.
The teacher’s questions were intended to guide students toward formalizing their ideas and strategies, especially given the complexity of the problem and the need to consider multiple variables. The teacher led the students to think aloud and reflect on their solutions in their own groups before presenting them to the others. Encouraging students to take a position in this phase equipped them to anticipate and address potential questions during the whole-class discussion.
3.5. Phase of Working Mathematically and Determining Results
When students worked mathematically to determine pay raises for the five employees, each group developed a different method. The variables organized in the previous phase were quantified, and the relationships between the quantities were discussed within the groups. One group centered their method around one key variable—the employee’s job performance—and used a graph to illustrate the pay distribution (see Figure 2). In this method, five employees were rated between one and five stars by customers; those with higher scores would be rewarded with higher pay raises.
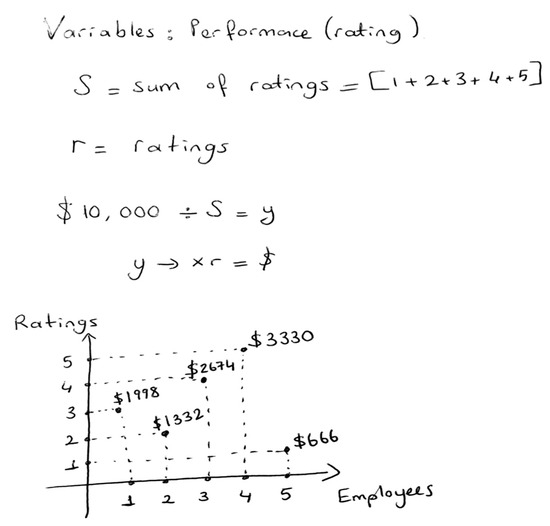
Figure 2.
Determining pay raises depending on employees’ work performance. Note: Cole’s group solution: Using the rating system in the distribution of raises.
The first vignette provided an illustrative example of an eliciting teacher move inviting students to review the equation and graph while emphasizing the mathematical connections between them. The teacher’s question focused on mathematical properties and relationships, as follows:
- T:
- How would you describe the relationship between your equation and graph?
- Cole:
- We first imagined this graph, and the equation came up later. The points on the x-axis represent workers, and the points on the y-axis represent the rating points. For example, Worker 2 receives two stars, and Worker 1 receives one star; thus, the little points on the coordinate graph represent each employee’s money.
- Cora:
- The equation we created there helped us find out unit money, which we then multiplied by each employee’s rating points.
While reflecting on their mathematical work, the students noticed the visual clue of the graph as the starting point in formalizing the central mathematical idea, which measured employees’ performance with rating points and distributed USD 10,000 based on the sum S of the rating points. The students’ mental image was modeled using the graph. Then, the graph became an object in the subsequent mathematical action, which was to create an equation.
When introducing terms and ideas in this phase of the modeling, the teacher reiterated the students’ ideas and aimed to extend their use of specific terms to articulate the mathematical ideas that they had constructed, as illustrated below:
- Cora:
- USD 10,000 is what we want to distribute. S is the sum of the ratings. Here, S is 15 [indicating 1 + 2 + 3 + 4 + 5]. We divide USD 10,000 by S to calculate the unit money.
- T:
- I see two variables in this equation: the independent variable S, which is the sum of the rating points you chose freely, and the dependent variable y, which depends on S.
- Alyse:
- Yes, unit money y is dependent on the sum of the rating points, which represent a worker’s performance, ensuring that we distribute USD10,000 using this equation.
The teacher introduced the terms “independent variable” and “dependent variable” to ensure the students correctly used and described the symbols they selected. The class continued to articulate other mathematical representations for the percentage increase from a total of USD 10,000, based on the salary of each employee. The teacher supported the students’ interaction with each other’s mathematical ideas by encouraging them to take a position in one group’s presentation. The following excerpt shows that, while students reflected on what they saw in others’ solutions (see Figure 3), with the teacher’s invitation, they became more precise in using appropriate mathematical terms in the discussion:
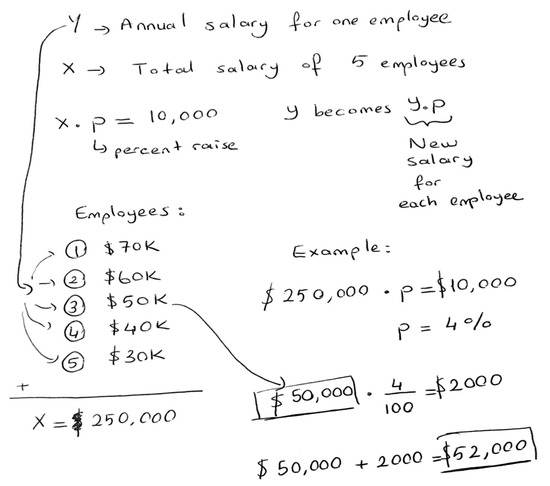
Figure 3.
Determining the percentage increase based on the salaries of five employees. Note: Ann’s group solution: Proportional distribution based on pre-assigned salaries.
- T:
- We have two methods for using percentages. For those who find this method [pointing out Figure 3] more convenient, convince us why.
- Burcin:
- This makes sense because our group randomly assigned percentages and multiplied them by salaries to determine the raises. However, we were not sure whether we had distributed exactly USD 10,000; we ended up with a total of USD 8000.
- Ann:
- Our method focuses on creating an equation to determine percent raise. Our variables are X, total salary of 5 employees; Y, annual salary for each employee.
- Burcin:
- Why do you divide 10,000 by X?
- Ann:
- To calculate the percent raise for each employee.
- Cora:
- Y is important to find each employee’s raise based on the salaries.
The teacher set the stage by asking students not only to present the mathematical properties of the solution but also to convince the class why one method might be more convenient. This emphasized the correct use of percentages in the mathematical models. One group developed a systematic method to ensure that USD 10,000 was distributed accurately among five employees with different incomes. The teacher’s guidance prompted the students to look for patterns in two different uses of percentages in two solutions, leading Burcin’s group to realize their mistake in randomly assigning percentage increases when distributing the USD 10,000. Ann and Cora explained the variables and their relationships within the presented solution.
3.6. Phase of Interpreting
This phase was important for drawing insights and conclusions from the developed models. The class evaluated whether the models were practical and understandable in the real-life context of the original problem. They examined their models based on the assumptions that they had made and the variables identified in the first phase. Their interpretations were of two types: recognizing the correspondence between the quantities in the problem context by providing examples or counterexamples and questioning the logic of the solution using personal knowledge and life experiences. The next vignette illustrates a teacher talk move aimed at eliciting students’ ideas by asking them for more details.
- Alyse:
- One advantage of our method is that it can be applied to other jobs.
- T:
- Could you explain what you mean by “applied to other jobs”?
- Ann:
- Let us say it is the office of a company that includes a manager, assistant, full-time and part-time workers, etc.
- Alyse:
- We could distribute raises for all types of workers.
The teacher encouraged students to clarify their reasoning and express their ideas more explicitly. The question encouraged the students to explain that knowing two key variables—salary and work hours—allowed them to distribute pay raises regardless of the company type. The class then discussed how the relationship between salary and working hours allowed Alyse’s model to work in different job settings. Building on this discussion, the teacher introduced the term “realistic”, emphasizing the need for students to check how “applicable” their models’ results were in real-world scenarios, as illustrated below:
- T:
- Regarding the applicability of Alyse’s group method, they concluded that their model is realistic because it can benefit any type of company and different workers through pay raises.
- Cora:
- So, are we looking at how realistic our models are?
- T:
- Yes, how practical and realistic your model is!
- Beth:
- I now think that the more variables are included in a model, the more realistic the results become.
- Cora:
- However, we cannot include all variables, even if they are important.
- T:
- Exactly! That is why we are choosing key variables. Models might have their own limitations, but we will determine which one seems the most realistic and applicable.
The teacher began by reiterating Alyse’s group’s conclusion regarding the applicability of their model to real life and connecting it to the broader discussion. This reiteration served to clarify the students’ understanding of the realistic results of the models. The teacher stated that, regardless of the limitations of a model, the focus should be on deciding which model seems realistic and applicable, guiding students toward the next step of modeling, collaboratively checking the results, and repeating the process, if necessary. To deepen the students’ understanding of each other’s ideas, the teacher encouraged them to take a position when interpreting the models, as illustrated below:
- Beth:
- The title on the y-axis [see Figure 2] should be “average rating points” if we want it to be more realistic.
- T:
- Can someone who agrees with Beth explain why “average rating points” are important?
- Cora:
- It’s because, currently, we do not know if each employee was rated by the same customers.
- Burcin:
- It is like—50 customers rated those five employees, and each employee received average points from those 50 customers.
The teacher’s move in encouraging students to take a position for or against using average rating points led them to reexamine what had been presented and achieve a more realistic understanding of the results. The move prompted students to elaborate on their understanding in their own words and allowed them to present different explanations and build on each other’s contributions. Cora’s response was reinforced by Burcin’s example, illustrating how students actively engaged with their peers’ ideas.
3.7. Phase of Checking Results and Repeating the Process
The checking and repeating phase was crucial for ensuring the accuracy and reliability of the models. The teacher facilitated the whole-class discussion, with students comparing their model’s outputs and reflecting on what worked and why. The teacher guided the students in identifying potential sources of error, revisiting assumptions, considering model limitations, and examining the accuracy of the mathematical methods. This phase led the students to think critically about the relationship between their mathematical models and the real-world situation. The vignette below offers an illustrative example of an eliciting teacher move inviting students to review their models by checking the accuracy of the solutions and comparing the results with the real situation:
- T:
- How do you know that your results are accurate and reliable? Are there any parts of your model that could be improved to make more sense?
- Cole:
- Compared to other groups, I would say that mathematically our solution [see Figure 2] is correct. We successfully distributed USD 10,000 among five employees using their rating points. However, we only considered job performance when deciding on the raises. We could multiply the years of experience by the rating points to help divide the USD 10,000 and determine the amount that each person should receive.
The teacher’s probing spurred the students to identify the strengths of their solution method, which was mathematically valid. Cole’s group decided that the model could be improved by incorporating other variables, such as years of experience, to increase the reliability of their model by bringing it closer to the real-world situation.
When introducing terms and ideas in this phase of the modeling, the teacher rephrased the groups’ solutions and highlighted the significance of a collaborative learning environment, using the terms “verifying” and “model refinement”, as shown below:
- T:
- Cole’s group decided to verify the accuracy of the calculations and determine whether the model needed refinement. We are doing this collectively to enhance our shared understanding.
- Ann:
- I think our model [see Figure 3]—the equation used to calculate percentages by considering years of work, annual salary, and the total salary of five different employees—results in correct calculations. We were able to distribute USD 10,000. With this system, we can distribute any amount of money.
- T:
- Okay, that is a strength of your model. It produces an accurate calculation.
- Ann:
- Our model considers more variables. However, we are missing the years of experience. This could have been another variable and made a part of the equation as a multiplier.
By highlighting Cole’s group decision, the teacher reinforced the idea that mathematical modeling is not just about arriving at an answer but also about evaluating it. This move emphasized the importance of the iterative process in mathematical modeling, with the initial solutions revised based on collective feedback. The teacher highlighted the importance of collaborative efforts to refine and enhance models.
To foster a sense of community, the teacher encouraged the students to take a position and exchange peer feedback during this phase. This approach prompted students to defend or reconsider their positions based on critiques of their model’s accuracy and reliability, as illustrated below.
- T:
- We have two suggestions for revising this model [see Figure 2]. One idea is to give raises to employees who get three stars or more. The other is to multiply years of experience by the rating points. Who supports the first idea? Convince us.
- Pera:
- I do. Just because someone has more experience, it does not mean they are doing a better job. The three-star system rewards performance and gives employees a clear goal to reach.
- Yang:
- I disagree! Experience matters, too. Someone with ten years at the company might not always get the highest ratings, but their experience still benefits the company in ways that ratings do not show. We could combine them.
- Beth:
- I agree with Yang. The three-star system is not clear on how it would work mathematically, but using experience with ratings is doable and USD 10,000 can be distributed.
- Cole:
- Yeah, adding experience as a multiplier makes the system more complex but also more reliable.
The teacher’s open-ended prompt invited students to take sides and explain their reasoning. This move opened up the door to debate and ensured that multiple perspectives were explored. The students needed to justify their views using logical arguments, as shown by Pera who argued that performance rather than experience should be rewarded. Yang and Beth challenged Pera’s view by suggesting a combined approach that balanced experience and performance. Cole’s comment showed how the teacher’s move led students to think about the complexity of applying such a model to real-world situations. Later, the class discussed how the rating system could be adjusted if a three-star condition was added to the model (see Figure 2), but they were unable to find a solution. This was a crucial moment for the teacher to emphasize that it could be challenging to mathematically represent all the variables that students wanted to include in their models.
4. Conclusions
In this study, we investigated how teacher talk moves help create a mathematical modeling classroom environment that promotes student participation in the phases of mathematical modeling and encourages the exchange of ideas among peers in both whole-class and small-group discussions. Our findings categorized teacher talk moves into three main types: eliciting students’ ideas, introducing terms and concepts used in mathematical modeling, and encouraging students to take a position. Eliciting ideas involves the teacher prompting students to share their strategies and solutions, using questions and restatements to clarify their thinking. Introducing terms and concepts related to mathematical modeling ensures that all students can follow and contribute to the discussion, fostering a shared understanding. Encouraging students to take a position involves the teacher interacting with students by acknowledging their perspectives and prompting them to argue for or against specific approaches to model development.
These findings align with previous studies, which found that, when combined with open-ended, real-life problems and consistent efforts to foster student interaction around each other’s ideas, teacher talk moves support the creation of a modeling community of learners engaged in collective sense making (Doerr, 2006; Jung & Brady, 2023). Within this community, classroom norms focus on listening, sharing, clarifying, comparing, interpreting, justifying, verifying results, describing agreement or disagreement with peers, and revising model solutions (Yenmez & Erbaş, 2023).
Unlike other studies on whole-class discussions in mathematical modeling classrooms (Brady & Jung, 2022; de Oliveira & Barbosa, 2013; Manouchehri et al., 2020), we observed that teacher talk moves appeared to facilitate the exchange of ideas during small-group work, which in turn contributed to students’ preparation for group presentations of their solutions to the whole class. Additionally, our study contributes to the research on modeling classrooms by documenting the distribution of teacher talk moves over four weeks. This evidence highlights the construction and evolution of classroom norms throughout the instructional sessions. Early on in this study, the majority of teacher talk moves focused on eliciting students’ ideas. In the later sessions, a greater proportion of the moves involved encouraging students to take a position during the discussions. As students became more accustomed to reflecting on their own and their peers’ ideas, classroom norms shifted toward formulating mathematical connections, creating alternative representations, and justifying solutions.
Our findings suggest a relationship between the types of teacher talk moves and students’ participation in different phases of the modeling process. In the phase of making assumptions and building a model, teacher talk moves concentrated on eliciting the students’ ideas. While students worked on problems in small groups, the teacher’s questions and comments aimed to activate prior knowledge and explore how students developed and implemented solution plans, including making assumptions and prioritizing selected variables. During the phases of working mathematically/determining results and interpreting, teacher moves were more focused on introducing key terms and ideas used in mathematical modeling, helping to establish a common problem space for defining variables and mathematical tools across groups. This encouraged students to become more attentive to the mathematizing practices of others. Notably, in the phase of interpreting, the teacher often reiterated the groups’ conclusions regarding the applicability of their models to real-life scenarios, connecting these conclusions to a broader discussion. This clarified the students’ understanding of the realistic outcomes of their models.
In the phase of checking results and repeating the process, the teacher moves were focused on encouraging students to actively participate in whole-class discussions. Initially, we observed that students were not naturally inclined to check their results or repeat processes. As noted by Galbraith and Stillman (2006), justifying results poses a particular challenge for students. However, similar to Jung and Brady’s (2023) study results, we observed that the teacher’s prompts encouraged students to take a stance during whole-class discussions and led to inductive reasoning about the mathematical results.
Implications and Limitations
In this study, we adopted the models and modeling theoretical perspective (R. Lesh & Lehrer, 2003) and used MEAs to introduce mathematical modeling to students. We also used an adapted version of the modeling cycle (R. A. Lesh & Doerr, 2003) to examine student participation in different phases of mathematical modeling and identify teacher talk moves that may contribute to fostering a mathematical modeling community. Our findings suggest a connection between specific talk moves and the nature of classroom discussions, particularly in the ways that students articulated, refined, and negotiated their ideas. However, we do not claim a direct causal relationship between talk moves and student learning, as other factors—such as task design, class structure, or the after-school learning environment—may have also played a role in shaping students’ creation and use of mathematical models. Employing alternative modeling perspectives and using different tasks may reveal additional teacher talk moves that are relevant to supporting student participation in mathematical modeling. Further research could explore how teachers intentionally select and sequence multiple modeling activities to align with their curricular goals.
This study was based on limited data from a four-week after-school program involving eight secondary students. The content coverage, assessments, and classroom discussions were shaped by students’ responses to the tasks and the research team’s adjustments to the instructional design for each session. Given the classroom context, we acknowledge that the structured modeling cycle and the carefully designed tasks likely contributed to the learning environment as much as, if not more than, the specific talk moves identified. Future studies could expand on this research by collaborating with multiple teachers across different classrooms to examine how various instructional approaches, teacher knowledge, and classroom contexts influence mathematical modeling discussions. As Geiger et al. (2022) noted, the investigation of teacher competencies required for effective modeling instruction remains an open area of research.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board of The Ohio State University (protocol code 2019B0331 and date of approval 21 August 2019).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the author.
Conflicts of Interest
The author declares no conflict of interest.
References
- Abassian, A., Safi, F., Bush, S., & Bostic, J. (2020). Five different perspectives on mathematical modeling in mathematics education. Investigations in Mathematics Learning, 12(1), 53–65. [Google Scholar] [CrossRef]
- Anhalt, C. O., & Cortez, R. (2015). Mathematical modeling: A structured process. The Mathematics Teacher, 108(6), 446–452. [Google Scholar] [CrossRef]
- Aroeira, A. J., Carreira, S., & da Ponte, J. P. (2024). Teacher strategic interventions to support students in constructing the model of the situation in a modelling task. In H.-S. Siller, V. Geiger, & G. Kaiser (Eds.), Researching mathematical modelling education in disruptive times (pp. 161–171). Springer Nature. [Google Scholar]
- Blum, W. (2015). Quality teaching of mathematical modelling: What do we know, what can we do? In S. J. Cho (Ed.), The proceedings of the 12th international congress on mathematical education (pp. 73–96). Springer. [Google Scholar]
- Borromeo Ferri, R. (2018). Learning how to teach mathematical modeling in school and teacher education. Springer. [Google Scholar]
- Brady, C., & Jung, H. (2022). Modeling presentations: Toward an assessment of emerging classroom cultures of modeling. Educational Studies in Mathematics, 109(2), 237–261. [Google Scholar] [CrossRef]
- Brady, C., Ramírez, P., & Lesh, R. (2024). Problem posing and modeling: Confronting the dilemma of rigor or relevance. In T. L. Toh, M. Santos-Trigo, P. H. Chua, N. A. Abdullah, & D. Zhang (Eds.), Problem posing and problem solving in mathematics education: International research and practice trends (pp. 33–50). Springer Nature. [Google Scholar]
- Campbell, T. (2023). Examining how middle grade mathematics students seize learning opportunities through conflict in small groups. Mathematical Thinking and Learning, 25(2), 208–231. [Google Scholar] [CrossRef]
- Campbell, T. G., & Yeo, S. (2021). Exploring in-the-moment teaching moves that support sociomathematical and general social norms in dialogic instruction. International Journal of Science and Mathematics Education, 21, 1–23. [Google Scholar] [CrossRef]
- Chapin, S. H., O’Connor, C., O’Connor, M. C., & Anderson, N. C. (2009). Classroom discussions: Using math talk to help students learn, grades K–6. Math Solutions. [Google Scholar]
- Cobb, P., Boufi, A., McClain, K., & Whitenack, J. (1997). Reflective discourse and collective reflection. Journal for Research in Mathematics Education, 28(3), 258–277. [Google Scholar] [CrossRef]
- de Oliveira, A. M. P., & Barbosa, J. C. (2013). Mathematical modelling, mathematical content and tensions in discourses. In G. A. Stillman, G. Kaiser, W. Blum, & J. Brown (Eds.), Teaching mathematical modelling: Connecting to research and practice (pp. 67–76). Springer. [Google Scholar]
- Doerr, H. M. (2006). Examining the tasks of teaching when using students’ mathematical thinking. Educational Studies in Mathematics, 62(1), 3–24. [Google Scholar] [CrossRef]
- Doerr, H. M., & English, L. D. (2006). Middle grade teachers’ learning through students’ engagement with modeling tasks. Journal of Mathematics Teacher Education, 9(1), 5–32. [Google Scholar] [CrossRef]
- Elia, I., Gagatsis, A., Panaoura, A., Zachariades, T., & Zoulinaki, F. (2009). Geometric and algebraic approaches in the concept of “limit” and the impact of the “didactic contract”. International Journal of Science and Mathematics Education, 7(4), 765–790. [Google Scholar] [CrossRef]
- English, L. D. (2003). Reconciling theory, research, and practice: A models and modelling perspective. Educational Studies in Mathematics, 54(2), 225–248. [Google Scholar] [CrossRef]
- English, L. D., & Doerr, H. M. (2004). Listening and responding to students’ ways of thinking. In I. Putt, R. Farragher, & M. McLean (Eds.), Mathematics education for the third millennium: Towards 2010 (pp. 215–222). MERGA. [Google Scholar]
- Galbraith, P., & Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. ZDM—Mathematics Education, 38(2), 143–162. [Google Scholar] [CrossRef]
- Garfunkel, S. A., Montgomery, M., Bliss, K., Fowler, K., Galluzzo, B., Giordano, F., Godbold, L., Gould, H., Levy, R., Libertini, J., & Long, M. (2016). GAIMME: Guidelines for assessment & instruction in mathematical modeling education. Consortium for Mathematics and Its Applications. [Google Scholar]
- Geiger, V., Galbraith, P., Niss, M., & Delzoppo, C. (2022). Developing a task design and implementation framework for fostering mathematical modelling competencies. Educational Studies in Mathematics, 109, 313–336. [Google Scholar] [CrossRef]
- Greefrath, G., Siller, H. S., Klock, H., & Wess, R. (2022). Pre-service secondary teachers’ pedagogical content knowledge for the teaching of mathematical modelling. Educational Studies in Mathematics, 109(2), 383–407. [Google Scholar] [CrossRef]
- Hofmann, R., & Ruthven, K. (2018). Operational, interpersonal, discussional and ideational dimensions of classroom norms for dialogic practice in school mathematics. British Educational Research Journal, 44(3), 496–514. [Google Scholar] [CrossRef]
- Illustrative Mathematics. (2016, May 4). HSN-Q.A. Reason quantitively and use units to solve problems. Available online: http://tasks.illustrativemathematics.org/content-standards/HSN/Q/A (accessed on 28 September 2024).
- Jung, H., & Brady, C. (2023). Modeling actions foregrounded in whole-class modeling discourse: A case study of a model-eliciting activity and a three-act task. Mathematical Thinking and Learning, 27, 1–24. [Google Scholar] [CrossRef]
- Jung, H., & Brady, C. (2024). Teachers posing model-eliciting activities to connect socially-relevant perspective with closely connected mathematical ideas. In H.-S. Siller, V. Geiger, & G. Kaiser (Eds.), Researching mathematical modelling education in disruptive times (pp. 317–327). Springer Nature Switzerland. [Google Scholar]
- Kaiser, G., Schwarz, B., & Tiedemann, S. (2010). Future teachers’ professional knowledge on modeling. In R. Lesh, P. L. Galbraith, C. R. Haines, & A. Hurford (Eds.), Modeling students’ mathematical modeling competencies (pp. 433–444). Springer. [Google Scholar]
- Kaiser, G., & Sriraman, B. (2006). A global survey of international perspectives on modelling in mathematics education. ZDM, 38, 302–310. [Google Scholar] [CrossRef]
- Kang, S. M., & Kim, M. K. (2016). Sociomathematical norms and the teacher’s mathematical belief: A case study from a Korean in-service elementary teacher. Eurasia Journal of Mathematics, Science and Technology Education, 12(10), 2733–2751. [Google Scholar]
- Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Mathematical Thinking and Learning, 18(2), 107–124. [Google Scholar] [CrossRef]
- Lesh, R., Hoover, M., Hole, B., Kelly, A., & Post, T. (2000). Principles for developing thought-revealing activities for students and teachers. In A. Kelly, & R. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 591–646). Lawrence Erlbaum Associates. [Google Scholar]
- Lesh, R., & Lehrer, R. (2003). Models and modeling perspectives on the development of students and teachers. Mathematical Thinking and Learning, 5(2–3), 109–129. [Google Scholar] [CrossRef]
- Lesh, R., & Sriraman, B. (2005). Mathematics education as a design science. ZDM—Mathematics Education, 37(6), 490–505. [Google Scholar] [CrossRef]
- Lesh, R. A., & Doerr, H. M. (Eds.). (2003). Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning, and teaching. Lawrence Erlbaum Associates. [Google Scholar]
- Manouchehri, A., Bekdemir, M., & Yao, X. (2020). Facilitating modelling activities in a grade 5 classroom. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical modelling education and sense-making (pp. 187–197). Springer. [Google Scholar]
- Mayring, P. (2015). Qualitative content analysis: Theoretical background and procedures. In A. Bikner-Ahsbahs, C. Knipping, & N. Presmeg (Eds.), Approaches to qualitative research in mathematics education: Examples of methodology and methods (pp. 365–380). Springer. [Google Scholar]
- National Council of Teachers of Mathematics. (2011). Cash or gas? NCTM. [Google Scholar]
- Ozturk, A. (2021). Examining the relationship between instructional practices and students’ mathematical modeling competencies [Doctoral dissertation, Ohio State University]. Available online: http://rave.ohiolink.edu/etdc/view?acc_num=osu1625748925881711 (accessed on 5 January 2025).
- Ozturk, A. (2023). Fostering quantitative reasoning through a question of fairness. Mathematics Teacher: Learning and Teaching PK-12, 116(4), 265–272. [Google Scholar] [CrossRef]
- Ozturk, A. (2024). Examining translanguaging practices in mathematical modelling. In H. S. Siller, V. Geiger, & G. Kaiser (Eds.), Researching mathematical modelling education in disruptive times. International perspectives on the teaching and learning of mathematical modelling. Springer. [Google Scholar] [CrossRef]
- Partanen, A. M., & Kaasila, R. (2015). Sociomathematical norms negotiated in the discussions of two small groups investigating calculus. International Journal of Science and Mathematics Education, 13(4), 927–946. [Google Scholar] [CrossRef]
- Savuran, R., & Akkoç, H. (2021). Examining pre-service mathematics teachers’ use of technology from a sociomathematical norm perspective. International Journal of Mathematical Education in Science and Technology, 54(1), 74–98. [Google Scholar] [CrossRef]
- Schukajlow, S., Kolter, J., & Blum, W. (2015). Scaffolding mathematical modelling with a solution plan. ZDM—Mathematics Education, 47(7), 1241–1254. [Google Scholar] [CrossRef]
- Schukajlow, S., Krawitz, J., Kanefke, J., Blum, W., & Rakoczy, K. (2023). Open modelling problems: Cognitive barriers and instructional prompts. Educational Studies in Mathematics, 114(3), 417–438. [Google Scholar] [CrossRef]
- Siller, H. S., Geiger, V., & Kaiser, G. (2024). Researching mathematical modelling education in disruptive times—An introduction. In Researching mathematical modelling education in disruptive times (pp. 3–11). Springer Nature Switzerland. [Google Scholar] [CrossRef]
- Siller, H. S., Nitzan-Tamar, O., & Kohen, Z. (2023). Scaffolding practices for modelling instruction in STEM-related contexts: Insights from expert and novice teachers. ZDM—Mathematics Education, 55(7), 1351–1364. [Google Scholar] [CrossRef]
- Steffe, L. P., & Ulrich, C. (2020). Constructivist teaching experiment. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 134–141). Springer. [Google Scholar]
- Stein, M. K., Engle, R. A., Smith, M. S., & Hughes, E. K. (2008). Orchestrating productive mathematical discussions: Five practices for helping teachers move beyond show and tell. Mathematical Thinking and Learning, 10(4), 313–340. [Google Scholar] [CrossRef]
- Stender, P. (2019). Heuristic strategies as a toolbox in complex modelling problems. In G. A. Stillman, & J. P. Brown (Eds.), Lines of inquiry in mathematical modelling research in education (pp. 197–212). Springer. [Google Scholar]
- Stephan, M. (2020). Sociomathematical norms in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 802–805). Springer. [Google Scholar]
- Tropper, N., Leiss, D., & Hänze, M. (2015). Teachers’ temporary support and worked-out examples as elements of scaffolding in mathematical modeling. ZDM—Mathematics Education, 47(7), 1225–1240. [Google Scholar] [CrossRef]
- Wickstrom, M. H., & Jung, H. (2024). Understanding preservice elementary teachers as mathematical modelers and their perceptions of the process. Journal for Research in Mathematics Education, 55(4), 182–209. [Google Scholar] [CrossRef]
- Wilhelm, A. G. (2014). Mathematics teachers’ enactment of cognitively demanding tasks: Investigating links to teachers’ knowledge and conceptions. Journal for Research in Mathematics Education, 45(5), 637–675. [Google Scholar] [CrossRef]
- Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458–477. [Google Scholar] [CrossRef]
- Yackel, E., Rasmussen, C., & King, K. (2000). Social and sociomathematical norms in an advanced undergraduate mathematics course. The Journal of Mathematical Behavior, 19(3), 275–287. [Google Scholar] [CrossRef]
- Yenmez, A. A., & Erbaş, A. K. (2023). Facilitating a sustainable transformation of sociomathematical norms through mathematical modeling activities. International Journal of Science and Mathematics Education, 21(3), 761–785. [Google Scholar] [CrossRef]
- Zahner, W., & Moschkovich, J. (2010). Talking while computing in groups: The not-so-private functions of computational private speech in mathematical discussions. Mind, Culture, and Activity, 17(3), 265–283. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).