Abstract
The differences in the math learning process and the underlying cognitive skills of students with a mathematical learning disability and those who are low achieving in math are important to consider when supporting their learning. Still, there is a lack of a comprehensive overview comparing these two groups’ cognitive skill deficits that are responsible for math learning difficulties. This systematic literature review aimed to fill this gap. This study revealed differences in the cognitive profiles of students with a mathematical learning disability and low-achieving students. Students with a mathematical learning disability showed significantly weaker domain-general cognitive skills than the control groups across most areas, while low-achieving students exhibited less pronounced differences compared to the controls. Additionally, students with a mathematical learning disability performed worse than low-achieving students in working memory and processing speed. In terms of domain-specific cognitive skills, both sample groups struggled with calculation compared to typical achievers, with students with a mathematical learning disability displaying weaker basic calculation skills than low achievers.
1. Introduction
Learning math can be complicated for students for many reasons. Geary et al. (2012) have identified two groups of students struggling with math: students with a math learning disability (MLD) and low-achieving (LA) students. According to Lewis (2014), LA students and those with MLDs learn math differently, and standard teaching strategies are unsuitable (Lewis & Fisher, 2016). Several studies highlight both similarities (e.g., Baglama et al., 2017; Bryant et al., 2003) and differences (e.g., Herold et al., 2020; Kajamies et al., 2010) in math teaching strategies used for students with an MLD and those with LA. In intervention studies, MLD and LA students are often grouped together based on achievement scores below the 25th percentile (Dennis et al., 2016). However, there is significant variation in individual responses, with a substantial proportion of participants not benefitting from interventions that are efficient at the group level (Kearns & Fuchs, 2013). This suggests that interventions may fail to target relevant deficits if it is assumed that all students struggling with math share similar profiles. The differences in the learning process and underlying cognitive skills must be considered when designing identification tools, appropriate instructional approaches, and effective practices to support learning (Nelson & Powell, 2018; Orosco & Reed, 2023; Van Herwegen et al., 2024). It has also been established that teachers lack knowledge in effectively identifying and supporting students with mathematical difficulties (Lewis, 2014; Orosco & Reed, 2023; Van Herwegen et al., 2024).
1.1. Definitions of the MLD and LA
Researchers have no consensus on identifying mathematical learning disabilities (Geary, 2010; Lewis & Fisher, 2016; Mazzocco, 2005). According to Mazzocco (2005), Nelson and Powell (2018), and Soares et al. (2018), math difficulties is a broader term to describe students with low math performance; it is often caused by a variety of factors, and it also includes students with a math disability. Soares et al. (2018) used the terms math learning disorder, math learning disability, and dyscalculia as synonyms in their study. In mathematics education research, math disorder is used instead of math learning disability (Deruaz et al., 2020). Ashkenazi et al. (2013) have described developmental dyscalculia as a part of a math learning disability, while Mazzocco (2005) marks math disability as biologically based math difficulties. According to Lewis and Fisher (2016), the studies that classify students based on achievement measures alone, not considering other aspects, use the terms students with mathematics learning difficulties or students at risk for mathematics learning disabilities rather than the term MLD.
By analyzing definitions, Fletcher et al. (2007) point out two components of dyscalculia: mathematical difficulties and cognitive deficits. Butterworth (2019) adds that dyscalculia is defined mainly as a deficit in basic numerical concepts and basic computational skills, and it does not include more abstract mathematical skills like algebra or geometry. Geary et al. (2004) give the following characteristics of MLD: a score on a mathematics achievement test that is lower than the 20th or 25th percentile, an IQ score that is low average or higher, often some form of the cognitive deficit, routine instructional intervention from the teacher in the classroom does not improve math achievement, and the persistence of learning disability.
Researchers have also defined the term low achievement differently. Yeo et al. (2008) describe low-achieving students as at-risk for academic failure. Kearns and Fuchs (2013) interpret low achievement quite widely: low performing with and without learning disabilities and with and without specific cognitive deficits. Kolikant and Broza (2011) point out two factors for the identification of low-achieving students in math: students that score below the 50th percentile on standardized tests but do not have learning disabilities. Also, the term severe difficulties in mathematics instead of low achieving in math is used in mathematics education research (Deruaz et al., 2020). According to Butterworth (2019), low scores in math are related to low IQ. Students with low IQ scores struggle with math problems that demand more complex concepts and problem-solving strategies, while the core problem of students with an MLD is struggling with basic calculation (Butterworth, 2019).
According to Shaw (2022), students with learning disabilities and LA may have similar poor results on achievement tests. Still, they tend to differ in general intelligence levels: students with specific learning disabilities typically have average or higher intelligence, while students with LA fall within the borderline-to-low range, though not to the extent of an intellectual disability. In 2012, Geary et al. excluded learning disabilities from low achievement by stating that low-achieving students score between the 11th and 25th percentile in math tests, whereas students with a math learning disability score at or below the 10th percentile. Moreover, students with an MLD experience significant and persistent challenges especially in learning mathematics, including difficulties with number sense, accurately and fluently performing calculations, and engaging in mathematical reasoning (World Health Organization [WHO], 2019).
In contrast, students with low academic achievement struggle with the development of a broad range of academic skills, including mathematics (Shaw, 2022). However, it is important to note that these learning difficulties do not include intellectual disability (World Health Organization [WHO], 2019; Shaw, 2022).
In this study, considering the diversity of definitions of math learning disability and low achievement, we interpret MLD as a specific learning disability with math test scores at or below the 10th percentile and take the terms “math learning disorder” and “math disability” as synonyms to MLD. Since dyscalculia also refers explicitly to difficulties in mathematics, especially when performing simple calculations (World Health Organization [WHO], 2019), this article categorizes it as a type of MLD. Low achievers are defined as having low academic performance in math. LA students’ math test scores are lower than those of typical achieving students but not as low as those of students with an MLD, staying between the 11th and 25th percentile.
1.2. Cognitive Profile of the Students with an MLD and LA
Mathematical competence is strongly influenced by language skills, visuospatial skills, and memory (Hannell, 2005). Furthermore, Butterworth (2019) claims that number sense, reasoning abilities, working memory, long-term memory, attention, and language are essential cognitive tools used when learning arithmetic. In addition, Butterworth (2019) divides cognitive abilities affecting arithmetic skills into two groups: domain-general abilities (cognitive abilities responsible for understanding a wide range of subjects, e.g., reasoning, working memory, long-term memory, attention, and language) and domain-specific abilities (cognitive abilities specific to numbers and arithmetic, e.g., number sense). According to Barnes and Raghubar (2017), domain-specific abilities are crucial developmental antecedents to eventual mathematical performance (e.g., complex calculation). However, domain-general abilities are essential in developing mathematical competencies (e.g., understanding and using mathematical concepts and procedures).
Several authors, such as Fletcher et al. (2007) and Lewis (2014), emphasize the relationship between the development of cognitive skills and MLDs. In the case of MLDs, multiple cognitive components of both domain-general and domain-specific cognitive functions may be deficient (Eidlin-Levy & Rubinsten, 2017). According to Geary (2004) and Shin and Bryant Pedrotty (2015), the executive functions of students with MLDs are impaired: There is evidence that connects MLDs with deficits in working memory (Chinn, 2020; Rubinsten & Henik, 2009), especially visuospatial working memory (Shin & Bryant Pedrotty, 2015), in the phonological loop on number-related tasks (Geary, 2004; Shin & Bryant Pedrotty, 2015), and attention problems (Rubinsten & Henik, 2009). Students with MLDs also show deficits in short-term memory (Chinn, 2020); moreover, students with MLDs often have disruptions in the ability to store and retrieve numerical facts from long-term memory (Butterworth, 2019; Geary, 2004), delayed procedural development (Geary, 2010), and difficulties in visuospatial processing (Augustyniak et al., 2005; Geary, 2010). However, the core deficit of the MLD is a number sense deficit (Geary, 2010; Butterworth, 2019). The difficulties described lead to more specific problems in counting and arithmetic (Geary, 2004; Shin & Bryant Pedrotty, 2015), copying numbers, and maintaining place values (Augustyniak et al., 2005). Not every person with an MLD has all of those deficits. Thus, Geary (2004) divides MLDs into three subtypes based on deficiencies in cognitive profiles: procedural, semantic memory, and visuospatial MLDs.
According to Shaw (2022), LA students have below-average cognitive abilities, including skills responsible for learning math, e.g., working memory, language, number sense, inattention, and organizational skills. Those students may solve basic arithmetic tasks with less difficulty than abstract complex math tasks (Shaw, 2022). Geary (2010) adds that students with LA have a moderate number sense, fact retrieval, and central executive deficits and have delayed procedural development to a lesser degree than MLD students.
It should be, however, noted that research on which cognitive skills are impaired in students with mathematics learning difficulties often yields contradictory findings. Mishra and Khan (2023) and Saga et al. (2022) highlight conflicting findings in their reviews regarding various cognitive skills, including verbal working memory, cognitive inhibition and shifting, number comprehension, and non-symbolic and symbolic number comparison. Furthermore, the recent longitudinal study by Kroesbergen et al. (2022) stated that the cognitive mechanisms for math development are broadly similar for students with an MLD and typically developed students, suggesting that an MLD can be defined as the worst performance on a continuous scale rather than as a discrete condition (Kroesbergen et al., 2022).
In summary, while numerous studies have focused on describing the cognitive skills of students with an MLD, considerably less research has explored the cognitive skills of LA students. Various authors have identified different, and sometimes overlapping, aspects of the cognitive profiles of MLD and LA students, making it difficult to form a cohesive understanding.
1.3. Previous Studies
There are some literature reviews written in the past 20 years about students with MLDs or/and LA (Baker et al., 2002; Deruaz et al., 2020; Lewis & Fisher, 2016; Kiru et al., 2018; Shin & Bryant Pedrotty, 2015). However, finding literature reviews comparing MLD and LA students is not easy. In several articles, different terms for describing samples are used, and it is complicated to understand whether the review article includes MLD or LA students (Benavides-Varela et al., 2020; Watt & Watkins, 2016). The literature review by Watt and Watkins (2016) identified effective interventions for teaching algebra to students with learning disabilities but did not specify the term learning disabilities. Nelson and Powell (2018) also grouped all students with math difficulties into one sample in their review, but there were, in fact, different subgroups of students struggling with math, MLD, and LA in math, for example. The authors acknowledged the difficulties when analyzing the results of the included articles, as well as the conclusions drawn about the cognitive performance of students with math difficulty, as the authors of the included studies have used different methods to compile the study samples (Nelson & Powell, 2018). Few literature reviews give information about the characteristics of MLDs. Still, there is even less information about LA. Deruaz et al. (2020) investigated in their literature review how an MLD is described in studies of mathematics education. They found that studies in this area mainly focused on the interventions instead of identification, and interventions were designed to consider the specific mathematical content instead of the characteristics of the students. The authors point out the importance of the collaboration of mathematics education, cognitive science, and special education to identify students with an MLD as early as possible and to develop more effective interventions to support students with an MLD in the classroom (Deruaz et al., 2020).
In their study, Lewis and Fisher (2016) aimed to determine how an MLD is identified in the research field of learning disabilities. There was significant variability in the methods used to identify MLDs: Many articles did not differentiate MLDs from low achievement, and it was unclear whether the difficulties in math persisted over the years. In addition, most of the articles focused on young children and basic calculations. Based on their research, the authors provide straightforward suggestions on how to increase the accuracy of the identification of MLDs:
- -
- There should be a clear description of how the participants were identified as having an MLD;
- -
- Standard measuring instruments for MLD identification should be used;
- -
- Cut-off scores below the 10th percentile on standardized math tests should be used to differentiate MLDs from LA;
- -
- There should be evidence that difficulties in math are persistent and not caused by social or environmental factors;
- -
- More research about older students with MLDs and more complex mathematical topics is needed (Lewis & Fisher, 2016).
To effectively identify and support students with learning difficulties in math, such as students with an MLD or LA, developing a comprehensive understanding of both their cognitive and mathematical skills is crucial. There are many studies describing the cognitive skills of students with an MLD (e.g., Butterworth, 2019; Fletcher et al., 2007). Still, we can find fewer articles about LA students’ cognitive profiles related to mathematics. According to Shaw (2022), there is a risk that students with LA may stay unidentified and without help because deficits in their cognitive and math skills are not as severe as those of students with an MLD or an intellectual disability. However, a survey that gives an extensive overview of the differences in deficits in cognitive skills responsible for math learning difficulties between students with LA and an MLD is missing.
This study aims to describe the differences in cognitive skills of students with a math learning disability (MLD) and low achievement (LA). The specific research questions are as follows:
RQ1: What are the differences in the domain-general profile related to mathematics between students with an MLD and LA?
RQ2: What are the differences in the domain-specific profile related to mathematics between students with an MLD and LA?
2. Method
This study took a literature review approach to identify similarities and differences in cognitive profiles between students with an MLD and LA. We used PRISMA’s principles and guidelines (Page et al., 2021) for this systematic review.
2.1. Database and Keywords
The authors conducted literature research in Boolean search mode using EBSCOhost Complete in November 2024. Keywords were (“low achieving students” OR “low achiev*” OR “learning difficult* in math*” OR “math* learning disabilit*” OR dyscalculia OR “learning disabilit* in math*”) AND (“cognitive skill*” OR “cognitive process*” OR “mental abilit*” OR “cognitive abilit*” OR “intellectual abilit*” OR cognit*).
2.2. Inclusion and Exclusion Criteria
The peer-reviewed articles published between January 2000 and November 2024 in international academic journals in English were included in this study. The year 2000 was chosen as a starting point because we considered 25 years of research as a representative period for answering the research questions. Articles that were not available as full texts were excluded. The papers needed to meet the following criteria to be considered for the current review:
- (1)
- Studies involving MLD and/or LA students of primary or secondary school age were included. Studies with participants younger than 6 years or older than 18 years and students with other disabilities were excluded. We followed the suggestions to increase the accuracy of identification of MLDs (Lewis & Fisher, 2016) and excluded articles that did not describe clearly how the sample(s) were classified;
- (2)
- The typical achieving students as the control group were included in this study;
- (3)
- A quantitative research method was used, and no review articles and studies with qualitative research methods were included in this study;
- (4)
- The research topic is participants’ domain-general or/and domain-specific abilities related to math learning.
2.3. Study Selection
A search in the database resulted in the identification of 1927 studies, which were reviewed in two phases. Initially, the first author reviewed the titles and keywords to eliminate duplicates (n = 112) and studies that were clearly outside the scope (n = 1696), altogether 1808 studies. During this phase, the second author also double-checked a subset of 58 articles for accuracy. An interrater agreement was calculated using Cohen’s kappa (k = 0.72). There was disagreement for eight articles, and a consensus was reached through discussion. One hundred nineteen studies were selected for further review. The second step was selection, based on the criteria for inclusion and exclusion, by reading the abstracts of the studies. The full text was reviewed when the abstract did not answer all the criteria. The first author coded all articles, and the second author coded 58 of them. The interrater agreement was 0.7 this time. There was disagreement regarding eight articles, and a consensus was reached via discussion. This process eliminated 62 studies. As a result, 57 articles were retrieved. Figure 1 illustrates the literature search and screening procedures.
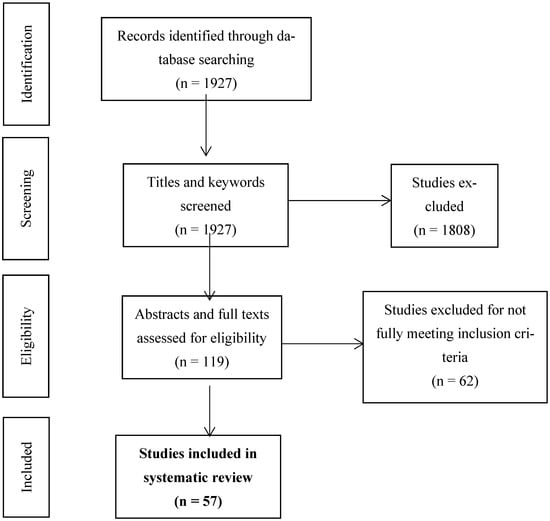
Figure 1.
Summary of systematic search and the screening procedure.
2.4. Data Analysis
The deductive content analysis (Mayring, 2014) was conducted to analyze the information from the selected studies.
Coding of the Studies
The first author developed coding forms to extract and record the relevant information from each study. The studies were coded, taking into account the following characteristics:
- (1)
- Description of the study (author, title, year, and journal);
- (2)
- Method of the study (number of participants, the sample group, and the selection criteria of the sample group, the control group, the age or grade, and the instrument);
- (3)
- Results of the study (the domain-general and domain-specific cognitive profiles and math skills) reported significantly different results from those of the control group and/or other sample group(s).
It was expected that the diagnostic criteria of the sample would vary across studies. Therefore, the following criteria were undertaken to categorize the sample as students with an MLD or LA (see Table 1): An MLD was defined as a specific learning disability with math test scores at or below the 10th percentile or at or below 1.5 standard deviations (SD) on math test scores or with the clinical diagnosis of an MLD or dyscalculia. In addition, we classified samples of nine studies as an MLD with math scores at or below the 15th percentile. LA was defined as low achievers in math whose math test scores are between the 11th and 25th percentile or 1 SD lower than average. We also decided to add a sample from one study to this group with math scores between the 9.5th and 32nd percentile. In addition, we created a different sample group called MLD + LA for studies with sample criteria at or below the 25th percentile or at least 1 SD below the age norm on math test scores. We also added to this group a sample with math scores less than the 30th percentile. When there were participants with other learning disabilities (e.g., dyslexia) included in the study, only data from students of the MLD, LA, or MLD + LA groups were used.

Table 1.
Characteristics of the samples in the selected studies.
According to previous studies, several cognitive skills are responsible for learning mathematics. In the present study, following Butterworth (2019), two groups of cognitive skills were formed to map the similarities and differences in the cognitive profile of students with an MLD and LA: domain-general and domain-specific cognitive skills (Butterworth, 2019).
The first author extracted the respective information from all the included studies, and the second author from ten studies. An interrater agreement of the coding results of 82% was calculated by dividing the number of agreements by the number of agreements plus the number of disagreements and multiplying by 100%. Disagreements were resolved through discussion.
3. Results
Fifty-seven studies from 28 different journals have been analyzed for this review (see Table S1). These studies spanned 19 years (2004–2022), and most of the articles were from the years 2012(9) and 2016(7). Sixteen of all the articles described longitudinal research. The descriptive data of the included articles are presented in Tables S1 and S2.
3.1. Participants
The number of participants described in the studies ranged between 20 and 1471 (see Table S2), with a mean size of 260 (SD = 332). The age of the participants ranged between 5 and 18 years, with a mean age of 9.45 (SD = 2.25) years. However, the participants in most studies were 8–10-year-old students. Fifteen studies included both MLD and LA samples. Other studies reported the data of the MLD (n = 24), LA (n = 2), or MLD + LA (n = 16) groups only. The mean size of the MLD, LA, and MLD + LA samples was 35 (SD = 29), 84 (SD = 97), and 31 (SD = 19), respectively.
As described above, we categorized sample groups according to math test scores. In 49 out of 57 studies, standardized math tests were used for sample selection. However, intelligence (Butterworth, 2019; Geary et al., 2004), persistence (Geary et al., 2004; Lewis & Fisher, 2016), and language skills (Emerson & Babtie, 2013; Farrell, 2013) can also be characteristics of the math learning disability. Considering this, we searched for additional selection criteria besides the math scores. We divided these criteria into three categories: IQ (scoring in standardized IQ tests), reading and spelling (scoring in reading and/or spelling tests/tasks), and permanence (the duration of low math test scores over the research period) (see Table 1, which presents the characteristics of the samples in the selected studies). The IQ score as a selection criterion was mentioned in 21 studies out of 39 for the MLD group, 8 out of 17 for the LA group, and 13 out of 16 for the MLD + LA group. In all studies, the IQ score of sample students had to be in the same range as the control group, described as “IQ in the normal range”. The lowest cut point was 74 (mainly in the range of 80), and the highest was 149 (mostly in the range of 120). The reading and/or spelling score was included in the selection criteria in eleven studies for the MLD group, in one study for the LA group, and in eight studies for the MLD + LA group. However, spelling was not mentioned as a selection criterion for MLD samples. The most described inclusion criteria were “average score on the reading/spelling test” and “reading score above the 25th percentile”. All but two of the reading or spelling tests used were standardized.
Interestingly, only nine studies (seven of them longitudinal) took the permanence of low math scoring as a selection criterion. The length of the period usually depended on the duration of the study (2–4 years). In addition, permanence was defined as “poor scores in at least two years from first through fourth grade” (article 50 according to the article IDs in Table S1) or “difficulties for more than six months according to parents and teachers” (21). Permanence as a selection criterion was reported in the case of all three groups.
3.2. Domain-General Cognitive Skills
We detected 18 domain-general cognitive skills from 52 articles (see Table S3). The most often measured cognitive skills were verbal working memory (n = 30), processing speed (n = 27), verbal processing (n = 25), and visuospatial working memory (n = 24). In more than ten studies, verbal short-term memory (n = 15), nonverbal reasoning (n = 14), the central executive component of working memory (n = 12), and visuospatial processing (n = 12) were measured. Cognitive processing was assessed in nine articles, and cognitive inhibition was assessed in eight. In five articles, visuospatial short-term memory was compared between the groups. In addition, long-term memory (n = 4) was assessed. However, auditory processing (n = 2), psychomotor abilities (n = 2), fluid reasoning (n = 1), mental representation (n = 1), and temporal processing (n = 1) were examined less often. The sample sizes of the studies reporting the findings varied from 15 to 99 for MLD students, 23–422 for LA students, and 14–75 for MLD + LA students.
The students with an MLD demonstrated significantly poorer performance in all three working memory components than the control group of typical achievers (CG) and LA students. For all three components, more studies confirmed a statistically significant difference between the groups compared to those that did not confirm it (see Table 2, which presents the cognitive skills of the students with an MLD, LA, and MLD + LA compared to each other and CG). The ages of the students in the analyzed studies ranged between 6 and 13 years, with the majority of students being 8–10 years of age. Several longitudinal studies (6, 38, 44, 19, and 32) emphasize the persistence of this finding. However, article 3 points out that students with an MLD have poorer verbal working memory than CG when measured by serial order information tasks but not when measured by item information tasks. LA students performed better than those with an MLD but were noticeably weaker than CG only in tasks involving the central executive component of working memory. In verbal and visuospatial working memory, there were an equal number of articles confirming and not confirming a statistically significant difference between low achievers and controls. Moreover, the results of the working memory tasks of MLD + LA students did not confirm the clear difference when compared to CG students for any component.

Table 2.
The cognitive and mathematical skills of the students with an MLD, LA, and MLD + LA in comparison to each other (MLD and LA) and the control group.
There is no clear evidence to suggest that the MLD group performs significantly worse than the control group in verbal and visuospatial short-term memory. Regarding low achievers’ short-term memory, it was assessed in only two studies on verbal short-term memory, both of which found that the LA group performed worse than the control group but showed no differences compared to the MLD group. For the MLD + LA group, verbal short-term memory did not differ from the control group, while one study reported a weakness in visuospatial short-term memory compared to the control group.
Studies on visual long-term and semantic memory did not reveal differences between the MLD and control groups. One study reported a difference between the MLD and control groups regarding verbal long-term memory, while another did not. A difference in verbal long-term memory was noted in one study between the LA and control groups, but no difference was found between the MLD and LA groups. Also, based on the results of the studies, the MLD + LA group did not differ from the control group in verbal short-term memory. However, the only study on visuospatial short-term memory reported a difference between the two groups. No studies examined long-term memory in the MLD + LA group.
The results revealed that the control group outperformed the MLD, LA, and MLD + LA groups across the various aspects of verbal processing, including reading, writing, comprehension, and phonological awareness. The differences between the MLD and LA groups were less pronounced. The control group showed slightly superior visuospatial processing compared to the sample groups. However, nearly an equal number of studies reported no significant differences between the MLD and LA groups in visuospatial processing. Studies on the MLD + LA group reported no differences compared to the control group.
The results for cognitive processing, processing speed, and cognitive inhibition suggest that these skills are weaker in students in the MLD group compared to the control group. Comparisons between the MLD and LA groups, as well as between the LA and control groups, do not show consistent differences. For the MLD + LA group, the majority of studies did not find significant differences compared to the control group.
The analyzed articles indicate that the MLD group has weaker nonverbal and verbal reasoning skills compared to the control group. For the LA group, reduced performance is evident only in nonverbal reasoning. Differences between the MLD and LA groups, as well as between the MLD + LA and control groups, were generally not observed.
Only a few articles investigated abilities such as mental representation, auditory perception, temporal processing, and psychomotor abilities. Based on these limited results, no conclusions can be drawn about differences between the groups.
3.3. Domain-Specific Cognitive and Math Skills
We found six different domain-specific cognitive skills from the analyzed articles, mainly related to number sense (see Supplementary Tables S2 and S3). The symbolic comparison was the most often mentioned skill in the studies (29 times). Non-symbolic magnitude comparison was analyzed in 24 articles, number comprehension in 11 articles, counting skills and reading and writing numbers in 8 articles, and conceptual knowledge in 2 articles. The sample sizes of the studies reporting the findings varied from 10 to 99 for MLD students, 20–422 for LA students, and 14–75 for MLD + LA students.
Although the math performance level was the primary selection criterion in the analyzed studies, some studies compared the math results of the samples and CG. Four math skills (place-value understanding (n = 3), basic calculation (n = 17), complex calculation (n = 10), and problem-solving (n = 8)) showing significant differences between the sample groups were detected in the studied articles. We describe the relationship between math skills and domain-specific skills.
The symbolic magnitude comparison was poorer in the MLD and LA sample groups than in CG. The number of articles reporting a statistically significant difference between the MLD + LA group and the control group was equal to the number of articles reporting no difference. The ages of students included in the studies ranged from 6 to 14 years, with the majority being 8–11 years of age. Few studies with substantial sample sizes focused on students aged from 11 to 13 with an MLD, and these studies revealed significant differences compared to the control group (1.43). However, only a few studies included results for the LA and MLD + LA groups. The non-symbolic comparison was tested mainly in studies that have included MLD as a sample group. The performance of the students with an MLD was inferior to CG only in estimating and subitizing tasks. Article 29 points out that the number comprehension skills of the MLD group were even more impaired than non-symbolic comparison skills when compared to CG, and article 10 specifies that the comprehension skills of the students with an MLD were at the same level with one grade younger typical achievers. The results generally do not indicate differences between CG and the remaining sample groups. For example, article 9 describes that the MLD and LA groups perform weaker than the control group in kindergarten, but the differences disappear by the second grade. Students with an MLD also had lower conceptual knowledge, place-value understanding, and counting skills than CG students. However, the conceptual knowledge level is similar to that of one year younger typical achievers; place-value understanding is even lower (10), and deficit in counting is persistent (8). The LA and MLD + LA groups also performed lower in those skills than CG in those few studies representing those two groups. Both number reading and writing of the MLD and MLD + LA groups were poorer than the results of the CG; MLD was also weaker than the LA group, being at the same skill level as one grade younger typical achievers (10).
Regarding basic calculation, students with an MLD performed persistently lower than CG and LA students, LA students performed persistently lower than CG, and the MLD + LA group was lower than CG, being two grade levels behind (14). In complex calculations, the deficit is more persistent in the MLD group than in CG and LA. LA students perform poorer than CG, while students in the MLD + LA group are two grade levels behind controls. LA students improve in complex calculations in higher grades; however, the difference between CG and LA remains significant (15). Problem-solving performance is lower in all three sample groups when compared to CG. In one article (18), the MLD and LA students have similar problem-solving abilities, while the other reports more severe deficits in MLD (44).
4. Discussion
This study aimed to find differences in the cognitive skills of students with an MLD and low achievement in mathematics. Our findings indicate a large area of domain-general and domain-specific cognitive skills that are impaired in students with an MLD and LA.
4.1. Domain-General Cognitive Skills
4.1.1. Memory
According to several authors, impaired working memory, long-term memory, and short-term memory are distinctive features of the domain-general cognitive skills of students with an MLD (Chinn, 2020; Geary, 2004; Shin & Bryant Pedrotty, 2015) and LA (Geary, 2004; Shaw, 2022). The present study confirms those statements regarding working memory. Also, some differences in working memory were observed between the students with an MLD and LA: LA students showed a stronger visuospatial component of working memory, but the evidence regarding differences in the central executive and verbal domains remains inconclusive. Visuospatial working memory plays a key role in domain-specific cognitive skills, such as understanding number sets and the number line (Geary et al., 2009). The weaker visuospatial working memory in students with an MLD may explain why their difficulties in mathematics arise early, especially during the acquisition of these domain-specific skills (Eidlin-Levy & Rubinsten, 2017). In contrast, low-achieving students typically face challenges primarily when tackling more complex mathematical problems (Shaw, 2022). However, it is also important to note that the central executive component of the low achievers’ working memory is clearly weaker than that of the typical achievers.
4.1.2. Processing Skills
While deficits in verbal processing are common predictors of reading and/or writing disabilities (Farrell, 2013; Fletcher et al., 2007), impaired language skills also have a significant impact on learning mathematics (Butterworth, 2019; Hannell, 2005), similar to the effects of difficulties in visuospatial processing (Augustyniak et al., 2005; Geary, 2010).
Findings in the present study describe the impairment of verbal processing in students with an MLD and LA. However, MLD students’ verbal processing skills are comparable to those of low achievers. While weak visuospatial processing is a common characteristic of MLD students, this study did not identify significant differences between the MLD and control groups. Instead, a more pronounced difference was observed between the LA and control groups.
The disturbance of cognitive processing, processing speed, and cognitive inhibition skills was expected based on several authors, both in students with an MLD (Geary, 2010; Rubinsten & Henik, 2009) and LA (Geary, 2010; Shaw, 2022). The present study met expectations only for the MLD group.
4.1.3. IQ and Reasoning Abilities
Although the general intelligence of the learner supports understanding mathematics (Butterworth, 2019), the learning disability in mathematics of the students with an MLD or LA is not caused by intellectual disability: the IQ level of those students is below average or higher (Geary, 2004), and there is no difference in IQ levels between the students with an MLD and LA (Fletcher et al., 2007). Most articles analyzed in the present study considered the IQ score as a selection criterion of the sample group, requiring that the IQ scores of the sample group fall within the same range as those of the control group. In 19 studies, the reasoning skills of the sample groups were also measured, revealing poorer nonverbal and verbal reasoning skills in students with an MLD and weaker nonverbal reasoning skills in LA compared to typical achievers. This supports the finding that both nonverbal (Partanen et al., 2020) and verbal (Kleemans et al., 2018) reasoning skills are closely related to mathematical performance. For instance, Geary et al. (2009) suggest that the relationship between IQ and number line performance in the first grade aligns with the capacity for logical and systematic thinking, which is essential for understanding the structure of the mathematical number line. The comparability of the data on reasoning abilities is strengthened by the use of standardized tests (e.g., WISC-IV and the Raven Progressive Matrices test) in the included studies.
4.1.4. Other Domain-General Cognitive Skills
Unfortunately, the other domain-general cognitive skills, such as mental representation, auditory reception, and temporal processing skills, were represented by only one study. This limits the ability to analyze the results more thoroughly.
4.2. Domain-Specific Cognitive Skills and Math Skills
Besides domain-general cognitive skills, several authors also confirm difficulties regarding the domain-specific abilities of students with an MLD (Fletcher et al., 2007; Lewis, 2014). According to Butterworth (2019) and Geary (2010), the number sense deficit is the core deficit of the MLD. The problems with writing numbers, place-value understanding (Augustyniak et al., 2005), arithmetic (Geary, 2004; Shin & Bryant Pedrotty, 2015), and procedural skills (Geary, 2010) are emphasized as well. In addition, LA students struggle with number sense, fact retrieval, and procedural skills, but their performance in these areas is moderate and notably better than that of students with an MLD (Geary, 2010). Shaw (2022) adds that more severe difficulties in LA students occur with abstract complex math. The present study showed that students with an MLD have problems in many domain-specific skills (non-symbolic and symbolic comparison, number comprehension, counting, and reading and writing numbers). Moreover, the deficit of students with an MLD is more severe than that of LA students who struggled only with symbolic comparison and counting. As expected from the group identification criteria, the math skills (place-value understanding, basic calculation, complex calculation, and problem-solving) of the students with an MLD and LA were significantly lower than those of their typically achieving peers. According to the results of the present study, it can be concluded that MLD students are significantly weaker than LA students in terms of basic calculation skills. For the other mathematical skills, the results were inconsistent. However, using different experimental approaches to measure domain-specific cognitive skills across the included studies may affect their comparability. The difference between the cognitive profiles of students with an MLD and LA is summarized in Table 3.

Table 3.
Differences in domain-general cognitive skills, domain-specific cognitive skills, and math skills between the students with an MLD and LA.
4.3. Practical Implications
Identifying students’ math difficulties as early as possible is essential. Moreover, awareness about the causes of these difficulties helps in designing or choosing appropriate interventions to improve the math skills of those students (Van Herwegen et al., 2024). According to Shaw (2022), identifying students with LA tends to stay in the shadow of diagnosing MLD and intellectual disability. As demonstrated in the present study, students with an MLD have severe deficits in many cognitive and core math skills. Students with LA have deficits in almost all the same math skills as students with an MLD but have different cognitive profiles. This fact indicates the need to take the identification of low-achieving learners more seriously. If LA students stay unidentified or mixed up with students with an intellectual disability, appropriate teaching and special education services will be unavailable for them. The findings of the current study may help identify students with math difficulties and differentiate LA students from MLD students.
4.4. Limitations
This study has several limitations. We limited our article search area by including only peer-reviewed quantitative research method articles published in international academic journals in English. Without this limitation, we could have a more extensive choice of articles. However, this decision was made to minimize biases in selected papers. As expected, there were difficulties in identifying the described samples as MLD or LA because of the variation in the diagnostic criteria. We made a different sample group called MLD + LA for the samples where it was impossible to identify if it was MLD or LA. Forming this group gives an extra tool for identifying students with math difficulties before further classification to MLD or LA. Furthermore, sample regrouping occurred in some cases because of the different cut-off points in standardized math test scores. For example, six articles used the 15th percentile cut point of a math test to determine the group of learners with mathematics learning difficulties, which we classified as an MLD sample instead of an MLD + LA sample. According to the directions for the accurate identification of MLD by Lewis and Fisher (2016), one important criterion is the persistence of math difficulties. Only nine articles in this study included persistence as a criterion for MLD or LA. Another limitation is that it was challenging to categorize the studies based on the sample age, as the age ranges used varied widely. A limitation is also related to the control groups’ age. In the studies included in the present review, the control groups were chronologically similar in age to the study groups with math learning difficulties. This makes it more challenging to distinguish specific cognitive deficits associated with math difficulties, as the cognitive abilities of struggling students may differ from their age peers but may be similar to those of a younger control group. Students with math challenges should be compared to a chronologically younger control group to accurately assess specific cognitive deficits related to learning mathematics.
5. Conclusions
In the present study, we have examined 57 articles to describe the differences in the cognitive skills of students with low achievement in mathematics and a math learning disability. The present study revealed that the cognitive profiles of students with an MLD and LA are different. The cognitive skills of students with an MLD were weaker than those of the typical achievers in nearly all domain-general and domain-specific cognitive skills related to learning mathematics. Contrary to our expectations, the LA group differed much less from the control group. The results of the MLD group were significantly weaker than those of the LA group in all components of working memory, processing speed, symbolic magnitude comparison, and counting. A common thread was that both groups were weaker than typical achieving students in all calculation skills. However, the MLD group was weaker than the LA group in terms of basic calculation. The domain-general, domain-specific, and math skills of students in the MLD + LA group were not similar to those of MLD or LA students, except for verbal processing, symbolic magnitude comparison, and calculation.
In addition to accurately identifying students with math difficulties, providing them with appropriate support when learning mathematics is necessary. There is a need to examine the similarities and differences in intervention strategies targeted toward students with a mathematical learning disability and low-achieving students.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/educsci15030361/s1, Table S1. Overview of the included studies. Table S2. Descriptive information from the included articles: Participants and cognitive and math skills. Table S3. Domain-general, domain-specific, and math skills retrieved from the studies included in the present study.
Author Contributions
Conceptualization, T.K.-K. and E.K.; methodology, T.K.-K.; software, T.K.-K.; validation, T.K.-K., E.K.; formal analysis, T.K.-K.; investigation, T.K.-K.; resources, E.K.; data curation, T.K.-K.; writing—original draft preparation, T.K.-K.; writing—review and editing, E.K.; visualization, T.K.-K.; supervision, E.K.; project administration, T.K.-K.; funding acquisition, E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashkenazi, S., Black, J. M., Abrams, D. A., Hoeft, F., & Menon, V. (2013). Neurobiological underpinnings of math and reading learning disabilities. Journal of Learning Disabilities, 46(6), 549–569. [Google Scholar] [CrossRef] [PubMed]
- Augustyniak, K., Murphy, J., & Phillips, D. K. (2005). Psychological perspectives in assessing mathematics learning needs. Journal of Instructional Psychology, 32(4), 277–286. [Google Scholar]
- Baglama, B., Yucesoy, Y., Uzunboylu, H., & Özcan, D. (2017). Can infographics facilitate the learning of individuals with mathematical learning difficulties? International Journal of Cognitive Research in Science, Engineering and Education, 5(2), 119–127. [Google Scholar] [CrossRef]
- Baker, S., Gersten, R., & Lee, D.-S. (2002). A synthesis of empirical research on teaching mathematics to low-achieving students. The Elementary School Journal, 103(1), 51–73. [Google Scholar] [CrossRef]
- Barnes, M. A., & Raghubar, K. P. (2017). Neurodevelopmental disorders as model systems for understanding typical and atypical mathematical development. In D. C. Geary, D. B. Berch, R. Ochsendorf, & K. M. Koepke (Eds.), Acquisition of complex arithmetic skills and higher-order mathematics concepts (pp. 67–97). Elsevier Inc. [Google Scholar]
- Benavides-Varela, S., Zandonella Callegher, C., Fagiolini, B., Leo, I., Altoè, G., & Lucangeli, D. (2020). Effectiveness of digital-based interventions for children with mathematical learning difficulties: A meta-analysis. Computers & Education, 157, 103953. [Google Scholar] [CrossRef]
- Bryant, D. P., Hartman, P., & Kim, S. A. (2003). Using explicit and strategic instruction to teach division skills to students with learning disabilities. Exceptionality, 11(3), 151–164. [Google Scholar] [CrossRef]
- Butterworth, B. (2019). Dyscalculia: From science to education. Routledge. [Google Scholar]
- Chinn, S. J. (2020). More trouble with maths: A complete manual to identifying and diagnosing mathematical difficulties (3rd ed.). Routledge. [Google Scholar]
- Dennis, M. S., Sharp, E., Chovanes, J., Thomas, A., Burns, R. M., Custer, B., & Park, J. (2016). A meta-analysis of empirical research on teaching students with mathematics learning difficulties. Learning Disabilities Research & Practice, 31(3), 156–168. [Google Scholar]
- Deruaz, M., Dias, T., Gardes, M.-L., Gregorio, F., Ouvrier-Buffet, C., Peteers, F., & Robotti, E. (2020). Exploring MLD in mathematics education: Ten years of research. The Journal of Mathematical Behavior, 60, 100807. [Google Scholar] [CrossRef]
- Eidlin-Levy, H., & Rubinsten, O. (2017). Developmental dyscalculia and automatic magnitudes processing: Investigating interference effects between area and perimeter. Frontiers in Psychology, 8, 2206. [Google Scholar] [CrossRef]
- Emerson, J., & Babtie, P. (2013). The dyscalculia assessment (2nd ed.). Bloomsbury Education. [Google Scholar]
- Farrell, M. (2013). The effective teacher’s guide to dyslexia and other learning difficulties (learning disabilities): Practical strategies (2nd ed.). Routledge. [Google Scholar] [CrossRef]
- Fletcher, J. M., Lyon, G. R., Fuchs, L. S., & Barnes, M. A. (2007). Learning disabilities: From identificaton to intervention. The Guilford Press. [Google Scholar]
- Geary, D. C. (2004). Mathematics and learning disabilities. Journal of Learning Disabilities, 37(1), 4–15. [Google Scholar] [CrossRef]
- Geary, D. C. (2010). Mathematical disabilities: Reflections on cognitive, neuropsychological, and genetic components. Learning and Individual Differences, 20(2), 130–133. [Google Scholar] [CrossRef]
- Geary, D. C., Bailey, D. H., Littlefield, A., Wood, P., Hoard, M. K., & Nugent, L. (2009). First-grade predictors of mathematical learning disability: A latent class trajectory analysis. Cognitive Development, 24(4), 411–429. [Google Scholar] [CrossRef] [PubMed]
- Geary, D. C., Hoard, M. K., & Bailey, D. H. (2012). Fact retrieval deficits in low achieving children and children with mathematical learning disability. Journal of Learning Disabilities, 45(4), 291–307. [Google Scholar] [CrossRef] [PubMed]
- Geary, D. C., Hoard, M. K., Byrd-Craven, J., & Catherine DeSoto, M. (2004). Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology, 88(2), 121–151. [Google Scholar] [CrossRef]
- Hannell, G. (2005). Dyscalculia. David Fulton Publishers Ltd. [Google Scholar]
- Herold, K. H., Bock, A. M., Murphy, M. M., & Mazzocco, M. M. M. (2020). Expanding task instructions may increase fractions problem difficulty for students with mathematics learning disability. Learning Disability Quarterly, 43(4), 201–213. [Google Scholar] [CrossRef]
- Kajamies, A., Vauras, M., & Kinnunen, R. (2010). Instructing low-achievers in mathematical word problem solving. Scandinavian Journal of Educational Research, 54(4), 335–355. [Google Scholar] [CrossRef]
- Kearns, D. M., & Fuchs, D. (2013). Does cognitively focused instruction improve the academic performance of low-achieving students? Exceptional Children, 79(3), 263–290. [Google Scholar] [CrossRef]
- Kiru, E. W., Doabler, C. T., Sorrells, A. M., & Cooc, N. A. (2018). A synthesis of technology-mediated mathematics interventions for students with or at risk for mathematics learning disabilities. Journal of Special Education Technology, 33(2), 111–123. [Google Scholar] [CrossRef]
- Kleemans, T., Segers, E., & Verhoeven, L. (2018). Role of linguistic skills in fifth-grade mathematics. Journal of Experimental Child Psychology, 167, 404–413. [Google Scholar] [CrossRef]
- Kolikant, Y. B.-D., & Broza, O. (2011). The effect of using a video clip presenting a contextual story on low-achieving students’ mathematical discourse. Educational Studies in Mathematics, 76(1), 23–47. [Google Scholar] [CrossRef]
- Kroesbergen, E. H., Huijsmans, M. D. E., & Friso-van Den Bos, I. (2022). A meta-analysis on the differences in mathematical and cognitive skills between individuals with and without mathematical learning disabilities. Review of Educational Research, 93(5), 718–755. [Google Scholar] [CrossRef]
- Lewis, K. E. (2014). Difference not deficit: Reconceptualizing mathematical learning disabilities. Journal for Research in Mathematics Education, 45(3), 351–396. [Google Scholar] [CrossRef]
- Lewis, K. E., & Fisher, M. B. (2016). Taking stock of 40 years of research on mathematical learning disability: Methodological issues and future directions. Journal for Research in Mathematics Education, 47(4), 338–371. [Google Scholar] [CrossRef]
- Mayring, P. (2014). Qualitative content analysis: Theoretical foundation, basic procedures and software solution. Available online: http://nbn-resolving.de/urn:nbn:de:0168-ssoar-395173 (accessed on 20 April 2023).
- Mazzocco, M. M. M. (2005). Challenges in identifying target skills for math disability screening and intervention. Journal of Learning Disabilities, 38(4), 318–323. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A., & Khan, A. (2023). Domain-general and domain-specific cognitive correlates of developmental dyscalculia: A systematic review of the last two decades’ literature. Child Neuropsychology, 29(8), 1179–1229. [Google Scholar] [CrossRef]
- Nelson, G., & Powell, S. R. (2018). A systematic review of longitudinal studies of mathematics difficulty. Journal of Learning Disabilities, 51(6), 523–539. [Google Scholar] [CrossRef] [PubMed]
- Orosco, M. J., & Reed, D. K. (2023). Effects of professional development on english learners’ problem solving. Journal of Learning Disabilities, 56(4), 324–338. [Google Scholar] [CrossRef]
- Page, M. J., Moher, D., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaf, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hróbjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., … McKenzie, J. E. (2021). PRISMA 2020 explanation and elaboration: Updated guidance and exemplars for reporting systematic reviews. BMJ, 372, n160. [Google Scholar] [CrossRef]
- Partanen, P., Jansson, B., & Sundin, Ö. (2020). Fluid reasoning, working memory and planning ability in assessment of risk for mathematical difficulties. Educational Psychology in Practice, 36(3), 229–240. [Google Scholar] [CrossRef]
- Rubinsten, O., & Henik, A. (2009). Developmental dyscalculia: Heterogeneity might not mean different mechanisms. Trends in Cognitive Sciences, 13(2), 92–99. [Google Scholar] [CrossRef] [PubMed]
- Saga, M., Rkhaila, A., Ounine, K., & Oubaha, D. (2022). Developmental dyscalculia: The progress of cognitive modeling in the field of numerical cognition deficits for children. Applied Neuropsychology: Child, 11(4), 904–914. [Google Scholar] [CrossRef] [PubMed]
- Shaw, S. R. (2022). Reaching and teaching students who don’t qualify for special education: Strategies for the inclusive education of diverse learners (1st ed). Routledge. [Google Scholar]
- Shin, M., & Bryant Pedrotty, D. (2015). A Synthesis of mathematical and cognitive performances of students with mathematics learning disabilities. Journal of Learning Disabilities, 48(1), 96–112. [Google Scholar] [CrossRef]
- Soares, N., Evans, T., & Patel, D. R. (2018). Specific learning disability in mathematics: A comprehensive review. Translational Pediatrics, 7(1), 48–62. [Google Scholar] [CrossRef] [PubMed]
- Van Herwegen, J., Outhwaite, L. A., & Herbert, E. (2024). Neuromyths about dyscalculia and dyslexia among educators in the UK. British Journal of Special Education, 51(2), 233–242. [Google Scholar] [CrossRef]
- Watt, S. J., & Watkins, J. R. (2016). Teaching algebra to students with learning disabilities. Journal of Learning Disabilities, 49(4), 437–447. [Google Scholar] [CrossRef]
- World Health Organization [WHO]. (2019). International classification of diseases, eleventh revision (ICD-11). WHO. [Google Scholar]
- Yeo, L. S., Ang, R. P., Chong, W. H., Huan, V. S., & Quek, C. L. (2008). Teacher efficacy in the context of teaching low achieving students. Current Psychology, 27(3), 192. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).